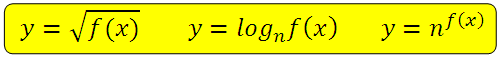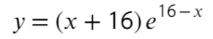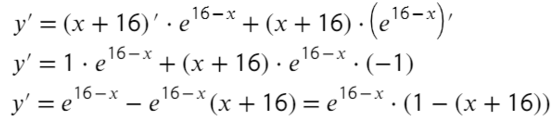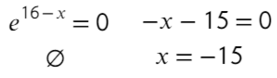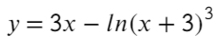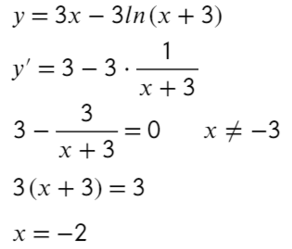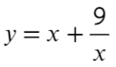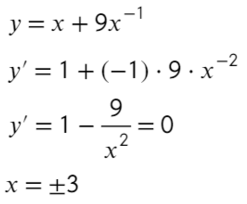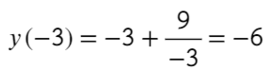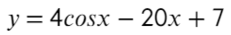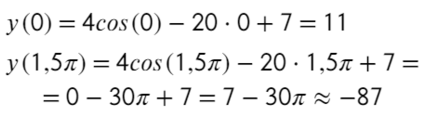СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Исследование функций без помощи производной
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 11 № 245173
i
Найдите точку максимума функции
Аналоги к заданию № 245173: 510390 286505 286603 … Все
Решение
·
Помощь
2
Тип 11 № 245174
i
Найдите точку минимума функции
Аналоги к заданию № 245174: 510409 286605 286703 … Все
Решение
·
Помощь
3
Тип 11 № 245175
i
Найдите наименьшее значение функции
Аналоги к заданию № 245175: 286705 286803 286707 … Все
Решение
·
Помощь
4
Тип 11 № 245176
i
Найдите наибольшее значение функции
Аналоги к заданию № 245176: 286805 286903 286807 … Все
Решение
·
Помощь
5
Тип 11 № 245177
i
Найдите точку максимума функции
Аналоги к заданию № 245177: 286905 287003 500916 … Все
Решение
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Здравствуйте! В этой статье речь пойдёт о задачах, которые можно решать без нахождения производной. В данной рубрике мы уже рассмотрели некоторые примеры с логарифмами, числом е, функции с произведениями. Смысл заданий тот же – требуется найти либо точку максимума (минимума) функции, либо определить максимальное (минимальное) значение функции.
В чём суть и каков «стандартный» алгоритм решения — можно посмотреть в этой статье. Но не для всех заданий применение этого алгоритма будет рационально. Если следовать ему в представленных ниже примерах, то процесс решения будет «перегружен» вычислениями. А потеря времени на экзамене вам не нужна. Так какие же задания имеются ввиду?
В условии дана иррациональная, логарифмическая или показательная функция:
при чём под корнем, под знаком логарифма или в показателе находится квадратичная функция вида:
Рассмотрим подход без нахождения производной. Вы увидите, что такие задачи можно решать устно.
Что необходимо знать? Свойство параболы, напомним его:
Если а > 0, то её ветви направлены вверх.
Если а < 0, то её ветви направлены вниз.
Далее вспомним координату (абсциссу) вершины параболы:
То есть, это точка экстремума квадратичной функции – в ней функция меняет своё поведение с возрастания на убывание или наоборот.
Следующий важный факт (ключевой для этих задач):
Если исходная функция монотонна (непрерывно возрастает или убывает), для нее указанная точка «х» также будет точкой экстремума.
Почему? Давайте рассмотрим отдельно функции подробнее.
Квадратичная функция в показателе степени (при чём n>1):
Смотрите! Представим, что ax2+bx+c=z. Можем записать:
Получается что значение z изменяется следующим образом.
Вариант когда a>0 (ветви параболы направлены вверх) – при х от минус бесконечности до –b/2a z уменьшается, в точке –b/2a значение будет минимальным, далее при х от –b/2a до бесконечности z увеличивается.
Это означает, что и сама функция у=nf(x) будет имет минимальное значение в точке х=–b/2a, так как при минимуме в показателе получится минимум в результате.
Вариант когда a<0 (ветви параболы направлены вниз) – при х от минус бесконечности до –b/2a z увеличивается, в точке –b/2a значение будет максимальным, далее при х от –b/2a до бесконечности z уменьшается.
Это означает, что и сама функция у=nf(x) будет иметь максимальное значение в точке х=–b/2a, так как при максимуме в показателе получится максимум в результате.
Квадратичная функция под знаком логарифма (при чём n>1):
Представим, что ax2+bx+c=z. Можем записать:
Получается что значение z изменяется следующим образом:
Вариант когда a>0 (ветви параболы направлены вверх) – при х от минус бесконечности до –b/2a z уменьшается, в точке –b/2a значение будет минимальным, далее при х от–b/2a до бесконечности z увеличивается.
Это означает, что и сама функция lognz будет имет минимальное значение в точке х=–b/2a. Так как логарифмическая функция уменьшается при уменьшении аргумента (видно по графику).
Вариант когда a<0 (ветви параболы направлены вниз) – при х от минус бесконечности до –b/2a z увеличивается, в точке –b/2a значение будет максимальным, далее при х от –b/2a до бесконечности z уменьшается.
Это означает, что и сама функция lognz будет имеет максимальное значение в точке х=–b/2a. Так как логарифмическая функция увеличивается при увеличении аргумента (видно по графику).
Квадратичная функция под знаком корня:
Представим, что ax2+bx+c=z. Можем записать:
Получается что:
При a>0 значение z минимально в точке х=–b/2a, а значит и сама функция будет иметь минимальное значение. *Корень из наименьшего значения в результате даст наименьшее число.
При a<0 значение z максимально в точке х=–b/2a, а значит и сама функция будет иметь максимальное значение.
Таким образом, сформулируем ключевое правило:
ВНИМАНИЕ! Конечно, если глубже уйти в тему, то возможны варианты когда сложная функция имеет отрицательный знак, когда логарифм находится в знаменателе дроби, когда основание логарифма или основание степени находится в пределах от 0 до 1. Разумеется, важно понимать как ведёт себя данная в условии функция (возрастает или убывает). Но для решения типовых заданий экзамена указанного вывода вам будет вполне достаточно.
И конечно, не теряйте из виду область допустимых значений заданной функции:
— выражение стоящее под знаком корня, больше или равно нулю (число неотрицательное).
— выражение стоящее под знаком логарифма, есть положительное число.
— выражение стоящее в знаменателе дроби не равно нулю.
В подобных задачах на нахождение наибольшего и наименьшего значения функции, я бы посоветовал находить область определения в любом случае (даже не смотря на то, что в представленных ниже примерах это ничего важного нам не даёт и не влияет на ответ).
Рассмотрим примеры:
Найдите точку максимума функции
Под корнем квадратичная функция 13+6х–х2. Ее график — парабола, ветви направлены вниз, поскольку а=–1<0. Значит максимальное значение функция приобретает в точке:
Проверим чему равно подкоренное выражение при х=3 То есть будет ли оно числом неотрицательным:
13 + 6∙3 – 32 = 13 + 18 – 9 = 22 > 0
Почему необходимо это сделать? Дело в том, что при полученной абсциссе квадратичная функция теоретически может дать отрицательное значение, то есть график такой параболы будет лежать ниже оси ох. Это будет означать что решения (таких вариантов заданий на самом ЕГЭ не будет).
Ответ: 3
Решите самостоятельно:
Найдите точку максимума функции
Посмотреть решение
Найдите наименьшее значение функции
Под корнем квадратичная функция х2 + 8х + 185.
Ее график — парабола, ветви направлены вверх, поскольку а = 1 > 0
Абсцисса вершины параболы:
Так как ветви параболы направлены вверх, то в точке х = – 4 функция
х2 + 8х + 185 принимает наименьшее значение.
Функция кважратного корня монотонно возрастает, значит х = 4 точка минимума всей функции, вычислим её наименьшее значение:
Ответ: 13
Решите самостоятельно:
Найдите наименьшее значение функции
Посмотреть решение
Найдите точку максимума функции у=log7(–2 – 12х – х2) + 10.
Под знаком логарифма квадратичная функция –2 – 12х – х2.
График — парабола, ветви направлены вниз, так как а = – 1 < 0
Абсцисса вершины параболы:
Проверим, принадлежит ли полученное значение х области определения (выражение под знаком логарифма должно быть число положительное):
– 2 – 12∙(–6) – (–6)2 = – 2 + 72 – 36 = 34 > 0
То есть, в точке х = – 6
функция f (х) = – 2 – 12х – х2 будет иметь максимальное значение.
Значит, и у=log7(–2–12х–х2)+10 в этой точке так же будет иметь максимальное значение.
Ответ: – 6.
Решите самостоятельно:
Найдите точку максимума функции у=log2(2 + 2х – х2) – 2
Посмотреть решение
Найдите наименьшее значение функции у=log9 (х2 – 10х + 754) + 3
Под корнем квадратичная функция х2 – 10х+754.
Ее график — парабола, ветви направлены вверх, поскольку а = 1 > 0
Абсцисса вершины параболы:
То есть, в точке х = 5 функция f (x) = х2 – 10х + 754 принимает наименьшее значение.
Функция log9х монотонная, значит у =log9 (х2 – 10х + 754) + 3 в точке х = 5 также принимает наименьшее значение, вычислим его:

Решите самостоятельно:
Найдите наименьшее значение функции у=log3(х2 – 6х + 10) + 2
Посмотреть решение
Найдите точку максимума функции
В показателе стоит квадратичная функция – 30 + 12х – х2.
График — парабола, ветви направлены вниз, так как а = –1 < 0.
Абсцисса вершины параболы:
То есть, в точке х = 6 функция f (х) = – 30 + 12х – х2 приобретёт максимальное значение. Значит и данная функция в этой точке будет иметь также максимальное значение.
Ответ: 6
Решите самостоятельно:
Найдите точку максимума функции:
Посмотреть решение
Найдите наименьшее значение функции
В показателе стоит квадратичная функция х2 + 16х + 66.
Ее график — парабола, ветви направлены вверх, поскольку а = 1 > 0
Абсцисса вершины параболы:
То есть, в точке х = – 8 функция х2 + 16х + 66 принимает наименьшее значение.
Показательная функция монотонна, поэтому её наименьшее значение будет также в точке х = – 8, вычислим его
Ответ: 36
Решите самостоятельно:
Найдите наименьшее значение функции
Посмотреть решение
Разумеется, что это краткая схема решения и, конечно же, нужно понимать свойства квадратичной, показательной, логарифмической, дробно-рациональной функции, но эта схема работает.
В данной рубрике мы ещё рассмотрим задания с тригонометрическими функциями, не пропустите! Успеха вам!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажите о сайте в социальных сетях.
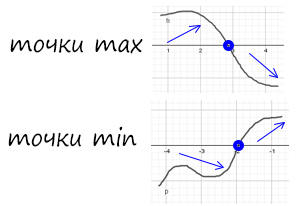
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

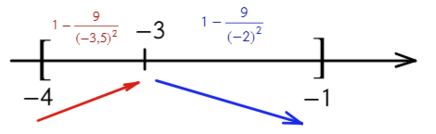
Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Значения функции и точки максимума и минимума

Наменьшее значение функции
Точки max
Точки min
Как говорил крестный отец: «Ничего личного». Только производные!
Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.
12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.
12 задание бывает двух видов:
- Найти точку максимума / минимума (просят найти значения «x»).
- Найти наибольшее / наименьшее значение функции (просят найти значения «y»).
Как же действовать в этих случаях?
Найти точку максимума / минимума
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный или найденные «х» и будут являться точками минимума или максимума.
- Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.
Задания с ЕГЭ:
Найдите точку максимума функции
- Берем производную:
- Приравняем ее к нулю:
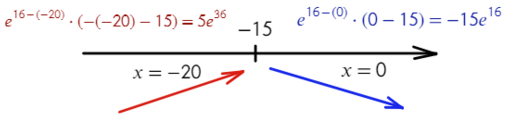
- Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):
Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15
Найдите точку минимума функции
- Преобразуем и возьмем производную:
- Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.
- Отлично! Сначала функция убывает, затем возрасает — это точка минимума!
Ответ: −2
Найти наибольшее / наименьшее значение функции
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный «х» и будет являться точкой минимума или максимума.
- Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
- В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
- Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции.
Задания с ЕГЭ:
Найдите наибольшее значение функции на отрезке [−4; −1]
- Преобразуем и возьмем производную:
- «3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?
- Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:
Ответ: −6
Найдите наибольшее значение функции на отрезке [0; 1,5π]
- Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».
Ответ: 11
Выводы:
- 70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
- Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
- Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
- В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
- А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.
Будь в курсе новых статеек, видео и легкого математического юмора.