Как найти точку максимума иррациональной

В этой статье мы рассмотрим несколько примеров на нахождение точек максимума (минимума) иррациональной функции. Алгоритм решения был уже неоднократно изложен в статьях с подобными заданиями, посмотрите его в одной из прошлых статей. 

У вас может возникнуть вопрос – а чем рациональная функция отличается от иррациональной? У иррациональной функции, говоря простыми словами, аргумент находится под корнем, или степень у него это дробное число (несокращаемая дробь). Другой вопрос –  в чём отличия в нахождении их точек максимума (минимума)? Да ни в чём. 

Сам принцип и алгоритм решения заданий на определения точек максимума (минимума) един. Просто для удобства и систематизации материала я разбил его на несколько статей – отдельно рассмотрел рациональные, логарифмические, тригонометрические и прочие, осталось ещё несколько примеров на нахождение наибольшего (наименьшего) значения иррациональной функции на отрезке. Их мы тоже рассмотрим.

Традиционно рекомендую ознакомится со статьёй «Исследование функций. Это нужно знать!», там же имеется таблица производных элементарных функций.

Давайте здесь подробно опишу нахождение производной, когда у аргумента имеется степень, во всех примерах ниже это используется.

Сама формула:

То есть, если у нас аргумент стоит в некоторой степени и требуется найти производную, то мы записывает это значение степени, умножаем его на аргумент, а его степень будет на единицу меньше, например:

Если же степень дробное число, то всё тоже самое:

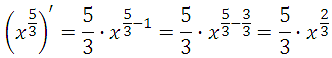
Следующий момент! Конечно же, вы должны помнить свойства корней и степеней, а именно:

То есть, если в примере вы увидите, например, выражение (или подобное с корнем):

То при решении, чтобы вычислить производную, его необходимо представить как х в степени, будет так:

Остальные табличные производные и правила дифференцирования вы должны знать!!!

Правила  дифференцирования:

Рассмотрим примеры:

77451. Найдите точку минимума функции y = x^3/2 – 3x + 1

Найдём производную заданной функции:

Найдем нули производной:

Решаем уравнение:

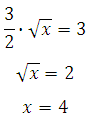
Определим знаки производной функции и изобразим на рисунке поведение функции. Для этого подставим произвольные значения из полученных интервалов в производную:

В точке х = 4, производная меняет знак с отрицательного на положительный, это означает, что данная точка является точкой минимума.

Ответ: 4

77455. Найдите точку максимума функции

Найдём производную заданной функции:

Найдем нули производной:

Решаем уравнение:

Определим знаки производной функции и изобразим на рисунке поведение функции. Для этого подставим произвольные значения из полученных интервалов в производную:

В точке х = 4, производная меняет знак с положительного на отрицательный, это означает, что данная точка является точкой максимума.

Ответ: 4

77457. Найдите точку максимума функции

Найдём производную заданной функции:

Найдем нули производной:

Решая уравнение:

Определим знаки производной функции и изобразим на рисунке поведение функции. Для этого подставим произвольные значения из полученных интервалов в производную:

В точке х = 9, производная меняет знак с положительного на отрицательный, это означает, что данная точка является точкой максимума.

Ответ: 9

77461. Найдите точку минимума функции

Найдём производную заданной функции:

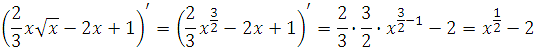
Найдем нули производной:

Решаем уравнение:

Определим знаки производной функции и изобразим на рисунке поведение функции. Для этого подставим произвольные значения из полученных интервалов в производную:

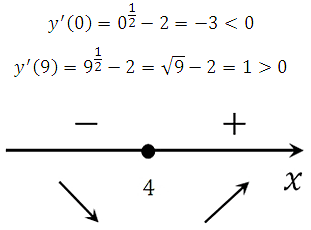
В точке х = 4, производная меняет знак с отрицательного на положительный, это означает, что данная точка является точкой минимума.

Ответ: 4

77463. Найдите точку максимума функции 

Посмотреть решение

На этом все. Успеха вам!

С уважением, Александр Крутиких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

В.К. Кузнецова,

учитель математики ГБОУ «Школа № 329» г.  Москва,

кандидат педагогических наук

Готовимся к ЕГЭ

Пособие для учащихся

«Исследование степенных и иррациональных функций»

В этой статье мы поговорим о задачах, в которых рассматриваются функции и в условии стоят вопросы, связанные с их исследованием.

Это целая группа задач входящих в ЕГЭ по математике. Обычно ставится вопрос о нахождении точек максимума (минимума) или определения наибольшего (наименьшего) значения функции на заданном интервале. 

Рассматриваются:

— Степенные и иррациональные функции.      

— Рациональные функции.     

— Исследование произведений и частных.    

— Логарифмические функции.         

— Тригонометрические функции.

Для успешного решения данных задач необходимо знать теорию пределов, понятие производной, свойства производной  для исследования графиков функций и её геометрический смысл. Свойства производной необходимы для исследования поведения функции на возрастание и убывание.

Что ещё необходимо знать для решения задач на исследование функций: таблицу производных  и  правила дифференцирования. Это базовые знания, в теме производной. Производные элементарных функций нужно  знать на отлично.

Свойства производной

1. Производная на интервалах возрастания имеет положительный знак (при подстановке значения из интервала в производную получается положительное число).

Значит, если производная в определённой точке из некоторого интервала имеет положительное значение, то график функции на этом интервале возрастает.

2. На интервалах убывания производная имеет отрицательный знак (при подстановке значения из интервала в выражение производной получается отрицательное  число). 

Значит, если производная в определённой точке из некоторого интервала имеет отрицательное значение,  то график функции на этом интервале убывает. 

Задачи на нахождение точек максимума и минимума

Алгоритм нахождения точек максимума (минимума) функции: 

1.  Находим производную функции f’(x).

2. Находим нули производной (приравниванием производную к нулю f’(x)=0  и решаем полученное уравнение). Также находим точки, в которых производная не существует (в частности это касается дробно-рациональных функций).

3.  Отмечаем полученные значения на числовой прямой и определяем знаки производной на этих интервалах путём подстановки значений из интервалов в выражение производной.

4.  Далее делаем вывод.

Вывод будет один из двух:

1. Точка максимума это точка, в которой производная меняет значение с положительного на отрицательное.

2. Точка минимума это точка, в которой производная меняет значение с отрицательного на положительное.

Задачи на нахождение наибольшего или наименьшего значения

функции на интервале.

В другом типе задач требуется найти наибольшее или наименьшее значение функции на заданном интервале.

Алгоритм нахождения наибольшего (наименьшего) значения функции:

1. Определяем, есть ли точки максимума (минимума). Для этого находим производную f’(x), затем решаем f’(x)=0 .

2.  Определяем, принадлежат ли полученные точки заданному интервалу и записываем  лежащие в его пределах.

3.  Подставляем в исходную функцию (не в производную, а в данную  в условии) границы данного интервала и точки (максимума-минимума), лежащие в пределах интервала.

4.  Вычисляем значения функции.

5.  Выбираем из полученных значений наибольшее (наименьше) значение, в зависимости от того, какой  вопрос был поставлен в задаче и  далее записываем ответ.

Рассмотрим примеры решения задач на исследование функций.

Пример 1.

Найдите точки максимума и минимума функции    .Решение:

Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке

поведение функции:

         +                          _                               +

              y                       -4                        4

                                    max                        min

Искомая точка максимума x= -4, искомая точка минимума x=4.

Ответ: −4; 4.

Пример 2.

Найдите наименьшее значение функции  на отрезке .
Решение.

Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

                                 _                     +

              y                       0                        3                   4

                                                                min

В точке x=3 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:

Ответ: −54.

Пример 3.

Найдите наибольшее значение функции  на отрезке .Решение.

Найдем производную заданной функции:

Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:

                                 _                     +

              y                       -2                       -1                 0

                                                                max

В точке x= -1 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:

Ответ: 6.

Предлагаем вам решить тренировочные варианты на нахождение точек максимума и точек минимума, наибольшего и наименьшего значения степенных и иррациональных функций. Задачи соответствуют заданию № 12 и взяты из открытого банка ФИПИ.

Тренинг по теме

«Исследование степенных и иррациональных функций»

Задание № 12

Вариант 1.

1. Найдите точку максимума функции 

2. Найдите точку минимума функции 

3. Найдите наименьшее значение функции  на отрезке 

4. Найдите наибольшее значение функции  

на отрезке 

Вариант 2.

1. Найдите точку максимума функции .

2. Найдите точку минимума функции .

3. Найдите наименьшее значение функции  на отрезке .

4. Найдите наибольшее значение функции  на отрезке .

Вариант 3.

1. Найдите точку максимума функции .

2. Найдите точку минимума функции .

3. Найдите наименьшее значение функции  

на отрезке .

4,. Найдите наибольшее значение функции  

на отрезке .

Вариант 4.

1. Найдите точку максимума функции 

2. Найдите точку минимума функции 

3. Найдите наименьшее значение функции  

на отрезке 

4. Найдите наибольшее значение функции  

на отрезке 

Вариант 5.

1. Найдите точку максимума функции .

2. Найдите точку минимума функции 

3. Найдите наименьшее значение функции  

на отрезке 

4. Найдите наибольшее значение функции  

на отрезке 

Вариант 6.

1. Найдите точку максимума функции 

2. Найдите точку минимума функции 

3. Найдите наименьшее значение функции  на отрезке 

4. Найдите наибольшее значение функции  на отрезке 

Вариант 7.

1. Найдите точку максимума функции 

2. Найдите точку минимума функции 

3. Найдите наименьшее значение функции  

    на отрезке 

4. Найдите наибольшее значение функции 

    на отрезке 

Вариант 8.

1. Найдите точку максимума функции 

2. Найдите точку минимума функции 

1. Найдите наименьшее значение функции  

на отрезке 

4. Найдите наибольшее значение функции  

    на отрезке 

Вариант 9.

1. Найдите точку минимума функции 
2. Найдите точку максимума функции .

3. Найдите наименьшее значение функции  на отрезке 

4. Найдите наибольшее значение функции  на отрезке       

Вариант 10.

1. Найдите точку минимума функции 
2. Найдите точку максимума функции 
3. Найдите наименьшее значение функции  

на отрезке 

4. Найдите наибольшее значение функции 

 на отрезке 

Вариант 11.

1. Найдите точку минимума функции 

2. Найдите наименьшее значение функции  

на отрезке 

3. Найдите точку минимума функции 

4. Найдите наибольшее значение функции 

 на отрезке 

Вариант 12.

1. Найдите точку максимума функции 
2. Найдите точку максимума функции .
3. Найдите наибольшее значение функции  

на отрезке 

 4. Найдите наименьшее значение функции  

на отрезке 

Вариант 13.

1. Найдите наибольшее значение функции 

 на отрезке 

2. Найдите наибольшее значение функции  

на отрезке 

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

Все вышесказанное можно обобщить следующими выводами:

– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

1. Найдите производную функции (f'(x)).
2. Найдите корни уравнения (f'(x)=0).
3. Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
4. Определите знак производной в каждом промежутке (методом интервалов).
5. Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
6. Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
   – если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
   – если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
   – если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Задание 11 Профильного ЕГЭ по математике

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции

Найдем производную функции.

Приравняем производную к нулю. Получим:

Исследуем знаки производной.

В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

Определим знаки производной.

В точке производная меняет знак с «минуса» на «плюс». Значит, — точка минимума функции

Исследование сложных функций

3. Найдите точку максимума функции

Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция монотонно возрастает, точка максимума функции .будет при том же , что и точка максимума функции А ее найти легко.

при . В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при

4. Найдите абсциссу точки максимума функции

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции является и точкой максимума функции

Это вершина квадратичной параболы

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

Найдем знаки производной.

В точке производная равна нулю и меняет знак с “+” на “-“. Значит, x = – 2 — точка максимума функции . Поскольку при функция убывает, В этой задаче значение функции на концах отрезка искать не нужно.

6. Найдите наименьшее значение функции на отрезке

Найдем производную функции и приравняем ее к нулю.

Найдем знаки производной.

Точка — точка минимума функции . Точка не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при Найдем это значение.

7. Найдите наименьшее значение функции на отрезке

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при

Если то Если , то

Значит, — точка минимума функции . В этой точке и достигается наименьшее значение функции на отрезке

8. Найдите наибольшее значение функции на отрезке

Найдем производную функции

Приравняем производную к нулю:

Найдем знаки производной на отрезке

При знак производной меняется с «плюса» на «минус». Значит, — точка максимума функции

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

9. Найдите наименьшее значение функции на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

Найдем производную функции

При знак производной меняется с «минуса» на «плюс». Значит, — точка минимума функции

10. Найдите наибольшее значение функции на отрезке

Как всегда, возьмем производную функции и приравняем ее к нулю.

По условию, . На этом отрезке условие выполняется только для Найдем знаки производной слева и справа от точки

В точке производная функции меняет знак с «плюса» на «минус». Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при

11.Найдите наименьшее значение функции на отрезке

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при

Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при

Как решать задачи B15 без производных

Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.

В этом случае работают другие приемы, один из которых — монотонность.

Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:

Функция f ( x ) называется на отрезке если для любых точек этого отрезка выполняется следующее:

Другими словами, для возрастающей функции Для убывающей функции все наоборот:

Например, логарифм монотонно возрастает, если основание и монотонно убывает, если Не забывайте про область допустимых значений логарифма:

f ( x ) = log _a x ( a > 0; a ≠ 1; x > 0)

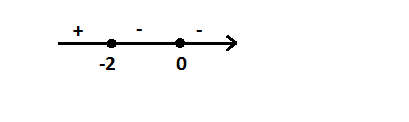
Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:

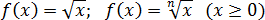
Показательная функция ведет себя аналогично логарифму: растет и убывает Но в отличие от логарифма, показательная функция определена для всех чисел, а не только

f ( x ) = a x (a > 0)

Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.

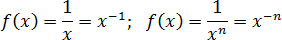
Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, становится тяжело считать производную. Что при этом происходит — сейчас разберем.

Координаты вершины параболы

Чаще всего аргумент функции заменяется на квадратный трехчлен вида Его график — стандартная парабола, в которой нас интересуют:

1. Ветви параболы — могут уходить вверх или вниз Задают направление, в котором функция может принимать бесконечные значения;
2. Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее или наибольшее значение.

Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:

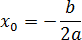
Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:

Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно для квадратного трехчлена, а на функцию — забить.

Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:

1. Отрезок [ a ; b ] в условии задачи отсутствует. Следовательно, вычислять не требуется. Остается рассмотреть лишь точки экстремума;
2. Но таких точек всего одна — это вершина параболы координаты которой вычисляются буквально устно и без всяких производных.

Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:

1. Выписать уравнение параболы и найти ее вершину по формуле:
2. Найти значение исходной функции в этой точке: Если никаких дополнительных условий нет, это и будет ответом.

На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.

Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.

Задача. Найдите наименьшее значение функции:

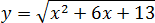
Под корнем стоит квадратичная функция График этой функции − парабола ветвями вверх, поскольку коэффициент

x ₀ = − b /(2 a ) = −6/(2 · 1) = −6/2 = −3

Поскольку ветви параболы направлены вверх, в точке функция принимает наименьшее значение.

Корень монотонно возрастает, значит точка минимума всей функции. Имеем:

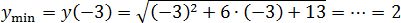
Задача. Найдите наименьшее значение функции:

Под логарифмом снова квадратичная функция: График — парабола ветвями вверх,

x ₀ = − b /(2 a ) = −2/(2 · 1) = −2/2 = −1

Итак, в точке квадратичная функция принимает наименьшее значение. Но функция монотонная, поэтому:

y _min = y (−1) = log ₂ ((−1) 2 + 2 · (−1) + 9) = . = log ₂ 8 = 3

Задача. Найдите наибольшее значение функции:

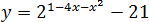
В показателе стоит квадратичная функция Перепишем ее в нормальном виде:

Очевидно, что график этой функции — парабола, ветви вниз Поэтому вершина будет точкой максимума:

Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке

Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.

Следствия из области определения функции

Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:

Аргумент логарифма должен быть положительным:

y = log _a f ( x ) ⇒ f ( x ) > 0

Арифметический квадратный корень существует только из неотрицательных чисел:

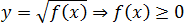
Знаменатель дроби не должен равняться нулю:

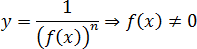
Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:

Задача. Найдите наибольшее значение функции:

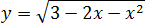
Под корнем снова квадратичная функция: Ее график — парабола, но ветви вниз, поскольку Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.

Выписываем область допустимых значений (ОДЗ):

3 − 2 x − x 2 ≥ 0 ⇒ x 2 + 2 x − 3 ≤ 0 ⇒

Теперь найдем вершину параболы:

Точка принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции а также на концах ОДЗ:

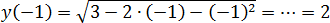
Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.

Задача. Найдите наименьшее значение функции:

Внутри логарифма стоит квадратичная функция Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:

6 x − x 2 − 5 > 0 ⇒ x 2 − 6 x + 5 x ₀ = − b /(2 a ) = −6/(2 · (−1)) = −6/(−2) = 3

Вершина параболы подходит по ОДЗ: Но поскольку концы отрезка нас не интересуют, считаем значение функции только

y _min = y (3) = log _0,5 (6 · 3 − 3 2 − 5) =

[spoiler title=”источники:”]

http://ege-study.ru/zadanie-12-profilnogo-EGE-po-matematike

http://www.berdov.com/ege/extremum/other_way/

[/spoiler]