Пришло время в данном разделе рассмотреть степенные функции. На блоге уже представлены задания на нахождение точек максимума и минимума различных функций, а именно: функций с числом е, с логарифмами, тригонометрические, рациональные.
Алгоритм нахождения данных точек оговаривался уже неоднократно, кратко повторюсь:
1. Находим производную функции.
2. Находим нули производной (приравниваем производную к нулю и решаем уравнение).
3. Далее строим числовую ось, на ней отмечаем найденные точки и определяем знаки производной на полученных интервалах. *Это делается путём подстановки произвольных значений из интервалов в производную.
4. Далее делаем вывод.
Если вы совсем не знакомы со свойствами производной для исследования функций, то обязательно изучите статью «Исследование функций. Это нужно знать!».Также повторите таблицу производных и правила дифференцирования (имеются в этой же статье). Рассмотрим задачи:
77431. Найдите точку максимума функции у = х3–5х2+7х–5.
Найдём производную функции:
Найдем нули производной:
3х2 – 10х + 7 = 0
Решая квадратное уравнение получим:
*Это точки возможного максимума (минимума) функции.
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(0)‘ = 3∙02 – 10∙0 + 7 = 7 > 0
у(2)‘ = 3∙22 – 10∙2 + 7 = – 1< 0
у(3)‘ = 3∙32 – 10∙3 + 7 = 4 > 0
В точке х = 1 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 1
77432. Найдите точку минимума функции у = х3+5х2+7х–5.
Найдём производную функции:
Найдем нули производной:
3х2 + 10х + 7 = 0
Решая квадратное уравнение получим:
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–3)‘ = 3∙(–3)2 + 10∙(–3) + 7 = 4 > 0
у(–2)‘= 3∙(–2)2 + 10∙(–2) + 7 = –1 < 0
у(0)‘= 3∙02 – 10∙0 + 7 = 7 > 0
В точке х = –1 производная меняет свой знак с отрицательного на положительный, значит это есть искомая точка минимума.
Ответ: –1
77435. Найдите точку максимума функции у = 7+12х–х3
Найдём производную функции:
Найдем нули производной:
12 – 3х2 = 0
х2 = 4
Решая уравнение получим:
*Это точки возможного максимума (минимума) функции.
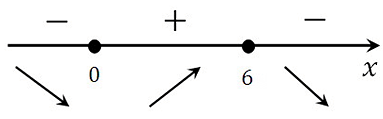
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–3)‘=12 – 3∙(–3)2 = –15 < 0
у(0)‘=12 – 3∙02 = 12 > 0
у(3)‘=12 – 3∙32 = –15 < 0
В точке х = 2 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 2
*Для этой же функции точкой минимума является точка х = – 2.
77439. Найдите точку максимума функции у = 9х2– х3.
Найдём производную функции:
Найдем нули производной:
18х –3х2 = 0
3х(6 – х) = 0
Решая уравнение получим:
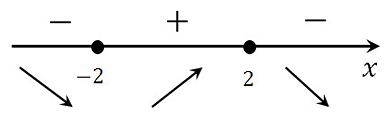
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–1)‘=18 (–1) –3 (–1)2 = –21< 0
у(1)‘=18∙1 –3∙12 = 15 > 0
у(7)‘=18∙7 –3∙72 = –1< 0
В точке х = 6 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 6
*Для этой же функции точкой минимума является точка х = 0.
77443. Найдите точку максимума функции у = (х3/3)–9х–7.
Найдём производную функции:
Найдем нули производной:
х2 – 9 = 0
х2 = 9
Решая уравнение получим:
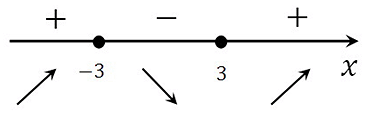
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–4)‘= (–4)2 – 9 > 0
у(0)‘= 02 – 9 < 0
у(4)‘= 42 – 9 > 0
В точке х = – 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: – 3
*Для этой же функции точкой минимума является точка х = 3.
77443. Найдите точку максимума функции у = 5+9х– (х3/3).
Найдём производную функции:
Найдем нули производной:
9 – х2 = 0
х2 = 9
Решая уравнение получим:
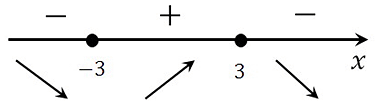
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–4)‘= 9 – (–4)2 < 0
у(0)‘= 9 – 02 > 0
у(4)‘= 9 – 42 < 0
В точке х = 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 3
*Для этой же функции точкой минимума является точка х = – 3.
77419. Найдите точку максимума функции у = х3– 48х+17. Решение.
77423. Найдите точку максимума функции у = х3–3х2+2. Решение.
77427. Найдите точку максимума функции у = х3+2х2+х+3. Решение.
На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Найдите наибольшее значение функции y=(7x^2-56x+56)e^x
на отрезке [-3; 2].
Показать решение
Решение
Найдём производную исходной функции по формуле производной произведения y”=
(7x^2-56x+56)”e^x,+
(7x^2-56x+56)left(e^xright)”=
(14x-56)e^x+(7x^2-56x+56)e^x=
(7x^2-42x)e^x=
7x(x-6)e^x.
Вычислим нули производной: y”=0;
7x(x-6)e^x=0,
x_1=0,
x_2=6.
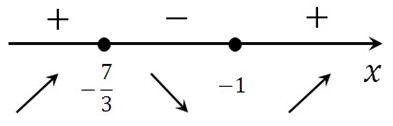
Расставим знаки производной и определим промежутки монотонности исходной функции на заданном отрезке.
Из рисунка видно, что на отрезке [-3; 0]
исходная функция возрастает, а на отрезке
— убывает. Таким образом, наибольшее значение на отрезке [-3; 2]
достигается при x=0
и равно y(0)=
7cdot 0^2-56cdot 0+56=56.
Ответ
Условие
Найдите наибольшее значение функции y=12x-12tg x-18
на отрезке left.
Показать решение
Решение
y”=
(12x)”-12(tg x)”-(18)”=
12-frac{12}{cos ^2x}=
frac{12cos ^2x-12}{cos ^2x}leqslant0.
Значит, исходная функция является невозрастающей на рассматриваемом промежутке и принимает наибольшее значение на левом конце отрезка, то есть при x=0.
Наибольшее значение равно y(0)=
12cdot 0-12 tg (0)-18=
-18.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Условие
Найдите точку минимума функции y=(x+8)^2e^{x+52}.
Показать решение
Решение
Будем находить точку минимума функции с помощью производной. Найдём производную заданной функции, пользуясь формулами производной произведения, производной x^alpha
и e^x:
y”(x)=
left((x+8)^2right)”e^{x+52}+(x+8)^2left(e^{x+52}right)”=
2(x+8)e^{x+52}+(x+8)^2e^{x+52}=
(x+8)e^{x+52}(2+x+8)=
(x+8)(x+10)e^{x+52}.
Расставим знаки производной и определим промежутки монотонности исходной функции. e^{x+52}>0
при любом x
. y”=0
при x=-8,
x=-10.
Из рисунка видно, что функция y=(x+8)^2e^{x+52}
имеет единственную точку минимума x=-8.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Условие
Найдите точку максимума функции y=8x-frac23x^tfrac32-106.
Показать решение
Решение
ОДЗ: x geqslant 0.
Найдём производную исходной функции:
y”=8-frac23cdotfrac32x^tfrac12=8-sqrt x.
Вычислим нули производной:
8-sqrt x=0;
sqrt x=8;
x=64.
Расставим знаки производной и определим промежутки монотонности исходной функции.
Из рисунка видно, что точка x=64
является единственной точкой максимума заданной функции.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Условие
Найдите наименьшее значение функции y=5x^2-12x+2ln x+37
на отрезке left[frac35; frac75right].
Показать решение
Решение
ОДЗ: x>0.
Найдём производную исходной функции:
y”(x)=
10x-12+frac{2}{x}=
frac{10x^2-12x+2}{x}.
Определим нули производной: y”(x)=0;
frac{10x^2-12x+2}{x}=0,
5x^2-6x+1=0,
x_{1,2}=
frac{3pmsqrt{3^2-5cdot1}}{5}=
frac{3pm2}{5},
x_1=frac15notinleft[frac35; frac75right],
x_2=1inleft[frac35; frac75right].
Расставим знаки производной и определим промежутки монотонности исходной функции на рассматриваемом промежутке.
Из рисунка видно, что на отрезке left[frac35; 1right]
исходная функция убывает, а на отрезке left
возрастает. Таким образом, наименьшее значение на отрезке left[frac35; frac75right]
достигается при x=1
и равно y(1)=
5cdot 1^2-12cdot 1+2 ln 1+37=
30.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Условие
Найдите наибольшее значение функции y=(x+4)^2(x+1)+19
на отрезке [-5; -3].
Показать решение
Решение
Найдём производную исходной функции, используя формулу производной произведения.
Приращения функции к приращению аргумента, который стремится к нулю. Для ее нахождения воспользуйтесь таблицей производных. Например, производная функции y = x3 будет равна y’ = x2.
Приравняйте данную производную к нулю (в данном случае x2=0).
Найдите значение переменной данного . Это будут те значения, при данная производная будет равна 0. Для этого подставьте в выражение произвольные цифры вместо x, при которых все выражение станет нулевым. Например:
2-2×2= 0
(1-x)(1+x) = 0
x1= 1, x2 = -1
Полученные значения нанесите на координатную прямую и высчитайте знак производной для каждого из полученных . На координатной прямой отмечаются точки, которые принимаются за начало отсчета. Чтобы высчитать значение на промежутках подставьте произвольные значения, подходящие по критериям. Например, для предыдущей функции до промежутка -1 можно выбрать значение -2. На от -1 до 1 можно выбрать 0, а для значений больше 1 выберите 2. Подставьте данные цифры в производную и выясните знак производной. В данном случае производная с x = -2 будет равна -0,24, т.е. отрицательно и на данном промежутке будет знак минус. Если x=0, то значение будет равно 2, а на данном промежутке ставится знак. Если x=1, то производная также будет равна -0,24 и ставится минус.
Если при прохождении через точку на координатной прямой производная меняет свой знак с минуса на плюс, то это точка минимума, а если с плюса на минус, то это точка максимума.
Видео по теме
Полезный совет
Для нахождения производной существуют онлайн-сервисы, которые подсчитывают нужные значения и выводят результат. На таких сайтах можно найти производную до 5 порядка.
Источники:
- Один из сервисов вычисления производных
- точку максимума функции
Точки максимума функции наряду с точками минимума называются точками экстремума. В этих точках функция меняет характер поведения. Экстремумы определяются на ограниченных числовых интервалах и всегда являются локальными.
Инструкция
Процесс нахождения локальных экстремумов называется функции и выполняется путем анализа первой и второй производной функции. Перед началом исследования убедитесь, что заданный интервал значений аргумента принадлежит к допустимым значениям. Например, для функции F=1/x значение аргумента х=0 недопустимо. Или для функции Y=tg(x) аргумент не может иметь значение х=90°.
Убедитесь, что функция Y дифференцируема на всем заданном отрезке. Найдите первую производную Y”. Очевидно, что до достижения точки локального максимума функция возрастает, а при переходе через максимум функция становится убывающей. Первая производная по своему физическому смыслу характеризует скорость изменения функции. Пока функция возрастает, скорость этого процесса является величиной положительной. При переходе через локальный максимум функция начинает убывать, и скорость процесса изменения функции становится отрицательной. Переход скорости изменения функции через ноль происходит в точке локального максимума.
Например, функция Y=-x²+x+1 на отрезке от -1 до 1 имеет непрерывную производную Y”=-2x+1. При х=1/2 производная равна нулю, причем при переходе через эту точку производная меняет знак с «+» на «-». Вторая производная функции Y”=-2. Постройте по точкам график функции Y=-x²+x+1 и проверьте, является ли точка с абсциссой х=1/2 локальным максимумом на заданном отрезке числовой оси.
Тип задания: 12
Тема:
Рациональные функции
Условие
Найдите наибольшее значение функции y=x+frac{36}{x}+10
на отрезке [-10; -1].
Показать решение
Решение
Исходная функция определена при x neq 0.
y”(x)=1-frac{36}{x^2}.
frac{36}{x^2}=1,
x^2=36,
x=pm 6.
Исследуемому промежутку принадлежит только значение x=-6.
Расставим знаки производной и определим промежутки монотонности исходной функции.
y=x+frac{36}{x}+10
возрастает на промежутке [-10; -6]
и убывает на промежутке [-6; -1].
Наибольшее значение достигается при x=-6
и равно y(-6)=-6+frac{36}{-6}+10=-2.
Ответ
Тип задания: 12
Тема:
Рациональные функции
Условие
Найдите наименьшее значение функции y=x+frac{25}{x}+2017
на отрезке .
Показать решение
Решение
y”(x)=1-frac{25}{x^2}.
Найдём нули производной: y”(x)=0
при frac{25}{x^2}=1,
x^2=25,
x=pm 5.
Исследуемому промежутку принадлежит только значение x=5.
Расставим знаки производной и определим промежутки монотонности исходной функции.
Из рисунка видно, что функция y=x+frac{25}{x}+2017
убывает на промежутке
и возрастает на промежутке .
Наименьшее значение достигается при x=5
и равно y(5)=5+frac{25}{5}+2017=2027.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Рациональные функции
Условие
Найдите точку минимума функции y=frac{x^2+10,000}{x}.
Показать решение
Решение
Исходная функция определена при x neq 0,
при этом y=-x-frac{10,000}{x}.
Тогда производная исходной функции y”(x)=-1+frac{10,000}{x^2}.
Найдём нули производной: y”(x)=0
при frac{10,000}{x^2}=1,
x^2=10,000,
x=pm 100.
Расставим знаки производной и определим промежутки монотонности исходной функции.
Из рисунка видно, что функция y=-frac{x^2+10,000}{x}
имеет единственную точку минимума x=-100.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Рациональные функции
Условие
y=-frac{x^2+144}{x}.
Показать решение
Решение
Исходная функция определена при xneq0,
при этом y=-x-frac{144}{x}.
Тогда производная исходной функции y”(x)=-1+frac{144}{x^2}.
Найдем нули производной: y”(x)=0
при frac{144}{x^2}=1,
x^2=144,
x=pm12.
Расставим знаки производной и определим промежутки монотонности исходной функции.
Из рисунка видно, что функция y=-frac{x^2+144}{x}
имеет единственную точку максимума x=12.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Рациональные функции
Условие
Найдите точку максимума функции y=-frac{x}{x^2+961}.
Показать решение
Решение
Находим производную: y”=-frac{1cdot(x^2+961)-xcdot2x}{(x^2+961)^2}=frac{x^2-961}{(x^2+961)^2}.
Решаем уравнение frac{x^2-961}{(x^2+961)^2}=0,
x^2-961=0;
x^2=961,
x=pm31.
Так как у дроби frac{x^2-961}{(x^2+961)^2}
знаменатель больше нуля, то ее знак совпадает со знаком числителя дроби, являющегося квадратным трехчленом x^2-961.
Таким образом, при y<-31
функция возрастает, а при -3131
опять возрастает:
В точке x=-31
будет максимум.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 12
Тема:
Рациональные функции
Условие
Найдите точку минимума функции y=frac{48}{x}+3x+204
.
Показать решение
Решение
Вычислим производную функции.
y”=-frac{48}{x^2}+3
Найдем точки, в которых производная функции обращается в нуль.
-frac{48}{x^2}+3=0
-frac{48+3x^2}{x^2}=0
48+3x^2=0
x^2=16
x=pm4
На числовой оси расставим знаки производной и посмотрим как ведет себя функция.
При переходе через точку x
= 4
производная меняет знак с минуса на плюс. Значит x
= 4
– точка минимума функции.
Алгоритм нахождения данных точек оговаривался уже неоднократно, кратко повторюсь:
1. Находим производную функции.
2. Находим нули производной (приравниваем производную к нулю и решаем уравнение).
3. Далее строим числовую ось, на ней отмечаем найденные точки и определяем знаки производной на полученных интервалах. *Это делается путём подстановки произвольных значений из интервалов в производную.
Если вы совсем не знакомы со свойствами производной для исследования функций, то обязательно изучите статью
«
».
Также повторите таблицу производных и правила дифференцирования (имеются в этой же статье). Рассмотрим задачи:
77431. Найдите точку максимума функции у = х 3 –5х 2 +7х–5.
Найдём производную функции:
Найдем нули производной:
3х 2 – 10х + 7 = 0
у(0)
”
= 3∙0
2 – 10∙0 + 7 = 7 > 0
у(2)
”
=
3∙2 2 – 10∙2 + 7 = – 1< 0
у(3)
”
=
3∙3 2 – 10∙3 + 7 = 4 > 0
В точке х = 1 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 1
77432. Найдите точку минимума функции у = х 3 +5х 2 +7х–5.
Найдём производную функции:
Найдем нули производной:
3х 2 + 10х + 7 = 0
Решая квадратное уравнение получим:
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(
–3
)
”
=
3∙(–3) 2 + 10∙(–3) + 7 = 4 > 0
у(
–2
)
“=
3∙(–2) 2 + 10∙(–2) + 7 = –1 < 0
у(0
)
“=
3∙0 2 – 10∙0 + 7 = 7 > 0
В точке х = –1 производная меняет свой знак с отрицательного на положительный, значит это есть искомая точка минимума.
Ответ: –1
77435. Найдите точку максимума функции у = 7+12х–х 3
Найдём производную функции:
Найдем нули производной:
12 – 3х 2 = 0
х 2 = 4
Решая уравнение получим:
*Это точки возможного максимума (минимума) функции.
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(
–3
)
“=
12 – 3∙(–3) 2 = –15 < 0
у(0
)
“=
12 – 3∙0 2 = 12 > 0
у(
3
)
“=
12 – 3∙3 2 = –15 < 0
В точке х = 2 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 2
*Для этой же функции точкой минимума является точка х = – 2.
77439. Найдите точку максимума функции у = 9х 2 – х 3 .
Найдём производную функции:
Найдем нули производной:
18х –3х 2 = 0
3х(6 – х) = 0
Решая уравнение получим:
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(
–1
)
“=
18 (–1) –3 (–1) 2 = –21< 0
у(1
)
“=
18∙1 –3∙1 2 = 15 > 0
у(7
)
“=
18∙7 –3∙7 2 = –1< 0
В точке х = 6 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 6
*Для этой же функции точкой минимума является точка х = 0.
77443. Найдите точку максимума функции у = (х 3 /3)–9х–7.
Найдём производную функции:
Найдем нули производной:
х 2 – 9 = 0
х 2 = 9
Решая уравнение получим:
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(
–4
)
“=
(–4) 2 – 9 > 0
у(0
)
“=
0 2 – 9 < 0
у(4
)
“=
4 2 – 9 > 0
В точке х = – 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: – 3
9 – х 2 = 0
х 2 = 9
Решая уравнение получим:
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(
–4
)
“=
9 – (–4) 2 < 0
у(0
Решение
.
На этом всё. Успеха вам!
С уважением, Александр Крутицких
.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
– Производная положительна там, где функция возрастает.
– Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после – производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
– Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
– Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
– если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
– если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
– если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Кубическая парабола задается функцией y=x3
График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции 
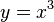
Перечислим основные свойства функции
1.Область определения – любое действительное число:.
2.Область значений – любое действительное число:.
3.Функция является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием .
Производная кубической функции 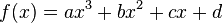
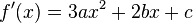





СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Исследование степенных и иррациональных функций
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 11 № 77419
i
Найдите точку максимума функции
Аналоги к заданию № 77419: 124217 124229 124261 … Все
Решение
·
1 комментарий
·
Видеокурс
·
Помощь
2
Тип 11 № 77421
i
Найдите наименьшее значение функции на отрезке
Аналоги к заданию № 77421: 124317 124361 124365 … Все
Решение
·
1 комментарий
·
Видеокурс
·
Помощь
3
Тип 11 № 77422
i
Найдите наибольшее значение функции на отрезке
Аналоги к заданию № 77422: 124367 124415 124369 … Все
Решение
·
Видеокурс
·
Помощь
4
Тип 11 № 77423
i
Найдите точку максимума функции
Аналоги к заданию № 77423: 124417 124515 124419 … Все
Решение
·
Видеокурс
·
Помощь
5
Тип 11 № 77424
i
Найдите точку минимума функции
Аналоги к заданию № 77424: 639109 124517 124615 … Все
Источник: ЕГЭ по математике 27.03.2023. Досрочная волна. Москва
Решение
·
Видеокурс
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023

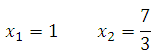

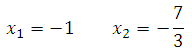
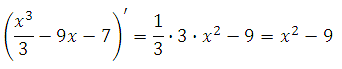
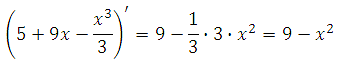
.png)
.png)
.png)
.png)
.png)
.png)

.png)
.png)












