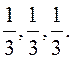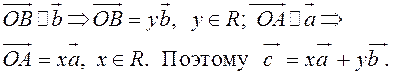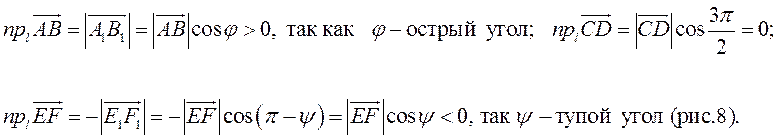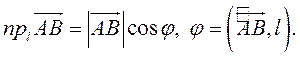Как найти точку медианы вектора - Сайт, где вы сможете решить свои вопросы

Уравнение медианы треугольника

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

What can I do to prevent this in the future?

Контрольная работа: Краткие сведения и задачи по курсу векторной и линейной алгебры

Как найти точку пересечения медиан треугольника, зная координаты его вершин?

1 способ

Поскольку все медианы треугольника пересекаются в одной точке, достаточно составить уравнения двух медиан и найти координаты их точки пересечения.

Пример.

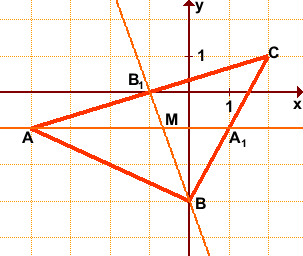
Найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1).

Решение:

Обозначим середины сторон BC и AC через A₁ и B₁ соответственно. По формулам координат середины отрезка

$[x_{A_1 } = frac{{x_B + x_C }}{2} = frac{{0 + 2}}{2} = 1,]$

$[y_{A_1 } = frac{{y_B + y_C }}{2} = frac{{ - 3 + 1}}{2} = - 1,]$

$[x_{B_1 } = frac{{x_A + x_C }}{2} = frac{{ - 4 + 2}}{2} = - 1,]$

$[y_{B_1 } = frac{{y_A + y_C }}{2} = frac{{ - 1 + 1}}{2} = 0.]$

Составим уравнения медиан AA₁ и BB₁.

Уравнение медианы AA₁ можно найти как уравнение прямой, проходящей через две точки A(-4;-1) и A₁(1;-1).

$[left{ begin{array}{l} - 1 = k cdot ( - 4) + b, \ - 1 = k cdot 1 + b, \ end{array} right. Rightarrow k = 0,b = - 1,]$

то есть уравнение прямой AA₁ y= -1.

B(0;-3), B₁(-1;0). Найдём уравнение медианы BB₁.

$[left{ begin{array}{l} - 3 = k cdot 0 + b, \ 0 = k cdot ( - 1) + b, \ end{array} right. Rightarrow k = - 3,b = - 3,]$

откуда уравнение прямой BB₁ y= -3x-3.

Координаты точки пересечения прямых AA₁ и BB₁ ищем как решение системы уравнений

$[left{ begin{array}{l} {rm{y = - 1}}, \ {rm{y = - 3x - 3}}{rm{,}} \ end{array} right. Rightarrow x = - frac{2}{3},y = - 1.]$

Ответ:

$[( - frac{2}{3}; - 1).]$

2 способ

Поскольку все медианы медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины, можно найти координаты концов любой медианы, а затем точку, которая делит медиану в отношении 2:1, начиная отсчёт от точки, которая является вершиной треугольника.

Например, в условиях предыдущей задачи — найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1), —

зная координаты A₁(1;-1), найдём координаты точки M. Точка M пересечения медиан треугольника делит отрезок AA₁ в отношении 2:1, считая от точки A.

По формулам деления отрезка в данном отношении

$[x = frac{{nx_1 + mx_2 }}{{m + n}},y = frac{{ny_1 + my_2 }}{{m + n}}]$

$[x_M = frac{{1 cdot x_A + 2 cdot x_{A_1 } }}{{2 + 1}} = frac{{1 cdot ( - 4) + 2 cdot 1}}{3} = - frac{2}{3},]$

$[y_M = frac{{1 cdot y_A + 2 cdot y_{A_1 } }}{{2 + 1}} = frac{{1 cdot ( - 1) + 2 cdot ( - 1)}}{3} = - 1.]$

Источник

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

Найти координаты середины отрезка по координатам его концов.
Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6e2006a50ac03a56 • Your IP : 85.95.188.35 • Performance & security by Cloudflare

то есть MM =

Краткие сведенияи задачи по курсу векторной и линейной алгебры

1. Найти скалярное произведение .

2. При каком значении α векторы и ортогональны?

;;;

Два вектора ортогональны, когда их скалярное произведение равно нулю.

3. Для прямой М₁ М₂ написать уравнение с угловым коэффициентом, в отрезках и общее уравнение. Начертить график прямой. М₁ (0,-3) М₂ (2,1).

Общий вид уравнения прямой с угловым коэффициентом записывается в виде:

Общий вид уравнения прямой, проходящей через две точки записывается в виде:

Общий вид уравнения прямой в отрезках записывается в виде:

Уравнения прямой в отрезках для прямой М₁ М₂

;

4. В треугольнике М₀ М₁ М₂ найти уравнение медианы, высоты, проведенных их вершины М₀ , а также уравнение средней линии EF, параллельной основанию М₁ М₂ .(М₀ (-1,-2); М₁ (0,-3); М₂ (2,1)).

Найдём координаты точки М₃ , координаты середины стороны М₁ М₂ :

уравнения прямой, проходящей через две точки записывается в виде:

уравнение для высоты М₀ М₃ :

Найдём уравнение прямой М₁ М₂ :

Из условия перпендикулярности (k₂ =-1/k₁ ) следует, что k₂ =1/2.

Уравнения прямой с угловым коэффициентом записывается в виде:

тогда уравнение для высоты примет вид:

Расстояние от точки М(x₀ ,y₀ ) до прямой Ax+By+c=0 находится по формуле:

Чтобы найти длину высоту, найдём расстояние от точки М₀ (-3,-5) до прямойМ₁ М₂ , уравнение которой имеет вид -x+2y-4=0. Подставим данные в формулу(1):

Найдём координаты точек Е иF.

Для точки Е: x=-1/2; y=-5/2; E(-1/2;-5/2).

Для точки F: x=1/2; y=-1/2; F(1/2;-1/2).

Уравнение прямой EF:

y+5/2=-2x-1 или 2x+y+3,5=0.

5. По каноническому уравнению кривой второго порядка определить тип кривой, начертить её график. Найти координаты фокусов, вершин и центра (для центральной кривой).

(1)

Воспользуемся параллельным переносом (O’(-3,-1))

(2)

Подставим (2) в (1), получим

кривая второго порядка является эллипсом.

т.к.

Координаты центра: O’(-3,-1).

6. Преобразовать к полярным координатам уравнения линии.

Первое уравнение представляет собой (при любых значениях φ) полюс О. Второе – дает все точки линии, в том числе полюс. Поэтому первое уравнение можно отбросить. Следовательно, получаем:

Ответы на вопросы

1. Дайте определение обратной матрицы. Какие вы знаете способы вычисления обратной матрицы?

Матрица В называется обратной для матрицы А, если выполняется условие АВ=ВА=Е, где Е – единичная матрица. Способы вычисления обратной матрицы: 1) использование алгебраических дополнений; 2) привести исходную матрицу к ступенчатому виду методом Гаусса, после чего необходимо преобразовать её в единичную .

2. Как записывается система уравнений в матрично-векторной форме? Как найти решение системы уравнений при помощи обратной матрицы?

Система уравнений в матрично-векторной форме записывается в виде: .

Решение системы уравнения при помощи обратной матрицы:

3. Сформулируйте, в чем состоит процедура Гаусса и для решения каких линейных задач применяется?

Процедура Гаусса используется для решения систем линейных уравнений и состоит в следующем:

Выполняются элементарные преобразования, вследствие чего можно получить два исхода:

1. получается строчка, в которой до черты стоят нули, а после – ненулевое число, тогда решения нет;

2. система приводится к лестничному виду.

Если в системе лестничного вида число уравнений совпадает с числом неизвестных, то решение единственное.

Если число уравнений меньше чем число неизвестных, то решений бесконечное множество. В этом случае неизвестные разделяются на зависимые и свободные. Число зависимых неизвестных совпадает с числом уравнений.

т.к. detA0, то матрица является невырожденной.

;

5. Найти скалярное произведение .

6. При каком значении α векторы и ортогональны?

;;;

Два вектора ортогональны, когда их скалярное произведение равно нулю.

7. Для прямой М₁ М₂ написать уравнение с угловым коэффициентом, в отрезках и общее уравнение. Начертить график прямой. М₁ (2,-2) М₂ (1,0).

Общий вид уравнения прямой с угловым коэффициентом записывается в виде:

Общий вид уравнения прямой, проходящей через две точки записывается в виде:

Общий вид уравнения прямой в отрезках записывается в виде:

здесь

Уравнения прямой в отрезках для прямой М₁ М₂

;

8. В треугольнике М₀ М₁ М₂ найти уравнение медианы, высоты, проведенных их вершины М₀ , а также уравнение средней линии EF, параллельной основанию М₁ М₂ .(М₀ (-3,-5); М₁ (2,-2); М₂ (1,0)).

Найдём координаты точки М₃ , координаты середины стороны М₁ М₂ :

уравнения прямой, проходящей через две точки записывается в виде:

уравнение для высоты М₀ М₃ :

Найдём уравнение прямой М₁ М₂ :

Из условия перпендикулярности (k₂ =-1/k₁ ) следует, что k₂ =-1/2.

Уравнения прямой с угловым коэффициентом записывается в виде:

тогда уравнение для высоты примет вид:

Расстояние от точки М(x₀ ,y₀ ) до прямой Ax+By+c=0 находится по формуле:

Чтобы найти длину высоту, найдём расстояние от точки М₀ (-3,-5) до прямойМ₁ М₂ , уравнение которой имеет вид 2x+y-2=0. Подставим данные в формулу(1):

Найдём координаты точек Е иF.

Для точки Е: x=-1/2; y=-7/2; E(-1/2;-7/2).

Для точки F: x=-1; y=-5/2; F(-1;-5/2).

Уравнение прямой EF:

y+7/2=-2x-1 или 2x+y+4,5=0.

9. По каноническому уравнению кривой второго порядка определить тип кривой, начертить её график. Найти координаты фокусов, вершин и центра (для центральной кривой).

(1)

Воспользуемся параллельным переносом (O’(-2,2))

(2)

Подставим (2) в (1), получим

кривая второго порядка является эллипсом.

т.к.

Координаты центра: O’(-2,2).

10. Преобразовать к полярным координатам уравнения линии.

Первое уравнение представляет собой (при любых значениях φ) полюс О. Второе – дает все точки линии, в том числе полюс,. Поэтому первое уравнение можно отбросить. Следовательно получаем:

Ответы на вопросы

4. Дайте определение обратной матрицы. Какие вы знаете способы вычисления обратной матрицы?

5. Как записывается система уравнений в матрично-векторной форме? Как найти решение системы уравнений при помощи обратной матрицы?

Система уравнений в матрично-векторной форме записывается в виде:

Решения системы уравнения при помощи обратной матрицы:

6. Сформулируйте, в чем состоит процедура Гаусса и для решения каких линейных задач применяется?

Процедура Гаусса используется для решения систем линейных уравнений и состоит в следующем:

Выполняются элементарные преобразования, вследствие чего можно получить два исхода:

3. получается строчка, в которой до черты стоят нули, а после – ненулевое число, тогда решения нет;

4. система приводится к лестничному виду.

Если в системе лестничного вида число уравнений совпадает с числом неизвестных, то решение единственное.

r=2; система совместима.

х 3,x4 – свободные переменные

т.к. detA0, то матрица невырождена.

[spoiler title=”источники:”]

http://mathvox.ru/geometria/dekartovi-koordinati-uravneniya-figur-v-dekartovoi-sisteme-koordinat/glava-5-uravneniya-nekotorih-elementov-treugolnika/uravnenie-mediani-treugolnika-po-koordinatam-ego-vershin/

http://www.bestreferat.ru/referat-114355.html

[/spoiler]

Название: Краткие сведения и задачи по курсу векторной и линейной алгебры
Раздел: Рефераты по математике
Тип: контрольная работа Добавлен 11:09:20 28 октября 2010 Похожие работы
Просмотров: 697 Комментариев: 21 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать

Источник

5. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1

ВЕКТОРНАЯ АЛГЕБРА

1. Векторы, базисы, координаты

№	Задание	Ответ
В треугольнике ABC разложите биссектрису CC по
	CB и b CA .
базису векторов a
РЕШЕНИЕ:

Пусть a CB , b CA ,
C лежит на стороне AB .

CC a b a ,

где a

Воспользуемся свойством биссектрисы треугольника

и тем, что BA BC C A. Отсюда

C A

следует, что

C A

CC 1 a

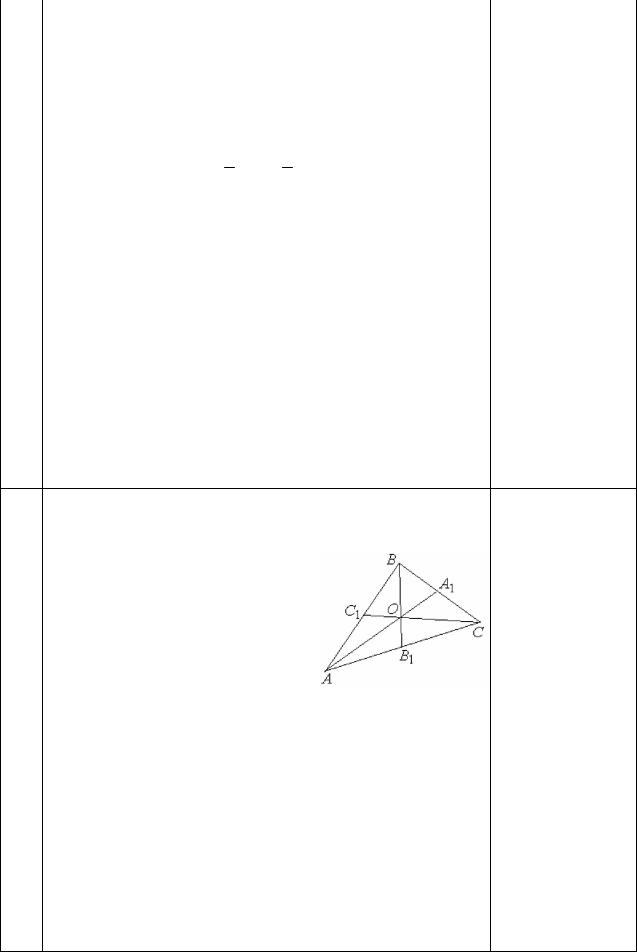
Докажите, что точка пе-

ресечения медиан тре-

угольника делит каждую

медиану в отношении

2 :1, считая от вершины.

РЕШЕНИЕ:


Пусть A – середина стороны BC , B	– середина
стороны AC . Отложим на медиане BB расстояние
	2	BB ‘		от вершины и поставим точку O . Тогда

3
		2		2

			AO AB		BB AB	BA AB
			3	3

1 AB 1 AC .

3 3

Отложим от вершины A по медиане AA	расстояние
	2	AA‘		и поставим точку M . Найдем координаты

3

вектора AM в базисе векторов AB и AC .
			2		2			1			2	1
		AM			AA				AB					AB	BA AC

										BC
					3							2	3	3
							3
						1	1	1			1
							AB		AC
									,		.
					3	3
							3			3

Но это координаты вектора AO . Таким образом, точка O и точка M совпадают, это точка пересечения медиан, и она делит медианы AA и BB в отношении 2 :1, считая от вершины.

В треугольнике ABC через O обозначена точка пе-

ресечения медиан. Найдите сумму векторов

OA OB OC .

РЕШЕНИЕ:

Обозначим

AB c , BC a , AC b,

b a c .

Из рисунка по свойству медиан

получаем, что

A1 A B1B C1C

OA OB OC

c c

a c b 0.

Точки E и F – середины сторон AD и BC четырех-

угольника ABCD . Докажите, что EF

AB DC

4Выведите теорему о средней линии трапеции. РЕШЕНИЕ:

EF EA AB BF , EF ED DC CF ,

							1
		BF CF , EA ED , EF	AB DC	.
		2
Если ABCD – трапеция, сторо-

ны AB и CD параллельны, то-
гда
		1			1
	EF			AB DC		AB
	2	2

– свойство средней линии трапеции.

На стороне AB и диагонали AC параллелограмма

ABCD	взяты соответственно точки E и F так, что
	1		1
AE		AB и AF		AC .
n	n 1

Докажите, что точки E , F и D лежат на одной прямой и определите отношение отрезков EF и FD .

5 ДОКАЗАТЕЛЬСТВО:

Пусть AB a , AD

b .Тогда a b AC .

EF AF AE

(a b)

b .

n 1

n(n 1)

n 1

FD AD AF b

( a b )

b .

n 1

EF || FD , то есть точки E ,

Отсюда | EF |:| FD |

F , D лежат на одной прямой.

Задан тетраэдр OABC . В базисе из ребер OA , OB и

OC найдите координаты векто-

ра OF , где F – точка пересече-

ния медиан основания ABC .

РЕШЕНИЕ:

6 Воспользуемся правилом треугольни-

ка:OF OA AF OA

AK .

K – середина ребра CB ; точка F находится на рас-

стоянии

длины медианы от вершины A.

AK AB

										1
					AO	OB	BO	OC .

													2
Подставим AK в OF :
							2
				OF OA	AO OB	1	BO OC
				3	3
						2			2			1			1
				OA			OA		OB		OB			OC
				3	3	3
																3
	1												1
		OA OB	OC								1			1
					,		OF =		,	,				.
3
											3	3		3
	В пространстве заданы треугольники ABC и
	A B C ; M и M		– точки пересечения медиан
	этих треугольников соответственно. Разложите
	вектор MM	по базису векторов AA , BB , CC .

РЕШЕНИЕ:

Пусть N – середина стороны BC , N – середина стороны B C .

MM MA AA A M

	.
	Найдем:
						2
	MA						NA ; NA	NB BA;
	3
														2	1	1		1
					1
	NB						CB ; M A	A M				N A ; N A N B B A ;

7										2							3				,	,
																	3	3	3
				1


	N B		2	C B ;

	C B C C CB BB ; B A B B BA AA .
	После последовательных подстановок		2
													2
	MM MA AA A M						NA AA

									N A
																3				3

				2
		NB BA AA	2	N	B B A
	3	3
				2								2	1
					1


				3 2						2				3 2
				2				1			1
							CB		BA AA			C C CB BB
	3		2	3	3
		2
		B B BA	AA	1	AA BB CC	,
	3	3

2. Декартов прямоугольный базис. Направляющие косинусы и координаты

В трапеции ABCD с основаниями AD и BC из-
вестны векторы
AB 2;2;5 ,
AC 3;6; 2 ,
AD 10;8; 14 . Найдите
сумму координат вектора					3
MN , где M и N – середины

сторон AB и CD .
РЕШЕНИЕ:
BC AC AB , MN	AD BC	AD AC AB	15	, 6,	21	.
2	2

2		2
3.
Даны точки A(8, 7, 4) , B(1, 2, 3) , C( 1, 1, 7) .
Найдите сумму координат точки D(x, y, z) , если
AB 2BC 3AD 0.
РЕШЕНИЕ:
AB 7,5,1 , BC 2,1, 4 ,	AD x 8, y 7, z 4 .

– 6

AB 2BC 3AD 0

7,5,1 4, 2,8 3x 24,3y 21,3z 12 0


	7 4 3x 24 0
		5 2 3y 21 0 (x, y, z) (9, 8, 7) .

		1 8 3z 12 0

	Сумма координат равна (- 6).
		2 и углы a 45 ,
	Дан модуль вектора	a

	b 60 и g 120 , которые он составляет с коор-
		2,1, 1
	динатными осями Ox , Oy и Oz соответственно.
	Вычислите проекции вектора a на координатные
	оси.

РЕШЕНИЕ:

ax a cosa 2cos 45 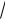2 ;

ay a cosb 2cos60 1;

az a cosg 2cos120 1.

a = 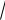2,1, 1

Даны векторы a												1, 1,		. Вы-
		2, 0, 1 и b		0
																							2b .
числите направляющие косинусы вектора a	cosa	0		,

РЕШЕНИЕ:																					5

																						2
																							cosb	,


																			5
a 2b 2, 0, 1 2 1, 1, 0		0, 2, 1 .
				1

				2			2			2
	a 2b		0		2		1	5 .								cos g

												5
cosa	0		; cosb	2		;	cos g	1	.


5								5					5
Может ли вектор составлять с координатными осями
следующие углы: a 45 , b 60 , g 120 ?
РЕШЕНИЕ:
Для направляющих косинусов выполняется равенство
cos2 a cos2 b cos 2g 1. Проверим его справедли-	да
вость.
															2
																				2	2
2					2						2			2		1	1

cos 45 cos	60 cos	120									1,


														2		2		2

равенство выполняется.

Даны точки A 3, 1, 5 , B 4, 2, 5 , C 4, 0, 3 .

Найдите длину медианы AA треугольника ABC .

РЕШЕНИЕ:							7

Координаты точки A (середины	AA ) A	0,1, 1	,

AA		3,2, 6		,	AA	3 2 22 6 2 7 .

Коллинеарны ли векторы c1	и c2 , построенные на	нет
векторах a и b , если a 9, 5,	3 ,

5b ?

b 7, 1, 2 , c1

, c2

РЕШЕНИЕ 1:

2a b 2

9, 5, 3

7, 1, 2

25, 9, 8

3a 5b

3 9, 5,

3 5

7, 1, 2

8, 20, 1

Пропорциональность компонент

c1y

c2 y

c2 z

c2 x

не выполняется, векторы неколлинеарны.

РЕШЕНИЕ 2

Векторы : a и b неколлинеарны, т.е. образуют базис. Векторы c1 и c2 неколлинеарны, так как их координаты в этом базисе не пропорциональны:

21 .

3. Скалярное произведение векторов

Найдите а)

a1 a2

и б)

3a1 2a2 , a1

2a2 , если

, a ,

РЕШЕНИЕ:

а)

a1 a2

, a1

а) 13 ,

, a1 a1,

a2 a2

a2 ,

б) 61

9 16

2 a1, a2

25 2

3 4cos

13.

б) 3a1

2a2 , a1 2a2

3a1 6 a1

, a2

2 a2 , a1 4a2

2π

3 9 4 a1,

a2 4 16 27 4 3 4 cos

64 61

Найдите

2a1 a2

, если a1 4, 2, 4 ,

a2 6, 3, 2 .

РЕШЕНИЕ:

105

2a1 a2 8, 4, 8 6, 3, 2 2, 1, 10 ,

105.

2a a

Найдите косинус угла между векторами AB и AC ,
	1,					0, 1,				3,
если A		2, 3	, B		2 ,	C	4, 5 .
РЕШЕНИЕ:
AB		0	1	, 1 2,						1, 1, 1 ,
	2 3		– 1
AC		2, 2, 2	,


								1 2	1	2 1	2


cos AB ,	AC					2					2	2

						12 1	12 2		22 2
1.

Вычислите синус угла, образованного векторами a 2, 2,1 и b 6, 3, 2 .

РЕШЕНИЕ:

Найдем косинус нужного угла:

cosj 2 6		2	3 1 2 12 6 2 4 ,
	5 17
	9 49			21		21		sinj
sin2 j 1 cos2 j 1	16		212 16		52 17	,	21

2	2	2
				21		21		21

sinj 517 . 21

Так как угол между векторами 0 j p,

sinj 517 . 21

Покажите, что

сумма квадратов

медиан треуголь-

ника относится к

сумме квадратов

b A

его сторон, как 3:4.

РЕШЕНИЕ:

b . Нахо-

Пусть CB a , CA b . Тогда

AB a

дим медианы треугольника:

a b

CC CB

BC a

b ,

BB BA AB

CA b

b .

Осталось найти требуемое отношение:

(ab)

2(ab)

Покажите, что четырехугольник ABCD

ромб, если

A(1,2,2) , B(3,5,8) , C( 3,2,6) , D( 5, 1,0).

Найдите угол при вершине А ромба.

РЕШЕНИЕ:

2, 3,

;

7 ;

;

p arccos

BC 6; 3; 2 ;

7 ;

;

7 .

и ABCD – ромб.

6 3

3 6

cos AB,

4 9 36

j p arccos

a, b

Докажите, что вектор

p b

перпендикуля-

рен вектору a .

РЕШЕНИЕ:

a, b

0 .

, a

a, b

Докажите: а) теорему косинусов; б) теорему Пифа-

гора.

ДОКАЗАТЕЛЬСТВО.

а) Рассмотрим треугольник

ABC , построенный на векто-

рах

AB и b

AC .

Пусть третья сторона

CB c .

Тогда

, a

cosg .

2 a,

б) При g 90

, получаем

теорему Пифагора.

Докажите, что диагонали ромба взаимно перпендикулярны.

РЕШЕНИЕ:

Пусть a AB и b AD –

стороны ромба.

b и

d1 AC a

d2 BD b

– его диагона-

ли.

a b

, b a

cos d1 , d2

так как для ромба

, и диагонали ромба

взаимно перпендикулярны.

4. Векторное произведение векторов

Найдите а)

a a

и б)

a 3a

3a a

если

2 , a ,

РЕШЕНИЕ:

а)

1 2 sin

3 ;

а) 3 ,

б)

б) 10 3

3 a1

a1 a1

a2 9 a2 a1 3 a2

10 a1 a2 10 3,

a1 a2 a2 a1

так как a1

a2 a2 0,

Найдите

, если

2a1

, 2a1

3, 1, 2

, a

1, 2, 1 .

РЕШЕНИЕ:

b 4 a1,

a2, a2

2 a1, a2

2 a2

4 a1, a2

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

ОПРЕДЕЛЕНИЕ. Разностью называется
сумма вектора и вектора, противоположного : (рис.
5).

Рис. 5

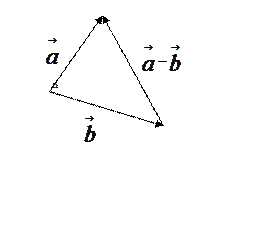
Начала и совмещаются в одной точке, и направлен от конца к концу .

СВОЙСТВА ЛИНЕЙНЫХ ОПЕРАЦИЙ

ОПРЕДЕЛЕНИЕ. Результат конечного числа линейных операций над
векторами называется их линейной комбинацией:, – линейная комбинация векторов с коэффициентами .

ПРИМЕР. Пусть М – точка пересечения медиан треугольника
АВС, а О – произвольная точка пространства. Представить как
линейную комбинацию

(рис. 6).

Рис. 6

. Так как точка пересечения медиан
треугольника делит их в отношении 2:1, считая от вершины, то из правила
параллелограмма следует, что .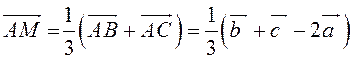

По
правилу треугольника 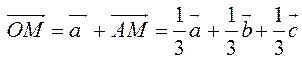, то есть – линейная комбинация с коэффициентами

ТЕОРЕМА 1. Пусть и – неколлинеарные векторы. Тогда любой
компланарный с ними вектор может быть представлен
в виде

, , (2.1)

где коэффициенты (2.1) определяются единственным
образом.

Представление вектора в виде
(2.1) называется разложением его по двум неколлинеарным векторам.

ДОКАЗАТЕЛЬСТВО.

1.
Пусть среди есть два коллинеарных, например:

2. Пусть среди коллинеарных
нет, тогда совместим начала всех трех векторов в одной точке. Построим
параллелограмм, диагональ которого совпадает с , а
стороны п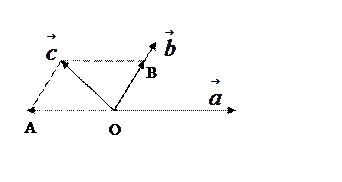араллельны прямым, на которых лежат и (рис.
7).

Тогда
но

Рис. 7

Докажем единственность разложения.
Предположим, что и Тогда,
вычитая одно равенство из другого, получим:. Если , то , что
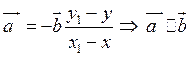
противоречит условию. Теорема доказана.

ТЕОРЕМА 2.
Пусть – некомпланарные векторы. Тогда любой
вектор может быть представлен в виде

, , (2.2)

причем
единственным образом.

Представление вектора в виде
(2.2) называется разложением его по трем некомпланарным.

Доказать самостоятельно.

ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ.

КООРДИНАТЫ ВЕКТОРА

Осью называется направленная прямая.

ОПРЕДЕЛЕНИЕ. Ортом оси называется
единичный вектор , направление которого совпадает
с направлением оси.

ОПРЕДЕЛЕНИЕ. Ортогональной проекцией точки М на ось называется основание М₁ перпендикуляра,
опущенного из М на .

ОПРЕДЕЛЕНИЕ. Ортогональной проекцией вектора на ось называется
длина отрезка А₁В₁ этой оси, заключенного между
ортогональными проекциями его начала и конца, взятая со знаком «+», если
направление вектора совпадает с направлением оси, и
со знаком «–», если эти направления противоположны (рис. 8).

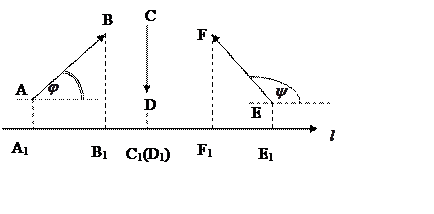Рис. 8

ОПРЕДЕЛЕНИЕ.
Углом между вектором и осью называется угол, на который нужно повернуть в
положительном направлении ось до совпадения ее направления с направлением
вектора (положительным считается поворот против часовой стрелки).

(рис.
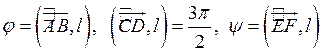
8).

Очевидно, проекцию вектора на ось можно найти по
формуле

Можно
показать, что проекция линейной комбинации векторов равна такой же линейной
комбинации их проекций:

В
частности, проекция суммы векторов равна сумме их проекций:

Рассмотрим
прямоугольную декартову систему координат ХОY. Обозначим – орт оси ОХ, – орт
оси OY. Выберем точку , и
пусть – проекции ее на ОХ и OY,то
есть координаты этой точки (рис. 9).