Нет. Кубическая парабола экстремумов не имеет.
Первая производная равна нулю в одной точке: х=0; у=0.
Но первая производная равна нулю не только в точках экстремума функции, но и в точках перегиба.
Разница между этими точками простая.
Экстремум – это есть максимум или минимум функции.
Это значит, что на подходе к максимуму функция возрастает, а после него убывает.
Для минимума наоборот – при подходе слева функция убывает, после минимума начинает возрастать (на то он и минимум).
А это значит, что по разные стороны от экстремума первая производная имеет разные знаки.
Как раз по этому признаку и можно определить экстремум – посмотреть (посчитать) знак первой производной до и после.
Перегиб не изменяет поведение функции – в смысле возрастания или убывания.
Геометрический смысл точки перегиба состоит в том, что график функции переходит в этой точке с одной стороны касательной на другую, т. е. кривая и касательная взаимно пересекаются.
При прохождении точки перегиба знак первой производной не изменяется.
Можно поступить по-другому – взять вторую производную.
Потому, что там, где вторая производная равна нулю – это и есть точки перегиба.
Пришло время в данном разделе рассмотреть степенные функции. На блоге уже представлены задания на нахождение точек максимума и минимума различных функций, а именно: функций с числом е, с логарифмами, тригонометрические, рациональные.
Алгоритм нахождения данных точек оговаривался уже неоднократно, кратко повторюсь:
1. Находим производную функции.
2. Находим нули производной (приравниваем производную к нулю и решаем уравнение).
3. Далее строим числовую ось, на ней отмечаем найденные точки и определяем знаки производной на полученных интервалах. *Это делается путём подстановки произвольных значений из интервалов в производную.
4. Далее делаем вывод.
Если вы совсем не знакомы со свойствами производной для исследования функций, то обязательно изучите статью «Исследование функций. Это нужно знать!».Также повторите таблицу производных и правила дифференцирования (имеются в этой же статье). Рассмотрим задачи:
77431. Найдите точку максимума функции у = х3–5х2+7х–5.
Найдём производную функции:
Найдем нули производной:
3х2 – 10х + 7 = 0
Решая квадратное уравнение получим:
*Это точки возможного максимума (минимума) функции.
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(0)‘ = 3∙02 – 10∙0 + 7 = 7 > 0
у(2)‘ = 3∙22 – 10∙2 + 7 = – 1< 0
у(3)‘ = 3∙32 – 10∙3 + 7 = 4 > 0
В точке х = 1 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 1
77432. Найдите точку минимума функции у = х3+5х2+7х–5.
Найдём производную функции:
Найдем нули производной:
3х2 + 10х + 7 = 0
Решая квадратное уравнение получим:
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–3)‘ = 3∙(–3)2 + 10∙(–3) + 7 = 4 > 0
у(–2)‘= 3∙(–2)2 + 10∙(–2) + 7 = –1 < 0
у(0)‘= 3∙02 – 10∙0 + 7 = 7 > 0
В точке х = –1 производная меняет свой знак с отрицательного на положительный, значит это есть искомая точка минимума.
Ответ: –1
77435. Найдите точку максимума функции у = 7+12х–х3
Найдём производную функции:
Найдем нули производной:
12 – 3х2 = 0
х2 = 4
Решая уравнение получим:
*Это точки возможного максимума (минимума) функции.
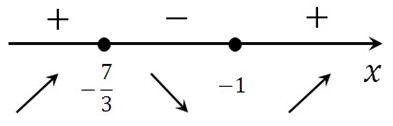
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–3)‘=12 – 3∙(–3)2 = –15 < 0
у(0)‘=12 – 3∙02 = 12 > 0
у(3)‘=12 – 3∙32 = –15 < 0
В точке х = 2 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 2
*Для этой же функции точкой минимума является точка х = – 2.
77439. Найдите точку максимума функции у = 9х2– х3.
Найдём производную функции:
Найдем нули производной:
18х –3х2 = 0
3х(6 – х) = 0
Решая уравнение получим:
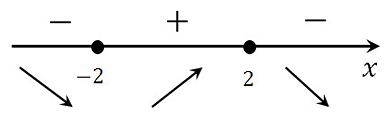
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–1)‘=18 (–1) –3 (–1)2 = –21< 0
у(1)‘=18∙1 –3∙12 = 15 > 0
у(7)‘=18∙7 –3∙72 = –1< 0
В точке х = 6 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 6
*Для этой же функции точкой минимума является точка х = 0.
77443. Найдите точку максимума функции у = (х3/3)–9х–7.
Найдём производную функции:
Найдем нули производной:
х2 – 9 = 0
х2 = 9
Решая уравнение получим:
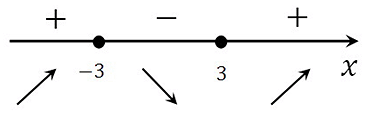
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–4)‘= (–4)2 – 9 > 0
у(0)‘= 02 – 9 < 0
у(4)‘= 42 – 9 > 0
В точке х = – 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: – 3
*Для этой же функции точкой минимума является точка х = 3.
77443. Найдите точку максимума функции у = 5+9х– (х3/3).
Найдём производную функции:
Найдем нули производной:
9 – х2 = 0
х2 = 9
Решая уравнение получим:
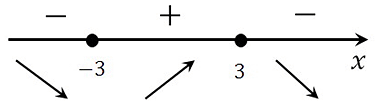
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–4)‘= 9 – (–4)2 < 0
у(0)‘= 9 – 02 > 0
у(4)‘= 9 – 42 < 0
В точке х = 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 3
*Для этой же функции точкой минимума является точка х = – 3.
77419. Найдите точку максимума функции у = х3– 48х+17. Решение.
77423. Найдите точку максимума функции у = х3–3х2+2. Решение.
77427. Найдите точку максимума функции у = х3+2х2+х+3. Решение.
На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Кубическая парабола задается функцией y=x3
График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции 
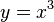
Перечислим основные свойства функции
1.Область определения – любое действительное число:.
2.Область значений – любое действительное число:.
3.Функция является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием .
Производная кубической функции 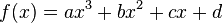
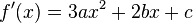





Кубическая парабола
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Кубическая парабола – это парабола, задаваемая уравнением вида $y=ax^3$, где $a ≠ 0$. Также в литературе можно встретить и другие формулы для кубической параболы, все они эквивалентны.
Рисунок 1. График кубической параболы
Свойства функции кубической параболы
- График кубической параболы определён на всём пространстве действительных чисел.
- Функция, задаваемая графиком кубической параболы, является нечётной, то есть:
$f(-x) =(-x)^3= – x^3 = f(x)$. - Из этого следует, что обратная функция кубической параболы, заданная уравнением $y = -x^3$ будет располагаться II и IV четвертях графика, тогда как для $y = x^3$ график располагается в I и III четвертях.
- График кубической параболы центрально-симметричен относительно начала координат или точки перегиба, если он сдвинут относительно начала координат. То есть форма кривой справа до точки перегиба полностью идентична форме кривой слева. График кубической параболы хотя бы 1 раз пересекает ось абсцисс.
- График кубической параболы возрастает на всей области определения.
Анализ графика функции кубической параболы
- Найдя производную $f'(x)$ кубической функции первого порядка и приравняв полученное выражение к нулю, вы получите критические точки для кубической параболы, называемые также локальными минимумами и максимумами.
- Вторая производная $f”(x)$ параболы определяет точку перегиба функции.
- Области значения и определения кубической параболы – все действительные числа.
Пример 1
Найдите точку перегиба для кубической параболы, заданной уравнением $y = 2x^3 + 6x^2 – x +2$.
- Сначала найдём первую производную функции, она равна: $y’ = 6x^2 + 12x – 1$.
- Теперь найдём вторую производную, $y” = 12x + 12$. Чтобы найти значение по оси абсцисс точки перегиба, приравняем вторую производную к нулю и решим уравнение: $12x + 12 = 0$, $x = -1$.
- Найдём значение по оси ординат, для этого в исходную функцию подставим значение найденного $x$: $y = -2 + 6 + 1 +2 = 7$. Точка перегиба кубической параболы, заданной уравнением $y = 2x^3 + 6x^2 – x +2$ находится по координатам $(-1; 7)$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 09.12.2022
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Задача о кубической функции (касательные, экстремум, …)
|
|
30/10/07 |
О кубической функции
Получил систему из 3-ёх уравнений: Решив её получил
|
|
|
|
|
Enne |
Re: Кубическая функция
|
|
08/02/08 |
|
|
|
|
|
Brukvalub |
|
||
01/03/06 |
KPEHgEJIb писал(а): Так как по условию это точка касания, то Для начала, странный у Вас дискриминант. Раньше его писали иначе. д
|
||
|
|
|||
|
незваный гость |
Re: Кубическая функция
|
||
17/10/05 |
KPEHgEJIb писал(а): Так как по условию это точка касания, то Этот вывод необоснован (или обоснован неправильно). KPEHgEJIb писал(а):
Зря!!! Это — теорема Ферма. KPEHgEJIb писал(а): А вот это откуда?! ~~~ При правильных вычислениях у Вас должно получиться два уравнения плюс условие, которое Вы пока не использовали. А именно, касательная с угловым — единственная.
|
||
|
|
|||
|
Алексей К. |
Re: Кубическая функция
|
|
29/09/06 |
KPEHgEJIb писал(а): Так как по условию это точка касания, то Вывод странный. Додумайте, детализируйте.
|
|
|
|
|
Azog |
|
|
29/01/07 |
1. В первом действии Вы двойку потеряли и с у вас непонятного происхождения.
|
|
|
|
|
KPEHgEJIb |
|
|
30/10/07 |
незваный гость , , только сильно не бейте. Я ошибся в записи функции, она выглядит так:
Д= KPEHgEJIb писал(а):
Зря!!! Это — теорема Ферма. KPEHgEJIb писал(а): А вот это откуда?!
Сам уже понял, что написал бред. , вы утверждаете что зря, а незваный гость говорит что это теорема Ферма
|
|
|
|
|
Azog |
|
|
29/01/07 |
дык, малая, а не большая.
|
|
|
|
|
KPEHgEJIb |
|
|
30/10/07 |
Azog , стоп, стоп. Гладкой функция – это ещё какая? Да я уверен в том что неправильно написал, потому что не имею представления ни о малой ни о большой
|
|
|
|
|
Azog |
|
|
29/01/07 |
Гладкая – то бишь дифференцируемая. Вы бы все таки матчасть почитали, а? Рекомендую Фихтенгольца для ознакомления.
|
|
|
|
|
Бодигрим |
|
||
22/11/06 |
KPEHgEJIb писал(а): Зря!!! Это — теорема Ферма. Сами-то поняли, что сказали? Что “ Теорем Ферма существует несколько. Есть среди них и такая, которая относится к матанализу. Цитата: У касательной только одна точка касания… Практически у любой касательной ровно одна точка касания. Может быть вы хотели сказать, что касательная с соответствующим угловым коэффициентом существует только в одной точке, а значит уравнение на Цитата: Но проверка не проходит А вы уверены, что верно разрешили записанную систему? По-моему, нет.
|
||
|
|
|||
|
KPEHgEJIb |
|
|
30/10/07 |
Azog , дело в том, что это задача из гос. экзамена (школьного) прошлого года. А у нас в программе нету ни Ферма, ни гладких функций, ни Фихтенгольца. То есть она должна решаться опираясь на более примитивные знания. Бодигрим писал(а): Может быть вы хотели сказать, что касательная с соответствующим угловым коэффициентом существует только в одной точке, а значит уравнение на Это я и хотел сказать
Систему утром тогда перерешаю. , Фихтенгольца.
|
|
|
|
|
Azog |
|
|
29/01/07 |
уважаемый, если у Вас в задаче есть производные, то ничего лучше чем прочитать соответствующий раздел в Фихтенгольце – я Вам предложить не могу.
|
|
|
|
|
незваный гость |
|
||
17/10/05 |
KPEHgEJIb писал(а): У касательной только одна точка касания Бодигрим писал(а): Практически у любой касательной ровно одна точка касания. Может быть вы хотели сказать, что касательная с соответствующим угловым коэффициентом существует только в одной точке, а значит уравнение на имеет ровно 1 корень? Это очень и очень важный момент! Обратите внимание на замечание Бодигрим а. KPEHgEJIb писал(а): Теорема Ферма ведь Я знаю по крайней мере три теоремы Ферма. Две из них в теории чисел, и одна в матане. Но я не верю своей памяти. Теорема Ферма говорит, что если функция дифференцируема в точке экстремума, то её производная в этой точке равна нулю. KPEHgEJIb писал(а): Azog , вы утверждаете что зря, а незваный гость говорит что это теорема Ферма Azog говорит, что Вы действительно зря сомневаетесь.
|
||
|
|
|||
|
bot |
|
||
21/12/05 |
KPEHgEJIb писал(а):
Это заподозрил сразу не дочитав до подтверждения. Исходя отсюда аккуратно учёл все условия и получилась система трёх уравнений – та же самая, что и в корневом сообщении. При решении этой системы получилось a=b=0, c=4, что заведомо не годится.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы


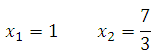

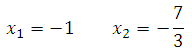
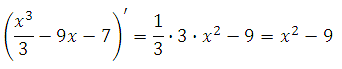
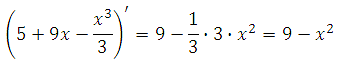


 известно, что среди касательных к её графику существует только единственная касательная, угловой коэффициент которой равен
известно, что среди касательных к её графику существует только единственная касательная, угловой коэффициент которой равен  , причём абсцисса точки касания
, причём абсцисса точки касания 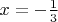 . Кроме этого известно, что данная кубическая функция имеет экстремум в точке
. Кроме этого известно, что данная кубическая функция имеет экстремум в точке  . Определите коэффициенты
. Определите коэффициенты  ,
,  и
и  .
. . Угловой коэффициент равен производной функции.
. Угловой коэффициент равен производной функции.


 .
.
 . Так как абсцисса точки касания
. Так как абсцисса точки касания 
 . Если в точке
. Если в точке  (вот в этом я не уверен).
(вот в этом я не уверен).
 ,
,  ,
,  . Но проверка не проходит
. Но проверка не проходит  . Поэтому производная получается
. Поэтому производная получается  .
.

 ?!
?! имеет ровно 1 корень?
имеет ровно 1 корень?