Как найти точку минимума под корнем

Сайты, меню, вход, новости

Здравствуйте! В этой статье речь пойдёт о задачах, которые можно решать без нахождения производной. В данной рубрике мы уже рассмотрели некоторые примеры с логарифмами, числом е, функции  с произведениями. Смысл заданий тот же –  требуется найти либо точку максимума (минимума) функции, либо определить максимальное (минимальное) значение функции. 

В чём суть и каков «стандартный» алгоритм решения — можно посмотреть в этой статье. Но не для всех заданий применение этого алгоритма будет рационально. Если следовать ему в представленных ниже примерах, то процесс решения будет «перегружен» вычислениями. А потеря времени на экзамене вам не нужна. Так какие же задания имеются ввиду?

В условии дана иррациональная, логарифмическая или показательная функция:

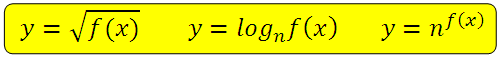
при чём под корнем, под знаком логарифма или в показателе находится квадратичная функция вида:

Рассмотрим подход без нахождения производной. Вы увидите, что такие задачи можно решать устно.

Что необходимо знать? Свойство параболы, напомним его:

Если а > 0, то её ветви направлены вверх.

Если а < 0, то её ветви направлены вниз.

Далее вспомним  координату  (абсциссу)  вершины параболы:

То есть, это точка экстремума квадратичной функции – в ней функция меняет своё поведение с возрастания на убывание или наоборот.

Следующий важный факт (ключевой для этих задач):

Если исходная функция монотонна (непрерывно возрастает или убывает), для нее указанная точка «х» также будет точкой экстремума.

Почему? Давайте рассмотрим отдельно функции подробнее.

Квадратичная функция в показателе степени (при чём n>1):

Смотрите! Представим, что ax²+bx+c=z. Можем записать:

Получается что значение z изменяется следующим образом.

Вариант когда a>0 (ветви параболы направлены вверх) – при х от минус бесконечности до –b/2a  z уменьшается, в точке –b/2a значение будет минимальным, далее при х от –b/2a  до бесконечности z увеличивается.

Это означает, что и сама функция у=n^f(x) будет имет минимальное значение в точке х=–b/2a, так как при минимуме в показателе получится минимум в результате.

Вариант когда a<0 (ветви параболы направлены вниз) – при х от минус бесконечности до  –b/2a  z увеличивается, в точке –b/2a значение будет максимальным, далее при х от –b/2a  до бесконечности z уменьшается.

Это означает, что и сама функция у=n^f(x) будет иметь максимальное значение в точке х=–b/2a, так как при максимуме в показателе получится максимум в результате.

Квадратичная функция под знаком логарифма (при чём n>1):

Представим, что ax²+bx+c=z. Можем записать:

Получается что значение z изменяется следующим образом:

Вариант когда a>0 (ветви параболы направлены вверх) –  при х от минус бесконечности до  –b/2a  z уменьшается, в точке –b/2a значение будет минимальным, далее при х от–b/2a  до бесконечности z увеличивается.

Это означает, что и сама функция log_nz будет имет минимальное значение в точке х=–b/2a. Так как логарифмическая функция уменьшается при уменьшении аргумента (видно по графику).

Вариант когда a<0 (ветви параболы направлены вниз) – при х от минус бесконечности до  –b/2a  z увеличивается, в точке –b/2a значение будет максимальным, далее при х от –b/2a  до бесконечности z уменьшается.

Это означает, что и сама функция log_nz будет имеет максимальное значение в точке х=–b/2a. Так как логарифмическая функция увеличивается при увеличении аргумента (видно по графику).

Квадратичная функция под знаком корня:

Представим, что ax²+bx+c=z. Можем записать:

Получается что:

При a>0 значение z минимально в точке х=–b/2a, а значит и сама функция будет иметь минимальное значение. *Корень из наименьшего значения в результате даст наименьшее число.

При a<0 значение z максимально в точке х=–b/2a, а значит и сама функция будет иметь максимальное значение.

Таким образом, сформулируем ключевое правило:

ВНИМАНИЕ! Конечно, если глубже уйти в тему, то возможны варианты когда сложная функция имеет отрицательный знак, когда логарифм находится в знаменателе дроби, когда основание логарифма или основание степени находится в пределах от 0 до 1. Разумеется,  важно понимать как ведёт себя данная в условии функция (возрастает или убывает). Но для решения типовых заданий экзамена указанного вывода вам будет вполне достаточно.

И конечно, не теряйте из виду область допустимых значений заданной функции:

— выражение стоящее под знаком корня, больше или равно нулю (число неотрицательное).

— выражение стоящее под знаком  логарифма, есть положительное число.

— выражение стоящее в знаменателе дроби не равно нулю.

В подобных задачах на нахождение наибольшего и наименьшего значения функции, я бы посоветовал находить область определения в любом случае (даже не смотря на то, что в представленных ниже примерах это ничего важного нам не даёт и не влияет на ответ).

Рассмотрим примеры:

Найдите точку максимума функции 

Под корнем  квадратичная функция  13+6х–х². Ее график — парабола, ветви направлены вниз, поскольку  а=–1<0. Значит максимальное значение  функция приобретает в точке:

Проверим чему равно подкоренное выражение при х=3 То есть будет ли оно числом неотрицательным:

13 + 6∙3 – 3² = 13 + 18 – 9 = 22 > 0 

Почему необходимо это сделать? Дело в том, что при полученной абсциссе квадратичная функция теоретически может дать отрицательное значение, то есть график такой параболы будет лежать ниже оси ох. Это  будет означать что решения (таких вариантов заданий на самом ЕГЭ не будет).

Ответ: 3

Решите самостоятельно:

Найдите точку максимума функции

Посмотреть решение

Найдите наименьшее значение функции

Под корнем  квадратичная функция   х² + 8х + 185.

Ее график — парабола,  ветви направлены вверх,  поскольку а =  1 > 0

Абсцисса вершины параболы:

Так как  ветви параболы направлены вверх, то в точке  х = – 4 функция

х² + 8х + 185 принимает наименьшее значение.

Функция кважратного корня монотонно возрастает, значит х = 4 точка минимума  всей функции, вычислим  её наименьшее  значение:

Ответ: 13

Решите самостоятельно:

Найдите наименьшее значение функции

Посмотреть решение

Найдите точку максимума функции у=log₇(–2 – 12х – х²) + 10. 

Под знаком логарифма квадратичная функция    –2 – 12х – х².

График — парабола, ветви направлены  вниз, так как а = – 1 < 0 

Абсцисса вершины параболы:

Проверим, принадлежит ли полученное значение х области определения (выражение под знаком логарифма должно быть число положительное):

– 2 – 12∙(–6) – (–6)² = – 2 + 72 – 36 = 34 > 0

То есть, в точке х = – 6

функция f (х) = – 2 – 12х – х²   будет иметь  максимальное значение.

Значит, и у=log₇(–2–12х–х²)+10  в этой точке так же будет иметь максимальное значение.

Ответ: – 6.

Решите самостоятельно:

Найдите точку максимума функции у=log₂(2 + 2х – х²) – 2

Посмотреть решение

Найдите наименьшее значение функции  у=log₉ (х² – 10х + 754) + 3

Под корнем  квадратичная функция   х² – 10х+754.

Ее график — парабола,  ветви направлены вверх,  поскольку а = 1 > 0

Абсцисса вершины параболы:

То есть, в точке х = 5 функция f (x) = х²  – 10х + 754 принимает наименьшее значение.  

Функция log₉х  монотонная, значит у =log₉ (х² – 10х + 754) + 3  в точке х = 5 также принимает наименьшее значение, вычислим его:

Ответ: 6

Решите самостоятельно:

Найдите наименьшее значение функции  у=log₃(х² – 6х + 10) + 2

Посмотреть решение

Найдите точку максимума функции 

В показателе стоит квадратичная функция   – 30 + 12х – х².     

График — парабола, ветви направлены  вниз, так как а = –1 < 0.

Абсцисса вершины параболы:

То есть, в точке х = 6 функция f (х) = – 30 + 12х – х² приобретёт максимальное значение. Значит и данная функция в этой точке будет иметь также максимальное значение.

Ответ: 6

Решите самостоятельно:

Найдите точку максимума функции: 

Посмотреть решение

Найдите наименьшее значение функции

В показателе стоит   квадратичная функция  х²  + 16х + 66.

Ее график — парабола,  ветви направлены вверх,  поскольку а = 1 > 0

Абсцисса вершины параболы:

То есть, в точке х = – 8 функция х²  + 16х + 66 принимает наименьшее значение.

Показательная  функция монотонна, поэтому её наименьшее значение будет также в точке х = – 8, вычислим его  

Ответ: 36

Решите самостоятельно:

Найдите наименьшее значение функции

Посмотреть решение

Разумеется,  что  это краткая схема решения и, конечно же, нужно понимать свойства квадратичной, показательной, логарифмической, дробно-рациональной функции,  но эта схема работает.

В данной рубрике мы ещё рассмотрим задания с тригонометрическими функциями, не пропустите! Успеха вам!

С уважением, Александр

P.S: Буду благодарен Вам, если расскажите о сайте в социальных сетях.

29 января 2012

Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.

В этом случае работают другие приемы, один из которых — монотонность.

Функция f (x) называется монотонно возрастающей на отрезке [a; b], если для любых точек x₁ и x₂ этого отрезка выполняется следующее:

x₁ < x₂ ⇒ f (x₁) < f (x₂).

Функция f (x) называется монотонно убывающей на отрезке [a; b], если для любых точек x₁ и x₂ этого отрезка выполняется следующее:

x₁ < x₂ ⇒ f (x₁) > f (x₂).

Другими словами, для возрастающей функции чем больше x, тем больше f (x). Для убывающей функции все наоборот: чем больше x, тем меньше f (x).

Например, логарифм монотонно возрастает, если основание a > 1, и монотонно убывает, если 0 < a < 1. Не забывайте про область допустимых значений логарифма: x > 0.

f (x) = log_a x (a > 0; a ≠ 1; x > 0)

Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:

Показательная функция ведет себя аналогично логарифму: растет при a > 1 и убывает при 0 < a < 1. Но в отличие от логарифма, показательная функция определена для всех чисел, а не только для x > 0:

f (x) = a ^x (a > 0)

Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.

Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, из-за которого становится тяжело считать производную. Что при этом происходит — сейчас разберем.

Координаты вершины параболы

Чаще всего аргумент функции заменяется на квадратный трехчлен вида y = ax² + bx + c. Его график — стандартная парабола, в которой нас интересуют:

1. Ветви параболы — могут уходить вверх (при a > 0) или вниз (a < 0). Задают направление, в котором функция может принимать бесконечные значения;
2. Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее (для a > 0) или наибольшее (a < 0) значение.

Наибольший интерес представляет именно вершина параболы, абсцисса которой рассчитывается по формуле:

Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее точка x₀ тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:

Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно искать x₀ для квадратного трехчлена, а на функцию — забить.

Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:

1. Отрезок [a; b] в условии задачи отсутствует. Следовательно, вычислять f (a) и f (b) не требуется. Остается рассмотреть лишь точки экстремума;
2. Но таких точек всего одна — это вершина параболы x₀, координаты которой вычисляются буквально устно и без всяких производных.

Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:

1. Выписать уравнение параболы y = ax² + bx + c и найти ее вершину по формуле: x₀ = −b/2a;
2. Найти значение исходной функции в этой точке: f (x₀). Если никаких дополнительных условий нет, это и будет ответом.

На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.

Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.

Задача. Найдите наименьшее значение функции:

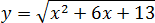
Под корнем стоит квадратичная функция y = x² + 6x + 13. График этой функции − парабола ветвями вверх, поскольку коэффициент a = 1 > 0.

Вершина параболы:

x₀ = −b/(2a) = −6/(2 · 1) = −6/2 = −3

Поскольку ветви параболы направлены вверх, в точке x₀ = −3 функция y = x² + 6x + 13 принимает наименьшее значение.

Корень монотонно возрастает, значит x₀ — точка минимума всей функции. Имеем:

Задача. Найдите наименьшее значение функции:

y = log ₂ (x² + 2x + 9)

Под логарифмом снова квадратичная функция: y = x² + 2x + 9. График — парабола ветвями вверх, т.к. a = 1 > 0.

Вершина параболы:

x₀ = −b/(2a) = −2/(2 · 1) = −2/2 = −1

Итак, в точке x₀ = −1 квадратичная функция принимает наименьшее значение. Но функция y = log ₂ x — монотонная, поэтому:

y_min = y(−1) = log ₂ ((−1)² + 2 · (−1) + 9) = … = log ₂ 8 = 3

Задача. Найдите наибольшее значение функции:

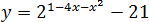
В показателе стоит квадратичная функция y = 1 − 4x − x². Перепишем ее в нормальном виде: y = −x² − 4x + 1.

Очевидно, что график этой функции — парабола, ветви вниз (a = −1 < 0). Поэтому вершина будет точкой максимума:

x₀ = −b/(2a) = −(−4)/(2 · (−1)) = 4/(−2) = −2

Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке x₀ = −2:

Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.

Следствия из области определения функции

Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка, а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:

1. Аргумент логарифма должен быть положительным:

   y = log_a f (x) ⇒ f (x) > 0

2. Арифметический квадратный корень существует только из неотрицательных чисел:

   

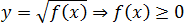
3. Знаменатель дроби не должен равняться нулю:

   

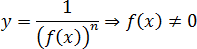
Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:

Задача. Найдите наибольшее значение функции:

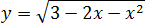
Под корнем снова квадратичная функция: y = 3 − 2x − x². Ее график — парабола, но ветви вниз, поскольку a = −1 < 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический квадратный корень из отрицательного числа не существует.

Выписываем область допустимых значений (ОДЗ):

3 − 2x − x² ≥ 0 ⇒ x² + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]

Теперь найдем вершину параболы:

x₀ = −b/(2a) = −(−2)/(2 · (−1)) = 2/(−2) = −1

Точка x₀ = −1 принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции в точке x₀, а также на концах ОДЗ:

y(−3) = y(1) = 0

Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.

Задача. Найдите наименьшее значение функции:

y = log _0,5 (6x − x² − 5)

Внутри логарифма стоит квадратичная функция y = 6x − x² − 5. Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:

6x − x² − 5 > 0 ⇒ x² − 6x + 5 < 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)

Обратите внимание: неравенство строгое, поэтому концы не принадлежат ОДЗ. Этим логарифм отличается от корня, где концы отрезка нас вполне устраивают.

Ищем вершину параболы:

x₀ = −b/(2a) = −6/(2 · (−1)) = −6/(−2) = 3

Вершина параболы подходит по ОДЗ: x₀ = 3 ∈ (1; 5). Но поскольку концы отрезка нас не интересуют, считаем значение функции только в точке x₀:

y_min = y(3) = log _0,5 (6 · 3 − 3² − 5) = log _0,5 (18 − 9 − 5) = log _0,5 4 = −2

Смотрите также:

1. Показательные функции в задаче B15: хитрости решения
2. Задача B15: работаем с показательной функцией без производной
3. Тест к уроку «Сложные выражения с дробями» (легкий)
4. Четырехугольная пирамида в задаче C2
5. Задача B5: площадь кольца
6. Решение задач на движение по воде