Как найти точку минимума показательной функции – Сайт, где вы сможете решить свои вопросы

28 апреля 2012

По определению, показательная функция — это выражение вида y = a^x, где a > 0. Но в задаче B15 встречаются только функции вида y = e^x. В крайнем случае, y = e^{kx + b}. Причина в том, что производные этих функций считаются очень легко:

(e^x)’ = e^x;
(e^{kx + b})’ = k · e^{kx + b}.

Как видите, если в показателе стоит просто переменная x, ничего не меняется. А если там будет линейное выражение вида kx + b, то спереди добавляется множитель k. Эта формула — частный случай производной сложной функции.

Задачи на вычисление наибольшего/наименьшего значения

Все задачи B15 с показательной функцией решаются по стандартной схеме — см. «Общая схема решения задач B15». Но если требуется найти наименьше/наибольшее значение функции, есть одна фишка:

Показатель должен быть равен нулю. Потому что e⁰ = 1 — нормальное число, его можно записать в ответ. В отличие от чисел e¹, e², которые вообще не представимы в виде десятичной дроби.

Данное замечание реально сокращает объем вычислений. Аналогичное правило есть у логарифмов — см. «Как считать логарифмы еще быстрее». И это вполне логично, поскольку логарифмы и показательные функции — родственные объекты.

А теперь разберем конкретные задачи.

Задача. Найдите наименьшее значение функции на отрезке [−1; 5]:

y = (x² − 5x + 5)e^{x − 3}

Сначала находим производную и раскладываем ее на множители:

y’ = ((x² − 5x + 5)e^{x − 3})’ = … = (x² − 3x)e^{x − 3} = x(x − 3)e^{x − 3}

Затем приравниваем полученное выражение к нулю и находим корни:

x(x − 3)e^{x − 3} = 0;
x₁ = 0; x₂ = 3.

Оба корня принадлежат отрезку [−1; 5]. Итого получаем четыре точки: два корня и два конца отрезка. Осталось вычислить значение функции в этих точках:

y(−1) = ((−1)² − 5 · (−1) + 5)e^{−1 − 3} = … = 11e⁻⁴;
y(0) = (0² − 5 · 0 + 5)e^{0 − 3} = … = 5e⁻³;
y(3) = (3² − 5 · 3 + 5)e^{3 − 3} = … = −1;
y(5) = (5² − 5 · 5 + 5)e^{5 − 3} = … = 5e².

Заметим, что из этих четырех чисел в бланк можно записать только y = −1. Кроме того, это единственное отрицательное число. Следовательно, это число и будет наименьшим.

Задача. Найдите наибольшее значение функции на отрезке [0; 6]:

y = (2x − 7)e^{8 − 2 · x}

Как и в прошлый раз, вычисляем производную функции и раскладываем ее на множители:

y’ = (y = (2x − 7)e^{8 − 2 · x})’ = … = (16 − 4x)e^{8 − 2 · x} = 4(4 − x)e^{8 − 2 · x}

Приравниваем производную к нулю и находим корни:

y’ = 0;
4(4 − x)e^{8 − 2 · x} = 0;
x = 4.

Корень x = 4 принадлежит отрезку [0; 6]. Мы ищем наибольшее значение, поэтому подставляем этот корень, а также концы отрезка в исходную функцию. Имеем:

y(0) = (2 · 0 − 7)e^{8 − 2 · 0} = … = −7e⁸;
y(4) = (2 · 4 − 7)e^{8 − 2 · 4} = … = 1;
y(6) = (2 · 6 − 7)e^{8 − 2 · 6} = … = 5e⁻⁴.

Итак, ответом может быть только число y = 1.

Задачи на вычисление точек максимума/минимума

В задачах на точки максимума/минимума нельзя применять приведенное выше правило, поэтому считаем все по стандартной схеме.

Задача. Найдите точку минимума функции:

y = (x − 12)e^{x − 11}

В первую очередь считаем производную:

y’ = (y = (x − 12)e^{x − 11})’ =
= (x − 12)’ · e^{x − 11} + (x − 12) · (e^{x − 11})’ =
= 1 · e^{x − 11} + (x − 12)e^{x − 11} =
= (1 + x − 12)e^{x − 11} =
= (x − 11)e^{x − 11}

Приравниваем производную к нулю:

y’ = 0;
(x − 11)e^{x − 11} = 0;
x − 11 = 0;
x = 11.

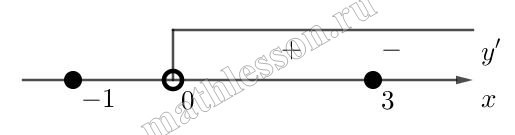
Множитель e^{x − 11} никогда не равен нулю, поэтому мы избавились от него. Осталось начертить координатную ось и расставить знаки производной:

Производная показательной функции

Итак, в точке x = 11 знак производной меняется с минуса на плюс. Считаем всегда в направлении оси — слева направо. Значит, x = 11 — это точка минимума.

Задача. Найдите точку максимума функции:

y = (2x² − 34x + 34)e^{6 − x}

Снова считаем производную:

y’ = ((2x² − 34x + 34)e^{6 − x})’ =
= (2x² − 34x + 34)’ · e^{6 − x} + (2x² − 34x + 34) · (e^{6 − x})’ =
= (4x − 34)e^{6 − x} + (2x² − 34x + 34) · (−1) · e^{6 − x}

Напомню, что производная сложной показательной функции считается по формуле:

(e^{kx + b})’ = k · e^{kx + b};
(e^{6 − x})’ = (−1) · e^{6 − x}.

Производная получилась довольно навороченная. Разложим ее на множители, для этого вынесем e^{6 − x} за скобку. Имеем:

(4x − 34)e^{6 − x} + (2x² − 34x + 34) · (−1) · e^{6 − x} =
= e^{6 − x} · (4x − 34 − 2x² + 34x − 34) =
= e^{6 − x} · (−2x² + 38x − 68)

Приравниваем полученное выражение к нулю:

e^{6 − x} · (−2x² + 38x − 68) = 0;
−2x² + 38x − 68 = 0;
x² − 19x + 34 = 0;
…
x₁ = 17; x₂ = 2.

Множитель e^{6 − x} снова можно безболезненно убрать, поскольку он никогда не равен нулю. Осталось отметить полученные точки и знаки производной на координатной прямой:

Производная: 2 корня

Обратите внимание: на рисунке отмечены знаки производной функции: y = e^{6 − x} · (−2x² + 38x − 68) — а вовсе не многочлена x² − 19x + 34, как думают некоторые ученики. В скобках стоит квадратичная функция, ее график — парабола ветвями вниз, поскольку a = −2 < 0.

В точке x = 17 знак производной меняется с плюса на минус. Значит, это точка максимума, что и требовалось найти.

Смотрите также:

Задача B15: частный случай при работе с квадратичной функцией
Специфика работы с логарифмами в задаче B15
Тест к уроку «Что такое числовая дробь» (легкий)
Типичные задачи B12 с функциями
Однородные тригонометрические уравнения: общая схема решения
ЕГЭ 2022, задание 6. Касательная и уравнение с параметром

Источник

Нахождение
точек минимума показательной функции.

Краткие
теоретические сведения

Определение. Точки,
в которых производная функции равна 0 или не существует называются критическими.

Среди этих точек могут быть точки максимума ( max ) и минимума ( min ), которые называются точками экстремума ( X_maxи X_min ). Значения функции в
этих точках называют экстремумами функции и обозначают f_max (X_max) и f_min (X_min).

Необходимым условием существования экстремумов является
равенство нулю производной или если производная не существует, то есть
необходимое условие – это наличие критических точек. (Это теорема Ферма), но
этого условия еще не достаточно. Чтобы функция имела экстремум в некоторой
точке, надо, чтобы при переходе через эту точку производная меняла свой знак,
то есть надо, чтобы возрастание менялось на убывание, или убывание на
возрастание. Если такой смены нет, то в этой критической точке не будет
экстремума.

Если
знак производной меняется с (+ ) на (- ) – это точка max, если знак производной меняется с (- )
на (+ ) – это точка min.

Вывод. Для существования
экстремумов необходимо выполнение двух условий:

1. Существование критических точек.

2. Смена знака производной при переходе через критическую точку.

Ответить на
вопросы.

1.
Что такое критические точки, как их
находят?

2.
Какие бывают точки экстремума?

3.
Что такое экстремумы функции?

4.
Какие существуют экстремумы функции?

5.
Что является необходимым условием
существования экстремума?

6.
Что является достаточным условием
существования экстремума?

7.
В каком случае функция будет иметь
максимум?

8.
В каком случае функция будет иметь
минимум?

Нахождение точек экстремумов функции осуществляют по следующему
плану:

1.
Найти
область определения функции.

2.
Найти
производную.

3.
Найти
критические точки ( приравнять производную к нулю).

4.
На
числовой прямой отметить найденные критические точки, выделить
полученные числовые промежутки и проверить знак производной в каждом из них.

5.
Записать,
где получились точки максимума или минимума, (а может быть и перегиба, если
знак производной не менялся при переходе через точку, или разрыва).

Самостоятельная
работа.

Вариант
1.

1.
Найдите точку минимума функции $y~=~(x+16){{e}^{x-16}}$ .

2.
Найдите точку минимума функции $y~=~(3-x){{e}^{3-x}}$ .

3.
Найдите точку минимума функции $y~=~(x^2-17x+17){{e}^{x-17}}$ .

4.
Найдите точку минимума функции $y~=~{{(x-2)}^{2}}{{e}^{x-5}}$ .

5.
Найдите точку минимума функции $y~=~{{(x+3)}^{2}}{{e}^{2-x}}$ .

6.
Найдите точку минимума функции $y~=~(3x^2-42x+42){{e}^{7-x}}$ .

7.
Найдите точку минимума функции $y=6^{x^2-8x+28}$ .

Вариант
2.

1. Найдите точку минимума функции $y~=~(x+18){{e}^{x-18}}$ .

2.
Найдите точку минимума функции $y~=~(25-x){{e}^{25-x}}$ .

3.
Найдите точку минимума функции $y~=~(3x^2-15x+15){{e}^{x-15}}$ .

4.
Найдите точку минимума функции $y~=~{{(x-7)}^{2}}{{e}^{x-4}}$ .

5.
Найдите точку минимума функции $y~=~{{(x+8)}^{2}}{{e}^{3-x}}$ .

6.
Найдите точку минимума функции $y~=~(2x^2-12x+12){{e}^{5-x}}$ .

7.
Найдите точку минимума функции $y=2^{x^2-26x+191}$ .

Вариант
3.

1.Найдите
точку минимума функции $y~=~(x+13){{e}^{x-13}}$ .

2.
Найдите точку минимума функции $y~=~(16-x){{e}^{16-x}}$ .

3.
Найдите точку минимума функции $y~=~(2x^2-24x+24){{e}^{x-24}}$ .

4.
Найдите точку минимума функции $y~=~{{(x-5)}^{2}}{{e}^{x-9}}$ .

5.
Найдите точку минимума функции $y~=~{{(x+6)}^{2}}{{e}^{2-x}}$ .

6.
Найдите точку минимума функции $y~=~(x^2-15x+15){{e}^{5-x}}$ .

7.
Найдите точку минимума функции $y=7^{x^2-30x+235}$ .

Вариант
4.

1.Найдите
точку минимума функции $y~=~(x+12){{e}^{x-12}}$ .

2.
Найдите точку минимума функции $y~=~(6-x){{e}^{6-x}}$ .

3.
Найдите точку минимума функции $y = (3x^2-24x+24){{e}^{x-17}}$ .

4.
Найдите точку минимума функции $y~=~{{(x-4)}^{2}}{{e}^{x-9}}$ .

5.
Найдите точку минимума функции $y~=~{{(x+12)}^{2}}{{e}^{2-x}}$ .

6.
Найдите точку минимума функции $y = (5x^2-40x+40){{e}^{2-x}}$ .

7.
Найдите точку минимума функции $y=5^{x^2-26x+176}$ .

Источник

28
Ноя 2013

Категория: 11 Исследование функции

2013-11-28
2021-09-24

Надеюсь, вы различаете понятия «точка минимума», «минимум», «наименьшее значение функции»… + показать

Задача 1. Найдите точку минимума функции $y=sqrt{x^2+20x+104}$ .

Решение: + показать

Задача 2. Найдите наименьшее значение функции $y=sqrt{x^2+8x+185}.$

Решение: + показать

Задача 3. Найдите точку максимума функции $y=8^{-30+12x-x^2}$ .

Решение: + показать

Задача 4. Найдите минимум функции .

Решение: + показать

Задача 5. Найдите наименьшее значение функции $y=5^{x^2-24x+148}$

Решение: + показать

Вы можете пройти тест (исследование функции без использования производной)

Автор: egeMax |

комментариев 28

Источник

Задание 942

Найдите наименьшее значение функции $$f(x)=(x^{2}-8x+8)*e^{2-x}$$ на отрезке [1; 7].

Ответ: -4

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Найдем производную функции: $$f^{‘}(x)=(2x-8)e^{2-x}+(-1)e^{2-x}(x^{2}-8x+8)=$$

$$=e^{2-x}(2x-8-x^{2}+8x-8)=e^{2-x}(-x^{2}+10x-16)$$

Приравняем производную к нулю:

$$e^{2-x}(-x^{2}+10x-16)=0$$ $$e^{2-x}=0$$

решений не имеет $$(-x^{2}+10x-16)=0$$ x₁=2 и x₂ =8

Отметим эти точки на координатной прямой и расставим знаки производной:

Точка минимума там, где производная меняет знак с – на +, то есть в точке 2

Подставим данное значение в первоначальную функцию и получим:

$$f(2)=(2^{2}-8*2+8)*e^{2-2}=(4-16+8)*1=-4$$

Задание 979

Найдите точку максимума функции $$f(x)=ln (x+5)-2x+9$$

Ответ: -4.5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Найдем производную функции и приравняем ее к нулю: $$f^{‘}(x)=frac{1}{x+5}-2=0Leftrightarrow frac{1-2x-10}{x+5}=0Leftrightarrow$$ $$ frac{-2x-9}{x+5}=0Leftrightarrow x=-4.5 ; xneq -5 $$ Отметим полученные точки на координатной прямой и расставим знаки производной. Получим, что точка -4,5 – точка максимума

Задание 1241

Найдите наибольшее значение функции $$f(x)=2^{x}(x+1)$$ , на отрезке [-1;2]

Ответ: 12

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Найдем производную этой функции и приравняем ее к нулю:

$$f'(x)=2^{x}ln 2(x+1)+2^{x}$$

$$2^{x}(ln 2(x+1)+1)=0$$

$$ln 2 * x+ ln 2 + 1 = 0$$

$$x = -1 – frac{1}{ln 2}$$

Данное значение меньше -1, значит точка экстремума левее нашего промежутка, а это означает, в свою очередь, что на заданном промежутке функция монотонна. Если мы подставим ноль в производную, то получим, что на промежутке, где расположен ноль, производная больше нуля, значит функция возрастает. Поэтому наибольшее значение функции будет в конце промежутка.

$$f(2)=2^{2}(2+1)=4*3=12$$

Задание 1295

Найдите точку минимума функции $$f(x) =x^{2}-3.75x- ln (x+2)$$

Ответ: 2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Найдем производную этой функции и приравняем к нулю:

$$f'(x) =2x-3.75- frac{1}{x+2}=0 $$

$$frac{2x^{2}+4x-3.75x-7.5-1}{x+2}=0$$

$$2x^{2}+0.25x-8.5=0 $$

$$x_{1}=frac{-34}{16}$$

$$x_{2}=2 $$

Начертим координатную прямую и посмотрим какие знаки принимает производная на полученных интервалах и получим, что точка 2 – точка минимума

Задание 2737

Найдите точку минимума функции: $$y=(73-x)cdot e^{73-x}$$

Ответ: 74

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y=(73-x)cdot e^{73-x}$$

$${y}’={(73-x)}’cdot e^{73-x}+(73-x){(e^{73-x})}’=$$ $$=- e^{73-x}+(73-x)cdot(-e^{73-x})=$$ $$-e^{73-x}(1+73-x)=0$$

$$x=74$$

Задание 2789

Найдите наибольшее значение функции $$y=10cdot ln(x+5)-10x-21$$ на отрезке [‐4,5; 0].

Ответ: 19

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$${y}’=frac{10}{x+5}-10=0$$ $$frac{10-10x-50}{x+5}=0$$ $$Leftrightarrow$$ $$frac{-10x-40}{x+5}=0$$ $$x=4$$ $$xneq -5$$ $$y=10cdot ln(-4+5)-10cdot(-4)-21=19$$

Задание 3117

Найдите точку максимума функции: $$y=(x^{2}-15x+15)cdot e^{x+3}$$

Ответ: 0

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y’=(2x-15)cdotexp^{x+3}+(x^{2}-15x+15)cdotexp^{x+3}=exp^{x+3}(x^{2}-13x)=0$$ $$x=0$$ $$x=13$$

Задание 3288

Найдите точку максимума функции $$y=0,5x^{2}-11x+28*ln x + 9$$

Ответ: 4

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y’=x-11+frac{28}{x}=0$$ $$frac{x^{2}-11x+28}{x}=0$$ $$x=7 ; x=4 ; xneq 0$$ Начертим координатную прямую и отметим полученные точки. На интервале от 0 до 4 производная имеет положительные значения, от 4 до 7 – отрицательные и от 7 до плюс бесконечности – положительные, значит: 7 – точка минимума 4 – точка максимума

Задание 3375

Найдите точку минимума функции $$f(x)=x^{8}cdot e^{5x+6}$$

Ответ: 0

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$f'(x)=(x^{8})’cdotexp^{5x+6}+x^{8}cdot(exp^{5x+6})’=$$ $$=8x^{7}cdotexp^{5x+6}+x^{8}cdotexp^{5x+6}cdot5=$$ $$=exp^{5x+6}cdot x^{7}cdot(8+5x)=0$$ $$x=0$$ или $$x=-frac{8}{5}=-1,6$$

Задание 5239

Найдите наименьшее значение функции $$y=(x^{2}-4x+4)cdot e^{2}$$ на отрезке $$[-1;3]$$

Ответ: 0

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Найдем производную данной функции и приравняем ее к нулю: $$y’=(2x-4)e^{x}+e^{x}*(x^{2}-4x+4)=0$$ $$e^{x}(2x-4+x^{2}-4x+4)=0$$ Число $$e^{x}$$ всегда положительно, поэтому можем его убрать: $$x^{2}-2x=0$$ Тогда $$x=0 ; x=2$$ Начертим координатную прямую, расставим знаки производной и получим, что $$x=2$$ – точка минимума, то есть в ней будет наименьшее значение функции на заданном в условии отрезке: $$y(2)=(2^{2}-4*2+4)e^{2}=0$$

Задание 5287

Найдите точку максимума функции $$y=(x-4)^{2}cdot e^{x}$$

Ответ: 2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Найдем производную этой функции и приравняем ее к нулю:

$$y’=((x-4)^{2})’e^{x}+(e^{x})'(x-4)^{2}=0$$

$$y’=2(x-4)e^{x}+e^{x}(x-4)^{2}=0$$

$$e^{x}(x-4)(2+x-4)=0$$

$$x=4 ; x=2$$

Начертим координатную прямую, отметим полученные точки и расставим знаки, которые принимает производная на полученных промежутках.

Тогда x=2 – точка максимума

Задание 6181

Найдите наименьшее значение функции $$y=log_{3} (x^{2}-6x+10)+2$$

Ответ: 2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y=log_{3}(x^{2}-6x+10)+2$$ Найдем минимальное значение функции; $$y_{min}$$ при $$x^{2}-6x+10rightarrow min$$ Минимальное значение квадратичная функция принимает в вершине параболы (ветви вверх): $$x_{0}=-frac{-6}{2}=3Rightarrow$$ $$y_{0}=9-6*3+10=1$$ Тогда минимальное значение функции: $$y_{min}=log_{3}(1)+2=2$$

Задание 6276

Найдите наибольшее значение функции $$y=sqrt{2lg x-1}-lg x$$

Ответ: 0

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$${y}’=frac{1}{2sqrt{2lg x-1}}*frac{2}{xln 10}-frac{1}{xln10}=0$$

$$frac{1}{xln 10}(frac{1}{2sqrt{2lg x-1}})=0$$

$$left{begin{matrix}xneq 0 \sqrt{2lg x-1}=1(1)end{matrix}right.$$

$$(1): sqrt{2lg x-1}=1Leftrightarrow$$ $$2lg x-1leq 1Leftrightarrow$$ $$2lg x=2Leftrightarrow$$ $$lg x=1Leftrightarrow x=10$$

$$y(10)=y=sqrt{2lg 10-1}-lg 10=1-1=0$$

Задание 6466

Найдите точку максимума функции $$y=6ln x – (x-2)^{2}$$

Ответ: 3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Так как дан логарифм, то будет ОДЗ: $$x>0$$

Найдем производную данной функции: $${y}’=frac{6}{x}-2(x-2)$$

Приравняем производную к нулю: $$frac{6-2x^{2}+4x}{x}=0$$

$$2x^{2}-4x+6=0Leftrightarrow$$$$x^{2}-2x+3=0Leftrightarrow$$$$(x-3)(x+1)=0$$

Тогда производная имеет вид: $${y}’=frac{-2(x-3)(x+1)}{x}$$. При этом, с учетом ОДЗ и знаков производной на полученных промежутках ((0;3) и $$(3;infty)$$) получим, что $$x(3)=x_{max}$$

Задание 6614

Найдите наибольшее значение функции $$y=frac{50}{2^{x}+3^{x}}$$ на промежутке [1;7]

Ответ: 1

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Функция $$f(x)=2^{x}$$ – возрастает, $$g(x)=3^{x}$$ – возрастает, тогда $$m(x)=2^{x}+3^{x}$$ – возрастает на всем промежутке, тогда $$y=frac{40}{2^{x}+3^{x}}$$ – убывает. Следовательно, $$y_{max}=y(1)=frac{40}{2+3}=8$$

Источник

1) Найдем производную функции (displaystyle f(x)=left(9-xright)e^{x+9}{small.})

(displaystyle f^{prime}(x)=left(left(9-xright)e^{x+9}right)^{prime}=-e^{x+9}+(9-x)e^{x+9}{small.})

Упростим выражение (displaystyle -e^{x+9}+(9-x)e^{x+9}{small.})

Вынесем (displaystyle e^{x+9}) за скобку, а затем приведем подобные слагаемые:

(displaystyle begin{aligned}-e^{x+9}+(9-x)e^{x+9}=left(-{color{red}{underline{underline{color{black}{1}}}}}+{color{red}{underline{underline{color{black}{9}}}}}-color{red}{underline{color{black}{x}}}right)e^{x+9}=left({color{red}{underline{underline{color{black}{8}}}}}-color{red}{underline{color{black}{x}}}right)e^{x+9}{small.}end{aligned})

Таким образом, получаем:

(displaystyle f^{prime}(x)=-e^{x+9}+(9-x)e^{x+9}=left(8-xright)e^{x+9}{small.})

2) Найдем точки, в которых (displaystyle f^{prime}(x)=0{small.})

Так как (displaystyle f^{prime}(x)=(8-x)e^{x+9}{small,}) то для этого необходимо решить уравнение (displaystyle (8-x)e^{x+9}=0{small.})

(displaystyle x=8) корень уравнения (displaystyle (8-x)e^{x+9}=0{small.})

3) Отметим корни производной на числовой прямой, а также определим ее знаки на получившихся интервалах.

на интервале (displaystyle color{green}{(-infty;,8)}) функция (displaystyle f^{prime}(x)>0{small,})
на интервале (displaystyle textcolor{blue}{(8;, +infty)}) функция (displaystyle f^{prime}(x)<0{small.})

Отмечая знаки производной на картинке, получаем:

4) Определим промежутки возрастания и убывания функции (displaystyle f(x)=left(9-xright)e^{x+9}{small ,}) пользуясь правилом.

Правило

Если для любой точки (displaystyle x_0in(a;,b)) производная (displaystyle f'(x_0)) существует и (displaystyle f'(x_0)>0{small,}) то

функция (displaystyle f(x)) возрастает (displaystyle nearrow) на всем интервале (displaystyle (a;,b){small.})

Если для любой точки (displaystyle x_0in(a;,b)) производная (displaystyle f'(x_0)) существует и (displaystyle f'(x_0)<0{small,}) то

функция (displaystyle f(x)) убывает (displaystyle searrow) на всем интервале (displaystyle (a;,b){small.})

Зная знаки производной (displaystyle f'(x){small,}) определим промежутки возрастания и убывания (displaystyle f(x){small:})

Схематически изобразим график (displaystyle f(x){small:})

Значит, (displaystyle x=8) – точка максимума функции (displaystyle f(x)=left(9-xright)e^{x+9}{small.})

Ответ: (displaystyle 8{small.})

Источник

Задачи на вычисление наибольшего/наименьшего значения

Задачи на вычисление точек максимума/минимума

Задание 942

Задание 979

Задание 1241

Задание 1295

Задание 2737

Задание 2789

Задание 3117

Задание 3288

Задание 3375

Задание 5239

Задание 5287

Задание 6181

Задание 6276

Задание 6466

Задание 6614

Вам также может понравиться

Как найти цепочку в море

Как составить формулу оксида кальция

Составить план социальные нормы как элемент социального контроля

Добавить комментарий Отменить ответ