Как найти точку на чертеже по координатам

Проецирование точки

Подробности

Категория: Основы начертательной геометрии

 

 ПРОЕЦИРОВАНИЕ ТОЧКИ НА ДВЕ ПЛОСКОСТИ ПРОЕКЦИЙ

Образование отрезка прямой линии АА₁   можно представить как результат перемещения точки А в какой-либо плоскости Н (рис. 84, а), а образование плоскости — как перемещение отрезка прямой линии АВ (рис. 84, б).

Точка — основной геометрический элемент линии и поверхности, поэтому изучение прямоугольного проецирования предмета начинается с построения прямоугольных проекций точки.

В пространство двугранного угла, образованного двумя перпендикулярными плоскостями — фронтальной (вертикальной) плоскостью проекций V и горизонтальной плоскостью проекций Н, поместим точку А (рис. 85, а).

Линия пересечения плоскостей проекций    — прямая, которая называется осью проекций и обозначается буквой    х.

Плоскость V здесь изображена в виде прямоугольника, а плоскость Н — в виде параллелограмма. Наклонную сторону этого параллелограмма обычно проводят под углом 45° к его горизонтальной стороне. Длина наклонной стороны берется равной 0,5 ее действительной длины.

Из точки А опускают перпендикуляры на плоскости V и Н. Точки а’и а пересечения перпендикуляров с плоскостями проекций V и Н являются прямоугольными проекциями точки А. Фигура Ааа_ха’ в пространстве — прямоугольник. Сторона аах этого прямоугольника на наглядном изображении уменьшается в 2 раза.

Совместим плоскости Н с плоскостью V ,вращая V вокруг линии пересечения плоскостей х. В результате получается комплексный чертеж точки А (рис. 85, б)

Для упрощения комплексного чертежа границы плоскостей проекций V и Н не указывают (рис. 85, в).

Перпендикуляры, проведенные из точки А к плоскостям проекций, называются проецирующими линиями, а основания этих проецирующих линий — точки а и а’ — называются проекциями точки А: а’ — фронтальная проекция точки А, а — горизонтальная проекция точки А.

Линия а’ а называется вертикальной линией проекционной связи.

Расположение проекции точки на комплексном чертеже зависит от положения этой точки в пространстве.

Если точка А лежит на горизонтальной плоскости проекций Н (рис. 86, а), то ее горизонтальная проекция а совпадает с заданной точкой, а фронтальная проекция а’ располагается на оси При расположении точки В на фронтальной плоскости проекций V ее фронтальная проекция совпадает с этой точкой , а горизонтальная проекция лежит на оси х. Горизонтальная и фронтальная проекции заданной точки С, лежащей на оси х, совпадают с этой точкой. Комплексный чертеж точек А, В и С показан на рис. 86, б.

ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ПЛОСКОСТИ ПРОЕКЦИЙ

В тех случаях, когда по двум проекциям нельзя представить себе форму предмета, его проецируют на три плоскости проекций. В этом случае вводится профильная плоскость проекций W, перпендикулярная плоскостям V и Н. Наглядное изображение системы из трех плоскостей проекций дано на рис. 87, а.

Ребра трехгранного угла (пересечение плоскостей проекций) называются осями проекций и обозначаются x, у и z. Пересечение осей проекций называется началом осей проекций и обозначается буквой О. Опустим из точки А перпендикуляр на плоскость проекций W и, отметив основание перпендикуляра буквой а”, получим профильную проекцию точки А.

Для получения комплексного чертежа точки А плоскости    Н и W совмещают с плоскостью V, вращая их вокруг осей Ох и Oz. Комплексный чертеж точки А показан на рис. 87, б и в.

Отрезки проецирующих линий от точки А до плоскостей проекций называются координатами точки А и обозначаются: х_А,    у_А и   z_A.

Например, координата z_A точки А, равная отрезку а’а_х (рис. 88, а и б), есть расстояние от точки А до горизонтальной плоскости проекций Н. Координата у точки А, равная отрезку аа_х, есть расстояние от точки А до фронтальной плоскости проекций V. Координата х_А, равная отрезку аа_у — расстояние от точки А до профильной плоскости проекций W.

Таким образом, расстояние между проекцией точки и осью проекции определяют координаты точки и являются ключом к чтению ее комплексного чертежа. По двум проекциям точки можно определить все три координаты точки.

Если заданы координаты точки А (например, х_А=20 мм,    у_А=22мм и z_A= 25 мм), то можно построить три проекции этой точки.

Для этого от начала координат О по направлению оси Oz откладывают вверх координату z_A и вниз координату у_А.Из концов отложенных отрезков — точек a_z и а_у (рис. 88, а) — проводят прямые, параллельные оси Ох, и на них откладывают отрезки, равные координате х_А. Полученные точки а’ и а — фронтальная и горизонтальная проекции точки    А.

По двум проекциям а’ и а точки А построить ее профильную проекцию можно тремя способами:

1)    из начала координат О проводят вспомогательную дугу радиусом Оа_у, равным координате    (рис. 87, б и в), из полученной точки а_у1 проводят прямую, параллельную оси Oz, и откладывают отрезок, равный z_A;

2)    из точки а_у проводят вспомогательную прямую под углом 45° к оси Оу (рис. 88, а), получают точку а_у1 и т. д.;

3)    из начала координат О проводят вспомогательную прямую под углом 45° к оси Оу (рис. 88, б), получают точку а_у1 и т. д.

Чертеж — важный конструкторский документ. Это проекционное изображения предмета. При создании чертежей в начертательной геометрии нужно следовать особым правилам. Все элементы должны находиться в строгой зависимости от положения в пространстве. Простым геометрическим образом пространства является точка. Что такое точки на чертеже? Как их использовать при создании чертежа? Разбираемся в нашем материале.

Что такое точка на чертеже?

Изображение предмета на чертеже состоит из двух или более геометрических фигур, только так можно передать форму изделия. В инженерной графике используются разные элементы графического языка. Одним из них является точка.

Точка — геометрический элемент, не имеющий размеров. Другими словами, все параметры точки равны нулю.

Чтобы изобразить изделие на чертеже, его необходимо перенести на плоскость. В построении любого изображения в инженерной графике применяется метод прямоугольного проецирования, который определяет расположение предмета на области за счет точек.

Проекция точки

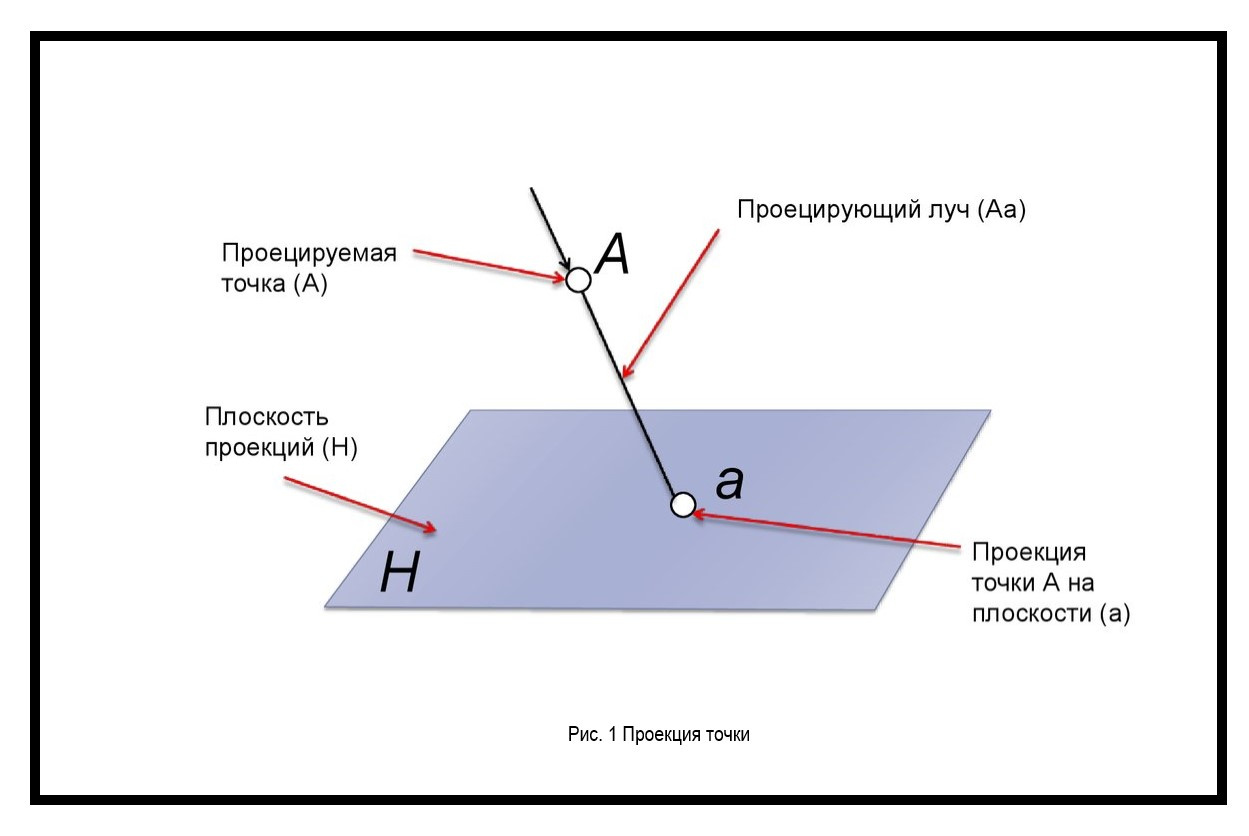
Проекция точки

Это точка пересечения прямой линии с плоскостью (рисунок 1).

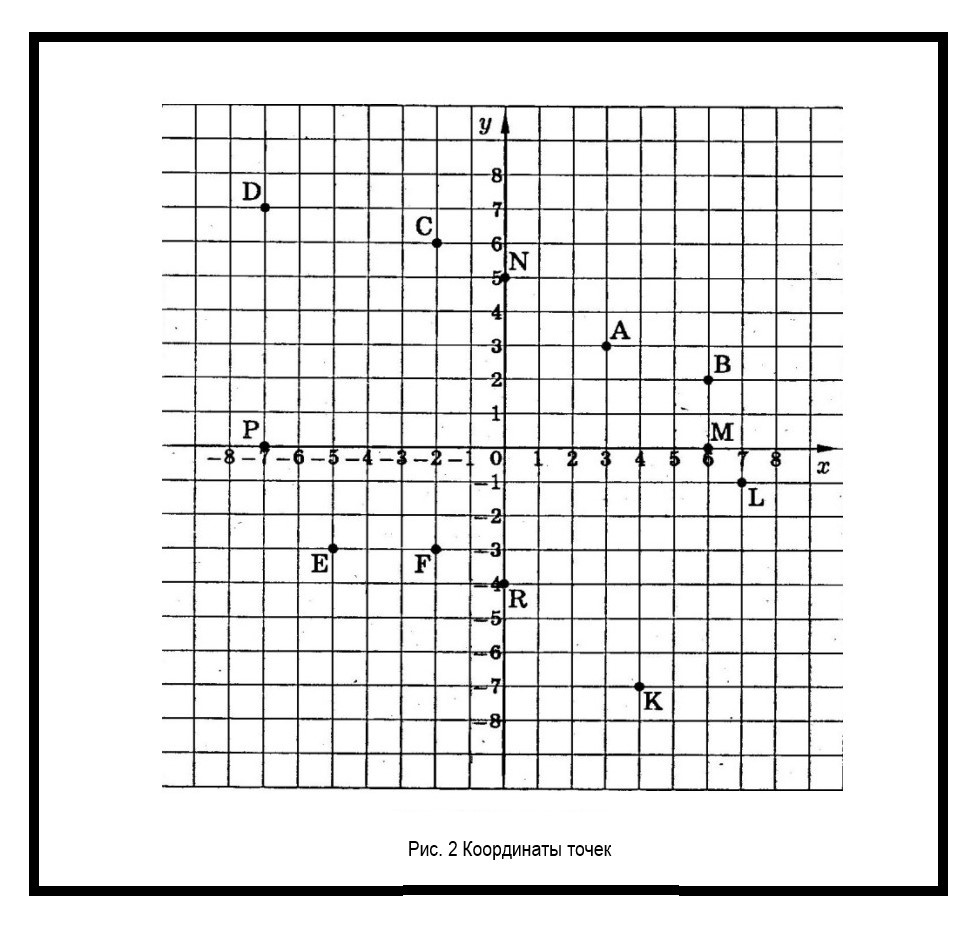
Проецируемая точка на плоскости обозначается как точка проекции. Это позволяет определить ее местоположение на плоскости. Каждая точка на чертеже имеет определенные координаты. Их используют для определения положения других элементов на комплексном чертеже (рисунок 2).

Как определить координаты по проекциям точки?

Для определения координат по проекциям точки используются две ортогональные проекции. Например, фронтальная и профильная. Они позволяют узнать конкретное значение координат точки, а также определить ее октант.

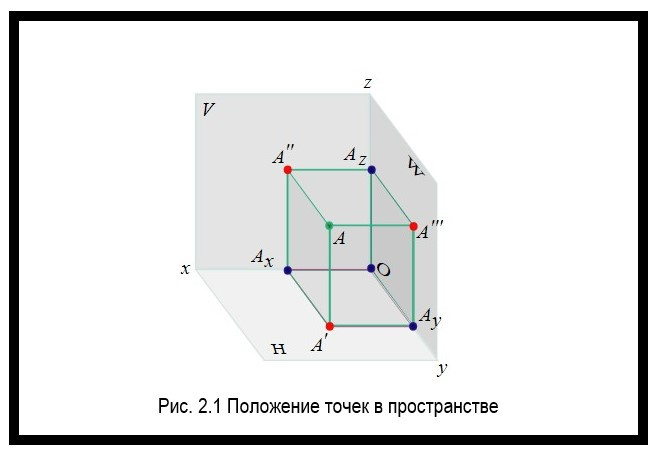
Как определить положение точки в пространстве?

Положение точки в пространстве определяется тремя координатами. Они показывают расстояние точки от плоскостей проекции. Пример представлен на рисунке рисунок 2.1.

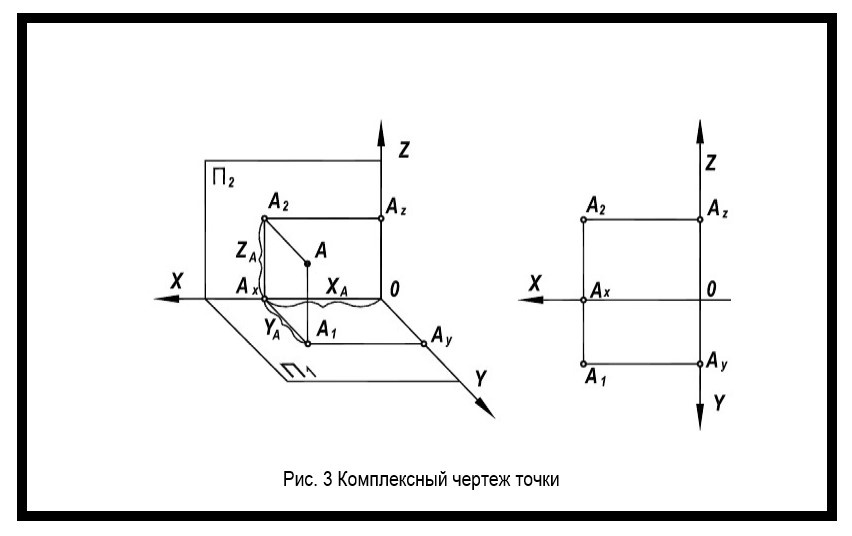
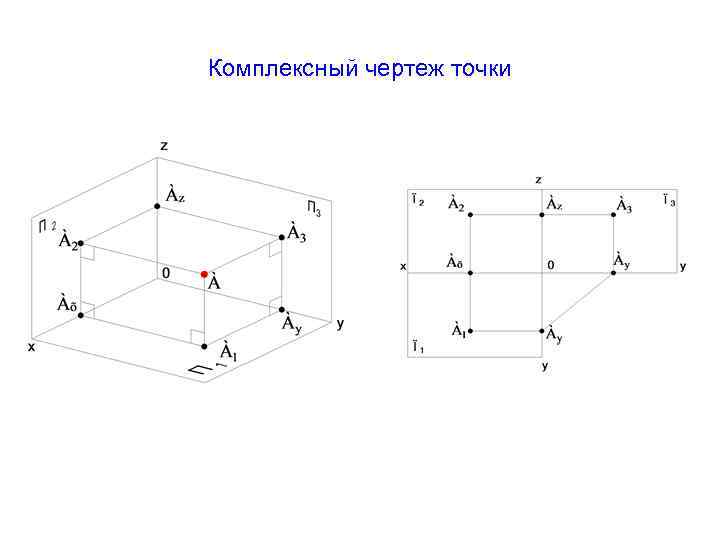
Комплексный чертеж точки

Чтобы изображение предмета было понятным, отражающим форму, размер и положение изделия в пространстве, необходимо использовать комплексный чертеж. Он представляет собой изображение предмета на совмещенных плоскостях проекции (рисунок 3).

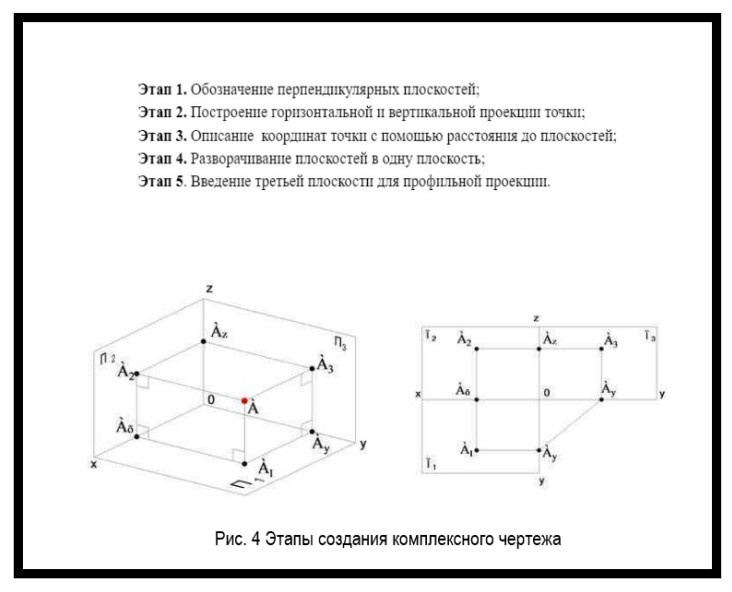
Построение комплексного чертежа состоит из нескольких этапов (рисунок 4).

Важно

На таких чертежах объемный предмет проецируется ортогонально на две взаимно перпендикулярные плоскости. Одна из них — вертикальная, другая — горизонтальная. Прямая пересечения этих плоскостей называется осью проекции

.

Изображение точки на комплексном чертеже

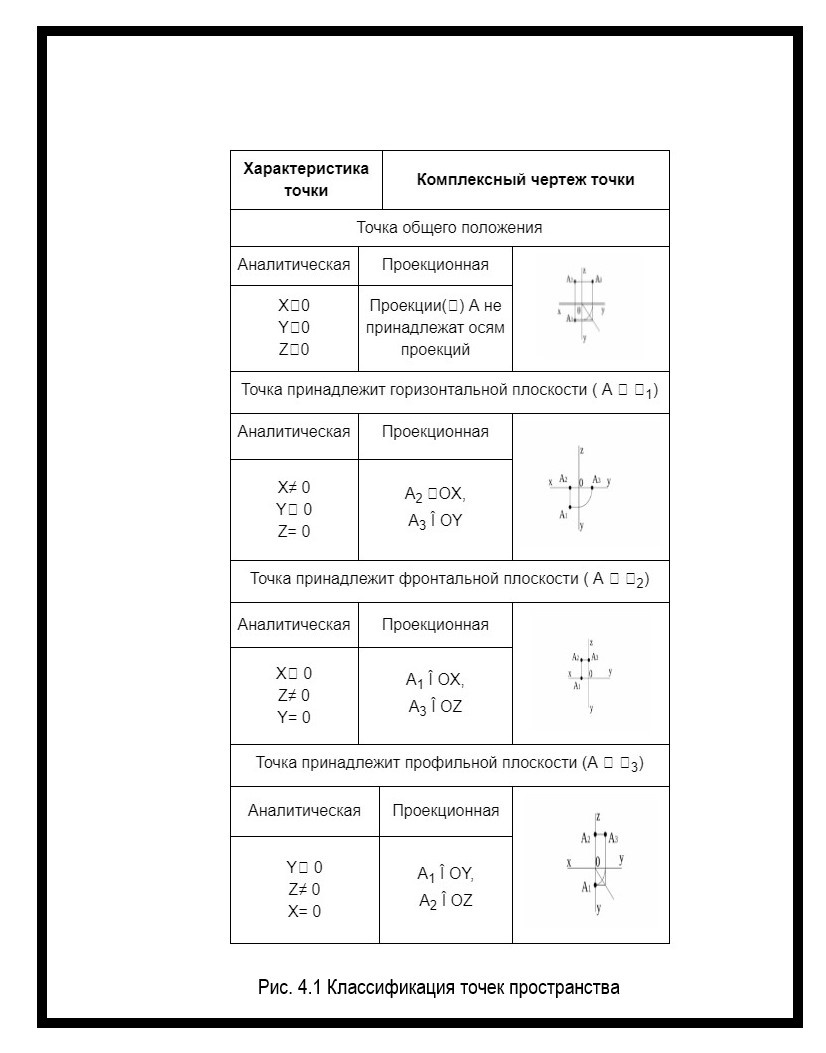
На комплексном чертеже точка — пара координат. Для изображения точки на чертеже нужно провести две перпендикулярные оси: горизонтальную и вертикальную ось. В зависимости от положения точки относительно плоскостей проекции, точки пространства могут быть нескольких видов (рисунок 4.1).

Обозначение точек на чертеже

Обозначение точек на чертеже осуществляется разными способами. Все параметры точек равны нулю, поэтому для их изображения используют условные обозначения (рис. 3.1).

Точка обозначаются буквами (например, точка A, B, C) или цифрами (например, точка 1, 2, 3). Кроме того, она может быть обозначена геометрическими символами кружочком или пересечением двух линий (рисунок 3).

Конкурирующие точки на чертеже

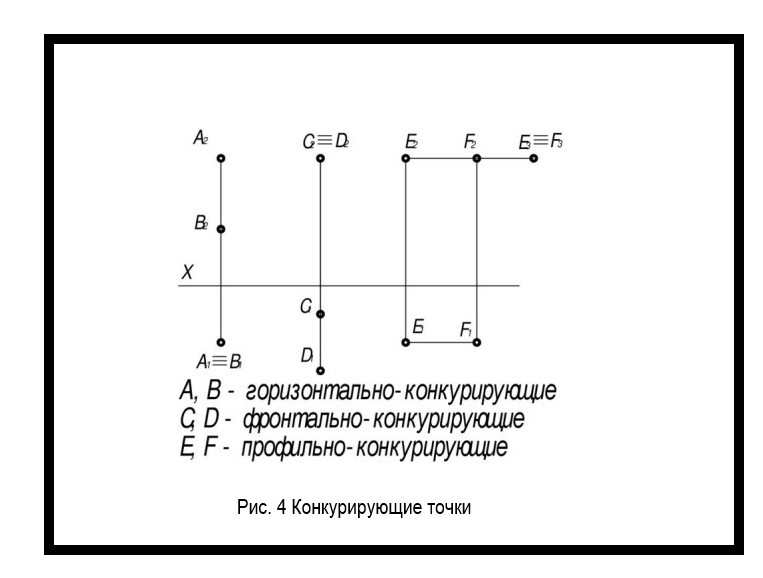
Точки на чертеже с двумя одинаковыми координатами называются конкурирующими (рисунок 4). Это точки, которые лежат на одном проецирующем луче.

Они могут быть нескольких видов, название которых определяет плоскость совпадающих проекций:

• Горизонтально конкурирующие — лежат на одном перпендикуляре к горизонтальной плоскости;
• Фронтально конкурирующие — лежат на одном луче к фронтальной плоскости;
• Профильно конкурирующие — лежат на одном перпендикуляре к профильной плоскости.

Видимые и невидимые конкурирующие точки на чертеже

Видимостью называют изображение близких к наблюдателю точек. Этот параметр помогает улучшить понимание геометрической формы и расположения предмета в пространстве.

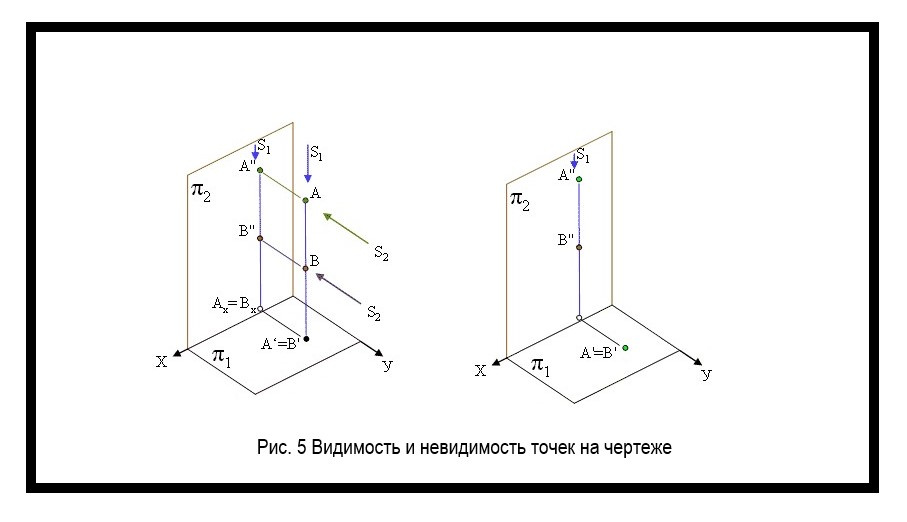
Для определения видимости, нужно найти точки предмета на одном луче и обозначить только те, которые расположены ближе к вам (рисунок 5). Без видимости определить положение объекта сложно.

Как обозначить видимость точек на чертеже

Видимость точек обозначается буквами (например, точка C”), невидимость — буквами с круглыми скобками (например, точка (С”)).

Типы точек на чертеже

Точки на чертеже по ГОСТу могут быть следующих типов:

Не хотите тратить время на чертежи? Вы можете заказать готовый чертеж у экспертов Студворк!

Точка – это геометрический абстрактный объект, который имеет координаты. Точки также участвуют в создании чертежа.

Комплексный чертеж и координаты точки

Комплексным называется чертеж, который был получен на фронтальной и горизонтальной плоскости проекции. Комплексный чертеж получается путем совмещения трех плоскостей проекций в одну.

Существует строгий порядок расположения проекций на чертеже, горизонтальная проекция должна располагаться под фронтальной, профильная проекция должна располагаться справа от фронтальной.

Как найти точки на чертеже

Рассматривая предмет как сочетание граней, вершин и ребер мы можем находить проекции отдельных точек. Для начала нужно определить, какой плоскости или грани точка принадлежит. Затем находят горизонтальные проекции точки, для этого проводят вертикальную прямую линию связи из проекции точек. Видимость проекций определяется исходя из направления взгляда.

Как правильно расставлять точки

Чтобы правильно вычертить вид детали, необходимо уметь строить проекции. С помощью проекций можно определить местоположение точки. Вспомогательные линии позволяют определить место, где ее можно поставить и используются в качестве опорных. Вспомогательные линии двух проекций пересекаются под углом в 45 градусов. В местах пересечения линий связи с проекциями поверхности расставляют точки.

Видимые и невидимые точки

Видимые проекции изображают на чертеже без скобок, а невидимые в скобках, например, А’’ относится к видимой проекции, а (B’’) к невидимой.

Точки сопряжения

В месте, где сопрягаются две линии образуется точка перехода или точка сопряжения. Для нахождения точки сопряжения линий прямого угла используется циркуль, его ставят в вершину угла и проводят дугу R до пересечения со сторонами. Чтобы найти центр сопряжения из найденных точек снова проводят окружности радиусом R, в месте их пересечения находится точка центра сопряжения, установив в нее циркуль проводят радиус сопряжения.

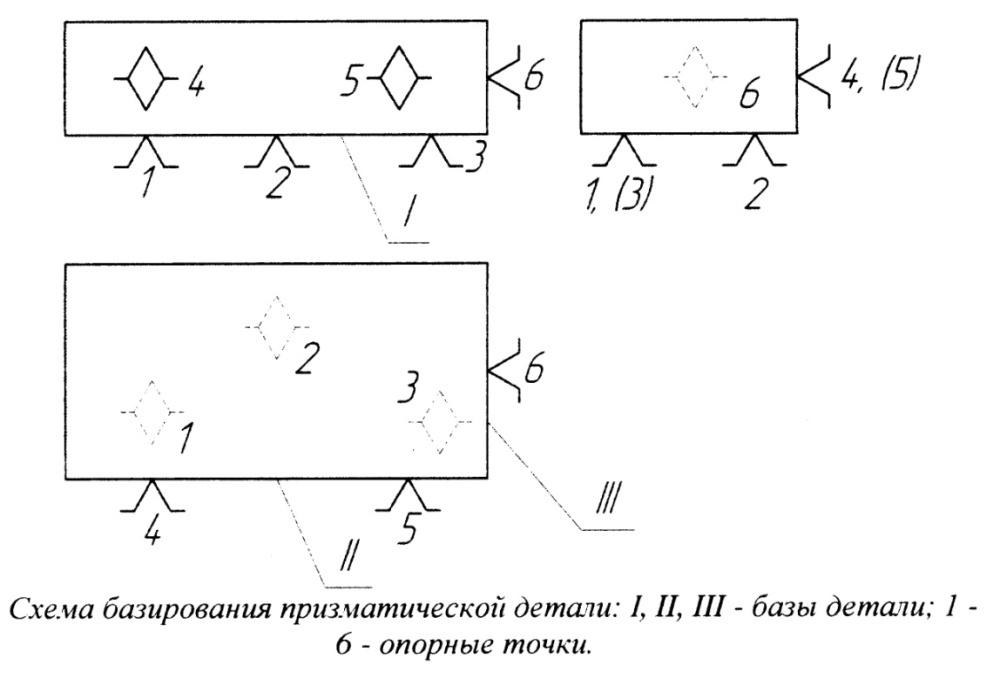
Опорные точки на чертеже

Опорные точки на схеме обозначают условными знакам согласно ГОСТ 21495-76, эти точки символизируют одну из связей заготовки иди изделия с выбранной системой координат. Нумерация опорных точек расставляется, начиная с базы, на которой расположено наибольшее число точек. Также опорные точки называют характерными, их число конечно, они выделяются своим особым положением относительно плоскости проекции и поверхности.

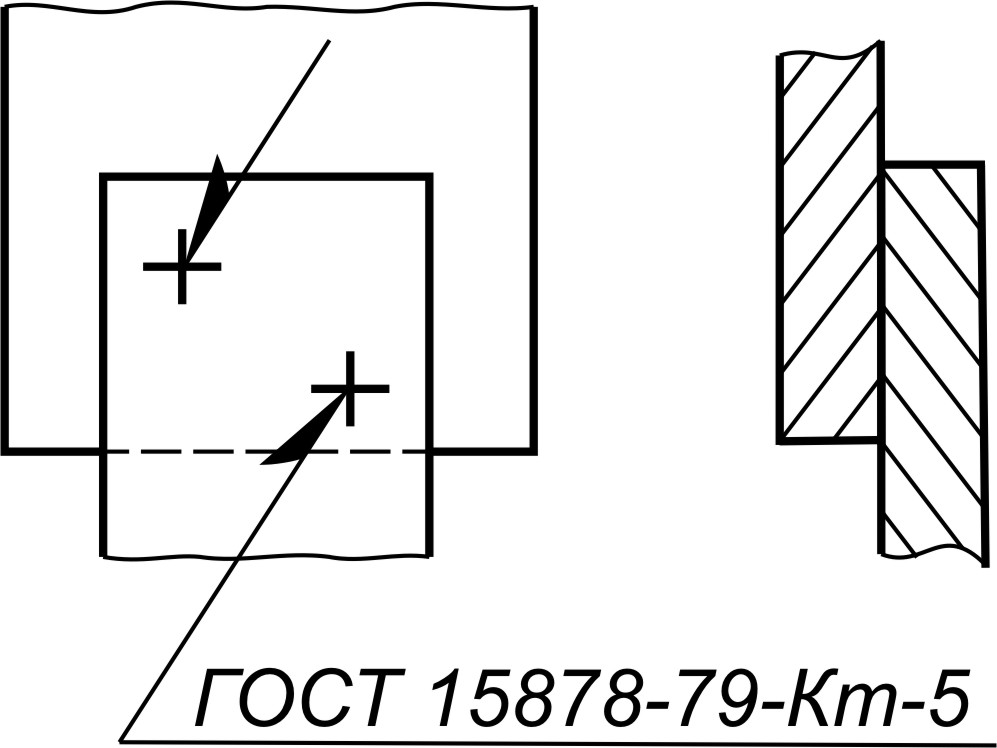
Сварные точки

Если детали соединяются сваркой, то ее также условно изображают на чертеже. В зависимости от расположения сварки можно увидеть шов или одиночную точку. Видимую одиночную точку обозначают знаком «+», невидимые одиночные точки на чертеже не обозначают. Видимый сварной шов обозначают основной сплошной линией, а невидимый штриховой линией.

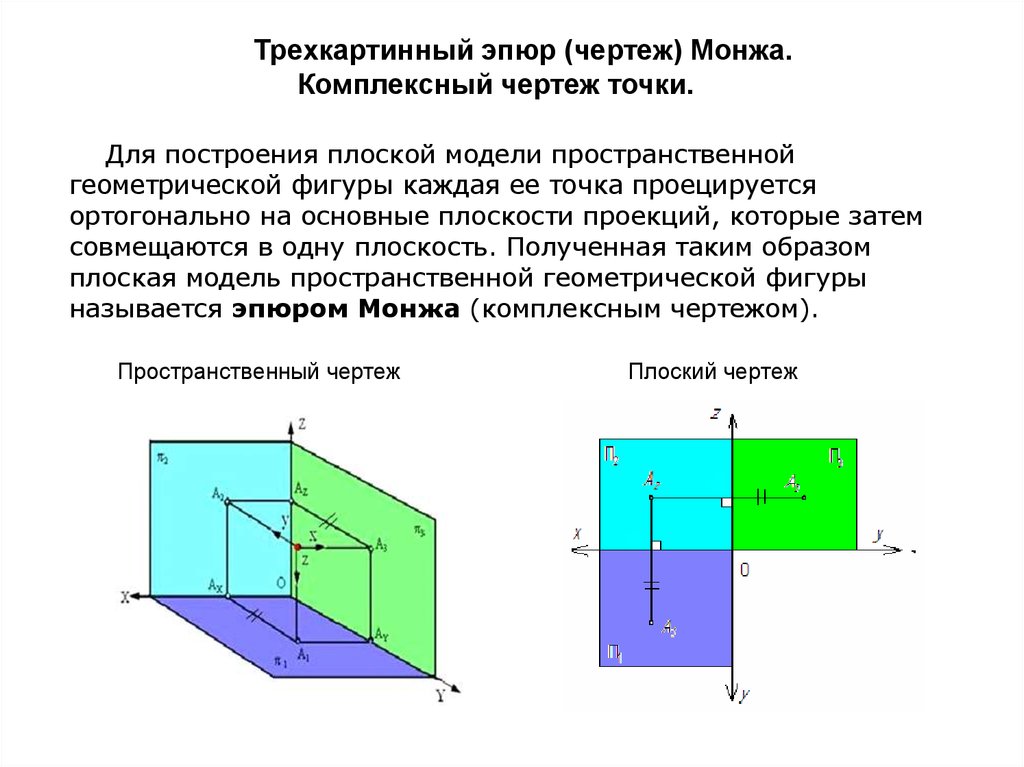
Трехкартинный чертеж точки

Трехкартинный чертеж или чертеж Монка представляет собой прямоугольник, сторонами которого являются линии связи, которые расположены перпендикулярно соответствующим осям проекции. При этом три вершины – проекции точки, а четвертая это точка перелома линии связи.

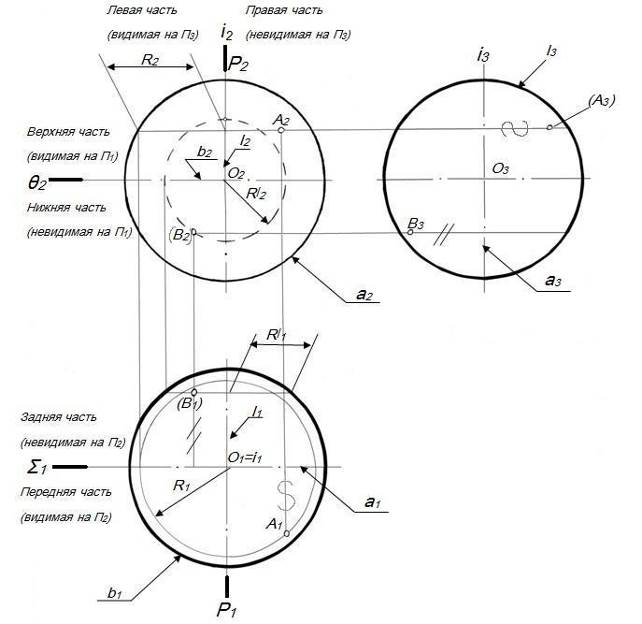
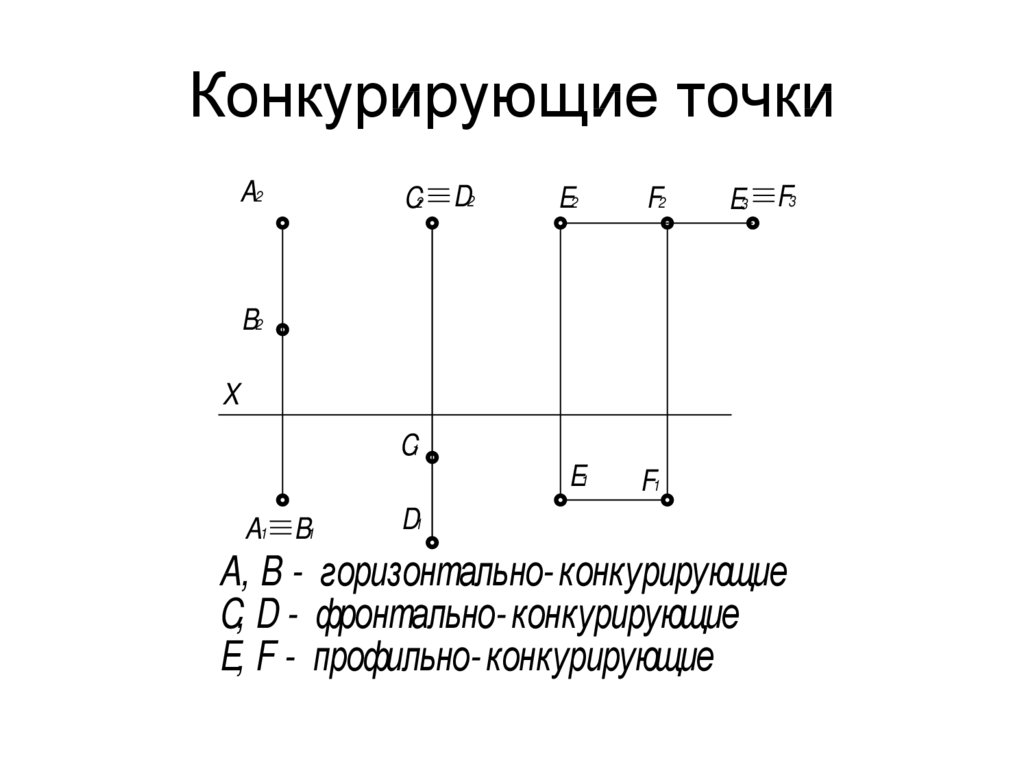
Конкурирующие точки на чертеже

Конкурирующие точки располагаются на одном проецирующем луче, таким образом для наблюдателя одна точка будет видимой, явной, а другая нет, что отразится и на чертеже.

Что такое явная точка на чертеже

Одним из важных понятий чертежа является база. Под базой понимается поверхность (точка, ось или сочетание поверхностей), принадлежащие заготовке, которая предназначена для придания изделию требуемого положения. Поверхность, используемая для базирования, может быть установочной ( лишает изделие возможностей перемещения), опорной (лишает одной степени свободы) или направляющей (лишает изделие или заготовку двух степеней свободы). По характеру базы могут быть скрытые и явные. Скрытые находятся в воображаемой плоскости или точке, а явные – в реальной поверхности или точке пересечения рисок.

Как построить комплексный чертеж точки: инструкция

Чтобы построить комплексный чертеж точки используется метод ортогональных или прямоугольных проекций, часто применяемый в инженерной графике. Проекция находится на пересечении проецирующего луча и плоскости.

Построение комплексного чертежа точки А состоит следующих этапов:

• возьмем две плоскости, которые перпендикулярны друг другу и назовем их П1 и П2;
• в результате пересечения проецирующих лучей, перпендикулярных каждой из плоскостей получаем горизонтальную и вертикальную проекцию точки А;
• координаты точки описываются с помощью расстояния до плоскостей;
• для построения плоского чертежа плоскость П1 разворачивают так, чтобы она совпадал с плоскостью П2, а прямая соединяющая А1 и А2 называется линией связи;
• третья плоскость вводится для построения профильной проекции.

Как поставить точку на чертеже в Компасе

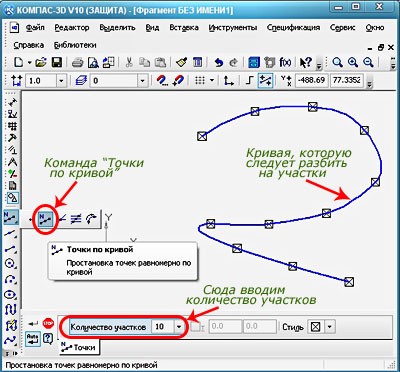
В меню программы Компас есть специальный инструмент «Точка», который позволяет сделать нужное действие за несколько шагов. Точку можно разместить, указав координаты, либо кликнув в месте рабочей области. Помимо основной функции команды, можно использовать расширенный список команд.

Как убрать точки на чертеже в Компасе

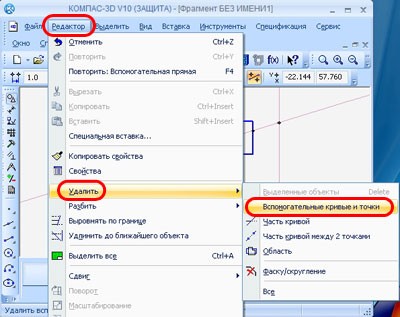
Убрать точки можно выделив их и нажав на клавишу «Delete», либо с помощью команды «Удалить вспомогательные кривые и точки».

Ответы на вопросы

Как правильно показать невидимую сварную точку?

Невидимые сварные точки не имеют обозначения, в отличие от швов.

Как на чертеже показать характерные точки отрезка?

Характерные точки зависят от объекта, у отрезка они находятся в начале и в конце прямой. Если какая-либо точка принадлежит прямой, то ее проекция принадлежит проекции прямой. При этом длина проекции отрезка прямой общего положения меньше длины самого отрезка.

Чем отличается двухкартинный чертеж точки от трехкартинного?

Разница состоит в количестве проекций на поверхности. В двухкартинном чертеже используются горизонтальная и фронтальная плоскости, такой чертеж вполне позволяет описать форму и размеры фигуры. В трехкартинном чертеже используется еще и третья плоскость.

Построение ортогональных проекций точек

Положение точки в пространстве может быть задано двумя её ортогональными проекциями, например, горизонтальной и фронтальной, фронтальной и профильной. Сочетание любых двух ортогональных проекций позволяет узнать значение всех координат точки, построить третью проекцию, определить октант, в котором она находится. Рассмотрим несколько типичных задач из курса начертательной геометрии.

По заданному комплексному чертежу точек A и B необходимо:

1. Записать их координаты.
2. Достроить проекции т. A и B на плоскость П₃.
3. Определить положение точек в пространстве (октант или плоскость проекций).
4. Построить наглядное изображение точек в системе плоскостей П₁, П₂, П₃.

Определение координат точек по их проекциям

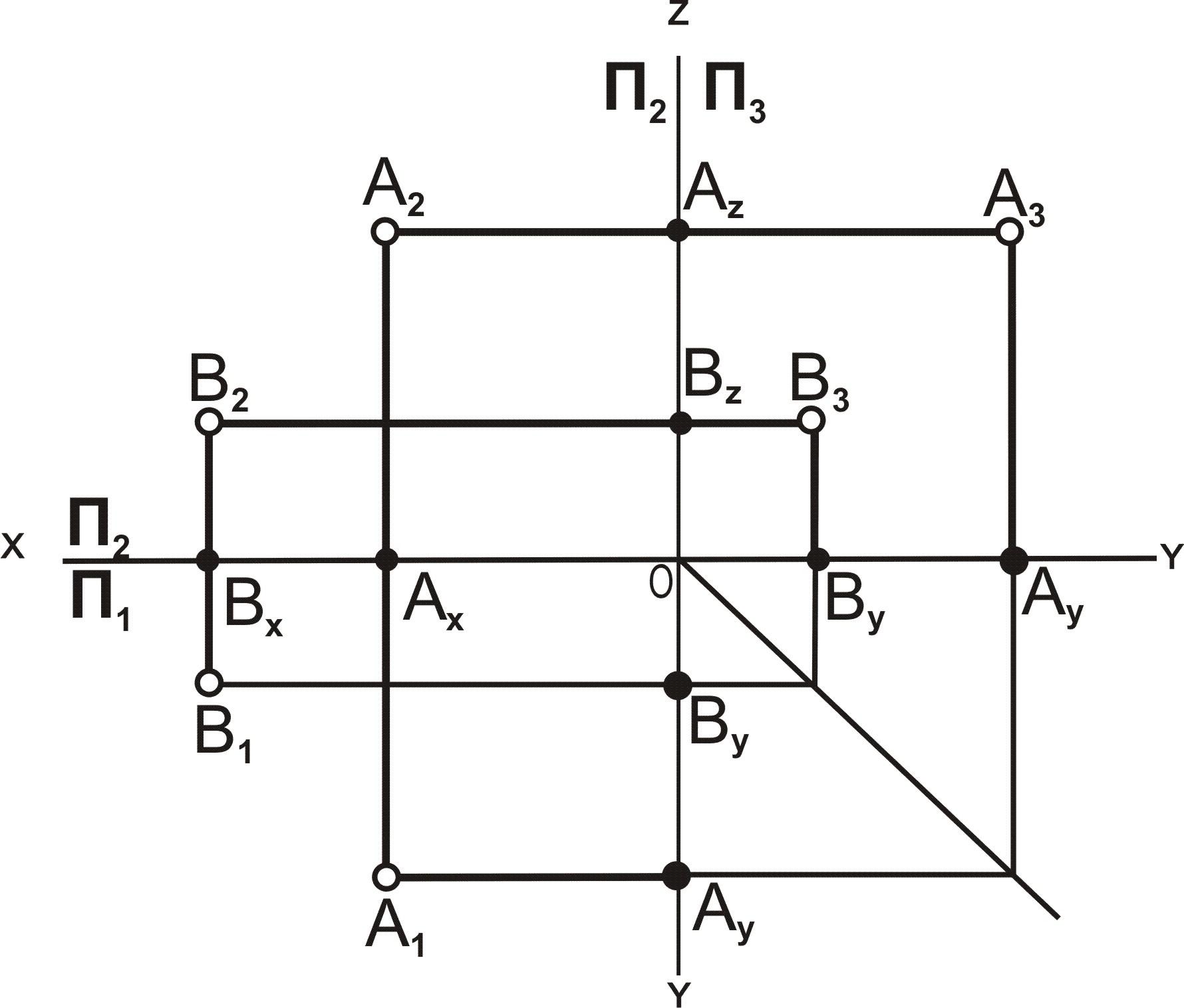
Определим сначала координаты т. A, которые можно записать в виде A (x, y, z). Горизонтальная проекция т. A – точка A’, имеющая координаты x, y. Проведем из т. A’ перпендикуляры к осям x, y и найдем соответственно A_х, A_у. Координата х для т. A равна длине отрезка A_хO со знаком плюс, так как A_х лежит в области положительных значений оси х. С учетом масштаба чертежа находим х = 10. Координата у равна длине отрезка A_уO со знаком минус, так как т. A_у лежит в области отрицательных значений оси у. С учетом масштаба чертежа у = –30. Фронтальная проекция т. A – т. A” имеет координаты х и z. Опустим перпендикуляр из A” на ось z и найдем A_z. Координата z точки A равна длине отрезка A_zO со знаком минус, так как A_z лежит в области отрицательных значений оси z. С учетом масштаба чертежа z = –10. Таким образом, координаты т. A (10, –30, –10).

Координаты т. B можно записать в виде B (x, y, z). Рассмотрим горизонтальную проекцию точки B –  т. В’. Так как она лежит на оси х, то B_x = B’ и координата B_у = 0. Абсцисса x точки B равна длине отрезка B_хO со знаком плюс. С учетом масштаба чертежа x = 30. Фронтальная проекция точки B – т. B˝ имеет координаты х, z. Проведем перпендикуляр из B” к оси z, таким образом найдем B_z. Аппликата z точки B равна длине отрезка B_zO со знаком минус, так как B_z лежит в области отрицательных значений оси z. С учетом масштаба чертежа определим значение z = –20. Таким образом, координаты B (30, 0, -20). Все необходимые построения представлены на рисунке ниже.

Построение проекций точек

Точки A и B в плоскости П₃ имеют следующие координаты: A”’ (y, z); B”’ (y, z). При этом A” и A”’ лежат одном перпендикуляре к оси z, так как координата z у них общая. Точно также на общем перпендикуляре к оси z лежат B” и B”’. Чтобы найти профильную проекцию т. A, отложим по оси у значение соответствующей координаты, найденное ранее. На рисунке это сделано с помощью дуги окружности радиуса A_уO. После этого проведем перпендикуляр из A_у до пересечения с перпендикуляром, восстановленным из точки A” к оси z. Точка пересечения этих двух перпендикуляров определяет положение A”’.

Точка B”’ лежит на оси z, так как ордината y этой точки равна нулю. Для нахождения профильной проекции т. B в данной задаче необходимо лишь провести перпендикуляр из B” к оси z. Точка пересечении этого перпендикуляра с осью z есть B”’.

Определение положения точек в пространстве

Наглядно представляя себе пространственный макет, составленный из плоскостей проекций П₁, П₂ и П₃, расположение октантов, а также порядок трансформации макета в эпюр, можно непосредственно определить, что т. A расположена в III октанте, а т. B лежит в плоскости П₂.

Другим вариантом решения данной задачи является метод исключений. Например, координаты точки A (10, -30, -10). Положительная абсцисса x позволяет судить о том, что точка расположена в первых четырех октантах. Отрицательная ордината y говорит о том, что точка находится во втором или третьем октантах. Наконец, отрицательная аппликата z указывает на то, что т. A расположена в третьем октанте. Приведенные рассуждения наглядно иллюстрирует следующая таблица.

Октанты	Знаки координат
x	y	z
1	+	+	+
2	+	–	+
3	+	–	–
4	+	+	–
5	–	+	+
6	–	–	+
7	–	–	–
8	–	+	–

Координаты точки B (30, 0, -20). Поскольку ордината т. B равна нулю, эта точка расположена в плоскости проекций П₂. Положительная абсцисса и отрицательная аппликата т. B указывают на то, что она расположена на границе третьего и четвертого октантов.

Построение наглядного изображения точек в системе плоскостей П₁, П₂, П₃

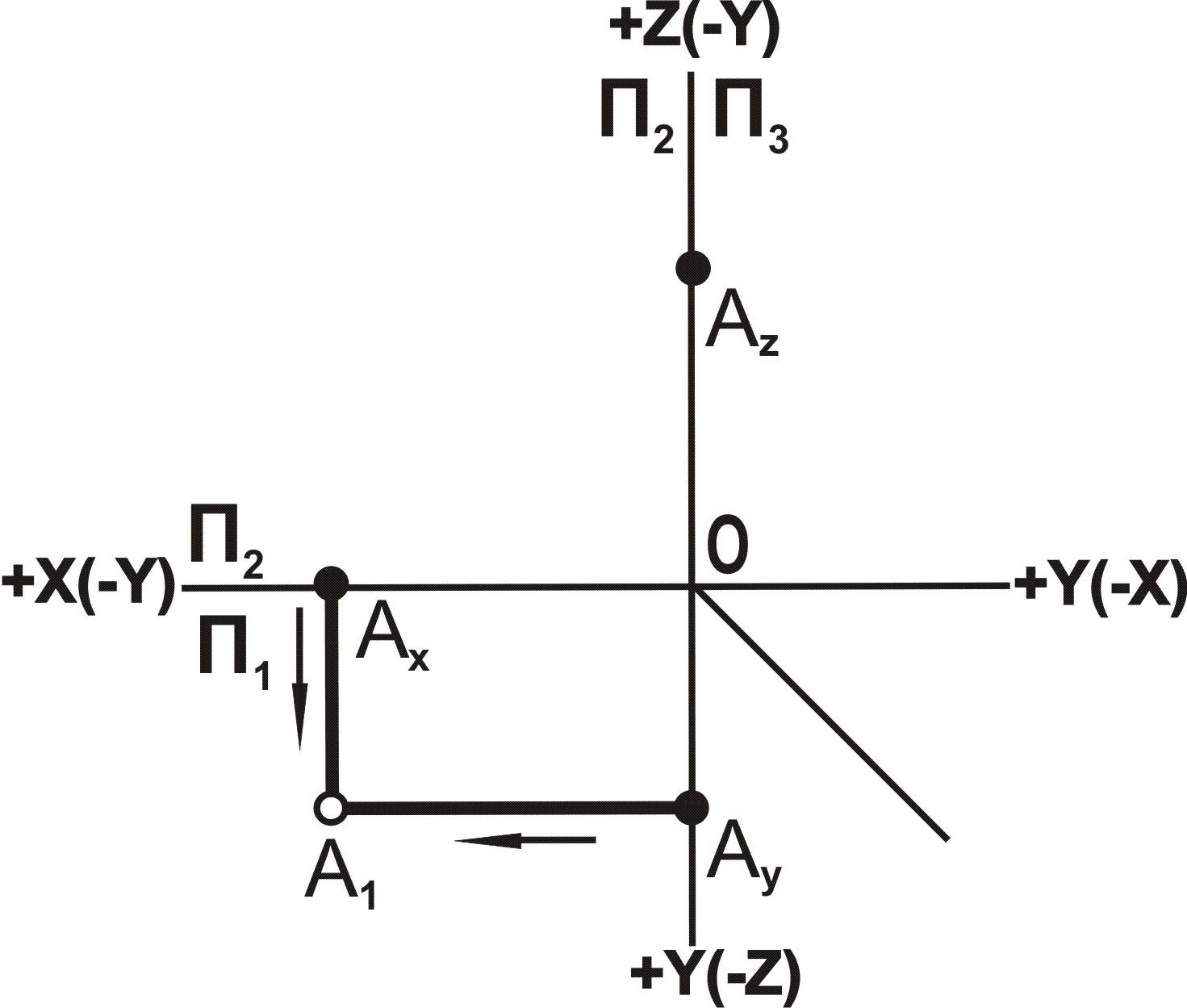
Используя фронтальную изометрическую проекцию, мы построили пространственный макет III октанта. Он представляет собой прямоугольный трехгранник, у которого гранями являются плоскости П₁, П₂, П₃, а угол (-y0x) равен 45 º. В этой системе отрезки по осям x, y, z будут откладываться в натуральную величину без искажений.

Построение наглядного изображения т. A (10, -30, -10) начнем с её горизонтальной проекции A’. Отложив по оси абсцисс и ординат соответствующие координаты, найдем точки A_х и A_у. Пересечение перпендикуляров, восстановленных из A_х и A_у  соответственно к осям x и y определяет положение т. A’. Отложив от A’ параллельно оси z в сторону её отрицательных значений отрезок AA’, длина которого равна 10, находим положение точки A.

Наглядное изображение т. B (30, 0, -20) строится аналогично – в плоскости П₂ по осям x и z нужно отложить соответствующие координаты. Пересечение перпендикуляров, восстановленных из B_х и B_z, определит положение точки B.

Алгоритм построения комплексного чертежа точки по координатам

Словесная форма	Графическая форма
1. Отложить на осях X, Y, Ζ соответствующие координаты точки А. Получаем точки Ax, Ay, Az
2. Горизонтальная проекция А1 находится на пересечении линий связи из точек Ax и Ay, проведенных параллельно осям X и Y
3. Фронтальная проекция А2 находится на пересечении линий связи из точек Ax и Az, проведенных параллельно осям X и Ζ
4. Профильная проекция А3 находится на пересечении линий связи из точек Az и Ay, проведенных параллельно осям Ζ и Y

3.2. Положение точки относительно плоскостей проекций

Положение точки в пространстве
относительно плоскостей проекций
определяется её координатами. Координатой
Х определяется удалённость точки от
плоскости П₃(проекция на П₂или П₁), координатой
У – удалённость
от плоскости П₂(проекция на П₃или П₁), координатой
Z – удаленность
от плоскости П₁(проекция на П₃или П₂). В зависимости от значения
этих координат точка может занимать в
пространстве как общее, так и частное
положение по отношению к плоскостям
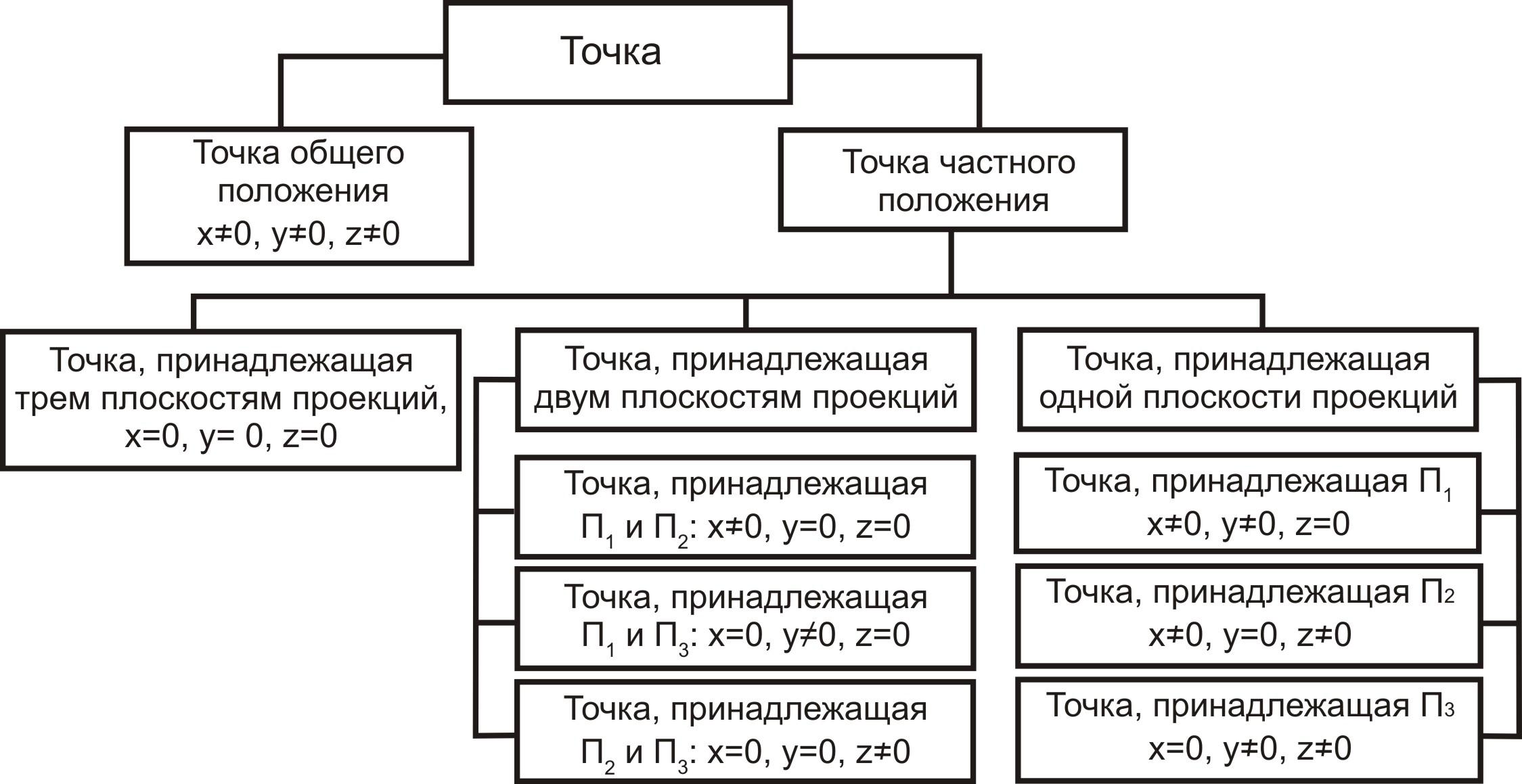
проекций (рис. 3.1).

Рис.
3.1. Классификация точек

Точка
общего
положения.
Координаты
точки общего положения не равны нулю
(x≠0,y≠0,z≠0),
и в зависимости от знака координаты
точка может располагаться в одном из
восьми октантов (табл.
2.1).

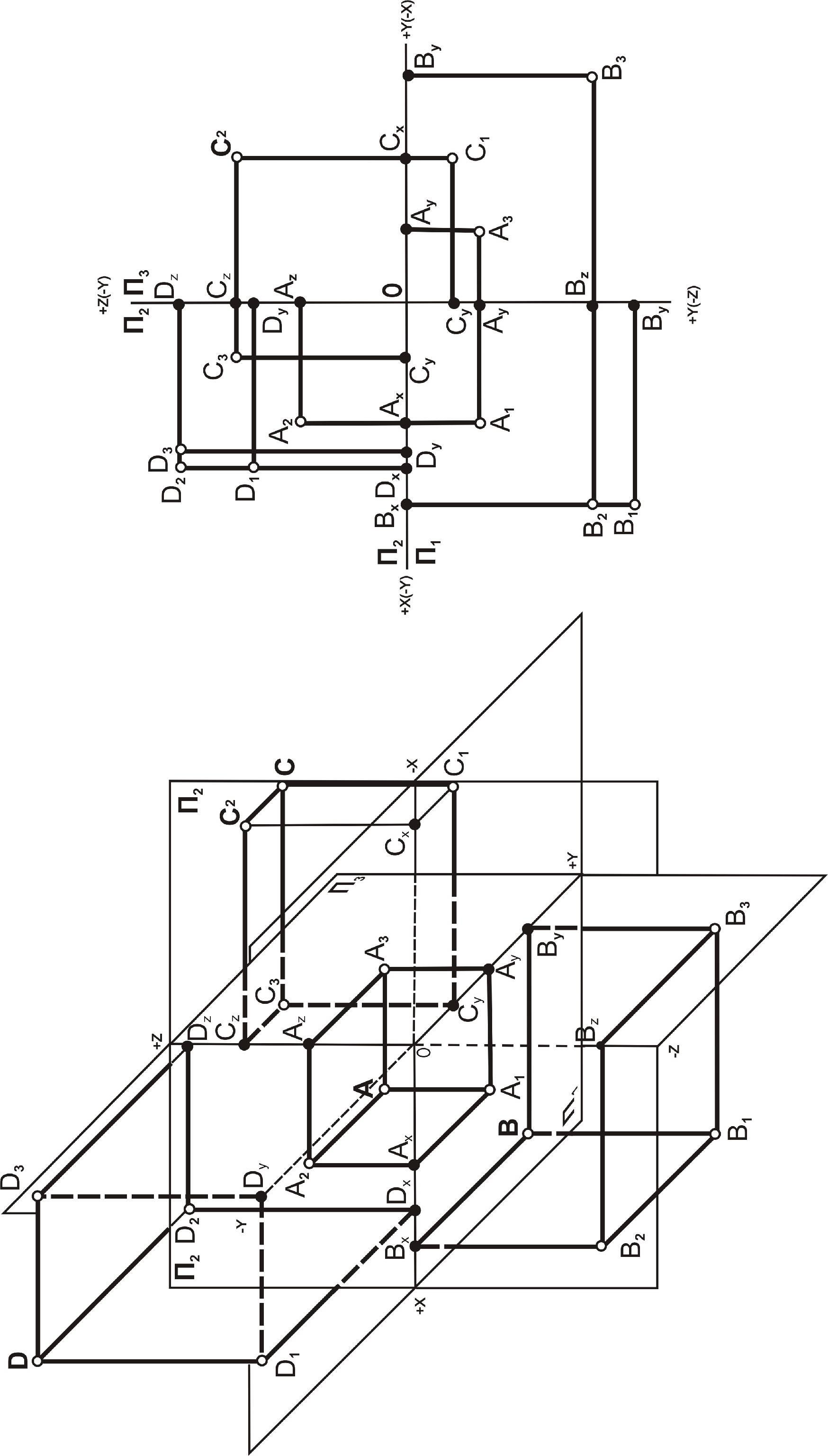
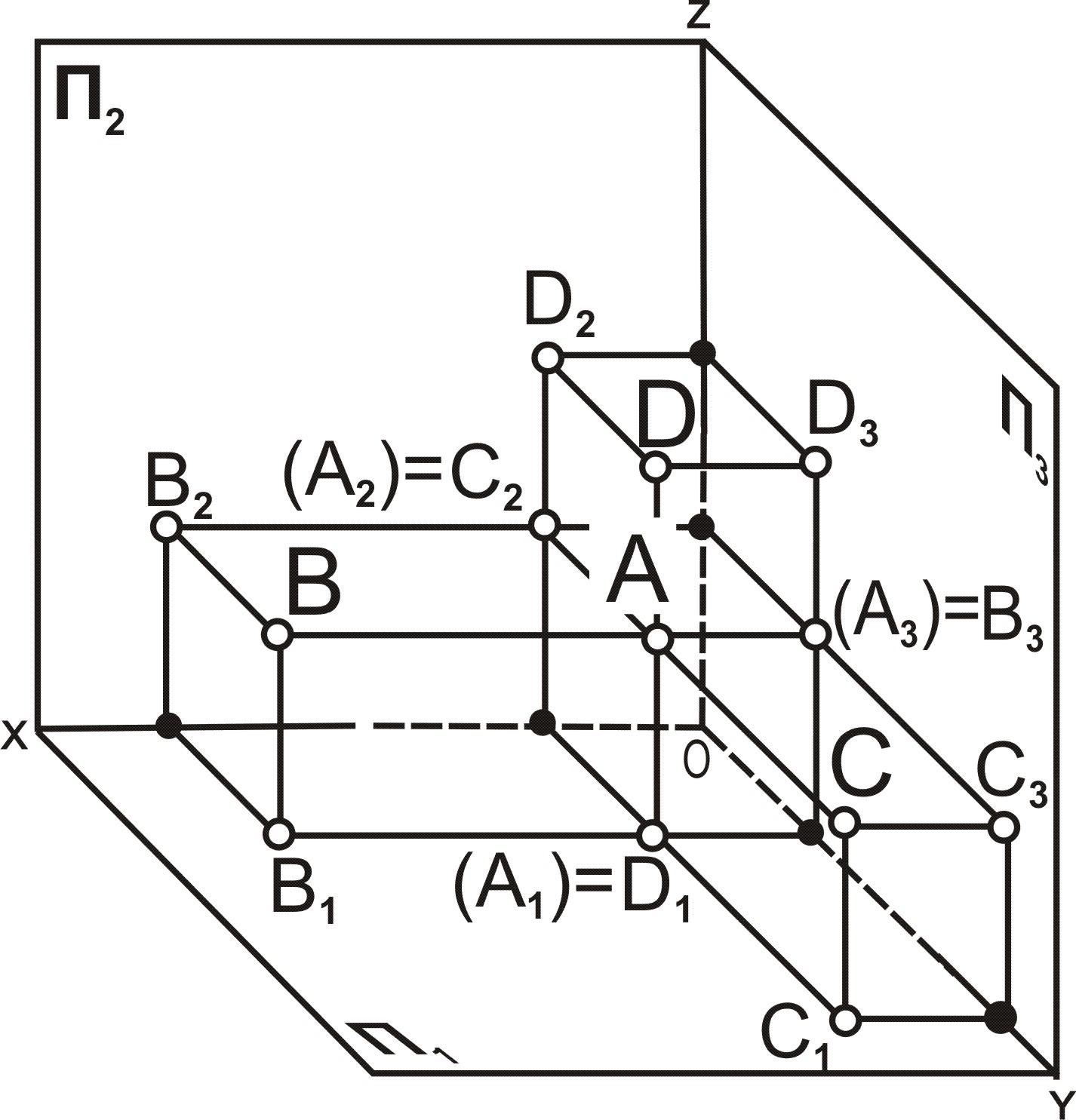
На рис. 3.2 даны чертежи точек общего
положения. Анализ их изображений
позволяет сделать вывод, что они
располагаются в следующих октантах
пространства: А(+X;+Y;
+Z(
Iоктанту;B(+X;+Y;-Z(
IVоктанту;C(-X;+Y;
+Z(
Vоктанту;D(+X;+Y;
+Z(
IIоктанту.

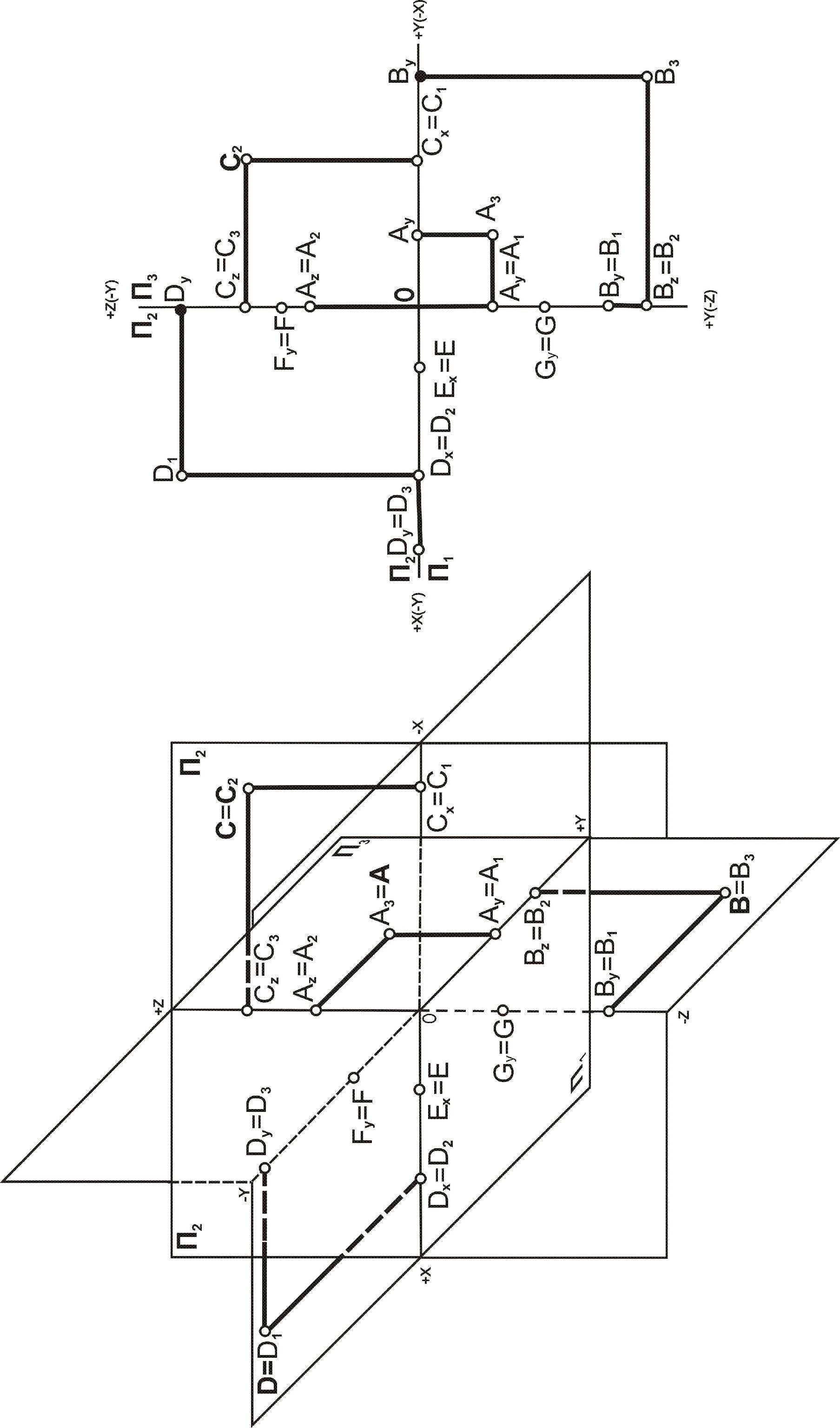
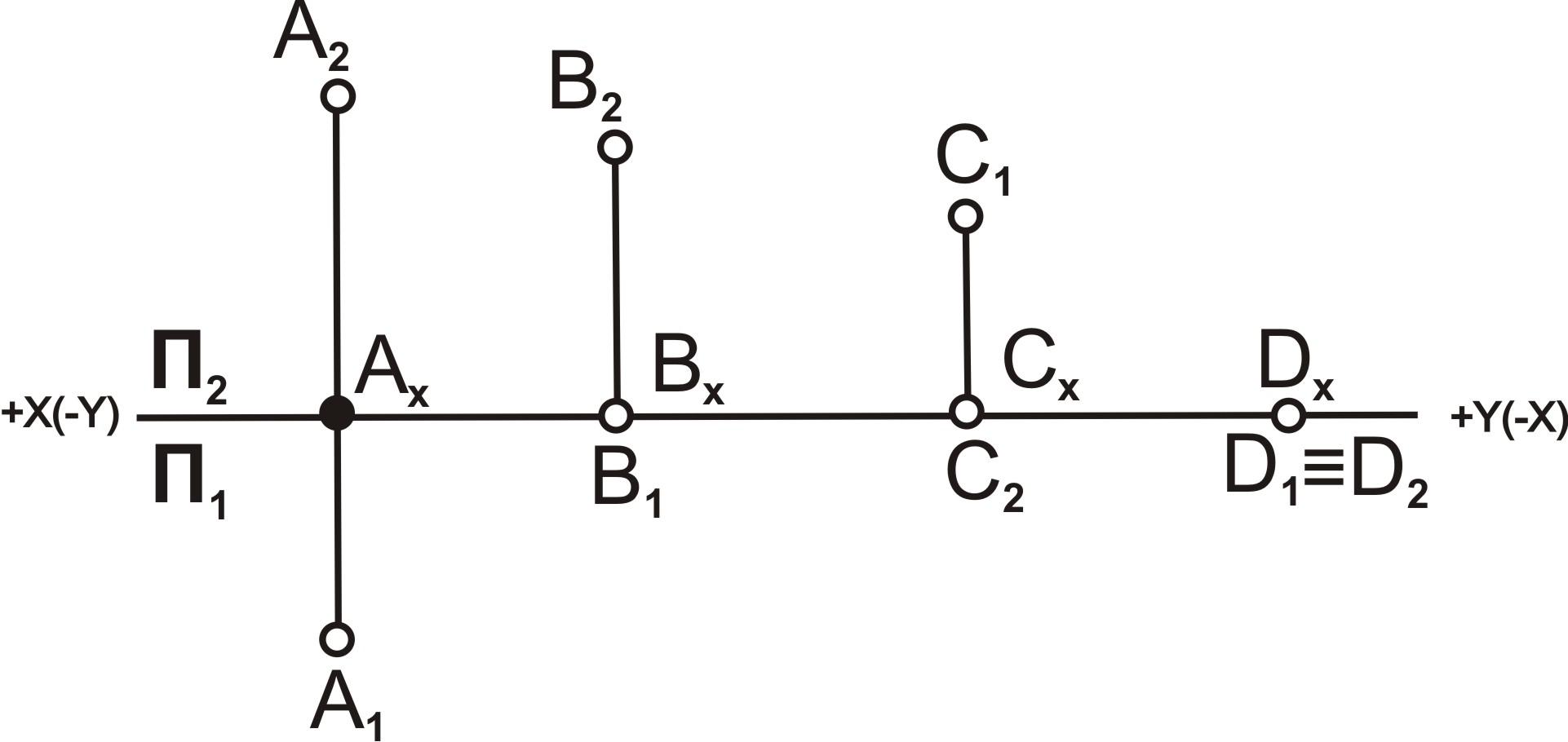
Точки частного положения. Одна из
координат у точки частного положения
равна нулю, поэтому проекция точки лежит
на соответствующем поле проекций, другие
две – на осях проекций. На рис. 3.3 такими
точками являются точки А, В,C,D,G.AП₃,то
точка Х_А=0; ВП₃,то
точка Х_В=0; СП₂,то
точкаY_C=0;DП₁,то
точкаZ_D=0.

Точка может принадлежать сразу двум
плоскостям проекций, если она лежит на
линии пересечения этих плоскостей –
оси проекций. У таких точек не равна
нулю только координата на этой оси. На
рис. 3.3 такой точкой
является точкаG(GOZ,то
точка Х_G=0,Y_G=0).

3.3. Взаимное положение точек в пространстве

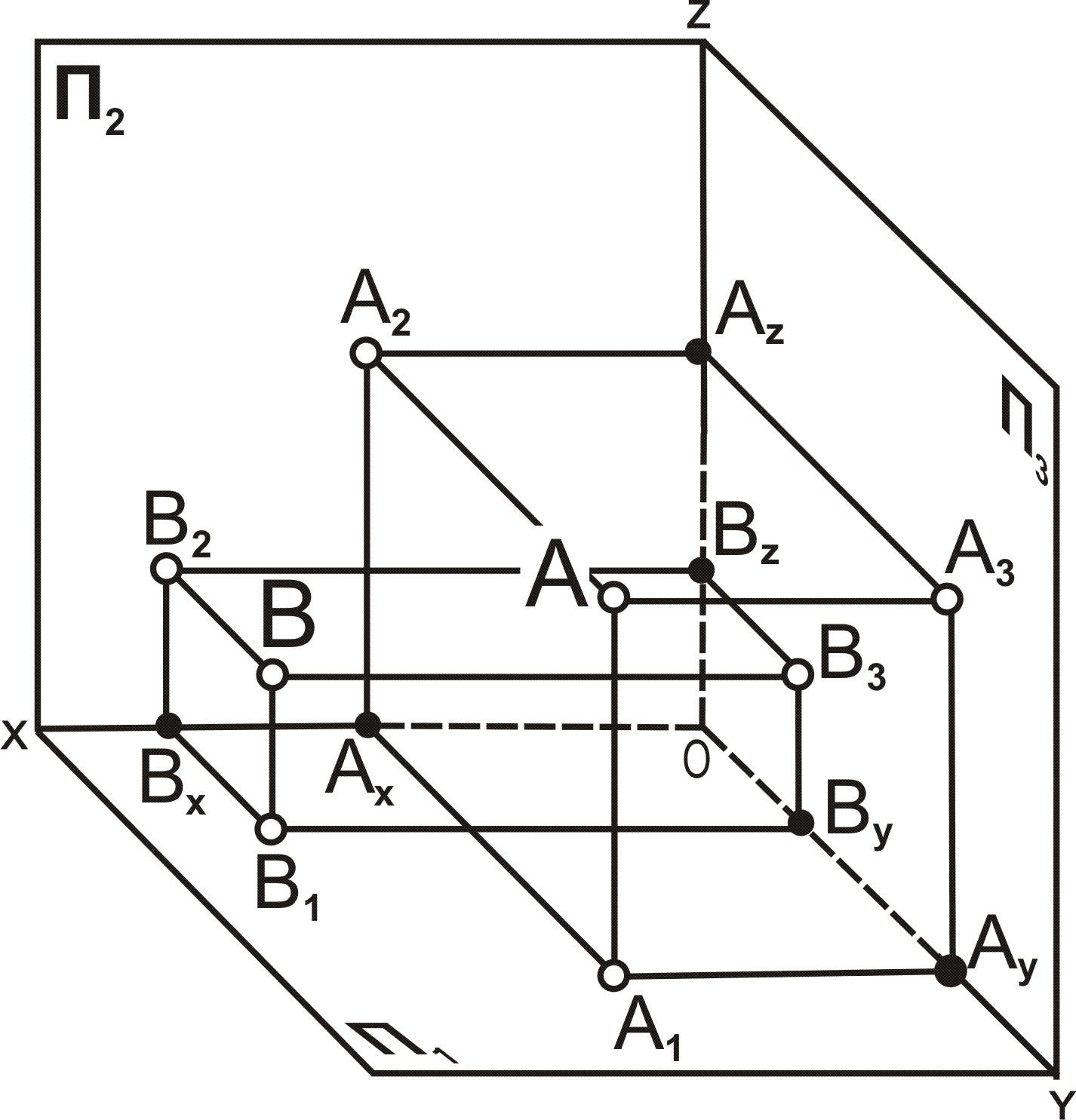
Рассмотрим три
варианта взаимного расположения точек
в зависимости от соотношения координат,
определяющих их положение в пространстве.

1. На
   рис. 3.4 точки AиBимеют различные координаты.

а	б
Рис. 3.4. Варианты взаимного расположения точек: а – наглядное изображение; б – комплексный чертёж

Их
взаимное расположение можно оценить
по удаленности к плоскостям проекций:
Y_А>Y_В, тогда точкаAрасположена дальше от плоскости П₂и ближе к наблюдателю, чем точкаB;
Z_А>Z_В, тогда точкаAрасположена дальше от плоскости П₁и ближе к наблюдателю, чем точкаB;
X_А<X_В, тогда точкаBрасположена дальше от плоскости П₃и ближе к наблюдателю, чем (при взгляде
слева) точка А.

1. На рис. 3.5 представлены точки A, B, С, D, у
   которых  одна из координат совпадает,
   а две другие  отличаются.

а	б
Рис. 3.5. Конкурирующие точки: а – наглядное изображение; б – комплексный чертёж

Их
взаимное расположение можно оценить
по удалённости к плоскостям проекций
следующим образом:

 Y_А=Y_В=Y_D,
то точки А, В и D
равноудалены от плоскости П₂,
и их горизонтальные и профильные
проекции расположены соответственно
на прямых [А₁В₁]llОХ
и [А₃В₃]llOZ.
Геометрическим местом таких точек
служит плоскость, параллельная П₂;

Z_А=Z_В=Z_С,
то точки А, В и С равноудалены от плоскости
П₁,
и их фронтальные и профильные проекции
расположены соответственно на прямых
[А₂В₂]llОХ
и [А₃С₃]llOY.
Геометрическим местом таких точек
служит плоскость, параллельная П₁;

X_А=X_C=X_D,
то точки А, 
C
и D
равноудалены от плоскости П₃
и их горизонтальные и фронтальные
проекции расположены соответственно
на прямых [А₁C₁]llOY
и [А₂D₂]llOZ
. Геометрическим местом таких точек
служит плоскость, параллельная П₃.

3.
Если у точек равны две одноименные
координаты, то они называются
конкурирующими.
Конкурирующие точки расположены на
одной проецирующей прямой. На рис. 3.3
даны три пары таких точек, у которых:
X_А=X_D;
Y_А=Y_D;
Z_D
>
Z_А;
X_A=X_C;
Z_A=Z_C;
Y_C
>
Y_A;
Y_A=Y_B;
Z_A=Z_B;
X_B
>
X_A.

Различают
горизонтально конкурирующие точки А и
D, расположенные на горизонтально
проецирующей прямой АD, фронтально
конкурирующие точки A и C, расположенные
на фронтально проецирующей прямой AC,
профильно конкурирующие точки A и B,
расположенные на профильно проецирующей
прямой AB.

Выводы
по теме

1.
Точка
– линейный геометрический образ, одно
из основных понятий начертательной
геометрии. Положение точки в пространстве
можно определить её координатами. Каждая
из трёх проекций точки характеризуется
двумя координатами, их название
соответствует названиям осей, которые
образуют соответствующую плоскость
проекций: горизонтальная – A₁(XA;
YA);
фронтальная – A₂(XA; ZA);
профильная – A₃(YA; ZA).
Трансляция координат между проекциями
осуществляется с помощью линий связи.
По двум проекциям можно построить
проекции точки либо с помощью координат,
либо графически.

3.
Точка по отношению к плоскостям проекций
может занимать в пространстве как общее,
так и частное положение.

4.
Точка общего положения – точка, не
принадлежащая ни одной
из плоскостей
проекций, т. е. лежащая в пространстве
между плоскостями проекций. Координаты
точки общего положения не равны нулю
(x≠0,y≠0,z≠0).

5.
Точка частного положения – это точка,
принадлежащая одной или двум плоскостям
проекций. Одна из координат у точки
частного положения равна нулю, поэтому
проекция точки лежит на соответствующем
поле плоскости проекций, другие две –
на осях проекций.

6.
Конкурирующие точки – точки, одноименные
координаты которых совпадают. Существуют
горизонтально конкурирующие точки,
фронтально конкурирующие точки, профильно
конкурирующие точки.

Ключевые
слова

• Точка

• Координаты
  точки

• Точка
  общего положения

• Точка
  частного положения

• Конкурирующие
  точки

Способы
деятельности, необходимые для решения
задач

– построение
точки по заданным координатам в системе
трех плоскостей проекций в пространстве;

– построение
точки по заданным координатам в системе
трех плоскостей проекций на комплексном
чертеже.

Вопросы
для самопроверки

1.
Как устанавливается связь расположения
координат на комплексном чертеже в
системе трех плоскостей проекций П₁П₂П₃
с координатами проекций точек?

2.
Какими координатами определяется
удалённость точек до горизонтальной,
фронтальной, профильной плоскостей
проекций?

3.
Какие координаты и проекции точки будут
изменяться, если точка перемещается в
направ­лении, перпендикулярном
профильной плоско­сти проекций П₃?

4.
Какие координаты и проекции точки будут
изменяться, если точка перемещается в
направ­лении, параллельном оси OZ?

5.
Какими координатами, определяется
горизонтальная (фронтальная, профильная)
проекция точки?

7.
В каком случае проекция точки совпадает
с самой точкой пространства и где
располагаются две другие проекции этой
точки?

8.
Может ли точка принадлежать одновременно
трём плоскостям проекций и в каком
случае?

9.
Как называют точки, одноимённые проекции
которых совпадают?

10.
Каким образом можно определить, какая
из двух точек ближе к наблюдателю, если
их фронтальные проекции совпадают?

Задания
для самостоятельного решения

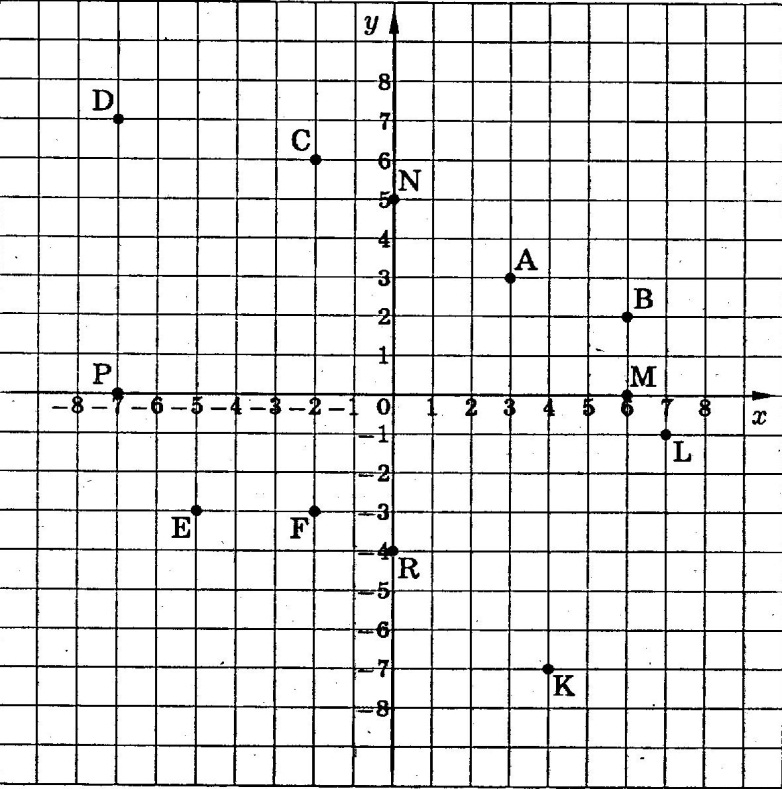
Рис. 3.6. Условие к заданию 1

1. Дать наглядное изображение точекA,B,C,Dотносительно плоскостей
проекций П₁, П₂. Точки заданы
своими проекциями (рис. 3.6).

2.
Построить проекции точек А и В по их
координатам на наглядном изображении
и комплексном чертеже: А(13,5; 20), В(6,5; –20).
Построить проекцию точки С, расположенной
симметрично точке А относительно
фронтальной плоскости проекций П₂.

3. Построить проекции точек А, В, С по их
координатам на наглядном изображении
и комплексном чертеже: А(–20; 0; 0), В(–30;
-20; 10), С(–10, –15, 0). Построить точку D,
расположенную симметрично точке С
относительно осиOХ.

Пример решения типовой задачи

Задача
1. Даны координатыX,Y,ZточекA,B,C,D,E,F(табл. 3.3)

Таблица 3.3

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #