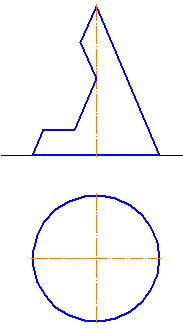
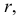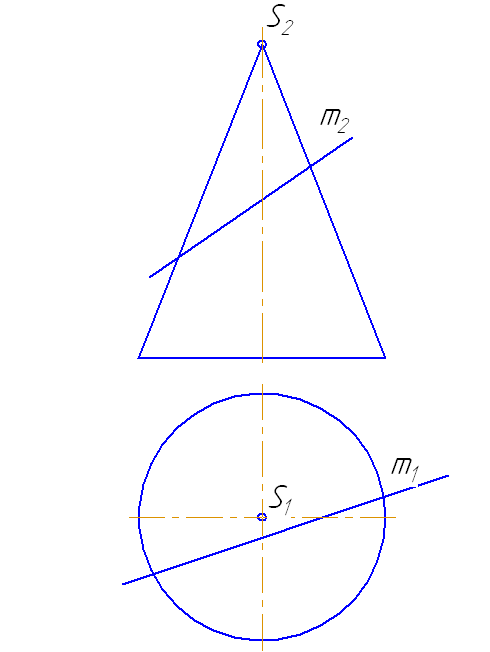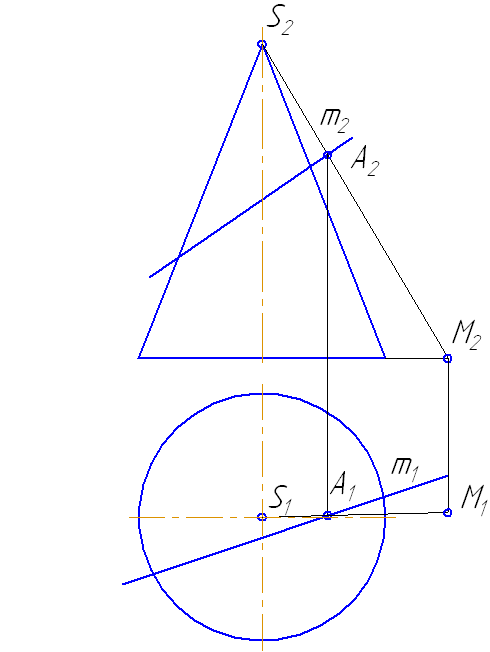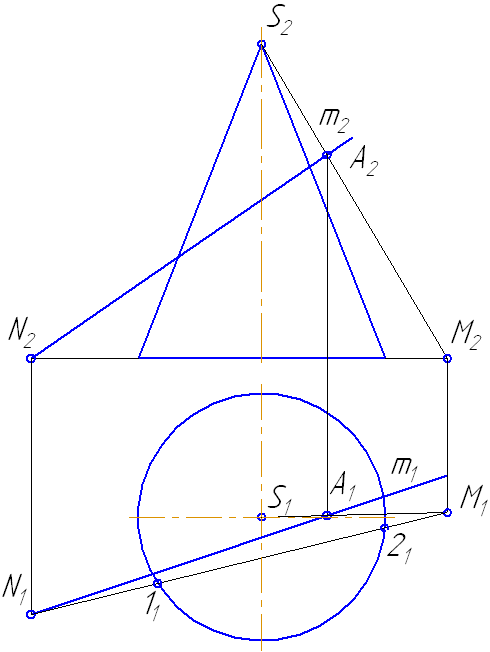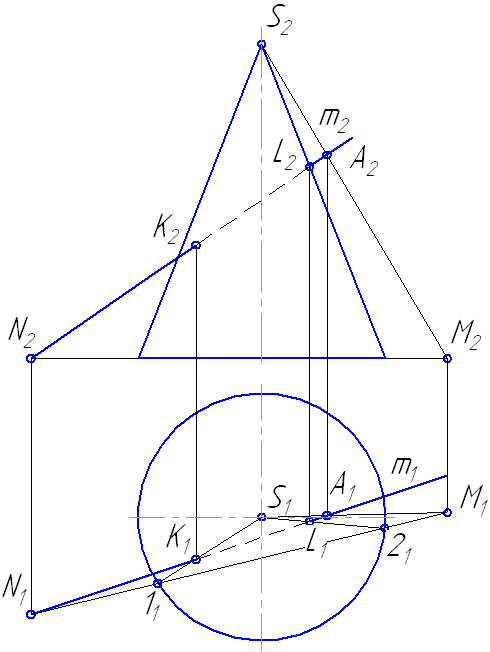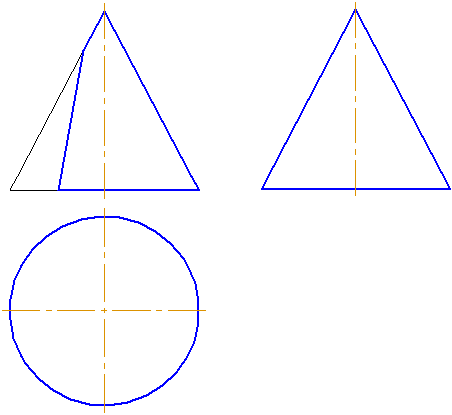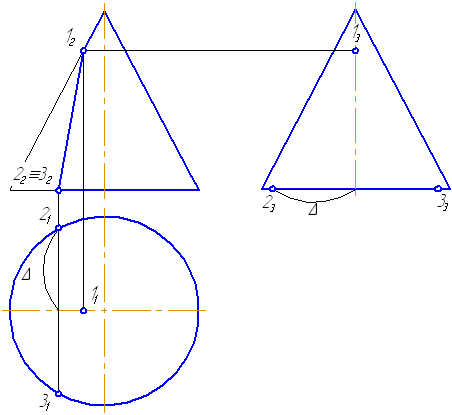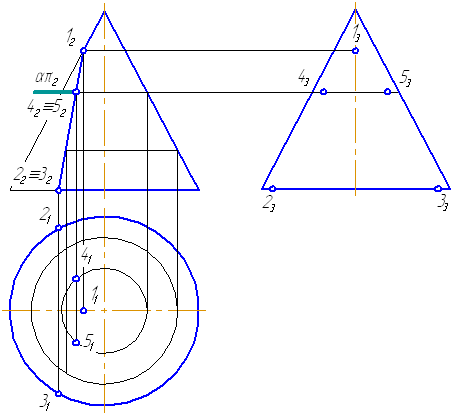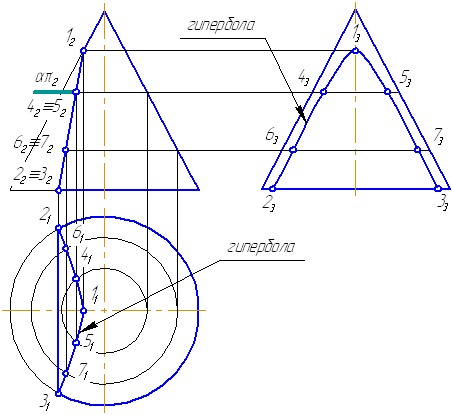Сферическая поверхность — шар
При вращении окружности вокруг ее диаметра образуется поверхность вращения, называемая сферой. Сферическая поверхность — геометрическое место точек, равноудаленных от ее центра. Сфера — единственная геометрическая поверхность, которая имеет бесконечное число осей, проходящих через ее центр, что удобно использовать при построении проекций точек на ее поверхности и при решении различных позиционных задач с геометрическими формами, в образование которых входит сфера.
Геометрическое тело, ограниченное сферой, называют шаром.
Проекции шара и проекции его очерковых окружностей
Все три очерка шара — фронтальный, горизонтальный и профильный -представляют собой окружности одного диаметра с центром в точке 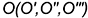
Каждая точка на поверхности шара описывает вокруг соответствующей оси окружности, называемые параллелями.
Фронтальный очерк шара — окружность 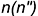
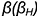
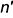
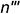
Горизонтальный очерк шара — это окружность 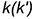
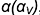
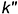
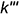
Профильный очерк шара — это окружность 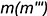
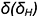
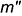
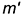
!!! Запомните характерные признаки шара на чертеже — три очерковые окружности одного диаметра.
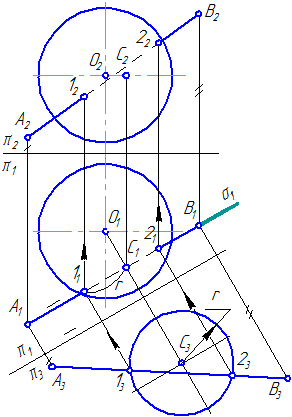
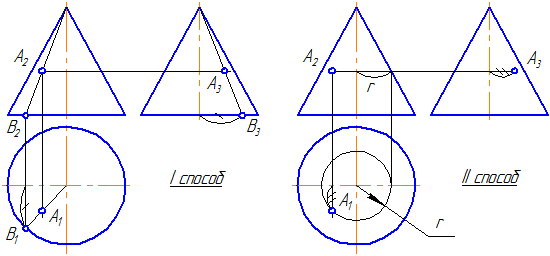
Построение проекций точек на поверхности шара
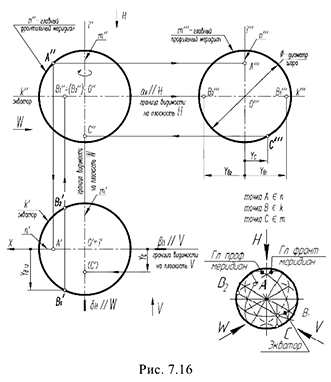
На рис. 7.16 показаны примеры построения проекций точек, лежащих на характерных очерковых окружностях шара.
Точка 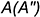
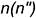
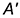
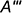
Точки 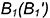
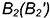
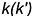
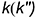
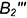
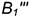
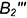
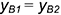
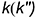
Точка 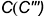
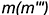
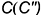
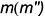
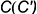
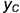
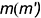
!!! Видимость проекций точки на проекциях шара определяется видимостью той части поверхности шара, на которой лежит точка, и определяется указанными границами видимости при взгляде на каждую плоскость проекций.
На рис. 7.17 показаны примеры построения проекций точек 
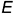
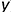
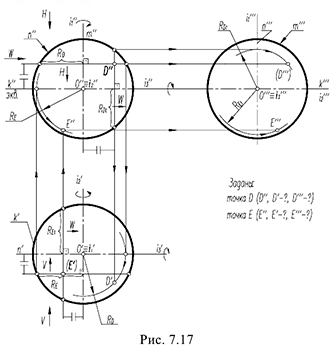
Точка 
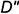
Для построения ее горизонтальной проекции 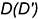
1-е действие. Провести через фронтальную проекцию точки 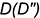
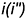
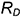

2-е действие. Провести горизонтальную проекцию этой параллели: окружность радиусом 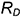
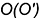
3-е действие. Построить по линии связи горизонтальную (видимую) проекцию точки 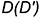
Точка 
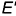
Для построения ее фронтальной проекции 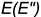
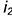
1-е действие. Провести через горизонтальную проекцию точки 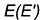
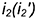
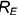
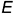
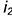
2-е действие. Провести фронтальную проекцию этой параллели: окружность радиусом 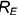
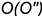
3-е действие. Построить по вертикальной линии связи фронтальную видимую проекцию точки 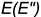
Для построения профильных проекций заданных точек 
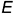
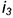
1-е действие. Провести через фронтальную проекцию точки 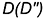
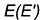
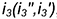
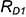
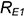

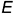
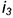
2-е действие. Провести профильные проекции этих параллелей: окружности радиусами 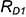
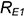
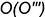
3-е действие. Построить по горизонтальным линиям связи профильные проекции точек 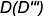
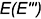
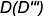
Построение проекций шара со срезами плоскостями частного положения
Всякая плоскость пересекает поверхность шара по окружностям (круговым параллелям). В зависимости от расположения секущих плоскостей относительно плоскостей проекций 
На рис. 7.18 показан пример построения проекций шара со срезами горизонтальной плоскостью 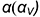
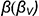
Окружность сечения шара горизонтальной плоскостью 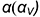
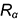
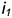
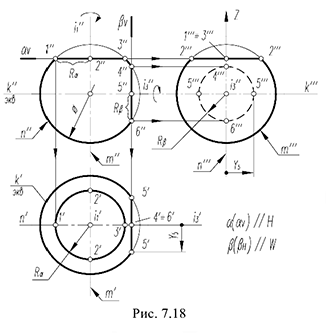
Окружность сечения шара профильной плоскостью 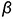
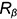
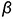
На этом же рисунке показано расположение проекции характерных точек 1,2, 3, 4, 5 и б, лежащих в плоскостях сечений на характерных очерковых окружностях шара:
- точки 1, 3, 4 и 6 лежат на главном фронтальном меридиане шара
и их проекции определяются на проекциях этого меридиана;
- точки 5 лежат на экваторе шара
и их проекции определяются на проекциях экватора;
- точки 2 лежат на профильном меридиане
и их проекции определяются на проекциях этого меридиана.
Оформление очерков проекций ясно из чертежа.
На рис. 7.19 показан пример построения проекций шара со срезом фронтально-проецирующей плоскостью 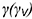
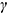
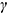
Проекции шара со срезом построены по проекциям точек, обозначенных на фронтальной проекции сечения
Горизонтальная проекция шара со срезом в виде эллипса построена по горизонтальным проекциям обозначенных точек:
-точки 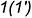
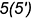
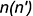
-точки 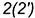
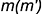
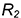
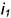
Построенные видимые горизонтальные проекции точек соединить плавной кривой эллипса с помощью лекала.
Очерк горизонтальной проекции определяет его экватор вправо от точек 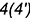
Профильная проекция шара со срезом в виде эллипса построена по профильным проекциям обозначенных точек:
Построенные видимые проекции точек соединить плавной кривой эллипса.
Очерк профильной проекции определяет профильный меридиан 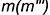
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
§ 19. Шар и сфера
19.1. Определения шара, сферы и их элементов
С шаром и сферой мы уже знакомы. Напомним их определения.
Определение. Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не большем данного R (R > 0). Данная точка называется центром шара, а данное расстояние R — радиусом шара.
Определение. Сферой называется множество всех точек пространства, находящихся от данной точки на расстоянии, равном данному R. Данные точка и расстояние R называются соответственно центром и радиусом сферы.
Рис. 193
На рисунке 193 изображён шар с центром О и радиусом R = OА.
Из определений шара и сферы следует, что шар с центром О и радиусом R является объединением двух множеств точек: 1) множества точек M пространства, для которых OM < R (они называются внутренними точками шара и образуют его внутренность); 2) множества всех М, для которых ОМ = R (эти точки являются граничными точками шара, а их объединение составляет границу шара, которая называется шаровой поверхностью и является сферой c центром О и радиусом R).
Радиусом шара называют также всякий отрезок, соединяющий центр шара с точкой шаровой поверхности. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара. Концы любого диаметра шара называются диаметрально nротивоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара (сферы). На рисунке 193 отрезки ОА, ОВ, ON, OS — радиусы шара; отрезки АВ, NS — диаметры шара; A и B — диаметрально противоположные точки шара. Из определения диаметра шара следует, что он равен удвоенному радиусу шара.
Рис. 194
Покажем, что шар — тело вращения. Для этого рассмотрим полукруг F с центром О и радиусом R (рис. 194, а). При вращении полукруга F вокруг прямой, содержащей его диаметр NS, образуется некоторое тело F1 (рис. 194, б). Так как вращение вокруг прямой — движение и точка О принадлежит оси l вращения, то каждая точка тела F1 удалена от точки O на расстояние, не большее R (движение сохраняет расстояния между точками). Это означает, что тело F1 есть шар с центром О и радиусом R. Кроме того, при вращении границы полукруга — полуокружности — вокруг прямой l образуется сфера. Прямая, содержащая любой диаметр шара, может быть рассмотрена как ось вращения. Следовательно, сечением шара плоскостью, перпендикулярной его оси вращения l и пересекающей шар, является круг, а сечением сферы такой плоскостью — окружность этого круга; центр круга (окружности) есть точка пересечения секущей плоскости с осью l.
Плоскость, проходящая через центр шара (сферы), называется диаметральной плоскостью шара (сферы). Сечением шара диаметральной плоскостью является круг, радиус которого равен радиусу шара. Такой круг называется большим кругом, а его окружность — большой окружностью; большая окружность является пересечением сферы и её диаметральной плоскости.
19.2. Изображение сферы
Рис. 195
Рассмотрим сферу, диаметр NS которой проведён вертикально (рис. 195, а). Большая окружность, по которой сферу пересекает диаметральная плоскость, перпендикулярная диаметру (оси) NS, называется экватором, а точки N и S — полюсами сферы. Окружность, ограничивающая круг — изображение сферы, — называется абрисом или очерковой линией.
Типичная ошибка (!) при изображении сферы (рис. 195, б) в том, что, изображая её экватор эллипсом, полюсы изображают расположенными на абрисе.
Для верного и наглядного изображения сферы вспомним, как в курсе черчения изображают фигуру на комплексном двухкартинном чертеже (эпюре) посредством ортогонального её проектирования на две взаимно перпендикулярные плоскости, одну из которых называют фронтальной (обозначают V), а другую — профильной (обозначают W) плоскостями проекций.
Сферу расположим так, чтобы её ось N′S′ была параллельна профильной (W), но не параллельна фронтальной (V) плоскостям проекций. Тогда ортогональные проекции сферы на плоскости V и W имеют вид, изображённый на рисунке 196. На нём: равные круги — проекции сферы на плоскости V и W; отрезки A1B1 и N1S1 — профильные проекции соответственно экватора и оси сферы; точки N, S — фронтальные проекции полюсов (строятся с помощью линий связи); точки А, В — фронтальные проекции концов диаметра экватора, параллельного фронтальной плоскости (строятся с помощью линий связи); отрезок CD — фронтальная проекция диаметра C′D′ сферы, перпендикулярного профильной плоскости; эллипс с осями АВ и CD — фронтальная проекция экватора. При таком расположении относительно плоскостей проекций сфера изображается так, как показано на рисунках 195, a; 196, a.
Рис. 196
Рис. 197
Обратите внимание! Полюсы N и S не лежат на абрисе, и экватор изображается эллипсом. При этом положение полюсов N и S и положение вершин А и В эллипса-экватора взаимосвязаны.
Действительно, из равенства △ ОBF = △ ЕNО (см. рис. 196, а) следует: OВ = EN, BF = NO. Это означает: а) если изображены полюсы N и S сферы, то вершины А и В эллипса — изображения экватора определяются из равенств OВ = ОА = NE, где NE || OD; б) если изображён экватор (т. е. дана малая ось AB эллипса-экватора), то положение полюсов N и S определяется из равенств ON = OS = BF, где BF || OD.
На рисунке 197, а — верное и наглядное изображение сферы, на рисунке 197, б — изображение сферы верное (почему?), но не наглядное; на рисунке 197, в — неверное изображение (почему?).
ЗАДАЧА (3.106). Найти в пространстве множество вершин всех прямых углов, опирающихся на данный отрезок АВ.
Решение. Если ∠ АМВ = 90°, то точка М принадлежит окружности с диаметром АВ (рис. 198, a).
Рис. 198
Проведём произвольную плоскость α, содержащую отрезок АВ. В этой плоскости множество всех точек М, из которых отрезок AB виден под прямым углом, есть окружность, для которой отрезок AB — диаметр. Точки А и В этому множеству точек не принадлежат. (Почему?) Таким образом, искомое множество вершин прямых углов, опирающихся на отрезок AB, есть сфера с диаметром AB. Точки А и В этому множеству точек-вершин не принадлежат.
19.3. Уравнение сферы
Составим уравнение сферы с центром А (a; b; с) и радиусом R в декартовой прямоугольной системе координат Oxyz.
Пусть М(x; у; z) — любая точка этой сферы (рис. 199). Тогда MA = R или MA2 = R2. Учитывая, что MA2 = (x – a)2 + (у – b)2 + (z – c)2, получаем искомое уравнение cферы
(x – a)2 + (у – b)2 + (z – c)2 = R2.
Если начало системы координат совпадает с центром A сферы, то a = b = c = 0, а сфера в такой системе координат имеет уравнение
x2 + y2 + z2 = R2.
Из полученных уравнений следует, что сфера — поверхность второго порядка.
Так как для любой точки М(х; у; z) шара с центром А (a; b; с) и радиусом R выполняется МА ⩽ R, то этот шар может быть задан неравенством
(x – a)2 + (у – b)2 + (z – c)2 ⩽ R2.
При этом для всех внутренних точек М шара выполняется условие МА2 < R2, т. е.
Рис. 199
(х – a)2 + (у – b)2 + (z – c)2 < R2,
для точек М шаровой поверхности — условие
МА = R,
т. е. (х – a)2 + (у – b)2 + (z – c)2 = R2,
для точек М вне шара — условие
МА > R,
т. е. (х – a)2 + (у – b)2 + (z – c)2 > R2.
19.4. Пересечение шара и сферы с плоскостью
Рассмотрим подробнее вопрос о пересечении шара и сферы с плоскостью. Имеет место следующая теорема.
Теорема 30 (о пересечении шара и сферы с плоскостью). 1) Если расстояние от центра шара до данной плоскости меньше радиуса шара, то пересечением шара с плоскостью является круг. Центром этого круга является основание перпендикуляра, проведённого из центра шара на плоскость, или сам центр шара, если плоскость проходит через этот центр. Пересечением сферы с плоскостью является окружность указанного круга. Радиус r сечения в этом случае равен r = 
Доказательство. Пусть точка О — центр шара, R — его радиус; α — данная плоскость, точка A — основание перпендикуляра, проведённого из центра O на плоскость α. Обозначим ρ(О; α) = | ОА | = d — расстояние от центра шара до плоскости α.
Рассмотрим каждый из случаев взаимного расположения шара и данной плоскости α.
Рис. 200
1) ρ(O; α) = d < R и плоскость α не проходит через центр О шара (рис. 200). Докажем, что пересечение шара и плоскости есть круг с центром А и радиусом r = 

Действительно, пусть М — произвольная точка шара, принадлежащая плоскости α (см. рис. 200). В прямоугольном треугольнике AOM по теореме Пифагора ОM2 = ОА2 + АМ2, откуда AM = 



Обратно, пусть М — произвольная точка плоскости α, принадлежащая кругу с центром А и радиусом r = 
Если неравенства, которые использовались в предыдущем доказательстве, заменить равенствами, то, рассуждая аналогично, можно доказать, что при d < R пересечением сферы и плоскости является окружность с центром А и радиусом r = 
Рис. 201
Если плоскость α проходит через центр O шара, то d = 0, значит, r = R, т. е. сечением шара такой плоскостью является большой круг, а сечением сферы — большая окружность (см. рис. 200).
2) ρ(O; α) = d = OA = R (рис. 201).
Так как ОА = ρ(O; α) = R, то точка А, являющаяся основанием перпендикуляра из центра О шара на плоскость α, принадлежит шаровой поверхности, ограничивающей данный шар.
Рис. 202
Пусть M — произвольная точка плоскости α, отличная от точки A (см. рис. 201). Тогда длины наклонной ОМ и перпендикуляра OA, проведённых из точки О к плоскости α, удовлетворяют неравенству OM > ОА = R. Значит, точка М не принадлежит шару. Следовательно, плоскость α имеет только одну общую точку с шаром — точку А.
3) ρ(О; α) = ОА = d > R (рис. 202). Для любой точки М плоскости α выполняется (почему?) ОМ ⩾ d > R. Это означает, что на плоскости α нет точек шара. Теорема доказана. ▼
ЗАДАЧА (3.161). Через середину радиуса шара проведена перпендикулярная к нему плоскость. Радиус шара равен R. Найти: а) площадь получившегося сечения; б) площади боковой и полной поверхностей конуса, основанием которого служит получившееся сечение шара, а вершиной — центр шара; в) площади боковой и полной поверхностей правильной треугольной пирамиды, вписанной в этот конус.
Решение. а) Пусть точка O — центр шара, OD — его радиус, точка С — середина радиуса OD; α — секущая плоскость, проходящая через точку С перпендикулярно OD.
Рассмотрим сечение шара диаметральной плоскостью, проходящей через его радиус OD. Этим сечением является большой круг с центром О и радиусом R (рис. 203); АВ — диаметр круга — сечения данного шара плоскостью α.
Так как АВ ⟂ OD и точка С — середина радиуса OD, то отрезок AB равен стороне правильного треугольника, вписанного в окружность радиуса R, значит, АВ = R
Рис. 203
АС = r = 

б) Найдём площадь поверхности конуса с вершиной О и радиусом основания r = 
Рис. 204
Образующая ОЕ конуса (рис. 204) равна радиусу R данного шара. Поэтому площадь боковой поверхности этого конуса равна
πr•R = π•

а площадь его полной поверхности — 



в) Найдём площадь поверхности правильной треугольной пирамиды OEFK, вписанной в конус, радиус основания которого СK = r = 
Так как △ ЕFK — правильный, вписанный в окружность радиуса r = 




Площадь боковой поверхности пирамиды равна 3S△ EOF = 
ОН = 


Тогда 

Следовательно, площадь полной поверхности пирамиды равна





Ответ: a) 






19.5. Плоскость, касательная к сфере и шару
Из теоремы 30 следует, что плоскость может иметь со сферой (с шаром) только одну общую точку.
Определение. Плоскость, имеющая только одну общую точку со сферой (с шаром), называется касательной плоскостью к сфере (шару), а их единственная общая точка называется точкой касания (рис. 205).
Рис. 205
Также говорят, что плоскость касается сферы (шара).
Любая прямая, лежащая в касательной плоскости к сфере и проходящая через точку их касания, называется касательной прямой к сфере; эта прямая имеет со сферой единственную общую точку — точку касания, и радиус сферы, проведённый в точку касания, перпендикулярен касательной прямой.

Справедливо и обратное: если прямая a касается окружности большого круга сферы в точке М, то эта прямая касается в точке М самой сферы.
Более того, так как прямая a, касающаяся сферы в точке М, имеет со сферой лишь одну общую точку — точку М, то эта прямая касается любой окружности, по которой пересекаются данная сфера и любая (не только диаметральная) плоскость, проходящая через прямую a. А поскольку радиус, проведённый в точку касания прямой и окружности, перпендикулярен касательной прямой, то центры всех этих окружностей — полученных сечений сферы — лежат в плоскости, проходящей через точку М перпендикулярно касательной прямой a. При этом, если точка О — центр данной сферы радиуса R, точка А — центр окружности радиуса r, по которой пересекает сферу одна (любая) из плоскостей, проходящих через касательную в точке М прямую к данной сфере, ϕ — величина угла между этой секущей плоскостью и проходящей через точку М диаметральной плоскостью данной сферы, то справедливо равенство r = R•cos ϕ (△ ОАМ — прямоугольный, так как отрезок ОА перпендикулярен секущей плоскости (почему?)).
Для плоскости, касательной к сфере, справедливы теоремы, аналогичные теоремам о прямой, касательной к окружности на плоскости.
Теорема 31. Если плоскость касается сферы, то она перпендикулярна радиусу, проведённому в точку касания.
Доказательство. Пусть дана сфера с центром O и радиусом R. Рассмотрим плоскость α, касающуюся данной сферы в точке M (см. рис. 205) и докажем, что ОM ⟂ α.
Предположим, что радиус ОM — не перпендикуляр, а наклонная к плоскости α. Значит, расстояние от центра сферы до плоскости α, равное длине перпендикуляра, проведённого из центра О на плоскость α, меньше радиуса. Тогда по теореме 30 плоскость α пересекает сферу по окружности. Но по условию теоремы плоскость α касается сферы и имеет с ней единственную общую точку M. Пришли к противоречию, которое и доказывает, что OM ⟂ α. Теорема доказана. ▼
Справедлива обратная теорема.
Теорема 32. Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведённому в эту точку, то она касается сферы.
Доказательство. Пусть плоскость α проходит через точку M сферы и перпендикулярна радиусу ОM (см. рис. 205). Значит, расстояние от центра сферы до плоскости равно радиусу ОM. Тогда по теореме 30 плоскость α и сфера имеют единственную общую точку M, следовательно, плоскость α касается сферы (в точке M). Теорема доказана.▼
Так как сечение шара плоскостью есть круг, то можно доказать, что для шара выполняются следующие метрические соотношения:
—диаметр шара, делящий его хорду пополам, перпендикулярен этой хорде;
—отрезки всех касательных прямых, проведённых к шару из одной расположенной вне шара точки, равны между собой (они образуют поверхность конуса с вершиной в данной точке, а точки касания этих прямых — окружность основания этого конуса);
—произведение длин отрезков хорд шара, проходящих через одну и ту же внутреннюю точку шара, есть величина постоянная (равная R2 – a2, где R — радиус шара, a — расстояние от центра шара до данной точки);
—если из одной и той же точки вне шара проведены к нему секущая и касательная, то произведение длины отрезка всей секущей на длину отрезка её внешней части равно квадрату длины отрезка касательной (и равно a2 – R2, где R — радиус шара, a — расстояние от центра шара до данной точки).
19.6. Вписанные и описанные шары и сферы
Определение. Шар называется вписанным в цилиндр, если основания и каждая образующая цилиндра касаются шара (рис. 206).
Рис. 206
Рис. 207
Цилиндр в таком случае называется описанным около шара. В цилиндр можно вписать шар тогда и только тогда, когда он равносторонний.
Определение. Шар называется описанным около цилиндра, если основания цилиндра служат сечениями шара (рис. 207).
Цилиндр при этом называют вписанным в шар. Около любого цилиндра можно описать шар. Центром шара служит середина оси цилиндра, а радиус шара равен радиусу круга, описанного около осевого сечения цилиндра.
Рис. 208
Рис. 209
Определение. Шар называется описанным около конуса, если основание конуса — сечение шара, а вершина конуса принадлежит поверхности шара (рис. 208).
Конус при этом называют вписанным в шар.
Центр шара, описанного около конуса, совпадает с центром круга, описанного около осевого сечения конуса, а радиус шара равен радиусу этого круга.
Определение. Шар называется вписанным в конус, если основание и все образующие конуса касаются шара.
Конус при этом называют описанным около шара (рис. 209). Центр вписанного в конус шара совпадает с центром круга, вписанного в осевое сечение конуса, а радиус шара равен радиусу этого круга.
Определение. Шар называется вписанным в многогранник, если он касается всех граней многогранника.
Многогранник в таком случае называют описанным около шара (рис. 210).
Не во всякий многогранник можно вписать шар. Например, вписать шар можно в любую треугольную или правильную пирамиду. А в прямую призму, в основании которой лежит прямоугольник, не являющийся квадратом, шар вписать нельзя.
Рис. 210
При нахождении радиуса r вписанного в многогранник шара (если таковой существует) удобно пользоваться соотношением
Vмногогр = 
Шар называется вписанным в двугранный угол, если он касается его граней. Центр вписанного в двугранный угол шара лежит на биссекторной плоскости этого двугранного угла. При этом для радиуса r шара, вписанного в двугранный угол, величины α этого угла и расстояния m от центра шара до ребра двугранного угла справедлива формула: r = m•sin 
Шар называется вписанным в многогранный угол, если он касается всех граней многогранного угла. При решении задач, в которых рассматриваются вписанные в многогранный угол шары, удобно пользоваться соотношением: r = m•sin 
Если все плоские углы трёхгранного угла равны по 60°, то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно 3r; если все плоские углы трёхгранного угла прямые, то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно r
Определение. Шар называется описанным около многогранника, если все вершины многогранника принадлежат поверхности шара (рис. 211). Многогранник при этом называют вписанным в шар.
Рис. 211
Не около всякого многогранника можно описать шар. Например, около любой правильной или любой треугольной пирамиды шар описать можно, а около четырёхугольной пирамиды, в основании которой лежит ромб, не являющийся квадратом, шар описать нельзя (около ромба нельзя описать окружность). Более того, нельзя описать шар около любой наклонной призмы.
Вообще, для того чтобы около многогранника можно было описать шар, необходимо, чтобы около любой его грани можно было описать круг. При этом центр описанного шара может лежать как внутри многогранника, так и вне его или на его поверхности (даже на ребре многогранника), и проектируется в центр описанного около любой грани круга. Кроме того, перпендикуляр, опущенный из центра описанного около многогранника шара на ребро многогранника, делит это ребро (как хорду шара) пополам.
Мы уже говорили о пирамидах, все рёбра которых одинаково наклонены к основанию. Около таких пирамид всегда можно описать шар, центр которого лежит на луче, содержащем высоту пирамиды.
Высота h пирамиды, радиус Rк описанного около основания пирамиды круга и радиус R описанного около этой пирамиды шара связаны соотношением:
(R – h)2 + 
Приведём формулы для вычисления радиусов вписанных и описанных шаров для правильных многогранников с ребром a.
В задачах иногда ещё рассматривают шары, касающиеся всех рёбер данного многогранника. Для куба, например, такой шар существует и его радиус равен 
19.7. Площади поверхностей шара и его частей
Часть шара, заключённая между секущей плоскостью и одной из двух частей его сферической поверхности, называется шаровым сегментом (рис. 212 и 214). Поверхность шарового сегмента называется сегментной поверхностью: она представляет собой часть шаровой поверхности, отсекаемую какой-нибудь плоскостью. Круг АВ, по которому плоскость пересекает шар, называется основанием шарового сегмента, а окружность этого круга — основанием сегментной поверхности. Отрезок ОС радиуса, перпендикулярного секущей плоскости, называется высотой шарового сегмента (сегментной поверхности).
Рис. 212
Часть шара, заключённая между двумя параллельными секущими плоскостями, называется шаровым слоем (см. рис. 212, 214). Поверхность шарового слоя называется шаровым поясом. Шаровой пояс — часть шаровой поверхности, заключённая между двумя параллельными секущими плоскостями. Перпендикуляр, проведённый из точки одного основания к плоскости другого, называется высотой шарового слоя (шарового пояса).
Сегментную поверхность и шаровой пояс можно рассматривать как поверхности вращения: в то время, как при вращении полуокружности CAA1D (см. рис. 212) вокруг диаметра CD образуется шаровая поверхность (сфера), при вращении дуги СА этой полуокружности вокруг того же диаметра образуется сегментная поверхность, а при вращении дуги AA1 — шаровой пояс.
Тело, образованное при вращении кругового сектора с углом ϕ (ϕ < 180°) вокруг прямой, которая содержит диаметр круга, не имеющий с круговым сектором общих внутренних точек, называется шаровым сектором.
Рис. 213
Из этого определения следует, что поверхность шарового сектора состоит из сегментной поверхности и боковой поверхности конуса (рис. 213, а, б) или из поверхности шарового пояса и боковых поверхностей двух конусов (рис. 213, в, г).
На рисунке 214 изображены различные элементы шара и сферы (шаровой сектор имеет простейший вид).
Рассмотрим вопрос о вычислении площадей сферы, сегментной поверхности, шарового пояса и шарового сектора.
Рис. 214
Рис. 215
а) Площадь сферы. Пусть ABCDEF — правильная ломаная линия, вписанная в данную полуокружность; a — длина её апофемы (рис. 215). При вращении полуокружности вокруг её диаметра AF образуется сфера, а при вращении ломаной ABCDEF вокруг этого же диаметра AF образуется некоторая поверхность Ф.
За площадь сферы, образованной вращением полуокружности вокруг её диаметра, принимают предел, к которому стремится площадь поверхности Ф, образованной вращением вокруг того же диаметра правильной n-звенной ломаной линии, вписанной в полуокружность, при n → +∞ (число сторон неограниченно возрастает).
Поверхность Ф является объединением поверхностей, образованных вращением звеньев ломаной линии, вписанной в полуокружность, вокруг её диаметра. Этими поверхностями являются боковые поверхности либо конуса (для первого и последнего звеньев ломаной), либо цилиндра (для звеньев, параллельных оси вращения; их может и не быть), либо усечённого конуса (для всех остальных звеньев ломаной).
При вычислении площадей получившихся поверхностей воспользуемся следствиями из теорем 26, 27, 29. Площадь Si (i = 1, 2, …, n) поверхности, образованной вращением любого звена, равна произведению 2π, расстояния bi от середины звена до центра сферы и длины mi проекции этого звена на ось вращения, т. е. Si вращ = 2π•bi•mi.
Так как ломаная — правильная, то все bi равны апофеме an данной n-звенной ломаной, а m1 + m2 + m3 + … + mn = 2R и S1 + S2 + S3 + … + Sn = 4π•an•R. Причём an = 

Следовательно, предел площади поверхности Ф при n → ∞ равен 4πR•R = 4πR2. Этот предел и принимается за величину площади сферы радиуса R:
Sсферы = 4πR2.
б) Площади сегментной поверхности и шарового пояса. Если правильная ломаная вписана не в полуокружность, а в некоторую её часть, например в дугу AD (см. рис. 215), при вращении которой образуется сегментная поверхность, то рассуждения, аналогичные предыдущим, приводят к выводу:
Sсегм. поверх = 2πRh,
где h — высота сферического сегмента.
Если же ломаная вписана в дугу ВЕ (см. рис. 215), при вращении которой образуется шаровой пояс, то получим:
Sшар. пояса = 2πRh,
где h — высота шарового пояса.
Проделайте эти рассуждения самостоятельно.
в) Площадь поверхности шарового сектора. Эта площадь может быть получена как сумма площадей поверхности сферического сегмента и боковой поверхности одного конуса (см. рис. 213, а, б) или как сумма площадей поверхности сферического слоя и боковых поверхностей двух конусов (см. рис. 213, в, г).
Рассмотрим частный случай (см. рис. 213, а, б). Если R — радиус сферы, h — высота шарового сегмента, то площадь боковой поверхности конуса с вершиной в центре сферы, образующей R, и радиусом основания 

Sшар. сект = πR(2h + 
ЗАДАЧА (3.418). Основанием треугольной пирамиды SABC является равносторонний треугольник АВС, сторона которого равна 4. Известно также, что AS = BS = 
Рис. 216
Решение. Решим эту задачу двумя методами.
Первый метод (геометрический). Пусть точка О — центр сферы, описанной около данной пирамиды; D — точка пересечения медиан правильного △ АВС; точка Е — середина отрезка АВ (рис. 216).
Центр О сферы равноудалён от всех вершин △ АBС, поэтому принадлежит прямой, проходящей через точку D перпендикулярно плоскости АВС.
Так как точка Е — середина отрезка АВ, то SE ⟂ АВ (AS = BS) и СЕ ⟂ АВ (△ АВС — правильный). Значит, по признаку перпендикулярности прямой и плоскости AB ⟂ (CSE), поэтому (CSE) ⟂ (ABC) (по признаку перпендикулярности двух плоскостей). Это означает, что прямая OD, а следовательно, и точка О — центр сферы — лежат в плоскости CSE.
Точка D является центром окружности, описанной около △ АВС. (По этой окружности плоскость АВС пересекает сферу, описанную около данной пирамиды.) Если L — точка пересечения прямой СЕ и упомянутой окружности, то CL — её диаметр. Найдём длину диаметра CL.
В правильном △ AВС имеем: CE = 




Далее △ BSE (∠ BES = 90°): SE2 = SB2 – BE2 = 19 – 4 = 15 (по теореме Пифагора); △ SEC (по теореме косинусов):
cos C = 


△ SLC (по теореме косинусов):
SL2 = SC2 + CL2 – 2SC•CL•cos C = 

Плоскость CSL проходит через центр О сферы, следовательно, пересекает сферу по большой окружности, которая описана около △ CSL. Значит, радиус R этой окружности равен радиусу сферы, описанной около данной пирамиды. Найдём длину радиуса R.
В треугольнике CSL имеем 







Находим площадь Q сферы:
Q = 4πR2 = 4π•

Второй метод (координатный). Введём в пространстве декартову прямоугольную систему координат так, чтобы её начало совпадало с вершиной А данной пирамиды, направление оси абсцисс — с направлением луча АС, ось аппликат была перпендикулярна плоскости основания АВС пирамиды (рис. 217).
В этой системе координат вершины основания пирамиды имеют координаты: А(0; 0; 0), B(2; 2 
Обозначив через х, у, z координаты вершины S пирамиды, найдём их из условий: AS = BS = 
Имеем
AS2 = x2 + y2 + z2 = 19,
ВS2 = (x – 2)2 + (y – 2 
CS2 = (x – 4)2 + y2 + z2 = 9.
Решая систему уравнений


находим: х = 


Рис. 217
Таким образом, вершина S имеет следующие координаты:
S 
Пусть центр O сферы имеет координаты a, b, с, а её радиус равен R. Так как сфера описана около пирамиды SABC, то OA2 = OB2 = OC2 = OS2 = R2. Это соотношение в координатном виде равносильно системе уравнений





Вычитая из первого уравнения четвёртое, получаем a = 2, после чего, вычитая из первого уравнения второе, получаем b = 
После вычитания третьего уравнения системы из первого её уравнения получаем:

Подставив в это уравнение вместо a и b найденные их значения, получаем с = 



Q = 4πR2 = 
Ответ: 
19.8. Объёмы шара и его частей
Рис. 218
Рассмотрим фигуру, образованную вращением равнобедренного прямоугольного треугольника с гипотенузой 2R вокруг прямой, проходящей через вершину прямого угла параллельно гипотенузе (рис. 218, а). Объём этой фигуры равен разности объёма цилиндра с высотой 2R, радиусом основания R и удвоенного объёма конуса высоты R, радиуса основания R:
V = π•R2•2R – 2•

Шар радиуса R (рис. 218, б) и образованную выше фигуру вращения расположим между двумя параллельными плоскостями, расстояние между которыми равно 2R. Шар при этом будет касаться каждой из данных плоскостей, а фигуру вращения расположим так, чтобы её ось вращения была перпендикулярна этим плоскостям (см. рис. 218). (Плоскость, которая содержит верхнее основание цилиндра и касается сферы в точке N, на рисунке не изображена.)
Будем пересекать наши фигуры плоскостями, параллельными данным плоскостям и удалёнными от центра шара на расстояние x (0 ⩽ x ⩽ R).
При х = 0 площади сечений обеих фигур равны π•R2; при х = R площади сечений равны нулю. В остальных случаях площадь сечения шара равна π•(
Vшара = 
гдe R — радиус шара.
Рис. 219
Для получения объёма шарового сегмента высоты h рассмотрим предыдущую ситуацию для R – h ⩽ x ⩽ R (при h < R) (рис. 218, 219). Применяя принцип Кавальери, получим: объём шарового сегмента равен разности объёма цилиндра высоты h и радиуса основания R и объёма усечённого конуса высоты h и радиусов оснований R и R – h, т. е.
V = π•h•R2 – 
= 
При h > R объём шарового сегмента можно найти как разность объёма шара и объёма шарового сегмента высоты 2R – h (рис. 220): V = 




Рис. 220
Мы показали, что в шаре радиуса R объём любого шарового сегмента высоты h может быть вычислен по формуле:
Vшар. сегм = 
или в другом виде
Vшар. сегм = π•h2•
Рис. 221
Рис. 222
Рис. 223
Выведем теперь формулу для вычисления объёма шарового сектора.
Сначала рассмотрим шаровой сектор, состоящий из шарового сегмента высоты h и конуса высоты (R – h) с вершиной в центре шара радиуса R (рис. 221). Для него имеем:
Vшар. сект = Vсегм + Vкон = 
+ 

Докажите самостоятельно, что и для других шаровых секторов (рис. 222, 223) их объём вычисляется по формуле:
Vшар. сект = 
Отметим, что объём шарового слоя с радиусами оснований r1 и r2 и высотой Н вычисляется по формуле
Vшар. слоя = 


ЗАДАЧА (3.457). Четыре шара радиуса R и четыре шара радиуса r расположены так, что каждый касается трёх шаров одного радиуса и трёх шаров другого радиуса. Найти отношение объёма шара радиуса R к объёму шара радиуса r (R > r).
Решение. Обозначим V1, V2 — объёмы шаров с радиусами соответственно R и r. Тогда V1 = 



Пусть А, В, С, Р — центры шаров радиуса R; A1, B1, С1, P1 — центры шаров радиуса r. Тогда:
1) AB = BC = CA = AP = BP = CP = 2R ⇒ РАВС — правильный тетраэдр с ребром 2R;
2) A1B1 = B1C1 = C1A1 = A1P1 = B1P1 = C1P1 = 2r ⇒ Р1А1В1С1 — правильный тетраэдр с ребром 2r.
Рис. 224
Обозначим точки A2, B2, C2, P2 — центры граней тетраэдра РАВС (рис. 224) и докажем, что все четыре высоты АA2, BB2, CC2, PP2 пересекаются в одной точке и делятся этой точкой в отношении 3 : 1, считая от вершин.
В самом деле, если М = AА2 ∩ PP2, то из подобия треугольников НАР и НР2А2 следует HP : НA2 = AP : A2P2 = 3 : 1, тогда из подобия треугольников APM и A2P2M следует, что AP : A2P2 = PM : MP2 = AM : MA2 = 3 : 1, т. е. PM = 
Аналогично доказывается, что высоты BB2 и CC2 делятся точкой M в отношении BM : MB2 = CM : MC2 = 3 : 1 и, таким образом, точки A2, B2, C2, P2 равноудалены от точки М.
Далее, так как шар с центром P1 и радиусом r касается шаров с центрами А, В, C и радиусами R, то P1А = P1B = P1С = R + r, т. е. точка P1 равноудалена от вершин А, В и С правильного тетраэдра РАВС. Так как (R + r) < 2R, то P1 принадлежит высоте РP2 этого тетраэдра: P1 ∈ PP2. Аналогично доказывается, что A1 ∈ АA2, B1 ∈ ВB2, C1 ∈ СC2.
Найдём дважды длину высоты РP2 тетраэдра РАВС: с одной стороны, как длину катета прямоугольного треугольника АPP2, с другой стороны, как сумму длин отрезков РМ, МР1 и P1P2.
В правильном △ AВС со стороной 2R имеем:
AP2 = 



Тогда в прямоугольном △ AРP2 :
РР2 = 


Найдём длину отрезка PP2 иначе. В прямоугольном △ AP1P2 имеем:
Аналогично можно убедиться, что A1A2 = B1B2 = C1C2 = P1P2 = 
Так как в правильном тетраэдре РАВС с ребром 2R для расстояния РМ от вершины Р до центра М этого тетраэдра выполняется РМ = 




Подставляя в равенство PP2 = РM + MP1 + P1P2 найденные значения длин отрезков РР2, РM, МP1 и P1P2, получаем:




или после элементарных преобразований:
R2 – 6Rr + r2 = 0.
Разделив это уравнение на r2 и введя новую переменную t = 








Ответ: (3 + 2 
Задания для работы с интернет-ресурсами
1. Посмотрите в Интернете и отберите рисунки по темам: «Тело вращения», «Поверхность вращения». Они помогут вам при построении рисунков к решению задач.
2. Сравните материалы Интернета и учебника по темам: «Цилиндр», «Конус», «Цилиндрическая и коническая поверхности вращения», «Касательная плоскость к цилиндру и конусу», «Формулы для вычисления площадей боковой и полной поверхностей цилиндра и конуса», «Формулы для вычисления объёма цилиндра и конуса», «Развёртки цилиндра и конуса», «Модели цилиндра и конуса». Что нового вы узнали из Интернета?
3. Вы узнаете много нового и интересного о замечательных кривых, сделав запрос в Интернете по темам: «Сечения цилиндра и конуса плоскостью», «Кривые второго порядка», «Конические сечения».
4. Найдите рисунки по темам: «Призма, вписанная в цилиндр и описанная около цилиндра», «Пирамиды, вписанные в конус и описанные около конуса». Удачные рисунки скопируйте в «Избранное» или в «Картотеку», чтобы можно было ими пользоваться при решении задач.
5. Найдите в Интернете теоремы о параллельных сечениях конуса. Посмотрите рисунки усечённых конусов. Найдите формулы для вычисления площадей боковой и полной поверхностей усечённого конуса и его объёма.
6. В Интернете посмотрите материал по темам: «Сфера», «Шар», «Изображение сферы», «Уравнение сферы», «Взаимное расположение сферы и плоскости», «Пересечение шара и сферы с плоскостью», «Плоскость, касательная к сфере и шару», «Шаровой сегмент, его основание и высота; сегментная поверхность», «Шаровой слой, его основания и высота», «Шаровой пояс», «Шаровой сектор и его поверхность».
7. Найдите в Интернете формулы для вычисления площадей сферы, сегментной поверхности, шарового пояса, поверхности шарового сектора, объёмов шара, шарового сегмента, шарового сектора, шарового слоя.
8. Обратите особое внимание на материал: «Шары и сферы, вписанные в двугранный угол и многогранный угол», «Шары и сферы, вписанные в многогранники (особенно в правильные многогранники) и описанные около них», «Шары и сферы, вписанные в цилиндр, конус и описанные около них».
9. Посмотрите рисунки и материалы по темам: «Комбинации геометрических тел», «Комбинации геометрических фигур в окружающем нас мире, в архитектуре». Тем, кто интересуется черчением и графикой, предлагаем найти статьи: «Техническое черчение: цилиндр и конус», «Пересечение двух цилиндров с перпендикулярными осями», «Резьбы и резьбовые соединения», «Цилиндрическая винтовая линия».
Вопросы для самооценки
1. Оцените результаты изучения этой главы. Довольны ли вы ими?
2.Что нового вы узнали в этой главе?
3.Как могут пригодиться вам эти знания в повседневной жизни?
4.Какие задания в этой главе были для вас самыми трудными? Почему?
5.Использовали ли вы при выполнении заданий дополнительные источники: справочники, пособия, интернет-ресурсы?
6.Обращались ли вы за помощью к одноклассникам, родителям, учителю?
Преподаватель который помогает студентам и школьникам в учёбе.
Шаровая поверхность в начертательной геометрии с примером
Шаровая поверхность:
Шаровой поверхностью (или сферой) называется поверхность, образованная при вращении окружности вокруг своего диаметра.
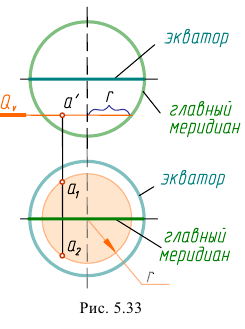
Если шаровая поверхность пересекается плоскостью, то в сечении всегда получается окружность. Эта окружность может спроецироваться:
- – в прямую, если секущая плоскость перпендикулярна плоскости проекций;
- – в окружность, если секущая плоскость параллельна плоскости проекций. Например, окружность с радиусом
- – в эллипс, если секущая плоскость не параллельна плоскости проекций.
Чтобы построить проекции точки, лежащей на поверхности шара, необходимо через нее провести секущую плоскость, параллельную плоскости проекций, затем построить окружность, на которой находится эта точка.
Пересечение шаровой поверхности плоскостью
Пересечем поверхность шара фронтально-проецирующей плоскостью 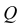
Развертка поверхности шара
Сферическая поверхность относится к неразвертываемым поверхностям, и поэтому развертка поверхности шара может быть выполнена только приближенными способами. Рассмотрим один из способов выполнения развертки шара.
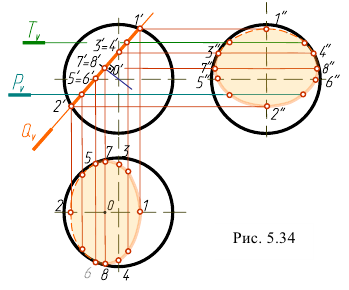
Для выполнения развертки поверхности шара поверхность делят меридианами на равные части. На рис. 5.35, а шар разделен на 12 равных частей. Представим себе, что все 12 частей поверхности шара отогнуты от полюсов и поставлены в вертикальное положение. Сферическая поверхность условно развернется как цилиндрическая поверхность, состоящая из 12 вертикально расположенных секций. Если эти секции разместить в одной плоскости, то получится приближенная развертка поверхности шара, рис. 5.35, б. Для построения 12 меридианов очерковые окружности шара на горизонтальной и фронтальной проекциях делят на 12 равных частей.
На горизонтальной проекции меридианы спроецируются в отрезки, проходящие через центр проекции шара. Фронтальные проекции этих меридианов будут кривыми, и их строят с помощью параллелей, проведенных через точки деления фронтального меридиана.
Для построения развертки достаточно знать размеры одной секции. На рис. 5.35, а выделена одна такая секция, на проекциях которой отмечены точки пересечения двух меридианов, являющихся ее сторонами, с параллелями. Так как экватор делит секцию на две одинаковые части (верхнюю и нижнюю). То точки взяты только на той части секции, которая расположена выше экватора.
Самый широкий участок секции расположен по экватору. Его ширина равна 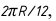
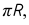
При развертке поверхности шара экватор развернется в отрезок, длина которого будет равна 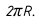
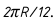
Через середину построенных отрезков проводят оси симметрий перпендикулярно экватору. Затем вверх и вниз от экватора откладывают длину развернутых участков меридианов, заключенных между параллелями. Их длина равна 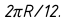
- Винтовые поверхности
- Способ вспомогательных секущих плоскостей
- Способ вспомогательных сфер
- Выполнение и оформление чертежей по ГОСТ и ЕСКД
- Построение проекций линии пересечения цилиндра плоскостью
- Развертка поверхности цилиндра
- Построение проекций линий пересечения конуса плоскостью
- Развертка поверхности конуса
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
7.1. Поверхности. Образование и задание поверхности на чертеже
Поверхности составляют широкое многообразие объектов трехмерного пространства. Инженерная деятельность человека связана непосредственно с проектированием, конструированием и изготовлением различных поверхностей. Большинство задач прикладной геометрии сводится к автоматизации проектно-конструкторского процесса и воспроизведения сложных поверхностей. Способы формообразования и отображения поверхностей составляют основу инструментальной базы трехмерного моделирования современных систем автоматизированного проектирования.
Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z)— многочлен n-ой степени и трансцендентные (F(x,y,z)— трансцендентная функция.
Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается поверхностью n-го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет исследуемая поверхность. Порядок поверхности может быть определен также числом точек её пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).
Поверхность можно рассматривать, как совокупность последовательных положений l1,l2… линии l перемещающейся в пространстве по определенному закону (Рисунок 7.1). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму — изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в виде одной линии или целого семейства линий (m, n, p…).
Подвижную линию принято называть образующей (li), неподвижные – направляющими (m). Такой способ образования поверхности принято называть кинематическим.
Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несёт на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество линий конгруэнтных профилю резца.
Рисунок 7.1 — Кинематическая поверхность
По виду образующей различают поверхности линейчатые и нелинейчатые, образующая первых – прямая линия, вторых – кривая.
Линейчатые поверхности в свою очередь разделяют на развертывающиеся, которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся.
Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Такие поверхности носят название циклические (Рисунок 7.2).
Рисунок 7.2 — Циклическая поверхность
Если группировать поверхности по закону движения образующей линии, то большинство встречающихся в технике поверхностей можно разделить на:
- поверхности вращения;
- винтовые поверхности;
- поверхности с плоскостью параллелизма;
- поверхности параллельного переноса.
Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов).
Для графического изображения поверхности на чертеже используется её каркас.
Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности.
Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом.
Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже.
Различают две части определителя: геометрическую и алгоритмическую.
Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности.
Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу.
Например, циклическая поверхность, каркас которой состоит из восьмиугольников (Рисунок 7.3), может быть задан следующим образом:
- Геометрическая часть определителя: три направляющих l, m, n.
- Алгоритмическая часть: выбираем плоскость α; находим точки А, В, С, в которых α пересекает соответственно направляющие l, m, n. Строим восьмиугольник, определяемый тремя найденными точками. Переходим к следующей плоскости и повторяем построение
Рисунок 7.3 –Образование циклической поверхности
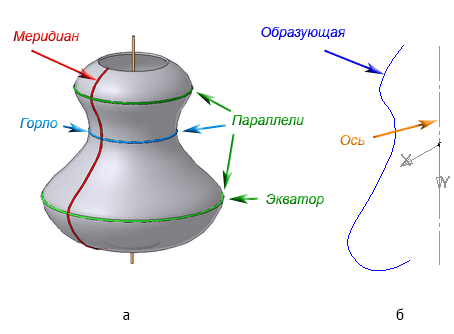
7.2. Поверхности вращения
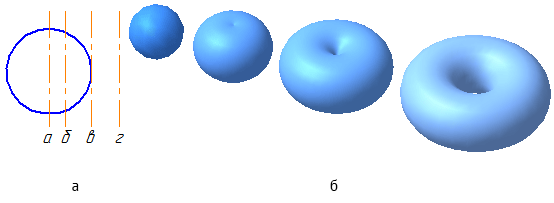
Поверхностями вращения называются поверхности, полученные вращением образующей вокруг неподвижной оси (Рисунок 7.5).
Цилиндрическая и коническая поверхности бесконечны (т.к. бесконечны образующие); сферическая, торовая поверхности — конечны.
Сферическая поверхность – частный случай торовой поверхности. При вращении окружности вокруг осей б, в, г (Рисунок 7.4, а) получим торовую поверхность (Рисунок 7.4, б), а вокруг оси а – сферическую.
Рисунок 7.4 – Образование поверхностей вращения
Рисунок 7.5 – Элементы поверхности вращения
Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости, перпендикулярной оси вращения. Эти окружности называются параллелями (Рисунок 7.5).
Наименьшая параллель называется горлом, наибольшая – экватором.
Линия пересечения поверхности вращения плоскостью, проходящей через ось, называется меридианом.
Линия пересечения поверхности вращения плоскостью, проходящая через ось, параллельно фронтальной плоскости проекций, называется главным меридианом.
7.3. Цилиндрическая поверхность
Цилиндрическая поверхность образуется движением прямой линии, которая в любом своём положении параллельна данному направлению и пересекает криволинейную направляющую (Рисунок 7.6).
Цилиндр – геометрическое тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими все образующие данной поверхности.
Взаимно параллельные плоские фигуры, ограниченные цилиндрической поверхностью, называются основаниями цилиндра.
Если нормальное сечение (плоскость сечения перпендикулярна образующим) имеет форму окружности, то цилиндрическая поверхность называется круговой.
Если образующие цилиндрической поверхности перпендикулярны к основаниям, то цилиндр называется прямым, в противном случае – наклонным.
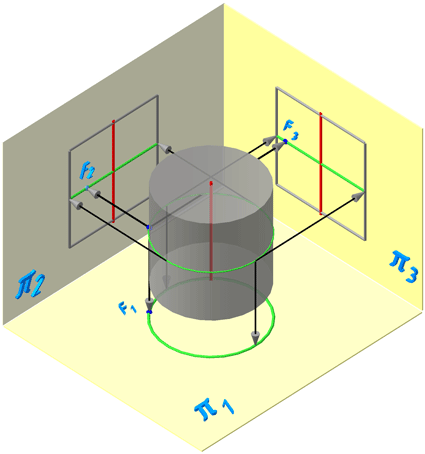
Рассмотрим проецирование прямого кругового цилиндра и принадлежащей ему точки F.
Условимся, что фронтальная проекция точки F – невидима (Рисунок 7.6).
Рисунок 7.6 – Проецирование цилиндра на плоскости проекций
Горизонтальная и профильная проекции точки F будут видимы.
При определении видимости, образующие, которые находятся на части, обращённой к наблюдателю и обозначенной на π1 сплошной зелёной линией – на плоскости проекции π2 видны, а которые находятся на части, обозначенной толстой штриховой линией – видны на π3.
Пусть точка А на π2 видима (Рисунок 7.7). Тогда на π1 она будет видима, а на π3 невидима.
Рисунок 7.7 – Эпюр прямого кругового цилиндра и принадлежащих ему точек
7.4. Пересечение прямой с поверхностью прямого кругового цилиндра
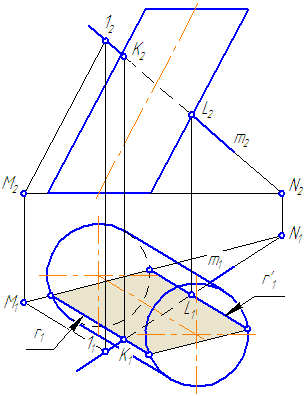
Для построения точек пересечения прямой линии с поверхностью прямого кругового цилиндра не требуется дополнительных построений. На горизонтальной плоскости проекций точки пересечения (1 и 2) находятся сразу. Фронтальные проекции строим по линиям связи.
Но в общем случае, алгоритм решения рассмотрим на следующем упражнении.
Рисунок 7.8 – Пересечение прямой с поверхностью прямого кругового цилиндра
Упражнение
Заданы: прямой круговой цилиндр с осью вращения, перпендикулярной плоскости проекций π1 и прямая а общего положения (Рисунок 7.8).
Построить точки пересечения прямой а с поверхностью цилиндра.
Решение:
Для построения точек пересечения прямой с поверхностью цилиндра необходимо:
- Заключить прямую во вспомогательную секущую плоскость частного положения σ (горизонтально-проецирующую).
- Построить фигуру пересечения поверхности цилиндра горизонтально-проецирующей плоскостью: результат пересечения — четырехугольник (на π2 условно заштрихован).
- Найти точки «входа» и «выхода» прямой: на пересечении её фронтальной проекции с фронтальными проекциями сторон четырёхугольника (они же — проекции образующей цилиндра);
Прямая а пересекается со сторонами сечения в двух точках – 1 и 2.
Определим видимость участков прямой: очевидно, что между точками 1-2 прямая невидима, а на плоскости проекций π2 будет ещё невидим участок прямой от точки 1 до левой крайней образующей.
7.5. Пересечение прямой с поверхностью наклонного цилиндра
Упражнение
Заданы: наклонный круговой цилиндр с осью вращения, наклонной к плоскости проекций π1 и прямая mобщего положения (Рисунок 7.9).
Построить точки пересечения прямой mс поверхностью цилиндра.
Решение:
Для построения точек пересечения прямой с поверхностью цилиндра необходимо:
Рисунок 7.9 – Пересечение прямой с наклонным цилиндром
- Заключить прямую m во вспомогательную плоскость σ, дающую в сечении наиболее простую фигуру – четырехугольник (σ параллельна оси цилиндра или образующим). Эту плоскость зададим двумя пересекающимися прямыми m∩(1M);
- Построить горизонтальный след плоскости σ (прямую пересечения σ с плоскостью проекций π1) как проходящую через горизонтальные следы прямых m и (1M) (точки пересечения прямых с плоскостью проекций π1 (основания)) – (MN);
- Найти точки пересечения MN с окружностью основания цилиндра. Через эти точки провести образующие r, по которым плоскость σ пересекает боковую поверхность цилиндра:
На анимации ниже представлена последовательность построения точек пересечения прямой с наклонным цилиндром.
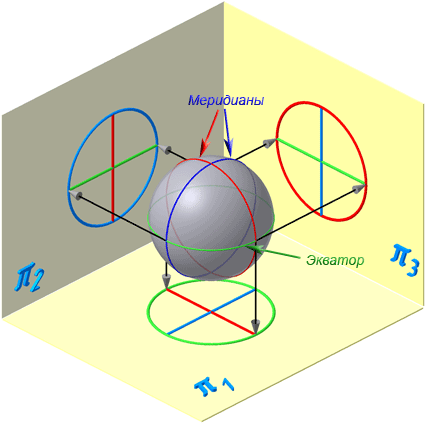
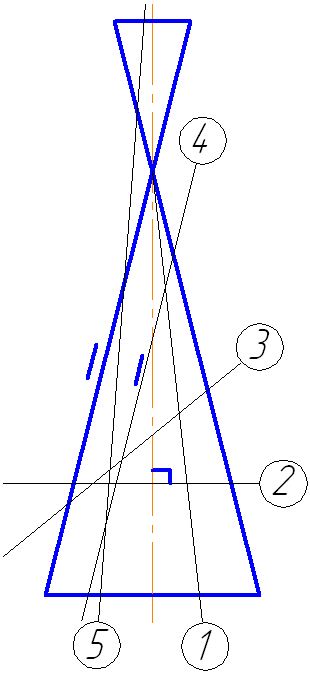
7.6. Сферическая поверхность
Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.
Шаром называется тело, ограниченное сферической поверхностью.
Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).
Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.
Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.
Рисунок 7.10 – Проецирование сферической поверхности
Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой.
Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек
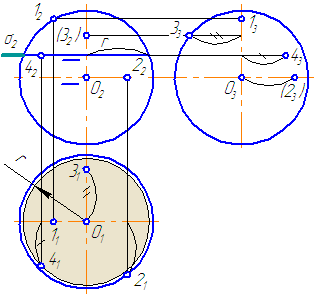
Упражнение
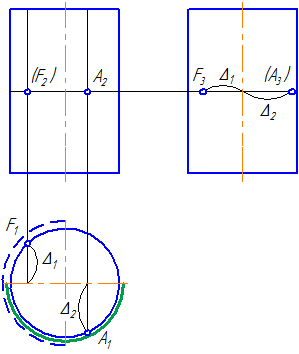
Заданы: сферическая поверхность тремя проекциями (Рисунок 7.11) и фронтальные проекции точек 1, 2, 3, 4.
Необходимо построить горизонтальные и профильные проекции заданных точек.
Решение.
- Проанализируем их расположение на поверхности сферы. Точки 1, 2, 3 лежат на очерковых образующих сферы.
- Точка 1 принадлежит главному меридиану (очерковой окружности на π2), проекция которого на π1 совпадает с проекцией горизонтальной оси, на π3 – с проекцией вертикальной оси.
- Недостающие проекции точки 1 находим посредством линий проекционной связи. Все проекции точки 1 видимы.
- Рассмотрим положение точки 2. Точка 2 принадлежит экватору (очерковой окружности на π1), проекции которого на π2 и π3 совпадают с проекцией горизонтальной оси. Горизонтальная проекция точки 2 строится посредством линии проекционной связи, для построения профильной проекции необходимо измерить расстояние, отмеченное дугой, и отложить его по линии связи от точки О3 вправо. Профильная проекция точки 2 невидима.
- Точка 3 принадлежит очерковой окружности на π3, которая также является меридианом, проекции которого на π2 и π1 совпадают с проекцией вертикальной оси. Профильная проекция точки строится посредством линии проекционной связи. Для построения горизонтальной проекции точки 3 необходимо расстояние, отмеченное на π3 двумя засечками, отложить на π1 вверх от точки О1. Горизонтальная и профильная проекции точки 3 видимы.
- Для построения проекций точки 4 необходимо ввести вспомогательную секущую плоскость (зададим плоскость σ//π1 и σ⊥π2). Плоскость σ пересекает поверхность сферы по окружности радиусом r. На π1 строим данное сечение и по линии проекционной связи находим 41. Для построения профильной проекции необходимо расстояние, отмеченное засечкой, отложить по линии проекционной связи на π3 вправо от оси. Все проекции точки 4 видимы.
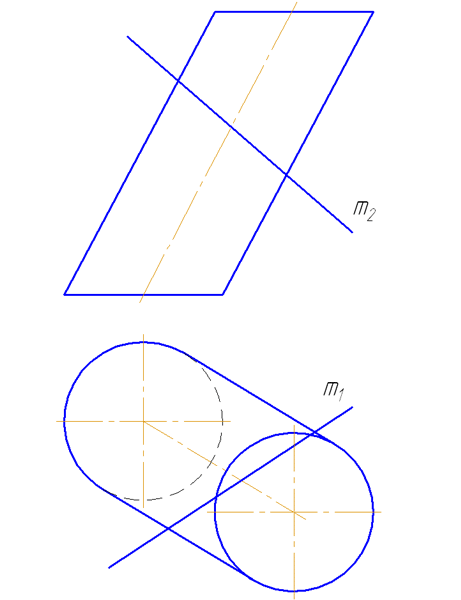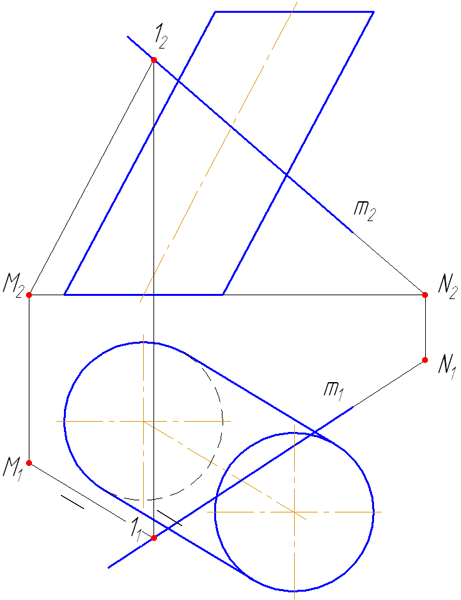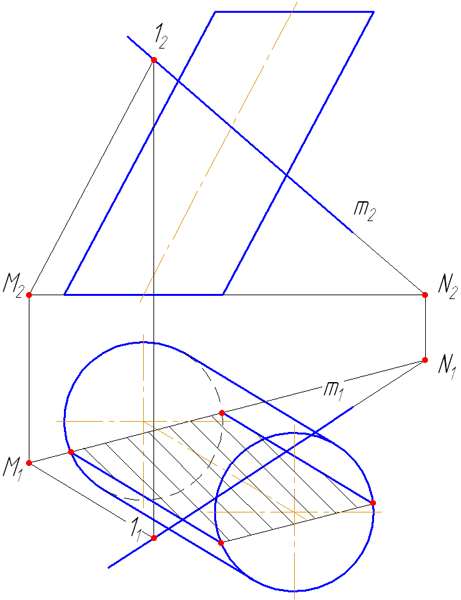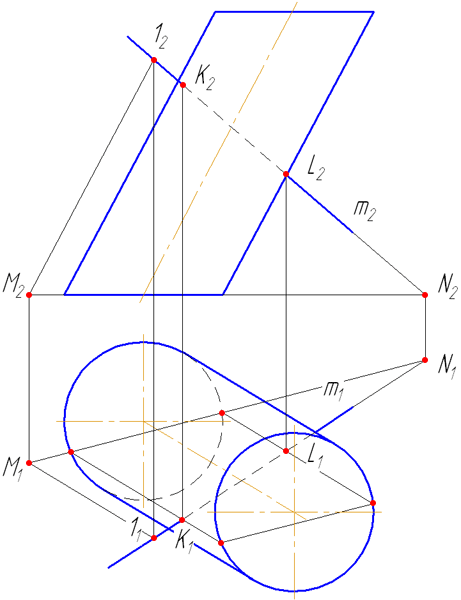
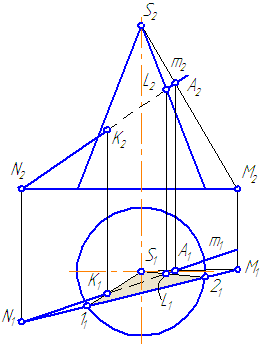
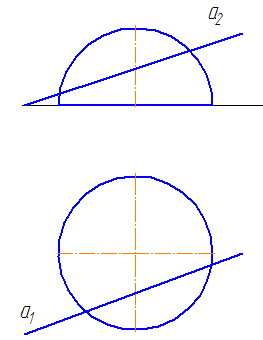
7.7. Пересечение прямой с поверхностью сферы
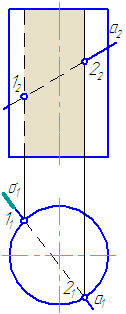
Упражнение
Заданы: сфера и прямая общего положения АВ.
Найти: точки пересечения прямой с поверхностью сферы (точки «входа» и «выхода»).
Чтобы найти точки пересечения прямой с поверхностью сферы необходимо:
- Заключить прямую во вспомогательную плоскость, пересекающую поверхность сферы так, чтобы получались простые фигуры (например, круг, ограниченный окружностью);
- Построить фигуру пересечения сферы вспомогательной плоскостью;
- Найти общие точки прямой и контура фигуры (окружность): так как прямая и окружность лежат в одной плоскости, то они, пересекаясь, образуют точки, общие для прямой и сферы, которые и будут являться искомыми точками (Рисунок 7.12).
Решение
- Через прямую проводим плоскость σ. Пусть σ⊥π1 и пересекает сферу по окружности радиусом r. С – центр окружности сечения ОС⊥σ:
Рисунок 7.12 – Пересечение прямой с поверхностью сферы
- Введём π3⊥π1 и π3//σ1. Построим проекцию окружности сечения на π3 и проекцию А3В3.
- Находим точки их пересечения 12 и 23.
- Определим видимость участков прямой.
- На π1 точки 1 и 2 находятся на переднем полушарии, следовательно, на π2 они видимы.
7.8. Коническая поверхность
Коническая поверхность образуется движением прямой линии (образующей), которая в любом своем положении проходит через неподвижную точку и пересекает криволинейную направляющую (имеет две полости).
Тело, ограниченное замкнутой конической поверхностью вершиной и плоскостью, называется конусом.
Плоская фигура, ограниченная конической поверхностью, называется основанием конуса.
Часть конической поверхности, ограниченная вершиной и основанием, называется боковой поверхностью конуса.
Если основание конуса является кругом, то конус называется круговым.
Если вершина конуса расположена на перпендикуляре к основанию, восстановленному из его центра, то конус называется прямым круговым.
Перемещая точку A» — можно изменять диаметр основания конуса;
перемещая точку O’ — можно менять положение точки на поверхности конуса.
Рисунок 7.13 – Принадлежность точки конической поверхности
Рассмотрим вопрос принадлежности точки А поверхности конуса.
Дана фронтальная проекция точки А и она видима (Рисунок 7.13).
1 способ. Для построения ортогональных проекций точки, расположенной на поверхности конуса, построим проекции образующей, проходящей через данную точку. При таком положении точки А все её проекции – видимы.
2 способ. Точка А лежит на параллели конуса радиусом r. На π1 строим проекцию окружности (параллели) и по линии проекционной связи находим А1. По двум проекциям точки строим третью.
7.9. Пересечение прямой с поверхностью конуса
Пусть задан прямой круговой конус и прямая общего положения m (Рисунок 7.14). Найти точки «входа» и «выхода» прямой с поверхностью конуса.
- Через прямую m проводим вспомогательную секущую плоскость σ, дающую в сечении наиболее простую фигуру.
- Применение в качестве вспомогательной секущей плоскости проецирующей плоскости в данном случае нецелесообразно, так как в сечении получится кривая второго порядка, которую нужно строить по точкам.
Наиболее простая фигура – треугольник. Для этого секущая плоскость σ должна пройти через вершину S. Плоскость зададим с помощью двух пересекающихся прямых σ=SM∩MN или, что, то же самое, (σ=SM∩m).
- Возьмем на прямой m точку А и соединим её с вершиной. Прямая SA пересечёт плоскость основания в точке М.
- Построим горизонтальные проекции этих объектов.
- Продлим фронтальную проекцию прямой m до пересечения с плоскостью основания в точке N.
Рисунок 7.14 – Построение точек пересечения прямой с поверхностью конуса
- Построим её горизонтальную проекцию.
- Соединим точки M1N1, на пересечении с окружностью основания получим точки 1 и 2.
- Строим треугольник сечения конуса плоскостью σ, соединив точки 1 и 2 с вершиной S.
- На пересечении образующих 1-S и 2-S с прямой m получим искомые точки K и L.
- Определим видимость прямой относительно поверхности конуса.
На анимации ниже представлена последовательность построения точек пересечения прямой с поверхностью конуса.
7.10. Пересечение цилиндра плоскостью
Пусть плоскость сечения γ – фронтально-проецирующая (Рисунок 7.15).
- Если плоскость сечения γ параллельна оси цилиндра, то она пересекает цилиндр по четырехугольнику.
- Если плоскость сечения γ перпендикулярна оси цилиндра, то она пересекает цилиндр по окружности.
- Если плоскость сечения γ не параллельна и не перпендикулярна оси цилиндра в сечении эллипс.
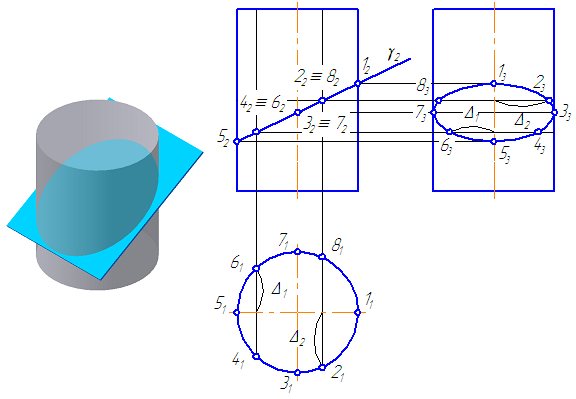
Рассмотрим алгоритм построения сечения – эллипс (Рисунок 7.15):
Рисунок 7.15 – пересечение цилиндра плоскостью
- Находим и строим характерные точки (точки, не требующие дополнительных построений) – в нашем случае, точки принадлежащие крайним образующим – 1, 3, 5, 7. Одновременно с этим, данные точки определяют величину большой и малой оси эллипса.
- Для построения участка эллипса необходимо построить не менее 5-ти точек (так как лекальная кривая второго порядка определяется как минимум пятью точками). Для построения точек 2, 4, 6, 8 возьмем на π1 произвольно расположенные образующие цилиндра, которые проецируются на данную плоскость проекции в точки.
- Построим вторые проекции данных образующих. Из точек пересечения вторых проекций образующих с проекцией плоскости сечения γ проводим линии связи к π3. Для построения третьей проекции, например, точки 6 измеряем расстояние Δ1 и откладываем его по соответствующей линии связи на π3. Симметрично ей, относительно оси вращения, строим точку 4. Аналогично строятся другие точки.
7.11. Пересечение сферы плоскостью
Плоскость пересекает поверхность сферы всегда по окружности. Задачу пересечения плоскости со сферой мы рассматривали при решении задачи построения точек пересечения прямой с поверхностью сферы (см. выше).
7.12. Пересечение конуса плоскостью
Рассмотрим пять возможных вариантов расположения плоскости относительно поверхности прямого кругового конуса. Пусть плоскость сечения перпендикулярна плоскости проекций π2 (Рисунок 7.16).
Рисунок 7.16
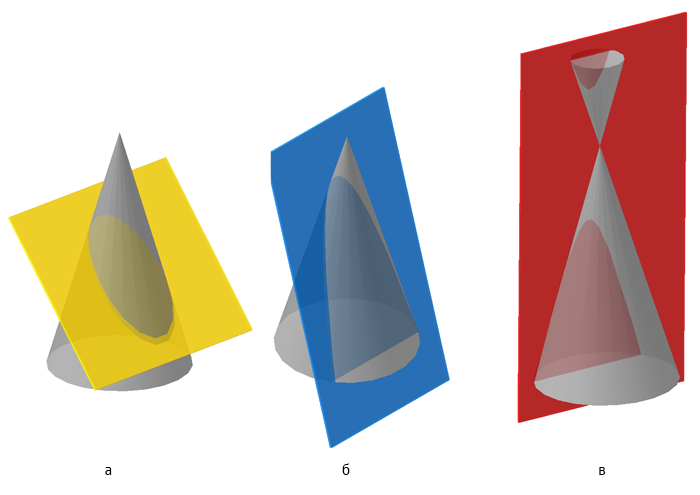
- Если плоскость проходит через вершину (1) – в сечении две образующие и прямая пересечения с плоскостью основания.
- Если плоскость перпендикулярна оси вращения конуса (2) – в сечении окружность.
- Если плоскость не параллельна ни одной образующей (пересекает все образующие (3)) – в сечении эллипс.
- Если плоскость параллельна одной образующей конуса – в сечении парабола (на примере – плоскость сечения (4) параллельна крайней образующей конуса).
- Если плоскость параллельна двум образующим (пересекает обе полости конической поверхности (5)) – в сечении гипербола (рисунок 7.17).
Рисунок 7.17. Плоскость сечения параллельна двум образующим конуса
Ниже, на моделях, представлены варианты положения секущей плоскости относительно поверхности конуса, при которых получаются сечения в виде эллипса, параболы и гиперболы.
Рисунок 7.18 – Сечение конической поверхности плоскостью (а — эллипс, б — парабола, в — гипербола)
Рассмотрим пример построения сечения конической поверхности плоскостью.
Рисунок 7.19 – Построение пересечения конической поверхности плоскостью
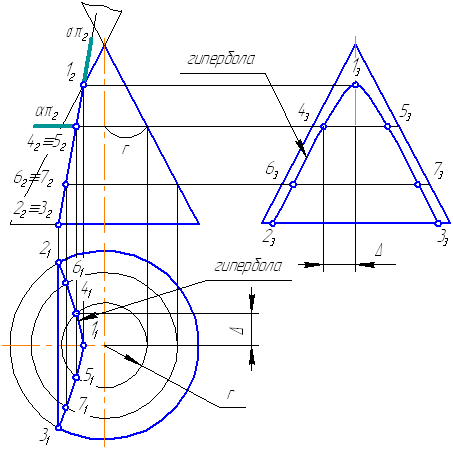
Пусть задана секущая проецирующая плоскость σ⊥π2 (Рисунок 7.19). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.
- Построим характерные точки. Это точки, лежащие на крайних образующих и на окружности основания конуса (1, 2, 3). Их проекции строятся по линиям проекционной связи.
- Для построения промежуточных точек, воспользуемся методом вспомогательных секущих плоскостей. Введём плоскость α⊥π2 и перпендикулярно оси вращения, что даст в сечении окружность радиусом r. Строим эту окружность на π1. Плоскость α пересекает и заданную плоскость сечения по прямой, проекции которой на π1 и π3 совпадают с линиями проекционной связи.
- На пересечении этих двух сечений на плоскости проекций π1 строим точки 4, 5. Профильные проекции этих точек строим по линии проекционной связи, откладывая расстояние от оси вращения конуса, равное Δ.
- Аналогично строим точки 6, 7. Плавно соединим построенные точки, образуя гиперболу.
- Обведём то, что осталось от конуса после такого среза с определением видимости. В нашем примере все проекции построенной кривой будут видимы.
На анимации ниже представлена последовательность построения пересечения конической поверхности плоскостью.
7.13. Задачи для самостоятельной работы
1. Достроить проекции сферы с заданным вырезом (Рисунок 7.20).
Рисунок 7.20
2-3. Построить три проекции конуса с призматическим отверстием (Рисунки 7.21, 7.22).
Рисунок 7.21
Рисунок 7.22
4. Построить точки «входа» и «выхода» прямой при пересечении её с поверхностью полусферы (Рисунок 7.23).
Рисунок 7.23
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.

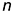 и их проекции определяются на проекциях этого меридиана;
и их проекции определяются на проекциях этого меридиана;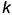 и их проекции определяются на проекциях экватора;
и их проекции определяются на проекциях экватора;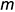 и их проекции определяются на проекциях этого меридиана.
и их проекции определяются на проекциях этого меридиана.