Как найти точку на циклоиде

В последующее сорокалетие трудами таких первоклассных ученых, как X. Гюйгенс, И Ньютон, Г В. Лейбниц и братья Бернулли, были исследованы механические применения циклоиды (см. пп. 15 и 16). Задача о брахистохроне в ее обобщенном виде явилась одним из основных истоков созданной в 18 веке трудами Л. Эйлера и Ж. Л. Лагранжа новой отрасли математики — вариационного исчисления.

Цикло́ида (от греч. κυκλοειδής «круглый») — плоская трансцендентная кривая.

Циклоида определяется кинематически как траектория фиксированной точки производящей окружности (радиуса ), катящейся без скольжения по прямой.

Уравнения[править | править код]

Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса . Циклоида описывается:

Свойства[править | править код]

Циклоиду можно рассматривать как:

• вид трохоиды в случае, когда производящая окружность катится по прямой;
• предельный случай циклогона^[en], когда число сторон многоугольника увеличивается до бесконечности.

Детали машин, которые совершают одновременно равномерное вращательное и поступательное движение, описывают циклоидальные кривые: циклоида, эпициклоида, гипоциклоида, трохоида, астроида (ср. построение лемнискаты Бернулли).

Циклоида — периодическая функция по оси абсцисс, с периодом . За границы периода удобно принять особые точки (точки возврата) вида , где  — произвольное целое число.

Для проведения касательной к циклоиде в произвольной её точке достаточно соединить эту точку с верхней точкой производящей окружности. Соединив с нижней точкой производящей окружности, мы получим нормаль.

Длина арки циклоиды равна . Другими словами, длина одной ветви циклоиды равна учетверённому диаметру производящей окружности. Это свойство открыл Кристофер Рен в 1658 году^[1]

Зависимость длины дуги циклоиды () от параметра следующая^[2]: .

Площадь под каждой аркой циклоиды втрое больше, чем площадь порождающего круга. Торричелли сообщил, что этот факт Галилей открыл экспериментально: сравнил вес пластинок с кругом и с аркой циклоиды.^[3] Математически этот факт первым доказал Роберваль около 1634 года с помощью метода неделимых.

Радиус кривизны у первой арки циклоиды равен .

«Перевёрнутая» циклоида является кривой наискорейшего спуска (брахистохроной). Более того, она имеет также свойство таутохронности: тяжёлое тело, помещённое в любую точку арки циклоиды, достигает горизонтали за одно и то же время.

Два нижеследующих свойства, открытые Гюйгенсом, были им использованы для создания точных механических часов.

• Период колебаний материальной точки, скользящей по перевёрнутой циклоиде, не зависит от амплитуды. Это непосредственное следствие таутохронности.
• Эволюта циклоиды является циклоидой, конгруэнтной исходной и параллельно сдвинутой от исходной так, что вершины переходят в «острия».

Площадь поверхности, образованной вращением арки циклоиды вокруг её основания, равна Она
превышает двойную площадь циклоиды (площадь осевого сечения) в раза^[4].

Исторический очерк[править | править код]

Первыми из учёных обратили внимание на циклоиду Николай Кузанский в XV веке и Шарль де Бовель в труде 1501 года. Но серьёзное исследование этой кривой началось только в XVII веке.

Название циклоида придумал Галилей (во Франции эту кривую сначала называли рулеттой). Содержательное исследование циклоиды провёл современник Галилея Мерсенн. Среди трансцендентных кривых (то есть кривых, уравнение которых не может быть записано в виде многочлена от ), циклоида — первая из исследованных.

Паскаль писал о циклоиде^[5][6]:

Рулетта является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели её древние… ибо это не что иное, как путь, описываемый в воздухе гвоздём колеса…

La Roulette est une ligne si commune, qu’apres la droitte, & la circulaire, il n’y en a point de si frequente; Et elle se décrit si fouuent aux yeux de tout le monde, qu’il y a lieu de s’estonner qu’elle n’ait point esté considerée par les anciens, dans lesquels on n’en trouue rien : Car ce n’est autre chose que le chemin que fait en l’air, le clou d’une rouë…

Новая кривая быстро завоевала популярность и подверглась глубокому анализу, в котором участвовали Декарт, Ферма, Ньютон, Лейбниц, братья Якоб и Иоганн Бернулли и другие корифеи науки XVII—XVIII веков. На циклоиде активно оттачивались методы появившегося в те годы математического анализа.

Тот факт, что аналитическое исследование циклоиды оказалось столь же успешным, как и анализ алгебраических кривых, произвёл большое впечатление и стал важным аргументом в пользу «уравнения в правах» алгебраических и трансцендентных кривых.

Применение[править | править код]

Один из самых популярных типов шестерёнок — с циклоидальными зубьями. Циклоидальные профили чаще встречаются в часовых механизмах^[7].

См. также[править | править код]

• Циклоидальная кривая

Примечания[править | править код]

Литература[править | править код]

• Берман Г. Н. Циклоида. М., Наука, 1980, 112 с.
• Выгодский М. Я. Справочник по высшей математике. — М.: АСТ, 2019. — 704 с. — ISBN 978-5-17-117741-6.
• Гиндикин С. Г. Рассказы о физиках и математиках. — издание третье, расширенное. — М.: МЦНМО, 2001. — С. 126-165. — ISBN 5-900916-83-9.
• Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 5.
• Маркушевич А. И. Замечательные кривые, Популярные лекции по математике, выпуск 4, Наука 1978 г., стр. 32.
• Циклоида // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.

Ссылки[править | править код]

• Веров С. Г. Тайны циклоиды // Квант. — 1975. — № 8. — С. 19—27.
• Циклоидальные кривые (Анимация).

3. Основные свойства касательной и нормали к циклоиде

Непосредственно очевидно, что ∟DOM равен 90° — φ.

Значит, ∟OMP = 90° — φ. Таким образом, получаем:

∟РМТ = ∟ОМТ – ∟ ОМР = 90° — — (90° — φ) = .

Получается замечательный результат: угол РМТ оказывается равным углу РМЕ (см. теорему 2). Следовательно, прямые ME и МТ сольются! Наш рис. 18 сделан не совсем правильно! Правильное расположение линий дано на рис. 19.

Сформулируем полученный результат виде теоремы 3.

Теорема 3 (первое основное свойство циклоиды). Нормаль к циклоиде проходит через «нижнюю» точку производящего круга.

Из этой теоремы получается простое следствие. Угол между касательной и нормалью, по определению, — прямой. Это угол, вписанный в окружность производящего круга. Поэтому он должен опираться на диаметр круга. Итак, ТТ₁— диаметр, и T₁ — «верхняя» точка производящего круга. Сформулируем полученный результат.

Следствие (второе основное свойство циклоиды). Касательная к циклоиде проходит через «верхнюю» точку производящего круга.

Что бы объяснить это свойство нам необходимо построить циклоиду.

Построение циклоиды.

Построение циклоиды производится в следующей последовательности:

1. На направляющей горизонтальной прямой откладывают отрезок АА₁₂, равный длине производящей окружности радиуса r, (2πr);

2. Строят производящую окружность радиуса r, так чтобы направляющая прямая была касательной к неё в точке А;

3. Окружность и отрезок АА₁₂ делят на несколько равных частей, например на 12;

4. Из точек делений 1¹, 2¹, …12¹ восстанавливают перпендикуляры до пересечения с продолжением горизонтальной оси окружности в точках 0₁, 0₂, …0₁₂;

5. Из точек деления окружности 1, 2, …12 проводят горизонтальные прямые, на которых делают засечки дугами окружности радиуса r;

6. Полученные точки А₁, А₂, …А₁₂ принадлежат циклоиде.

На рис. 20 основание циклоиды разделено на 6 равных частей;

чем число делений будет больше, тем, как мы знаем, чертеж получится точнее. В каждой точке циклоиды, построенной нами, проведем касательную, соединяя точку кривой с «верхней» точкой производящего круга. На нашем чертеже получилось семь касательных (из них две — вертикальные). Проводя теперь циклоиду от руки, будем заботиться, чтобы она действительно касалась каждой из этих касательных: это значительно увеличит точность чертежа. При этом сама циклоида будет огибать все эти касательные ¹).

Проведем на том же рис. 20 нормали во всех найденных точках циклоиды. Всего будет, не считая направляющей, пять нормалей. Можно построить от руки сгибающую этих нормалей. Если бы мы вместо шести взяли 12 или 16 точек деления, то нормалей на чертеже было бы больше, и огибающая наметилась бы ясней. Такая огибающая всех нормалей играет важную роль при изучении свойств любой кривой линии. В случае циклоиды обнаруживается любопытный факт: огибающей нормалей циклоиды служит точно такая же циклоида, только сдвинутая на 2а вниз и на πа вправо. Этот факт характерен именно для циклоиды.

4. Геометрическое определение циклоиды

Теперь мы дадим определение циклоиды как геометрического места точек, не пользуясь механикой. Проще всего поступить так. Рассмотрим произвольную прямую АВ (будем условно считать ее направление горизонтальным) и на ней точку М₀. Далее рассмотрим всевозможные круги определенного радиуса, касающиеся этой прямой и расположенные по одну сторону от нее. На каждом круге от точки Т касания его с прямой АВ отложим (в направлении к точке М₀) дугу ТМ, по длине равную отрезку М₀Т. Геометрическое место точек М (взятых на всех упомянутых нами кругах) и будет циклоидой.

Установим еще одно важное свойство циклоиды и попробуем именно его положить в основу изучения этой кривой.

Рассмотрим треугольник МТТ₁ (рис. 21), образованный вертикальным диаметром производящего круга, касательной к циклоиде и нормалью к ней.

Связь между «высотой» и наклоном касательной

Угол МТ₁Т, как вписанный в окружность, равен половине центрального угла, опирающегося на ту же дугу, т. е. равен . Проведем МК||АВ и ME ┴ АВ. Отрезок МЕ будет играть в дальнейшем значительную роль, поэтому дадим ему имя и обозначение: будем называть его «высотою» точки М циклоиды и обозначать буквою h. Итак, высота точки М циклоиды — это расстояние ее от направляющей прямой.

Обратим внимание на угол КМТ. Он равен углу МТ₁Т. Из треугольника ТМТ₁ получаем:

МТ = 2а sin

а из треугольника ТКМ:

КТ = МТ sin- .

Сопоставляя эти результаты и замечая, что КТ = h, получим окончательно:

h = 2a sin²

Мы выразили высоту точки М через угол между касательной в точке М и вертикалью (горизонталью мы по-прежнему считаем направление прямой АВ). Теперь выразим синус этого угла через «высоту». Получим, очевидно:

где через k обозначена постоянная для данной циклоиды величина Полученный результат изложим в теореме.

Теорема 4. Синус угла между касательной к циклоиде в точке М и вертикалью пропорционален корню квадратному из «высоты» точки М.

Этим свойством обладает, очевидно, любая циклоида. Возникает вопрос: в какой мере это свойство характеризует именно циклоиду: будет ли всякая кривая, обладающая этим свойством, непременно циклоидой? Можно доказать, что это будет именно так, — что верна и следующая (обратная) теорема:

Теорема 5. Если даны прямая АВ и точка М, то единственной кривой, удовлетворяющей условиям теоремы 4 и проходящей через точку М, будет циклоида.

При этом радиус производящего круга этой циклоиды связан с коэффициентом k, о котором говорится в теореме 4, следующим соотношением:

(Разумеется, расстояние точки М от АВ должно быть меньше, чем 2а.)

Строгое доказательство этой теоремы средствами элементарной математики очень громоздко, и мы его приводить здесь не будем.

Семейство циклоид

Если в условии теоремы 5 не оговорить, что искомая кривая проходит через наперед указанную точку М, то получится не одна, а бесконечное множество циклоид, которые получаются друг из друга параллельным сдвигом по направлению прямой АВ (одна из них проходит через точку М, другая — через М₁ третья — через М₂ и т. д.). Это множество, или, как его называют, семейство циклоид изображено на рис. 22.

5. Параметрическое уравнение циклоиды и уравнение в декартовых координатах

Допустим, что у нас дана циклоида, образованная окружностью радиуса а с центром в точке А.

Если выбрать в качестве параметра, определяющего положение точки, угол t=∟NDM на который успел повернуться радиус, имевший в начале качения вертикально е положение АО, то координаты х и у точки М выразятся следующим образом:

х= OF = ON – NF = NM – MG = at-a sin t,

y= FM = NG = ND – GD = a – a cos t

Итак параметрические уравнения циклоиды имеют вид:

(0

≤ t ≤ 2π).

При изменении t от -∞ до +∞ получится кривая, состоящая из бесчисленного множества таких ветвей, какая изображена на данном рисунке.

Так же, помимо параметрического уравнения циклоиды, существует и ее уравнение в декартовых координатах:

, где r – радиус окружности, образующей циклоиду.

6. Задачи на нахождение частей циклоиды и фигур, образованных циклоидой

Задача №1. Найти площадь фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрически

и осью Ох.

Решение. Для решения данной задачи, воспользуемся известными нам фактами из теории интегралов, а именно:

Площадь криволинейного сектора.

Рассмотрим некоторую функцию r = r(ϕ), определенную на [α, β].

Будем считать, что r и ϕ — полярные координаты точки. Тогда любому

ϕ₀ ∈ [α, β] соответствует r₀ = r(ϕ₀) и, значит, точка M₀(ϕ₀, r₀), где ϕ₀,

r₀ — полярные координаты точки. Если ϕ будет меняться, «пробегая» весь[α, β], то переменная точка M опишет некоторую кривую AB, заданную

уравнением r = r(ϕ).

Определение 7.4. Криволинейным сектором называется фигура, ограниченная двумя лучами ϕ = α, ϕ = β и кривой AB, заданной в полярных

координатах уравнением r = r(ϕ), α ≤ ϕ ≤ β.

Справедлива следующая

Теорема. Если функция r(ϕ) > 0 и непрерывна на [α, β], то площадь

криволинейного сектора вычисляется по формуле:

Эта теорема была доказана ранее в теме определенного интеграла.

Исходя из приведенной выше теоремы, наша задача о нахождении площади фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрические x= a (t – sin t) , y= a (1 – cos t) , и осью Ох, сводится к следующему решению.

Решение. Из уравнения кривой dx = a(1−cos t) dt. Первая арка циклоиды соответствует изменению параметра t от 0 до 2π. Следовательно,

Задача №2. Найти длину одной арки циклоиды

Так же в интегральном исчислении изучалась следующая теорема и следствие из нее.

Теорема. Если кривая AB задана уравнением y = f(x), где f(x) и f^’(x) непрерывны на [a, b], то AB является спрямляемой и

Следствие. Пусть AB задана параметрически

L_AB = (1)

Пусть функции x(t), y(t) непрерывно-дифференцируемые на [α, β]. Тогда

формулу (1) можно записать так

Сделаем замену переменных в этом интеграле x = x(t), тогда y’(x)= ;

dx= x’(t)dt и, следовательно:

From Wikipedia, the free encyclopedia

In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another curve.

The cycloid, with the cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object’s starting position (the tautochrone curve). In physics, when a charged particle at rest is put under a uniform electric and magnetic field perpendicular to one another, the particle’s trajectory draws out a cycloid.

History[edit]

The cycloid has been called “The Helen of Geometers” as, like Helen of Troy, it caused frequent quarrels among 17th-century mathematicians, while Sarah Hart sees it named as such “because the properties of this curve are so beautiful”.^[1][2]

Historians of mathematics have proposed several candidates for the discoverer of the cycloid. Mathematical historian Paul Tannery speculated that such a simple curve must have been known to the ancients, citing similar work by Carpus of Antioch described by Iamblichus.^[3] English mathematician John Wallis writing in 1679 attributed the discovery to Nicholas of Cusa,^[4] but subsequent scholarship indicates that either Wallis was mistaken or the evidence he used is now lost.^[5] Galileo Galilei’s name was put forward at the end of the 19th century^[6] and at least one author reports credit being given to Marin Mersenne.^[7] Beginning with the work of Moritz Cantor^[8] and Siegmund Günther,^[9] scholars now assign priority to French mathematician Charles de Bovelles^[10][11][12] based on his description of the cycloid in his Introductio in geometriam, published in 1503.^[13] In this work, Bovelles mistakes the arch traced by a rolling wheel as part of a larger circle with a radius 120% larger than the smaller wheel.^[5]

Galileo originated the term cycloid and was the first to make a serious study of the curve.^[5] According to his student Evangelista Torricelli,^[14] in 1599 Galileo attempted the quadrature of the cycloid (determining the area under the cycloid) with an unusually empirical approach that involved tracing both the generating circle and the resulting cycloid on sheet metal, cutting them out and weighing them. He discovered the ratio was roughly 3:1, which is the true value, but he incorrectly concluded the ratio was an irrational fraction, which would have made quadrature impossible.^[7] Around 1628, Gilles Persone de Roberval likely learned of the quadrature problem from Père Marin Mersenne and effected the quadrature in 1634 by using Cavalieri’s Theorem.^[5] However, this work was not published until 1693 (in his Traité des Indivisibles).^[15]

Constructing the tangent of the cycloid dates to August 1638 when Mersenne received unique methods from Roberval, Pierre de Fermat and René Descartes. Mersenne passed these results along to Galileo, who gave them to his students Torricelli and Viviana, who were able to produce a quadrature. This result and others were published by Torricelli in 1644,^[14] which is also the first printed work on the cycloid. This led to Roberval charging Torricelli with plagiarism, with the controversy cut short by Torricelli’s early death in 1647.^[15]

In 1658, Blaise Pascal had given up mathematics for theology but, while suffering from a toothache, began considering several problems concerning the cycloid. His toothache disappeared, and he took this as a heavenly sign to proceed with his research. Eight days later he had completed his essay and, to publicize the results, proposed a contest. Pascal proposed three questions relating to the center of gravity, area and volume of the cycloid, with the winner or winners to receive prizes of 20 and 40 Spanish doubloons. Pascal, Roberval and Senator Carcavy were the judges, and neither of the two submissions (by John Wallis and Antoine de Lalouvère) was judged to be adequate.^[16]: 198 While the contest was ongoing, Christopher Wren sent Pascal a proposal for a proof of the rectification of the cycloid; Roberval claimed promptly that he had known of the proof for years. Wallis published Wren’s proof (crediting Wren) in Wallis’s Tractus Duo, giving Wren priority for the first published proof.^[15]

Fifteen years later, Christiaan Huygens had deployed the cycloidal pendulum to improve chronometers and had discovered that a particle would traverse a segment of an inverted cycloidal arch in the same amount of time, regardless of its starting point. In 1686, Gottfried Wilhelm Leibniz used analytic geometry to describe the curve with a single equation. In 1696, Johann Bernoulli posed the brachistochrone problem, the solution of which is a cycloid.^[15]

Equations[edit]

The cycloid through the origin, generated by a circle of radius r rolling over the x–axis on the positive side (y ≥ 0), consists of the points (x, y), with

where t is a real parameter corresponding to the angle through which the rolling circle has rotated. For given t, the circle’s centre lies at (x, y) = (rt, r).

The Cartesian equation is obtained by solving the y-equation for t and substituting into the x–equation:

or, eliminating the multiple-valued inverse cosine:

When y is viewed as a function of x, the cycloid is differentiable everywhere except at the cusps on the x-axis, with the derivative tending toward or near a cusp. The map from t to (x, y) is differentiable, in fact of class C^∞, with derivative 0 at the cusps.

The slope of the tangent to the cycloid at the point is given by .

A cycloid segment from one cusp to the next is called an arch of the cycloid, for example the points with and .

Considering the cycloid as the graph of a function , it satisfies the differential equation:^[17]

Involute[edit]

The involute of the cycloid has exactly the same shape as the cycloid it originates from. This can be visualized as the path traced by the tip of a wire initially lying on a half arch of the cycloid: as it unrolls while remaining tangent to the original cycloid, it describes a new cycloid (see also cycloidal pendulum and arc length).

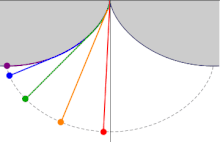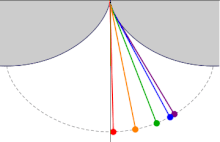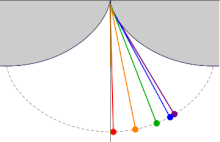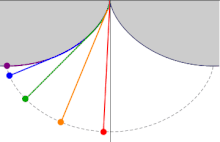
Demonstration[edit]

This demonstration uses the rolling-wheel definition of cycloid, as well as the instantaneous velocity vector of a moving point, tangent to its trajectory. In the adjacent picture, and are two points belonging to two rolling circles, with the base of the first just above the top of the second. Initially, and coincide at the intersection point of the two circles. When the circles roll horizontally with the same speed, and traverse two cycloid curves. Considering the red line connecting and at a given time, one proves the line is always tangent to the lower arc at and orthogonal to the upper arc at . Let be the point in common between the upper and lower circles at the given time. Then:

• are colinear: indeed the equal rolling speed gives equal angles , and thus . The point lies on the line therefore and analogously . From the equality of and one has that also . It follows .
• If is the meeting point between the perpendicular from to the line segment and the tangent to the circle at , then the triangle is isosceles, as is easily seen from the construction: and . For the previous noted equality between and then and is isosceles.
• Drawing from the orthogonal segment to , from the straight line tangent to the upper circle, and calling the meeting point, one sees that is a rhombus using the theorems on angles between parallel lines
• Now consider the velocity of . It can be seen as the sum of two components, the rolling velocity and the drifting velocity , which are equal in modulus because the circles roll without skidding. is parallel to , while is tangent to the lower circle at and therefore is parallel to . The rhombus constituted from the components and is therefore similar (same angles) to the rhombus because they have parallel sides. Then , the total velocity of , is parallel to because both are diagonals of two rhombuses with parallel sides and has in common with the contact point . Thus the velocity vector lies on the prolongation of . Because is tangent to the cycloid at , it follows that also coincides with the tangent to the lower cycloid at .
• Analogously, it can be easily demonstrated that is orthogonal to (the other diagonal of the rhombus).
• This proves that the tip of a wire initially stretched on a half arch of the lower cycloid and fixed to the upper circle at will follow the point along its path without changing its length because the speed of the tip is at each moment orthogonal to the wire (no stretching or compression). The wire will be at the same time tangent at to the lower arc because of the tension and the facts demonstrated above. (If it were not tangent there would be a discontinuity at and consequently unbalanced tension forces.)

Area[edit]

Using the above parameterization , the area under one arch, is given by:

This is three times the area of the rolling circle.

Arc length[edit]

The arc length S of one arch is given by

Another geometric way to calculate the length of the cycloid is to notice that when a wire describing an involute has been completely unwrapped from half an arch, it extends itself along two diameters, a length of 4r. This is thus equal to half the length of arch, and that of a complete arch is 8r.

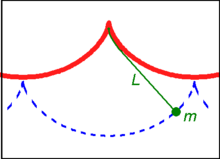
Cycloidal pendulum[edit]

If a simple pendulum is suspended from the cusp of an inverted cycloid, such that the string is constrained to be tangent to one of its arches, and the pendulum’s length L is equal to that of half the arc length of the cycloid (i.e., twice the diameter of the generating circle, L = 4r), the bob of the pendulum also traces a cycloid path. Such a pendulum is isochronous, with equal-time swings regardless of amplitude. Introducing a coordinate system centred in the position of the cusp, the equation of motion is given by:

where is the angle that the straight part of the string makes with the vertical axis, and is given by

where A < 1 is the “amplitude”, is the radian frequency of the pendulum and g the gravitational acceleration.

The 17th-century Dutch mathematician Christiaan Huygens discovered and proved these properties of the cycloid while searching for more accurate pendulum clock designs to be used in navigation.^[18]

[edit]

Several curves are related to the cycloid.

• Trochoid: generalization of a cycloid in which the point tracing the curve may be inside the rolling circle (curtate) or outside (prolate).
• Hypocycloid: variant of a cycloid in which a circle rolls on the inside of another circle instead of a line.
• Epicycloid: variant of a cycloid in which a circle rolls on the outside of another circle instead of a line.
• Hypotrochoid: generalization of a hypocycloid where the generating point may not be on the edge of the rolling circle.
• Epitrochoid: generalization of an epicycloid where the generating point may not be on the edge of the rolling circle.

All these curves are roulettes with a circle rolled along another curve of uniform curvature. The cycloid, epicycloids, and hypocycloids have the property that each is similar to its evolute. If q is the product of that curvature with the circle’s radius, signed positive for epi- and negative for hypo-, then the similitude ratio of curve to evolute is 1 + 2q.

The classic Spirograph toy traces out hypotrochoid and epitrochoid curves.

Other uses[edit]

The cycloidal arch was used by architect Louis Kahn in his design for the Kimbell Art Museum in Fort Worth, Texas. It was also used by Wallace K. Harrison in the design of the Hopkins Center at Dartmouth College in Hanover, New Hampshire.^[19]

Early research indicated that some transverse arching curves of the plates of golden age violins are closely modeled by curtate cycloid curves.^[20] Later work indicates that curtate cycloids do not serve as general models for these curves,^[21] which vary considerably.

See also[edit]

• Cyclogon
• Cycloid gear
• List of periodic functions
• Tautochrone curve

References[edit]

Further reading[edit]

• An application from physics: Ghatak, A. & Mahadevan, L. Crack street: the cycloidal wake of a cylinder tearing through a sheet. Physical Review Letters, 91, (2003). link.aps.org
• Edward Kasner & James Newman (1940) Mathematics and the Imagination, pp 196–200, Simon & Schuster.
• Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. 445–47. ISBN 0-14-011813-6.

External links[edit]

• O’Connor, John J.; Robertson, Edmund F., “Cycloid”, MacTutor History of Mathematics archive, University of St Andrews
• Weisstein, Eric W. “Cycloid”. MathWorld. Retrieved April 27, 2007.
• Cycloids at cut-the-knot
• A Treatise on The Cycloid and all forms of Cycloidal Curves, monograph by Richard A. Proctor, B.A. posted by Cornell University Library.
• Cycloid Curves by Sean Madsen with contributions by David von Seggern, Wolfram Demonstrations Project.
• Cycloid on PlanetPTC (Mathcad)
• A VISUAL Approach to CALCULUS problems by Tom Apostol