-
Метод проекций.
Проекция (лат. projectio — выбрасывание
вперёд) — изображение трёхмерной фигуры
на так называемой картинной (проекционной)
плоскости.
Термин проекция также означает метод
построения такого изображения и
технические приёмы, в основе которых
лежит этот метод.
Принцип
Проекционный метод изображения предметов
основан на их зрительном представлении.
Если соединить все точки предмета
прямыми линиями (проекционными лучами)
с постоянной точкой S(центр проекции), в которой предполагается
глаз наблюдателя, то на пересечении
этих лучей с какой-либо плоскостью
получается проекция всех точек предмета.
Соединив эти точки прямыми линиями в
том же порядке, как они соединены в
предмете, получим на плоскостиперспективное изображение предмета
или центральную проекцию.
Если центр проекции бесконечно удалён
от картинной плоскости, то говорят о
параллельной проекции, а если при
этом проекционные лучи падают
перпендикулярно к плоскости — то обортогональной проекции.
Проекция широко применяется в инженерной
графике, архитектуре, живописи и
картографии.
Изучением проекций и методов проектирования
занимается начертательная геометрия.
Проекционный чертеж– чертеж,
построенный методом проецирования
пространственных объектов на плоскость.
Является основным средством для анализа
свойств пространственных фигур.
Аппарат проецирования:
-
Центр проецирования (S)
-
Проекционные лучи
-
Объект проецирования
-
Проекция
Комплексный чертеж– эпюр Монжа.
Декартова система координат, ось (x,y,z)
Плоскости:
Фронтальная – вид спереди;
Горизонтальная – вид сверху;
Профильная – вид сбоку.
Состав комплексного чертежа:
1) Плоскости проекций
2) Оси проекций (пересечение плоскостей
проекций)
3) Проекции
Линии связи.
-
Основные свойства ортогонального
проецирования.
2 связанные между собой ортогональные
проекции однозначно определяют положение
точки относительно плоскостей проекции.
3-яя проекция не может быть задана
произвольно.
Ортогональные проекции.
Ортогональное (прямоугольное) проецирование
есть частный случай проецирования
параллельного, когда все проецирующие
лучи перпендикулярны плоскости проекций.
Ортогональным проекциям присущи все
свойства параллельных проекций, но при
прямоугольном проецировании проекция
отрезка, если он не параллелен плоскости
проекций, всегда меньше самого отрезка
(рис. 58). Это объясняется тем, что сам
отрезок в пространстве является
гипотенузой прямоугольного треугольника,
а его проекция — катетом: А’В’ = ABcosa.
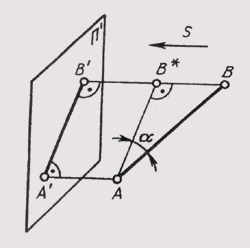
Рис. 58
При прямоугольном проецировании прямой
угол проецируется в натуральную величину,
когда обе стороны его параллельны
плоскости проекций, и тогда, когда лишь
одна из его сторон параллельна плоскости
проекций, а вторая сторона не перпендикулярна
этой плоскости проекций.
Теорема о проецировании прямого угла.
Если одна сторона прямого угла параллельна
плоскости проекций, а вторая ей не
перпендикулярна, то при ортогональном
проецировании прямой угол проецируется
на эту плоскость в прямой же угол.
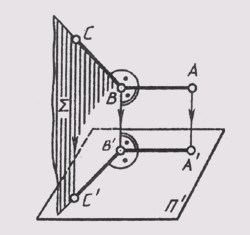
Рис. 59
Пусть дан прямой угол ABC,
у которого сторона АВ параллельна
плоскости п’ (рис. 59). Проецирующая
плоскость перпендикулярна плоскости
п’. Значит, АВ _|_S, так как
АВ _|_ ВС и АВ _|_ ВВ, отсюда АВ _|_ В’С’. Но
так какАВ || А’В’ _|_ В’С’, т. е. на плоскости
п’ угол между А’В’ и В’С равен 90°.
Обратимость чертежа. Проецирование на
одну плоскость проекций дает изображение,
которое не позволяет однозначно
определить форму и размеры изображенного
предмета. Проекция А (см. рис. 53) не
определяет положение самой точки в
пространстве, так как не известно, на
какое расстояние она удалена от плоскости
проекций п’. Любая точка проецирующего
луча, проходящего через точку А, будет
иметь своей проекцией точку А’. Наличие
одной проекции создает неопределенность
изображения. В таких случаях говорят о
необратимости чертежа, так как по такому
чертежу невозможно воспроизвести
оригинал. Для исключения неопределенности
изображение дополняют необходимыми
данными. В практике применяют различные
способы дополнения однопроекционного
чертежа. В данном курсе будут рассмотрены
чертежи, получаемые ортогональным
проецированием на две или более взаимно
перпендикулярные плоскости проекций
(комплексные чертежи) и путем
перепроецирования вспомогательной
проекции предмета на основную
аксонометрическую плоскость проекций
(аксонометрические чертежи).
-
Комплексный чертеж.
Прямая на комплексном чертеже:
-
Проекциями 2 точек
-
Непосредственно проекциями самой
прямой
Прямая общего положения– не
параллельна и не перпендикулярна к
плоскостям проекции.
Линии уровня– линии, параллельные
плоскостям проекции:
-
Горизонталь
-
Фронталь
-
Профильная
Общее свойство: у линий уровня одна
проекция равна натуральной величине,
другие проекции параллельны осям
проекций.
Проецирующие прямые– дважды линии
уровня (если перпендикулярны одной из
плоскостей, то параллельны 2 другим):
-
Горизонтально-проецирующая
-
Фронтально-проецирующая
-
Профильно-проецирующая
Конкурирующие точки– точки, лежащие
на одной линии связи.
Взаимное расположение 2 прямых:
-
Пересекающееся – имеют 1 общую точку
и общие проекции этой точки -
Параллельные – проекции всегда
параллельны у 2 параллельных прямых -
Скрещивающиеся – не имеют общих точек,
пересекаются только проекции, а не сами
прямые -
Конкурирующие – прямые лежат в плоскости
перпендикулярной к одной из плоскостей
проекций (н-р, горизонтально-конкурирующие)
Элементы трехпроекционного комплексного
чертежа точки.
Для определения положения геометрического
тела в пространстве и получения
дополнительных сведений на их изображениях
может возникнуть необходимость в
построении третьей проекции. Тогда
третью плоскость проекций располагают
справа от наблюдателя перпендикулярно
одновременно горизонтальной плоскости
проекций П1 и фронтальной плоскости
проекций П2 (рис. 62, а). В результате
пересечения фронтальной П2 и профильной
П3 плоскостей проекций получаем новую
ось П2/П3, которая располагается на
комплексном чертеже параллельно
вертикальной линии связи A1A2
(рис. 62, б). Третья проекция точки А —
профильная — оказывается связанной с
фронтальной проекцией А2 новой линией
связи, которую называют горизонталь-
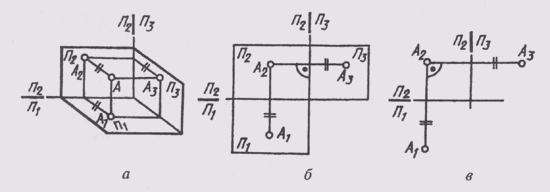
Рис. 62
ной. Фронтальная и профильная проекции
точки всегда лежат на одной горизонтальной
линии связи. Причем A1A2
_|_ А2А1 и А2А3, _|_ П2/П3.
Положение точки в пространстве в этом
случае характеризуется ее широтой —
расстоянием от нее до профильной
плоскости проекций П3, которое обозначим
буквой р.
Полученный комплексный чертеж точки
называется трехпроек-ционным.
В трехпроекционном чертеже глубина
точки АА2 проецируется без искажений
на плоскости П1и П2 (рис. 62, а). Это
обстоятельство позволяет построить
третью — фронтальную проекцию точки А
по ее горизонтальной А1 и фронтальной
А2 проекциям (рис. 62, в). Для этого через
фронтальную проекцию точки нужно
провести горизонтальную линию связи
A2A3 _|_A2A1.
Затем в любом месте на чертеже провести
ось проекций П2/П3 _|_ А2А3, измерить глубинуfточки на горизонтальном
поле проекции и отложить ее по
горизонтальной линии связи от оси
проекций П2/П3. Получим профильную
проекцию А3 точки А.
Таким образом, на комплексном чертеже,
состоящем из трех ортогональных проекций
точки, две проекции находятся на одной
линии связи; линии связи перпендикулярны
соответствующим осям проекций; две
проекции точки вполне определяют
положение ее третьей проекции.
Необходимо отметить, что на комплексных
чертежах, как правило, не ограничивают
плоскости проекций и положение их задают
осями (рис. 62, в). В тех случаях, когда
условиями задачи этого не требу-
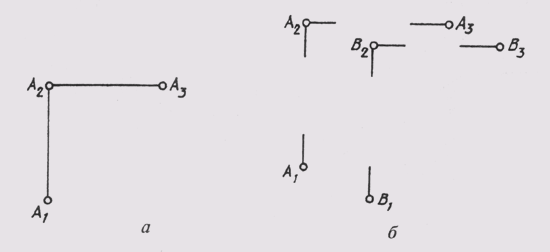
Рис. 63
ется, проекции точек могут быть даны
без изображения осей (рис. 63, а, б). Такая
система называется безосновой. Линии
связи могут также проводиться с разрывом
(рис. 63, б).
5. Прямая на комплексном чертеже. Основные положения.
Комплексный чертеж прямой линии.
Учитывая то, что прямую линию в пространстве
можно определить положением двух ее
точек, для построения ее на чертеже
достаточно выполнить комплексный чертеж
этих двух точек, а затем соединить
одноименные проекции точек прямыми
линиями. При этом получаем соответственно
горизонтальную и фронтальную проекции
прямой.
На рис. 69, а показаны прямая l и принадлежащие
ей точки А и В. Для построения фронтальной
проекции прямой l2 достаточно построить
фронтальные проекции точек А2 и В2 и
соединить их прямой. Аналогично строится
горизонтальная проекция, проходящая
через горизонтальные проекции точек
А1 и В1. После совмещения плоскости П1 с
плоскостью П2 получим двухпроекционный
комплексный чертеж прямой l (рис. 69, б).
Профильную проекцию прямой можно
построить с помощью профильных проекций
точек А и В. Кроме того, профильную
проекцию прямой можно построить,
используя разность расстояний двух ее
точек до фронтальной плоскости проекций,
т. е. разность глубин точек (рис. 69, в). В
этом случае отпадает необходимость
наносить оси проекций на чертеж. Этот
способ, как более точный, и используется
в практике выполнения технических
чертежей.
6. Определение натуральной величины
отрезка прямой общего положения.
Определение натуральной величины
отрезка прямой линии.
При решении задач инженерной графики
в ряде случаев появляется необходимость
в определении натуральной величины
отрезка прямой линии. Решить эту задачу
можно несколькими способами: способом
прямоугольного треугольника, способом
вращения, плоскопараллельного перемещения,
заменой плоскостей проекций.
Рассмотрим пример построения изображения
отрезка в истинную величину на комплексном
чертеже способом прямоугольного
треугольника. Если отрезок расположен
параллельно какой-либо из плоскостей
проекций, то на эту плоскость он
проецируется в натуральную величину.
Если же отрезок представлен прямой
общего положения, то на одной из плоскостей
проекций нельзя определить его истинную
величину (см. рис. 69).
Возьмем отрезок общего положения АВ (A
^ П1) и построим его ортогональную проекцию
на горизонтальной плоскости проекций
(рис. 78, а). В пространстве при этом
образуется прямоугольник А1ВВ1, в котором
гипотенузой является сам отрезок, одним
катетом — горизонтальная проекция
этого отрезка, а вторым катетом —
разность высот точек А и В отрезка. Так
как по чертежу прямой определить разность
высот точек ее отрезка не составляет
труда, то можно построить по горизонтальной
проекции отрезка (рис. 78, б) прямоугольный
треугольник, взяв вторым катетом
превышение одной точки над второй.
Гипотенуза этого треугольника и будет
натуральной величиной отрезка АВ.
Аналогичное построение можно сделать
на фронтальной проекции отрезка, только
в качестве второго катета надо взять
разность глубин его концов (рис. 78, в),
замеренную на плоскости П1.
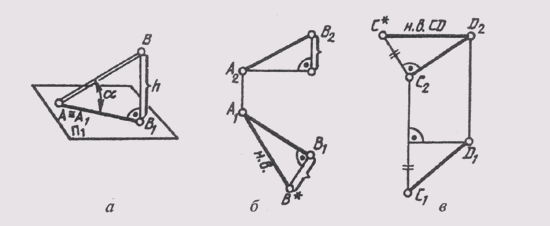
Рис. 78
Для определения натуральной величины
отрезка прямой можно воспользоваться
поворотом ее относительно плоскостей
проекций, чтобы она расположилась
параллельно одной из них (см. § 36) или
вводом новой плоскости проекций (заменой
одной из плоскостей проекций) так, чтобы
она была параллельна одной из проекций
отрезка (см. §§58, 59).
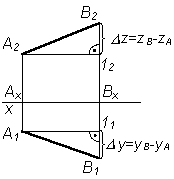
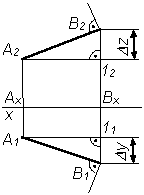
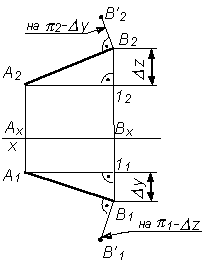
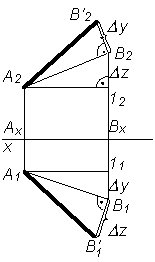
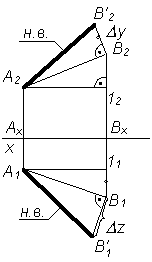
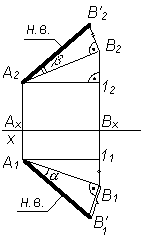
треугольника.
Для определения натуральной величины
отрезка прямой линии общего положения
по ее проекциям применяют метод
прямоугольного треугольника.
|
Вербальная форма |
Графическая форма |
|
1. D z – D y – разность |
|
|
2. а) б) либо перпендикуляр |
|
|
3. На или от точки B1 отложить |
|
|
4. Соединить A2 и В’2; |
|
|
5. |АВ| = А1В’1 = А2В’2 |
|
|
6. a – б – |
|
При решении подобной задачи находить
натуральную величину отрезка можно
только один раз (либо на p 1, либо на p 2).
Если требуется определить углы наклона
прямой к плоскостям проекций, то данное
построение выполняется дважды – на
фронтальной и горизонтальной проекциях
отрезка.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Точка – это геометрический абстрактный объект, который имеет координаты. Точки также участвуют в создании чертежа.
Комплексный чертеж и координаты точки
Комплексным называется чертеж, который был получен на фронтальной и горизонтальной плоскости проекции. Комплексный чертеж получается путем совмещения трех плоскостей проекций в одну.
Существует строгий порядок расположения проекций на чертеже, горизонтальная проекция должна располагаться под фронтальной, профильная проекция должна располагаться справа от фронтальной.
Рисунок 1. Координаты точки
Как найти точки на чертеже
Рассматривая предмет как сочетание граней, вершин и ребер мы можем находить проекции отдельных точек. Для начала нужно определить, какой плоскости или грани точка принадлежит. Затем находят горизонтальные проекции точки, для этого проводят вертикальную прямую линию связи из проекции точек. Видимость проекций определяется исходя из направления взгляда.
Как правильно расставлять точки
Чтобы правильно вычертить вид детали, необходимо уметь строить проекции. С помощью проекций можно определить местоположение точки. Вспомогательные линии позволяют определить место, где ее можно поставить и используются в качестве опорных. Вспомогательные линии двух проекций пересекаются под углом в 45 градусов. В местах пересечения линий связи с проекциями поверхности расставляют точки.
Видимые и невидимые точки
Видимые проекции изображают на чертеже без скобок, а невидимые в скобках, например, А’’ относится к видимой проекции, а (B’’) к невидимой.
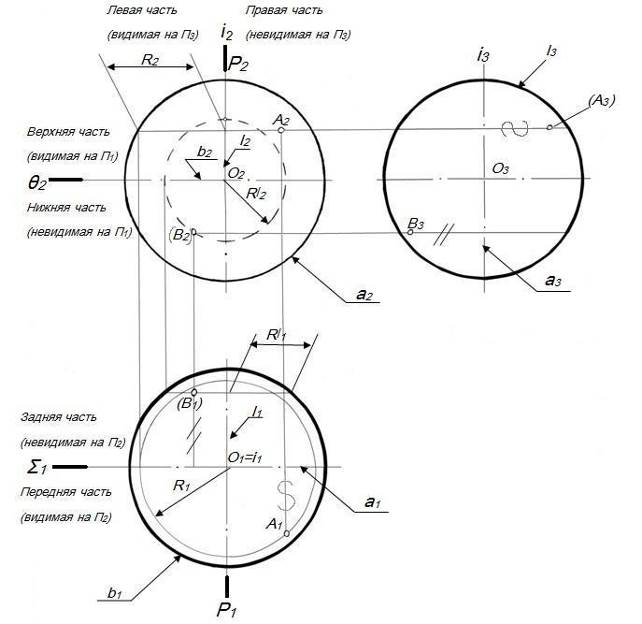
Рисунок 2. Видимые и невидимые точки
Точки сопряжения
В месте, где сопрягаются две линии образуется точка перехода или точка сопряжения. Для нахождения точки сопряжения линий прямого угла используется циркуль, его ставят в вершину угла и проводят дугу R до пересечения со сторонами. Чтобы найти центр сопряжения из найденных точек снова проводят окружности радиусом R, в месте их пересечения находится точка центра сопряжения, установив в нее циркуль проводят радиус сопряжения.
Опорные точки на чертеже
Опорные точки на схеме обозначают условными знакам согласно ГОСТ 21495-76, эти точки символизируют одну из связей заготовки иди изделия с выбранной системой координат. Нумерация опорных точек расставляется, начиная с базы, на которой расположено наибольшее число точек. Также опорные точки называют характерными, их число конечно, они выделяются своим особым положением относительно плоскости проекции и поверхности.
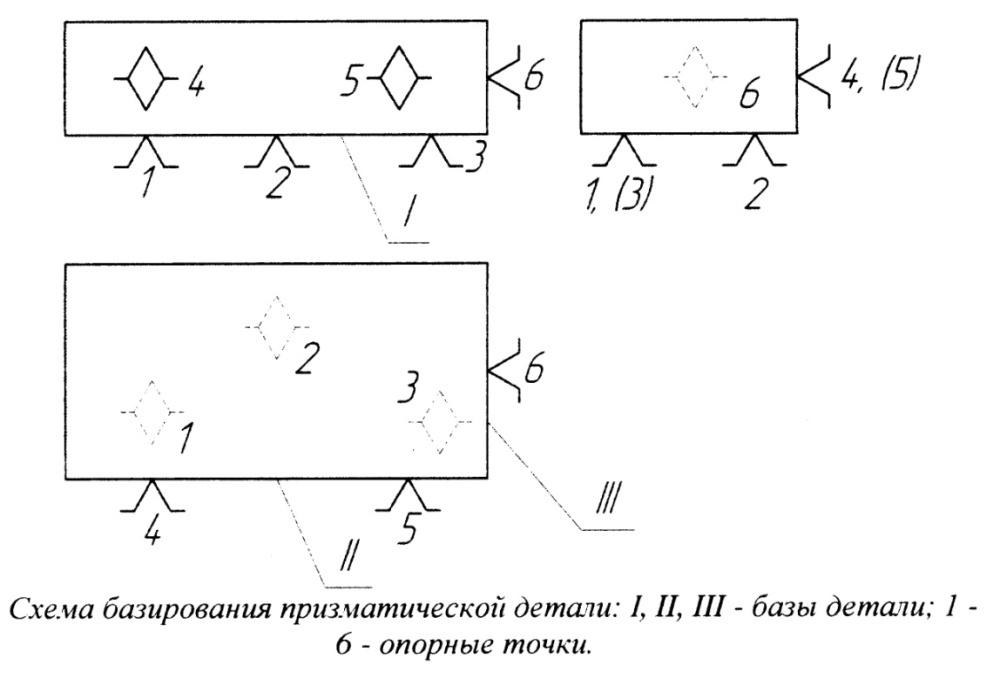
Рисунок 3. Опорные точки на чертеже
Сварные точки
Если детали соединяются сваркой, то ее также условно изображают на чертеже. В зависимости от расположения сварки можно увидеть шов или одиночную точку. Видимую одиночную точку обозначают знаком «+», невидимые одиночные точки на чертеже не обозначают. Видимый сварной шов обозначают основной сплошной линией, а невидимый штриховой линией.
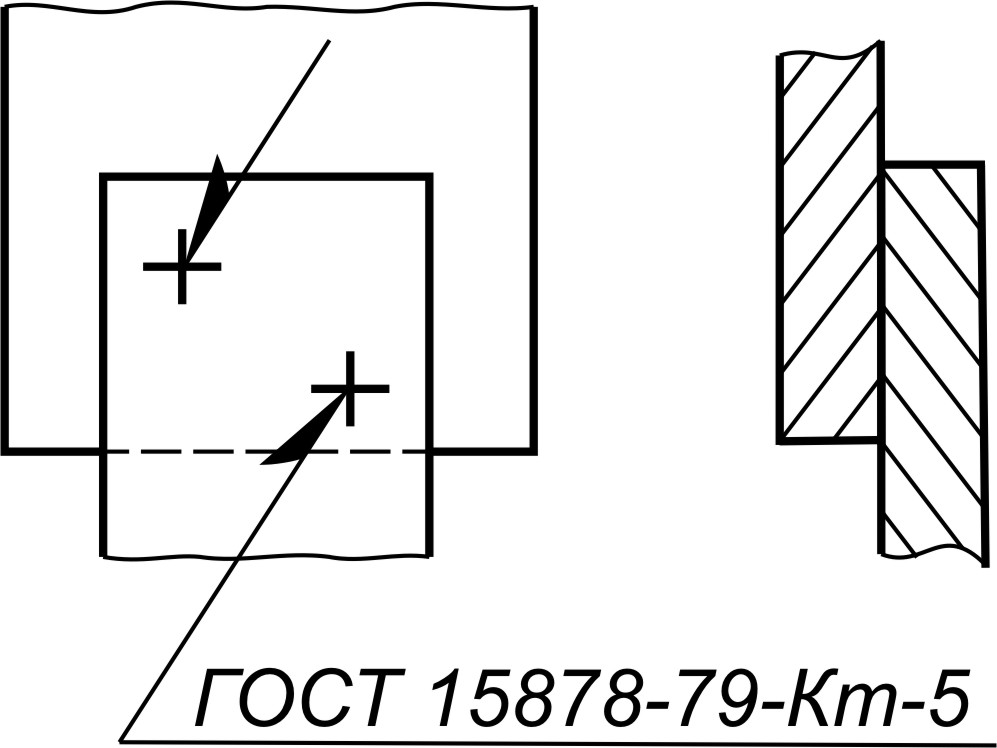
Рисунок 4. Сварные точки на чертеже
Трехкартинный чертеж точки
Трехкартинный чертеж или чертеж Монка представляет собой прямоугольник, сторонами которого являются линии связи, которые расположены перпендикулярно соответствующим осям проекции. При этом три вершины – проекции точки, а четвертая это точка перелома линии связи.
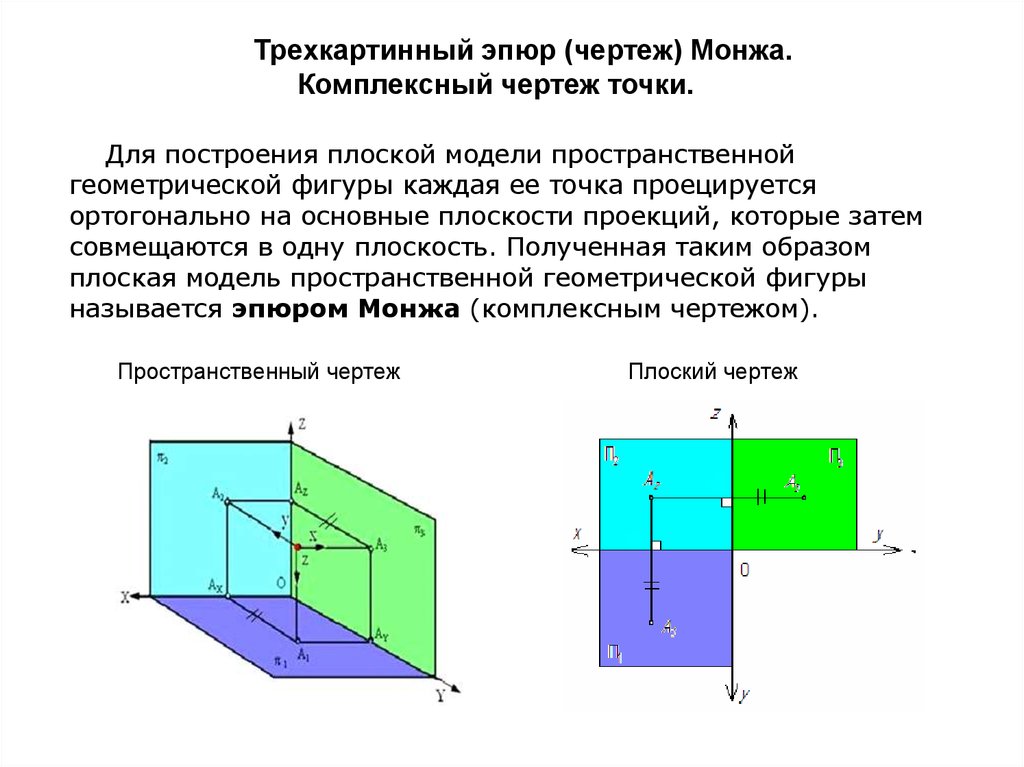
Рисунок 5. Трехкартинный чертеж точки
Конкурирующие точки на чертеже
Конкурирующие точки располагаются на одном проецирующем луче, таким образом для наблюдателя одна точка будет видимой, явной, а другая нет, что отразится и на чертеже.
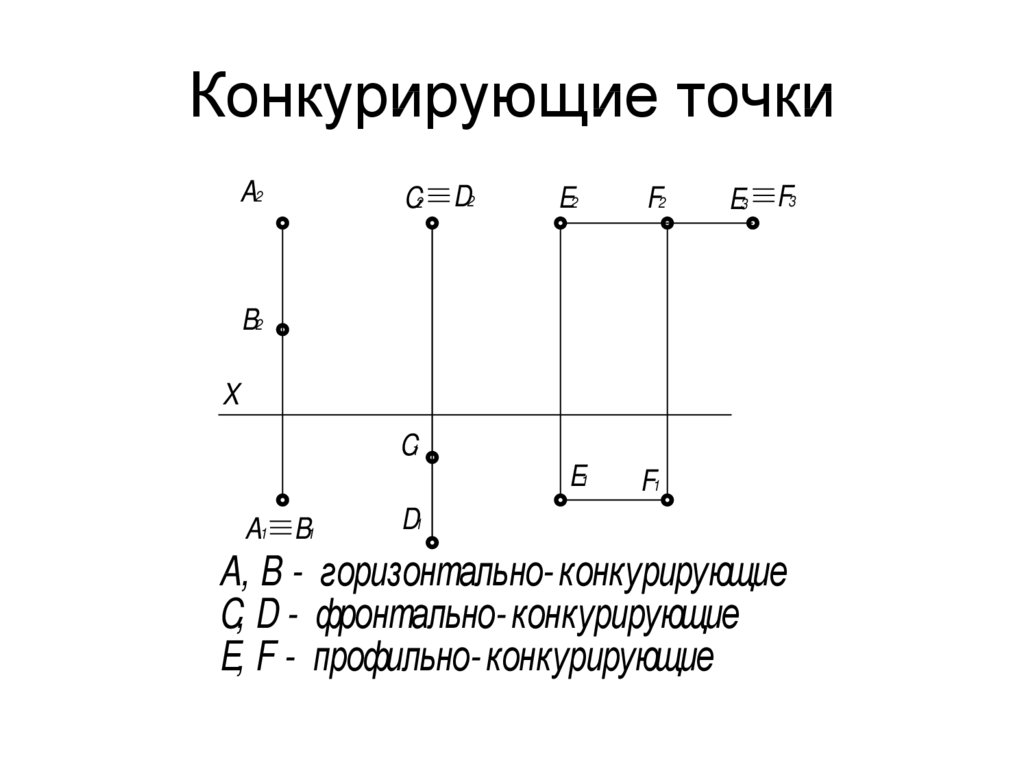
Рисунок 6. Конкурирующие точки на чертеже
Что такое явная точка на чертеже
Одним из важных понятий чертежа является база. Под базой понимается поверхность (точка, ось или сочетание поверхностей), принадлежащие заготовке, которая предназначена для придания изделию требуемого положения. Поверхность, используемая для базирования, может быть установочной ( лишает изделие возможностей перемещения), опорной (лишает одной степени свободы) или направляющей (лишает изделие или заготовку двух степеней свободы). По характеру базы могут быть скрытые и явные. Скрытые находятся в воображаемой плоскости или точке, а явные – в реальной поверхности или точке пересечения рисок.
Как построить комплексный чертеж точки: инструкция
Чтобы построить комплексный чертеж точки используется метод ортогональных или прямоугольных проекций, часто применяемый в инженерной графике. Проекция находится на пересечении проецирующего луча и плоскости.
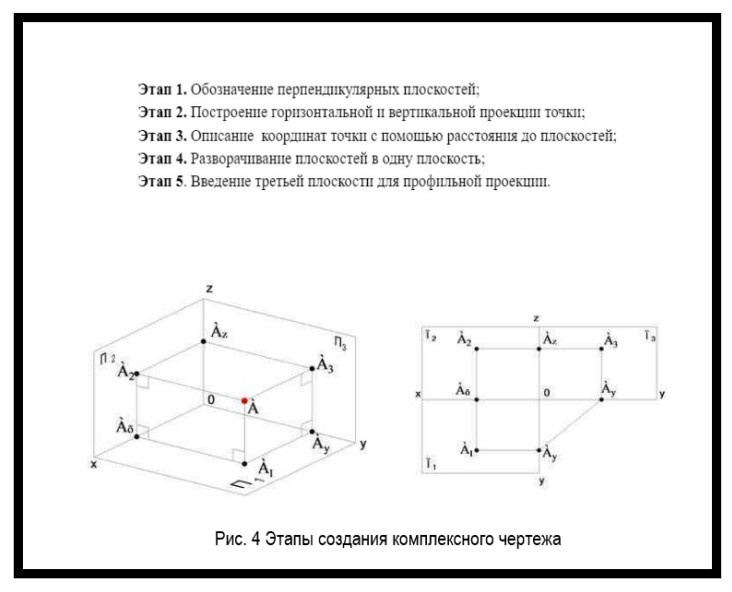
Построение комплексного чертежа точки А состоит следующих этапов:
- возьмем две плоскости, которые перпендикулярны друг другу и назовем их П1 и П2;
- в результате пересечения проецирующих лучей, перпендикулярных каждой из плоскостей получаем горизонтальную и вертикальную проекцию точки А;
- координаты точки описываются с помощью расстояния до плоскостей;
- для построения плоского чертежа плоскость П1 разворачивают так, чтобы она совпадал с плоскостью П2, а прямая соединяющая А1 и А2 называется линией связи;
- третья плоскость вводится для построения профильной проекции.
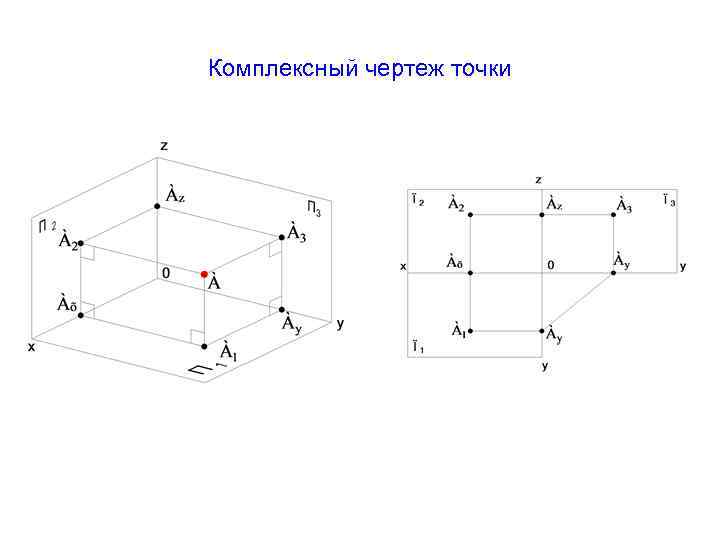
Рисунок 7. Построение комплексного чертежа точки
Как поставить точку на чертеже в Компасе
В меню программы Компас есть специальный инструмент «Точка», который позволяет сделать нужное действие за несколько шагов. Точку можно разместить, указав координаты, либо кликнув в месте рабочей области. Помимо основной функции команды, можно использовать расширенный список команд.
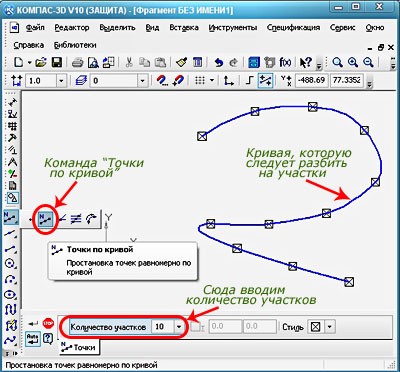
Рисунок 8. Как поставить точку в программе Компас
Как убрать точки на чертеже в Компасе
Убрать точки можно выделив их и нажав на клавишу «Delete», либо с помощью команды «Удалить вспомогательные кривые и точки».
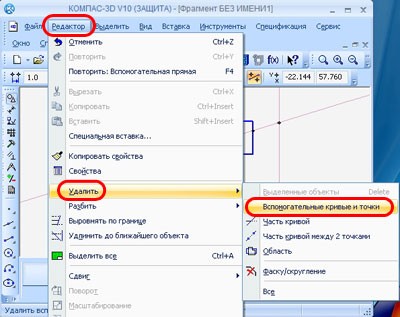
Рисунок 9. Как убрать точку в программе Компас
Ответы на вопросы
Как правильно показать невидимую сварную точку?
Невидимые сварные точки не имеют обозначения, в отличие от швов.
Как на чертеже показать характерные точки отрезка?
Характерные точки зависят от объекта, у отрезка они находятся в начале и в конце прямой. Если какая-либо точка принадлежит прямой, то ее проекция принадлежит проекции прямой. При этом длина проекции отрезка прямой общего положения меньше длины самого отрезка.
Чем отличается двухкартинный чертеж точки от трехкартинного?
Разница состоит в количестве проекций на поверхности. В двухкартинном чертеже используются горизонтальная и фронтальная плоскости, такой чертеж вполне позволяет описать форму и размеры фигуры. В трехкартинном чертеже используется еще и третья плоскость.
Содержание:
Чертежи точки, отрезка прямой:
Эпюр Монжа, построенный по схеме рассмотренной выше, позволяет однозначно судить как о форме и положении объектов в пространстве, так и о расположении их по отношению к плоскостям проекции.
Комплексные чертежи точки
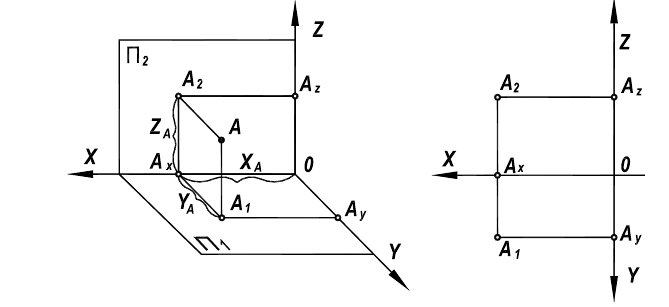
Рисунок 2.1 – Чертеж точки в пространстве
На этом чертеже присутствуют две ее проекции: горизонтальная –  и, соответствующая ей, фронтальная –
и, соответствующая ей, фронтальная – 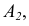 объединенные линией связи
объединенные линией связи 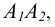 ортогональной оси чертежа Ох.
ортогональной оси чертежа Ох.
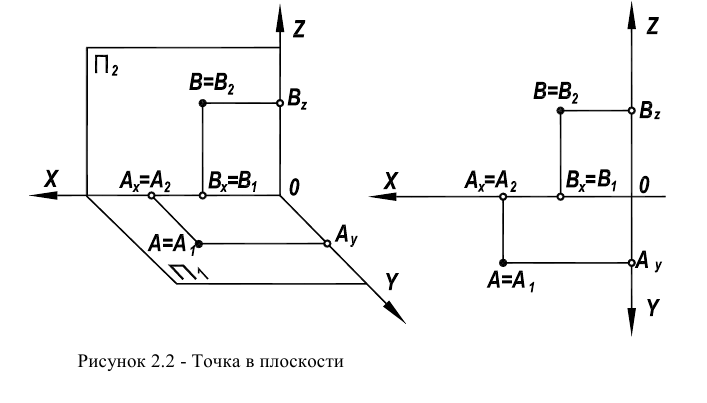
Чертеж точек, лежащих в плоскостях проекций, представлен на рисунке 2.2. Точка 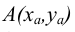 лежит в горизонтальной плоскости проекции
лежит в горизонтальной плоскости проекции 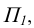 а вторая точка
а вторая точка 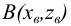 – во фронтальной плоскости проекции
– во фронтальной плоскости проекции 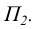
Отличием этого чертежа от предыдущего является то, что одна из проекций этих точек оказывается на оси чертежа Ох.
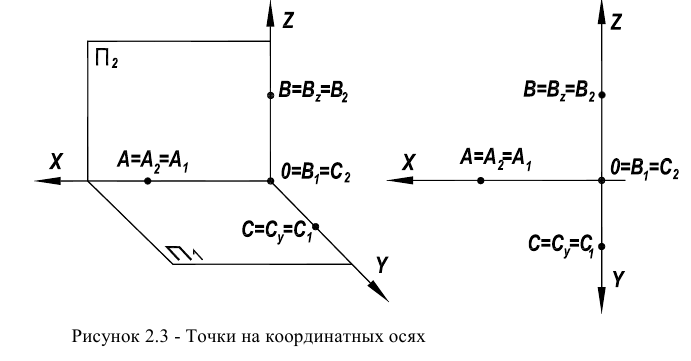
Точки, лежащие на координатных осях, изображены на рисунке 2.3. Точка 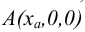 лежит на оси Ох, точка
лежит на оси Ох, точка 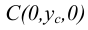 – на оси Оу, а точка
– на оси Оу, а точка 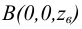 -на оси Oz. Для чертежей этих точек характерно следующее.
-на оси Oz. Для чертежей этих точек характерно следующее.
Обе проекции точки А, лежащей на оси чертежа , совпадают 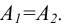
У точки С, лежащей на оси Оу, фронтальная проекция совпадает с точкой начала координат 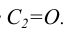
Аналогичная ситуация и с точкой В, лежащей на оси Oz, ее горизонтальная проекция совпадает с точкой начала координат 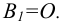
Комплексные чертежи прямых
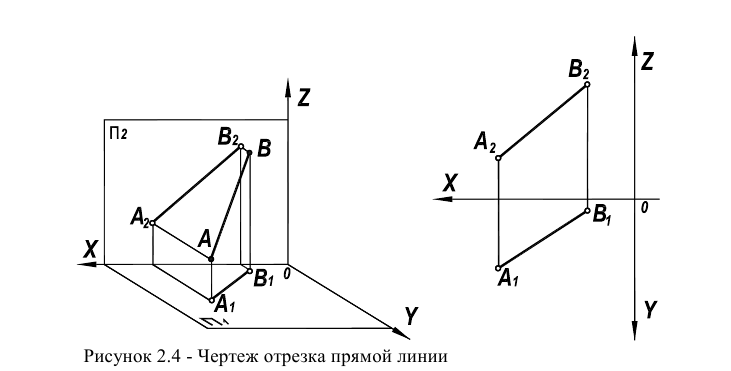
Будем прямую на чертеже задавать ее симплексом (отрезком). Для этого достаточно на чертеже задать две произвольные точки (в случае их совпадения длина отрезка будет нулевой). Чертеж отрезка прямой АВ приведен на рисунке 2.4.
Все прямые могут быть классифицированы в зависимости от их расположения по отношению к плоскостям проекций.
Прямая, не параллельная ни одной плоскости проекции, получила название прямой общего положения. Чертеж такой прямой приведен выше на рисунке 2.4.
Характерной особенностью чертежа такой прямой является непараллельность ее проекций ни одной из координатных осей.
Прямые, параллельные плоскостям проекций, получили название линий уровня.
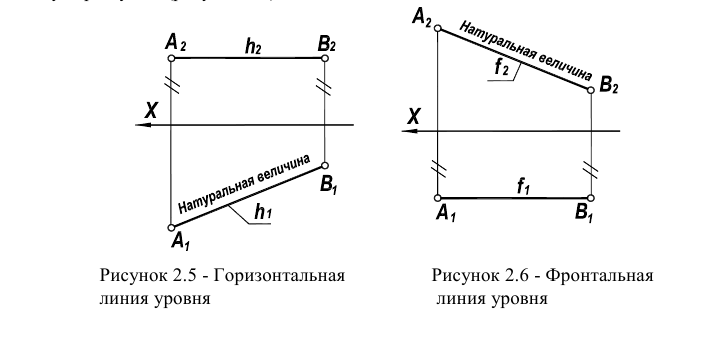
Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной линией уровня.
Фронтальная проекция  такой прямой параллельна оси чертежа, а горизонтальная проекция
такой прямой параллельна оси чертежа, а горизонтальная проекция  проецируется в отрезок, равный по длине самому отрезку АВ (рисунок 2.5).
проецируется в отрезок, равный по длине самому отрезку АВ (рисунок 2.5).
Прямая, параллельная фронтальной плоскости проекций, называется фронтальной линией уровня.
Горизонтальная проекция  такой прямой параллельна оси чертежа, а фронтальная проекция
такой прямой параллельна оси чертежа, а фронтальная проекция  проецируется в отрезок, равный по длине отрезку АВ (рисунок 2.6).
проецируется в отрезок, равный по длине отрезку АВ (рисунок 2.6).
Характерным для чертежей линий уровня является то, что одна из их проекций параллельна оси чертежа.
Линии, перпендикулярные плоскостям проекций, получили название проецирующих прямых.
Прямая, перпендикулярная фронтальной плоскости проекции  называется фронтально – проецирующей прямой. Такая прямая параллельная координатной оси Оу. На чертеже такой прямой (рисунок 2.8) фронтальная проекция
называется фронтально – проецирующей прямой. Такая прямая параллельная координатной оси Оу. На чертеже такой прямой (рисунок 2.8) фронтальная проекция 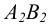 вырождается в точку, а горизонтальная проекция
вырождается в точку, а горизонтальная проекция 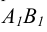 перпендикулярна оси чертежа (совпадает по направлению с линиями связи).
перпендикулярна оси чертежа (совпадает по направлению с линиями связи).
Прямая, перпендикулярная горизонтальной плоскости проекции  называется горизонтально – проецирующей прямой. Такая прямая параллельна координатной оси Oz.
называется горизонтально – проецирующей прямой. Такая прямая параллельна координатной оси Oz.
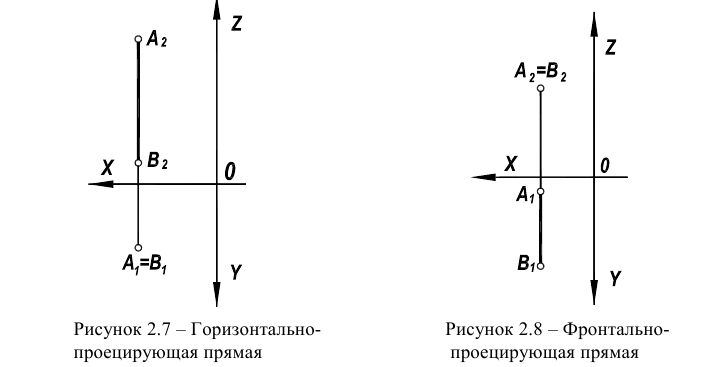
На чертеже прямой (рисунок 2.7) горизонтальная проекция 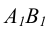 вырождается в точку, а фронтальная
вырождается в точку, а фронтальная 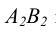 перпендикулярна оси чертежа (совпадает по направлению с линиями связи).
перпендикулярна оси чертежа (совпадает по направлению с линиями связи).
Характерной особенностью чертежей проецирующих прямых является то, что одна из проекций у них вырожденная, а вторая – параллельна одной из координатных осей (рисунок 2.7, 2.8).
Линии уровня и проецирующие прямые объединяют в одну группу – линий частного положения.
- Заказать чертежи
Следы прямой
Очевидно, что прямая и плоскость пересекаются в точке. Точки пересечения прямой с плоскостями проекции получили название следов прямой. Точка пересечения прямой с фронтальной плоскостью проекций 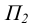 называется фронтальным следом, а с горизонтальной плоскостью проекций
называется фронтальным следом, а с горизонтальной плоскостью проекций 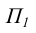 – горизонтальным следом.
– горизонтальным следом.
Следы прямой, заданной на чертеже отрезком AВ, можно найти исходя из определения данного выше.
След – это одна из точек прямой, лежащая в плоскости проекции. Следовательно, одна из координат этой точки должна быть равна нулю (в соответствии с рисунком 2.1).
При определении положения фронтального следа N прямой необходимо продлить горизонтальную проекцию 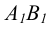 до пересечения с осью чертежа (рисунок 2.9). Эта точка пересечения
до пересечения с осью чертежа (рисунок 2.9). Эта точка пересечения 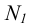 может быть принята за горизонтальную проекцию искомого следа. Фронтальная проекция
может быть принята за горизонтальную проекцию искомого следа. Фронтальная проекция 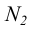 следа найдется по соответствию на фронтальной проекции прямой
следа найдется по соответствию на фронтальной проекции прямой 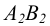 (см. рисунок 2.9). Очевидно, что точка N лежит на прямой АВ (ее проекции лежат на соответствующих проекциях этой прямой).
(см. рисунок 2.9). Очевидно, что точка N лежит на прямой АВ (ее проекции лежат на соответствующих проекциях этой прямой).
Вместе с этим у нее координата Y равна нулю (горизонтальная проекция 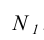 лежит на оси чертежа). Следовательно, можно утверждать, что точка N- это фронтальный след прямой.
лежит на оси чертежа). Следовательно, можно утверждать, что точка N- это фронтальный след прямой.
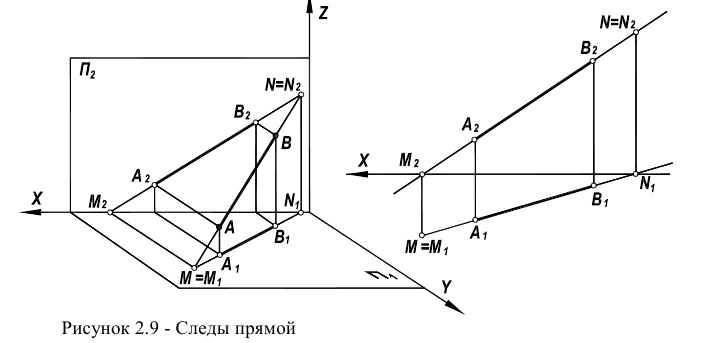
Аналогично может быть построен и горизонтальный след М. Для этого
следует продлить фронтальную проекцию отрезка А 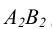 до пересечения с осью чертежа и принять точку пересечения за фронтальную проекцию искомого следа
до пересечения с осью чертежа и принять точку пересечения за фронтальную проекцию искомого следа 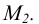 Горизонтальная проекция следа
Горизонтальная проекция следа 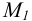 найдется по соответствию на горизонтальной проекции прямой
найдется по соответствию на горизонтальной проекции прямой 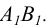
Взаимное расположение прямых
Прямые могут быть классифицированы и по такому признаку, как взаимное расположение в пространстве
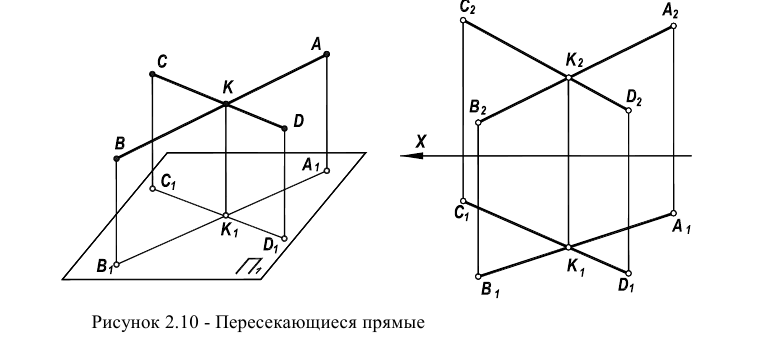
Рассмотрим вариант пересекающихся прямых, лежащих в произвольной плоскости. По определению две прямые пересекаются, если имеют одну общую точку.
На рисунке 2.10 изображен чертеж пересекающихся прямых АВ и CD. Точка пересечения К одновременно принадлежит двум этим прямым.
Это является следствием того, что на комплексном чертеже соответствующие проекции этой точки одновременно принадлежат соответствующим проекциям прямых (фронтальные проекции – фронтальным, а горизонтальные -горизонтальным).
Частным случаем пересечения прямых являются параллельность. Параллельные прямые пересекаются в несобственной точке.
Характерной особенностью чертежа параллельных прямых является параллельность одноименных проекций. В соответствие с рисунком 2.11
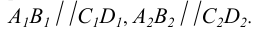
Прямые в пространстве, не имеющие общих точек, называются скрещивающимися (рисунок 2.12).
Точки пересечения их горизонтальных 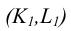 и фронтальных
и фронтальных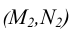 являются совпадающими проекциями различных точек. Такие точки, принадлежащие разным прямым, называют конкурирующими.
являются совпадающими проекциями различных точек. Такие точки, принадлежащие разным прямым, называют конкурирующими.
Конкурирующие точки используются для анализа видимости и глубины сцены в системах машинной графики.
- Чертежи плоскости
- Взаимное положение двух плоскостей, прямой линии и плоскости
- Решение задач на тему: перпендикулярности прямой и плоскости
- Проекции с числовыми отметками
- Геометрические тела
- Комплексный чертеж
- Определение видимости
- Конструктивное отображение пространства

Чертеж — важный конструкторский документ. Это проекционное изображения предмета. При создании чертежей в начертательной геометрии нужно следовать особым правилам. Все элементы должны находиться в строгой зависимости от положения в пространстве. Простым геометрическим образом пространства является точка. Что такое точки на чертеже? Как их использовать при создании чертежа? Разбираемся в нашем материале.
Что такое точка на чертеже?
Изображение предмета на чертеже состоит из двух или более геометрических фигур, только так можно передать форму изделия. В инженерной графике используются разные элементы графического языка. Одним из них является точка.
Точка — геометрический элемент, не имеющий размеров. Другими словами, все параметры точки равны нулю.
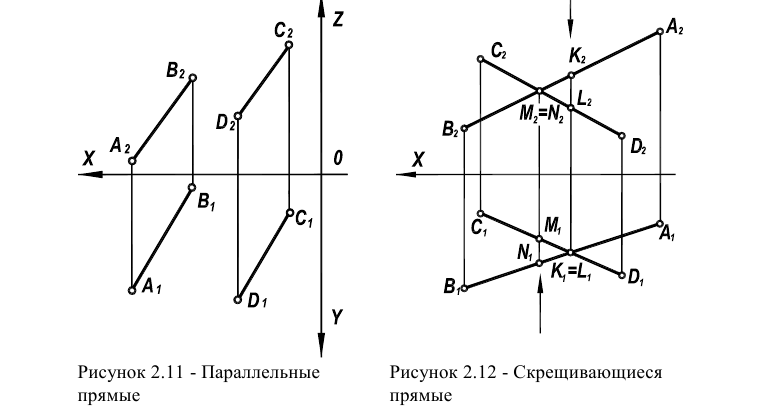
Чтобы изобразить изделие на чертеже, его необходимо перенести на плоскость. В построении любого изображения в инженерной графике применяется метод прямоугольного проецирования, который определяет расположение предмета на области за счет точек.
Проекция точки
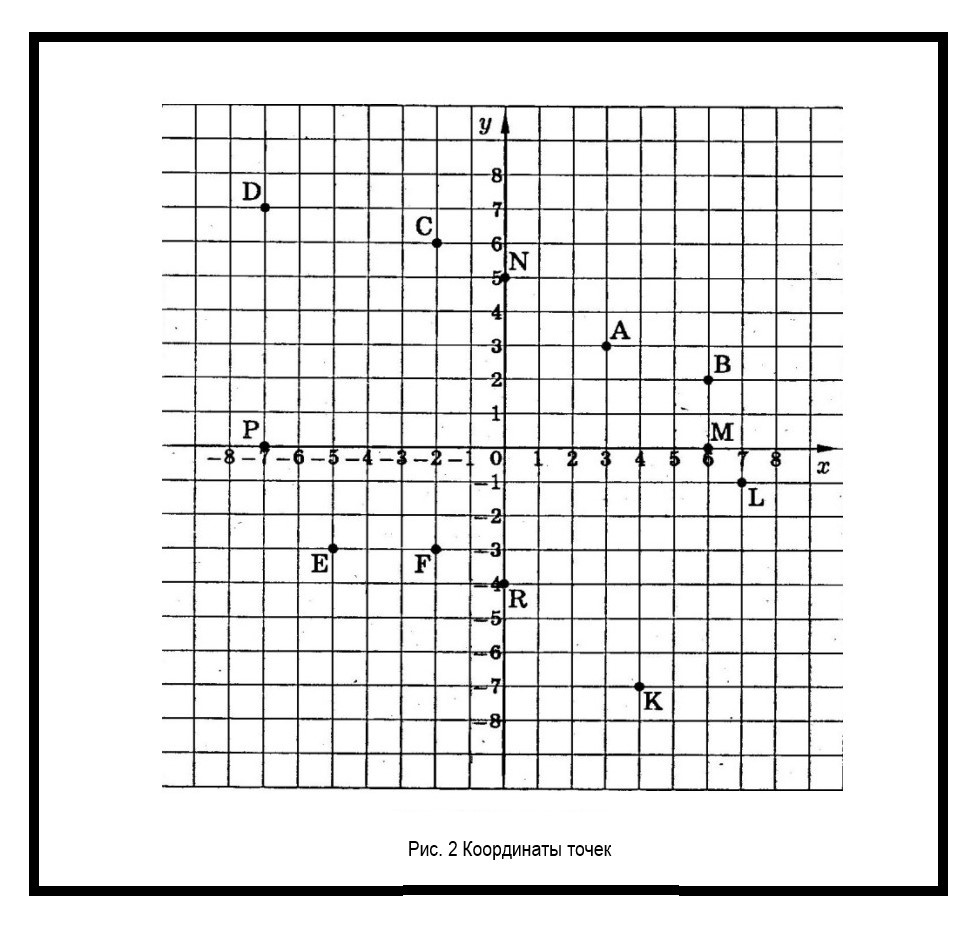
Это точка пересечения прямой линии с плоскостью (рисунок 1).
Проецируемая точка на плоскости обозначается как точка проекции. Это позволяет определить ее местоположение на плоскости. Каждая точка на чертеже имеет определенные координаты. Их используют для определения положения других элементов на комплексном чертеже (рисунок 2).
Как определить координаты по проекциям точки?
Для определения координат по проекциям точки используются две ортогональные проекции. Например, фронтальная и профильная. Они позволяют узнать конкретное значение координат точки, а также определить ее октант.
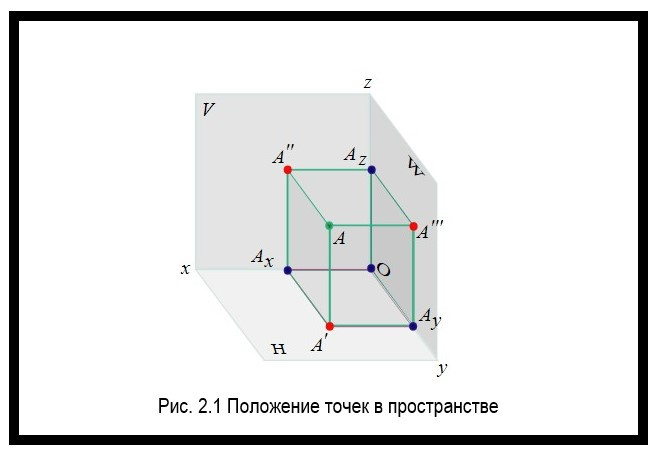
Как определить положение точки в пространстве?
Положение точки в пространстве определяется тремя координатами. Они показывают расстояние точки от плоскостей проекции. Пример представлен на рисунке рисунок 2.1.
Комплексный чертеж точки
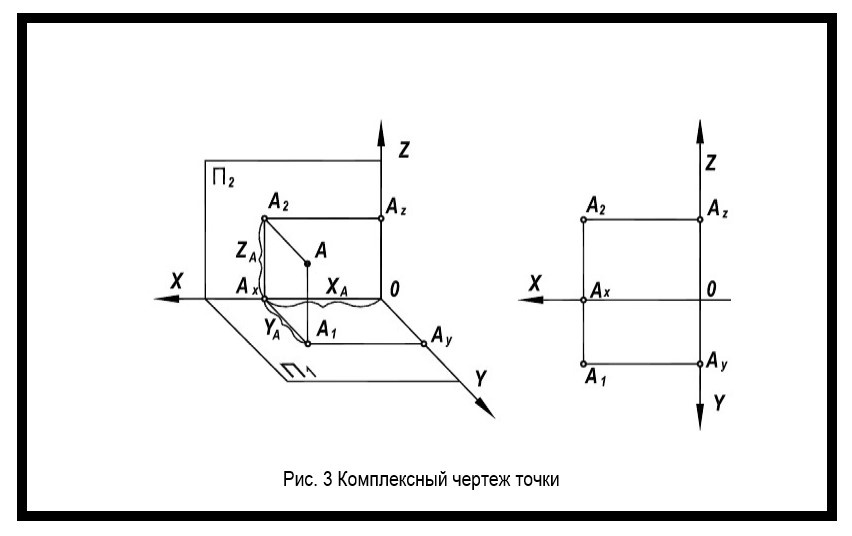
Чтобы изображение предмета было понятным, отражающим форму, размер и положение изделия в пространстве, необходимо использовать комплексный чертеж. Он представляет собой изображение предмета на совмещенных плоскостях проекции (рисунок 3).
Построение комплексного чертежа состоит из нескольких этапов (рисунок 4).
На таких чертежах объемный предмет проецируется ортогонально на две взаимно перпендикулярные плоскости. Одна из них — вертикальная, другая — горизонтальная. Прямая пересечения этих плоскостей называется осью проекции
.
Изображение точки на комплексном чертеже
На комплексном чертеже точка — пара координат. Для изображения точки на чертеже нужно провести две перпендикулярные оси: горизонтальную и вертикальную ось. В зависимости от положения точки относительно плоскостей проекции, точки пространства могут быть нескольких видов (рисунок 4.1).
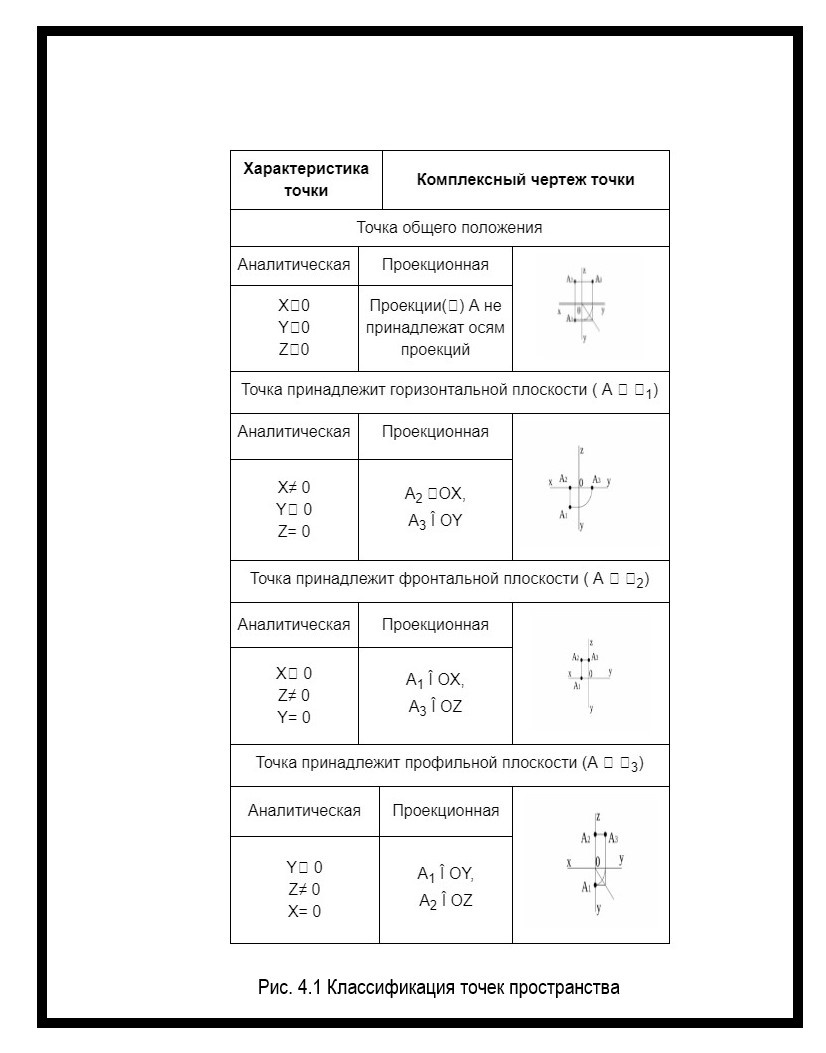
Обозначение точек на чертеже
Обозначение точек на чертеже осуществляется разными способами. Все параметры точек равны нулю, поэтому для их изображения используют условные обозначения (рис. 3.1).
Точка обозначаются буквами (например, точка A, B, C) или цифрами (например, точка 1, 2, 3). Кроме того, она может быть обозначена геометрическими символами кружочком или пересечением двух линий (рисунок 3).

Конкурирующие точки на чертеже
Точки на чертеже с двумя одинаковыми координатами называются конкурирующими (рисунок 4). Это точки, которые лежат на одном проецирующем луче.
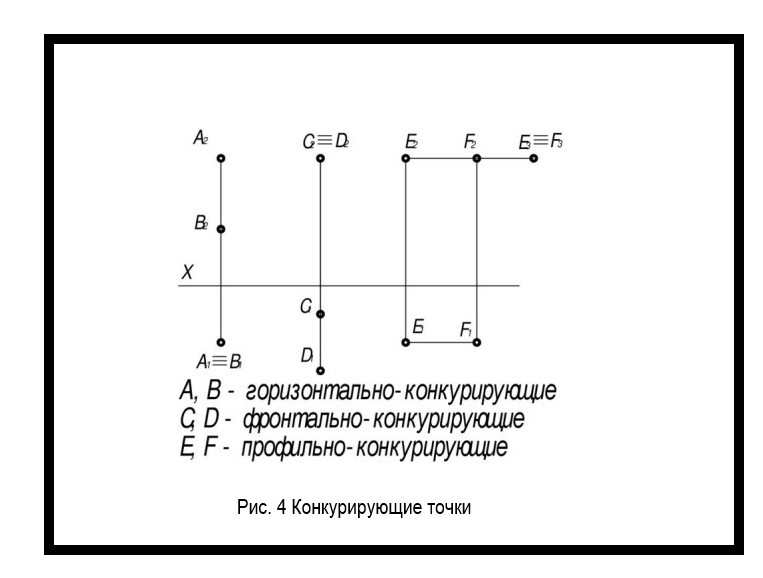
Они могут быть нескольких видов, название которых определяет плоскость совпадающих проекций:
- Горизонтально конкурирующие — лежат на одном перпендикуляре к горизонтальной плоскости;
- Фронтально конкурирующие — лежат на одном луче к фронтальной плоскости;
- Профильно конкурирующие — лежат на одном перпендикуляре к профильной плоскости.
Видимые и невидимые конкурирующие точки на чертеже
Видимостью называют изображение близких к наблюдателю точек. Этот параметр помогает улучшить понимание геометрической формы и расположения предмета в пространстве.
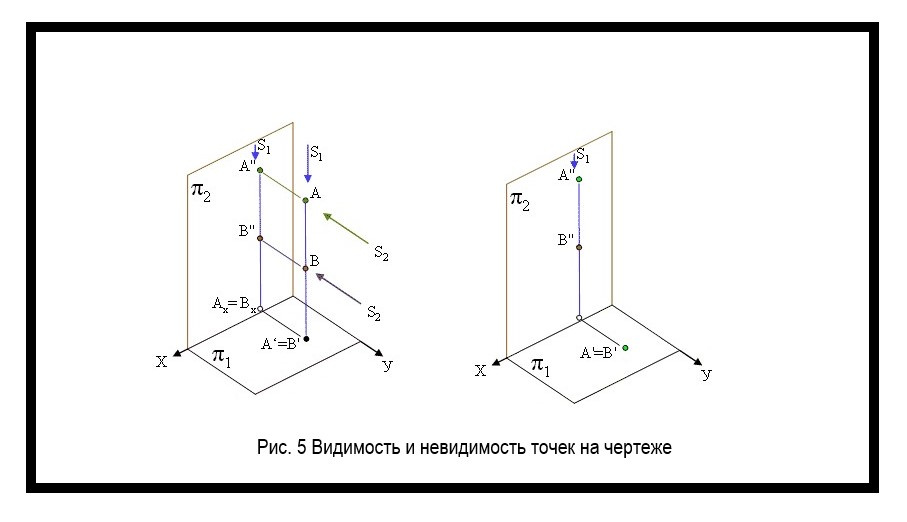
Для определения видимости, нужно найти точки предмета на одном луче и обозначить только те, которые расположены ближе к вам (рисунок 5). Без видимости определить положение объекта сложно.
Как обозначить видимость точек на чертеже
Видимость точек обозначается буквами (например, точка C”), невидимость — буквами с круглыми скобками (например, точка (С”)).
Типы точек на чертеже
Точки на чертеже по ГОСТу могут быть следующих типов:
Не хотите тратить время на чертежи? Вы можете заказать готовый чертеж у экспертов Студворк!
Глава 6. ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ
§ 32. Комплексный чертеж точки
Чтобы построить изображение предмета, сначала изображают отдельные его элементы в виде простейших элементов пространства. Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.д
Правила построения изображений на чертежах в инженерной графике основываются на методе проекций. Одно изображение (проекция) геометрического тела не позволяет судить о его геометрической форме или форме простейших геометрических образов, составляющих это изображение. Таким образом, нельзя судить о положении точки в пространстве по одной ее проекции; положение ее в пространстве определяется двумя проекциями.
Рассмотрим пример построения проекции точки А, расположенной в пространстве двугранного угла (рис. 60). Одну из плоскостей проекции расположим горизонтально, назовем ее горизонтальной плоскостью проекций и обозначим буквой П1. Проекции элементов

Рис. 60
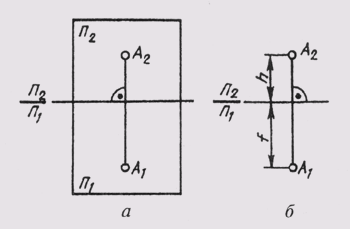
Рис. 61
пространства на ней будем обозначать с индексом 1 : А1, а1, S1 … и называть горизонтальными проекциями (точки, прямой, плоскости).
Вторую плоскость расположим вертикально перед наблюдателем, перпендикулярно первой, назовем ее вертикальной плоскостью проекций и обозначим П2. Проекции элементов пространства на ней будем обозначать с индексом 2: А2, <a2, S2 и называть фронтальными проекциями (точки, прямой, плоскости). Линию пересечения плоскостей проекций назовем осью проекций.
Спроецируем точку А ортогонально на обе плоскости проекций:
АА1_|_ П1;AА1 ^П1=A1;
АА2_|_ П2;AА2 ^П2=A2;
Проецирующие лучи АА1 и АА2 взаимно перпендикулярны и создают в пространстве проецирующую плоскость АА1АА2, перпендикулярную обеим сторонам проекций. Эта плоскость пересекает плоскости проекций по линиям, проходящим через проекции точки А.
Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П1 с фронтальной плоскостью П2 вращением вокруг оси П2/П1 (рис. 61, а). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси П2/П1. Прямая А1А2, соединяющая горизонтальную А1 и фронтальную А2 проекции точки, называется вертикальной линией связи.
Полученный плоский чертеж называется комплексным чертежом. Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.
Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки а относительно этих плоскостей (рис. 61, б) ее высотой h (АА1 =h) и глубиной f(AA2 =f), то эти величины на комплексном чертеже существуют как отрезки вертикальной линии связи. Это обстоятельство позволяет легко реконструировать чертеж, т. е. определить по чертежу положение точки относительно плоскостей проекций. Для этого достаточно в точке А2 чертежа восстановить перпендикуляр к плоскости чертежа (считая ее фронтальной) длиной, равной глубине f. Конец этого перпендикуляра определит положение точки А относительно плоскости чертежа.