Нахождение проекций точек на поверхности конуса
Для нахождения недостающих проекций точек на поверхности конуса могут применяться следующие линии, принадлежащие поверхности конуса: окружность — параллель конуса (рис. 2.7, а), прямая — образующая конуса (рис. 2.7, б). Рассмотрим оба способа.
Пример 2.1. На поверхности конуса заданы проекции А2 и В, (см. рис. 2.7). Найдите недостающие проекции точек Ли В на поверхности конуса.
Рис. 2.7. Нахождение проекций точек на поверхности конуса
Способ 1. На рис. 2.7, а точка А задана проекцией А. Для нахождения недостающих проекций точки А воспользуемся вышеизложенным алгоритмом.
- 1. Через заданную проекцию точки Аг проводим линию, принадлежащую поверхности конуса — параллель.
- 2. Строим проекции параллели на других изображениях конуса. Па виде сверху она представляет собой окружность радиусом Rvна виде слева — отрезок.
- 3. На проекциях линии находим соответствующие проекции точек.
- 4. На пересечении окружности радиусом Л., с вертикальной линией связи, опущенной из А2, отмечаем проекцию Л,.
- 5. На виде сверху измеряем координату от проекции А, до горизонтальной оси и откладываем ее на проведенной линии связи на виде слева — получаем проекцию Л3.
- 6. Отмечаем проекцию А.л как невидимую. Проекция А., задана как видимая, следовательно, точка лежит в той части конической поверхности, которая обращена к наблюдателю (на виде сверху это часть, расположенная ниже горизонтальной оси). Таким образом, на виде слева ее проекция не видна.
Способ 2. Па рис. 2.7, 6 точка В задана проекцией В,. Построение недостающих проекций аналогично построению проекций точки А, за исключением того, что вместо окружности используется образующая конуса, пересекающая его основание в точке 1.
Коническая поверхность вращения
Коническая поверхность вращения — это линейчатая поверхность, образованная вращением прямолинейной образующей, которая пересекает криво-линейную направляющую (окружность) и проходит через неподвижную точку оси вращения, называемую вершиной.
Конусом называют геометрическое тело, ограниченное конической поверхностью и плоскостью основания, пересекающего все его образующие.
Конус называют прямым, если ось вращения перпендикулярна его основанию. Конус называют круговым, так как направляющей является окружность Конус с двумя параллельными основаниями, т.е. конус со срезанной вершиной, называют усеченным.
Построение проекций прямого кругового конуса
На рис. 4.71 показан пример построения проекций прямою кругового конуса с горизонтально-проецирующей осью вращения 

Для построения проекций конуса требуется выполнить графо-аналитические действия в следующем порядке:
1-е действие. По заданному условию построить горизонтальную проекцию очерка прямого кругового конуса, которая представляет собой окружность заданного радиуса 
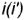
2-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса:
- Круг радиуса
является невидимой проекцией основания конуса.
- Круг радиуса
с вершиной конуса
является видимой проекцией боковой поверхности конуса.
- Обозначить на горизонтальной проекции характерные образующие конуса
и
которые будут определять очерки фронтальной и профильной проекций конуса.
3-е действие. Построить фронтальную проекцию (очерк) конуса, которая представляет собой треугольник 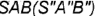
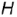
4-е действие. Построить профильную проекцию (очерк) конуса:
- ‘Задать на окружности горизонтальной проекции конуса положение базовой линии (б.о.), совпадающей с горизонтальной линией оси этой окружности.
- Выбрать положение базовой оси
(б.о.), которая будет совпадать с вертикальной осью
вращения на профильной проекции конуса.
- Профильная проекция конуса представляет собой треугольник
ограниченный:
слева и справа очерковыми образующими 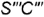
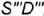
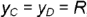
вершиной 
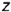
профильными проекциями характерных образующих 
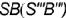
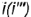
. Запомните характерные признаки очерков прямого круговою конуса на чертеже — окружность основания и два треугольника.
. Характерные признаки очерков прямого кругового усеченного конуса окружность основания и две равнобокие трапеции.
Построение проекции точек, лежащих на поверхности конуса
Принадлежность точки поверхности конуса определяется ее принадлежностью образующей поверхности и принадлежностью круговым параллелям (окружностям), по которой точка вращается вокруг оси конуса. Следовательно, проекции точки можно строить либо по принадлежности образующей, либо по принадлежности круговой параллели.
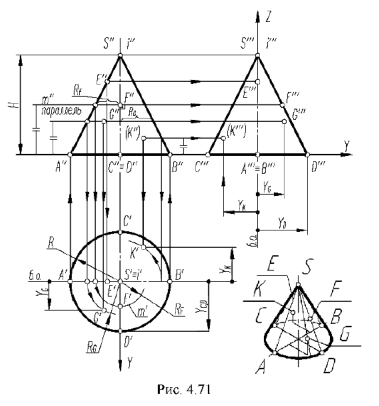
На рис. 4.71 показан пример построения горизонтальных и профильных проекций точек 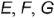
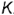
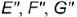
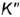
Посфоение горизонтальных проекций заданных точек:
горизонтальные проекции точек 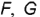
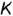
Рассмотрим графический алгоритм для построения горизонтальных проекции точек, лежащих на боковой поверхности конуса (на примере заданной точки , по их при надежности круговым параллелям:
Графический алгоритм I:
1-е действие. Провести фронтальную проекцию вспомогательной круговой параллели 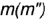
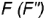
2-е действие. Провести окружность горизонтальной проекции параллели 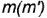
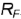
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки 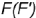
Повторить действия графического алгоритма 1 и построить аналогично горизонтальные проекции 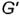
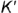
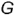
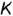
Построение профильных проекций заданных точек. Точки 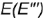
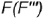
точка 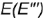
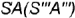
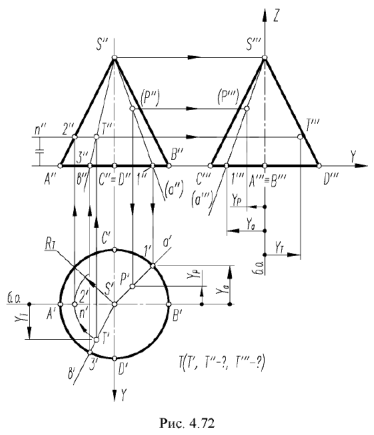
На рис. 4.72 показан пример построения горизонтальной и профильной проекции точки 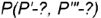
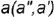
- Построение горизонтальной проекции точки по принадлежности образующей выполняется по графическому алгоритму II:
1-е действие. Провести через вершину конуса 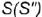
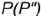
2-е действие. Построить горизонтальную проекцию образующей 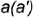
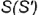
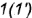
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки 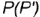
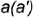
- Построение профильной проекции невидимой точки
выполняется по принадлежности образующей
, построенной но координате
.
На рис. 4.72 показано построение фронтальной и профильной проекции точки по ее заданной горизонтальной проекции. Построение выполнено по приведенным алгоритмам I и II, но в обратном порядке:
1-е действие. Провести на горизонтальной проекции конуса радиусом 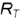
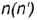
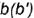
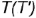
2-е действие. Построить фронтальные проекции вспомогательной параллели 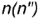
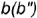
параллель 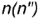
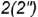
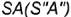
образующую 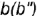
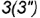
3-е действие. Построить по вертикальной линии связи фронтальную проекцию точки 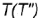
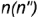
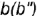
Конические сечения
Рассмотрим пять возможных случаев расположения секущей плоскости относительно оси конуса и его образующих, определяющих форму линии ее пересечения с поверхностью конуса (математические доказательства не приводятся):
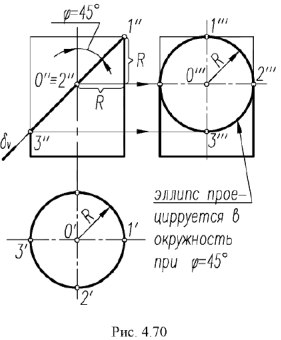
1-й случаи. Гели секущая плоскость проходит через вершину конуса, то эта плоскость пересекает коническую поверхность по двум образующим 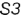

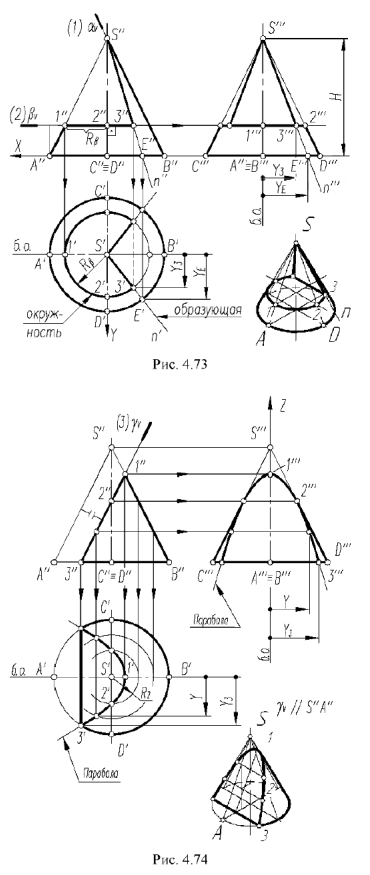
2-й случай. Если секущая плоскость расположена перпендикулярно оси конуса, то эта плоскость пересекает коническую поверхность но окружности (горизонтальная плоскость рис. 4.73).
3-й случай. Если секущая плоскость расположена параллельно одной образующей конуса, то эта плоскость пересекает коническую поверхность по параболе (фронтально-проецирующая плоскость 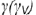

4-и случай. Если секущая плоскость расположена параллельно двум образующим конуса, то эта плоскость пересекает коническую поверхность по гиперболе (фронтальная плоскость 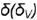

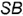
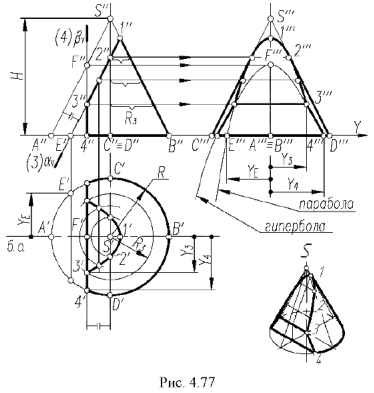
5-й случай. Если плоскость пересекает все образующие конуса под углом, отличным от прямого (или иначе, не параллельна ни одной образующей конуса), то эта плоскость пересекает коническую поверхность по эллипсу (фронтально-проецирующая плоскость ), рис 4.76).
Рассмотрим построение на проекциях конуса линии пересечения для всех пяти случаев сечений.
1-й и 2-й случаи. На рис. 4.73 показано построение проекций прямого кругового конуса с вырезом, образованным сечениями конической поверхности фронтально-проецирующей плоскостью 

Плоскость 

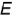
Плоскость пересекает поверхность конуса по окружности радиуса ограниченной линией 3-3 пересечения плоскостей выреза.
Построение горизонтальной и профильной проекций конуса с вырезом и оформление очерков этих проекций видно из чертежа.
3-й случай. На рис. 4.74 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью 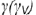

Плоскость пересекает поверхность конуса по параболе, горизонтальная и профильная проекции которой строятся по отмеченным характерным точкам 1, 2 и 3 и промежуточной точке (не обозначена)
Построение проекций этих точек выполнено по их принадлежности:
- проекции промежуточной точки построены по ее принадлежности соответствующей параллели (профильные проекции — по координате
).
Оформление очерков проекций видно из чертежа.
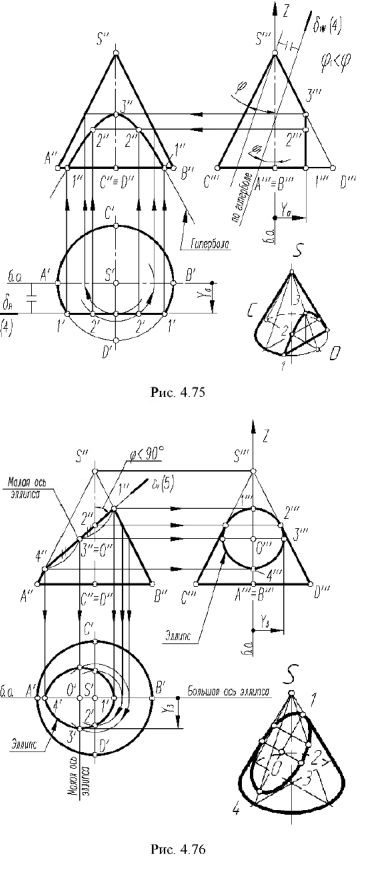
4-й случай. На рис. 4.75 показано построение проекций конуса со срезом фронтальной плоскостью 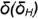


Плоскость 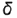
Оформление очерков проекций видно из чертежа.
На рис 4 75 на профильной проекции конуса показано положение секущей плоскости 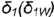
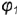
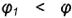
5-й ыучай. На рис. 4.76 показано построение проекции конуса со срезом фронтально-проецирующей плоскостью 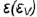
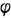
Плоскость 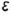
Оформление очерков проекций видно из чертежа.
. Количество взятых промежуточных точек должно быть минимальным, но достаточным, чтобы построить на проекциях конуса формы кривых второго порядка (параболы, гиперболы и эллипса), которые выполняют на чертеже по построенным характерным и промежуточным точкам с помощью лекала.
Построении проекции прямого конуса со срезами плоскостями частного положения
На рис. 4.77 показан пример построения проекций прямого круговою конуса со срезами фронтально-проецирующей плоскостью 

Для построения проекций конуса со срезами следует выполнить графический алгоритм, определяющий порядок действий при решении всех подобных задач.
1-е действие. Построить на чертеже тонкими линиями по заданному радиусу основания 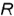
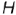


2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основанием конуса и выпол-иить графический анализ сечений:
1. Фронтально-проецирующая плоскость 
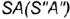
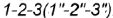
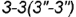


- Профильная плоскость
параллельна двум образующим конуса
и
и пересекает его поверхность по участку гиперболы
, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов
и
и плоскости
с основанием конуса (4-4).
3-е действие. Достроить горизонтальную проекцию конуса со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек и определить видимость плоскостей срезов:
1. Плоскость среза 
- Плоскость среза
определяет вертикальный видимый отрезок
вырожденной в линию проекции профильной плоскости, точки
которой лежат на очерковой окружности основания конуса.
. Поскольку горизонтальная проекция имеет вертикальную симметрию, точки обозначены на одной ее половине (нижней).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса для определения ее очерка и внутреннего контура:
- Горизонтальный очерк определяют участок окружности и отрезок
.
- Внутренний контур определяет видимый участок параболы
.
5-е действие. Достроить профильную проекцию конуса со срезами, пост-роив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов:
1. Плоскость среза а определяет видимый участок параболы , построенный по профильным проекциям обозначенных точек:
- Плоскость среза
определяют видимые участки гиперболы
, ограниченные видимым отрезком
(построен) и видимым отрезком
. точки которого построены но координате
.
6-е действие. Выполнить графический анализ построенной профильной проекции конуса для определения ее очерка и внутреннего контура.
- Профильный очерк определяют:
- Внутренний контур определяют:
7-е действие. Оформить чертеж конуса, выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой его проекции (оставить сплошными тонкими линиями полные очерки проекций и линии построения).
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Сечение поверхности конуса плоскостью общего положения
При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности.
Ниже мы рассмотрим задачу, в которой требуется построить проекции и натуральную величину сечения конуса ω плоскостью α . Начальные данные представлены на рисунке ниже.
Определение высшей и низшей точки сечения. Границы видимости
Построение линии пересечения следует начинать с нахождения её характерных точек. Они определяют границы сечения и его видимость по отношению к наблюдателю.
Через ось конической поверхности проведем вспомогательную плоскость γ, параллельную П2. Она пересекает конус ω по двум образующим, а плоскость α по фронтали fγ. Точки 1 и 2 пересечения fγ с образующими являются граничными точками. Они делят сечение на видимую и невидимую части.
Определим высшую и низшую точки линии пересечения. Для этого через ось конуса перпендикулярно h0α введем дополнительную секущую плоскость β. Она пересекает коническую поверхность по образующим SL и SK, а плоскость α по прямой MN. Искомые точки 3 = SL ∩ MN и 4 = SK ∩ MN определяют большую ось эллипса. Его центр находится в точке O, которая делит отрезок 3–4 пополам.
Определение промежуточных точек и построение проекций эллипса
Чтобы построить проекции сечения наиболее точно, найдем ряд дополнительных точек. В случае с эллипсом целесообразно определить величину его малого диаметра. Для этого через центр O проводим вспомогательную горизонтальную плоскость δ. Она пересекает коническую поверхность по окружности диаметром AB, а плоскость α – по горизонтали hδ. Строим горизонтальные проекции окружности и прямой hδ. Их пересечение определяет точки 5′ и 6′ малого диаметра эллипса.
Для построения промежуточных точек 7 и 8 вводим вспомогательную горизонтальную плоскость ε. Проекции 7′ и 8′ определяются аналогично 5′ и 6′, как это показано на рисунке.
Соединив найденные точки плавной кривой, мы получили контур эллиптического сечения. На рисунке он обозначен красным цветом. Фронтальная проекция контура меняет свою видимость в точках 1 и 2, как это было отмечено выше.
Построение натуральной величины сечения методом совмещения
Чтобы найти натуральную величину сечения, повернем плоскость α до совмещения её с горизонтальной плоскостью. В качестве оси вращения будем использовать след h0α. Его положение в процессе преобразований останется неизменным.
Построение начинается с определения направления фронтального следа f1α. На прямой f0α возьмем произвольную точку E и определим её проекцию E’. Из E’ опустим перпендикуляр к h0α. Пересечение данного перпендикуляра с окружностью радиусом XαE» определяет положение точки E’1. Через Xα и E’1 проводим f1α.
Строим проекцию горизонтали h’1δ ∥ h0α, как это показано на рисунке. Точки O’1 и 5′1, 6′1 лежат на пересечении h’1δ с прямыми, проведенными перпендикулярно h0α из O’ и 5′, 6′. Аналогично на горизонтали h’1ε находим 7′1 и 8′1.
Строим проекции фронталей f’1γ ∥ f1α, f’3 ∥ f1α и f’4 ∥ f1α. Точки 1′1, 2′1, 3′1 и 4′1 лежат на пересечении этих фронталей с перпендикулярами, восстановленными к h0α из 1′, 2′, 3′ и 4′ соответственно.
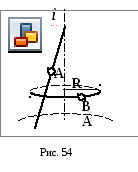
Точка принадлежит
поверхности конуса, если она принадлежит
линии этой поверхности.
В качестве
линии берется либо образующая конуса
(для точки А), либо параллель, проходящая
через данную точку (для точки В). Радиус
параллели R
замеряют от оси вращения до образующей
конуса (рис.54).
Дано:
– прямой круговой конус 1,2,3,4
Построить:
11
,21
, 31,
41 -?
.
1.
Постройте горизонтальную проекцию
точки 1.
Эта точка является
опорной точкой, так как принадлежит
очерку поверхности – главному фронтальному
меридиану.
Очерковая
образующая проецируется на горизонтальную
плоскость проекций в виде отрезка
прямой, проходящей через горизонтальную
осевую.
Спроецируйте
точку 1 на горизонтальную проекцию
очерковой образующей.
2.
Постройте горизонтальную проекцию
точки 2.
Точка 2 является
опорной точкой, так как принадлежит
очерку поверхности – экватору.
Экватор
проецируется на горизонтальную плоскость
проекций в виде окружности.
3.
Спроецируйте
точку 2 на горизонтальную проекцию
экватора.
Так как
вертикальная линия связи дважды
пересекает горизонтальную проекцию
экватора, получают две проекции 21
и 21I.
Точка 2 – видимая,
а 2I
– невидимая.
4.
Постройте горизонтальную проекцию
точки 3.
Для построения
недостающей проекции точки воспользуйтесь
вспомогательной линией – образующей
конуса.
5.
Постройте
горизонтальную проекцию образующей
конуса (задача имеет два решения).
6.
Спроецируйте
точку 3 на горизонтальные проекции
вспомогательных образующих. Для этого
проведите из фронтальной проекции
точки 32
вертикальную линию связи до пересечения
с горизонтальными проекциями
вспомогательных образующих. Получится
две проекции 31
и 31I.
7.
Постройте горизонтальную проекцию
точки 4.
Для построения
недостающей проекции точки воспользуйтесь
вспомогательной линией – параллелью.
8.
Через
фронтальную проекцию точки 42
проведите параллель (фронтальная
проекция параллели – отрезок прямой).
9. Замерьте радиус
параллели R.
10. Горизонтальную
проекцию параллели проведите радиусом
R
11. Спроецируйте
точку 4 на горизонтальную проекцию
параллели. Получится две проекции 41
и 41I.
7.4 Цилиндр
Цилиндр
– геометрическое тело, ограниченное
цилиндрической поверхностью и двумя
плоскостями.
Цилиндрическая
поверхность
образуется при вращении прямой линии
(образующей) вокруг неподвижной оси i,
параллельной образующей (рис.55).
1.Спроецируйте
нижнее основание цилиндра
на горизонтальную плоскость проекций.
Получится окружность, а на фронтальной
и профильной проекции – отрезок прямой,
равный диаметру окружности. Аналогично
спроецируйте верхнее основание.
2.Спроецируйте
контурные образующие на
фронтальную и профильную плоскости
проекций в виде прямых, перпендикулярных
к проекции основания и равных высоте
цилиндра. На П1
образующие проецируются в точки.
3.Постройте
комплексный чертеж цилиндра.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сечение поверхности конуса плоскостью общего положения
При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности.
Ниже мы рассмотрим задачу, в которой требуется построить проекции и натуральную величину сечения конуса ω плоскостью α . Начальные данные представлены на рисунке ниже.
Содержание
- Определение высшей и низшей точки сечения. Границы видимости
- Построение промежуточных точек и проекций эллипса
- Построение натуральной величины сечения методом совмещения
Определение высшей и низшей точки сечения. Границы видимости
Построение линии пересечения следует начинать с нахождения её характерных точек. Они определяют границы сечения и его видимость по отношению к наблюдателю.
Через ось конической поверхности проведем вспомогательную плоскость γ, параллельную П2. Она пересекает конус ω по двум образующим, а плоскость α по фронтали fγ. Точки 1 и 2 пересечения fγ с образующими являются граничными точками. Они делят сечение на видимую и невидимую части.
Определим высшую и низшую точки линии пересечения. Для этого через ось конуса перпендикулярно h0α введем дополнительную секущую плоскость β. Она пересекает коническую поверхность по образующим SL и SK, а плоскость α по прямой MN. Искомые точки 3 = SL ∩ MN и 4 = SK ∩ MN определяют большую ось эллипса. Его центр находится в точке O, которая делит отрезок 3–4 пополам.
Определение промежуточных точек и построение проекций эллипса
Чтобы построить проекции сечения наиболее точно, найдем ряд дополнительных точек. В случае с эллипсом целесообразно определить величину его малого диаметра. Для этого через центр O проводим вспомогательную горизонтальную плоскость δ. Она пересекает коническую поверхность по окружности диаметром AB, а плоскость α – по горизонтали hδ. Строим горизонтальные проекции окружности и прямой hδ. Их пересечение определяет точки 5′ и 6′ малого диаметра эллипса.
Для построения промежуточных точек 7 и 8 вводим вспомогательную горизонтальную плоскость ε. Проекции 7′ и 8′ определяются аналогично 5′ и 6′, как это показано на рисунке.
Соединив найденные точки плавной кривой, мы получили контур эллиптического сечения. На рисунке он обозначен красным цветом. Фронтальная проекция контура меняет свою видимость в точках 1 и 2, как это было отмечено выше.
Построение натуральной величины сечения методом совмещения
Чтобы найти натуральную величину сечения, повернем плоскость α до совмещения её с горизонтальной плоскостью. В качестве оси вращения будем использовать след h0α. Его положение в процессе преобразований останется неизменным.
Построение начинается с определения направления фронтального следа f1α. На прямой f0α возьмем произвольную точку E и определим её проекцию E’. Из E’ опустим перпендикуляр к h0α. Пересечение данного перпендикуляра с окружностью радиусом XαE” определяет положение точки E’1. Через Xα и E’1 проводим f1α.
Строим проекцию горизонтали h’1δ ∥ h0α, как это показано на рисунке. Точки O’1 и 5′1, 6′1 лежат на пересечении h’1δ с прямыми, проведенными перпендикулярно h0α из O’ и 5′, 6′. Аналогично на горизонтали h’1ε находим 7′1 и 8′1.
Строим проекции фронталей f’1γ ∥ f1α, f’3 ∥ f1α и f’4 ∥ f1α. Точки 1′1, 2′1, 3′1 и 4′1 лежат на пересечении этих фронталей с перпендикулярами, восстановленными к h0α из 1′, 2′, 3′ и 4′ соответственно.
Проекции точек на поверхностях геометрических тел
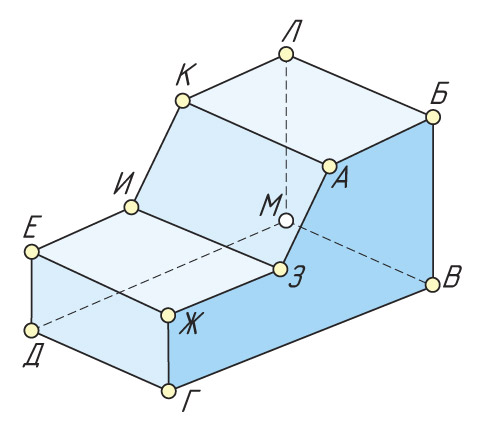
Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.
Укажите количество вершин, ребер и граней изображенного предмета.
|
Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки. |
 |
|
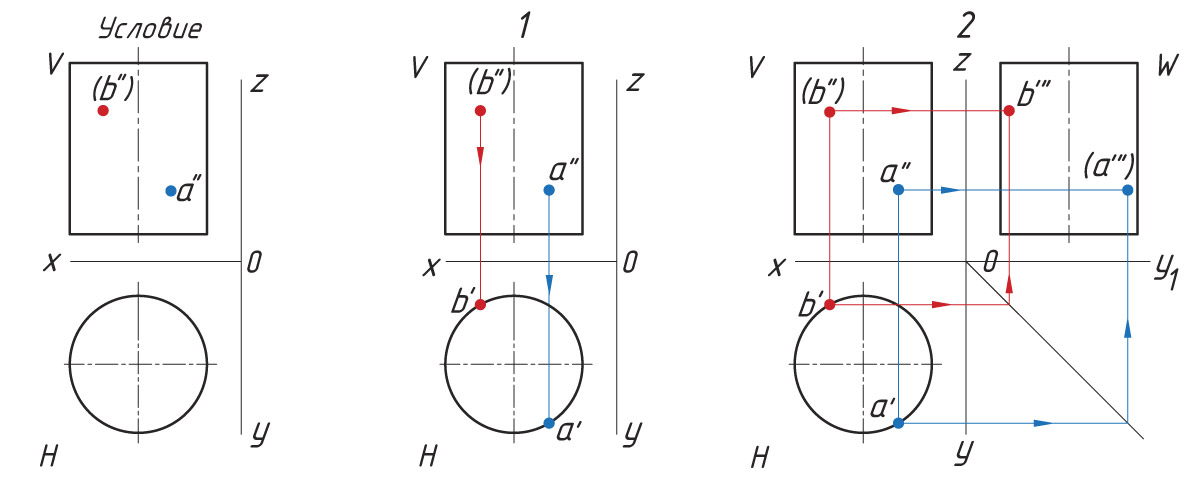
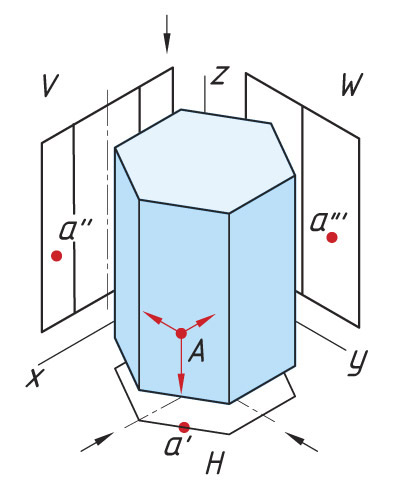
Рассмотрим проекции точки на геометрических телах. Проецирование точек на поверхности цилиндра Последовательность проецирования точек 1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью. 2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи. |
 |
Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).
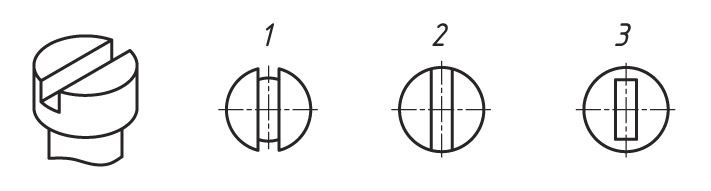
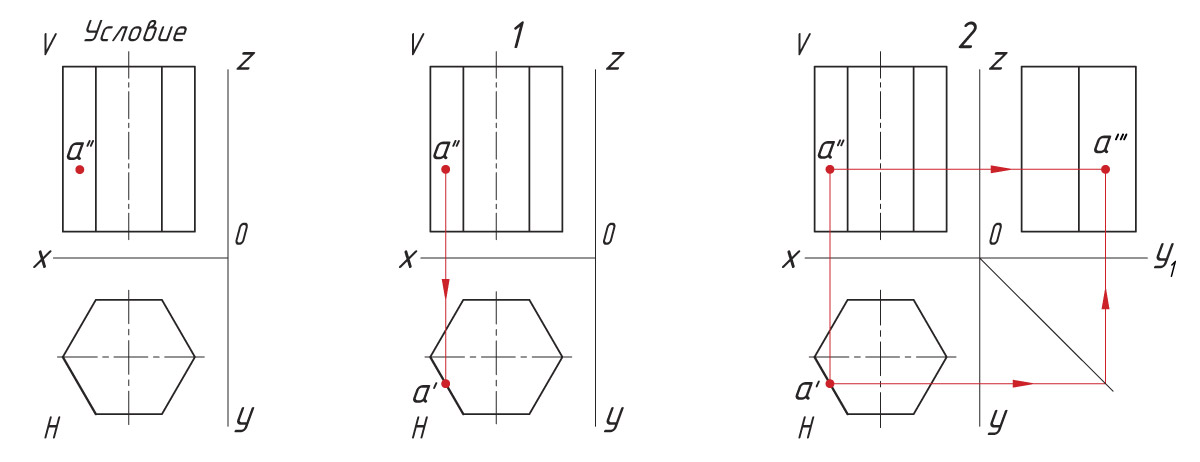
Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.
|
Проецирование точек на поверхности призмы Последовательность проецирования точек 1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы). 2. Проекцию точки а′″ находят на пересечении линий проекционной связи. |
 |
Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.
Проецирование точек на поверхности пирамиды
Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.
Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.
Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.
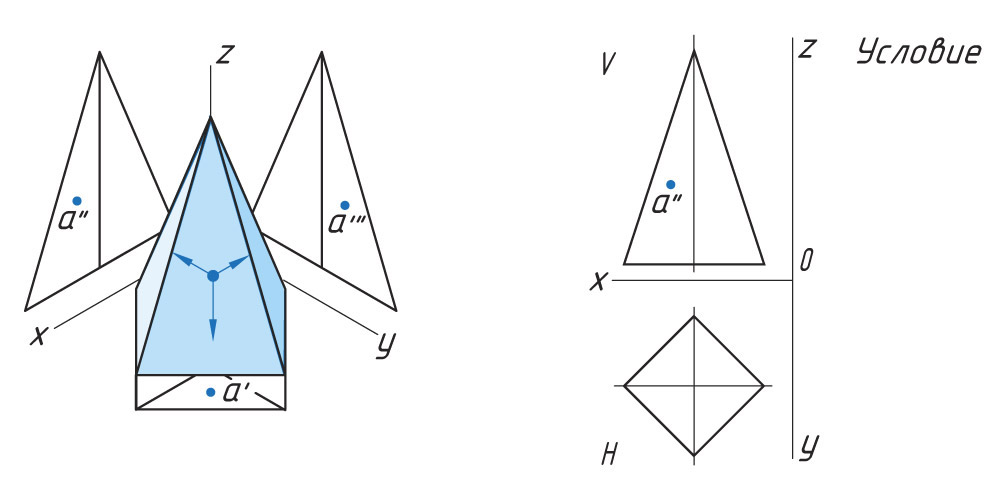
Построение проекции точки, лежащей на грани
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.
Проекции точек можно определить несколькими способами. Рассмотрим каждый из них.
|
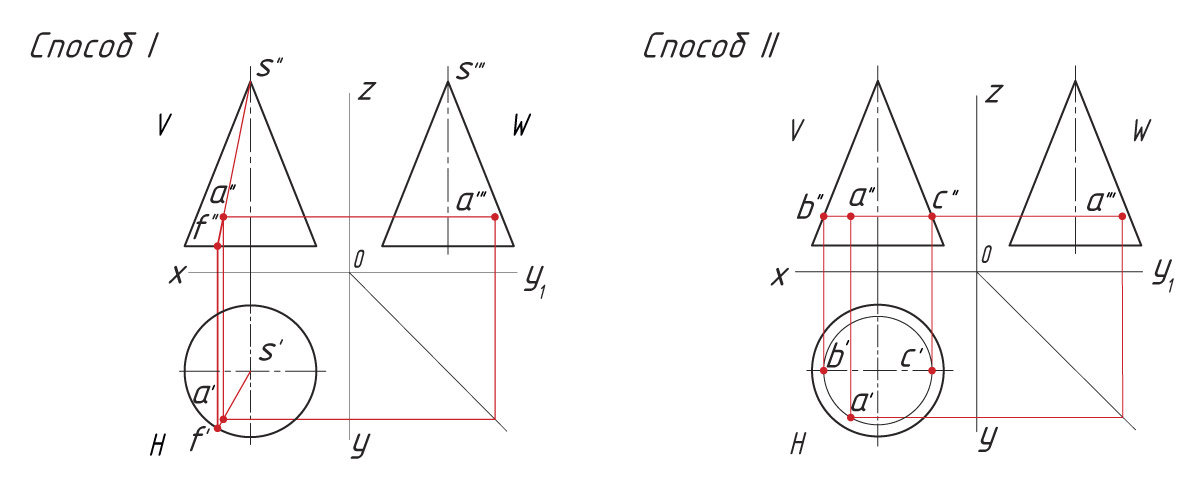
Способ I. 1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″. |
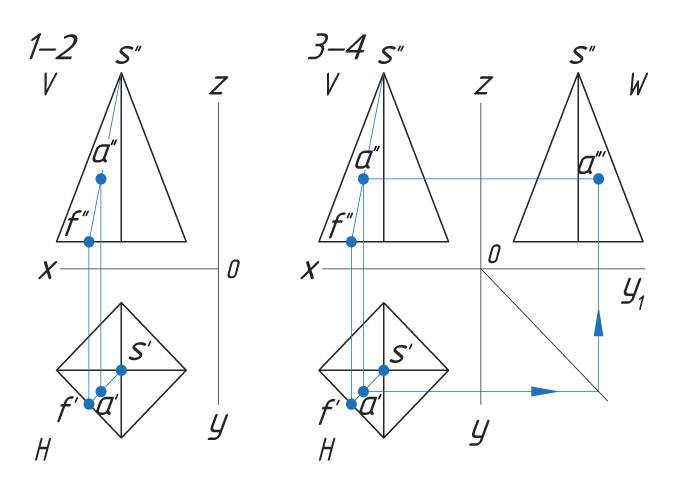 |
|
Способ II. 1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″. |
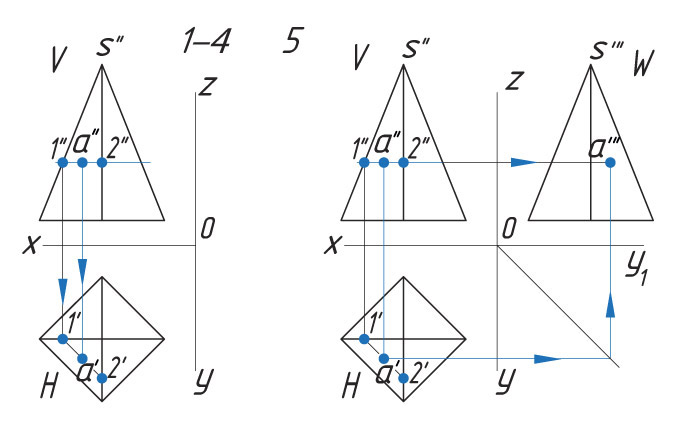 |
На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?
|
Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами. Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А. |
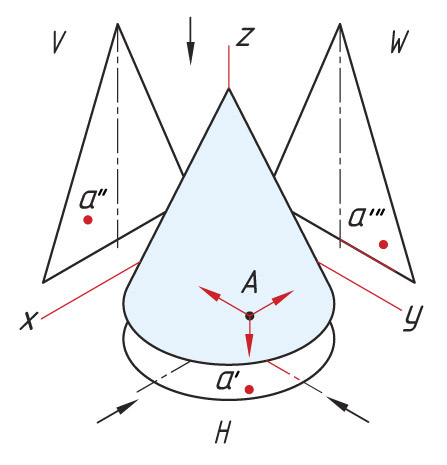 |
Преподаватель который помогает студентам и школьникам в учёбе.
Построение проекций линий пересечения конуса плоскостью с примером
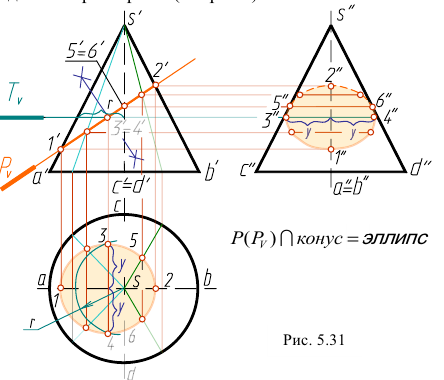
Построение проекций линий пересечения конуса плоскостью:
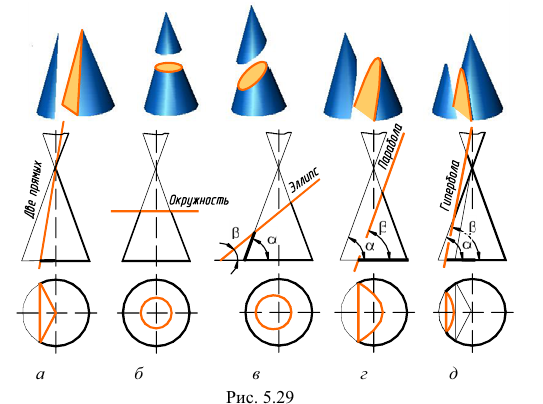
В зависимости от направления секущей плоскости в сечении конуса вращения могут получиться различные линии. Они называются линиями конических сечений.
Если секущая плоскость проходит через вершину конуса, в его сечении получается две прямые – образующие (треугольник) (рис. 5.29, а). В результате пересечения конуса плоскостью, перпендикулярной оси конуса, получается окружность (рис. 5.29, б). Если секущая плоскость наклонена к оси вращения конуса и не проходит через его вершину, в сечении конуса могут получиться эллипс, парабола или гипербола (рис. 5.29, в, г, д) – в зависимости от величины угла наклона секущей плоскости.
Эллипс получается в том случае, когда угол
Если углы 
Если секущая плоскость направлена под углом, который изменяется в пределах 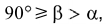
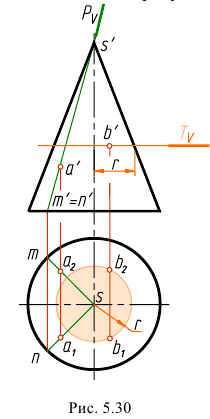
Известно, что точка принадлежит поверхности, если она принадлежит какой-нибудь линии поверхности. Для конуса наиболее простыми линиями являются прямые (образующие) и окружности. Следовательно, если требуется найти горизонтальные проекции точек А и В, принадлежащих поверхности конуса, то нужно через точки провести одну из этих линий.
Горизонтальную проекцию точки А найдем с помощью образующей. Для этого через точку А и вершину конуса S проведем вспомогательную фронтально – проецирующую плоскость 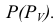
Задача имеет два ответа: точки 
Горизонтальную проекцию точки В найдем, построив окружность, на которой она лежит. Для этого через точку проведем горизонтальную плоскость 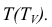
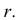
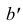
Рассмотрим пример построения проекций линии пересечения конуса фронтально – проецирующей плоскостью 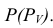
Фронтальная проекция линии сечения совпадает с фронтальным следом плоскости
Для удобства решения задачи обозначим крайние образующие конуса и определим характерные (опорные) точки.
Нижняя точка 1 лежит на образующей AS, верхняя – 2 на образующей BS. Эти точки определяют положение большой оси эллипса. Малая ось эллипса перпендикулярна большой оси. Чтобы найти малую ось, разделим отрезок 1-2 на две равные части. Точки 3 и 4 определяют малую ось эллипса. Точки 5 и 6, расположенные на образующих CS и DS, являются точками границы видимости для профильной плоскости проекций. Проекции точек 1, 2, 5 и 6 находятся на соответствующих проекциях образующих. Чтобы найти проекции точек 3 и 4, проводим дополнительную секущую плоскость 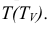
На горизонтальную плоскость проекций окружность проецируется в натуральную величину. Проведя линию связи, находим горизонтальные проекции точек 3 и 4. Профильные проекции находим, отложив на линии связи от оси конуса у координаты точек 3 и 4 (рис. 5.3 I).
Для точного построения эллипса недостаточно перечисленных точек. Поэтому необходимо определить дополнительные (случайные точки). Проекции этих точек находим аналогично точкам 3 и 4. Их можно найти также проводя через эти точки образующие. Найдя проекции всех точек, соединяем их. Определяем видимость. На горизонтальной плоскости все точки, лежащие на поверхности конуса, видимы. На профильной -точки 5, З, 1,4, 6 видимы, остальные – нет.
- Развертка поверхности конуса
- Шаровая поверхность
- Винтовые поверхности
- Способ вспомогательных секущих плоскостей
- Пирамида с вырезом
- Коническая и цилиндрическая поверхности
- Построение проекций линии пересечения цилиндра плоскостью
- Развертка поверхности цилиндра

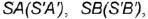
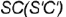 и
и 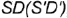 которые будут определять очерки фронтальной и профильной проекций конуса.
которые будут определять очерки фронтальной и профильной проекций конуса.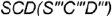 ограниченный:
ограниченный: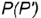
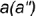
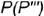 выполняется по принадлежности образующей
выполняется по принадлежности образующей 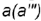 , построенной но координате
, построенной но координате 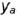 .
.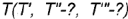
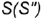
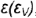
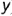 ).
).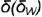
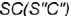 и
и  и пересекает его поверхность по участку гиперболы
и пересекает его поверхность по участку гиперболы 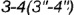 , которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов
, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов 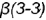 и плоскости
и плоскости 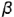 определяет вертикальный видимый отрезок
определяет вертикальный видимый отрезок 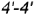 вырожденной в линию проекции профильной плоскости, точки
вырожденной в линию проекции профильной плоскости, точки 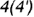 которой лежат на очерковой окружности основания конуса.
которой лежат на очерковой окружности основания конуса.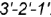 .
.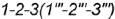
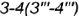 , ограниченные видимым отрезком
, ограниченные видимым отрезком 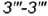 (построен) и видимым отрезком
(построен) и видимым отрезком 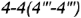 . точки которого построены но координате
. точки которого построены но координате 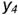 .
.