Как найти точку общую для двух плоскостей – Сайт, где вы сможете решить свои вопросы

В данном разделе продолжим изучение темы уравнения прямой в пространстве с позиции стереометрии. Это значит, что мы будем рассматривать прямую линию в трехмерном пространстве как линию пересечения двух плоскостей.

Согласно аксиомам стереометрии, если две плоскости не совпадают и имеют одну общую точку, то они также имею одну общую прямую, на которой лежат все точки, которые являются общими для двух плоскостей. Используя уравнения двух пересекающихся плоскостей, мы можем определить прямую линию в прямоугольной системе координат.

По ходу рассмотрения темы приведем многочисленные примеры, ряд графических иллюстраций и развернутых решений, необходимых для лучшего усвоения материала.

Уравнения двух плоскостей, задающих прямую линию в пространстве

Пусть даны две плоскости, которые не совпадают между собой и пересекаются. Обозначим их как плоскость α и плоскость β. Разместим их в прямоугольной системе координат Oхуz трехмерного пространства.

Как мы помним, любую плоскость в прямоугольной системе координат задает общее уравнение плоскости вида Ax+By+Cz+D=0. Будем считать, что плоскости α соотвествует уравнение A1x+B1y+C1z+D1=0, а плоскости β уравнение A2x+B2y+C2z+D2=0. В этом случае нормальные вектора плоскостей α и β n1→=(A1, B1, C1) и n2→=(A2, B2, C2) не коллинеарны, так как плоскости не совпадают между собой и е размещаются параллельно друг другу. Запишем это условие следующим образом:

n1→≠λ·n2→⇔A1, B1, C1≠λ·A2, λ·B2, λ·C2 , λ∈R

Чтобы освежить в памяти материал по теме «Параллельность плоскостей», смотрите соответствующий раздел нашего сайта.

Линию пересечения плоскостей обозначим буквой a. Т.е. a=α∩β. Эта прямая представляет собой множество точек, которые являются общими для обеих плоскостей α и β. Это значит, что все точки прямой линии a удовлетворяют обоим уравнениям плоскости A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0. Фактически, они являются частным решением системы уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0.

Общее решение системы линейных уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 определяет координаты всех точек линии, по которой происходит пересечение двух плоскостей α и β. Это значит, что с его помощью мы можем определить положение прямой в прямоугольной системе координат Oxyz.

Уравнения двух плоскостей, задающих прямую линию в пространстве

Рассмотрим описанную теорию еще раз, теперь уже на конкретном примере.

Пример 1

Прямая Ox – это прямая, по которой пересекаются координатные плоскости Oxy и Oxz. Зададим плоскость Oxy уравнением z=0, а плоскость Oxz уравнением у=0. Такой подход мы подробно разобрали в разделе «Неполное общее уравнение плоскости», так что, в случае затруднений, можно обратиться к этому материалу повторно. В этом случае координатная прямая Ox определяется в трехмерной системе координат системой из двух уравнений вида y=0z=0.

Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости

Рассмотрим задачу. Пусть в трехмерном пространстве задана прямоугольная система координат Oхуz. Линия, по которой пересекаются две плоскости a, задана системой уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0. Дана точка трехмерного пространства M0 x0, y0, z0.

Давайте определим, принадлежит ли точка M0 x0, y0, z0 заданной прямой линии a.

Для того, чтобы получить ответ на вопрос задачи, подставим координаты точки М0 в каждое из двух уравнений плоскости. Если в результате подстановки оба уравнения превратятся в верные равенства A1x0+B1y0+C1z0+D1=0 и A2x0+B2y0+C2z0+D2=0, то точка М0 принадлежит каждой из плоскостей и принадлежит заданной линии. Если хотя бы одно из равенств A1x0+B1y0+C1z0+D1=0 и A2x0+B2y0+C2z0+D2=0 окажется неверным, то точка М0 не принадлежит прямой линии.

Рассмотрим решение примера

Пример 2

Прямая линия задана в пространстве уравнениями двух пересекающихся плоскостей вида 2x+3y+1=0x-2y+z-3=0. Определите, принадлежат ли точки M0(1, -1, 0) и N0(0, -13, 1) прямой линии пересечения плоскостей.

Решение

Начнем с точки М0_.Подставим ее координаты в оба уравнения системы 2·1+3·(-1)+1=01-2·(-1)+0-3=0⇔0=00=0.

В результате подстановки мы получили верные равенства. Это значит, что точка М0 принадлежит обеим плоскостям и расположена на линии их пересечения.

Подставим в оба уравнения плоскости координаты точки N0(0, -13, 1). Получаем 2·0+3·-13+1=00-2·-13+1-3=0⇔0=0-113=0.

Как вы видите, второе уравнение системы превратилось в неверное равенство. Это значит, что точка N0 не принадлежит заданной прямой.

Ответ: точка М0принадлежит прямой линии, а точка N0не принадлежит.

Теперь предлагаем вам алгоритм нахождения координат некоторой точки, принадлежащей прямой линии, если прямая в пространстве в прямоугольной системе координат Oxyz определяется уравнениями пересекающихся плоскостей A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0.

Количество решений системы из двух линейных уравнений с темя неизвестными A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 бесконечно. Любое из этих решений может стать решением задачи.

Приведем пример.

Пример 3

Пусть в трехмерном пространстве задана прямая линия уравнениями двух пересекающихся плоскостей вида x+3z+7=02x+3y+3z+2=0. Найдите координаты любой из точек этой прямой.

Решение

Перепишем систему уравнений x+3z+7=02x+3y+3z+2=0⇔x+0y+3z=-72x+3y+3z=-2.

Возьмем отличный от нуля минор второго порядка в качестве базисного минора основной матрицы системы 1023=3≠0. Это значит, что z – это свободная неизвестная переменная.

Перенесем слагаемые, содержащие свободную неизвестную переменную z в правые части уравнений:

x+0y+3z=-72x+3y+3z=-2⇔x+0y=-7-3z2x+3y=-2-3z

Введем произвольное действительное число λ и примем, что z=λ.

Тогда x+0y=-7-3z2x+3y=-2-3z⇔x+0y=-7-3λ2x+3y=-2-3λ.

Для решения полученной системы уравнений применим метод Крамера:

∆=1023=1·3-0·1=2∆x=-7-3λ0–3λ3=-7-3λ·3-0·(-2-3λ)=21-9λ⇒x=∆x∆=-7-3λ∆y=1-7-3λ2-2-3λ=1·-2-3λ–7-3λ·=12+3λ⇒y=∆y∆=4+λ

Общее решение системы уравнений x+3z+7=02x+3y+3z+2=0 будет иметь вид x=-7-3λy=4+λz=λ, где λ∈R.

Для получения частного решения системы уравнений, которое даст нам искомые координаты точки, принадлежащей заданной прямой, нам необходимо взять конкретное значение параметра λ . Если λ=0, то x=-7-3·0y=4+0z=0⇔x=-7y=4z=0.

Это позволяет нам получить координаты искомой точки -7, 4, 0.

Проверим верность найденных координат точки методом подстановки их в исходные уравнения двух пересекающихся плоскостей -7+3·0+7=02·(-7)+3·4+3·0+2=0⇔0=00=0.

Ответ: -7, 4, 0

Направляющий вектор прямой, по которой пересекаются две плоскости

Давайте рассмотрим, как определить координаты направляющего вектора прямой, которая задана уравнениями двух пересекающихся плоскостей A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0. В прямоугольной системе координат 0хуz направляющий вектор прямой неотделим от прямой линии.

Как мы знаем, прямая перпендикулярна по отношению к плоскости в том случае, когда она перпендикулярна по отношению к любой прямой, лежащей в данной плоскости. Исходя из вышесказанного, нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в данной плоскости. Эти два факта помогут нам в нахождении направляющего вектора прямой.

Плоскости α и β пересекаются по линии a. Направляющий вектор a→ прямой линии a расположен перпендикулярно по отношению к нормальному вектору n1→=(A1, B1, C1) плоскости A1x+B1y+C1z+D1=0 и нормальному вектору n2→=(A2, B2, C2) плоскости A2x+B2y+C2z+D2=0.

Направляющий вектор прямой a представляет собой векторное произведение векторов n→1=(A1, B1, C1) и n2→=A2, B2, C2.

a→=n→1×n2→=i→j→k→A1B1C1A2B2C2

Зададим множество всех направляющих векторов прямой как λ·a→=λ·n1→×n2→, где λ – это параметр, который может принимать любые действительные значения, отличные от нуля.

Пример 4

Пусть прямая в пространстве в прямоугольной системе координат Oхуz задана уравнениями двух пересекающихся плоскостей x+2y-3z-2=0x-z+4=0. Найдем координаты любого направляющего вектора этой прямой.

Решение

Плоскости x+2y-3z-2=0 и x-z+4=0 имеют нормальные векторы n1→=1, 2, -3 и n2→=1, 0, -1. Примем за направляющий вектор прямой линии, являющейся пересечением двух заданных плоскостей, векторное произведение нормальных векторов:

a→=n→1×n2→=i→j→k→12-310-1=i→·2·(-1)+j→·(-3)·1+k→·1·0–k→·2·1-j→·1·(-1)-i→·(-3)·0=-2·i→-2j→-2k→

Запишем ответ в координатной форме a→=-2, -2, -2. Тем, кто не помнит, как это делается, рекомендуем обратиться к теме «Координаты вектора в прямоугольной системе координат».

Ответ: a→=-2, -2, -2

Переход к параметрическим и каноническим уравнениям прямой в пространстве

Для решения ряда задач проще использовать параметрические уравнения прямой в пространстве вида x=x1+ax·λy=y1+ay·λz=z1+az·λ или канонические уравнения прямой в пространстве вида x=x1+ax·λy=y1+ay·λz=z1+az·λ. В этих уравнениях ax, ay, az – координаты направляющего вектора прямой, x1, y1, z1 – координаты некоторой точки прямой, а λ – параметр, принимающий произвольные действительные значения.

От уравнения прямой вида A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 можно перейти к каноническим и параметрическим уравнениям прямой линии в пространстве. Для записи канонических и параметрических уравнений прямой нам понадобятся навыки нахождения координат некоторой точки прямой, а также координат некоторого направляющего вектора прямой, заданной уравнениями двух пересекающихся плоскостей.

Рассмотрим написанное выше на примере.

Пример 5

Зададим прямую линию в трехмерной системе координат уравнениями двух пересекающихся плоскостей 2x+y-z-1=0x+3y-2z=0. Напишем канонические и параметрические уравнения этой прямой.

Решение

Найдем координаты направляющего вектора прямой, который является векторным произведением нормальных векторов n1→=2, 1, -1 плоскости 2x+y-z-1=0и n2→=(1, 3, -2) плоскости x+3y-2z=0:

a→=n1→×n2→=i→j→k→21-113-2=i→·1·(-2)+j→·(-1)·1+k→·2·3–k→·1·1-j→·2·(-2)-i→·(-1)·3=i→+3·j→+5·k→

Координаты направляющего вектора прямой a→=(1, 2, 5).

Следующим шагом является определение координат некоторой точки заданной прямой линии, которыми является одно из решений системы уравнений: 2x+y-z-1=0x+3y-2z=0⇔2x+y-z=1x+3y-2z=0.

Возьмем в качестве минорной матрицы системы определитель 2113=2·3-1·1=5 , который отличен от нуля. В этом случае переменная z является свободной. Перенесем слагаемые с ней в правые части каждого уравнения и придаем переменной произвольное значение λ:

2x+y-z=1x+3y-2z=0⇔2x+y=1+zx+3y=2z⇔2x+y=1+λx+3y=2λ, λ∈R

Применяем для решения полученной системы уравнений метод Крамера:

∆=2113=2·3-1·1=5∆x=1+λ12λ3=(1+λ)·3-1·2λ=3+λ⇒x=∆x∆=3+λ5=35+15·λ∆y=21+λ12λ=2·2λ-(1+λ)·1=-1+3λ⇒y=∆y∆=-1+3λ5=-15+35·λ

Получаем: 2x+y-z-1=0x+3y-2z=0⇔x=35+15y=-15+35z=λ

Примем λ=2 для того, чтобы получить координаты точки прямой линии: x1=35+15·2y1=-15+35·2z1=2⇔x1=1y1=1z1=2. Теперь мы имеем достаточно данных для того, чтобы записать канонические и параметрические уравнения данной прямой в пространстве: x-x1ax=y-y1ay=z-z1az⇔x-11=y-13=z-25x=x1+ax·λy=y1+ay·λz=z1+az·λ⇔x=1+1·λy=1+3·λz=2+5·λ⇔x=1+λy=1+3·λz=2+5·λ

Ответ: x-11=y-13=z-25 и x=1+λy=1+3·λz=2+5·λ

Данная задача имеет еще один способ решения.

Нахождение координат некоторой точки прямой проводится при решении системы уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0.

В общем случае ее решения можно записать в виде искомых параметрических уравнений прямой в пространстве x=x1+ax·λy=y1+ay·λz=z1+az·λ.

Получение канонических уравнений проводится следующим образом: решаем каждое из полученных уравнений относительно параметра λ, приравниваем правые части равенства.

x=x1+ax·λy=y1+ay·λz=z1+az·λ⇔λ=x-x1axλ=y-y1ayλ=z-z1az⇔x-x1ax=y-y1ay=z-z1az

Применим данный способ к решению задачи.

Пример 6

Зададим положение прямой линии уравнениями двух пересекающихся плоскостей 2x+y-z-1=0x+3y-2z=0. Напишем параметрическое и каноническое уравнения для этой прямой линии.

Решение

Решение системы из двух уравнений с тремя неизвестными проводится аналогично тому, как мы делали это в предыдущем примере. Получаем: 2x+y-z-1=0x+3y-2z=0⇔x=35+15·λy=-15+35·λz=λ.

Это параметрические уравнения прямой в пространстве.

Канонические уравнения получаем следующим образом: x=35+15·λy=-15+35·λz=λ⇔λ=x-3515λ=y+1535λ=z1⇔x-3515=y+1535=z1

Полученные в обоих примерах уравнения отличаются внешне, однако они эквивалентны, так как определяют одно и то же множество точек трехмерного пространства, а следовательно и одну и ту же прямую линию.

Ответ: x-3515=y+1535=z1 и x=35+15·λy=-15+35·λz=λ

Источник

Параллельные плоскости.

Плоскости будут параллельными:

если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости (рис. 6);
если плоскости параллельны, то параллельны их одноименные следы (рис. 7).

рис. 6

рис. 7

Плоскости пересекаются

Для построения линии пересечения двух плоскостей необходимо

или найти две точки, каждая из которых принадлежит обеим плоскостям;
или найти одну точку, принадлежащей двум плоскостям, и направление линии пересечения.

В обоих случаях задача заключается в нахождении точек, общих для двух плоскостей.

Плоскости в пространстве могут занимать различное положение. рассмотрим три случая построения линии их пересечения.

Линия пересечения двух проецирующих плоскостей

Если плоскости занимают частное положение, например, как на рис. 8, являются горизон- тально-проецирующими, то проекцией линии пересечения на плоскость проекций, которой данные плоскости перпендикулярны (в данном случае горизонтальной), будет точка. Фронтальная проекция линии пересечения перпендикулярна оси проекций.

рис. 8

Линия пересечения плоскости общего положения и проецирующей плоскости

В этом случае одна проекция линии пересечения совпадает с проекцией проецирующей плоскости на той плоскости проекций, которой она перпендикулярна.

На рис. 9 показано построение проекций линии пересечения горизонтально-проецирующей плоскости, заданной следами, c плоскостью общего положения (треугольник ABC).

На горизонтальной проекции (рис. 9) в пересечении следа плоскости P_Н и сторон АС и ВС треугольника АВС находим горизонтальные проекции n и m линии пересечения. По линиям связи находим фронтальные проекции точек M и N линии пересечения.

При взгляде по стрелке на плоскость V по горизонтальной проекции видно, что часть треугольника правее линии пересечения МN (mn) находится перед плоскостью Р, то есть будет видимой на фронтальной плоскости проекций. Остальная часть — за плоскостью Р, то есть невидима.

рис. 9

Линия пересечения двух плоскостей общего положения

Построение линии пересечения двух плоскостей общего положения осуществляется с помощью дополнительных плоскостей- посредников.

Общий прием построения линии пересечения таких плоскостей заключается в следующем. Вводим вспомогательную плоскость (посредник) и строим линии пересечения вспомогательной плоскости с двумя заданными. В пересечении построенных линий находим общую точку двух плоскостей. Чтобы найти вторую общую точку, повторяем построение с помощью еще одной вспомогательной плоскости.

Соединяем полученные точки М и N и определяем взаимную видимость фигур.

Рис. 10

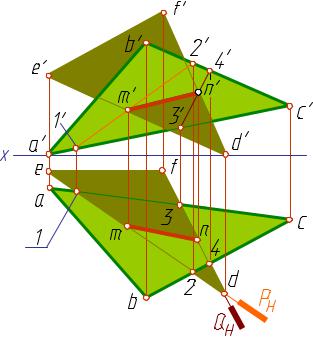
Задача. Построить линию пересечения двух плоских фигур, заданных треугольниками с координатами вершин:

ΔABC — A(16,2,0), B(10,9,7), C(1,4,3)

ΔDEF — D (5,9,0), E (16,1,5), F (9,1,9)

На рис. 11 дано построение линии пересечения двух треугольников. Решение выполняем в следующей последовательности. Проводим две вспомогательные горизонтально-проецирующие плоскости — плоскость P через сторону ED и плоскость Q через сторону DF треугольника DEF. Плоскость P пересекает треугольник ABC по прямой 1-2.

В пересечении фронтальных проекций 1′-2′ и d’e‘ находим фронтальную проекцию точки M(m’) линии пересечения. Плоскость Q пересекает треугольник ABC по прямой 3-4. В пересечении фронтальных проекций 3′-4′ и b‘c‘ находим фронтальную проекцию точки N(п’) линии пересечения. Горизонтальные проекции этих точек, а следовательно, и линии пересечения, находим, проводя линии связи.

Соединяем точки M и N. Взаимную видимость треугольников на плоскостях проекций определяем с помощью конкурирующих точек.

рис. 11

Источник

3. Так как прямые AB и MN лежат в одной плоскости P, то определяют точку их пересечения (точку K), которая является точкой пересечения прямой AB с плоскостью Q.

3.(•)K = (AB) ∩(MN)

4. Определяют взаимную видимость прямой AB и плоскости Q.

Задача: Определить точку пересечения прямой АВ с плоскостью треугольника СDE (рис. 5). Точки задаются координатами:

A(9,1,2), B(2,7,6), C(11,7,4), D(2,4,2), E(5,0,7)

Задачу решаем по выше рассмотренному плану.

• Через прямую AB проводим вспомогательную фронтальнопроецирующую плоскость P.

(AB) P V

• Строим линию пересечения (12) заданной плоскости Q (∆ CDE) и вспомогательной плоскости P.

(12) = P ∩Q( CDE)

• Так как прямые (AB) и (12) лежат

в одной плоскости P, то определяем точку

их пересечения (точку K), которая являет-

ся точкой пересечения прямой AB с плос-

костью Q.

(•)K = (12)∩(AB)

•	Определяем взаимную видимость
прямой AB и плоскости Q.
Для определения видимых участков
прямой AB анализируем положение точек
на скрещивающихся прямых (конкури-
рующих точек).
	(•)1 CD	(•)4 АВ
	(•)3 AB	(•)5 СD
Рис. 5	Y1 >Y3	Z4 > Z5

Взаимное положение двух плоскостей

Параллельные плоскости. Плоскости будут параллельными:

•если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости (рис. 6);

•если плоскости параллельны, то параллельны их одноименные следы

(рис. 7).

Плоскости пересекаются

Для построения линии пересечения двух плоскостей необходимо

•или найти две точки, каждая из которых принадлежит обеим плоскостям;

•или найти одну точку, принадлежащей двум плоскостям, и направление линии пересечения.

Вобоих случаях задача заключается в нахождении точек, общих для двух плоскостей.

1.Линия пересечения двух проецирующих плоскостей

Если плоскости занимают частное положение, например, как на рис. 8, являются горизон- тально-проецирующими, то проекцией линии пересечения на плоскость проекций, которой данные плоскости перпендикулярны (в данном случае горизонтальной), будет точка. Фронталь- ная проекция линии пересечения перпендикулярна оси проекций.

Рис. 8

2. Линия пересечения плоскости общего положения и проецирующей плоскости

В этом случае одна проекция линии пересечения совпадает с проекцией проецирующей плоскости на той плоскости проекций, которой

	она перпендикулярна. На рис. 9 по-
	казано построение проекций линии
	пересечения	горизонтально-
	проецирующей плоскости, заданной
	следами, c плоскостью общего по-
	ложения (треугольник ABC).
	На горизонтальной проекции
	(рис. 9) в пересечении следа плоско-
	сти PН и сторон АС и ВС треуголь-
	ника АВС находим горизонтальные
	проекции n и m линии пересечения.
	По линиям связи находим фрон-
	тальные проекции точек M и N ли-
	нии пересечения.
Рис. 9	При взгляде по стрелке на
плоскость V по горизонтальной про-

екции видно, что часть треугольника правее линии пересечения MN (mn)
находится перед плоскостью P, то есть будет видимой на фронтальной
плоскости проекций. Остальная часть − за плоскостью P, то есть неви-
дима.

Линия пересечения двух плоскостей общего положения

Построение линии пересечения двух плоскостей общего положения осуществляется с помощью дополнительных плоскостейпосредников.

(12) = Q ∩∆ABC

(34) = Q ∩∆EFK

(•)M = (12) ∩(34)

(56) = P ∩∆ABC

(78) = P ∩∆EFK

(•)N = (56) ∩(78)

Соединяем полученные точки М и N и определяем взаимную

видимость фигур.

Рис. 10

При решении подобных задач удобнее в качестве посредников применять проецирующие плоскости.

Задача. Построить линию пересечения двух плоских фигур, заданных треугольниками с координатами вершин:

∆ABC – A(16,2,0), B(10,9,7), C(1,4,3)

∆DEF – D(5,9,0), E(16,1,5), F(9,1,9)

На рис. 11 дано построение линии пересечения двух треугольников. Решение выполняем в следующей последовательности. Проводим

две вспомогательные горизонтально-проецирующие плоскости − плоскость P через сторону ED и плоскость Q через сторону DF треугольника DEF. Плоскость P пересекает треугольник ABC по прямой 1-2. В пересечении фронтальных проекций 1′-2′ и d′e′ находим фронтальную проекцию точки M(m′) линии пересечения. Плоскость Q пересекает треугольник ABC по прямой 3-4. В пересечении фронтальных проекций 3′-4′ и b′c′ находим фронтальную проекцию точки N(n′) линии пересечения. Горизонтальные проекции этих точек, а следовательно, и линии пересечения, находим, проводя линии связи.

1.(ED) P H

2.(12) = P ∩ ∆ABC 3.(•)M = (12) ∩(ED)

4.(FD) Q H

5.(34) = Q ∩∆ABC 6.(•)N = (34) ∩(FD)

Лекция5.Поверхности

Способы задания поверхности

Существуют различные способы задания поверхности.

1. Аналитический способ

Поверхность в этом случае описана математическим выражением и представляется как геометрическое место точек или линий, удовлетворяющих уравнению F(x, y, z) = 0.

Например, поверхность шара задана уравнением: x2+y2+z2=r2. 2. Задание поверхности каркасом.

Этот способ используется при задании сложных поверхностей. Поверхность задается семейством линий, принадлежащих поверхности (каркасом). Каркасы могут быть сетчатые, линейчатые, точечные.

При задании поверхности каркасом необходимо иметь ряд ее параллельных сечений, которые можно рассматривать как положения образующей переменного вида. Такой способ применяется при изготовлении кузовов автомобилей, в самолетостроении и судостроении.

Способ задания поверхности каркасом с помощью линий пересечения поверхности плоскостями уровня применяется в топографии, горном и дорожном деле. Проекции линии уровня на плоскость проекций с соответствующими отметками представляют собой карту рельефа местности. Поверхность, отнесенная к земной поверхности, называется топо-

графической (рис. 1).

Рис. 1

3. Кинематический способ

В начертательной геометрии поверхности рассматриваются как

	множество последовательных по-
Образующая	ложений движущейся линии. Та-
	кой способ образования поверх-
	ности называется кинематиче-
	ским.
	Линия (кривая или прямая)
Направляющая	движется в пространстве и созда-
ет поверхность. Она называется
Рис. 2

образующей. Как правило, образующая движется по второй линии. Эта линия называется направляющей (рис. 2).

Классификация поверхностей

Поверхности можно разделить на несколько классов в зависимости от формы образующей, а также от формы, числа и расположения направляющих:

1.Поверхности закономерные и незакономерные.

2.Линейчатые (образованные перемещением прямой линии) и нелинейчатые (криволинейные) поверхности.

3.Поверхности развертывающиеся (или торсы) и неразвертываю-

щиеся.

Развертывающиеся поверхности – поверхности, которые после разреза их по образующей могут быть односторонне совмещены с плоскостью без наличия разрывов и складок.

Неразвертывающиеся поверхности – поверхности, которые не мо-

гут быть совмещены с плоскостью без наличия разрывов и складок.

4.Поверхности с образующей постоянной формы и поверхности с образующей переменной формы.

5.Поверхности с поступательным, вращательным или винтовым движением образующей.

Задание поверхности на чертеже

Чтобы задать поверхность на комплексном чертеже, достаточно иметь на нем такие элементы поверхности, которые позволяют построить каждую ее точку. Совокупность этих элементов называется определи-

телем поверхности.

Определитель поверхности состоит из двух частей:

•геометрической части,

включающей постоянные геометри-

Ωl ческие элементы (точки, линии), ко-

	торые участвуют в образовании по-
	верхности;
	• алгоритмической	части,
	задающей закон движения обра-
	зующей, характер изменения ее
	формы.
	Когда какая-нибудь поверх-
	ность Ω проецируется с помощью
Рис. 3	параллельных лучей на	плоскость
проекций P, то проецирующие пря-

мые, касающиеся поверхности Ω, образуют цилиндрическую поверхность (рис. 3). Эти проецирующиеся

прямые касаются поверхности Ω в точках, образующих некоторую линию m, которая называется контурной линией.

Проекция контурной линии m на плоскость P, mp, называется очер-

ком поверхности.

Чтобы сделать чертеж более наглядным строят очерк поверхности, а также ее наиболее важные линии и точки.

Линейчатые поверхности

Гранные поверхности Гранной поверхностью называется поверхность, образованная пе-

ремещением прямолинейной образующей по ломаной направляющей. Гранные поверхности можно разделить на два вида: пирамидальные (рис. 4, а) и призматические (рис. 4, б).

Пирамидальная поверхность Призматическая поверхность

Рис. 4

Пирамидальной называется поверхность, образованная перемещением прямолинейной образующей по ломаной направляющей. При этом все образующие проходят через некоторую неподвижную точку S. Определитель поверхности – ломаная направляющая m и точка S.

Призматической называется поверхность, образованная перемещением прямолинейной образующей по ломаной направляющей. При этом все образующие проходят параллельно некоторому заданному направлению l. Определитель поверхности – ломаная направляющая m и направление l.

Точка на поверхности

Точка принадлежит поверхности, если она принадлежит какой-

нибудь линии, принадлежащей поверхности.

Линия принадлежит поверхности, если она проходит через точки,

принадлежащие поверхности.

Следовательно, если точка принадлежит поверхности, то ее проекции принадлежат одноименным проекциям линии этой поверхности.

Точки M и N принадлежат соответственно пирамидальной и призматической поверхностям, так как принадлежат прямым, расположенным на этих поверхностях.

Часть пространства, ограниченная со всех сторон поверхностью, называется телом.

Многогранники

Многогранником называется тело, ограниченное плоскими многоугольниками. Рассмотрим два многогранника – пирамиду и призму.

Пирамида представляет собой многогранник, у которого одна грань − основание (произвольный многоугольник). Остальные грани (боковые) − треугольники с общей вершиной S, называемой вершиной пирамиды.

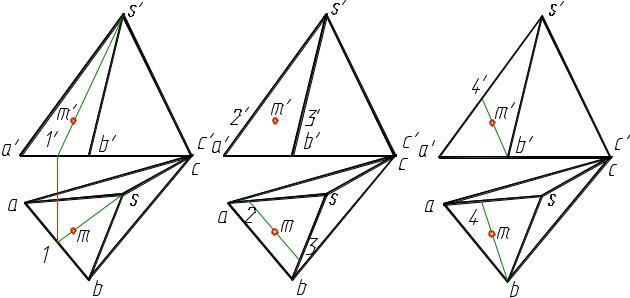
Для задания на чертеже пирамиды достаточно задать ее основание и вершину. Чтобы построить проекции точки на поверхности пирамиды, нужно через эту точку провести вспомогательную прямую, принадлежащую поверхности пирамиды (рис. 5).

Ω – пирамида SABC. (•) М (m′) Ω.	m – ?
(•) М S1	(•) М 2–3	(•) М B4

Рис. 5

Призмой называется многогранник, у которого основания – равные многоугольники с соответственно параллельными сторонами. Боковые грани призмы − параллелограммы. Если ребра боковых граней перпендикулярны основанию, то призму называют прямой (рис. 6), если нет – наклонной (рис. 7). Для задания призмы достаточно задать одно ее основание и боковое ребро. Чтобы построить недостающую проекцию точки, лежащей на грани призмы, нужно через эту точку провести прямую.

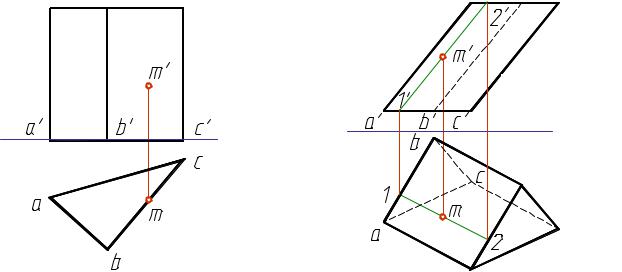
Σ – призма ABC. (•) М (m′) Σ. m – ?

Пересечение многогранников плоскостями

В пересечении гранных поверхностей плоскостями получаются многоугольники. Их вершины определяются как точки пересечения ребер гранных поверхностей с секущей плоскостью.

Многоугольник сечения может быть построен двумя способами:

1.Вершины многоугольника находятся как точки пересечения прямых (ребер) с секущей плоскостью;

2.Стороны многоугольника находятся как линии пересечения плоскостей (граней) многогранника с секущей плоскостью.

В качестве примера построим сечение призмы (рис. 8) и пирамиды (рис. 9) фронтально-проецирующими плоскостями.

Секущая плоскость является фронтально – проецирующей, следовательно, все линии, лежащие в этой плоскости (в том числе и фигура

сечения на фронтальной проекции), совпадут с фронтальным следом QV плоскости Q. Таким образом, фронтальные проекции фигур сечения

1′2′3′ определятся при пересечении фронтальных проекций ребер призмы и пирамиды со следом QV. Горизонтальные проекции точек 1, 2 и 3 находим при помощи линий связи на горизонтальных проекциях соответствующих ребер.

Грани прямой призмы на плоскость, которой они перпендикулярны, проецируются в линии, ребра – в точки. Поэтому все точки и линии, находящиеся на гранях и ребрах призмы проецируется соответственно на эти линии и точки. Проекция фигуры сечения призмы совпадает с горизонтальной проекцией самой призмы (рис. 8).

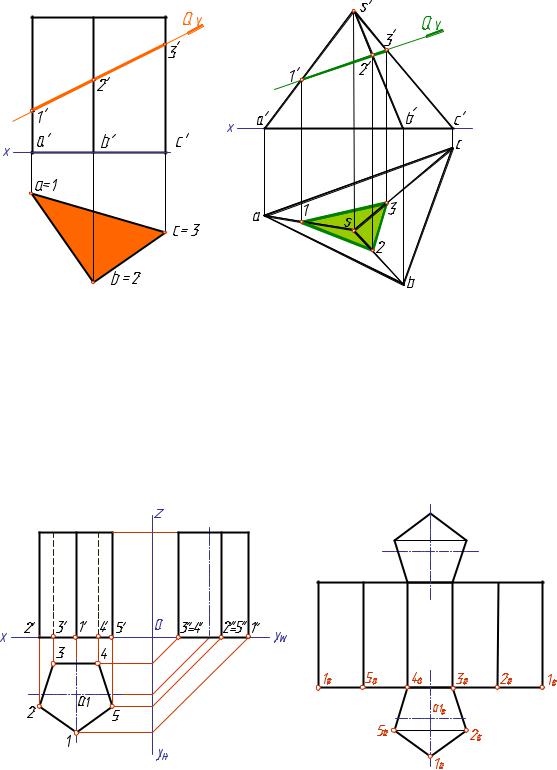
Ω – призма ABC.	Q V
Ω∩Q =	123
	Рис. 8

Ω – пирамида SABC. Q V

Ω∩Q = 123

Развертки многогранников Развертка поверхности призмы

При построении развертки поверхности любого многогранника все его грани располагают в одной плоскости. В результате построения развертки получают плоскую фигуру, в которой все грани многогранника сохраняют свою форму, натуральные размеры и последовательность расположения.

Рассмотрим построение развертки поверхности пятиугольной призмы (рис. 5.9).

Для построения развертки боковой поверхности проводим горизонтальную прямую линию, на которой откладываем пять отрезков, каждый из которых равен ширине грани или стороне пятиугольного основа-

ния. Можно взять величину этого отрезка с ортогонального чертежа, где сторона основания проецируется без искажения. Получаем точки 10…50. Затем из этих точек вверх проводим перпендикуляры (ребра боковой поверхности призмы), на которых откладываем высоту призмы, взятую на фронтальной или профильной проекции.

Далее строим два основания. Для этого через середину стороны грани 3040 (или любой другой) проводим центровую линию, на которую с горизонтальной проекции переносим расстояние от стороны 34 до центра О1 и вершины основания. Строим точку О10 и проводим вторую центровую линию основания. Для нахождения точек 20 и 50 на горизонтальной проекции точки 2 и 5 соединяем прямой линией. Измеряем расстояние от точки пересечения этой линии с центровой до стороны 34 и переносим это расстояние на соответствующую центровую линию на развертке. Проводим параллельно стороне 3040 прямую, на которую с горизонтальной проекции переносим расстояние от осевой линии до точек 2 и 5. Полученные точки 10 … 50 соединяем отрезками, получаем основание. Таким же образом строим второе основание.

Развертка поверхности правильной пирамиды

Так как боковые ребра правильной пирамиды равны между собой и все грани равнобедренные треугольники, то развертку боковой поверхности пирамиды начинаем строить с проведения дуги радиусом, равным размеру ребра боковой поверхности пирамиды (рис. 11).

На фронтальную и горизонтальную плоскости проекций ребра пирамиды проецируются с искажением, так как расположены наклонно относительно плоскостей H и V. На профильной плоскости проекций ребра S2 и S3 тоже проецируются с искажением, так как расположены наклонно к плоскости W, а ребро S1 проецируется в натуральную величину, потому что располагается параллельно плоскости W. Радиусом, равным

длине ребра S1 (s′′1′′), описываем дугу. На ней от произвольно выбранной точки откладываем три хорды, равные стороне основания. Размер стороны основания берем с горизонтальной проекции пирамиды. Затем для построения основания на развертке из точек 10 и 30 радиусом, равным стороне основания, проводим дуги до взаимного пересечения в точ-

ке 20. Развертка поверхности неправильной пирамиды

Развертка поверхности неправильной пирамиды будет состоять из неправильных треугольников боковой поверхности и неправильного треугольника, лежащего в основании, совмещенных в одну плоскость, причем их взаимное расположение на развертке должно соответствовать взаимному расположению на ортогональных проекциях. Так как у неправильной пирамиды стороны основания разные и ребра боковой поверхности не равны между собой, сначала находим натуральную величину всех боковых ребер (рис. 12).

Для этого используем один из способов определения натуральной величины отрезка прямой общего положения. В данном случае использован способ вращения. Боковые ребра вращаем вокруг оси, проведенной через вершину пирамиды S перпендикулярно плоскости Н. На чертеже

фронтальная проекция оси i′i′ проведена через фронтальную проекцию

вершины s′ перпендикулярно оси Ox. Горизонтальные проекции ребер s1, s2, и s3 поворачиваем до положения, параллельного оси Ox. При этом горизонтальные проекции точек 1, 2 и 3 займут положение 11, 21 и 31. От этих точек проводим линии проекционной связи на фронтальную плоскость проекций для получения их фронтальных проекций 1′1, 2′1 и 3′1. Затем фронтальные проекции точек соединяем с фронтальной проекцией

s′ вершины S прямыми линиями, которые и будут натуральными величи-

нами ребер (1′1s′, 2′1s′и 3′1s′).

Стороны основания 12, 23 и 13 спроецировались в натуральную величину на горизонтальную плоскость проекций. Зная натуральные величины всех элементов пирамиды, приступаем к построению развертки ее поверхности. При построении развертки боковой поверхности используем способ построения треугольников по трем заданным сторонам. Построение можно начать с любой грани боковой поверхности, например с грани 1S3 (рис. 5.12). Сначала на свободном месте чертежа проводим произвольную прямую и на ней откладываем натуральную величину стороны основания 1030, взятую с горизонтальной проекции. Затем из точки 10 радиусом, равным натуральной величине ребра S1 (s′1′1), а из точки 30 радиусом, равным натуральной величине ребра S3 (s′3′1), делаем засечки до пересечения в точке S0, которая будет вершиной развертки боковой поверхности пирамиды. Далее строим боковую грань 3S2. Для этого на фронтальной проекции циркулем измеряем натуральную величину ребра S2 (s′2′1) и на развертке этим радиусом из вершины S0, а из точки 30 радиусом 32, взятым с горизонтальной проекции, делаем засечки до пересечения в точке 20. Соединив точку 20 прямой линией с вершиной S0, получим вторую грань 30S020 боковой поверхности пирамиды. Третья грань и основание сроятся тем же способом.

Криволинейные поверхности

Коническая поверхность образуется движением прямолинейной образующей по криволинейной направляющей. При этом образующая проходит через некоторую неподвижную точку S, которая называется вершиной (рис. 13).

( m, s)

Рис. 13

Коническая поверхность определена на чертеже, если заданы направляющая и вершина. Тело, ограниченное конической поверхностью и плоскостью, называется конусом. Конус будет круговым, если в его основании лежит круг.

Точка N принадлежит конической поверхности, так как она принадлежит образующей f этой поверхности; nочка K принадлежит кониче-

	ской	поверхности, так как она принадлежит образующей S1 (k s1,
	k′s′1′) данной поверхности (рис. 13).
		Цилиндрическая поверхность образуется движением прямолиней-
	ной образующей параллельно заданной прямой линии l по криволиней-
	ной направляющей (рис. 14).
	( m, l)
		Рис. 14
		Цилиндрическая поверхность определена, если задана направляю-
	щая и образующая. Для построения чертежа цилиндрической поверхно-
	сти удобно выбирать в качестве направляющей линию пересечения ци-
	линдрической поверхности с плоскостью проекций или другой плоско-
	стью, ей параллельной.
		Цилиндрическая поверхность также может быть незамкнутой или
	замкнутой. Тело, ограниченное цилиндрической замкнутой поверхно-
	стью и двумя параллельными плоскостями, называется цилиндром. Ци-
	линдрические поверхности различают по виду нормального сечения, на-
	пример, круговой цилиндр, эллиптический цилиндр и т.д.
		Точка N принадлежит цилиндрической поверхности, так как она
		принадлежит образующей f этой поверхности;
		точка K принадлежит цилиндрической поверхно-
		сти, так как она принадлежит образующей, про-
		ходящей через точку 1 параллельно направлению
		S данной поверхности (рис. 14).
		Торс (поверхность с ребром возврата) обра-
		зуется движением прямолинейной образующей,
		касающейся во всех своих положениях некоторой
	Рис. 15	пространственной кривой, называемой ребром
	возврата (от франц. tors − витой, крученный).

		Ребро возврата m является направляющей торса. Торс состоит из
	двух полостей, разделенных ребром возврата (рис. 15).
		Если ребро возврата вырождается в точку, поверхность торса пре-
	вращается в коническую. В случае, когда ребро возврата вырождается в
	бесконечно удаленную точку, торсовая поверхность превращается в ци-
	линдрическую.
		46

Лекция6.Поверхности вращения

Поверхностью вращения называется поверхность, образованная вращением образующей вокруг неподвижной оси (рис. 1). Эта поверхность определяется на чертеже заданием образующей и оси вращения.

Рис. 1

Каждая точка образующей l описывает при своем вращении окружность, лежащую в плоскости, перпендикулярной оси вращения, с центром на оси. Эти окружности называются параллелями. Наибольшая из этих параллелей называется экватором, наименьшая − горлом.

Плоскость, проходящую через ось поверхности вращения, называют меридианальной. Линию ее пересечения с поверхностью – меридианом. Меридиан, параллельный фронтальной плоскости проекций, называется главным меридианом. Все меридианы равны между собой.

На чертеже ось вращения II располагают перпендикулярно к одной из плоскостей проекций, например горизонтальной. Тогда все параллели проецируются на эту плоскость в истинную величину. Экватор и горло определят горизонтальный очерк поверхности. Фронтальным очерком такой поверхности будет главный меридиан, то есть меридиан, расположенный во фронтальной плоскости.

Точки на поверхностях вращения могут быть построены с помощью параллелей, то есть окружностей на поверхности.

Цилиндр вращения

Цилиндром вращения называется поверхность, образованная вращением прямой вокруг параллельной ей оси.

Если ось цилиндра перпендикулярна горизонтальной плоскости проекций, то горизонтальные проекции точек, лежащих на его поверхно-

сти, будут расположены на окружности, в которую спроецируется ци-
линдр на горизонтальную плоскость Н (рис. 2).
Задача. Найти недостающие проекции точек M и K (рис. 2).
	ϕ(l, II)
	M (m′)
	K(k)
	m (m1	, m2	) – ?
	k′ (k′1	, k′2	) – ?
	Для того, чтобы найти горизонтальную проек-
	цию точки М, проведем линию связи от фронталь-
	ной проекции М(m′) до пересечения с горизонталь-
	ной проекцией цилиндра (окружностью). Задача
	имеет два ответа: точки m1 и m2.
	Однозначно определить положение фронталь-
	ной проекции точки К по одной только горизон-
	тальной проекции k невозможно. По линии связи,
Рис. 2	проведенной от горизонтальной проекции этой точ-
ки, на	поверхности цилиндра может находиться
бесчисленное множество точек. В этом случае необходима дополнитель-
ная информация о положении точки К.
При пересечении цилиндра вращения плоскостью, параллельной
оси вращения, в сечении получаются две прямые – образующие (рис. 3).
Если секущая плоскость перпендикулярна оси вращения, в резуль-
тате сечения получится окружность (рис. 4).
В общем случае, когда секущая плоскость наклонена к оси враще-
ния цилиндра, в сечении получается эллипс (рис. 5).

Рис. 3

Рис. 4

Рис. 5

Рис. 6
Сечение цилиндра плоскостью
	В общем случае построение
	линии пересечения	поверхности
	плоскостью заключается в нахож-
	дении общих точек, то есть точек,
	принадлежащих одновременно се-
	кущей плоскости и поверхности.
	Для нахождения этих точек
	применяют способ	дополнитель-
Рис. 7	ных секущих плоскостей:
1.Проводят дополнительную

	плоскость.

2.Строят линии пересечения дополнительной плоскости с поверхностью и дополнительной плоскости с заданной плоскостью.

3.Определяют точки пересечения полученных линий. Дополнительные плоскости проводят таким образом, чтобы они

пересекали поверхность по наиболее простым линиям.

Нахождение точек линии пересечения начинают с определения характерных (опорных) точек. К ним относятся

•верхние и нижние, левая и правая и точки границы видимости;

•точки, характеризующие данную линию пересечения (для эл-

липса − точки большой и малой осей).

Для более точного построения линии пересечения необходимо построить еще и дополнительные (промежуточные) точки.

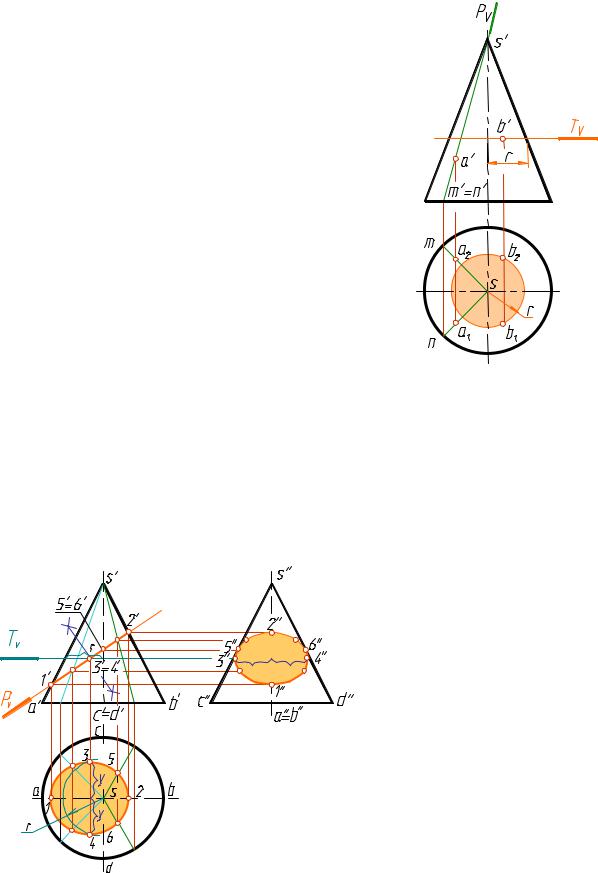
Прямой круговой конус Сечение конуса плоскостью

В зависимости от направления секущей плоскости в сечении конуса вращения могут получиться различные линии.

•Если секущая плоскость проходит через вершину конуса, в его сечении получается две прямые − образующие (треугольник) (рис. 8, а).

•В результате пересечения конуса плоскостью, перпендикулярной оси конуса, получается окружность (рис. 8, б).

Если секущая плоскость наклонена к оси вращения конуса и не проходит через его вершину, в сечении конуса могут получиться эллипс, парабола или гипербола (рис. 8, в, г, д) – в зависимости от величины угла наклона секущей плоскости.

•Эллипс получается в том случае, когда угол β наклона секущей плоскости меньше угла наклона α образующих конуса к его основанию

(0<β < α), т.е. когда плоскость пересекает все образующие данного конуса (рис. 8, в).

•Если углы α и β равны (то есть секущая плоскость параллельна

одной из образующих конуса), в сечении получается парабола

(рис. 8, г).

• Если секущая плоскость направлена под углом, который изменяется в пределах 90° β > α, то в сечении получается гипербола. В этом случае секущая плоскость параллельна двум образующим конуса. Гипербола имеет две ветви, так как коническая поверхность двухполостная

(рис. 8, д).

β	α	β	β
α	α

Рис. 8

Точка на конусе
Для конуса наиболее простыми линиями
являются прямые (образующие) и окружности.
Горизонтальную проекцию точки A найдем
с помощью образующей. Проведем через точку A
и вершину конуса S вспомогательную фронталь-
но-проецирующую плоскость P(PV). Она пересе-
кает конус по двум образующимSM и SN. Их фрон-
тальные проекции совпадают. Строим горизон-
тальные проекции образующих. Затем проводим
через точку a′ линию связи. На пересечении ли-
нии связи и горизонтальных проекций образую-
щих определим горизонтальную проекцию точки.
Задача имеет два ответа: точки a1	и a2 (рис. 9).
(•)A SN	или	(•)A SM
Горизонтальную проекцию точки B найдем,
построив окружность, на которой она лежит. Для
этого через точку	проведем	горизонтальную	Рис. 9
плоскость T(TV), которая пересекает конус по ок-

ружности радиуса r.

(•)B Окр r

Строим горизонтальную проекцию этой окружности. Через точку b′ проведем линию связи до ее пересечения с окружностью. Задача также

имеет два ответа − точки b1 и b2.
Рассмотрим пример построения проекций линии пересечения ко-
нуса фронтально – проецирующей плоскостью P(PV). В этом случае в се-
	чении получается	эллипс
	(рис. 10).
	Сначала	определим
	характерные	(опорные)
	точки.
	Фронтальная	проек-
	ция линии сечения совпа-
	дает с фронтальным следом
P(PV ) конус=	плоскости PV. Нижняя точ-
ка 1 лежит на образующей

	AS, верхняя − 2 на обра-
Рис. 10	зующей ΒS. Эти точки оп-
ределяют положение боль-
	шой оси эллипса. Малая
	ось эллипса	перпендику-

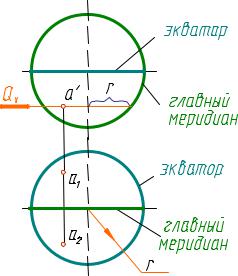
Сечение шаровой поверхности плоскостью

Пересечем поверхность шара фронтально-проецирующей плоскостью Q(QV) (рис. 12). Построение начинаем с определения характерных точек.

(•)1,2 гл. меридиану

Точки 1 и 2 находятся на главном меридиане. Эти точки − концы малой оси эллипса, а также это самая высокая и самая низкая точки. Их

(•)A Окр. r

Рис. 11

Шаровой поверхностью (или сфе-

рой) называется поверхность, образованная при вращении окружности вокруг своего диаметра.

Если шаровая поверхность пересе-

кается плоскостью, то в сечении всегда

получается окружность, которая может спроецироваться:

– в прямую, если секущая плоскость

перпендикулярна плоскости проекций;

– в окружность, если секущая плос-

кость параллельна плоскости проекций.

Например, окружность с радиусом r, равным расстоянию от оси вращения шара до очерка (рис. 11);

– в эллипс, если секущая плоскость не параллельна плоскости проекций.

Чтобы построить проекции точки, лежащей на поверхности шара, необходимо через нее провести секущую плоскость, параллельную плоскости проекций, затем построить окружность, на которой находится эта точка.

лярна большой оси. Чтобы найти малую ось, разделим отрезок 1-2 на две равные части. Точки 3 и 4 определяют малую ось эллипса. Точки 5 и 6, расположенные на образующих CS и DS, являются точками границы видимости для профильной плоскости проекций. Проекции точек 1, 2, 5 и 6 находятся на соответствующих проекциях образующих. Чтобы найти проекции точек 3 и 4, проводим дополнительную секущую плоскость T(TV). Она рассекает конус по окружности радиуса r. На этой окружности находятся проекции данных точек. Для точного построения необходимо определить дополнительные (случайные точки). Проекции этих точек находим аналогично точкам 3 и 4 или проводя через эти точки образующие. Соединяем полученные проекции точек. Определяем видимость. На горизонтальной плоскости все точки, лежащие на поверхности конуса, видимы. На профильной − точки 5, 3, 1, 4, 6 видимы, остальные − нет.

Шаровая поверхность

горизонтальные и профильные проекции строим по фронтальным проекциям.

Рис. 12	(•)3,4 профильному очерку
Точки 3 и 4 находятся на
	профильном меридиане и оп-
	ределяют видимость на про-

фильной плоскости проекций. Горизонтальные проекции точек находим по профильным проекциям.

(•)5,6 экватору

Точки 5 и 6 принадлежат экватору и являются точками границы видимости на горизонтальной проекции. Профильные проекции точек находим по горизонтальным проекциям.

Чтобы найти положение большой оси эллипса (точки 7 и 8) разделим отрезок 1′2′ пополам. Фронтальные проекции точек (точки 7′ и 8′) совпадают с серединой этого отрезка. В этой же точке находится фронтальная проекция центра окружности сечения. На горизонтальную плоскость диаметр окружности проецируется без искажения. Поэтому точки 7 и 8 будут находиться на расстоянии R от центра окружности сечения

(рис. 12).

Для большей точности строим несколько дополнительных точек. Полученные точки соединяем плавной кривой линией с учетом ее

видимости.

Тор Тор − поверхность, полученная вращением окружности вокруг оси,

лежащей в плоскости этой окружности, но не проходящей через ее центр.

Если ось вращения проходит вне окружности, то поверхность называется «открытый тор» или «тор − кольцо» (рис. 13); если ось касается окружности, поверхность называется «закрытый тор» (рис. 14 – 16). Тор, изображенный на рис. 15, называется также «тор-яблоко», а на рис. 16 – «тор-лимон». Сфера – частный случай торовой поверхности.

Рис. 13

Рис. 14

Рис. 15

Рис. 16

(•)А окр.r

Поверхности, образованные вращением кривых второго порядка:

а) эллипсоид вращения − поверхность, полученная вращением эллипса вокруг оси (рис. 17). Поверхность, образованная вращением эллипса вокруг его большой оси, называется вытянутым эллипсоидом вра-

щения (рис. 17, б), при вращении вокруг малой оси − сжатым эллипсоидом вращения (рис. 17, а, в);

б) параболоид вращения − поверхность, образованная вращением параболы вокруг ее оси (рис. 18);

в) двухполостный гиперболоид вращения − поверхность, обра-

зованная вращением гиперболы вокруг ее действительной оси (рис. 19).

бв

Развертка поверхности цилиндра

Развертка поверхности цилиндра представляет собой развернутую боковую поверхность цилиндра и его оснований, совмещенных в одной плоскости (рис. 20).

Для ее построения проводим прямую линию, на которой откладываем отрезок, равный длине окружности основания (2πR). Из концов отрезка проводим перпендикулярные отрезки, равные высоте цилиндра, и полученные точки соединяем. К боковой поверхности цилиндра пристраиваем два основания, как показано на рис. 20, б.

Развертку боковой поверхности цилиндра можно выполнить приближенно, разделив окружность основания на 12 равных частей и отложив на прямой 12 хорд. Далее построение ведется, как описано выше.

а	б
Рис. 20
Развертка поверхности конуса

Развертка боковой поверхности конуса представляет собой круговой сектор, у которого радиус равен длине образующей конуса, а длина дуги сектора равна длине окружности основания конуса. Если радиус окружности основания обозначить буквой R, длину образующей боковой поверхности – L, то угол сектора α можно определить по формуле α=360°×R/L. На рис. 21 показано построение развертки поверхности конуса. Сначала проводим дугу радиусом, равным длине образующей (L), которую берем с фронтальной или профильной проекции крайних образующих, потому что на эти плоскости проекций крайние образующие проецируются без искажения, так как они располагаются параллельно плоскостям проекций. Затем строим угол α, который определяем по приведенной выше формуле. Получаем сектор, являющийся развернутой боковой поверхностью конуса. К любой точке дуги сектора пристраиваем основание конуса.

Развертку боковой поверхности конуса можно выполнить приближенно, разделив окружность основания на 12 равных частей и отложив по дуге радиуса 12 хорд. Далее построение ведется, как описано выше.

Развертка поверхности шара

Сферическая поверхность относится к неразвертываемым поверхностям, и поэтому развертка поверхности шара может быть выполнена только приближенными способами. Рассмотрим один из способов выполнения развертки шара.

Для выполнения развертки поверхности шара поверхность делят меридианами на равные части. На рис. 22, а шар разделен на 12 равных частей. Представим себе, что все 12 частей поверхности шара отогнуты от полюсов и поставлены в вертикальное положение. Сферическая поверхность условно развернется как цилиндрическая поверхность, состоящая из 12 вертикально расположенных секций. Если эти секции разместить в одной плоскости, то получится приближенная развертка поверхности шара, рис. 22, б.

Для построения 12 меридианов очерковые окружности шара на горизонтальной и фронтальной проекциях делят на 12 равных частей. На горизонтальной проекции меридианы спроецируются в отрезки, проходящие через центр проекции шара. Фронтальные проекции этих меридианов будут кривыми, и их строят с помощью параллелей, проведенных через точки деления фронтального меридиана.

Для построения развертки достаточно знать размеры одной секции. На рис. 22, а выделена одна такая секция, на проекциях которой отмечены точки пересечения двух меридианов, являющихся ее сторонами, с па-

раллелями. Так как экватор делит секцию на две одинаковые части (верхнюю и нижнюю). То точки взяты только на той части секции, которая расположена выше экватора.

Самый широкий участок секции расположен по экватору. Его ширина равна 2πR/12, то есть 1/12 части экватора. Длина выпрямленной секции равна πR, то есть длине половины развернутого меридиана.

При развертке поверхности шара экватор развернется в отрезок, длина которого будет равна 2πR. Построение начинают с проведения прямой, на которой откладывают 12 отрезков, равных 2πR/12. На рис. 22, б показано построение только части развертки поверхности шара, так как все секции одинаковы.

Через середину построенных отрезков проводят оси симметрии перпендикулярно экватору. Затем вверх и вниз от экватора откладывают длину развернутых участков меридианов, заключенных между параллелями. Их длина равна 2πR/12. Через полученные точки параллельно экватору проводят прямые линии, на которых откладывают отрезки развернутых параллелей (3040, 5060). Эти отрезки равны 1/12 длины окружности, в которую проецируется соответствующая параллель на горизонтальной проекции. Построенные точки соединяют плавной кривой линией и обводят по лекалу.

Эту же развертку можно выполнить, заменяя развернутые дуги хордами, измеренными на ортогональных проекциях.

Лекция7.Винтовыеповерхности.Пересечениеповерхностей

Винтовая линия

Винтовая линия (гелиса) – это про- странственная кривая, образованная движе- нием точки, совершающей одновременно поступательное и вращательное движение. Рассмотрим цилиндрическую винто- вую линию (рис. 1) и построим две ее про- екции.

Для этого используем две проекции

цилиндра, каждую из которых делим на

двенадцать равных частей. При перемеще-

нии точки из первого положения во второе

ее горизонтальная проекция перемещается

по окружности на одну двенадцатую часть,

а фронтальная – вверх на одну двенадцатую.

	Совершая полный оборот, точка в
	пространстве опишет винтовую линию. Вы-
Рис. 1	сота, на которую поднимается точка по
прямой за полный оборот, называется ша-
	гом винтовой линии. Если ось винтовой ли-
нии перпендикулярна горизонтальной плоскости проекций, то горизон-
тальная проекция винтовой линии есть окружность, а фронтальная – си-
нусоида.
На одной поверхности цилиндра может быть несколько винтовых
линий.

Винтовые поверхности

Винтовой поверхностью называется поверхность, образованная при перемещении какой-либо линии (образующей) по винтовой линии (направляющей).

Если образующей винтовой поверхности является прямая линия, то поверхность называется линейчатой винтовой поверхностью или гели-

коидом (от франц. helic − спираль, винтовая линия). Геликоид называется прямым или наклонным в зависимости от того, перпендикулярна образующая оси геликоида или наклонна.

Рассмотрим некоторые виды линейчатых винтовых поверхностей. 1.Прямой геликоид образуется движением прямолинейной образующей l по двум направляющим. Одна из направляющих является цилинд-

рической винтовой линией m, а другая − ее осью II. Причем во всех своих положениях образующая l параллельна плоскости, которая называется

плоскостью параллелизма, перпендикулярной оси II (рис. 2). У прямого геликоида образующая l пересекает ось II под прямым углом.

2. Наклонный геликоид отличается от прямого геликоида тем, что его образующая l пересекает ось геликоида под постоянным углом α, не равным прямому углу. Во всех своих положениях образующая l параллельна образующим некоторого конуса вращения. У этого конуса угол

между образующей и осью, параллельной оси геликоида, равен ϕ. Он на-

зывается направляющим конусом наклонного геликоида (рис. 3).

Его направляющими являются цилиндрическая винтовая линия m и ее ось II. Образующие геликоида параллельны соответствующим образующим направляющего конуса.

Если образующие геликоида пересекают его ось, то геликоид на-

зывается закрытым, если нет – открытым.

3. Открытый геликоид образуется при винтовом движении прямолинейной образующей l, касающейся во всех свих положениях поверхности малого цилиндра и параллельно плоскости параллелизма, проведенной перпендикулярно оси геликоида (рис. 4).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Пересечение двух плоскостей

Пересечение двух плоскостей общего положения представляет собой прямую линию, поэтому для ее определения достаточно найти две
точки, принадлежащие одновременно каждой из двух заданных плоскостей – так называемые общие точки.

Чтобы найти общие точки, достаточно ввести одну или две вспомогательные секущие плоскости γ₁
и γ₂.

Найти пересечение двух плоскостей общего положения линию l, если плоскости заданны пересекающимися прямыми b c и
параллельными прямыми d e.

Пересечение двух плоскостей

Вспомогательная плоскость γ₁ пересекает заданные плоскости по прямым n1 и n2, которые пересекаясь между собой дают первую точку искомой линии.

Вспомогательная плоскость γ₂ пересекает заданные плоскости по прямым m1 и m2, которые пересекаясь между собой дают вторую точку искомой линии.
Проведя через найденные точки L1 и L2 прямую линию получаем искомое, пересечение двух плоскостей – линию l.

Определить линию пересечения l плоскостей заданных следами α_H,
α_V и β_H, β_V.

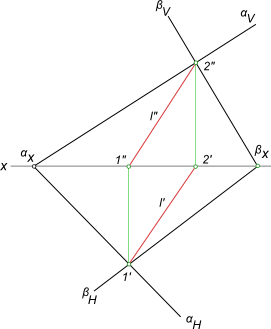
Пересечение двух плоскостей

Задача на пересечение плоскостей заданных следами α_H,
α_V и β_H, β_V.

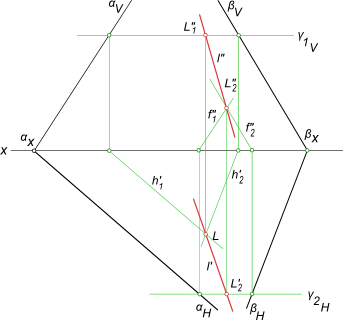
Пересечение двух плоскостей

Задача на пересечение плоскостей заданных следами α_H,
α_V и β_H, β_V причем α_V ║ β_V.

Пересечение двух плоскостей

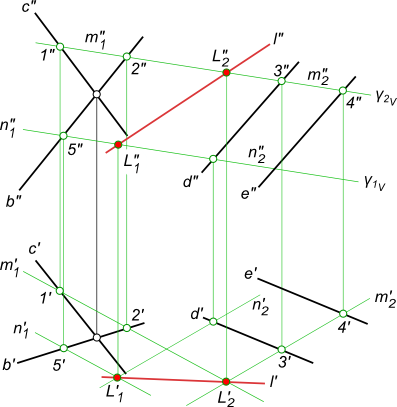
Пересечение двух плоскостей, заданных треугольниками ABC и DEF.

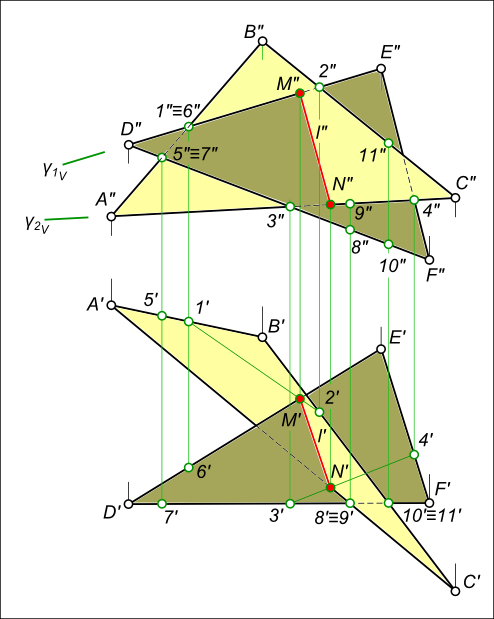
Пересечение двух плоскостей

Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым 1-2 и DE, которые пересекаясь между собой дают первую точку искомой линии – точка M.

Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым 3-4 и AC, которые пересекаясь между собой дают вторую точку искомой линии – точка N.

Соединяем точки MN прямой линией получаем искомую линию l пересечения двух плоскостей.

Определение видимости пересекающихся плоскостей на плоскостях проекций выполняем, используя Конкурирующие точки:
на фронтальной плоскости проекций – 1″≡6″; 1`, 6` и 5″≡ 7″; 5`, 7` – будет видна вершина D с прилегающими сторонами до линии пересечения.
на горизонтальной плоскости проекций – 8`≡9`; 8″, 9″ и 10`≡ 11`; 10″, 11″ – будет видна вершина C с прилегающими сторонами до линии пересечения.

Построить линию пересечения двух плоскостей треугольник ABC и α(αH, αV)

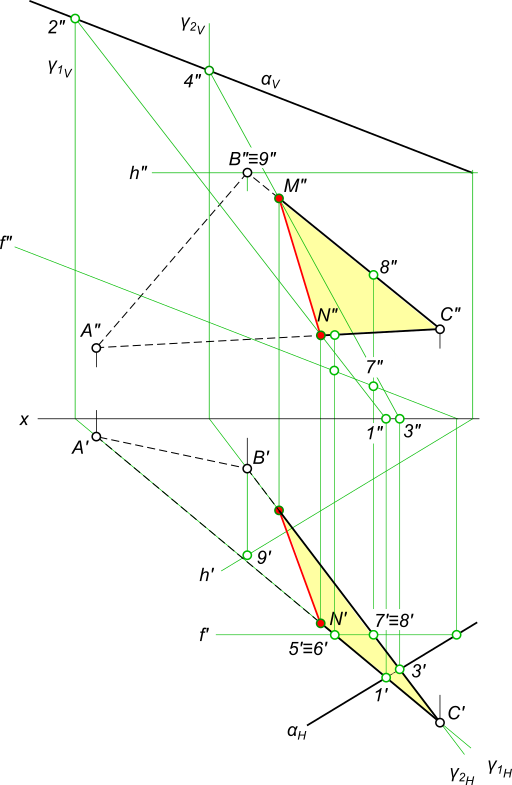
Пересечение двух плоскостей

Графическая работа 1 представляет задачу на пересечение двух плоскостей заданных треугольником и ромбом

Источник

5.4.4. Прямая, заданная пересечением двух плоскостей

Если плоскости пересекаются, то система линейных уравнений задаёт прямую в пространстве.

То есть прямая задана уравнениями двух плоскостей. Типовая и распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:

Задача 151

Записать канонические уравнения прямой

Решение: чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор. А у нас даны уравнения двух плоскостей….

1) Сначала найдём какую-либо точку, принадлежащую данной прямой. Как это сделать? Методом подбора. В системе уравнений обнулим какую-нибудь координату, например, . Тогда получается система двух линейных уравнений с двумя неизвестными: . Почленно складываем уравнения и находим решение системы:

Таким образом, точка принадлежит данной прямой. Но принадлежит ли? Выполним проверку – подставим её координаты в исходную систему уравнений:

Получены верные равенства, значит, действительно .

В процессе подбора обратите внимание на следующий технический момент: желательно найти точку с целыми координатами. Если бы в системе мы обнулили «икс» или «зет», то не факт, что получилась бы «хорошая» точка без дробных координат. Такой анализ и подбор точки следует проводить мысленно или на черновике.

2) Как найти направляющий вектор прямой? Существует готовая формула: если прямая задана пересечением двух плоскостей , то вектор является направляющим вектором данной прямой.
В нашей задаче:

Однако всех формул не упомнишь и поэтому очень важно понимать, откуда они взялись. Направляющий вектор нашей прямой ортогонален нормальным векторам плоскостей: и , поэтому вектор «пэ» можно найти как векторное произведение векторов нормали: .
Из уравнений плоскостей «снимаем» их векторы нормали:
и находим направляющий вектор прямой:

Проверим результат с помощью скалярного произведения:
, ч.т.п.

И, наконец, завершающий этап:

3) Составим канонические уравнения прямой по точке и направляющему вектору :

Ответ:

Аналогичная задача для самостоятельного решения:

Задача 152

Записать канонические уравнения прямой

Будьте внимательны! Ваш ответ может отличаться от моего ответа (смотря, какую точку подберёте). Если отличие есть, то для проверки возьмите точку из вашего уравнения и подставьте в моё уравнение (или наоборот).

Полное решение и ответ в конце книги.

И сейчас самое время перейти к простейшим задачам с пространственной прямой:

Уравнения прямой в пространстве – это уравнения двух пересекающихся плоскостей

Уравнения двух плоскостей, задающих прямую линию в пространстве

Пусть даны две плоскости, которые не совпадают между собой и пересекаются. Обозначим их как плоскость α и плоскость β . Разместим их в прямоугольной системе координат O х у z трехмерного пространства.

Как мы помним, любую плоскость в прямоугольной системе координат задает общее уравнение плоскости вида A x + B y + C z + D = 0 . Будем считать, что плоскости α соотвествует уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а плоскости β уравнение A 2 x + B 2 y + C 2 z + D 2 = 0 . В этом случае нормальные вектора плоскостей α и β n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) не коллинеарны, так как плоскости не совпадают между собой и е размещаются параллельно друг другу. Запишем это условие следующим образом:

n 1 → ≠ λ · n 2 → ⇔ A 1 , B 1 , C 1 ≠ λ · A 2 , λ · B 2 , λ · C 2 , λ ∈ R

Линию пересечения плоскостей обозначим буквой a . Т.е. a = α ∩ β . Эта прямая представляет собой множество точек, которые являются общими для обеих плоскостей α и β . Это значит, что все точки прямой линии a удовлетворяют обоим уравнениям плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Фактически, они являются частным решением системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

Общее решение системы линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определяет координаты всех точек линии, по которой происходит пересечение двух плоскостей α и β . Это значит, что с его помощью мы можем определить положение прямой в прямоугольной системе координат O x y z .

Рассмотрим описанную теорию еще раз, теперь уже на конкретном примере.

Прямая O x – это прямая, по которой пересекаются координатные плоскости O x y и O x z . Зададим плоскость O x y уравнением z = 0 , а плоскость O x z уравнением у = 0 . Такой подход мы подробно разобрали в разделе «Неполное общее уравнение плоскости», так что, в случае затруднений, можно обратиться к этому материалу повторно. В этом случае координатная прямая O x определяется в трехмерной системе координат системой из двух уравнений вида y = 0 z = 0 .

Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости

Рассмотрим задачу. Пусть в трехмерном пространстве задана прямоугольная система координат O х у z . Линия, по которой пересекаются две плоскости a , задана системой уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Дана точка трехмерного пространства M 0 x 0 , y 0 , z 0 .

Давайте определим, принадлежит ли точка M 0 x 0 , y 0 , z 0 заданной прямой линии a .

Для того, чтобы получить ответ на вопрос задачи, подставим координаты точки М 0 в каждое из двух уравнений плоскости. Если в результате подстановки оба уравнения превратятся в верные равенства A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 , то точка М 0 принадлежит каждой из плоскостей и принадлежит заданной линии. Если хотя бы одно из равенств A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 окажется неверным, то точка М 0 не принадлежит прямой линии.

Рассмотрим решение примера

Прямая линия задана в пространстве уравнениями двух пересекающихся плоскостей вида 2 x + 3 y + 1 = 0 x – 2 y + z – 3 = 0 . Определите, принадлежат ли точки M 0 ( 1 , – 1 , 0 ) и N 0 ( 0 , – 1 3 , 1 ) прямой линии пересечения плоскостей.

Решение

Начнем с точки М 0 _. Подставим ее координаты в оба уравнения системы 2 · 1 + 3 · ( – 1 ) + 1 = 0 1 – 2 · ( – 1 ) + 0 – 3 = 0 ⇔ 0 = 0 0 = 0 .

В результате подстановки мы получили верные равенства. Это значит, что точка М 0 принадлежит обеим плоскостям и расположена на линии их пересечения.

Подставим в оба уравнения плоскости координаты точки N 0 ( 0 , – 1 3 , 1 ) . Получаем 2 · 0 + 3 · – 1 3 + 1 = 0 0 – 2 · – 1 3 + 1 – 3 = 0 ⇔ 0 = 0 – 1 1 3 = 0 .

Как вы видите, второе уравнение системы превратилось в неверное равенство. Это значит, что точка N 0 не принадлежит заданной прямой.

Ответ: точка М 0 принадлежит прямой линии, а точка N 0 не принадлежит.

Теперь предлагаем вам алгоритм нахождения координат некоторой точки, принадлежащей прямой линии, если прямая в пространстве в прямоугольной системе координат O x y z определяется уравнениями пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

Количество решений системы из двух линейных уравнений с темя неизвестными A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 бесконечно. Любое из этих решений может стать решением задачи.

Пусть в трехмерном пространстве задана прямая линия уравнениями двух пересекающихся плоскостей вида x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 . Найдите координаты любой из точек этой прямой.

Решение

Перепишем систему уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = – 7 2 x + 3 y + 3 z = – 2 .

Возьмем отличный от нуля минор второго порядка в качестве базисного минора основной матрицы системы 1 0 2 3 = 3 ≠ 0 . Это значит, что z – это свободная неизвестная переменная.

Перенесем слагаемые, содержащие свободную неизвестную переменную z в правые части уравнений:

x + 0 y + 3 z = – 7 2 x + 3 y + 3 z = – 2 ⇔ x + 0 y = – 7 – 3 z 2 x + 3 y = – 2 – 3 z

Введем произвольное действительное число λ и примем, что z = λ .

Тогда x + 0 y = – 7 – 3 z 2 x + 3 y = – 2 – 3 z ⇔ x + 0 y = – 7 – 3 λ 2 x + 3 y = – 2 – 3 λ .

Для решения полученной системы уравнений применим метод Крамера:

∆ = 1 0 2 3 = 1 · 3 – 0 · 1 = 2 ∆ x = – 7 – 3 λ 0 – – 3 λ 3 = – 7 – 3 λ · 3 – 0 · ( – 2 – 3 λ ) = 21 – 9 λ ⇒ x = ∆ x ∆ = – 7 – 3 λ ∆ y = 1 – 7 – 3 λ 2 – 2 – 3 λ = 1 · – 2 – 3 λ – – 7 – 3 λ · = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ

Общее решение системы уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 будет иметь вид x = – 7 – 3 λ y = 4 + λ z = λ , где λ ∈ R .

Это позволяет нам получить координаты искомой точки – 7 , 4 , 0 .

Проверим верность найденных координат точки методом подстановки их в исходные уравнения двух пересекающихся плоскостей – 7 + 3 · 0 + 7 = 0 2 · ( – 7 ) + 3 · 4 + 3 · 0 + 2 = 0 ⇔ 0 = 0 0 = 0 .

Ответ: – 7 , 4 , 0

Направляющий вектор прямой, по которой пересекаются две плоскости

Давайте рассмотрим, как определить координаты направляющего вектора прямой, которая задана уравнениями двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . В прямоугольной системе координат 0хуz направляющий вектор прямой неотделим от прямой линии.

Плоскости α и β пересекаются по линии a . Направляющий вектор a → прямой линии a расположен перпендикулярно по отношению к нормальному вектору n 1 → = ( A 1 , B 1 , C 1 ) плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и нормальному вектору n 2 → = ( A 2 , B 2 , C 2 ) плоскости A 2 x + B 2 y + C 2 z + D 2 = 0 .

Направляющий вектор прямой a представляет собой векторное произведение векторов n → 1 = ( A 1 , B 1 , C 1 ) и n 2 → = A 2 , B 2 , C 2 .

a → = n → 1 × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2

Зададим множество всех направляющих векторов прямой как λ · a → = λ · n 1 → × n 2 → , где λ – это параметр, который может принимать любые действительные значения, отличные от нуля.

Пусть прямая в пространстве в прямоугольной системе координат O х у z задана уравнениями двух пересекающихся плоскостей x + 2 y – 3 z – 2 = 0 x – z + 4 = 0 . Найдем координаты любого направляющего вектора этой прямой.

Решение

Плоскости x + 2 y – 3 z – 2 = 0 и x – z + 4 = 0 имеют нормальные векторы n 1 → = 1 , 2 , – 3 и n 2 → = 1 , 0 , – 1 . Примем за направляющий вектор прямой линии, являющейся пересечением двух заданных плоскостей, векторное произведение нормальных векторов:

a → = n → 1 × n 2 → = i → j → k → 1 2 – 3 1 0 – 1 = i → · 2 · ( – 1 ) + j → · ( – 3 ) · 1 + k → · 1 · 0 – – k → · 2 · 1 – j → · 1 · ( – 1 ) – i → · ( – 3 ) · 0 = – 2 · i → – 2 j → – 2 k →

Запишем ответ в координатной форме a → = – 2 , – 2 , – 2 . Тем, кто не помнит, как это делается, рекомендуем обратиться к теме «Координаты вектора в прямоугольной системе координат».

Ответ: a → = – 2 , – 2 , – 2

Переход к параметрическим и каноническим уравнениям прямой в пространстве

Для решения ряда задач проще использовать параметрические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ или канонические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В этих уравнениях a x , a y , a z – координаты направляющего вектора прямой, x 1 , y 1 , z 1 – координаты некоторой точки прямой, а λ – параметр, принимающий произвольные действительные значения.

От уравнения прямой вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 можно перейти к каноническим и параметрическим уравнениям прямой линии в пространстве. Для записи канонических и параметрических уравнений прямой нам понадобятся навыки нахождения координат некоторой точки прямой, а также координат некоторого направляющего вектора прямой, заданной уравнениями двух пересекающихся плоскостей.

Рассмотрим написанное выше на примере.

Зададим прямую линию в трехмерной системе координат уравнениями двух пересекающихся плоскостей 2 x + y – z – 1 = 0 x + 3 y – 2 z = 0 . Напишем канонические и параметрические уравнения этой прямой.

Решение

Найдем координаты направляющего вектора прямой, который является векторным произведением нормальных векторов n 1 → = 2 , 1 , – 1 плоскости 2 x + y – z – 1 = 0 и n 2 → = ( 1 , 3 , – 2 ) плоскости x + 3 y – 2 z = 0 :

a → = n 1 → × n 2 → = i → j → k → 2 1 – 1 1 3 – 2 = i → · 1 · ( – 2 ) + j → · ( – 1 ) · 1 + k → · 2 · 3 – – k → · 1 · 1 – j → · 2 · ( – 2 ) – i → · ( – 1 ) · 3 = i → + 3 · j → + 5 · k →

Координаты направляющего вектора прямой a → = ( 1 , 2 , 5 ) .

Следующим шагом является определение координат некоторой точки заданной прямой линии, которыми является одно из решений системы уравнений: 2 x + y – z – 1 = 0 x + 3 y – 2 z = 0 ⇔ 2 x + y – z = 1 x + 3 y – 2 z = 0 .

Возьмем в качестве минорной матрицы системы определитель 2 1 1 3 = 2 · 3 – 1 · 1 = 5 , который отличен от нуля. В этом случае переменная z является свободной. Перенесем слагаемые с ней в правые части каждого уравнения и придаем переменной произвольное значение λ :

2 x + y – z = 1 x + 3 y – 2 z = 0 ⇔ 2 x + y = 1 + z x + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ , λ ∈ R

Применяем для решения полученной системы уравнений метод Крамера:

∆ = 2 1 1 3 = 2 · 3 – 1 · 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = ( 1 + λ ) · 3 – 1 · 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 · λ ∆ y = 2 1 + λ 1 2 λ = 2 · 2 λ – ( 1 + λ ) · 1 = – 1 + 3 λ ⇒ y = ∆ y ∆ = – 1 + 3 λ 5 = – 1 5 + 3 5 · λ

Получаем: 2 x + y – z – 1 = 0 x + 3 y – 2 z = 0 ⇔ x = 3 5 + 1 5 y = – 1 5 + 3 5 z = λ

Примем λ = 2 для того, чтобы получить координаты точки прямой линии: x 1 = 3 5 + 1 5 · 2 y 1 = – 1 5 + 3 5 · 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2 . Теперь мы имеем достаточно данных для того, чтобы записать канонические и параметрические уравнения данной прямой в пространстве: x – x 1 a x = y – y 1 a y = z – z 1 a z ⇔ x – 1 1 = y – 1 3 = z – 2 5 x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x = 1 + 1 · λ y = 1 + 3 · λ z = 2 + 5 · λ ⇔ x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ

Ответ: x – 1 1 = y – 1 3 = z – 2 5 и x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ

Данная задача имеет еще один способ решения.

Нахождение координат некоторой точки прямой проводится при решении системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

Получение канонических уравнений проводится следующим образом: решаем каждое из полученных уравнений относительно параметра λ , приравниваем правые части равенства.

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ λ = x – x 1 a x λ = y – y 1 a y λ = z – z 1 a z ⇔ x – x 1 a x = y – y 1 a y = z – z 1 a z

Применим данный способ к решению задачи.

Зададим положение прямой линии уравнениями двух пересекающихся плоскостей 2 x + y – z – 1 = 0 x + 3 y – 2 z = 0 . Напишем параметрическое и каноническое уравнения для этой прямой линии.

Решение

Решение системы из двух уравнений с тремя неизвестными проводится аналогично тому, как мы делали это в предыдущем примере. Получаем: 2 x + y – z – 1 = 0 x + 3 y – 2 z = 0 ⇔ x = 3 5 + 1 5 · λ y = – 1 5 + 3 5 · λ z = λ .

Это параметрические уравнения прямой в пространстве.

Канонические уравнения получаем следующим образом: x = 3 5 + 1 5 · λ y = – 1 5 + 3 5 · λ z = λ ⇔ λ = x – 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x – 3 5 1 5 = y + 1 5 3 5 = z 1

Ответ: x – 3 5 1 5 = y + 1 5 3 5 = z 1 и x = 3 5 + 1 5 · λ y = – 1 5 + 3 5 · λ z = λ

Линия пересечения плоскостей онлайн

С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Линия пересечения плоскостей − теория, примеры и решения

Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α₁ и α₂:

α₁: A₁x+B₁y+C₁z+D₁=0,

(1)

α₂: A₂x+B₂y+C₂z+D₂=0,

(2)

Найдем уравнение линии пересеченя плоскостей α₁ и α₂. Для этого рассмотрим следующие случаи:

Умножив уравнение (2) на λ, получим:

α₂: A₁x+B₁y+C₁z+λD₂=0,

(3)

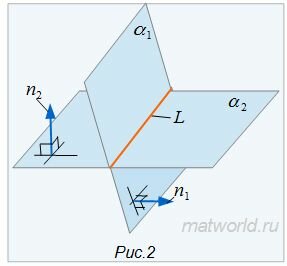
Если векторы n₁ и n₂ не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:

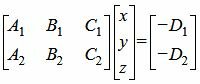(4)

Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.

Так как в системе линейных уравнений (4) векторы n₁=<A₁, B₁, C₁> и n₂=<A₂, B₂, C₂> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:

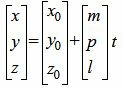(5)

Равенство (5) можно записать в следующем виде:

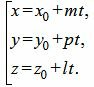(6)

Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α₁ и α₂. Полученное уравнение прямой можно записать в каноническом виде:

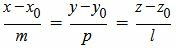Пример 1. Найти линию пересечения плоскостей α₁ и α₂:

Поскольку направляющие векторы n₁ и n₂ неколлинеарны, то плолскости α₁ и α₂ пересекаются.

Для нахождения линии пересечения влоскостей α₁ и α₂ нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:

(9)

Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

(10)

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строку 2 со строкой 1, умноженной на −2:

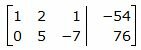Второй этап. Обратный ход Гаусса.

Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:

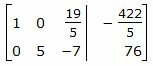Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

(11)

где t− произвольное действительное число.

Запишем (11) в следующем виде:

(12)

Получили уравнение линии пересечения плоскостей α₁ и α₂ в параметрическом виде. Запишем ее в каноническом виде.

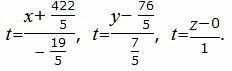(13)

Из равентсв выше получим каноническое уравнение прямой:

Ответ. Уравнение линии пересечения плоскостей α₁ и α₂имеет вид:

Пример 2. Найти линию пересечения плоскостей α₁ и α₂:

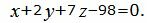(14)

(15)

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/2), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/2:

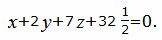(16)

Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α₁ и α₂ не совпадают. Следовательно они параллельны, т.е. не пересекаются.

Пример 3. Найти линию пересечения плоскостей α₁ и α₂:

(17)

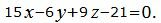(18)

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/3), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/3:

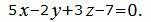(19)

Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α₁ и α₂ совпадают.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenija-prjamoj-v-prostranstve-eto-uravnenija-d/

http://matworld.ru/analytic-geometry/linija-peresechenija-ploskostej.php

[/spoiler]

Источник

Уравнения двух плоскостей, задающих прямую линию в пространстве

Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости

Направляющий вектор прямой, по которой пересекаются две плоскости

Переход к параметрическим и каноническим уравнениям прямой в пространстве

Взаимное положение двух плоскостей

Пересечение двух плоскостей

5.4.4. Прямая, заданная пересечением двух плоскостей

Уравнения прямой в пространстве – это уравнения двух пересекающихся плоскостей

Уравнения двух плоскостей, задающих прямую линию в пространстве

Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости

Направляющий вектор прямой, по которой пересекаются две плоскости

Переход к параметрическим и каноническим уравнениям прямой в пространстве

Линия пересечения плоскостей онлайн

Предупреждение

Линия пересечения плоскостей − теория, примеры и решения

Вам также может понравиться

Как найти сообщения на чужом телефоне

Мышка делает двойное нажатие как исправить

Как найти уважение персонала

Добавить комментарий Отменить ответ