Как найти точку отметки горизонтали - Сайт, где вы сможете решить свои вопросы

Содержание

Определение отметок точек и превышений
Определение отметки (высоты) точки
Вычисление уклона линии.
6. Определение отметок точек по горизонталям
Сплошные горизонтали проведены через 2,5 м
Построение продольного профиля по заданному направлению

Определение отметок точек и превышений

Системы вертикальных (высотных) координат

Основной величиной в этой системе является высота. Высотой точки называется расстояние по отвесной линии от уровенной поверхности до данной точки. Числовое значение высоты точки является ее отметкой.

Если высоты отсчитываются от основной уровенной поверхности, то они называются абсолютными и входят в абсолютную систему высот. Если же высоты отсчитываются от любой другой уровенной поверхности, условно принятой за начальную, то они называются условными и входят в условную систему высот.

В России и сопредельных государствах положение основной уровенной поверхности, совпадающей со средним многолетним уровнем Балтийского моря, фиксируется нулевым горизонтальным штрихом на бронзовой доске, прикрепленной к устою моста через обводной канал в Кронштадте. Эта доска с нулевым штрихом, от которого ведется отсчет абсолютных высот, называется Кронштадским футштоком.

Высота одной точки (В) относительно другой (А) называется относительной высотой или превышением (h). Из рисунка видно, что превышение равно разности абсолютных или условных высот двух точек:

Рис. Абсолютные (HA и HB), условные H’A и H’B и относительные (h) высоты Рельеф земной поверхности и его изображение

На топографических картах

Рельеф – это совокупность всех неровностей земной поверхности, различных по своей форме и размерам. Изображение рельефа на топокартах должно быть наглядным, отражать количественные характеристики неровностей местности (абсолютные высоты, превышения точек, крутизну склонов и др.). Рельеф на топокартах изображается горизонталями в сочетании с отметками высот и условными обозначениями форм, которые нельзя изобразить горизонталями. Способ изображения рельефа горизонталями позволяет геометрически наиболее точно передать форму рельефа и отразить его особенности.

Горизонтали– это кривые линии, соединяющие на карте точки с одинаковыми высотами. Горизонтали представляют проекции сечения местности уровенными поверхностями через определенные высоты.

При изображении рельефа местности горизонталями обязательным является условие, чтобы уровенные поверхности, рассекающие земную поверхность, отстояли одна от другой на одно и то же расстояние h, называемое высотой сечения рельефа. Горизонтали проектируются на горизонтальную плоскость М (или на поверхность эллипсоида) для изображения их на плане (или карте). Для того чтобы отличить изображения положительных (гор) и отрицательных (котловин) форм рельефа, от одной или нескольких горизонталей проводятся скатштрихи (бергштрихи) в сторону понижения ската (рис. 1). Отметки горизонталей, кратные высоте сечения, подписываются либо в разрыве горизонталей, либо у их концов так, чтобы нижняя часть цифр располагалась ниже по скату, указывая на понижение рельефа. Высота сечения выбирается в зависимости:

— от масштаба карты (плана): чем крупнее масштаб, тем меньше высота сечения;

— от характера местности: для горной местности высота сечения больше, чем для равнинной;

— от требуемой точности и детальности, определяемой хозяйственно-техническими соображениями: чем точнее и детальнее требуется изобразить рельеф, тем меньше должна быть высота рельефа.

Как мы уже выяснили, расстояние между соседними секущими уровенными поверхностями называется высотой сечения рельефа h. Расстояние на карте между смежными горизонталями называется заложением d. Высота сечения рельефа зависит от масштаба карты и характера рельефа местности. Нормальной высотой сечения принято считать высоту, равную 0,02 см в масштабе карты. В зависимости от условий рельефа местности для различных масштабов карт установлены стандартные нормальные высоты сечения рельефа. Так, в пределах равнинных территорий для топокарт масштаба 1:10 000 – 2,5 м; 1:25 000 – 5 м; 1:50 000 – 10 м; 1:100 000 – 20 м.

Горизонтали нормального сечения проводят сплошными линиями коричневого цвета толщиной 0,12–0,15 мм и называют основными или сплошными горизонталями. Для улучшения читаемости рельефа каждая пятая горизонталь (для масштаба 1:10 000 – каждая десятая), вычерчивается утолщенной линией 0,2 – 0,25 мм. Такие горизонтали называются утолщенными. Для отражения форм рельефа, не выражающихся основными горизонталями применяются дополнительные и вспомогательные горизонтали. Дополнительные, или полугоризонтали проводятся в половине основного сечения прерывистыми линиями длиной штрихов 5 мм, а вспомогательные или четвертьгоризонтали – в ¼ высоты сечения длиной штрихов – 2 мм. Формы рельефа, не выражающиеся горизонталями, изображаются специальными условными знаками. Это – обрывы, оползни, осыпи, овраги, промоины, воронки, курганы и др. Изображение элементов местности горизонталями представлено на рис. 3.10.

Горизонтали имеют следующие свойства:

1. Все точки, лежащие на одной горизонтали, имеют одинаковые отметки высот, кратные принятой высоте сечения рельефа.

2. Горизонтали – непрерывные замкнутые линии. Если горизонталь не замыкается внутри карты, то может обрываться только у рамки карты.

3. Горизонтали никогда не пересекаются, т. к. относятся к разным по высоте плоскостям.

4. Горизонтали одного и того же склона имеют внешнее сходство в рисунке.

5. Расстояние между горизонталями характеризует крутизну склона (ската).

Для улучшения читаемости рельефа, на карте подписываются абсолютные отметки вершин, седловин, тальвегов, перегибов склонов, а также относительные высоты обрывов, курганов, уступов террас, которые отсчитываются от подошв и бровок.

1. Отметка точки, расположенной на горизонтали, равна отметке этой горизонтали (напр., на рис. 6 Н₁=152,5 м).

2. Отметку точки, расположенной между горизонталями (напр., точки 2), определяют из выражения:

(1)

где Н_мл_. – отметка младшей горизонтали, (Н_мл.= 150,0 м), Δh₁ – превышение точки 2 над младшей горизонталью; d–заложение ската,l₁–расстояние в плане от младшей горизонтали до точки; h – высота сечения рельефа, м.

Для приведенного на рис. 6 примера

Для контроля отметку точки следует определить относительно старшей горизонтали как

(2)

3. Отметку точки, расположенной между горизонталями с одинаковыми отметками (точка 3 – седловина) либо внутри замкнутой горизонтали (точка 4 – вершина), можно определить лишь приближенно. При этом отметку точки принимают меньше или больше отметки этой горизонтали на половину высоты сечения рельефа, т. е. 0,5 h. Например:

;

Превышения между точками определяют как разность отметок последующей и предыдущей отметок, т. е.

(3)

Определение отметок точек и превышений

Точки	Отметки точек Н, м	Превышения h, м
152,50
— 1,50
151,00
+ 2,75
153,75
+ 7,50
161,25
— 8,75
152,50

Контролем правильности вычислений является равенство нулю суммы всех превышений т. е. .

Лучшие изречения:

Студент всегда отчаянный романтик! Хоть может сдать на двойку романтизм. © Эдуард А. Асадов
==> читать все изречения. 391 — | 269 —

Источник

Определение отметки (высоты) точки

При определении высоты точки по карте могут встретиться следующие случаи:

1.Точка лежит на горизонтали. Ее отметка равна отметке горизонтали.

2.Точка М лежит между горизонталями с отметками НК и НN (Рис.1.). В этом

случае отметку точки определяют посредством интерполирования, для чего измеряют расстояния d1 и d2 от точки М до ближайших горизонталей с помощью линейки.

Отметку НМ точки М вычисляют дважды с учетом направления понижения местности:

НМ = НК + (h*d1)/( d1 + d2); НМ = НN — (h*d2)/( d1 + d2),

где НК, НN – отметки горизонталей, м ; d1 и d2 – расстояния от точки М до горизонталей, м ; h – высота сечения рельефа ( на рис.1 h = 2,5 м).

За окончательное значение принимают среднюю отметку.

3.Точка расположена внутри замкнутой горизонтали. Точка Р лежит внутри замкнутой горизонтали и является вершиной высоты. Очевидно, что ее отметка НР больше отметки горизонтали, окружающей точку, на величину, меньшую высоты сечения рельефа. Можно принять, что отметка НР приближенно равна отметке соседней горизонтали плюс половина высоты сечения рельефа, т.е. НР = 151,25 м. Если точка является дном котловины, ее отметка будет меньше высоты ближайшей горизонтали на величину, равную половине высоты сечения рельефа. Точность определения отметки точки по горизонталям на среднепересеченной местности равна примерно 1/3 высоты сечения рельефа.

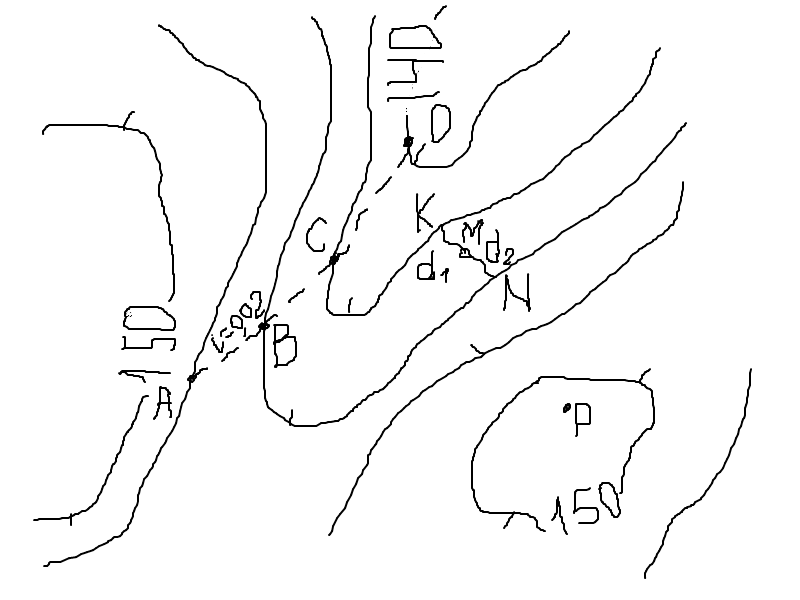
Рис.1 — Определение отметки (высоты) точки.

5) вычислить превышение точки 2 над точкой 1;

6) определить расстояние между точками 1 и 2;

7) вычислить уклон линии 1- 2;

Вычисление уклона линии.

Решение данной задачи можно выполнить двумя способами: по масштабу (графику) заложений и по приближенной формуле.

При первом способе в раствор циркуля-измерителя берется расстояние между двумя смежными горизонталями по линии наибольшей крутизны, т. е. по кратчайшему расстоянию между ними и, приложив иглы циркуля к графику заложений, определить угол наклона (рис.3). График заложений (рис.2) помещается под южной стороной рамки листа топографической карты. В случае очень близкого расположения горизонталей друг к другу, когда затруднительно взять расстояние между ними, крутизну склона определяют между утолщенными горизонталями, пользуясь при этом графиком заложений между утолщенными горизонталями (правый график заложений).

Пусть требуется определить крутизну ската вдоль отрезка ef. Взяв отрезок в раствор циркуля-измерителя, перемещаем нижнюю ножку циркуля вдоль основания основного (левого) масштаба заложений до тех пор, пока верхняя точка не окажется на кривой. В данном примере крутизна ската равна 2,5˚

Приближенная формула для определения величина угла ν, характеризующего крутизну склона, следующая: i = tg = h/d ; где h – превышение (высота сечения рельефа); d– заложение в метрах на местности. Эту формулу можно использовать для определения среднего угла наклона для двух точек, лежащих на одном склоне (рис.1).

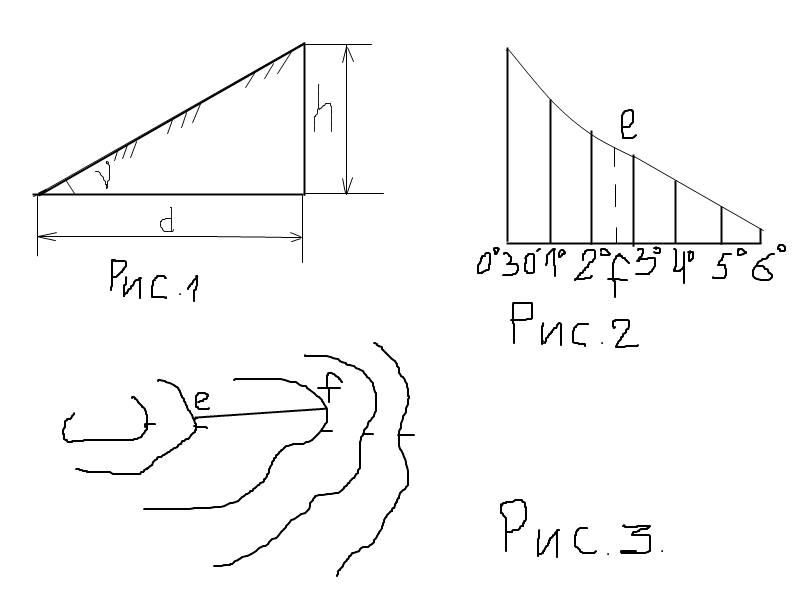
8) определить дирекционный угол линии 1 – 2 и обратный 2 – 1;

Источник

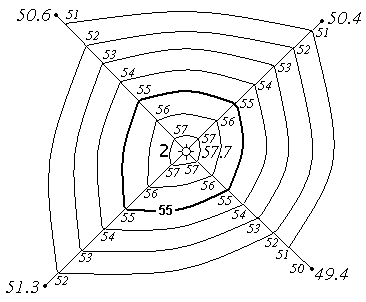
6. Определение отметок точек по горизонталям

Рассмотрим три случая:

1-й случай: точка А находится на горизонтали;

2-й случай: точки В и С находятся между горизонталями;

3-й случай: точка Д находится между точкой с отметкой и горизонталью.

Когда точка А расположена на горизонтали (1-й случай), то ее отметка равна отметке горизонтали. Отметка горизонтали может быть определена следующим образом:

– под южной рамкой карты указывается высота сечения рельефа, т.е. превышение между двумя сплошными соседними горизонталями (h_с);

– отыскиваем в районе расположения точки А подписанную горизонталь или точку с отметкой и устанавливаем, в какую сторону от точки А идет понижение рельефа. Понижение отметок рельефа можно определить по расположению бергштрихов, по надписанным горизонталям (основание цифры обращено в сторону понижения отметок) или по вторичным признакам (понижение идет к рекам, ручьям и т.д.). Зная высоту сечения рельефа h_с, производим оцифровку горизонталей (все сплошные горизонтали имеют высоты, кратные h_с; в нашем примере высоты горизонталей оканчиваются на 2,5м; 5м; 7,5 м; 0 м, горизонтали, вычерченная штрих-пунтирной линией — полугоризонталь отличается по высоте от сплошной горизонтали на ½ высоты сечения (в нашем случае на 1,25м).

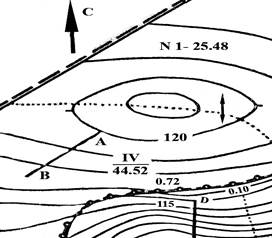
В нашем случае ( рис.14) высота сечения рельефа h_с равна 2,5 м, тогда, учитывая, что точка А лежит на горизонтали, расположенной на 3 сечения выше, чем горизонталь с отметкой 100м, получим

Рис. 14. Определение отметок по горизонталям.

Сплошные горизонтали проведены через 2,5 м

Если точка расположена между горизонталями (случай 2), то вначале производят оцифровку сплошных горизонталей и полугоризонталей, так, как описано в первом случае, а затем производят интерполяцию по расстоянию до ближайшей горизонтали.

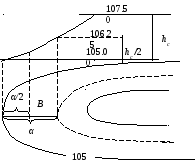
Рис. 15. Определение высоты точки В

На рис. 15 точка В расположена между сплошной горизонталью 105 м и полугоризонталью 106,25 м посередине, поэтому ее высота будет равна

Точка С расположена выше горизонтали 102,5 на величину Δh, которая находится из пропорции

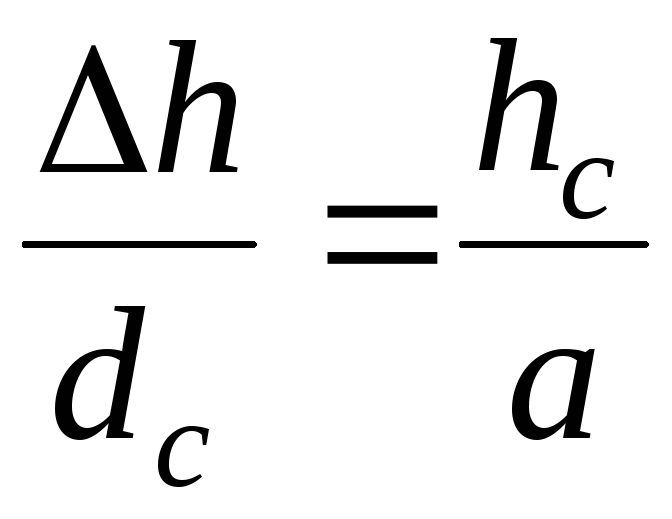, (27)

где 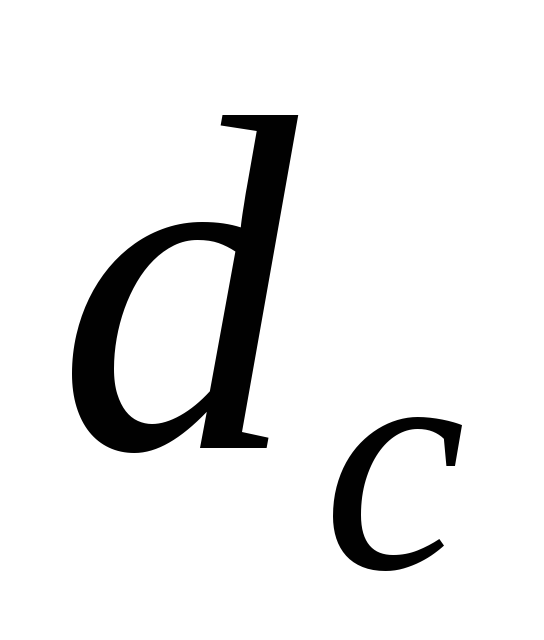– расстояние от горизонтали с отметкой 102,5м до точки С; – заложение расстояния между горизонталями в плане.

Отметка точки С будет равна:

Если точка Д находится между горизонталью и точкой К с известной отметкой (случай 3), то ее отметка находится так же, как и у точек В и C. Разница в данном случае только в том, что отметка точки К уже известна.

где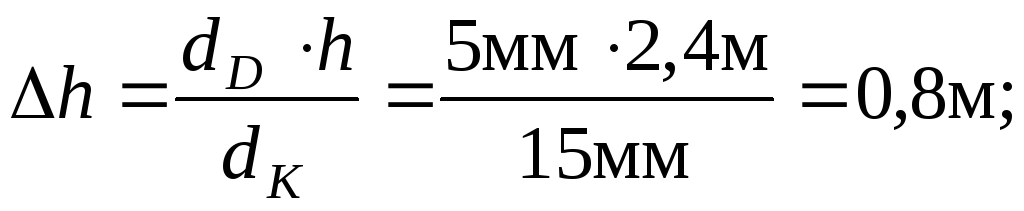

; ; .

Тогда

Построение продольного профиля по заданному направлению

На карте задано направление, например АВ, для которого необходимо построить продольный профиль (рис. 17)

Источник

Рассмотрим три
случая:

1-й
случай: точка А
находится на горизонтали;

2-й
случай: точки В
и С
находятся между горизонталями;

3-й
случай: точка Д
находится между точкой с отметкой и
горизонталью.

Когда
точка А
расположена на горизонтали (1-й случай),
то ее отметка равна отметке горизонтали.
Отметка горизонтали может быть определена
следующим образом:

– под
южной рамкой карты указывается высота
сечения рельефа, т.е. превышение между
двумя сплошными соседними горизонталями
(h_с);

– отыскиваем
в районе расположения точки А
подписанную
горизонталь или точку с отметкой и
устанавливаем, в какую сторону от точки
А идет
понижение рельефа. Понижение отметок
рельефа можно определить по расположению
бергштрихов, по надписанным горизонталям
(основание цифры обращено в сторону
понижения отметок) или по вторичным
признакам (понижение идет к рекам,
ручьям и т.д.). Зная высоту сечения рельефа
h_с,
производим оцифровку горизонталей (все
сплошные горизонтали имеют высоты,
кратные h_с;
в нашем примере высоты горизонталей
оканчиваются на 2,5м; 5м; 7,5 м; 0 м, горизонтали,
вычерченная штрих-пунтирной линией –
полугоризонталь отличается по высоте
от сплошной горизонтали на ½ высоты
сечения (в нашем случае на 1,25м).

В
нашем случае ( рис.14) высота сечения
рельефа h_с
равна 2,5 м, тогда, учитывая, что точка А
лежит на
горизонтали, расположенной на 3 сечения
выше, чем горизонталь с отметкой 100м,
получим

Рис. 14. Определение
отметок по горизонталям.

Сплошные горизонтали проведены через 2,5 м

Если
точка расположена между горизонталями
(случай 2), то вначале производят оцифровку
сплошных горизонталей и полугоризонталей,
так, как описано в первом случае, а затем
производят интерполяцию по расстоянию
до ближайшей горизонтали.

Рис.
15. Определение высоты точки В

На
рис. 15 точка В
расположена
между сплошной горизонталью 105 м и
полугоризонталью 106,25 м посередине,
поэтому ее высота будет равна

Δh

_{Рис. 16. Определение

высоты точки}_С.

Точка
С
расположена выше горизонтали 102,5 на
величину Δh,
которая находится из пропорции

, (27)

где
–
расстояние от горизонтали с отметкой
102,5м до точки С;
–
заложение расстояния между горизонталями
в плане.

Тогда

Отметка
точки С
будет равна:

Если
точка Д
находится между горизонталью и точкой
К
с известной отметкой (случай 3), то ее
отметка находится так же, как и у точек
В
и C.
Разница в данном случае только в том,
что отметка точки К
уже известна.

где

;

;
.

Тогда

Построение продольного профиля по заданному направлению

На
карте задано направление, например АВ,
для которого необходимо построить
продольный профиль (рис. 17)

190

185

180

175

170

165

160

155

150

155

150

Рис. 17. Высотный
план местности и продольный

профиль
вдоль линии АВ
М_г=1:10000,
М_в=1:500

Для
построения профиля к линии АВ
прикладывают согнутую полоску
миллиметровой бумаги, по краю которой
отмечают карандашом точки пересечения
линии АВ
с горизонталями. Развернув лист
миллиметровой бумаги, по сгибу проводят
горизонтальную линию и выписывают над
точками пересечения их отметки. В
этом случае горизонтальный масштаб
профиля равен масштабу карты М_Г1:10000.

Задаваясь
вертикальным масштабом, строят продольный
профиль. Вертикальный масштаб обычно
берут в 10 раз крупнее горизонтального
или принимают таким, чтобы рельеф был
выражен. В нашем примере возьмем М_В
1:500.

Построение профиля
ведут в следующей последовательности:

– вычерчивают
вертикальную линию, левее точки А
на расстоянии 0,5-1см;

– вычисляют
условный горизонт (УГ)
– отметку, от которой начинают построение
профиля. Условный горизонт выбирают
кратным основанию вертикального масштаба
при условии свободного пространства
от минимальной отметки профиля до линии
условного горизонта в 4-5 см.

В нашем случае

Точки
профиля получают на пересечении точек,
отмеченных на горизонтальной линии
профиля и соответствующих им высот,
подписанных на вертикальной шкале
профиля. Соединив точки профиля плавной
кривой, получаем линию профиля вдоль
заданного направления АВ.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В.А. Тарбаев, Р.Р. Гафуров Р., Л.М. Хончева
Геодезия с основами землеустройства
Учебно-методическое пособие. Саратов: Саратовский ГАУ, 2009. — 67 с.

Содержание статьи:

1 2. Рельеф местности. Составление картограммы
- 1.1 2.3. Определение отметок точек по горизонталям

2. Рельеф местности. Составление картограммы

2.3. Определение отметок точек по горизонталям

Отметка любой точки на карте или плане определяется в зависимости от ее положения относительно горизонталей. Если точка А (рис. 7) лежит на горизонтали, то ее отметка равна значению этой горизонтали, т.е.120м.

М 1 : 5000

Рис.7. Определение отметок точек по горизонталям

Если точка В находится между горизонталями, то ее отметка равна:

Н_в=Н₀±h_в (1)

где Н₀ – отметка горизонтали, ближайшая к точке (Н₀=117 м);

h_в – превышение точки В над этой горизонталью.

Превышение вычисляется по формуле:

(2)

где L – расстояние от точки В до ближайшей горизонтали (L=3 мм);

а – заложение ската, расстояние между соседними горизонталями (а=8мм);

h – сечение рельефа (h=1 м);

Крутизна склона характеризуется углом наклона α, либо уклоном i, значение которого вычисляется по формуле:

(3)

где h – превышение между точками, м (h=Н_А-Н_В=120-117,4=2,6 м);

d – расстояние между этими же точками, м.

Измеряется по карте и берется в ее масштабе (d= 2 см, в масштабе 1:5000 соответствует 100 м).

Средний уклон линии АВ равен:

, tg 1° = 0,0175, тогда

Источник

План урока №1

Этап 1. Тема урока

Цели и задачи дисциплины. Понятия о форме и размерах Земли. Определение положений точек на земной поверхности.

Этап II. Цель урока:
-дать представление о форме и размерах Земли -научиться определять положение точек на земной поверхности
Этап III. Тип урока Урок ознакомления с новым материалом

Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Отраслевой каталог (топография, геодезия, картография,) [Электронный ресурс]. – Режим доступа: http://www.geocontent.ru, свободный. – Загл. с экрана.

Этап VI. Ход урока -организационный момент – изучение темы – закрепление темы – подведение итогов – домашнее задание

Урок №1

Понятие о форме и размерах Земли

В геодезии для обозначения формы земной поверхности используют термин «фигура Земли».

Знание фигуры и размеров Земли необходимо во многих областях и прежде всего для определения положения объектов на земной поверхности и правильного её изображения в виде карт, планов и цифровых моделей местности.

Физическая поверхность Земли состоит из подводной (70,8 %) и надводной (29,2 %) частей. Подводная поверхность включает в себя систему срединно-океанических хребтов, подводные вулканы, океанические желоба, подводные каньоны, океанические плато и абиссальные равнины. Надводная часть земной поверхности также характеризуется многообразием форм. С течением времени поверхность Земли из-за тектонических процессов и эрозии постоянно изменяется.

Рис. 2. Фигура Земли (вид из космоса)

Представление о фигуре Земли (рис. 2) в целом можно получить, вообразив, что вся планета ограничена мысленно продолженной поверхностью океанов в спокойном состоянии.

Уровенных поверхностей, огибающих Землю, можно вообразить множество. Та из них, что совпадает со средним уровнем воды океанов в спокойном состоянии, т.е. в момент полного равновесия всей массы находящейся в ней воды под влиянием силы тяжести, называется основной уровенной поверхностью Земли.

В геодезии, как и в любой другой науке, одним из основополагающих принципов является принцип перехода от общего к частному. Исходя из него, для решения научных и инженерных задач по изучению физической поверхности Земли, а также других геодезических задач, сначала необходимо определиться с математической моделью поверхности Земли.

Что принимается за математическую поверхность Земли? Что является фигурой Земли? Какие у неё размеры?

Математическая поверхность Земли

Рассмотрим любую материальную точку А на физической поверхности Земли (рис. 3).

На эту точку оказывают влияние две силы: сила притяжения F_п, направленная к центру Земли, и центробежная сила вращения Земли вокруг своей оси F_ц, направленная от оси вращения по перпендикуляру. Равнодействующая этих сил называется силой тяжести F_т.

В любой точке земной поверхности направление силы тяжести, называемое ещё вертикальной или отвесной линией, можно легко и просто определить с помощью уровня или отвеса. Оно играет очень большую роль в геодезии. По направлению силы тяжести ориентируется одна из осей пространственной системы координат.

Если через точку А построить замкнутую поверхность, которая в каждой своей точке будет перпендикулярна отвесной линии (направлению силы тяжести), то данную поверхность можно принять в качестве математической при решении некоторых частных задач в геодезии. Такая поверхность получила название уровенной или горизонтальной. Её недостаток в том, что она содержит элемент неопределенности, т.е. через любую точку можно провести свою уровенную поверхность, и таких поверхностей будет бесчисленное множество.

Проектирование земной поверхности. Системы координат

Топографическое изучение земной поверхности заключается в определении положения ситуации и рельефа относительно математической поверхности Земли, т.е. в определении пространственных координат характерных точек, необходимых и достаточных для моделирования местности. Модель местности может быть представлена в виде геодезических чертежей, изготовление которых называют картографированием, и аналитически – в виде совокупности координат характерных точек. Для построения моделей местности в геодезии применяют метод проекций и различные системы координат.

Метод горизонтальной проекции заключается в том, что изучаемые точки (A, B, C, D, E) местности с помощью вертикальных (отвесных) линии проектируются на уровенную поверхность У (рис. 5), в результате чего получают горизонтальные проекции этих точек (a, b, c, d, e). Отрезки Аa, Bb, Cc, Dd, Ee называются высотами точек, а численные их значения – отметками.

Высота точки является одной из её пространственных координат. Отметка называется абсолютной, если в качестве уровенной поверхности принимается геоид, и относительной или условной, если для этого принимается произвольная уровенная поверхность.

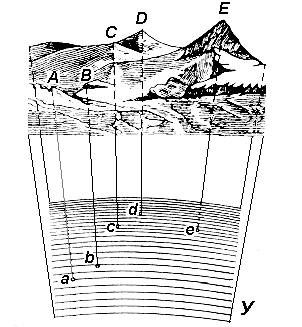
Рис. 5. Проектирование точек местности на уровенную поверхность Земли

Две другие недостающие координаты точки определяются с помощью системы координат, построенной на математической поверхности Земли (рис. 6).

Через любую точку поверхности референц-эллипсоида можно провести две взаимно перпендикулярные плоскости:

плоскость геодезического меридиана – плоскость, проходящая через ось вращения Земли PP’;
плоскость геодезической широты, которая перпендикулярна плоскости геодезического меридиана.

Следы сечения поверхности референц-эллипсоида этими плоскостями называют меридианом (М) и параллелью.

Меридиан, проходящий через астрономическую обсерваторию в Гринвиче, называется начальным или нулевым (М₀).

Параллель, плоскость которой проходит через центр Земли O, называется экватором (Э).

Плоскость, проходящая через центр Земли O перпендикулярно к её оси вращения PP’, называется экваториальной.

Основой для всех систем координат являются плоскости меридиана и экватора.

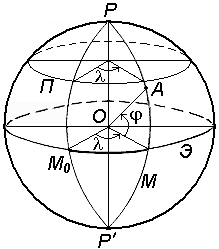
Рис. 6. Система географических координат

Системы координат подразделяются на угловые, линейные и линейно – угловые.

Примером угловых координат являются географические координаты (рис.6): широта  и долгота . Вдоль соответствующих параллели и меридиана широта и долгота точек постоянны.

В геодезии применяются следующие системы координат:

геодезические;
астрономические;
географические;
плоские прямоугольные геодезические (зональные);
полярные;
местные.

Геодезические координаты

Геодезические координаты определяют положение точки земной поверхности на референц-эллипсоиде (рис.7).

Рис. 7. Система геодезических координат

Геодезическая широта B – угол, образованный нормалью к поверхности эллипсоида в данной точке и плоскостью его экватора. Широта отсчитывается от экватора к северу или югу от 0° до 90° и соответственно называется северной или южной широтой.

Геодезическая долгота L – двугранный угол между плоскостями геодезического меридиана данной точки и начального геодезического Гринвичского меридиана.

Долготы точек, расположенных к востоку от начального меридиана, называются восточными, а к западу – западными.

Астрономические координаты (для геодезии)

Астрономическая широта  и долгота  определяют положение точки земной поверхности относительно экваториальной плоскости и плоскости начального астрономического меридиана (рис.8).

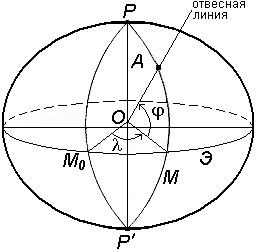
Рис. 8. Система астрономических координат

Астрономическая широта  – угол, образованный отвесной линией в данной точке и экваториальной плоскостью.

Астрономическая долгота  – двугранный угол между плоскостями астрономического меридиана данной точки и начального астрономического меридиана.

Плоскостью астрономического меридиана является плоскость, проходящая через отвесную линию в данной точке и параллельная оси вращения Земли.

Астрономическая широта  и долгота  определяются астрономическими наблюдениями.

Геодезические и астрономические координаты отличаются (имеют расхождение) из-за отклонения отвесной линии от нормали к поверхности эллипсоида. При составлении географических карт этим отклонением пренебрегают.

Географические координаты

Географические координаты – величины, обобщающие две системы координат: геодезическую и астрономическую, используют в тех случаях, когда отклонение отвесных линий от нормали к поверхности не учитывается (рис.9).

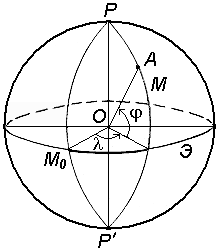
Рис. 9. Система географических координат

Географическая широта  – угол, образованный отвесной линией в данной точке и экваториальной плоскостью.

Географическая долгота  – двугранный угол между плоскостями меридиана данной точки с плоскостью начального меридиана.

Плоские прямоугольные геодезические координаты (зональные).

При решении инженерно-геодезических задач в основном применяют плоскую прямоугольную геодезическую и полярную системы координат.

Для определения положения точек в плоской прямоугольной геодезической системе координат используют горизонтальную координатную плоскость ХОУ (рис. 10), образованную двумя взаимно перпендикулярными прямыми. Одну из них принимают за ось абсцисс X, другую – за ось ординат Y, точку пересечения осей О – за начало координат.

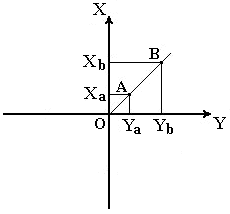
Рис. 10. Плоская прямоугольная система координат

Изучаемые точки проектируют с математической поверхности Земли на координатную плоскость ХОУ. Так как сферическая поверхность не может быть спроектирована на плоскость без искажений (без разрывов и складок), то при построении плоской проекции математической поверхности Земли принимается неизбежность данных искажений, но при этом их величины должным образом ограничивают. Для этого применяется равноугольная картографическая проекция Гаусса – Крюгера (проекция названа по имени немецких ученых, предложивших данную проекцию и разработавших формулы для её применения в геодезии), в которой математическая поверхность Земли проектируется на плоскость по участкам – зонам, на которые вся земная поверхность делится меридианами через 6° или 3°, начиная с начального меридиана (рис. 11).

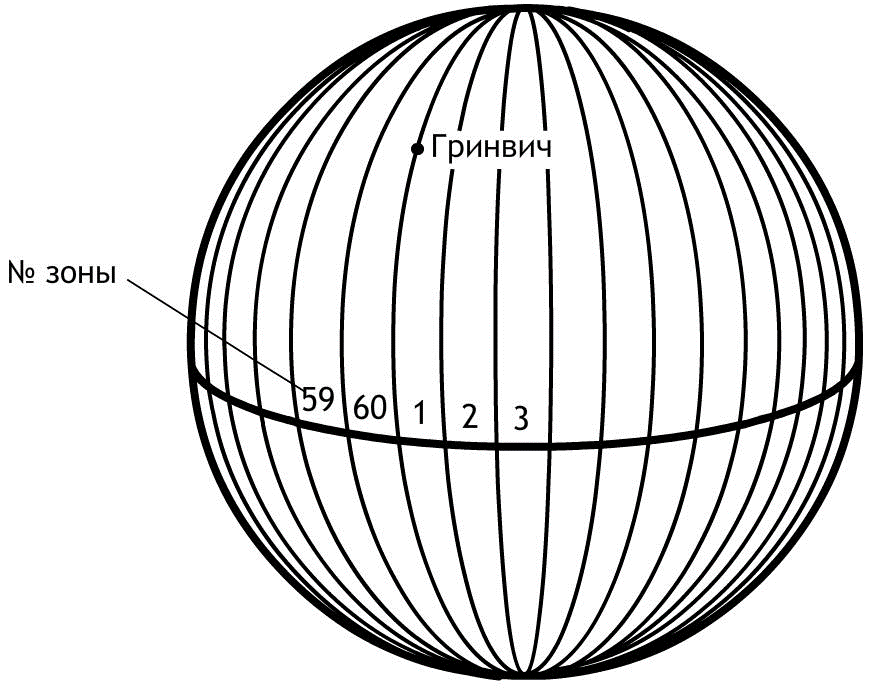
Рис. 11. Деление математической поверхности Земли на шестиградусные зоны

В пределах каждой зоны строится своя прямоугольная система координат. С этой целью все точки данной зоны проецируются на поверхность цилиндра (рис. 12, а), ось которого находится в плоскости экватора Земли, а его поверхность касается поверхности Земли вдоль среднего меридиана зоны, называемого осевым. При этом соблюдается условие сохранения подобия фигур на земле и в проекции при малых размерах этих фигур.

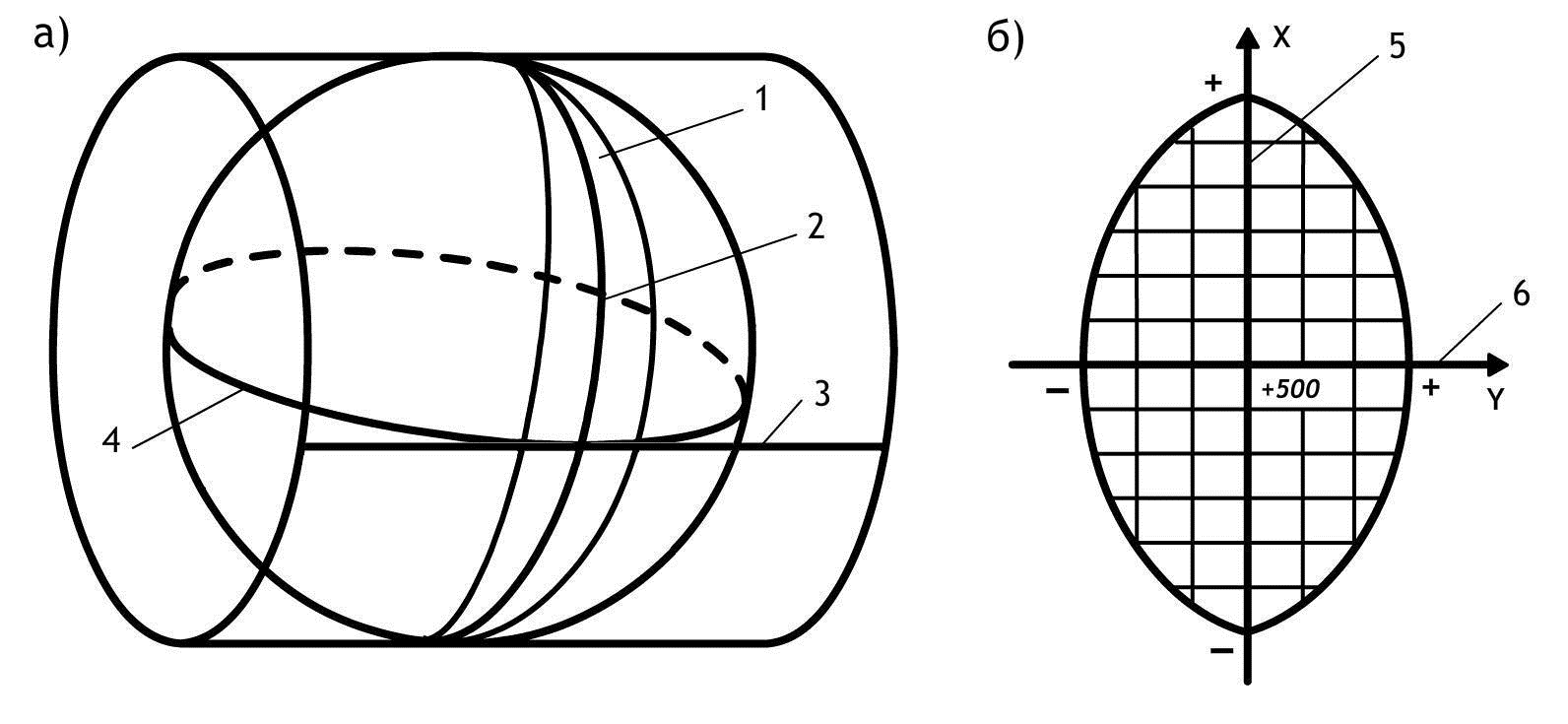
Рис. 12. Равноугольная картографическая проекция Гаусса – Крюгера (а) и зональная система координат (б):

1 – зона, 2 – осевой (средний) меридиан зоны, 3 – проекция экватора на поверхность цилиндра, 4 – экватор,

5 – ось абсцисс – проекция осевого меридиана, 6 – ось ординат – проекция экватора

После проектирования точек зоны на цилиндр, он развертывается на плоскость, на которой изображение проекции осевого меридиана и соответствующего участка экватора будет представлена в виде двух взаимно перпендикулярных прямых (рис. 12, б). Точка пересечения их принимается за начало зональной плоской прямоугольной системы координат, изображение северного направления осевого меридиана – за положительную ось абсцисс, а изображение восточного направления экватора – за положительное направление оси ординат.

Для всех точек на территории нашей страны абсциссы имеют положительное значение. Чтобы ординаты точек также были только положительными, в каждой зоне ординату начала координат принимают равной 500 км (рис. 12, б). Таким образом, точки, расположенные к западу от осевого меридиана, имеют ординаты меньше 500 км, а к востоку – больше 500 км. Эти ординаты называют преобразованными.

Искажения длин линий в данной проекции увеличиваются по мере удаления от осевого меридиана к краям зоны. На границах зон в пределах широт от 30° до 70° относительные ошибки, происходящие от искажения длин линий в этой проекции, колеблются от 1 : 1000 до 1 : 6000. Когда такие ошибки недопустимы, прибегают к трехградусным зонам.

На картах, составленных в равноугольной картографической проекции Гаусса – Крюгера, искажения длин в различных точках проекции различны, но по разным направлениям, выходящим из одной и той же точки, эти искажения будут одинаковы. Круг весьма малого радиуса, взятый на уровенной поверхности, изобразится в этой проекции тоже кругом. Поэтому говорят, что рассматриваемая проекция конформна, т. е. сохраняет подобие фигур на сфере и в проекции при весьма малых размерах этих фигур. Таким образом, изображения контуров земной поверхности в этой проекции весьма близки к тем, которые получаются.

Четверти прямоугольной системы координат нумеруются. Их счет идет по ходу стрелки от положительного направления оси абсцисс (рис.13).

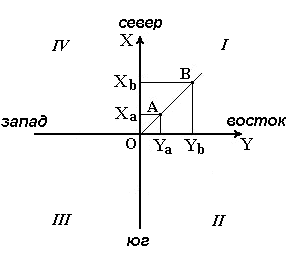
Рис. 13. Четверти прямоугольной системы координат

Если за начало плоской прямоугольной системы координат принять произвольную точку, то она будет называться относительной или условной.

Полярные координаты

При выполнении съемочных и разбивочных геодезических работ часто применяют полярную систему координат (рис.14). Она состоит из полюса О и полярной оси ОР, в качестве которых принимается прямая с известным началом и направлением.

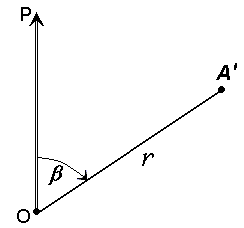
Рис. 14. Полярная система координат

Для определения положения точек в данной системе используют линейно-угловые координаты: угол β, отсчитываемый по часовой стрелке от полярной оси ОР до направления на горизонтальную проекцию точки А’, и полярное расстояние r от полюса системы О до проекции А’.

Системы высот

Высота точки является третьей координатой, определяющей её положение в пространстве.

В геодезии для определения отметок точек применяются следующие системы высот (рис.15):

ортометрическая (абсолютная);
геодезическая;
нормальная (обобщенная);
относительная (условная).

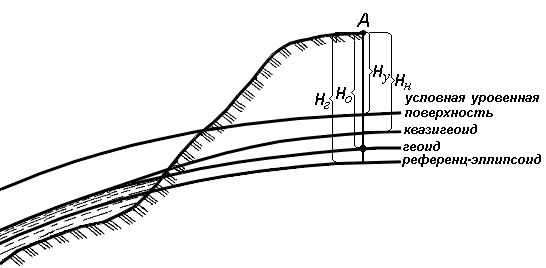
Рис. 15. Системы высот в геодезии

Ортометрическая (абсолютная) высота H_о – расстояние, отсчитываемое по направлению отвесной линии от поверхности геоида до данной точки.

Геодезическая высота H_г – расстояние, отсчитываемое по направлению нормали от поверхности референц-эллипсоида до данной точки.

В нашей стране все высоты реперов государственной нивелирной сети определены в нормальной системе высот. Это связано с тем, что положение геоида под материками определить сложно. Поэтому с конца 40-х годов в СССР было принято решение не применять ортометрическую систему высот.

В нормальной системе высот отметка точки H_н отсчитывается по направлению отвесной линии от поверхности квазигеоида, близкой к поверхности геоида. Отличие реального среднего уровня моря от геоида может достигать 1 м.

Квазигеоид («якобы геоид») – фигура, предложенная в 1950-х г.г. советским учёным М.С. Молоденским в качестве строгого решения задачи определения фигуры Земли путем тщательных измерений гравитационного поля Земли. Квазигеоид определяется по измеренным значениям потенциалов силы тяжести согласно положениям теории М.С. Молоденского.

В России абсолютные высоты точек определяются в Балтийской системе высот (БСВ) относительно нуля Кронштадтского футштока – горизонтальной черты на медной пластине, прикрепленной к устою моста через обводной канал в г. Кронштадте.

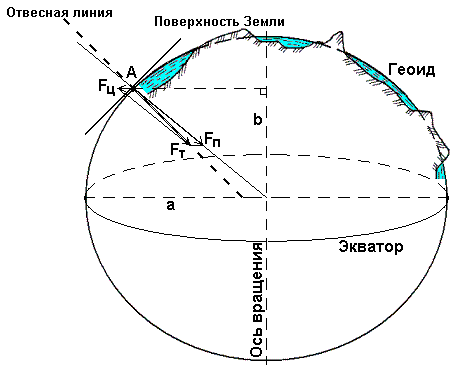
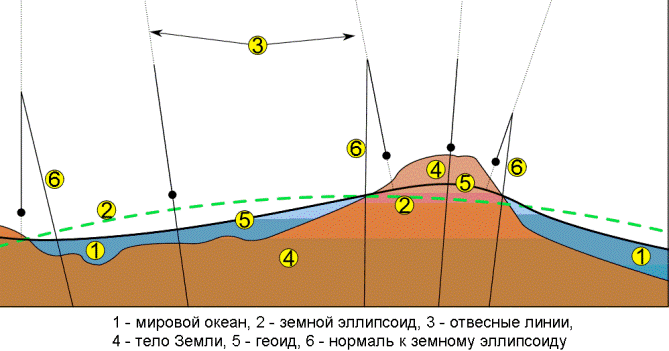
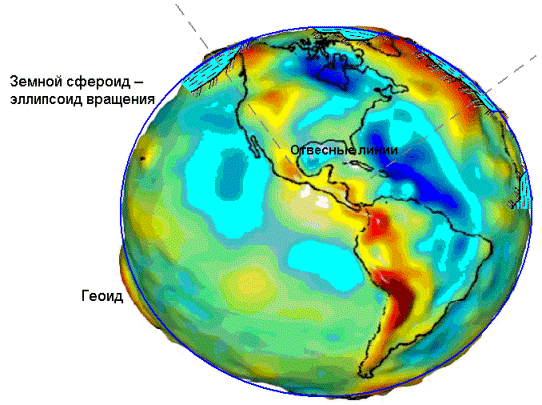
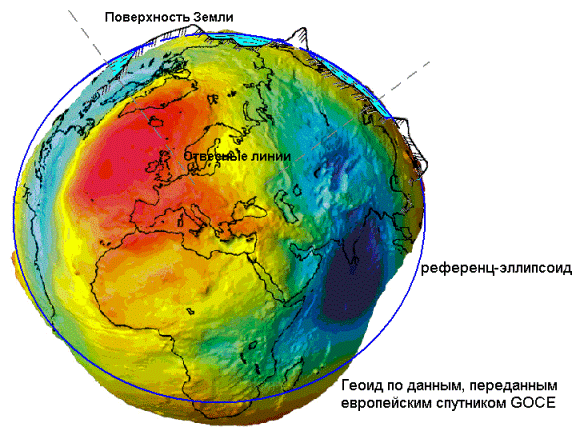
Рис. 3. Моделирование фигуры Земли

Для устранения этой неопределенности при решении общих геодезических задач принимается так называемая общая математическая поверхность, т.е. уровенная поверхность, которая в каждой своей точке совпадает со средним уровнем морей и океанов в момент полного равновесия всей массы воды под влиянием силы тяжести. Такая поверхность носит название общей фигуры Земли или поверхности геоида.

Геоид – выпуклая замкнутая поверхность, совпадающая с поверхностью воды в морях и океанах в спокойном состоянии и перпендикулярная к направлению силы тяжести в любой её точке (см. рис. 3).

Фигура геоида зависит от распределения масс и плотностей в теле Земли. Из-за неравномерного распределения масс внутри Земли геоид не имеет правильной геометрической формы, и в математическом отношении его поверхность характеризуется слишком большой сложностью. Поэтому там, где это допустимо, поверхность геоида заменяется приближенными математическими моделями, в качестве которых принимается в одних случаях земной сфероид, в других – земной шар, а при топографическом изучении незначительных по размеру территорий – горизонтальная плоскость, т.е. плоскость, перпендикулярная к вертикальной линии в данной точке.

Земной сфероид – эллипсоид вращения получается вращением эллипса вокруг его малой оси b (см. рис. 3), совпадающей с осью вращения Земли, причем центр эллипсоида совмещается с центром Земли.

Размеры эллипсоида подбирают при условии наилучшего совпадения поверхности эллипсоида и геоида в целом (общеземной эллипсоид) или отдельных его частей (референц-эллипсоид).

Фигура референц-эллипсоида наилучшим образом подходит для территории отдельной страны или нескольких стран. Как правило, референц-эллипсоиды принимают для обработки геодезических измерений законодательно.

Наиболее удачная математическая модель Земли в виде референц-эллипсоида была предложена проф. Ф. Н. Красовским с большой полуосью a=6378245 м, малой – b=6356863 м и коэффициентом сжатия у полюсов a = (a-b)/a = 1/298.3 ~ 1/300. Отклонения эллипсоида Красовского от геоида на территории СНГ не превышают 150 м.

Постановлением Совета Министров СССР № 760 от 7 апреля 1946 года эллипсоид Красовского принят для территории нашей страны в качестве математической поверхности Земли.

В инженерной геодезии для практических расчетов за математическую поверхность Земли принимают шар со средним радиусом R=6371.11 км. Объем шара равен объему земного эллипсоида.

При топографическом изучении физической поверхности Земли надводная и подводная части рассматриваются отдельно. Надводная часть (суша) – местность (территория)является предметом изучения топографии. Подводную часть – акваторию (поверхность, покрытую водами морей и океанов) изучает океанография.

План урока №2

Этап 1. Тема урока

Ориентирование линий на местности. Сближение меридианов. Склонение магнитной стрелки. Румбы , дирекционные углы, азимут

Этап II. Цель урока

-дать представление о ориентировании линий на местности -научиться определять румбы, дирекционные углы.
Этап III. Тип урока Урок ознакомления с новым материалом

Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Урок №2

Понятие об ориентировании

При выполнении геодезических работ на местности, а также при решении инженерно-геодезических задач на топографических картах и планах возникает необходимость в определении положения линий местности относительно какого-либо направления, принимаемого за основное (исходное). Такое определение называется ориентированием.

Чаще всего за основное принимается направление меридиана, и положение линий местности определяется относительно сторон горизонта – севера, востока, юга и запада. Такое ориентирование называется ориентированием относительно стран света.

В геодезии при ориентировании за основное направление принимают направление осевого, истинного или магнитного меридианов. При этом положение линии определяют с помощью соответствующих углов ориентирования: дирекционного угла, истинного или магнитного азимута.

Дирекционные углы и осевые румбы

Осевой (средний) истинный меридиан зоны часто принимают за основное направление. В этом случае положение линии местности относительно осевого меридиана определяет угол ориентирования, называемый дирекционным (рис. 16).

Дирекционный угол измеряется от северного направления осевого меридиана в направлении движения часовой стрелки через восток, юг и запад. Следовательно, градусная величина дирекционного угла может иметь любое значение от 0° до 360°.

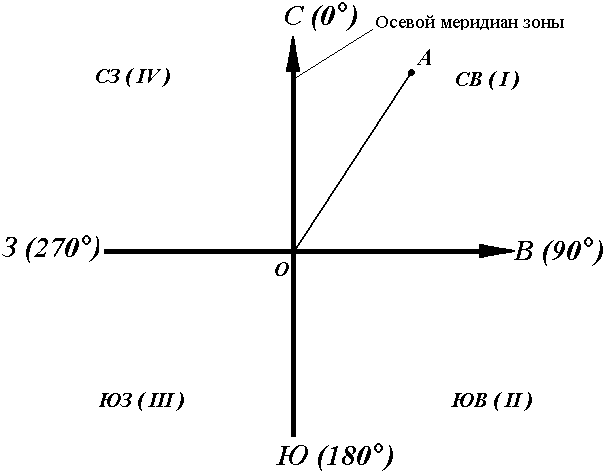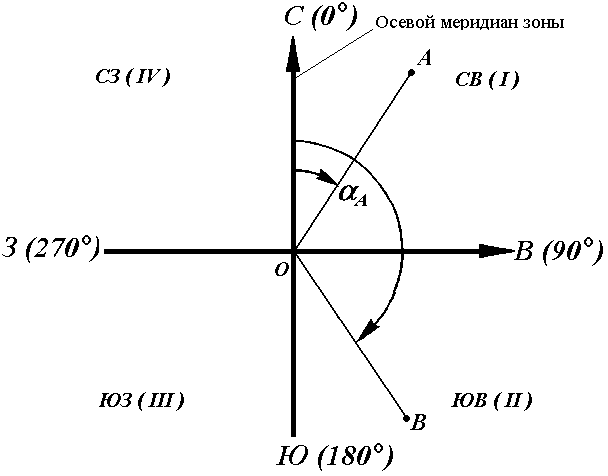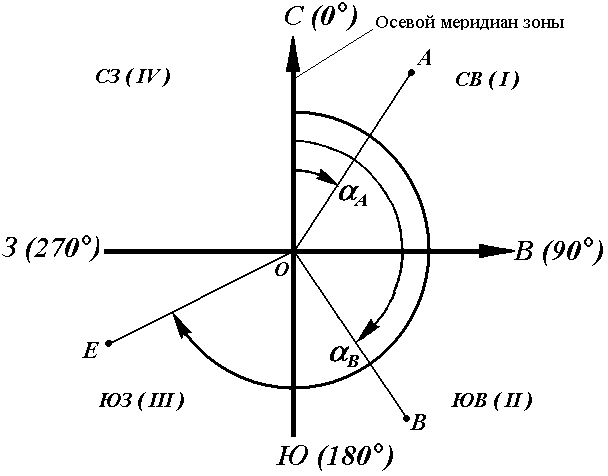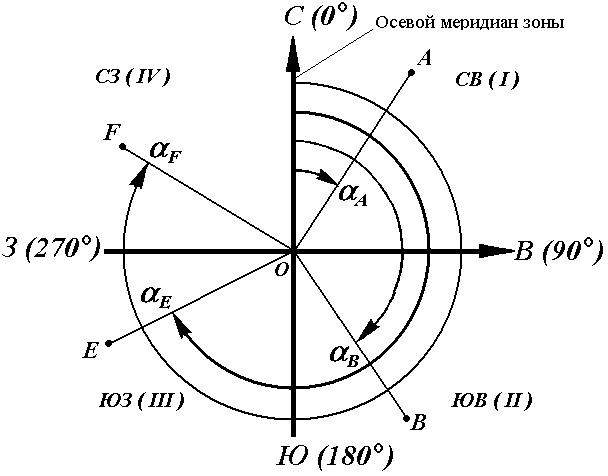
Рис. 16. Дирекционные углы

Для линии ОА её дирекционным углом в точке О является горизонтальный угол α_ОA между северным направлением осевого меридиана и направлением линии. Для линий ОВ, ОЕ и ОF – α_ОВ , α_ОE , α_ОF.

Таким образом, дирекционным углом является угол в горизонтальной плоскости, отсчитываемый от северного направления осевого меридиана по ходу часовой стрелки до данной линии.

В геодезии принято различать прямое и обратное направление линии (рис. 17). Так, если ВС считать прямым направлением линии, то СВ будет обратным направлением той же линии. В соответствии с этим α_BC является прямым дирекционным углом линии ВС в точке М, а угол α_CB – обратным дирекционным углом этой же линии в той же точке.

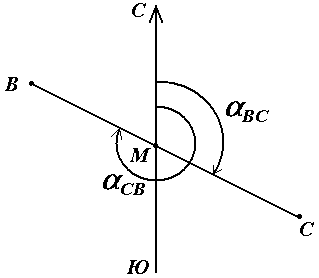
Рис. 17. Прямое и обратное направление линии

Из рисунка видно, что α_CB = α_BC + 180°, т.е. прямой и обратный дирекционные углы отличаются друг от друга на 180°.

Иногда для ориентирования линии местности пользуются не дирекционными углами, а румбами (рис. 18).

Осевым румбом называется острый горизонтальный угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии. Румбы обозначают буквой r с индексом, указывающим четверть, в которой находится румб.

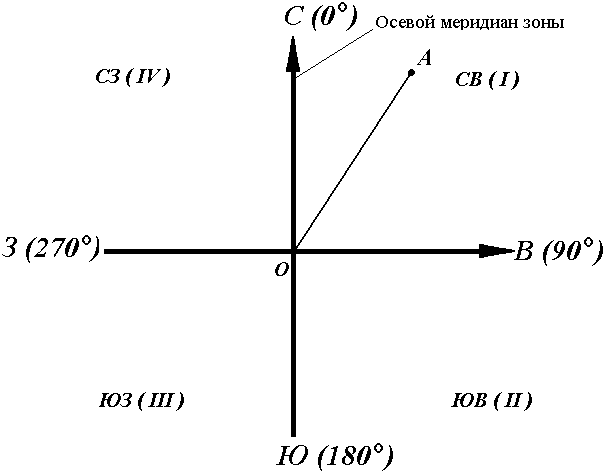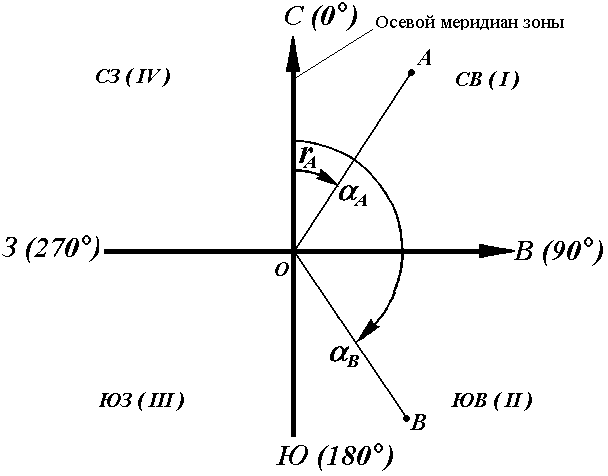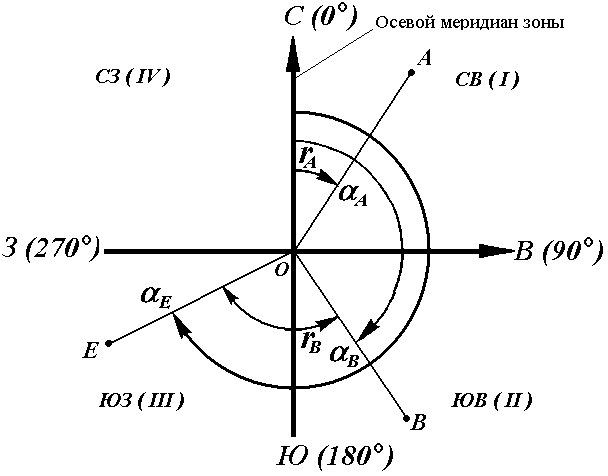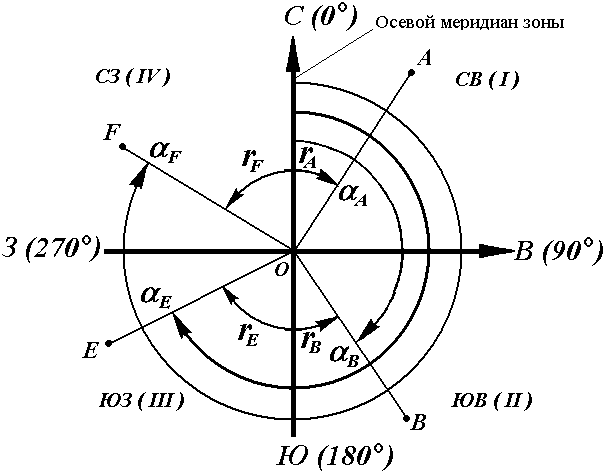
Рис. 18. Румбы и дирекционные углы

Название четвертей составлены из соответствующих обозначений главных точек горизонта: север (С), юг (Ю), восток (В), запад (З).

Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:

I четверть (СВ) r = α

II четверть (ЮВ) r = 180° – α

III четверть (ЮЗ) r = α – 180°

IV четверть (СЗ) r = 360° – α

Румб в точке М направления ВС называется прямым, а противоположного направления СВ – обратным. Прямой и обратный румб в одной и той же точке данной линии равны по численному значению, но имеют индексы противоположных четвертей.

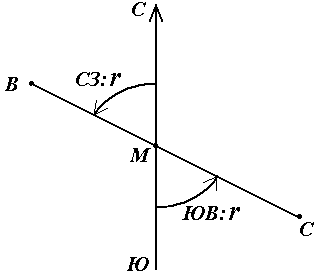
Рис. 19. Прямой и обратный румбы

Истинные азимуты и румбы

Кроме осевого меридиана зоны при ориентировании линий местности за основное направление может приниматься направление истинного (географического) меридиана.

Истинный меридиан – линия пересечения земной поверхности с плоскостью, проходящей через отвесную линию и ось вращения Земли.

Положение линии местности относительно истинного меридиана определяется истинным азимутом или истинным румбом.

Истинный азимут линии – угол в горизонтальной плоскости, отсчитываемый от северного направления истинного меридиана по ходу часовой стрелки до данной линии (рис. 20).

Истинный румб линии – острый горизонтальный угол, отсчитываемый от ближайшего направления истинного меридиана (северного или южного) до данной линии.

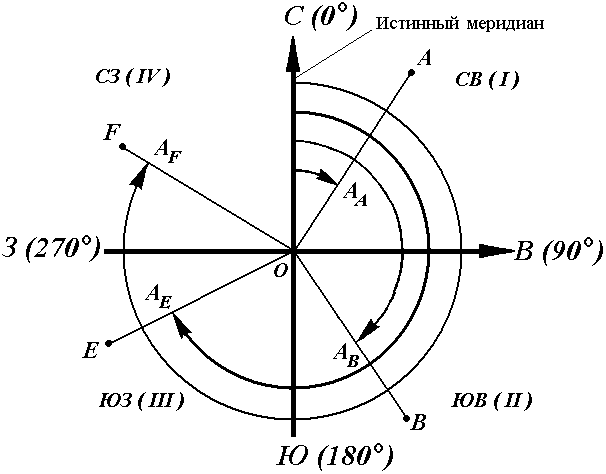
Рис. 20. Истинные азимутыы

Истинный азимут A измеряется от 0° до 360°. Зависимость между истинными азимутами и румбами такая же, как и между дирекционными углами и осевыми румбами.

Истинные меридианы, проходящие через точки Земли с разной долготой, не параллельны между собой и сходятся на полюсах. Поэтому азимуты одной и той же прямой линии, определяемые относительно разных истинных меридианов, отличаются на величину γ (рис. 21), которую называют углом сближения меридианов. Его приближенное значение можно рассчитать по формулам:

γ = 0,54 · l · tgφ или γ = sinφ · Δλ,

где l – длина прямой линии между точками (км); φ – средняя широта линии; Δλ – разность долгот. При l = 1 км и широте Хабаровска φ = 48°28′ угол сближения меридианов γ = 0,6′ = 36″.

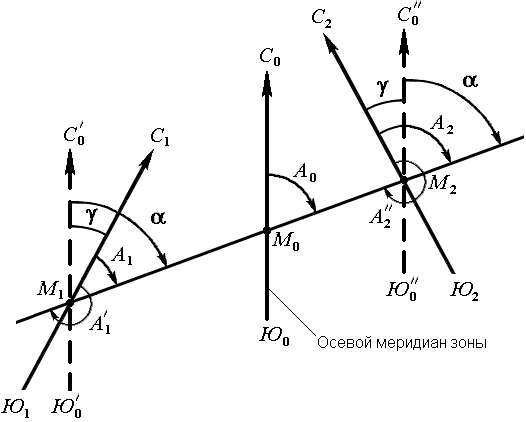
Рис. 21. Зависимость между истинным азимутом и дирекционным углом

Для перехода от дирекционного угла к истинному азимуту и наоборот необходимо знать угол сближения γ между осевым и истинным меридианом (рис. 21). Зависимость между истинным азимутом и дирекционным углом следующая

А = α + γ .

Если точка расположена к западу от осевого меридиана, то величину угла сближения γ между осевым и истинным меридианом принято считать отрицательной, если к востоку – положительной (рис. 21). Например, истинные азимуты линии при дирекционном угле α = 70° и углах сближения γ = – 0°50′ для западной точки М1, γ = 0°50′ для восточной –М2 соответственно равны

А₁= 70° – 0°50′ = 69°50′,

А₂= 70° + 0°50′ = 70°50′.

Магнитные азимуты и румбы

При ориентировании линий местности за основное направление может также приниматься направление магнитного меридиана.

Магнитная стрелка на концах имеет точки, в которых сосредоточены магнитные массы. Соединяющая их линия называется магнитной осью стрелки.

Вертикальная плоскость, проходящая через магнитную ось стрелки, является плоскостью магнитного меридиана.

Линия пересечения плоскости магнитного меридиана с горизонтальной плоскостью дает направление магнитного меридиана.

Горизонтальный угол, отсчитываемый от северного направления магнитного меридиана по ходу часовой стрелки до данной линии, называется магнитным азимутом А_м(рис. 22).

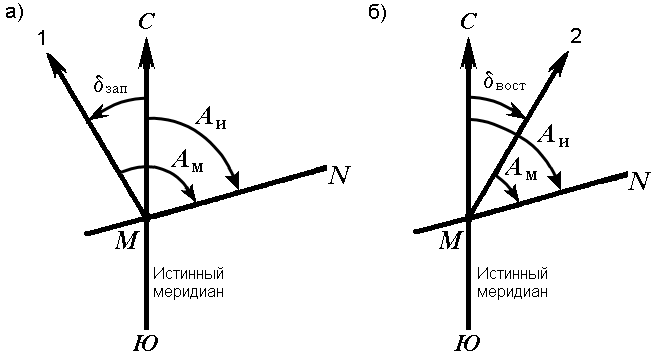
Рис. 22. Магнитный азимут и склонение магнитной стрелки: а) западное; б) восточное

В каждой точке на поверхности Земли магнитный и истинный меридианы образуют между собой угол, называемый склонением магнитной стрелки δ (рис. 22). Северный конец магнитной стрелки может отклоняться от истинного меридиана к западу или востоку. В зависимости от этого различают западное и восточное склонения. Восточное склонение принято считать положительным, западное – отрицательным:

А_и= А_м + δ_вост ,

А_и = А_м – δ_зап .

Магнитное склонение в разных пунктах Земли различно и непостоянно. Различают вековые, годовые и суточные изменения склонения. В связи с этим магнитная стрелка указывает направление магнитного меридиана приблизительно и ориентировать линию по нему можно только тогда, когда не требуется большая точность ориентирования.

Вопросы для самоконтроля

1. Что называется ориентированием на местности?

2. Что называется дирекционным углом линии, и в каких пределах он измеряется?

3. Что такое румб линии, и в каких пределах он измеряется?

4. Что называется истинным и магнитным азимутами?

5. Какова зависимость между дирекционным углом и истинным азимутом и между истинным азимутом и магнитным азимутом?

6. Что называется сближением меридианов?

7. Что называется склонением магнитной стрелки?

План урока №3

Этап 1. Тема урока

Прямая и обратная геодезические задачи на плоскости. Измерения и построения в геодезии

Этап II. Цель урока: -дать представление о прямой и обратной геодезической задаче -научиться решать прямую и обратную геодезическую задачу
Этап III. Тип урока Урок ознакомления с новым материалом

Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Этап VI. Ход урок -организационный момент – актуализация знаний учащихся по предыдущей теме –изучение темы -закрепление материала – подведение итогов -домашнее задание

Урок №3

Прямая геодезическая задача

В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояние S_AB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол α_AB или румб r_AB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.

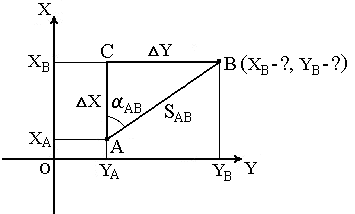
Рис. 23. Прямая геодезическая задача

Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом.

Дано: Точка А( X_A, Y_A ), S_AB и α_AB.

Найти: точку В( X_B, Y_B ).

Непосредственно из рисунка имеем:

ΔX = X_B – X_A ;

ΔY = Y_B – Y_A .

Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:

ΔX = S_AB · cos α_AB ;

ΔY = S_AB · sin α_AB .

Так как в этих формулах S_AB всегда число положительное, то знаки приращений координат ΔX и ΔY зависят от знаков cos α_AB и sin α_AB. Для различных значений углов знаки ΔX и ΔY представлены в табл.1.

Таблица 1.

Знаки приращений координат ΔX и ΔY

Приращения координат	Четверть окружности в которую направлена линия
I (СВ)	II (ЮВ)	III (ЮЗ)	IV (СЗ)
ΔX	+	–	–	+
ΔY	+	+	–	–

При помощи румба приращения координат вычисляют по формулам:

ΔX = S_AB · cos r_AB ;

ΔY = S_AB · sin r_AB .

Знаки приращениям дают в зависимости от названия румба.

Вычислив приращения координат, находим искомые координаты другой точки:

X_B = X_A + ΔX ;

Y_B = Y_A + ΔY .

Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения.

Обратная геодезическая задача

Обратная геодезическая задача заключается в том, что при известных координатах точек А( X_A, Y_A ) и В( X_B, Y_B ) необходимо найти длину S_AB и направление линии АВ: румбr_AB и дирекционный угол α_AB (рис.24).

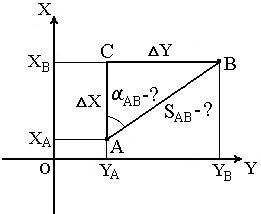
Рис. 24. Обратная геодезическая задача

Даннная задача решается следующим образом.

Сначала находим приращения координат:

ΔX = X_B – X_A ;

ΔY = Y_B – Y_A .

Величину угла r_AB определем из отношения

ΔY	= tg r_AB
ΔX

По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находимα_AB.

Для контроля расстояние S_AB дважды вычисляют по формулам:

S_AB=	ΔX	=	ΔY	= ΔX · sec α_AB = ΔY · cosec α_AB
cos α_AB	sin α_AB

S_AB=	ΔX	=	ΔY	= ΔX · sec r_AB = ΔY · cosec r_AB
cos r_AB	sin r_AB

Расстояние S_AB можно определить также по формуле

Вопросы для самоконтроля

1. Что называется ориентированием на местности?

2. Что называется дирекционным углом линии, и в каких пределах он измеряется?

3. Что такое румб линии, и в каких пределах он измеряется?

4. Что называется истинным и магнитным азимутами?

6. Что называется сближением меридианов?

План урока №4

Этап 1. Тема урока

Понятия о геодезических планах, картах и чертежах .Масштабы

Номенклатура планов и карт.

Этап II. Цель урока: -дать представление о геодезических планах, картах и чертежах
Этап III. Тип урока Урок ознакомления с новым материалом

Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Этап VI. Ход урок -организационный момент – актуализация знаний учащихся по теме. –изучение темы -закрепление темы – подведение итогов -домашнее задание

Урок №4

План, карта, профиль

Чтобы спроектировать линию местности на горизонтальную плоскость, нужно определить её горизонтальное проложение (проекцию линии на горизонтальную плоскость) и уменьшить его до определенного масштаба. Для проектирования на горизонтальную плоскость какого-либо многоугольника (рис. 26) измеряют расстояния между его вершинами и горизонтальные проекции его углов.

Совокупность линейных и угловых измерений на земной поверхности называется геодезической съемкой. По результатам геодезической съемки составляют план или карту.

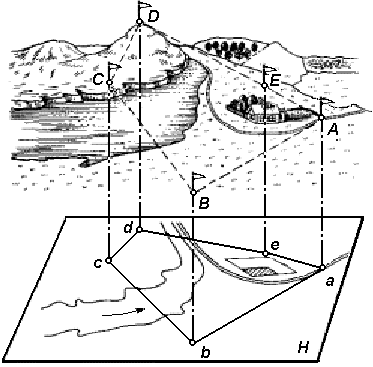
Проектирование участка земной поверхности на горизонтальную плоскость

План – чертеж, на котором в уменьшенном и подобном виде изображается горизонтальная проекция небольшого участка местности.

Карта – уменьшенное и искаженное изображение картографической проекции значительной части или всей земной поверхности, построенное по определенным математическим законам, учитывающим влияние кривизны Земли.

Таким образом, и план, и карта – это уменьшенные изображения земной поверхности на плоскости. Различие между ними состоит в том, что при составлении карты проектирование производят с искажениями поверхности за счет влияния кривизны Земли, на плане изображение получают практически без искажений.

В зависимости от назначения планы и карты могут быть контурные и топографические. На контурных планах и картах условными знаками изображают ситуацию, т.е. только контуры (очертания) горизонтальных проекций местных предметов (дорог, строений, пашен, лугов, лесов и т.п.).

На топографических картах и планах кроме ситуации изображают ещё рельеф местности.

Для проектирования железных, шоссейных дорог, каналов, трасс, водопроводов и других сооружений необходимо иметь вертикальный разрез или профиль местности.

Профилем местности называется чертеж, на котором изображается в уменьшенном виде сечение вертикальной плоскостью поверхности Земли по заданному направлению.

Как правило, разрез местности (рис. 27, а) представляет собой кривую линию ABC…G. На профиле (рис. 27, б) она строится в виде ломаной линии abc…g. Уровенную поверхность изображают прямой линией. Для большей наглядности вертикальные отрезки (высоты, превышения) делают крупнее, чем горизонтальные (расстояния между точками).

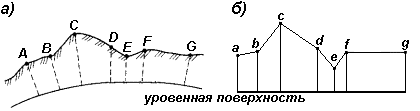
Рис. 27. Вертикальный разрез (а) и профиль (б) местности

Рельефом (от лат. relevo – поднимаю) называют совокупность неровностей суши, дна океанов и морей, разнообразных по очертаниям, размерам, происхождению, возрасту и истории развития.

Рельеф как совокупность неровностей физической поверхности Земли рассматривается по отношению к её уровенной поверхности.

Рельеф местности

Рельеф слагается из положительных (выпуклых) и отрицательных (вогнутых) форм (рис. 4) и образуется главным образом в результате длительного одновременного воздействия на земную поверхность эндогенных (внутренних) и экзогенных (внешних) процессов.

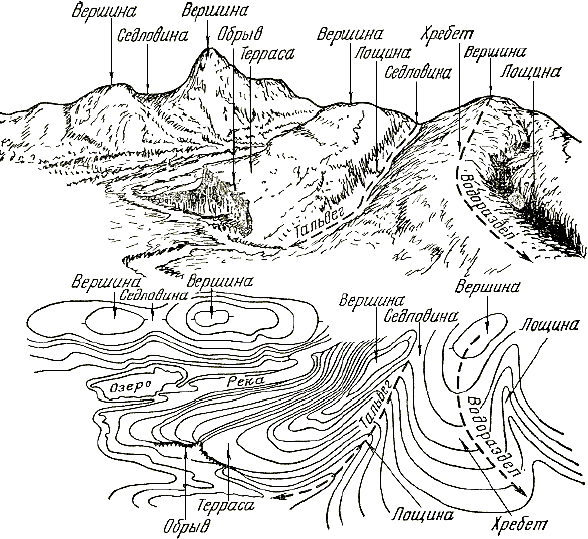
Изображение форм рельефа горизонталями

Для изображения рельефа горизонталями выполняют топографическую съемку участка местности. По результатам съемки определяют координаты (две плановые и высоту) для характерных точек рельефа и наносят их на план (рис. 33). В зависимости от характера рельефа, масштаба и назначения плана выбирают высоту сечения рельефа h.

Изображение рельефа горизонталями

Для инженерного проектирования обычно h = 1 м. Отметки горизонталей в этом случае будут кратны одному метру.

Положение горизонталей на плане или карте определяется с помощью интерполирования. На рис. 33 приведено построение горизонталей с отметками 51, 52, 53, 54, 55, 56, 57 м. Горизонтали кратные 5 или 10 м проводят на чертеже утолщенными и подписывают. Подписи наносят таким образом, чтобы верх цифр указывал сторону повышения рельефа. На рис. 33 подписана горизонталь с отметкой 55 м.

Там, где заложения больше, наносят штриховые линии (полугоризонтали). Иногда, чтобы сделать чертеж более наглядным, горизонтали сопровождают небольшими черточками, которые ставятся перпендикулярно горизонталям, по направлению ската (в сторону стока воды). Эти черточки называются бергштрихи.

План урока №5

Этап 1. Тема урока

Условные знаки на планах и картах, геодезических и строительных чертежах.

Рельеф местности и способы его обозначения.

Этап II. Цель урока: -дать представление о рельефе местности и способах его обозначения. -рассказать, какие условные знаки используются на планах и картах
Этап III. Тип урока Урок ознакомления с новым материалом

Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Этап VI. Ход урок -организационный момент – актуализация знаний учащихся по предыдущей теме –изучение темы -закрепление темы – подведение итогов

Урок №5

Изображение рельефа на планах и картах

Для решения инженерных задач изображение рельефа должно обеспечивать: во-первых, быстрое определение с требуемой точностью высот точек местности, направления крутизны скатов и уклонов линий; во-вторых, наглядное отображение действительного ландшафта местности.

Рельеф местности на планах и картах изображают различными способами (штриховкой, пунктиром, цветной пластикой), но чаще всего с помощью горизонталей (изогипсов), числовых отметок и условных знаков.

Горизонталь на местности можно представить как след, образованный пересечением уровенной поверхности с физической поверхностью Земли. Например, если представить холм, окружённый неподвижной водой, то береговая линия воды и есть горизонталь (рис. 30). Лежащие на ней точки имеют одинаковую высоту.

Допустим, что высота уровня воды относительно уровенной поверхности 110 м (рис. 30). Предположим теперь, что уровень воды упал на 5 м и часть холма обнажилась. Кривая линия пересечения поверхностей воды и холма будет соответствовать горизонтали с высотой 105 м. Если последовательно снижать уровень воды по 5 м и проектировать кривые линии, образованные пересечением поверхности воды с земной поверхностью, на горизонтальную плоскость в уменьшенном виде, то получим изображение рельефа местности горизонталями на плоскости.

Таким образом кривая линия, соединяющая все точки местности с равными отметками, называется горизонталью.

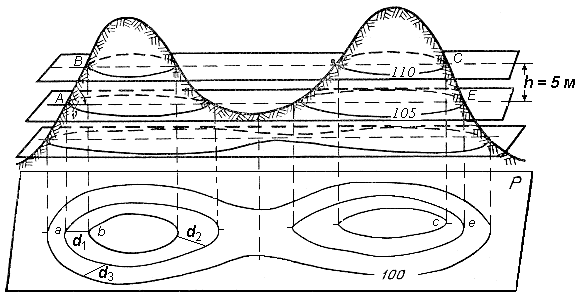
Рис. 30. Способ изображения рельефа горизонталями

При решении ряда инженерных задач необходимо знать свойства горизонталей:

1. Все точки местности, лежащие на горизонтали, имеют равные отметки.

2. Горизонтали не могут пересекаться на плане, поскольку они лежат на разных высотах. Исключения возможны в горных районах, когда горизонталями изображают нависший утес.

3. Горизонтали являются непрерывными линиями. Горизонтали, прерванные у рамки плана, замыкаются за пределами плана.

4. Расстояние между соседними горизонтальными секущими плоскостями h (см. рис. 30) называется высотой сечения рельефа. Оно равно разности высот двух соседних горизонталей.

Высота сечения рельефа в пределах плана или карты строго постоянна. Её выбор зависит от характера рельефа, масштаба и назначения карты или плана. Для определения высоты сечения рельефа иногда пользуются формулой

h = 0,2 мм · М,

где М – знаменатель масштаба.

Такая высота сечения рельефа называется нормальной.

5. Расстояние между соседними горизонталями на плане или карте называется заложением ската или склона. Заложение есть любое расстояние между соседними горизонталями (см. рис. 30), оно характеризует крутизну ската местности и обозначается d.

Вертикальный угол, образованный направлением ската с плоскостью горизонта и выраженный в угловой мере, называется углом наклона ската ν (рис. 31). Чем больше угол наклона, тем круче скат.

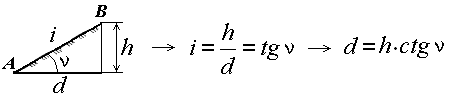
Рис. 31. Определение уклона и угла наклона ската

Другой характеристикой крутизны служит уклон i. Уклоном линии местности называют отношение превышения к горизонтальному проложению. Из формулы следует (рис. 31), что уклон безразмерная величина. Его выражают в сотых долях (%) или тысячных долях – промиллях (‰).

Если угол наклона ската до 45°, то он изображается горизонталями, если его крутизна более 45°, то рельеф обозначают специальными знаками. Например, обрыв показывается на планах и картах соответствующим условным знаком (рис. 32).

Изображение основных форм рельефа горизонталями приведено на рис. 32.

Изображение форм рельефа горизонталями

Изображение рельефа горизонталями

Для инженерного проектирования обычно h = 1 м. Отметки горизонталей в этом случае будут кратны одному метру.

План урока №6

Этап 1. Тема урока

Уклон линий. График заложений. Ориентирование на местности с помощью карты.

Этап II. Цель урока: -дать представление об уклоне линий, графике заложения -научить ориентироваться на местности с помощью карты.
Этап III. Тип урока Урок ознакомления с новым материалом

Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Этап VI. Ход урок -организационный момент – актуализация знаний учащихся по теме. –изучение темы -закрепление темы. – подведение итогов

Урок №6

Определение отметок точек местности по горизонталям

а) Точка лежит на горизонтали.
В этом случае отметка точки равна отметке горизонтали (см. рис. 35): H_А = 75 м; Н_С = 55 м.

б) Точка лежит на скате между горизонталями.
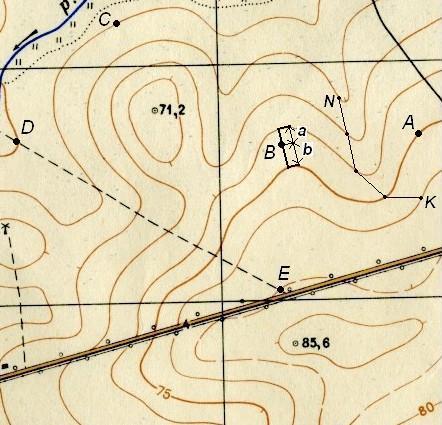
Если точка лежит между горизонталями, то через нее проводят кратчайшее заложение, масштабной линейкой измеряют длину отрезков а и b (см. рис. 35, точка В) и подставляют в выражение

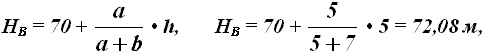
где h – высота сечения рельефа. Если точка лежит между горизонталью и полугоризонталью, то вместо h в формулу подставляют 0,5h.

Решение задач на карте с горизонталям

Определение крутизны ската

Крутизна ската по направлению заложения определяется двумя показателями – уклоном и углом наклона по формуле

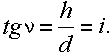
Следовательно, тангенс угла наклона линии к горизонту называется её уклоном. Уклон выражают в тысячных – промиллях (‰) или в процентах (%). Например: i = 0,020 = 20‰ = 2%.

Для графического определения углов наклона по заданному значению заложения d, масштабу М и высоте сечения рельефа h строят график заложений (см. рис. 36).

Вдоль прямой линии основания графика намечают точки, соответствующие значениям углов наклона. От этих точек перпендикулярно к основанию графика откладывают в масштабе карты отрезки, равные соответствующим заложениям, а именно

Концы этих отрезков соединяют плавной кривой (см. рис. 36).

Заложение линии, угол наклона которой надо определить, снимают с карты при помощи измерителя, а затем, укладывая на графике между основанием и кривой измеренный отрезок, находят соответствующее ему значение угла наклона.

График заложений для углов наклона

Аналогично строят и пользуются графиком заложений для уклонов (рис. 37).

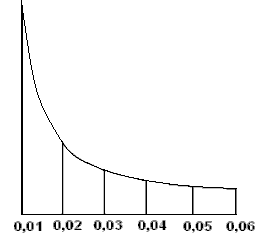
График заложений для уклонов

Построение линии с заданным уклоном

Задача построения линии с заданным уклоном решается в проектировании трасс железных, автомобильных и других линейных сооружений. Она заключается в том, что из некоторой точки, обозначенной на карте, необходимо провести линию с заданным уклоном i по заданному направлению. Для этого сначала определяют значение заложения d, соответствующее заданным i и h. Его находят по графику заложения уклонов или вычисляют по формуле

d = h/i .

Далее, установив раствор измерителя равным полученному значению d, ставят одну его ножку в начальную точку K, а другой засекают ближайшую горизонталь и тем намечают точку трассы, из которой в свою очередь засекают следующую горизонталь, и т.д. (см. рис. 38).

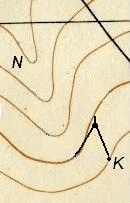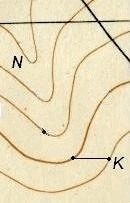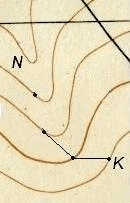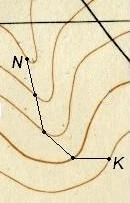
Построение линии с заданным уклоном

Построение профиля по топографической карте

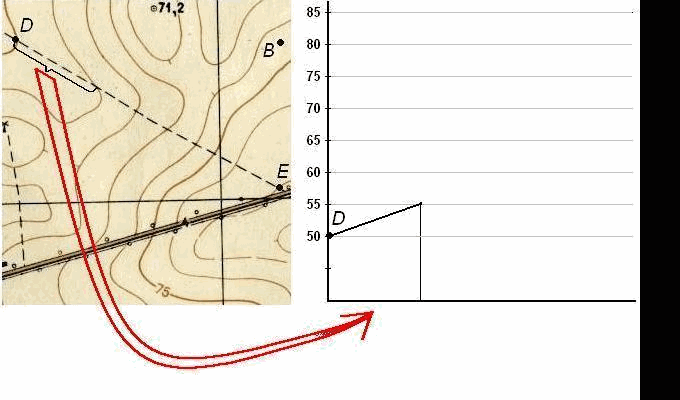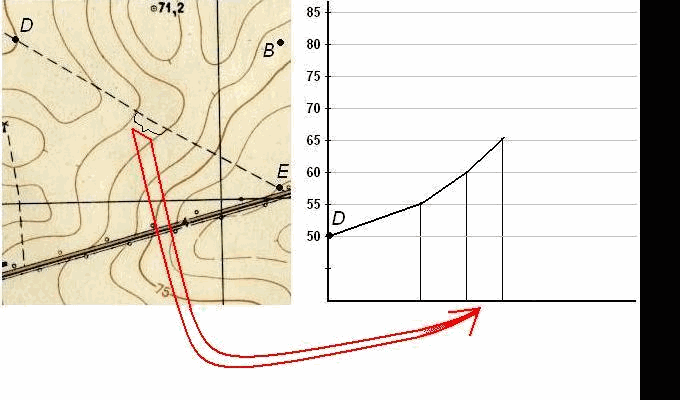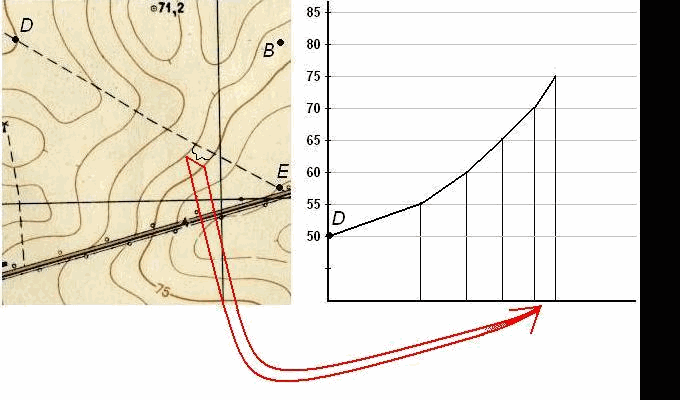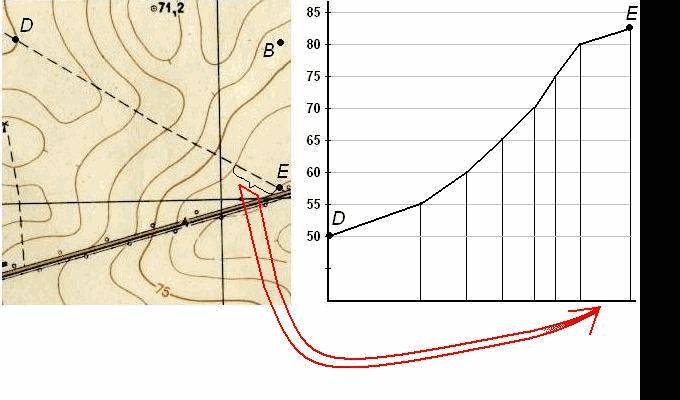
Профилем местности называют уменьшенное изображение вертикального разреза местности по заданному направлению.

Пусть требуется построить профиль местности по линии DE, указанной на карте (рис. 39). Для построения профиля на листе бумаги (как правило, используется миллиметровая бумага) проводят горизонтальную прямую и на ней, обычно в масштабе карты (плана), откладывают линию DE и точки её пересечения с горизонталями и полугоризонталями. Далее из этих точек по перпендикулярам откладывают отметки соответствующих горизонталей (на рис. 39 это отметки 50, 55, 60, 65, 70, 75, 80 и 82,5 м). Чтобы отобразить профиль более рельефно, отметки точек обычно откладывают в масштабе в 10 раз крупнее масштаба плана. Соединив прямыми концы перпендикуляров, получают профиль по линии DE.

Вопросы для самоконтроля

1. Что понимают под рельефом местности?

2. Назовите формы рельефа.

3. Что такое горизонталь? Назовите её основные свойства.

4. Что такое высота сечения рельефа?

5. Что называется заложением горизонталей?

6. Что такое уклон линии?

7. Как определяется нормальная высота сечения рельефа?

8. Как определить на карте высоту точки и крутизну ската линии?

План урока №7

Этап 1. Тема урока

Погрешности измерений. Свойства случайных погрешностей измерений. Предельная, абсолютная и относительная погрешности.

Двойные измерения. Понятия о правилах и технике геодезических измерений.
Этап II. Цель урока: -дать представление о погрешности измерений Этап III. Тип урока Урок ознакомления с новым материалом
Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Этап VI. Ход урок -организационный момент – актуализация знаний учащихся по предыдущей теме –изучение темы -закрепление темы. – подведение итогов -домашнее задание

Урок №7

Погрешность – это отклонение результата измерения от истинного значения измеряемой величины.

Истинное значение ФВ может быть установлено лишь путем проведения бесконечного числа измерений, что невозможно реализовать на практике. Истинное значение измеряемой величины является недостижимым, а для анализа погрешностей в качестве значения ближайшего к истинному, используют действительное значение измеряемой величины, значение получают с использованием самых совершенных методом измерений и самых высокоточных средств измерений. Таким образом, погрешность измерений представляет собой отклонение от действительного значения ∆=Xд – Хизм

Погрешность сопровождает все измерения и связана с несовершенством метода, средства измерения, условия измерения (когда они отличаются от н.у.).

В зависимости от принципов действия прибора те или иные факторы оказывают влияние.

Различают погрешности СИ и результата измерений за счет влияния внешних условий, особенностей измеряемой величины, несовершенства СИ.

Погрешность результата измерений включает в себя погрешность и средства измерений, также влияние условий проведения измерений, свойств объекта и измеряемой величины ∆ри=∆си+∆ву+∆св.о+∆сив.

Классификация погрешностей:

1) По способу выражения:

a) Абсолютная – погрешность, выраженная в единицах измеряемой величины ∆=Хд-Хизм

b) Относительная – погрешность, выраженная отношением абсолютной погрешности к результате измерений или действительному значению измеряемой величины γотн=(∆/Xд)* 100 .

c) Приведенная – это относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условию, принятому значению величины постоянному во всем диапазоне измерений (или части диапазона) γприв=(∆/Xнорм)*100, где Хнорм – нормирующее значение, установленное для приведенных значений. Выбор Хнорм производится в соответствии с ГОСТом 8.009-84. Это может быть верхний предел средства измерений, диапазон измерений, длина шкалы и т.л. Для множества средств измерений по приведенной погрешности устанавливают класс точности. Приведенная погрешность вводится потому что относительная характеризует погрешность только в данной точке шкалы и зависит от значения измеряемой величины.

2) По причинам и условиям возникновения:

a) Основная – это погрешность средств измерения, которое находятся в нормальных условиях эксплуатации, возникает из-за неидеальности функции преобразования и вообще неидеальности свойств средств измерений и отражает отличие действительной функции преобразования средств измерения в н.у. от номинальной нормированной документами на средства измерений (стандарты, тех. условия). Нормативными документами предусматриваются следующие н.у.:

Температура окружающей среды (20±5)°С;
Относительная влажность (65±15)%;
напряжение питания сети (220±4,4)В;
частота питания сети (50±1)Гц;
отсутствие эл. и магн. полей;
положение прибора горизонтальное, с отклонением ±2°.

Рабочие условия измерений – это условия, при которых значения влияющих величин находятся в пределах рабочих областей, для которых нормируют дополнительную погрешность или изменение показаний СИ.

Например, для конденсаторов нормируют дополнительную погрешность, связанную с отклонением температуры от нормальной; для амперметра отклонение частоты переменного тока 50 Гц.

b) Дополнительная – это составляющая погрешности средств измерений, возникающая дополнительно к основной, вследствие отклонения какой-либо из влияющих величин от нормы её значения или вследствие её выхода за пределы нормированной области значений. Обычно нормируется наибольшее значение дополнительной погрешности.

Предел допускаемой основной погрешности – наиб. основная погрешность средств измерения, при которой СИ может быть годным и допущено к применению по тех. условиям.

Предел допускаемой дополнительной погрешности – наибольшая дополнительная погрешность, при которой СИ допущено к применению.

Например, для прибора с КТ 1.0 приведенная дополнительная погрешность по температуре не должна превышать ±1% при изменении температуры на каждые 10°.

Пределы, допустимой основной и дополнительной погрешности могут быть выражены в форме абсолютной, относительной или приведенной погрешности.

Для того чтобы иметь возможность выбирать СИ путем сравнения их характеристик вводят обобщенную характеристику данного типа СИ – класс точности (КТ). Обычно это предел допускаемых основной и дополнительной погрешностей. КТ позволяет судить в каких пределах находится погрешность СИ одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью каждого из этих СИ, т.к. погрешность зависит также от метода, условий измерений и т.д. Это нужно учитывать при выборе СИ в зависимости от заданной точности.

Значения КТ устанавливаются в стандартах или в технических условиях или других нормативных документах и выбираются в соответствии с ГОСТ 8.401-80 из стандартного ряда значений. Например, для электромеханических приборов: 0,05; 0,1; 0,2; 0,5; 1.0; 2,5; 4.0; 6.0.

Зная КТ СИ можно найти максимально допустимое значение абсолютной погрешности для всех точек диапазона измерений из формулы для приведенной погрешности: ∆maxдоп=(γприв*Xнорм)/100.

КТ обычно наносят на шкалу прибора в разных формах, например,(2.5) (в кружочке).

3) По характеру изменений:

a) систематические – составляющая погрешности, остающаяся постоянной или изменяющаяся по известной закономерности во все время проведения измерений. Может быть исключена из результатов измерения путем регулировки или введением поправок. К ним относят: методические П, инструментальные П, субъективные П и т д. Такое качество СИ, когда систематическая погрешность близка к нуля называют правильностью.

b) случайные – это составляющие погрешности, изменяющиеся случайным образом, причины нельзя точно указать, а значит, и устранить нельзя. Приводят к неоднозначности показаний. Уменьшение возможно при многократных измерениях и последующей статистической обработке результатов. Т.е. усредненный результат многократных измерений ближе к действительному значению, чем результат одного измерения. Качество, которое характеризуется близостью к нулю случайной составляющей погрешности называется сходимостью показаний этого прибора.

c) промахи – грубые погрешности, связанные с ошибками оператора или неучтенными внешними воздействиями. Их обычно исключают из результатов измерений, не учитывают при обработке результатов.

4) По зависимости от измеряемой величины:

a) Аддитивные погрешности (не зависит от измеряемой величины)

b) Мультипликативные погрешности (пропорционально значению измеряемой величины).

Мультипликативная погрешность по-другому называется погрешностью чувствительности.

Аддитивная погрешность обычно возникает из-за шумов, наводок, вибраций, трения в опорах. Пример: погрешность нуля и погрешность дискретности (квантования).

Мультипликативная погрешность вызывается погрешностью регулировки отдельных элементов измерительных приборов. Например, из-за старения (погрешность чувствительности СИ).

В зависимости от того, какая погрешность прибора является существенной, нормируют метрологические характеристики.

Если существенна аддитивная погрешность, то предел допустимой основной погрешности нормируют в виде приведенной погрешности.

Если существенна мультипликативная погрешность, то предел допустимой основной погрешности определяют по формуле относительной погрешности.

Тогда относительная суммарная погрешность: γотн=Δ/Х= γадд + γмульт= γадд+ γмульт+ γадд*Xнорм/Х– γадд=±, где с= γадд+ γмульт; d= γадд.

Это способ нормирования метрологических характеристик когда аддитивная и мультипликативная составляющие погрешности соизмеримы, т.е. предел относительной допустимой основной погрешности выражается в двучленной формуле соответственно и обозначение КТ состоит из двух чисел, выражающих c и d в %, разделенных косой чертой. Например, 0.02/0,01. Это удобно, т.к. число с – это относит.погрешность СИ в н.у. Второй член формулы характеризует увеличение относительной погрешности измерения при увеличении величины Х, т.е. характеризует влияние аддитивной составляющей погрешности.

5) В зависимости от влияния характера изменения измеряемой величины:

a) Статическая – погрешность СИ при измерении неизменной или медленно изменяющейся величины.

b) Динамическая – погрешность СИ, возникающая при измерении быстро меняющейся во времени ФВ. Динамическая погрешность является следствием инерционности прибора.

План урока №8

Этап 1. Тема урока

Принцип измерения углов. Зрительная труба.

Уровни и их устройство.

Этап II. Цель урока: -дать представление о принципе измерения углов. -рассмотреть устройство зрительной трубы
Этап III. Тип урока Урок ознакомления с новым материалом

Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Этап VI. Ход урок -организационный момент – актуализация знаний учащихся по предыдущей теме. –изучение темы -закрепление темы – подведение итогов -домашнее задание

Урок №8

Принцип измерения горизонтального угла

Углы обычно измеряют в градусной мере (градусы, минуты, секунды), реже – в радианной. За рубежом широко применяется градовая мера измерения углов.

При геодезических работах измеряют не углы между сторонами на местности, а их ортогональные (горизонтальные) проекции, называемые горизонтальными углами. Так, для измерения угла АВС, стороны которого не лежат в одной плоскости, нужно предварительно спроектировать на горизонтальную плоскость точки А, В, и С (рис. 40) и измерить горизонтальный угол abc = β (рис.39).

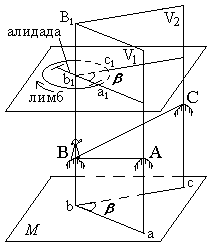
Рис. 40. Принцип измерения горизонтального угла

Рассмотрим двугранный угол между вертикальными плоскостями V₁и V₂ , проходящими через стороны угла АВС. Угол β для данного двугранного угла является линейным. Следовательно, углу β равен всякий другой линейный угол, вершина которого находится в любой точке на отвесном ребре ВВ₁ двугранного угла, а стороны его лежат в плоскости, параллельной плоскости М. Итак, для измерения величины угла abc = β можно в любой точке, лежащей на ребре ВВ₁ двугранного угла, допустим в точке b₁, установить горизонтальный круг с градусными делениями и измерить на нем дугу a₁c₁, заключенную между сторонами двугранного угла, которая и будет градусной мерой углаa₁b₁c₁, равной β , т.е. угол abc = β.

Уровни геодезических инструментов. Назначение, устройство, чувствительность уровней

В геодезических приборах используются цилиндрические и круглые уровни, различающиеся между собой ценой деления, чувствительностью и конструктивными особенностями.

Цилиндрический уровень представляет стеклянную трубку, верхняя внутренняя поверхность которой отшлифована по дуге определенного радиуса (от 3,5 до 80 м). Трубка помещается в металлическую оправу. Для регулировки уровень снабжен исправительным винтом. На наружной поверх-

ности трубки нанесены штрихи. Расстояние между штрихами должно быть 2 мм. Точка в средней части ампулы называется нульпунктом уровня.

Линия касательная к внутренней поверхности уровня в его нультпункте называется осью уровня.

Круглый уровень представляет собой стеклянную ампулу, отшлифованную по внутренней сферической поверхности определенного радиуса. За нуль-пункт круглого уровня принимается центр окружности. Осью кругового уровня является нормаль проходящая через нульпункт, перпендикулярно к плоскости, касательной к внутренней поверхности уровня в его центре.

Для более точного приведения пузырька в нуль-пункт применяются контактные уровни. В них над цилиндрическим уровнем устанавливается призменное оптическое устройство, которое передает изображение концов пузырька в поле зрения трубы. Пузырек находиться в нуль-пункте, если его концы видны совмещенными.

Ценой деления уровня t называется угол, на который наклониться ось уровня, если пузырек сместиться на одно деление ампулы, т.е.

t = l / R или t”=(l/R) r”, где r”=206265″.

В геодезических приборах применяют цилиндрические уровни с ценой деления от 5 до 60″, круглые – от 5 до 20′.

Под чувствительностью уровня понимают минимальное линейное перемещение пузырька, которое можно заметить невооруженным

глазом, обычно принимаемое в 0.1 деления, т.е. 0.2 мм.

План урока №9

Этап 1. Тема урока

Теодолиты .Поверки и юстировки теодолитов. Центрирование теодолитов.

Измерение горизонтальных и вертикальных углов.

Этап II. Цель урока: -дать представление об устройстве теодолита и его поверках. -научиться измерять горизонтальные и вертикальные углы.
Этап III. Тип урока Урок ознакомления с новым материалом

Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Урок №9

Теодолит, его составные части

Измерения горизонтальных проекций углов между линиями местности производят геодезическим угломерным прибором теодолитом. Для этого теодолит имеет горизонтальный угломерный круг с градусными делениями, называемый лимбом. Стороны угла проектируют на лимб с использованием подвижной визирной плоскости зрительной трубы. Она образуется визирной осью трубы при её вращении вокруг горизонтальной оси. Данную плоскость поочередно совмещают со сторонами угла ВА и ВС, последовательно направляя визирную ось зрительной трубы на точки А и С. При помощи специального отсчетного приспособления алидады, которая находится над лимбом соосно с ним и перемещается вместе с визирной плоскостью, на лимбе фиксируют начало и конец дуги a₁c₁ (см. рис. 40), беря отсчеты по градусным делениям. Разность взятых отсчетов является значением измеряемого угла β.

Лимб и алидада, используемые для измерения горизонтальных углов, составляют в теодолите горизонтальный круг. Ось вращения алидады горизонтального круга называют основной осью теодолита.

В теодолите также имеется вертикальный круг с лимбом и алидадой, служащий для измерения вертикальных проекций углов – углов наклона. Принято считать углы наклона выше горизонта положительными, а ниже горизонта – отрицательными. Лимб вертикального круга обычно наглухо скреплён со зрительной трубой и вращается вместе с ней вокруг горизонтальной оси теодолита.

Перед измерением углов центр лимба с помощью отвеса или оптического центрира устанавливают на отвесной линии, проходящей через вершину измеряемого угла, а плоскость лимба приводят в горизонтальное положение, используя с этой целью три подъемных винта 3 и цилиндрический уровень 12 (рис. 41). В результате данных действий основная ось теодолита должна совпасть с отвесной линией, проходящей через вершину измеряемого угла.

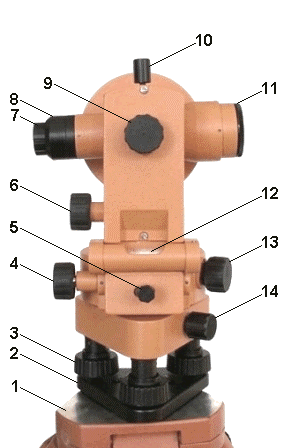
Рис. 41. Устройство теодолита 4Т30П:
1 – головка штатива; 2 – основание; 3 – подъемный винт; 4 – наводящий винт алидады; 5 – закрепительный винт алидады; 6 – наводящий винт зрительной трубы; 7 – окуляр зрительной трубы; 8 – предохранительный колпачок сетки нитей зрительной трубы; 9 – кремальера; 10 – закрепительный винт зрительной трубы; 11 – объектив зрительной трубы; 12 – цилиндрический уровень; 13 – кнопочный винт для поворота лимба; 14 – закрепительный винт; 15 – окуляр отсчетного микроскопа с диоптрийным кольцом; 16 – зеркальце для подсветки штрихов отсчетного микроскопа; 17– колонка; 18 – ориентир-буссоль; 19 – вертикальный круг; 20 – визир; 21 – диоптрийное кольцо окуляра зрительной трубы; 22 – исправительные винты цилиндрического уровня; 23 – подставка.

Для установки, настройки и наведения теодолита на цели в нем имеется система винтов: становой и подъемные винты, закрепительные (зажимные) и наводящие (микрометренные) винты, исправительные (юстировочные) винты.

Становым винтом теодолит крепят к головке штатива, подъемными винтами – горизонтируют.

Закрепительными винтами скрепляют подвижные части теодолита (лимб, алидаду, зрительную трубу) с неподвижными. Наводящими винтами сообщают малое и плавное вращение закрепленным частям.

Чтобы теодолит обеспечивал получение неискаженных результатов измерений, он должен удовлетворять соответствующим геометрическим и оптико-механическим условиям. Действия, связанные с проверкой этих условий, называют поверками. Если какое-либо условие не соблюдается, с помощью исправительных винтов производят юстировку прибора.

Основные узлы теодолита

Отсчетные приспособления

Отсчетные приспособления служат для отсчитывания делений лимба и оценки их долей. Они делятся на штриховые (теодолит Т30) и шкаловые (2Т30, Т5, 2Т5) микроскопы (рис.42) и микрометры (теодолит Т2). Угловая цена деления лимба называется ценой деления лимба.

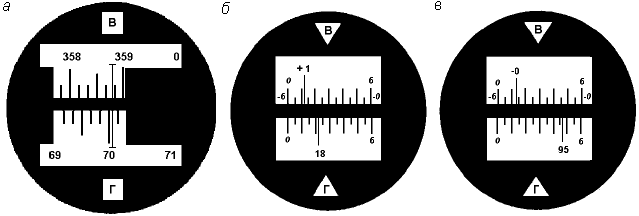
Рис.42. Поле зрения отсчетных устройств:
штрихового микроскопа с отсчетами по вертикальному кругу – 358° 48′ , по горизонтальному – 70° 04′ (а); шкалового микроскопа с отсчетами: по вертикальному кругу – 1° 11,5′, по горизонтальному – 18° 22′ (б); по вертикальному кругу – -0° 46,5′, по горизонтальному – 95° 47′ (в).

В штриховом микроскопе теодолита Т30 в середине поля зрения виден штрих, относительно которого осуществляется отсчет по лимбу (рис. 42, а). Перед отсчетом по лимбу необходимо определить цену деления лимба. В теодолите Т30 цена деления лимба составляет 10 угловых минут, т.к. градус разделен на шесть частей. Число минут оценивается на глаз в десятых долях цены деления лимба. Точность отсчета составляет 1′.

В шкаловом микроскопе теодолита 2Т30 в поле зрения видна шкала, размер которой соответствует цене деления лимба (рис. 42, б, в). Для теодолита технической точности размер шкалы и цена деления лимба равны 60′. Шкала разделена на двенадцать частей и цена ее деления составляет 5 угловых минут. Если перед числом градусов знака минус нет, отсчет производится по шкале от 0 до 6 в направлении слева направо (рис.42, б). Если перед числом градусов стоит знак минус, в этом случае минуты отсчитываются по шкале вертикального круга, где перед цифрами от 0 до 6 стоит знак минус в направлении справа налево (рис.42, в). Десятые доли цены деления шкалы берутся на глаз с точностью до 30”.

Уровни

Уровни служат для приведения отдельных осей и плоскостей геодезических приборов в горизонтальное или вертикальное положение. Они состоят из ампулы, оправы и регулировочного приспособления.

В зависимости от формы ампулы уровни бывают цилиндрические и круглые. Ампулу цилиндрического уровня, внутренняя поверхность которой отшлифована по дуге круга радиуса R, заполняют нагретым серным эфиром или спиртом и запаивают. Свободную от жидкости часть ампулы, заполненную парами жидкости, называют пузырьком уровня. На внешней поверхности рабочей части такой ампулы через 2 мм нанесены штрихи. Точка, соответствующая средней части центрального деления ампулы, называется нуль-пунктом уровня.

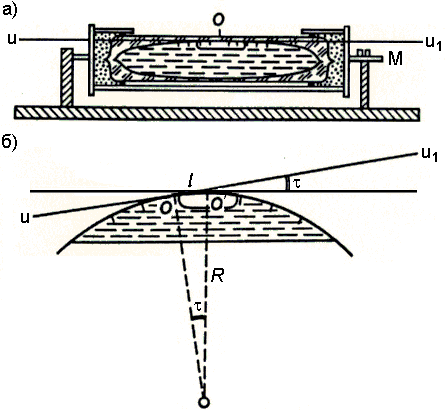
Рис. 43. Цилиндрический уровень

Прямая uu₁ – касательная к внутренней поверхности ампулы в нуль-пункту О, называется осью цилиндрического уровня (рис. 43). При любом положении ампулы уровня его пузырек будет всегда занимать наивысшее положение, а касательная, проведенная к самой высокой точке О‘ пузырька, будет горизонтальна. Если совместить точки О и О‘, то ось цилиндрического уровня тоже займет горизонтальное положение.

Центральный угол τ соответствующий одному делению ампулы, определяет чувствительность уровня, т.е. способность пузырька быстро и точно занимать в ампуле наивысшее положение. Величину этого угла называют ценой деления уровня и рассчитывают по формуле

τ = ρ” ∙ l / R ,

где R – радиус внутренней поверхности ампулы, мм; ρ” – величина радиана в секундах; l – длина деления ампулы, мм.

Чем больше R, тем меньше цена одного деления и тем точнее уровень. У точных теодолитов цена деления уровня колеблется в пределах 15 – 40″ на 2 мм, а у технических – в пределах 45 – 60″ на 2 мм.

ПОВЕРКИ И ЮСТИРОВКИ ТЕОДОЛИТОВ

До начала работы с теодолитом внешним осмотром проверяют его устойчивость на штативе, плавность хода подъемных и наводящих винтов, прочность фиксации вращающихся частей закрепительными винтами.

Если теодолит получен с завода, после ремонта, от другого специалиста, до ввода теодолита в эксплуатацию выполняют поверки. В процессе поверок удостоверяются в правильном взаимном положении осей прибора (рис. 8.11, а).

1. Ось UU цилиндрического уровня горизонтального круга должна быть перпендикулярна оси VV вращения прибора (рис. 8.11,6).

Поверку выполняют в такой последовательности. Теодолит устанавливают на штативе так, чтобы уровень был расположен по направлению двух любых подъемных винтов и, вращая их в разные стороны, приводят пузырек уровня в нуль-пункт, затем поворачивают горизонтальный круг теодолита на 180°. Если пузырек остался на середине или отклонился не более чем на одно деление, уровень исправен, если более чем на одно деление — неисправен.

Для устранения неисправности пузырек перемещают исправительными винтами уровня к нуль-пункту на одну половину дуги отклонения, подъемными винтами — на вторую.

После выполнения поверки удостоверяются, что теодолит сохраняет рабочее положение. Для этого горизонтальный круг поворачивают на 90°, приводят пузырек цилиндрического уровня на середину и поворачивают горизонтальный круг в произвольном направлении. Если при различных положениях круга относительно подъемных винтов пузырек остался на середине, поверка считается выполненной.

2. Визирная ось РР трубы должна быть перпендикулярна оси ННвращения трубы (рис. 8.11, в).

Поверку выполняют в такой последовательности. Вертикальную ось теодолита приводят в отвесное положение. Для этого сначала устанавливают уровень теодолита по направлению двух подъемных винтов и, вращая их в разные стороны, приводят пузырек на середину ампулы. Поворачивают теодолит на 90° и вращением третьего подъемного винта приводят пузырек снова на середину. Наводят трубу на удаленную, ясно видимую точку, закрепляют лимб и берут отсчет а₁ по горизонтальному кругу. Отпускают зажимной винт зрительной трубы и переводят трубу через зенит. Открепляют зажимной винт алидады и, наводя трубу на ту же точку, берут повторный отсчет а₂. Если отсчеты а₁ и а₂ равны или отличаются не более чем на двойную точность отсчетного устройства, теодолит исправен, если больше — неисправен.

Чтобы устранить неисправность, из отсчетов a₁ и а₂ находят среднее значение: a=(a₁+a₂)/2. Микрометренным винтом устанавливают на горизонтальном круге средний отсчет а (изображение точки сместится от вертикальной нити). Снимают с окулярного колена трубы колпачок, ослабляют вертикально расположенные винты и вращением боковых исправительных винтов смещают сетку до совпадения перекрестия сетки нитей с точкой визирования. После юстировки закрепляют винты.

Можно измерять угол и при нарушенном соотношении осей. В этом случае отсчеты берут при двух положениях трубы — левом и правом (Л и П) и из этих отсчетов определяют среднее.

3. Ось НН вращения трубы должна быть перпендикулярна осиVV вращения прибора (рис. 8.11, г).

Поверку выполняют в такой последовательности. Теодолит устанавливают на расстоянии 8…10 м от стены здания. Вертикальную ось вращения приводят в отвесное положение. Трубу наводят на точку, высоко расположенную на здании, и закрепляют горизонтальный круг. Трубу плавно опускают до горизонтального положения. На стене отмечают проекцию точки. Переводят трубу через зенит, опускают закрепительный винт алидады и снова наводят на ту же точку. Проецируют точку на тот же уровень и закрепляют. Если проекции точки совпадают, теодолит исправен, если не совпадают — неисправен.

Условия этой поверки гарантируются заводом-изготовителем. При нарушении условия прибор направляют в мастерскую для ремонта.

При работе с нарушенным соотношением осей выполняют следующее. Измерения делают только при двух положениях круга. При подъеме трубы до 30° и расстоянии до проектируемой точки до 20 м допускается несовпадение проекций до 30 мм; за окончательный результат принимают среднее из двух наведении.

4. Вертикальная нить АА сетки зрительной трубы должна быть перпендикулярна оси НН ее вращения (рис. 8.11, д).

Поверку выполняют в такой последовательности. Вертикальную ось вращения теодолита приводят в отвесное положение. На расстоянии 8…10 м от теодолита закрепляют отвес. Вертикальную нить наводят на отвес. Если вертикальная нить сетки совпадает с нитью отвеса, теодолит исправен, если отклонилась от отвеса — неисправен.

Чтобы исправить соотношение осей, снимают с окулярного колена трубы колпачок, ослабляют исправительные винты сетки и поворачивают диафрагму так, чтобы вертикальная нить сетки совместилась с нитью отвеса.

При нарушении условия поверки визируют только перекрестием сетки нитей.

После выполнения этой поверки повторно делают вторую поверку.

5. Компенсатор вертикального круга должен обеспечивать неизменный отсчет по вертикальному кругу при наклонах вертикальной оси теодолита в пределах +2′ (для теодолитов ЗТ5К).

Поверку выполняют в такой последовательности. Вертикальную ось вращения теодолита приводят в отвесное положение, расположив один из подъемных винтов в направлении выбранной точки местности. Трубу наводят на точку, расположенную на расстоянии 50 м, и закрепляют закрепительными винтами, наклоняют теодолит на 3…4 деления уровня, вновь наводят трубу на ту же точку и делают отсчет по вертикальному кругу. Повторяют те же действия, наклонив теодолит на 3…4 деления уровня в другую сторону. Если разность отсчетов, полученных при первом и втором наклонах теодолита, не превышает ±0,Г, то теодолит исправен, если превышает — неисправен.

При нарушении этого условия работать нельзя, теодолит направляют в оптико-механическую мастерскую для исправления.

6. Визирная ось KK’K” оптического отвеса должна совпадать с осью К’К” вращения теодолита, т. е. VV (рук:. 8.11, е).

Поверку выполняют в такой последовательности. Вертикальную ось вращения теодолита приводят в отвесное положение. Отмечают на местности точку, в которую проецируется наблюдаемый в окуляр центр отвеса. Повернув теодолит на 180°, снова отмечают проекцию центра отвеса. Если проекции точек совпадают до 1 мм, теодолит исправен, если не совпадают до 1 мм — неисправен.

Чтобы устранить неисправность, снимают крышку, под которой расположены два винта, скрепляющие отвес с теодолитом, отпускают винты и передвигают окулярную часть до совмещения проекций первой и второй точек. Нельзя выполнять работы при несовпадении проекций центра отвеса свыше 3 мм; теодолит в этом случае отправляют в ремонт.

Вопросы для самоконтроля

1. Назначение теодолита.

2. Основные части теодолита.

3. Какие бывают отсчетные приспособления в теодолитах?

4. Назначение цилиндрического уровня при алидаде горизонтального круга.

5. Назначение зрительной трубы теодолита.

6. Характеристики зрительной трубы.

7. Какие установки зрительной трубы при наблюдениях?

План урока №10

Этап 1. Тема урока

Измерение длины линий мерными приборами.

Измерение длины линий дальномерами.

Этап II. Цель урока: -дать представление об измерении длины линий мерными приборами. -научиться измерять длину линий
ЭТАП III. Тип урока Урок ознакомления с новым материалом
Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Урок №10

Приборы непосредственного измерения линий

Для измерения длин линий посредством откладывания мерного прибора используют стальные мерные ленты, которые обычно изготавливают из ленточной углеродистой стали. В геодезической практике чаще всего применяются штриховые и шкаловые ленты.

Штриховые ленты (рис. 47, а) имеют длину 20 и 24 м, ширину 15 – 20 мм и толщину 0,3 – 0,4 мм.

Рис. 47. Мерные ленты.

На ленте нанесены метровые деления, обозначенные прикрепленными бляшками, и дециметровые деления, обозначенные отверстиями. Метровые деления на обеих сторонах оцифрованы. Счет оцифровки делений ведется на одной стороне от одного конца ленты, а на другом – от другого конца. За длину ленты принимают расстояние между штрихами, нанесенными на крюках у концов ленты. К крюкам приделаны ручки. К ленте прилагается 6 или 11 шпилек на кольце. Шпильки сделаны из стальной проволоки диаметром 5 – 6 мм и длиной 30 – 40 см в нерабочем положении ленту наматывают на кольцо (рис. 47, в).

Шкаловая лента (рис.47, б) выпускается длиной 20 – 24 м, шириной 6 – 10 мм и толщиной 0,15 – 0, 20 мм. На обоих концах ленты, в пределах второго дециметра, имеются миллиметровые шкалы длиной по 100 мм каждая.

Для измерения небольших расстояний применяют стальные и тесьмяные рулетки длиной 5, 10, 20, 50 м.

Компарирование мерных лент и рулеток

Мерные ленты и рулетки перед измерением ими линий должны быть проверены. Данная проверка называется компарированием и состоит в установлении действительной длины мерного прибора путем его сравнения с образцовым прибором, длина которого точно известна.

Для компарирования штриховых лент за образцовый мерный прибор принимают одну из лент, имеющихся на производстве, длину которой выверяют в лаборатории Государственного надзора за стандартами и измерительной техникой Государственного комитета стандартов РФ и пользуются ею при сравнении с рабочими лентами. Компарирование шкаловых лент производят на специальных приборах, называемых стационарными компараторами.

Простейший способ компарирования штриховых лент состоит в следующем. На горизонтальной поверхности, например, на полу, укладывают образцовую ленту. Рядом с ней кладут проверяемую ленту так, чтобы их края касались друг друга, а нулевые штрихи совмещались. Жестко закрепив концы с нулевыми штрихами, ленты натягивают с одинаковой силой и измеряют миллиметровой линейкой величину несовпадения конечных штрихов на других концах лент. Данная величина показывает на сколько миллиметров рабочая лента короче или длиннее образцовой и называется поправкой за компарирование Δℓ.

Длина проверяемой 20-метровой ленты не должна отличаться от длины образцовой ленты более чем на ±2 мм. В противном случае в результаты измерения линий вводят поправки. При этом, выполняя измерения линий рабочей лентой, полагают, что её длина равняется 20 м. Поправки определяют по формуле

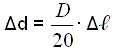
где D – длина измеренной линии.

Поправку вычитают из результатов измерения, когда рабочая лента короче образцовой, и прибавляют, когда она длиннее.

Порядок измерения линий штриховой лентой

Измерение линий на местности штриховыми лентами производят двое рабочих. По направлению измерения один из них считается задним, второй – передним. Ленту аккуратно разматывают с кольца. Её оцифровка должна возрастать по ходу измерения. Для закрепления мерной ленты в створе линии используется 6 шпилек. Перед началом измерения 5 шпилек берет передний мерщик и одну – задний. Задний мерщик совмещает с началом линии нулевой штрих ленты. Используя прорезь в ленте, закрепляет шпилькой её конец рядом с колышком, обозначающим начальную точку линии (рис. 49, а).

Передний мерщик, имея в руке 5 шпилек, по указанию заднего мерщика, встряхнув ленту, натягивает её в створе линии и фиксирует первой шпилькой передний конец ленты. Затем задний мерщик вынимает свою шпильку из земли, вешает её на кольцо, и оба мерщика переносят ленту вперед вдоль линии. Дойдя до воткнутой в землю передним мерщиком шпильки, задний мерщик закрепляет на ней свой конец ленты, а передний, натянув ленту, закрепляет её передний конец следующей шпилькой (рис. 49, б). В таком порядке мерщики укладывают ленту в створе линии 5 раз.

После того как передний мерщик зафиксирует пятой шпилькой свой конец ленты, задний мерщик передает ему кольцо с пятью шпильками, которые он собрал в процессе измерения (рис. 49, в). Число таких передач (т.е. отрезков по 100 м при длине ленты в 20 м) записывают в журнале измерений. Последний измеряемый остаток линии обычно меньше полной длины ленты. При определении его длины метры и дециметры отсчитывают по ленте, а сантиметры оценивают на глаз (рис. 49, е).

Рис. 49. Измерение линии мерной лентой

Измеренная длина линии D вычисляется по формуле :

D = 100 · a + 20 · b + c,

где a – число передач шпилек;

b – число шпилек у заднего мерщика на кольце;

c – остаток.

Для контроля линию измеряют вторично 24-метровой или той же 20-метровой в обратном направлении. За окончательный результат принимают среднее арифметическое из двух измерений, если их расхождение не превышает:

– 1/3000 части от длины линии при благоприятных условиях измерений;

– 1/2000 – средних условиях измерений;

– 1/1000 – неблагоприятных условиях измерений.

Т.е. допускаются абсолютные ошибки на 100 м длины линии 3 см, 5 см и 10 см.

Косвенные измерения длин линий

При измерении расстояний лентой или рулеткой встречаются случаи, когда местное препятствие (река, овраг, здание, дорога и т.п.) делает непосредственное измерение невозможным. Тогда применяют косвенные методы определения расстояний.

Различают три случая определения недоступных расстояний.

1. При взаимной видимости точек разбивают базис b и измеряют горизонтальные углы и (рис. 51).

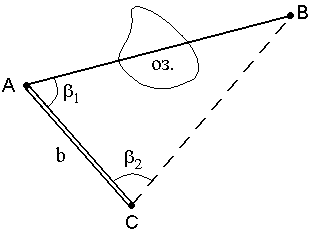
Рис. 51. Косвенное измерение расстояния через озеро

Для определения расстояния АВ используют теорему синусов

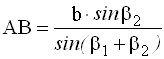
2. При взаимной невидимости точек (рис. 52) выбирают точку С из которой видны точки А и В, измеряют расстояния S₁, S₂и угол .

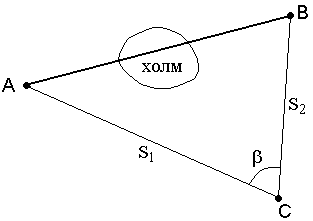
Рис. 52. Косвенное измерение расстояния через

Используя теорему косинусов, находят расстояние АВ

3. Если обе точки измеряемого расстояния недоступны, то разбивают базис b и из точек С и Д измеряют углы

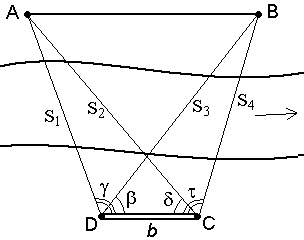
Рис. 53. Косвенное измерение расстояний если недоступны обе точки

По теореме синусов дважды для контроля находят с контролем расстояние АВ.

Вопросы для самоконтроля

1. Что называется вешением линии?

2. Что такое створ линии?

3. Какие приборы применяются для непосредственного измерения расстояний?

4. Что такое компарирование мерных приборов?

5. Как измеряются линии стальной мерной штриховой лентой?

6. Как приводятся наклонные расстояния к горизонту?

7. От чего зависит точность измерения линии мерной лентой?

План урока №11

Этап 1. Тема урока

Сущность и методы измерения превышений. Геометрическое нивелирование.

Нивелиры и их устройство. Лазерный нивелир. Нивелирная рейка.

Этап II. Цель урока: -дать представление о геометрическом нивелировании. – рассказать об устройстве нивелиров
ЭТАП III. Тип урока Урок ознакомления с новым материалом
Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Урока№11

Сущность и методы измерения превышений

Нивелированием называется совокупность геодезических измерений для определения превышений между точками, а также их высот.

Нивелирование производят для изучения рельефа, определения высот точек при проектировании, строительстве и эксплуатации различных инженерных сооружений. Результаты нивелирования имеют большое значение для решения научных задач как самой геодезии, так и для других наук о Земле.

В зависимости от применяемых приборов и измеряемых величин нивелирование делится на несколько видов.

1. Геометрическое нивелирование – определение превышения одной точки над другой посредством горизонтального визирного луча. Осуществляют его обычно с помощью нивелиров, но можно использовать и другие приборы, позволяющие получать горизонтальный луч.

2. Тригонометрическое нивелирование – определение превышений с помощью наклонного визирного луча. Превышение при этом определяют как функцию измеренного расстояния и угла наклона, для измерения которых используют соответствующие геодезические приборы (тахеометр, кипрегель).

3. Барометрическое нивелирование – в его основу положена зависимость между атмосферным давлением и высотой точек на местности.

4. Гидростатическое нивелирование – определение превышений основывается на свойстве жидкости в сообщающихся сосудах всегда находиться на одном уровне, независимо от высоты точек, на которых установлены сосуды.

5. Аэрорадионивелирование – превышения определяются путем измерения высот полета летательного аппарата радиовысотомером.

6. Механическое нивелирование – выполняется с помощью приборов, устанавливаемых в путеизмерительных вагонах, тележках, автомобилях, которые при движении вычерчивают профиль пройденного пути. Такие приборы называются профилографы.

7. Стереофотограмметрическое нивелирование основано на определении превышения по паре фотоснимков одной и той же местности, полученных из двух точек базиса фотографирования.

8. Определение превышений по результатам спутниковых измерений. Использование спутниковой системы ГЛОНАСС – Глобальная Навигационная Спутниковая Система позволяет определять пространственные координаты точек.

Классификация нивелиров

Согласно действующему ГОСТу 10528-90 [9] нивелиры изготавливают трёх типов: высокоточные Н-05, точные Н-3 (Н-3К, Н-3КЛ) и технические Н-5 (Н-5К и Н-5КЛ).

В названии Н – нивелир; 05, 3 и 5 – средняя квадратическая ошибка измерения превышения в миллиметрах на 1 км двойного нивелирного хода; К – компенсатор; Л – лимб.

В зависимости от того, каким способом визирный луч устанавливается в горизонтальное положение, нивелиры изготавливают в двух исполнениях:

– с цилиндрическим уровнем при зрительной трубе, с помощью у которого осуществляется горизонтирование визирного луча (рис. 63);

– с компенсатором – свободно подвешенная оптико-механическая система, которая приводит визирный луч в горизонтальное положение. В названии нивелира буква К обозначает компенсатор (Н-3К, Н-3КЛ)(рис. 64).

Н-3

Рис. 63. Точный нивелир Н-3 с цилиндрическим уровнем при зрительной трубе: 1 – подъемные винты; 2 – круглый уровень; 3 – элевационный винт; 4 – окуляр зрительной трубы с диоптрийным кольцом; 5 – визир; 6 – кремальера; 7 – объектив зрительной трубы; 8 – закрепительный винт; 9 – наводящий винт; 10 – контактный цилиндрический уровень; 11 – юстировочные винты цилиндрического уровня

Схема горизонтирования визирного луча в нивелире с компенсатором

ЗН-3КЛ

Рис. 65. Точный нивелир ЗН-3КЛ с компенсатором и лимбом: 1 – лимб; 2 – наводящий винт; 3 – кремальера; 4 – визир.

Точные нивелиры Н-3 и 3Н-3КЛ предназначены для нивелирования III и IV классов.

3Н-5КЛ

Рис. 65. Технический нивелир 3Н-5КЛ

Техническими нивелирами выполняют техническое нивелирование для определения высот точек высотного съемочного обоснования и при решении различных инженерно-технических задач при изыскании, строительстве и эксплуатации линейных сооружений и промышленно-гражданском строительстве.

Лазерный нивелир

Нивелирные рейки

Нивелирные рейки для нивелирования III – IV класса и технического изготавливают из деревянных брусьев двутаврового сечения шириной 8 – 10 и толщиной 2 – 3 см.

Рейка РН-3 (рис. 66) имеет длину 3 м. Деления нанесены через 1 см. Нижняя часть рейки заключена в металлическую оковку и называется пяткой.

Основная шкала имеет деления черного и белого цвета, ноль совмещен с пяткой рейки. Дополнительная шкала на другой стороне рейки имеет чередующиеся красные и белые деления. С пяткой рейки совмещен отсчет больше 4000 мм. Часто встречаются комплекты реек, у которых с пятками красных сторон совпадают отсчеты 4687 и 4787 мм. Поэтому превышения, измеренные по красным сторонам реек, будут больше или меньше на 100 мм измеренных по черным сторонам реек.

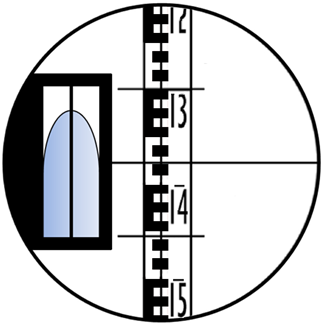
Рис. 66. Нивелирная рейка (а) и поле зрения зрительной трубы нивелира с цилиндрическим уровнем (б)

Вопросы для самоконтроля

1. Что называется нивелированием?

2. Назовите виды нивелирования?

3. Назовите способы геометрического нивелирования?

4. В чем заключается способ нивелирования из середины и вперед?

5. В чем сущность последовательного нивелирования?

6. В чем сущность тригонометрического, барометрического и гидростатического нивелирования?

7. Как нивелиры классифицируются по точности?

План урока №12

Этап 1. Тема урока

Поверки и юстировки нивелиров. Тригонометрическое нивелирование. Барометрическое нивелирование. Гидростатическое нивелирование.

Производство геометрического нивелирования.

Нивелирование по квадратам
Этап II. Цель урока: -дать представление о поверках и юстировках нивелиров – рассказать о способах нивелирования
ЭТАП III. Тип урока Урок ознакомления с новым материалом
Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Этап VI. Ход урок -организационный момент – актуализация знаний учащихся по теме. –изучение темы –закрепление темы – подведение итогов -домашнее задание

Урок №12

Поверки и юстировки нивелиров.

Прежде чем начать работу с нивелиром, как и с любым геодезическим прибором, его осматривают.

Если при внешнем осмотре нивелира повреждения не обнаружены, приступают к поверкам. Поверки- это действия, которыми контролируют правильность взаимного расположения основных осей прибора, если при выполнении поверок обнаруживается

несоответствие взаимного расположения частей прибора, его юстируют исправительными винтами.

Рассмотрим, какие поверки выполняют при подготовке нивелира с цилиндрическими уровнями к работе.

1. Ось круглого уровня UU должна быть параллельна оси вращения JJ нивелирования (рис. 7.14, а).

Чтобы проверить параллельность осей, выполняют следующие действия: пузырек круглого уровня приводят подъемными винтами на середину; верхнюю часть нивелира поворачивают на 180°. Нивелир считается исправным, если пузырек остался в центре, неисправным, если пузырек сместился.

Для устранения этой неисправности нивелир приводят в отвесное положение, перемещая пузырек к центру на первую половину дуги отклонения исправительными винтами уровня, на вторую половину – подъемными винтами.

2. Горизонтальная нить АА сетки должна быть перпендикулярна оси вращения JJ нивелира (рис. 7.14, б).

Это условие гарантируется заводом-изготовителем прибора, но небольшое исправление и доводка могут быть выполнены исполнителем.

Поверку выполняют в такой последовательности: ось вращения нивелира приводят по круглому уровню в отвесное положение; на расстоянии 20…30 м от нивелира устанавливают рейку и берут отсчет; наводят левый конец средней горизонтальной нити на рейку и берут отсчет, перемещают винтом трубу в горизонтальной плоскости до пересечения правого конца средней горизонтальной нити и берут отсчет. Если нивелир исправен, отсчет по рейке не изменится или изменится в пределах 1 мм, если неисправен – изменится более чем на 1 мм.

Чтобы устранить неисправность, ослабляют исправительные винты сетки и развертывают диафрагму с сеткой нитей за счет люфта винтов.

3. Визирная ось VV зрительной трубы должна быть параллельна оси UU цилиндрического уровня (рис. 7.14, в, г).

Последовательность выполнения поверки: на местности выбирают две точки А и В с расстоянием между ними 70…80 м; точки закрепляют кольями, нивелир устанавливают в точке С1 и берут отсчеты a1, b1 по рейкам. После этого вычисляют превышение h1 = a1 – b1. Далее нивелир устанавливают в точке С2 на расстоянии 3…5 м от одной из реек, по рейкам берут отсчеты а2 и b2 и вычисляют превышение h2=a2-b2.

При равенстве превышений или разнице между ними менее 4 мм нивелир пригоден к эксплуатации. Если разница превышений больше 4 мм, вычисляют правильный отсчет по дальней рейке a2=b2+h1.

Горизонтальную нить сетки наводят винтом на этот отсчет (при этом пузырек отклонится от середины). Ослабляют боковые исправительные винты уровня и возвращают вертикальными винтами пузырек уровня на середину, или смещают сетку нитей ее исправительными винтами. У самоустанавливающихся нивелиров устанавливают горизонтальную нить сетки на правильный отсчет с помощью исправительных винтов сетки нитей.

Способы геометрического нивелирования

Геометрическое нивелирование – это наиболее распространенный способ определения превышений. Его выполняют с помощью нивелира, задающего горизонтальную линию визирования.

Устройство нивелира достаточно простое. Он имеет две основные части: зрительную трубу и устройство, позволяющее привести визирный луч в горизонтальное положение.

Геометрическое нивелирование можно выполнять по следующей схеме:

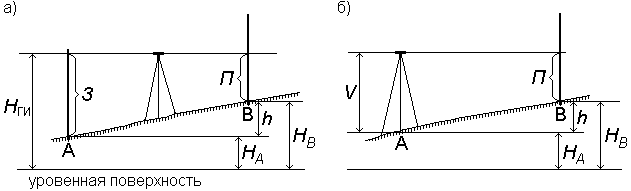
Рис. 61. Способы нивелирования

При нивелировании из середины нивелир располагают между двумя точками примерно на одинаковых расстояниях (рис.61, а). В точках устанавливают отвесно рейки с сантиметровыми делениями. Их ставят на колышек, вбитый вровень с землей, или на специальный костыль, так как рейка под собственной тяжестью будет давить на землю и отсчет по ней будет меняться. Визирный луч зрительной трубы нивелира последовательно наводят на рейки и берут отсчеты З и П, которые записывают в миллиметрах в журнал нивелирования. Отсчет по рейке производят по средней нити нивелира, т.е. по месту, где проекция средней нити пересекает рейку. Превышение между точками определяют по формуле

h = З – П

где З – отсчет назад на заднюю точку А; П – отсчет вперед на переднюю точку B.

При нивелировании вперед прибор устанавливают над точкой А (рис. 61, б), измеряют его высоту V и берут отсчет П по рейке в точке В. Превышение определяют вычитанием из высоты прибора V отсчета П.

h = V – П.

Высоту передней точки В вычисляется по формуле:

Высоту визирного луча на уровенной поверхностью называют горизонтом инструмента H_ГИ (рис. 61) и вычисляют

Н_ГИ = Н_А + З = Н_А + V.

Место установки нивелира называется станцией. Если для определения превышения между точками А и В достаточно установить прибор один раз, то такой случай называется простым нивелированием.

Если же превышение между точками определяют только после нескольких установок нивелира, такое нивелирование называют сложным или последовательным (рис. 62).

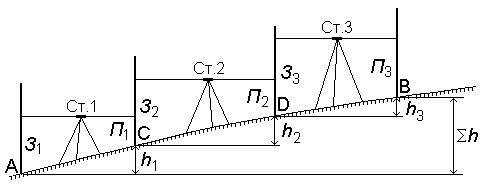
Рис. 62. Последовательное нивелирование.

В этом случае точки С и D называют связующими. Превышение между ними определяют как при простом нивелировании:

; ;

h = ∑З – ∑П

Такую схему нивелирования называют нивелирным ходом.

План урока №13

Этап 1. Тема урока

Лазерные геодезические приборы. Электронные приборы и теодолиты.

Приборы вертикального проектирования. Использование спутниковых технологий в инженерной геодезии.

Геодезические сети. Общие сведения о геодезических сетях. Плановые геодезические сети. Высотные геодезические сети.

Топографические съемки.

Этап II. Цель урока: -дать представление об лазерных геодезических приборах. -рассказать о геодезических сетях – научиться производить топографическую съемку
ЭТАП III. Тип урока Урок ознакомления с новым материалом
Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Урок №13

Лазерные геодезические приборы

В лазерных геодезических приборах в качестве излучателя светового потока используют оптические квантовые генераторы (ОКГ).

Оптические квантовые генераторы (лазеры) бывают: твердотельные, газовые, жидкостные и полупроводниковые. В геодезических приборах используют газовые и полупроводниковые лазеры. Газовые лазеры применяют в приборах, задающих положение вертикальной или горизонтальной опорной линии: лазерных нивелирах, указателях направлений, лазерных центрирах и других приборах различного назначения. В практике геодезического обеспечения строительства используют газовые гелий-неоновые лазеры непрерывного излучения, работающие в видимой части светового диапазона и излучающие узконаправленный пурпурно-красный пучок света. Полупроводниковые лазеры применяют в основном в приборах для измерения расстояний — свето-дальномерах.

Лазерные геодезические приборы конструируют таким образом, чтобы лазер был установлен параллельно визирной оси прибора, на котором он смонтирован, или лазерный пучок направлялся бы через зрительную трубу прибора. Как правило, при измерениях используют визуальную или фотоэлектрическую индикацию лазерного пучка. При визуальной индикации для отсчетов по лучу применяют экран в виде сетки квадратов или концентрических окружностей, а также нивелирную рейку. При более точной фотоэлектрической индикации используют специальные фотоприемные устройства с фотоэлементами.

Рассмотрим некоторые типы известных лазерных приборов, применяемых в строительстве.

Лазерные нивелиры предназначены для измерения превышений и передачи высотных отметок. Нивелир излучает видимый пучок света, относительно которого производят измерения превышений. В одних приборах пучок лазерного излучения направляют по оптической оси зрительной трубы, в других зрительная труба соединена параллельно с излучателем О КГ.

В нивелирах с уровнем ось пучка приводят в горизонтальное положение цилиндрическим уровнем, а в нивелирах-автоматах — компенсатором. По условиям геометрического нивелирования оси лазерного пучка и цилиндрического уровня должны быть параллельны.

В настоящее время лазерные нивелиры выпускают в основном с автоматически горизонтирующимся пучком излучения, вращающимся лазерным пучком и другими особенностями.

Многоцелевые приборы, предназначенные для контрольно-измерительных операций при установке конструкций, опалубки, выемке грунта, устройстве земляного полотна, укладке бетона, совмещают в себе визирную оптическую трубу и установленный на нее квантовый генератор. Рассмотрим некоторые из этих приборов.

Конструкция штатива позволяет в широких пределах изменять высоту ПГЛ-1 над местностью. Угол сканирования (поворота)

Прибор задания вертикали ПВЗЛ-1 имеет передающую и приемную части. Передающая часть включает в себя: лазерный передатчик в виде цилиндра диаметром 120 мм и длиной 382 мм (масса 3,1 кг), горизонтирующее устройство и автономный блок питания размерами 200 х 106 х 138 (масса 2,6 кг) на гальванических элементах. Световой пучок попадает в насадку и, проходя через пентапризму (пятиугольную стеклянную призму), изменяет направление с горизонтального на вертикальное.

Насадка с пентапризмой съемная, что позволяет использовать ^лУч прибора в горизонтальной плоскости. Приемная часть состоит из регистратора и фотомишени, перемещающейся по взаимно-перпендикулярным измерительным линейкам.

Лазерный передатчик устанавливают на исходном горизонте по уровням, что формирует в пространстве вертикальную световую линию. Фотомишень с регистратором размещают на монтажном горизонте и по линейкам перемещают до совмещения с центром проекции лазерного пучка. При совмещении показания индикаторов регистратора будут нулевыми. Возможные отклонения от задаваемой вертикали считывают по линейкам фотомишени. Дальность действия прибора с фотоэлектрической регистрацией составляет 20 м, погрешность измерения отклонения объекта от задаваемой вертикали — 1 мм, а задания вертикали — 2 мм. Некоторые типы лазерных приборов устроены так, что испускаемый луч направляется вертикально вверх, и тогда с помощью насадки с пентапризмой при необходимости изменяют его направление на горизонтальное.

Особую группу приборов составляют лазерные указки. К ним относятся лазерные указки укладки труб, визирования, вертикали и др.

Так, лазерная указка укладки труб состоит из корпуса, на одном конце которого прикреплена горизонтирующая основа. В ней устроены оправа с лазером, уровень и шкала уклонов, что позволяет направлять луч под заданным углом к горизонту. Погрешность задания уклона составляет не более ±10 мм на 100 м длины.

Лазерные указки просты в обращении, дешевы в изготовлении, имеют автономное питание (12 В) от батареек для карманных фонарей, могут включаться и выключаться с помощью дистанционного управления.

Применение лазерных указок повышает производительность труда пользователей на 50 %, машин и механизмов — на 10 %.

Геодезические сети

Геодезические измерения сводятся к определению взаимного положения точек на земной поверхности. Чтобы ослабить влияние ошибок измерений и не допустить их накопления при геодезической съемке участков местности, принято за правило вести работу от общего к частному. Для этого из множества определяемых точек участка земной поверхности выделяют наиболее характерные и определяют в первую очередь их положение. Такие точки называют опорными. Эти точки образуют геодезическую опорную сеть (геодезическое основание), т.е. составляют как бы общую канву, на основе которой с необходимой, хотя и более низкой точностью производится дальнейшая съемка.

Для того, чтобы результаты съемок были надежны, все важнейшие геодезические действия должны выполняться с контролем. Поэтому в основе качества геодезических работ лежит принцип ни одного шага вперед без контроля предыдущих действий.

Назначение и виды государственных геодезических сетей

С 1919 года в нашей стране было положено начало научно-обоснованной организации всех топографо-геодезических работ. Исполнительные, контрольные, разрешительные и надзорные функции при их производстве были объединены в Высшем геодезическом управлении (ВГУ). В последствии оно было преобразовано в Главное управление геодезии и картографии. С 1 марта 2009 года эти функции переданы Федеральной службе государственной регистрации, кадастра и картографии.

Одной из важнейших задач данного государственного органа является создание государственной геодезической сети (ГГС) на территории нашей страны.

Государственной геодезической сетью является совокупность опорных геодезических пунктов, прочно закрепленных на местности, взаимное расположение которых точно определено в единой государственной системе координат и высот.

Геодезические сети подразделяются на государственную геодезическую сеть, геодезическую сеть сгущения и съемочную геодезическую сеть.

Государственная геодезическая сеть является исходной для других геодезических сетей. Она делится на плановую и высотную.

Плановая государственная геодезическая сеть создается астрономическим или геодезическим методами.

При астрономическом методе плановое положение каждого из отдельных пунктов сети определяется независимо друг от друга из астрономических наблюдений.

Геодезический метод состоит в том, что для определения координат точек находят из астрономических наблюдений координаты только нескольких точек, называемых исходными. Дальнейшее определения планового положения точек производят путем геодезических измерений на местности.

Высотная государственная геодезическая сеть создается методом геометрического нивелирования.

Плановые государственные геодезические сети. Методы их создания

Основными методами создания государственной геодезической сети являются триангуляция, трилатерация, полигонометрия и спутниковые координатные определения.

Триангуляция (рис. 68, а) представляет собой цепь прилегающих друг к другу треугольников, в каждом из которых измеряют высокоточными теодолитами все углы. Кроме того, измеряю длины сторон в начале и конце цепи.

Рис. 68. Схема триангуляции (а) и полигонометрии (б).

В сети триангуляции известными являются базис L и координаты пунктов А и В. Для определения координат остальных пунктов сети измеряют в треугольниках горизонтальные углы.

Триангуляция делится на классы 1, 2, 3, 4. Треугольники разных классов различаются длинами сторон и точностью измерения углов и базисов.

Развитие сетей триангуляции выполняется с соблюдением основного принципа «от общего к частному», т.е. сначала строится триангуляция 1 класса, а затем последовательно 2, 3 и 4 классов.

Пункты государственной геодезической сети закрепляются на местности центрами. Для обеспечения взаимной видимости между пунктами над центрами устанавливают геодезические знаки деревянные или металлические. Они имеют приспособление для установки прибора, платформу для наблюдателя и визирное устройство.

В зависимости от конструкции, наземные геодезические знаки подразделяются на пирамиды и простые и сложные сигналы.

Типы подземных центров устанавливаются в зависимости от физико-географических условий региона, состава грунта и глубины сезонного промерзания грунта. Например, центр пункта государственной геодезической сети 1-4 классов типа 1 согласно инструкции «Центры и реперы государственной геодезической сети» (М., Недра, 1973) предназначен для южной зоны сезонного промерзания грунтов. Он состоит из железобетонного пилона сечением 16Х16 см (или асбоцементной трубы 14-16 см, заполненной бетоном) и бетонного якоря. Пилон цементируется в якорь. Основание центра должно располагаться ниже глубины сезонного промерзания грунта не менее 0,5 м и не менее 1,3 м от поверхности земли. В верхней части знака на уровне поверхности земли бетонируется чугунная марка. Над маркой в радиусе 0,5 м насыпается грунт слоем 10-15 см. В 1,5м от центра устанавливается опознавательный столб с охранной плитой.

В настоящее время широко используют радиотехнические средства для определения расстояний между пунктами сети с относительными ошибками 1:100 000 – 1:1 000 000. Это дает возможность строить геодезические сети методом трилатерации, при которой в сетях треугольников производится только измерение сторон. Величины углов вычисляют тригонометрическим способом.

Метод полигонометрии(рис. 68, б) состоит в том, что опорные геодезические пункты связывают между собой ходами, называемыми полигонометрическими. В них измеряют расстояния и справа лежащие углы.

Спутниковые методы создания геодезических сетей подразделяются на геометрические и динамические. В геометрическом методе искусственный спутник Земли используют как высокую визирную цель, в динамическом – ИСЗ является носителем координат.

Высотные государственные геодезические сети

Государственная высотная геодезическая сеть – это нивелирная сеть I, II, III и IV классов. При этом сети I и II классов являются высотной основой, с помощью которой устанавливается единая система высот на всей территории страны.

На линиях I, II, III и IV классов закладывают вековые, фундаментальные, грунтовые, скальные, стенные и временные реперы.

Вековые и фундаментальные реперы закладываются в скальные породы или в грунт. Они отличаются повышенной устойчивостью и обеспечивают сохранность высотной основы на длительное время. Вековыми реперами закрепляют места пересечений линий нивелирования I класса, а фундаментальные – закладывают на линиях I и II классов не реже, чем через 60 км.

Временные реперы используют в качестве высотной основы при топографических съёмках, а также включают в линии нивелирования II, III и IV классов.

Геодезические съемочные сети

Съемочные сети являются геодезической основой при решении инженерно-геодезических задач. Их создают в качестве съемочного обоснования для производства топографических съемок, выноса на местность инженерных сооружений, а также для плановой и высотной привязки отдельных объектов.

Съемочное обоснование разбивается от пунктов плановых и высотных опорных сетей.

Самый распространенный вид съемочного обоснования – теодолитные ходы (рис. 69), опирающиеся на один или два исходных пункта. Они представляют собой геодезические построения в виде ломаных линий, в которых углы измеряют одним полным приёмом с помощью технического теодолита, а стороны – стальной 20-метровой лентой или дальномерами, обеспечивающими заданную точность. Теодолитные ходы могут быть замкнутыми или разомкнутыми.

Рис. 69. Теодолитные ходы: замкнутый (а); разомкнутый (б).

Длины линий (сторон) теодолитных ходов зависят от масштаба съемки и условий снимаемой местности и должны быть не более 350 м и не менее 20 м. Относительные линейные невязки в ходах должны быть менее 1:2000, при неблагоприятных условиях измерений допускается 1:1000.

Углы поворота на точках хода измеряют теодолитом со средней квадратической ошибкой 0,5′ одним приемом. Расхождение значений углов в полуприемах не более двойной точности теодолита.

Точки съемочного обоснования, как правило, закрепляют на местности временными знаками: деревянными кольями, столбами, металлическими штырями, трубами.

Если эти точки предполагается использовать в дальнейшем для других целей, их закрепляют постоянными знаками.

Плановая привязка вершин теодолитного хода к пунктам ГГС

Совокупность геодезических измерений и вычислений, необходимых для определения положения вершин теодолитного хода в государственной системе координат, называется привязкой.

Привязку можно выполнить несколькими методами.

1. Плановая привязка методом угловой засечки (рис. 70).

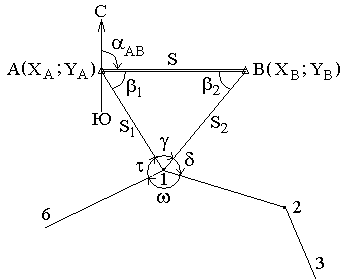
Рис. 70. Привязка теодолитного хода методом угловой засечки.

Дано: А ; В .

Измереные углы:

Контроль измерений: ;

Найти координаты точки 1 ; дирекционный угол .

1. Решение обратной геодезической задачи

Контроль :

2. Решение треугольника привязки

;

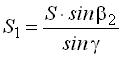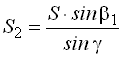
3. Передача дирекционных углов

Контроль вычислений:

4. Решение прямой геодезической задачи

Если расхождение в координатах не более 0,02 м, то находят средние значения координат X₁ и Y₁.

2. Метод снесения координат (рис. 71).

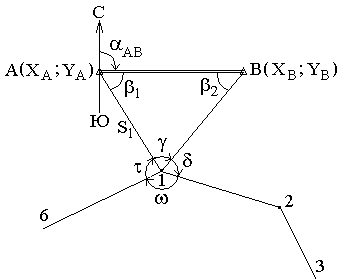
Рис. 71. Привязка методом снесения координат

Дано: А (X_A ; Y_A ) ; В (X_В ; Y_В ).

Измеренные:

Контроль:

Найти координаты точки 1 (X₁ ; Y₁ ); дирекционный угол (1 – 2) .

1. Решение обратной геодезической задачи.

2. Решение треугольника привязки

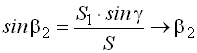
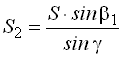
3. Передача дирекционных углов.

4. Решение прямой геодезической задачи.

3. Метод привязки теодолитного хода к одному опорному пункту с известным направлением в нем (рис. 72)..

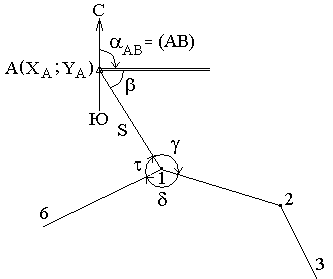
Рис. 72. Привязка к одному пункту с известным направлением.

Дано: А (X_A ; Y_A ) ;

Измерено: S; углы:

Контроль:

Найти координаты точки 1 (X₁ ; Y₁ ); дирекционный угол (1 – 2) .

1. Передача дирекционных углов

2.Решение прямой геодезической задачи.

Для контроля привязки необходимо другую вершину теодолитного хода привязать к опорному пункту

Вопросы для самоконтроля

1. В чем состоят основные принципы построения геодезических сетей?

2. В чем сущность метода триангуляции?

3. В чем сущность метода трилатерации?

4. В чем сущность метода полигонометрии?

5. Как измеряют углы и линии при создании теодолитного хода?

6. В чем состоит задача плановой привязки теодолитного хода к опорным пунктам?

7. В чем сущность прямой и обратной геодезических задач?

План урока №14

Этап 1. Тема урока

Инженерные изыскания для строительства

Этап II. Цель урока: -дать представление о инженерных изысканиях для строительства
Этап III. Тип урока Урок ознакомления с новым материалом

Этап IV. Оборудование Наглядные и раздаточные материалы, учебник М.И.Киселев. Геодезия

Этап VI. Ход урок -организационный момент – актуализация знаний учащихся по теме. –изучение темы -закрепление темы – подведение итогов

Урок №14

Инженерно-геодезические изыскания.

Инженерно-геодезические изыскания для строительства должны обеспечивать получение топографо-геодезических материалов и данных о ситуации и рельефе местности (в том числе дна водотоков, водоемов и акваторий), существующих зданиях и сооружениях (наземных, подземных и надземных), элементах планировки (в цифровой, графической, фотографической и иных формах), необходимых для комплексной оценки природных и техногенных условий территории строительства и обоснования проектирования, строительства и эксплуатации объектов.

В состав инженерно-геодезических изысканий для строительства входят:

сбор и обработка материалов инженерных изысканий прошлых лет, топографо-геодезических, картографических, аэрофотосъемочных и других материалов и данных;

рекогносцировочное обследование территории;

создание (развитие) опорных геодезических сетей, включая геодезические сети специального назначения для строительства;

создание планово-высотных съемочных геодезических сетей;

топографическая (наземная, аэрофототопографическая, стереофотограмметрическая и др.) съемка, включая съемку подземных и надземных сооружений;

обновление топографических (инженерно-топографических) и кадастровых планов в графической, цифровой, фотографической и иных формах;

инженерно-гидрографические работы;

геодезические работы, связанные с переносом в натуру и привязкой горных выработок, геофизических и других точек инженерных изысканий;

геодезические стационарные наблюдения за деформациями оснований зданий и сооружений, земной поверхности и толщи горных пород в районах развития опасных природных и техноприродных процессов;

инженерно-геодезическое обеспечение информационных систем поселений и государственных кадастров (градостроительного и др.);

создание (составление) и издание (размножение) инженерно-топографических планов, кадастровых и тематических карт и планов, атласов специального назначения (в графической, цифровой и иных формах);

камеральная обработка материалов;

составление технического отчета.

В состав инженерно-геодезических изысканий для строительства линейных сооружений дополнительно входят:

камеральное трассирование и предварительный выбор конкурентоспособных вариантов трассы для выполнения полевых работ и обследований;

полевое трассирование;

съемки существующих железных и автомобильных дорог, составление продольных и поперечных профилей, пересечений линий электропередачи (ЛЭП), линий связи (ЛС), объектов радиосвязи, радиорелейных линий и магистральных трубопроводов;

координирование основных элементов сооружений и наружные обмеры зданий (сооружений);

определение полной и полезной длины железнодорожных путей на станциях и габаритов приближения строений.

Техническое задание на производство инженерно-геодезических изысканий дополнительно, должно содержать:

сведения о принятой системе координат и высот;

данные о границах и площадях топографической съемки (обновления планов);

указания о масштабе топографической съемки и высоте сечения рельефа по отдельным площадкам, включая требования к съемке подземных и надземных сооружений;

данные к трассированию линейных сооружений;

требования к стационарным геодезическим наблюдениям в районах развития опасных природных и техноприродных процессов;

требования к составу, форме и срокам представления отчетной технической документации.

В программе инженерно-геодезических изысканий дополнительно к требованиям, приведенным в п. 4.14, должны быть представлены:

обоснование видов и схемы построения опорной геодезической сети, в том числе геодезической сети специального назначения для строительства, плотности геодезических пунктов и точности определения их планово-высотного положения;

сведения о способе закрепления пунктов (точек) на местности;

данные о методе выполнения топографической съемки;

данные по трассированию линейных сооружений;

данные по инженерно-геодезическому обеспечению выполнения других видов инженерных изысканий (исследований);

сведения об использовании программных средств для камеральной обработки результатов геодезических измерений и создания инженерно-топографических планов (цифровых инженерно-топографических планов).

Топографическая съемка при инженерных изысканиях для строительства предприятий, зданий и сооружений выполняется в масштабах 1:200; 1:500; 1:1000; 1:2000; 1:5000 и 1:10 000.

Ситуация и рельеф местности, подземные и надземные сооружения должны изображаться на инженерно-топографических планах условными знаками, утвержденными или согласованными федеральной службой геодезии и картографии России.

В районах с рельефом, имеющим углы наклона свыше 6° (для планов в масштабах 1:5000 и 1:2000) и свыше 10° (для планов в масштабах 1:1000 и 1:500), число горизонталей должно соответствовать разности высот, определенных на перегибах скатов, а средние погрешности высот, определенных на характерных точках рельефа, не должны превышать ¹/₃ принятой высоты сечения рельефа.

По результатам выполненных инженерно-геодезических изысканий по каждому объекту должен быть составлен технический отчет.

^ Общие сведения — основание для производства работ, задачи инженерно-геодезических изысканий, местоположение района (площадки, трассы), административная принадлежность, данные о землепользовании и землевладельцах, сведения о проектируемом объекте строительства, система координат и высот, виды и объемы выполненных работ, сроки их проведения, сведения об исполнителе.

^ Краткая физико-географическая характеристика района (площадки) работ — характеристика рельефа (в том числе углы наклона поверхности), геоморфология, гидрография, сведения о наличии опасных природных и техноприродных процессов.

^ Топографо-геодезическая изученность района (площадки) инженерных изысканий — обеспеченность территории топографическими картами, инженерно-топографическими планами, фотопланами (аэро- и космофотопланами), специальными (земле-, лесоустроительными и др.) планами соответствующих масштабов, данные о кадастрах, сведения о геодезических сетях (типы центров и наружных знаков) и возможности их использования на основе результатов их оценки, наименование организаций — исполнителей карт (планов), времени и методов их создания, техническая характеристика геодезических, картографических и топографических материалов.

^ Сведения о методике и технологии выполненных работ — создание (развитие) опорных и съемочных геодезических сетей или геодезических сетей специального назначения для строительства, производство топографической съемки и создание (составление) инженерно-топографических планов, выполнение инженерно-гидрографических работ, трассирование линейных сооружений, геодезическое обеспечение производства других видов инженерных изысканий, выполнение геодезических наблюдений и исследований (в том числе в районах развития опасных природных и техноприродных процессов), характеристика точности и детальности изыскательских работ.

^ Сведения о проведении технического контроля и приемки работ — результаты выполненного контроля работ при инженерно-геодезических изысканиях.

Заключение — краткие результаты выполненных работ и их оценка, рекомендации по производству последующих топографо-геодезических работ.

Графическая часть технического отчета в зависимости от выполненных работ должна содержать:

— картограмму топографо-геодезической изученности;

—схемы созданной планово-высотной опорной и (или) съемочной геодезической сети;

— абрисы закрепленных пунктов (точек) и каталог их координат и высот;

— инженерно-топографические и кадастровые планы;

— планы (схемы) сетей подземных сооружений с их техническими характеристиками, согласованные с эксплуатирующими организациями;

— графики результатов наблюдений за осадками и деформациями оснований зданий, сооружений, земной поверхности и толщи горных пород.

В результате выполненных инженерно-гидрографических работ дополнительно представляются:

— инженерно-топографические планы прибрежной части и акваторий (в изобатах), внутренних водоемов и рек;

— топографо-батиметрические планы (при изысканиях в шельфовой зоне морей);

— продольные профили водной поверхности (в табличном и графическом виде).

По трассам проектируемых сооружений дополнительно представляются:

— инженерно-топографический план трассы и ее вариантов, план съемки участков индивидуального проектирования;

— продольный профиль трассы с вариантами;

— планы подходов к конечным пунктам трассы проектируемого линейного сооружения (подстанциям и др.);

— совмещенный план трассы проектируемого линейного сооружения с существующими инженерными сетями;

— абрисы привязок характерных точек трассы к элементам ситуации;

— ведомости углов поворота, прямых и кривых (прямых и углов), пересекаемых угодий и лесов, водотоков, автомобильных и железных дорог, надземных и подземных сооружений, в том числе сносимых сооружений и отчуждаемых угодий, оврагов, лощин, заболоченных и косогорных участков, технические показатели по трассам.

В результате инженерно-геодезических изысканий в районах развития опасных природных и техноприродных процессов (карст, склоновые процессы, переработка берегов рек, озер, морей и водохранилищ, разрывные тектонические смещения, подрабатываемые территории и др.) в соответствии с требованиями технического задания заказчика должен представляться технический отчет.

В текстовой части технического отчета в дополнение к требованиям п. 5.13 должны приводиться:

— основные результаты геодезических наблюдений и характеристика динамики опасного процесса — активизация или стабилизация деформаций;

— скорости смещения деформационных геодезических знаков и изменение их положения по сезонам года (во времени) по отдельным участкам территории;

— влияние выявленных факторов на динамику развития опасного природного и техноприродного процесса;

— рекомендации по учету полученных результатов при проектировании, строительстве и эксплуатации предприятий, зданий и сооружений;

— предложения по дальнейшему выполнению или прекращению геодезических наблюдений.

Топографические материалы должны сопровождаться пояснительной запиской с характеристикой изученности территории, сведениями о времени их составления, исполнителях, порядке получения, а также другими данными в соответствии с техническим заданием заказчика на выполнение этих работ.

При выполнении геодезических работ по созданию разбивочной основы в период строительства и эксплуатации предприятий, зданий и сооружений должны быть представлены:

разбивочный чертеж с привязкой к знакам геодезической основы разбивочных осей зданий и сооружений;

каталоги координат и высот пунктов геодезической основы;

чертежи геодезических знаков;

технический отчет.

Источник

Определение отметок точек и превышений

Определение отметки (высоты) точки

Вычисление уклона линии.

6. Определение отметок точек по горизонталям

Сплошные горизонтали проведены через 2,5 м

Построение продольного профиля по заданному направлению

Сплошные горизонтали проведены через 2,5 м

Построение продольного профиля по заданному направлению

2. Рельеф местности. Составление картограммы

2.3. Определение отметок точек по горизонталям

Вам также может понравиться

Как составить жалобу в авито на продавца

Чат рулетка как найти по лицу

Ошибка датчика падения mi robot как исправить ошибку

Добавить комментарий Отменить ответ