Задача 22099 1) Дан треугольник ABC с вершинами…
Условие
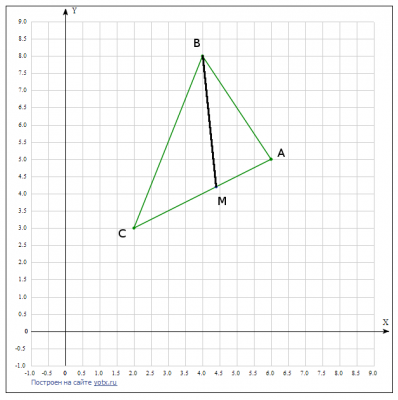
1) Дан треугольник ABC с вершинами А(1;5), B(4; 1), С(13; 10). Найти точку пересечения биссектрисы внутреннего угла А со стороной BC.
математика 10-11 класс
12375
Решение
★
|АВ|=sqrt((4-1)^2+(1-5)^2)=sqrt(9+16)=sqrt(25)=5
|AC|=sqrt((13-1)^2+(10-5)^2)=sqrt(144+25)=sqrt(169)=13
Пусть АК – биссектриса, К ∈ BC.
Применяем свойство биссектрисы внутреннего угла треугольника.
Биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
ВК:КС=АВ:АС=5:13
Точка К делит отрезок ВС в отношении 5:13
лямбда =5/13
Применяем формулу нахождения координат точки, делящей отрезок в данном отношении
x_(K)=(x_(B)+ лямбда x_(C))/(1+ лямбда )
y_(K)=(y_(B)+ лямбда y_(C))/(1+ лямбда )
x_(K)=(4+(5/13)*13)/(1+(5/13))=13/2
y_(K)=(1+(5/13)*10)/(1+(5/13))=63/18=7/2
К(13/2; 7/2)
О т в е т. К(13/2; 7/2)
Все решения
Вариант решения через уравнение биссектрис.
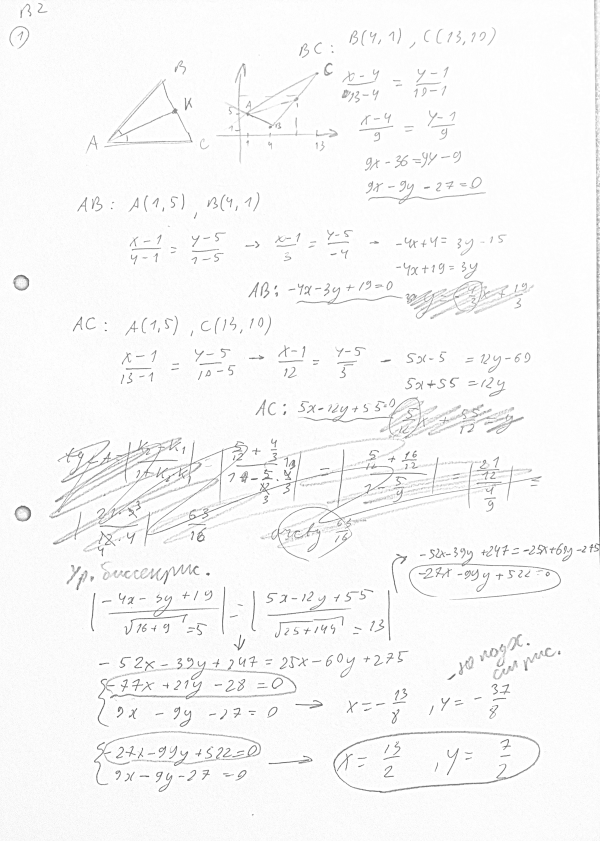
Написать комментарий
Если точка М(x; y) лежит на прямой, проходящей
через две данные точки
(
,
)
и
(
,
), и дано отношение
, в
котором точка М делит отрезок
, то координаты
точки М определяются по формулам
,
.
| 86 | Даны концы А(3; -5), В(-1; 1) однородного стержня. Определить координаты его центра масс. |
|
| 87 | Центр мас однородного стержня находится в точке М(1; 4), один из его концов Р(-2; 2). Определить координаты точки Q – другого конца этого стержня. |
|
| 88 | Даны вершины треугольника А(1; -3), В(3; -5), С(-5; 7). Определить середины его сторон. |
|
| 89 | Даны точки А(3; -1), С(2; 1). Определить: | |
| 89.1 | Координаты точки М, симметричной точке А относительно точки В; |
|
| 89.2 | Координаты точки N, симметричной точке В относительно точки А. |
|
| 90 | Точки А(2; -1), N (-1; 4), P(-2; 2) являются серединами сторон треугольника. Определить его вершины. |
|
| 91 | Даны три вершины параллелограмма А(3; -5), B(5; -3), C(-1; 3). Определить четвертую вершину D, противоположную B. |
|
| 92 | Даны две смежные вершины параллелограмма А(-3; 5), B(1; 7) и точка пересечения его диагоналей M(1; 1). Определить две другие вершины. |
|
| 93 | Даны три вершины А(2; 3), B(4; -1), C(0; 5) параллелограмма ABCD. Найти его четвертую вершину D. |
|
| 94 | Даны вершины треугольника A(1; 4), B(3; -9), C(-5; 2). Определить длину его медианы, проведенной из вершины B. |
|
| 95 | Отрезок, ограниченный точками A(1; -3), B(4; 3) разделен на три равные части. Определить координаты точек деления. |
|
| 96 | Даны вершины треугольника A(2; -5), B(1; -2), C(4; 7). Найти точку пересечения биссектрисы его внутреннего угла при вершине В со стороной АС. |
|
| 97 | Даны вершины треугольника A(3; -5), B(-3; 3), C(-1; -2). Определить длину биссектрисы его внутреннего угла при вершине А. |
|
| 98 | Даны вершины треугольника А(-1; -1), B(3; 5), C(-4; 1). Найти точку пересечения биссектрисы его внешнего угла при вершине А с продолжением стороны ВС. |
|
| 99 | Даны вершины треугольника А(3; -5), B(1; -3), C(2; -2). Определить длину биссектрисы его внешнего угла при вершине В. |
|
| 100 | Даны точки А(1; 1), В(3; 3), С(4; 7). Определить отношение отрезок, ограниченный двумя другими. |
|
| 101 | Определить координаты концов А и В отрезка, который точками P(2; 2), Q(1; 5) разделен на три равные части. |
|
| 102 | Прямая проходит через точки M1(-12; -13), M2(-2; -5). На этой прямой найти точку, абсцисса которой равна 3. |
|
| 103 | Прямая проходит через точки M(2; -3), N(-6, 5). На этой прямой найти точку, ордината которой равна –5. |
|
| 104 | Прямая проходит через точки A(7; -3), B(23; -6). Найти точку пересечения этой прямой с осью абсцисс. |
|
| 105 | Прямая проходит через точки A(5; 2), B(-4; -7). Найти точку пересечения этой прямой с осью ординат. |
|
| 106 | Даны вершины четырехугольника А(-3; 12), B(3; -4), C(5; -4), D(5; 8). Определить, в каком отношении его диагональ AC делит диагональ BD. |
|
| 107 | Даны вершины четырехугольника A(-2; 14), B(4; -2), C(6; -2), D(6; 10). Определить точку пересечения его диагоналей AC и BD. |
|
| 108 | Даны вершины однородной треугольной пластинки A(x1; y1), B(x2; y2), C(x3; y3). Определить координаты ее центра масс. Центр масс находится в точке пересечения медиан. |
|
| 109 | Точка M пересечения медиан треугольника лежт на оси абсцисс, две вершины его – точки А(2; -3) и B(-5; 1), третья вершина C лежит на оси ординат. Определить координаты точек M и C. |
|
| 110 | Даны вершины однородной треугольной пластинки A(x1; y1), B(x2; y2), C(x3; y3). Если соединить середины ее сторон, то образуется новая однородная треугольная пластинка. Доказать, что центры масс обеих пластинок совпадают. |
|
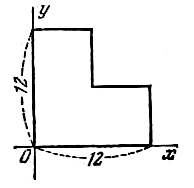
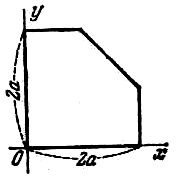
| 111 | Однородная пластинка имеет форму квадрата со стороной, равной 12, в которой сделан квадратный вырез, прямые разрезы проходят через центр квадрата, оси координат направлены по ребрам пластинки (рис.). Определить центр масс этой пластинки. |
|
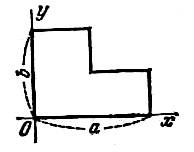
| 112 | Однородная пластинка имеет форму прямоугольника со сторонами, равными a и b, в котором сделан прямоугольный вырез; прямые разреза проходят через центр, оси координат направлены по ребрам пластинки (Рис). Определить центр масс этой пластинки. |
|
| 113 | Однородная пластинка имеет форму квадрата со стороной, равной 2a, от которого отрезан треугольник; прямая разреза соединяет середины двух смежных сторон, оси координат направлены по ребрам пластинки (Рис). Определить центр масс пластинки. |
|
| 114 | В точках A(x1; y1), B(x2; y2), C(x3; y3) сосредоточены массы m, n, p. Определить координаты центра тяжести этой системы. |
|
| 115 | Точки A(4; 2), B(7; -2), C(1; 6) являются вершинами треугольника, сделанного из однородной проволоки. Определить центр масс этого треугольника. |
Точка пересечения биссектрис – свойства, теорема и соотношения
Общие сведения
Треугольник — геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и отрезков, соединяющих их. Точки имеют другое название — вершины. Обозначается треугольник символом Δ, после которого идут 3 латинских буквы. Например, ΔMNO. Допускается использовать и русские литеры, но злоупотреблять этим не стоит.
В высших учебных заведениях преподаватели требуют от студентов международное обозначение. Кроме того, большинство программных продуктов и онлайн-сервисов воспринимают только латинские символы.
Существует определенная классификация Δ, на основании которой доказываются теоремы, выводятся формулы, свойства и решаются задачи. В последнем случае следует правильно производить идентификацию, чтобы избежать ошибок при расчетах.
Классификация треугольников
Необходимо отметить, что Δ различаются между собой по некоторым критериям.
Они бывают нескольких типов:
- Произвольные.
- Прямоугольные.
- Равнобедренные.
- Равносторонние.
- Тупоугольные.
- Остроугольные.
В первом случае стороны фигуры не равны между собой. Чтобы идентифицировать прямоугольный треугольник, необходимо рассмотреть его углы. Если один из них является прямым (равен 90 градусам), такая фигура называется прямоугольной. В третьем виде основным критерием считается наличие двух, равных между собой сторон.
В равностороннем треугольнике все стороны равны между собой. Математики его называют «правильным». Он обладает важным свойством — вокруг него можно описать окружность. Пятый тип определяет наличие тупого угла, градусная мера которого больше 90. Если фигура является остроугольной, это значит, что все 3 его угла меньше 90, т. е. являются острыми.
Один треугольник может относиться к нескольким типам. Например, прямоугольный Δ может быть равнобедренным на основании свойства геометрии: если Δ является равнобедренным, то углы (∠), образованные боковыми сторонами с основанием, равны между собой. В этом случае их градусные меры эквивалентны 45, поскольку сумма ∠ любого Δ составляет 180. Следовательно, 180 — 90 = 2k, где неизвестная величина «к» соответствует углу при основании.
Решая уравнение, можно получить искомое значение угла: k = 45. Исходя из вычислений, треугольник является прямоугольным и равнобедренным.
Дополнительные элементы
У любого Δ существуют определенные дополнительные элементы, необходимые при построении чертежей или схематических рисунков, доказательства теорем и решения задач по геометрии.
К ним относятся:
Биссектриса — отрезок (прямая), проходящий через вершину Δ и делящий угол на 2 равные части. Медиана — единственный отрезок для каждой вершины, соединяющий ее с серединой стороны, на которую он опущен.
Высотой является перпендикуляр, опущенный из вершины на противоположную сторону.
В равнобедренном и равностороннем треугольниках биссектриса является медианой и высотой. В последнем случае их можно провести всего 3.
Однако в произвольном Δ – по 3, т. е. 3 высоты, 3 медианы и 3 биссектрисы.
Теорема о биссектрисах
Теорема о биссектрисах треугольника звучит таким образом: в любом Δ биссектрисы пересекаются только в одной точке — инцентре фигуры. Для доказательства нужно построить произвольный ΔКLМ, а затем следовать по такому алгоритму:
- Провести биссектрисы LN (к стороне КМ) и КU (к LM).
- На рисунке видно, что LN и KU пересекаются в одной точке (W).
- Доказывать теорему следует от противного — пусть биссектрисы не пересекаются.
- Если прямые не пересекаются, значит, они параллельны, т. е. LN || KU. Следовательно, KL — секущая.
- Сумма градусных мер односторонних углов эквивалентна 180, т. е. (∠К/2) + (∠L/2) = 180 (свойство параллельных прямых и секущей).
- Из соотношения в 5 пункте следует, что сумма ∠К + ∠L = 360.
- Сумма углов Δ эквивалентна 180. Однако при сложении значений двух ∠ величина их суммы больше 180. Следовательно, биссектрисы треугольника пересекаются в одной точке.
Необходимо доказать, что третья биссектриса (МV), проведенная из вершины М, проходит через точку W. Это делается таким образом:
- Из W следует опустить перпендикуляры на стороны Δ: WG, WF и WE.
- Нужно рассмотреть 2 ΔGBW и ΔBFW, которые являются прямоугольными, поскольку WG и WF — перпендикуляры, а BW — общая сторона. Углы ∠GBW и ∠WВF равны, т. к. их образует биссектриса LN (общий угол будет делиться на 2 равные части). Следовательно, ΔGBW и ΔBFW равны.
- Из равенства ΔGBW и ΔBFW получается отношение WG и WF.
- Аналогично доказывается равенство сторон WG и WЕ.
Далее следует рассмотреть ∠М. Следовательно, что координата точки W равноудалена от вершины М. На основании признака биссектрисы, W лежит на МV, поскольку W — точка пересечения биссектрис треугольника КLМ. Утверждение доказано.
Свойства и соотношения
На основании теоремы о биссектрисах Δ были получены некоторые важные свойства, которые рекомендуется применять при решении задач и доказательства других утверждений:
- Центр вписанной окружности соответствует точке их пересечения.
- Точка при пересечении делит биссектрису по такому соотношению: отношение суммарного значения прилежащих к противолежащей стороне.
- Угол между биссектрисами двух смежных углов является прямым.
- В равнобедренном Δ равны только 2 биссектрисы, а в равностороннем — 3. Кроме того, она является медианой и высотой.
При решении задач нужно находить их длину (L).
Для удобства необходимо обозначить стороны таким образом: КМ = d, КL = e и LМ = f, чтобы воспользоваться следующими формулами через известные параметры треугольника:
- Все стороны: Lm = [2 * (d * e * p * (p — f))^(½)] / (d + e), Lк = [2 * (d * f * p * (p — e))^(½)] / (d + f) и Ll = [2 * (d * f * p * (p — e))^(½)] / (d + f). Параметр «р» — полупериметр, т. е. р = (d + e + f) / 2.
- Стороны и угол: Lm = (2 * d * e * cos (∠M)) / (d + e), Lk = (2 * d * f * cos (∠K)) / (d + f) и Ll = (2 * f * e * cos (∠L)) / (f + e).
Соотношения позволяют найти не только длины Lk, Lm и Ll, но и другие параметры треугольников. Следует отметить, что углы во второй группе формул соответствуют биссектрисам, исходящим из них.
Таким образом, для решения задач на нахождение длины биссектрис необходимо знать теорию, доказательство теоремы, свойства, а также основные соотношения.
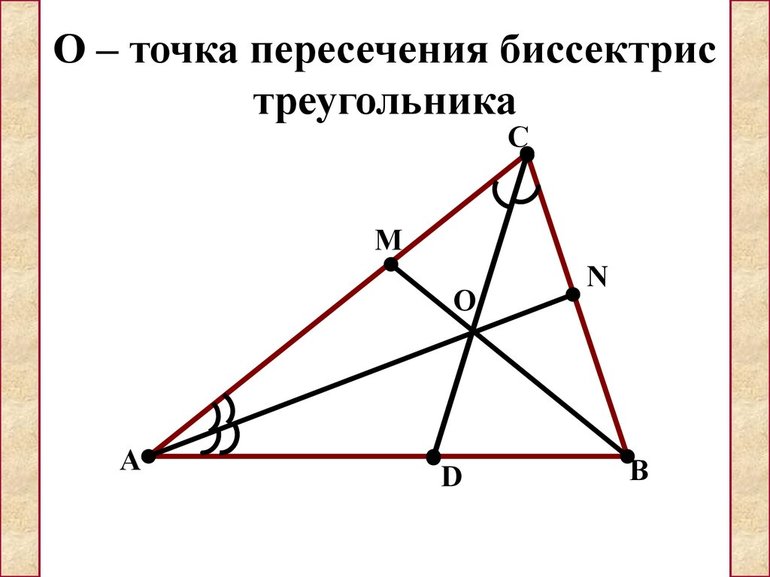
Точка пересечения биссектрис
Как найти точку пересечения биссектрис треугольника по координатам его вершин?
Как найти радиус вписанной в треугольник окружности по координатам его вершин?
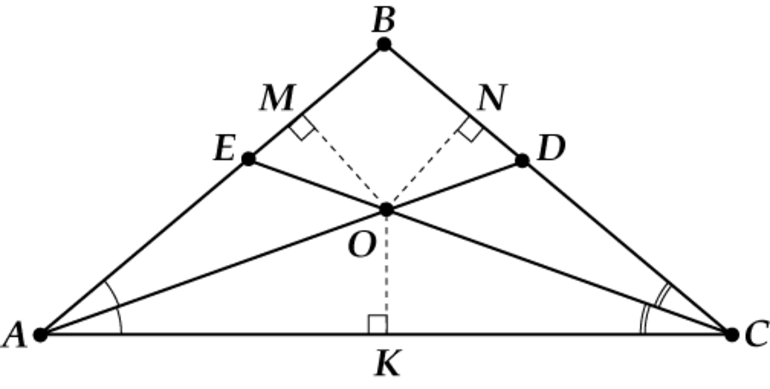
Точка пересечения биссектрис треугольника является центром вписанной в этот треугольник окружности.
Эта точка равноудалена от сторон треугольника. Расстояние от точки пересечения биссектрис до сторон треугольника равно радиусу вписанной окружности.
Следовательно, все три задачи сводятся к нахождению точки пересечения биссектрис треугольника.
Для этого надо сначала составить уравнения биссектрис треугольника и найти точку их пересечения.
Дан треугольник ABC с вершинами в точках A(0;-3), B(12;-12) и C(3,36;-0,48).
1) Найти точку пересечения биссектрис треугольника ABC.
2) Найти радиус вписанной в треугольник ABC окружности.
3) Составить уравнение вписанной в треугольник ABC окружности.
1) Составим уравнения прямых, содержащих стороны треугольника.
Уравнение прямой AC:
Уравнение прямой BC:
Составим уравнение биссектрисы треугольника ABC, исходящей из угла B. Она образована прямыми AB и BC:
откуда уравнения биссектрис угла B: x-y-24=0 или x+y=0. Чтобы понять, которое из двух уравнений является биссектрисой внутреннего угла треугольника, следует подставить в уравнения координаты точек A и C. Поскольку они лежат по разные стороны от биссектрисы внутреннего угла B, то подстановка их координат в уравнение биссектрисы даёт числа разных знаков.
A(0;-3) и C(3,36;-0,48) в x-y-24=0: 0-(-3)-24 0. Получили числа разных знаков, x+y=0 — биссектриса угла B треугольника ABC.
Составим уравнение биссектрисы угла C. Угол C образован прямыми AC и BC, откуда
уравнения биссектрис угла C: 7x-y-24=0 и x+7y=0.
A(0;-3), B(12;-12) в 7x-y-24=0: 7·0-(-3)-24 0. Получили числа разных знаков, значит 7x-y-24=0 — уравнение биссектрисы внутреннего угла C.
Поскольку все три биссектрисы треугольника пересекаются в одной точке, третью биссектрису находить не требуется.
Точку пересечения биссектрис углов B и C найдём из системы уравнений
O(3;-3) — точка пересечения биссектрис треугольника ABC. Эта точка является центром вписанной в треугольник окружности.
2) Радиус вписанной в треугольник ABC окружности можно найти как расстояние от точки O до прямой AB, BC или AC. Найдем, например, расстояние от O до AB:
3) Чтобы найти уравнение вписанной в треугольник ABC окружности, в уравнение окружности подставляем координаты центра O(3;-3) и r=9/5:
Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):
Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.
Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).
Свойство 4
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC
Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
- CD – внутренняя биссектриса ∠ACB;
- CE – биссектриса угла, смежного с ∠ACB;
- ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Пример задачи
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.
Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):
Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
[spoiler title=”источники:”]
[/spoiler]
|
18 / 18 / 4 Регистрация: 05.05.2013 Сообщений: 88 |
|
|
1 |
|
Точка пересечения бисектрис треугольника09.06.2013, 00:24. Показов 16998. Ответов 12
Нужно найти точку пересечения бисектрис в произвольном треугольнике. Миниатюры
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
09.06.2013, 00:24 |
|
Ответы с готовыми решениями: М- точка пересечения медиан треугольника ABC AB=BC A(-1;-2) , C(3;6). Точка М лежит на оси ординат найти координаты точки B Точка пересечения треугольника и окружности
Написать уравнение плоскости, проходящей через прямую DM, параллельно ребру BC, М-точка пересечения медиан треугольника 12 |
|
753 / 458 / 49 Регистрация: 13.05.2012 Сообщений: 947 |
|
|
09.06.2013, 15:47 |
2 |
|
чтобы найти точку пересечения биссектрис треугольника, нужно знать уравнения этих биссектрис(достаточно иметь два уравнения биссектрис).
1 |
|
1764 / 968 / 180 Регистрация: 24.02.2013 Сообщений: 2,782 Записей в блоге: 12 |
|
|
09.06.2013, 17:14 |
3 |
|
Решение Можно проще:
3 |
|
753 / 458 / 49 Регистрация: 13.05.2012 Сообщений: 947 |
|
|
09.06.2013, 17:33 |
4 |
|
Проще… Смотря на каком этапе знаний мы находимся. Если студент, например, не изучал аналитическую геометрию в пространстве- вряд ли он знает, что такое направляющий вектор прямой. Ведь термин “направляющий вектор” встречается в аналитической геометрии в пространстве.
0 |
|
18 / 18 / 4 Регистрация: 05.05.2013 Сообщений: 88 |
|
|
09.06.2013, 18:29 [ТС] |
5 |
|
Да, с направляющим вектором я действительно не знаком.
0 |
|
1764 / 968 / 180 Регистрация: 24.02.2013 Сообщений: 2,782 Записей в блоге: 12 |
|
|
09.06.2013, 19:40 |
6 |
|
(x-x0)/X=(y-y0)/Y
1 |
|
4526 / 3520 / 358 Регистрация: 12.03.2013 Сообщений: 6,038 |
|
|
10.06.2013, 13:27 |
7 |
|
Есть замечательно красивая формула: если I – центр окружности, вписанной в треугольник ABC, и a, b, c – длины сторон, то
2 |
|
496 / 204 / 18 Регистрация: 19.03.2013 Сообщений: 463 |
|
|
11.06.2013, 07:52 |
8 |
|
helter, формула, действительно, красивая. Но ее использование требует доказательства.
0 |
|
4526 / 3520 / 358 Регистрация: 12.03.2013 Сообщений: 6,038 |
|
|
11.06.2013, 09:43 |
9 |
|
ее использование требует доказательства. Какой вы суровый.
0 |
|
18 / 18 / 4 Регистрация: 05.05.2013 Сообщений: 88 |
|
|
11.06.2013, 15:03 [ТС] |
10 |
|
Хмм…..
0 |
|
1074 / 655 / 68 Регистрация: 10.02.2011 Сообщений: 518 |
|
|
11.06.2013, 17:05 |
11 |
|
Посмотрите рисунок: Миниатюры
1 |
|
135 / 112 / 13 Регистрация: 03.06.2013 Сообщений: 270 |
|
|
11.06.2013, 17:23 |
12 |
|
Так Вы воспользуйтесь той теоремой, что предложил Helter, вот она http://fxdx.ru/page/centr-vpis… kruzhnosti И в начало координат точку О засуньте. А-а, ну да, всё уже…
1 |
|
18 / 18 / 4 Регистрация: 05.05.2013 Сообщений: 88 |
|
|
11.06.2013, 17:30 [ТС] |
13 |
|
Cute, спасибо. P.S. тему можно закрывать.
0 |
Все ответы
|
|
 |
|














 Даны координаты двух вершин треугольника и точка пересечения его высот
Даны координаты двух вершин треугольника и точка пересечения его высот
 Пожалуй, тут достаточно пару раз применить свойство биссектрисы (делит сторону в отношении, равным отношению прилежащих сторон). А можно от ответа: найти, в каком отношении прямая AI делит отрезок BC (причём в силу симметричности другие стороны можно не рассматривать).
Пожалуй, тут достаточно пару раз применить свойство биссектрисы (делит сторону в отношении, равным отношению прилежащих сторон). А можно от ответа: найти, в каком отношении прямая AI делит отрезок BC (причём в силу симметричности другие стороны можно не рассматривать).