2.6. Призма, параллелепипед
Определение 20
Призмой называется многогранник, все вершины которого расположены в двух параллельных плоскостях, причём в этих же двух плоскостях лежат две грани призмы, представляющие собой равные многоугольники с соответственно параллельными сторонами, а все рёбра, не лежащие в этих плоскостях, параллельны.
Эти две равные грани называются основаниями призмы. Все остальные грани призмы называются боковыми, они образуют боковую поверхность призмы. Все боковые грани призмы являются параллелограммами.

Рис. 61

Рис. 62
Рёбра, не лежащие в основаниях, называются боковыми рёбрами призмы. Призму называют n–угольной, если её основаниями являются n-угольники.
На рисунке 61 изображена пятиугольная призма ABCDEA1B1C1D1E1. Здесь использован наиболее распро- странённый (стандартный) способ обозначения вершин призмы и стандартная запись: сначала в порядке обхода указывают вершины одного основания, а затем в том же порядке — вершины другого; концы каждого бокового ребра обозначают одинаковыми буквами, только вершины, лежащие в одном основании, обозначают буквами без индекса, а в другом — с индексом.
Хорошо известный параллелепипед (рис. 62) является частным случаем призмы: параллелепипед — это четырёхугольная призма, основаниями которой являются параллелограммы. Причём за основание можно взять любую грань параллелепипеда.
Призма называется прямой, если её боковые рёбра перпендикулярны основаниям.
Призма называется правильной, если она прямая, а её основания — правильные многоугольники.
Как было отмечено, параллелепипед является частным случаем призмы. Особо выделим прямоугольный параллелепипед — параллелепипед, все грани которого прямоугольники (рис. 63).

Рис. 63
Диагональ параллелепипеда — это отрезок, соединяющий его противоположные вершины. У параллелепипеда четыре диагонали.
Теорема 2.7 (свойство диагоналей параллелепипеда)
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Точка пересечения диагоналей параллелепипеда является центром симметрии параллелепипеда, или просто центром параллелепипеда.
Уточним, что мы называем центром симметрии фигуры или тела точку, при симметрии относительно которой тело переходит само в себя. Заметим также, что образ параллелепипеда при симметрии однозначно задаётся образами его вершин. Поэтому точка пересечения диагоналей будет центром симметрии параллелепипеда (если мы докажем теорему 2.7).
Доказательство. Рассмотрим параллелепипед ABCDA1B1C1D1 (см. рис. 62). Докажем, что любые две его диагонали пересекаются и делятся точкой пересечения пополам. Возьмём, например, диагонали AC1 и CA1. Рёбра AA1 и CC1 равны и параллельны, поскольку каждое из них равно и параллельно ребру BB1. Значит, AA1C1C — параллелограмм, диагонали AC1 и CA1 которого пересекаются и делятся точкой пересечения пополам. ▼
Следствие
Параллелепипед имеет центр симметрии. Это — точка пересечения его диагоналей. Двенадцать рёбер параллелепипеда образуют три четвёрки соответственно равных между собой и параллельных отрезков.
Теорема 2.8
Диагонали прямоугольного параллелепипеда равны.
Доказательство. Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1 (см. рис. 63). Рёбра AA1 и CC1 равны и перпендикулярны граням ABCD и A1B1C1D1, в которых лежат отрезки AC и A1C1. Следовательно, AA1C1C — прямоугольник и AC1 = CA1. То же верно для любой пары диагоналей. ▼
Теорема 2.9 (теорема Пифагора для прямоугольного параллелепипеда)
Пусть a, b и c — длины трёх непараллельных рёбер прямоугольного параллелепипеда, d — его диагональ. Тогда a2 + b2 + c2 = d 2. (Эта теорема представляет собой один из многих пространственных аналогов теоремы Пифагора.)
Доказательство. Пусть в прямоугольном параллелепипеде ABCDA1B1C1D1 (см. рис. 63) AB = a, AD = b, AA1 = c. (Такими же соответственно будут и длины параллельных им рёбер.) Так как AA1C1C — прямоугольник, то
 ▼
▼
|
|
|
1.Разрежьте треугольную призму на три треугольные пирамиды. |
|
2.Разрежьте куб на три равные четырёхугольные пирамиды. |
|
3.Сумма трёх чисел, равных количеству вершин, рёбер и граней некоторого многогранника, равна: а) 102; б) 104. Определите вид многогранника, если известно, что это либо пирамида, либо призма. |
|
4(в). Найдите диагональ единичного куба. |
|
5.Три отрезка, не лежащие в одной плоскости, имеют общую точку и делятся этой точкой пополам. Докажите, что концы этих отрезков служат вершинами параллелепипеда. |
|
6.Найдите расстояние от центра грани единичного куба до вершин противоположной грани. |
|
7.Рёбра прямоугольного параллелепипеда равны 2, 3 и 4. Найдите угол между его диагоналями. |
|
8.Проекции отрезка на три попарно перпендикулярные прямые равны 1, 2 и 3. Найдите длину этого отрезка. |
|
9.Найдите расстояние между серединами непараллельных сторон разных оснований правильной треугольной призмы, все рёбра которой равны 2. |
|
10.Покажите, что в кубе можно выбрать четыре вершины, являющиеся вершинами правильного тетраэдра, причём сделать это можно двумя способами. |
|
11.Рассмотрим две треугольные пирамиды, вершинами которых служат вершины данного параллелепипеда. (Каждая вершина параллелепипеда является вершиной одной пирамиды.) Возможно ли, чтобы каждая вершина одной из пирамид принадлежала плоскости грани другой пирамиды, и наоборот? |
|
12.Через точку на ребре треугольной пирамиды проведены две плоскости, параллельные двум граням этой пирамиды. Эти плоскости отсекают две треугольные пирамиды. Разрежьте оставшийся многогранник на две треугольные призмы.
|
|
13(в). Диагонали трёх различных граней прямоугольного параллелепипеда равны m, n и p. Найдите диагональ этого параллелепипеда. |
|
14(в). Диагональ прямоугольного параллелепипеда образует с его рёбрами углы a, b и g. Докажите, что cos2 a + cos2 b + cos2 g = 1. |
|
15(в). В каком отношении диагональ AC1 параллелепипеда ABCDA1B1C1D1 делится плоскостью A1BD ? |
|
16(т). В одном старом учебнике дано такое определение призмы: «Призмой называется многогранник, у которого две грани — равные многоугольники с соответственно параллельными сторонами, а все остальные грани — параллелограммы». Приведите пример многогранника, удовлетворяющего этому определению, но не являющегося призмой. |
|
17(т). Станет ли верным определение, приведённое в предыдущей задаче, если перед словом «многогранник» поставить слово «выпуклый»? Указание. Возьмём куб и на каждой его грани, как на основании, во внешнюю сторону построим правильную четырёхугольную пирамиду с двугранными углами при основании 45°. |
|
18(т). Найдите ребро куба, одна грань которого лежит в плоскости основания правильной пирамиды, а четыре оставшиеся вершины — на её боковой поверхности, если сторона основания пирамиды равна a, а высота h. Решите эту задачу: а) для правильной четырёхугольной пирамиды; б) для правильной треугольной пирамиды. |
|
19(п). Рёбра прямоугольного параллелепипеда равны a, b и c (a ⩽ b ⩽ c). Найдите: а) углы между его диагоналями; б) угол между диагональю параллелепипеда и скрещивающейся с ней диагональю грани со сторонами a и b; в) угол между скрещивающимися диагоналями двух граней с общим ребром a. |
|
20.Пусть K, L и M — середины рёбер AD, A1B1 и CC1 прямоугольного параллелепипеда ABCDA1B1C1D1, в котором AB = a, AA1 = b, AD = c. Найдите периметр треугольника KLM. |
|
21(т). Укажите все точки на диагонали AC1 параллелепипеда ABCDA1B1C1D1, через которые нельзя провести прямую, пересекающую прямые: а) BC и DD1; б) A1B и B1C. |
|
22(т). Два ребра прямоугольного параллелепипеда равны 1 и 2. Плоскость, параллельная этим рёбрам, делит параллелепипед на два неравных, но подобных между собой параллелепипеда. Найдите длину ребра, отличного от данных. |
|
23(т). На рёбрах A1B1 и A1D1 единичного куба ABCDA1B1C1D1 взяты точки K и M так, что A1K = A1M = x. Найдите x, если известно, что при повороте куба вокруг диагонали AC1 на угол a точка K переходит в M. |
|
24(п). Постройте изображение призмы ABCA1B1C1, если на плоскости даны изображения следующих точек: а) A, B, B1 и C1; б) середин AA1, BC, CC1 и A1C1. |
|
25.Постройте изображение параллелепипеда ABCDA1B1C1D1, если даны изображения следующих точек: а) A, B, D, A1; б) A, B, C, D1; в) A, C, B1, D1; г) середин AB1, BC1, CD, A1D1; д) A, B и центров граней A1B1C1D1 и CDD1C1. |
|
26.Дано изображение призмы ABCA1B1C1. Постройте изображение точки M пересечения плоскостей A1BC, AB1C и ABC1. Пусть высота призмы равна h. Чему равно расстояние от точки M до оснований призмы? |
|
27(пт). Пусть O — середина высоты правильной треугольной пирамиды. Вторая пирамида симметрична данной относительно точки O. Как называется многогранник, являющийся общей частью двух указанных пирамид? (Если вы не знаете его названия, опишите, как он устроен.) Чему равна площадь поверхности этого многогранника, если площадь боковой грани равна S ? |
|
28(т). Рёбра прямоугольного параллелепипеда равны a, b и c (a < b < c). Некоторое сечение этого параллелепипеда является квадратом. Найдите сторону этого квадрата. |
|
29.Проекция вершины A параллелепипеда ABCDA1B1C1D1 на некоторую плоскость лежит внутри проекции треугольника A1BD на эту плоскость. Докажите, что площадь проекции параллелепипеда в два раза больше площади проекции треугольника A1BD. |
|
30(т). Используя результат предыдущей задачи, найдите, чему равно наибольшее значение площади проекции прямоугольного параллелепипеда с рёбрами a, b и c на некоторую плоскость. |
|
31(т). Через центр единичного куба проведена плоскость, делящая его на два многогранника. Докажите, что в каждом из получившихся многогранников найдётся диагональ, длина которой не меньше . |
|
32.Многогранники изучают, их свойства используют представители самых различных профессий. Например, свойствам многогранников посвящены разделы таких наук, как минералогия и кристаллография. Известный русский минералог и кристаллограф Е. С. Фёдоров (1853—1919) сделал немало замечательных открытий, связанных со свойствами многогранников. Некоторые из открытых им многогранников называют «фёдоровскими». Вот один из них. Возьмём куб и соединим его центр со всеми вершинами. Для каждого из восьми полученных таким образом отрезков построим плоскость, перпендикулярную ему и проходящую через середину. Рассмотрим многогранник, ограниченный этими плоскостями и поверхностью куба (в него входит центр куба). Сколько граней имеет получившийся многогранник? Какими многоугольниками являются его грани? Докажите, что такими многогранниками можно заполнить всё пространство без пропусков и пересечений. |
Параллелепипед
Что за слово такое мудреное – «параллелепипед»? Что за многогранник скрывается за этим словом?
Что-то должно быть связано с параллельностью, не правда ли?
Так и есть.
Читай статью, смотри вебинар и ты все про него будешь знать!
Параллелепипед — коротко о главном
Параллелепипед — это четырехугольная призма (многогранник с ( displaystyle 6) гранями), все грани которой — параллелограммы.
Прямой параллелепипед —это параллелепипед, у которого ( displaystyle 4) боковые грани — прямоугольники.
Прямоугольный параллелепипед — параллелепипед, у которого все грани — прямоугольники
Куб — параллелепипед, у которого все грани квадраты.
Высота параллелепипеда – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Свойства параллелепипеда
- Противолежащие грани параллелепипеда параллельны и равны.
- Диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
- Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через точку пересечения диагоналей (центр параллелепипеда), делится ею пополам.
- Все диагонали прямоугольного параллелепипеда равны между собой и равны сумме квадратов его измерений. ( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}).
Параллелепипед — подробнее
Параллелепипед – многоугольник, образованный пересечением трех пар параллельных плоскостей.
Если слишком сложно, просто посмотри на картинку.
Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?
Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.
Далее смотри на картинки, запоминай и не путай!
Высота – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Та грань, на которую опущена высота, называется основанием.
Прямой параллелепипед
Прямым называется параллелепипед, у которого боковые ребра перпендикулярны основанию.
Вот так:
У прямого параллелепипеда в основании – параллелограмм, а боковые грани – прямоугольники.
Прямоугольный параллелепипед
Прямоугольным называется параллелепипед, у которого в основании прямоугольник, а боковые ребра перпендикулярны основанию.
Это такая обувная коробка:
У прямоугольного параллелепипеда все грани – прямоугольники.
Давай-ка теперь выведем одну интересную формулу для диагонали прямоугольного параллелепипеда.
Диагональ прямоугольного параллелепипеда равна сумме квадратов его измерений.( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}).
Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.
Смотри:
Куб
Куб – параллелепипед, у которого все грани квадраты.
Все ребра куба равны.
Кстати, заметь, что куб – частный вид прямоугольного параллелепипеда.
Поэтому для диагонали куба действует формула, которую мы получили для прямоугольного параллелепипеда.
( displaystyle {{d}^{2}}={{a}^{2}}+{{a}^{2}}+{{a}^{2}}),
То есть
( displaystyle d=asqrt{3})
Давай убедимся в пользе этой формулы.
Представь, что у тебя задача: «Диагональ куба равна ( displaystyle 5sqrt{3}). Найти полную поверхность».
Решим ее.
Бонус. Видео из нашего курса по подготовке к ЕГЭ по математике
А теперь пора закрепить знания и порешать задачки. Иначе твои знания будут не полными!
На этом вебинаре мы на примере самых простых объемных фигур (куб, параллелепипед, призма — задание №8 из ЕГЭ) научимся находить важнейшие вещи в стереометрии — расстояния и углы в пространстве.
Бери ручку, тетрадь и решай задачи вместе с Алексеем!
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
![]()
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Диагональ прямоугольного параллелепипеда


4.6
Средняя оценка: 4.6
Всего получено оценок: 90.
4.6
Средняя оценка: 4.6
Всего получено оценок: 90.
В геометрии 10 класса есть разделы, изучающие свойства диагонали прямоугольного параллелепипеда. Свойства изучаются не просто так, много задач на нахождение диагонали этой фигуры встречаются в ЕГЭ. Поэтому имеет смысл подробно поговорить о характеристиках диагонали прямоугольного параллелепипеда.

Опыт работы учителем математики – более 33 лет.
Определение понятия
В общем случае диагональ представляет собой отрезок, соединяющий вершины двух углов, не принадлежащих одной стороне многогранника. Прямоугольный параллелепипед в свою очередь состоит из шести граней, являющихся прямоугольниками.
Диагонали в прямоугольном параллелепипеде могут быть проведены не только во внутреннем пространстве фигуры, но и на боковых гранях, и в гранях оснований. В последнем случае обычно уточняется, что речь идет о диагонали боковой грани или диагонали основания.
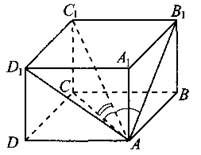
У параллелепипеда есть четыре диагонали. Причем, эти отрезки не принадлежат ни одной боковой грани или основаниям, а проводятся внутри фигуры.
Характеристики диагонали
Существует две теоремы, касающиеся диагоналей параллелограмма. Чтобы их доказать, используются дополнительные построения. К примеру, часто диагональ нижнего основания данной объемной геометрической фигуры служит стороной для нескольких треугольников.
Первая Теорема
Квадрат диагонали прямоугольного параллелепипеда можно найти, суммировав квадраты трех измерений этой геометрической фигуры.
Здесь речь идет о длине, ширине и высоте рассматриваемого многогранника. Чтобы доказать данную теорему необходимо использовать свойства прямоугольных треугольников.
Диагональ, проведенная в основании будет являться гипотенузой прямоугольного треугольника $АВС$, значит ее можно найти по теореме Пифагора через сумму квадратов $АВ$ и $ВС$.
Но $АВ$ и $ВС$ это длина и ширина параллелепипеда.
$$АC=sqrt{AB^2+BC^2}$$
Затем рассмотрим прямоугольный треугольник $АСС’$. Диагональ $АС’$ также можно найти через теорему Пифагора, как корень из суммы катетов $АС$ и $СС’$. Но $АС$ мы уже находили как корень из суммы квадратов $АВ$ и $АС$:
$(ACʹ)^2= (CCʹ)^2+(CD)^2+(CB)^2$, где
$CCʹ$ – высота;
$CD$ – длина;
$CB$ – ширина.
Так выглядит формула, отражающая содержание данной теоремы.
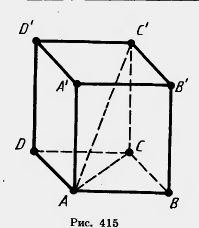
Обычно больший отрезок, лежащий в основании параллелепипеда, считается ее длиной. Меньший отрезок – шириной.
Вторая теорема
В любом параллелепипеде четыре диагонали пересекаются в одной точке, которую называют точкой симметрии, и делятся ею пополам. Это свойство доказывают, рассматривая две любые диагонали, и проводя соответствующие отрезки.
Для доказательства этой теоремы нужно вспомнить, что плоскость может задаваться двумя пересекающимися прямыми. В рассматриваемом случае, сечение плоскостью, заданной двумя пересекающимися диагоналями, принимает форму прямоугольника. А диагонали прямоугольника, как известно, точкой пересечения делятся пополам.
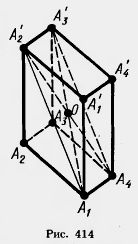
Из этой же теоремы можно сделать вывод о том, что все его диагонали будут равными между собой отрезками.

Что мы узнали?
Мы поговорили о диагоналях прямоугольного параллелепипеда. Узнали, что, используя свойства диагоналей параллелепипеда, можно найти ширину, длину и высоту параллелепипеда. Поговорили о том, как найти центр симметрии, и определить длину диагоналей прямоугольного параллелепипеда.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 90.
А какая ваша оценка?
На чтение 4 мин Просмотров 4.4к. Опубликовано 12 декабря, 2020
Параллелепипед — тело строгих геометрических форм, противоположные грани которого находятся в параллельных плоскостях. Все плоскости, или грани, включая основание, параллелограммы. Научно определение параллелепипеда — призма, основанием которой служит параллелограмм. Часто ученики затрудняются ответить, чем отличается параллелограмм от параллелепипеда. Отличие в том, что параллелограмм — фигура плоская, двухмерная, а параллелепипед — объемное геометрическое тело, протяженное в трех измерениях, имеющее ширину, высоту и длину. Как выглядит параллелепипед, посмотрите на рисунке:
![]()
Виды параллелепипеда
Параллелепипед — многогранник. Его ограничивают шесть плоскостей, два основания, и четыре боковые грани. Линии, по которым соединяются грани, называются ребрами, а точки, в которых сходятся три ребра — вершинами. У фигуры 8 вершин.
Если грани имеют общее ребро, то их называют смежными, а те, у которых такого ребра нет — противоположными. Это же касается и вершин, если они не лежат на одной грани, то их тоже называют противоположными. Высота, ширина и длина прямоугольного параллелепипеда называются измерениями, они выходят из одной вершины. Если фигура не прямоугольная, то измерения и ребра не совпадают.
![]()
При построении параллелепипеда на рисунке можно провести ряд дополнительных линий, которые помогают при вычислении объема, площади поверхности, неизвестных длин и других параметров. Если линии проходят через противоположные вершины, то их называют диагоналями. У параллелепипеда их насчитывается четыре.
В геометрии выделяют несколько типов параллелепипедов, которые отличаются некоторыми свойствами:
- Прямой — фигура, у которой боковые грани являются прямоугольниками;
- Прямоугольный — все грани прямоугольники, не только боковые, но и основания. Объемный прямоугольник — это т есть такой параллелепипед.
- Наклонный — боковые грани находятся по отношению к основанию под углами, отличными от 900;
- Ромбоэдр — все грани представляют собой равные ромбы;
- Куб — все грани квадратны.
Свойства параллелепипеда
Для всех типов параллелепипедов можно выделить общие свойства, характеризующие фигуру. Таких свойств немного, запомнить их не сложно:
- Диагонали параллелепипеда в точке пересечения делятся пополам;
- Параллелепипед симметричен относительно точки пересечения диагоналей;
- Любой отрезок, соединяющий две точки на гранях параллелепипеда и проходящий через точку пересечения диагоналей, делится пополам;
- Противоположные грани равны и параллельны (вытекает из определения);
- Сумма квадратов измерений равна квадрату диагонали.
Твердо запомнив эти свойства несложно решить большинство задач школьной геометрии.
Основные формулы параллелепипеда
Кроме свойств этой фигуры нужно запомнить ряд несложных формул. Конечно, в процессе решения задачи можно вывести эти выражения самостоятельно. Но часто на это нет времени, лучше воспользоваться готовыми шаблонами.
Формула площади боковой поверхности прямого параллелепипеда — одна из самых простых. Sб=Ро∙h. В этой формуле только три величины, но одна из них составная:
H – высота параллелепипеда;
Р – периметр, АВ+ВС+АD+ CD.
Воспользоваться такой формулой можно только в том случае, если известны длины сторон основы и высота.
Площадь полной поверхности параллелепипеда определяется по формуле Sп=Sб+2Sо.
Как найти площадь боковой поверхности мы знаем из предыдущего пункта, а площадь Sо рассчитывается в зависимости от вида четырехугольника, лежащего в основании.
Объем прямого параллелепипеда тоже найти несложно, для этого достаточно умножить площадь основания на высоту. Объём V=Sо∙h
Формулы для прямоугольного параллелепипеда тоже не отличаются сложностью:
Sб=2c(a+b) в этой формуле а и b – стороны основания, с – высота, равна длине бокового ребра.
Площадь полной поверхности равна Sп=2(ab+bc+ac);
Объем V=abc, то есть, произведение всех трех измерений.
Когда же приходится вычислять площади и объем произвольного параллелепипеда, то показанные формулы не всегда срабатывают. Необходимо использовать законы векторной геометрии. При вычислении объема параллелепипеда через длину диагонали, необходимо использовать проекции на разные оси. Видимая простота формул — это только основа для сложной работы, требующей пространственного воображения и смекалки.
Вновь поступил вопрос про прямоугольный параллелепипед. И вопрос этот не простой, смотрите сами:
Рёбра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите площадь его поверхности. Подскажите, как это переварить?
Вопрос, конечно, не простой — что такое прямоугольный параллелепипед, как и с чем его едят? В частности, как найти рецепт приготовления площади поверхности этого то ли фрукта, то ли овоща? Так, для начала давайте посмотрим, что это вообще такое — прямоугольный параллелепипед? Вот картинка прямоугольного параллелепипеда.
Как видите, прямоугольный параллелепипед — это, собственно, обыкновенный кирпич. Кстати, если бы Ньютону на голову упала не сфера в виде яблока, а прямоугольный параллелепипед в виде кирпича, то в школе мы вряд ли бы учили его законы. Прямоугольная комната — это тоже прямоугольный параллелепипед, который позволяет вам совершить обзорную экскурсию по его достопримечательностям прямо изнутри. Если вы хотите произвести внешний осмотр достопримечательностей сего математического чуда, тогда возьмите в руки коробку из-под обуви и можете вертеть её, сколько душе угодно.
И так, прямоугольный параллелепипед на картинке дает нам возможность увидеть вершины, ребра и диагонали. Вершины мы можем потрогать пальцем, ребра мы можем измерять, диагональ можем высчитать. Нам сейчас диагональ не нужна. Закон движения учеников в классе знаете? Если леди-учитель покидает класс, класс движется быстрее. Закон решения задач очень похож: чем меньше всякой ерунды нам нужно искать, тем проще задача.
Первая проблема, с которой мы сталкиваемся в задаче, это проблема сленга. Задача сформулирована на бытовом сленге, а все формулы и определения в математике формулируются на математическом сленге. Поэтому нам самим предстоит выполнить перевод. Приступаем к поэтапному переводу, по фразам.
«Рёбра прямоугольного параллелепипеда, выходящие из одной вершины …» — собственно, здесь говорится о тех ребрах, которые позволяют нам определить размеры прямоугольного параллелепипеда и на основании этих размеров выполнить все необходимые вычисления. На картинке это ребра a, b и c. Кто бы сомневался, что именно эти три ребра нам дадут по условию, но только не я. Ни один математик вам этого не скажет (не потому, что они этого не знают, а из боязни нарваться на очень неудобные вопросы), но если в условии задачи дать две длины параллельных ребер и одного перпендикулярного им, то нашу задачу в принципе решить будет невозможно. В прямоугольном параллелепипеде из любой вершины всегда выходит три взаимно перпендикулярных ребра. Вот по этому в нашей задаче прямо говорится об этом. Если верить Священным Писаниям разных религий, то именно из одного такого ребра сотворены все прямоугольные параллелепипеды, задачи о которых решает вся прекрасная половина человечества.
Следующая фраза «… равны 1, 2, 3» обозначает, что нам не нужно искать этот злополучный прямоугольный параллелепипед и свою линейку, чтобы измерить длины его граней, как это показано на рисунке. Тот, кто эту задачу придумал, уже сам всё измерил (или выдумал эти размеры, что в данном случае принципиального значения не имеет). Кто есть кто в этом списке чисел? Где длина, ширина, высота нашего параллелепипеда? Нам это без разницы. Как бы мы этот прямоугольный параллелепипед не крутили, площадь его поверхности всегда будет оставаться неизменной. Предыдущие поколения математиков этот факт не единожды проверили. Когда мы доберемся до решения, мы сами в этом убедимся.
Теперь вопрос, в чём же конкретно измеряется наш прямоугольный параллелепипед и площадь его поверхности? В каких единицах измерения? Ответ довольно прост — в любых единицах измерения длины. Англичане и американцы любят дюймы, футы, мили. Мы предпочитаем сантиметры, метры, километры. В чем измеряют длину инопланетяне? Мы вообще не знаем. Да нам эти единицы измерения и не важны. В чем бы мы не измеряли длину граней, циферки возле длин и площади будут одинаковыми. Циферки остаются, единицы измерения меняются. Вот два способа получения результата в математике.
разные числа + одинаковые единицы измерения = разный результат
одинаковые числа + разные единицы измерения = разный результат
Приблизительно, как в этом счетчике. Крутим одно колесико — меняются числа. Крутим другое колесико — меняются единицы измерения. Так устроена настоящая математика, маленький кусочек которой мы сейчас рассматриваем.
Это уже не детская математика, придуманная специально для того, чтобы мучить нас задачками. Это взрослая математика, одинаковая для всех.
В нашей задаче мы измеряем всё в абстрактных единицах измерения длины. Соответственно, полученная нами площадь будет измеряться в этих же единицах измерения, возведенных в квадрат.
Теперь нам осталось только достать из глубокого кармана шпаргалку с формулами для прямоугольного параллелепипеда и посмотреть, чего полезного для нас там имеется.
Что вообще есть в этой шпаргалке? Формула диагонали прямоугольного параллелепипеда, формула объема. Есть несколько формул для площади поверхности: полная, основания, боковая. Вот одна из этих формул нам как раз нужна. Разберемся в площадях на примере коробки для обуви. Площадь основания — это площадь донышка или крышки коробки. Площадь боковой поверхности — это боковые стеночки коробки без донышка и крышки. Полная площадь — это боковые стеночки вместе с донышком и крышкой.
Теперь смотрим в условие задачи и определяем, «чё тебе надобно, старче?». А надобно ему (ей, им) «площадь поверхности». Если уточнений типа «боковой» или «основания» нет, значит искать нужно полную площадь поверхности прямоугольного параллелепипеда. Длины трех граней у нас есть, формула тоже, можно произвести расчет. Заморачиваться с основаниями и боками нам нет смысла.
Как видим, полная площадь поверхности нашего прямоугольного параллелепипеда получилась равной 22 единицы в квадрате. Какие именно единицы? А какие вам не жалко или какие вы больше всего любите.
По просьбе учащихся добавляю картинку про сумму длин ребер прямоугольного параллелепипеда.
 |
| Сумма ребер прямоугольного параллелепипеда |
Сумму длин всех ребер параллелепипеда я обозначил через букву «P», поскольку она очень похожа на периметр прямоугольника. Кстати, в формуле длин всех ребер я этого не записал, но если мы возьмем три фигурообразующие грани прямоугольного параллелепипеда, которыми являются прямоугольники, то сумма длин всех ребер параллелепипеда будет равна сумме периметров этих прямоугольников.







