Как найти точку пересечения диагоналей параллелограмма векторы

Онлайн калькулятор. Площадь параллелограмма построенного на векторах.

Этот онлайн калькулятор позволит вам очень просто найти площадь параллелограмма построенного на векторах.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади параллелограмма построенного на векторах и закрепить пройденый материал.

Калькулятор для вычисления площади параллелограмма построенного на векторах

Выберите каким образом задается параллелограмм:

Введите значения векторов: Введите координаты трех любых вершин параллелограмма:

Инструкция использования калькулятора для вычисления площади параллелограмма построенного на векторах

Ввод данных в калькулятор для вычисления площади параллелограмма построенного на векторах

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления площади параллелограмма построенного на векторах

• Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.

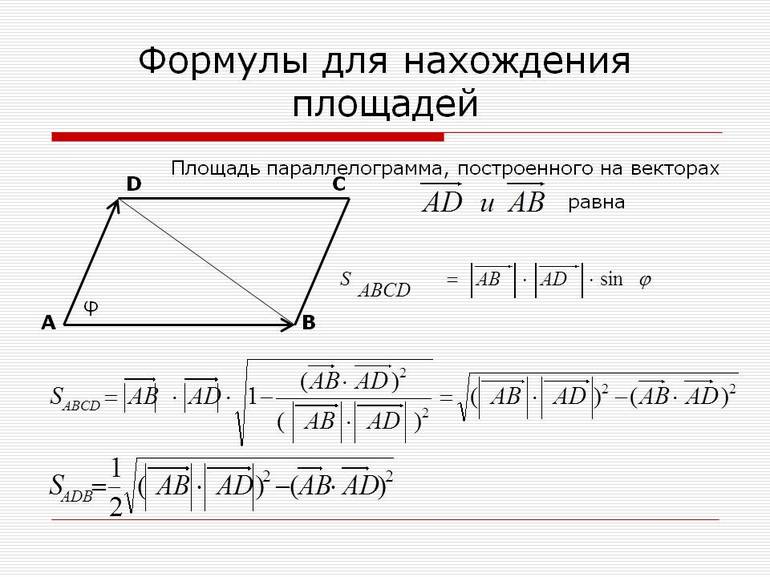
Теория. Площадь параллелограмма построенного на векторах.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Найти четвертую вершину параллелограмма

Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?

В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.

Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.

Дано: ABCD — параллелограмм,

1) Найдём координаты точки O — середины диагонали AC.

2) По свойству диагоналей параллелограмма, точка O также является серединой BD:

Дано: ABCD — параллелограмм,

1) Ищем координаты точки O — середины отрезка BD:

2) Точка O также является серединой AC:

2 Comments

А как вы получили -14 в первом примере.

Можно применить основное свойство пропорции: 12+xD=2∙(-1), xD=-2-12=-14.

Площадь параллелограмма, построенного на векторах – формула и примеры решения задач

Четырехугольник и вектор на плоскости

Каждый школьник понимает, что параллелограмм является специальным видом плоских четырехугольников. Эта фигура состоит из двух пар параллельных пересекающихся отрезков. Она обладает следующими важными свойствами:

• ее противоположные стороны и углы равны друг другу;
• сумма всех четырех углов составляет 360 градусов;
• если просуммировать лишь два смежных (прилежащих к одной стороне) угла, то получится значение 180 градусов;
• любая диагональ делит фигуру на две равные части (треугольники);
• пересечение диагоналей происходит в точке, которая является геометрическим и массовым центром параллелограмма;
• любая секущая, которая проходит через геометрический центр, делит фигуру на две равные по площади части.

Специальные типы

Исходя из определения параллелограмма, как четырехугольника с параллельными и равными по длине противоположными сторонами, можно привести несколько видов фигуры, которые обладают высокой симметрией по отношению к ряду элементарных операций. Это следующие геометрические типы:

1. Квадрат. Все четыре стороны его равны по длине между собой, а углы составляют 90 градусов. Он является фигурой с достаточно высокой симметрией, и его площадь вычисляется просто как квадрат длины любой его стороны.
2. Прямоугольник. Еще один вид параллелограмма, все углы которого являются прямыми. Его симметрия несколько ниже, чем у квадрата, поскольку длины сторон равны лишь попарно. Площадь фигуры можно вычислить, перемножив длины смежных сторон.
3. Ромб. Специальный геометрический тип параллелограмма, который характеризуется тем, что длины всех его сторон являются одинаковыми. Углы фигуры попарно равны и отличаются от 90 градусов (два тупых и два острых).

Направленные отрезки и операция умножения

Площадь параллелограмма через векторы рассчитать легко, если знать понятие направленного отрезка и уметь работать с соответствующими математическими операциями. Поскольку любая точка на плоскости может быть представлена в виде набора двух координат в декартовой прямоугольной системе, то для P и Q можно записать:

P (x1, y1); Q (x2, y2).

Где числа x1, y1, x2 и y2 являются соответствующими координатами для точек P и Q по осям абсцисс и ординат. Чтобы получить вектор PQ-, который будет направлен из P в точку Q, необходимо из координат Q попарно вычесть значения для P:

PQ- = Q — P = (x2-x1, y2-y1).

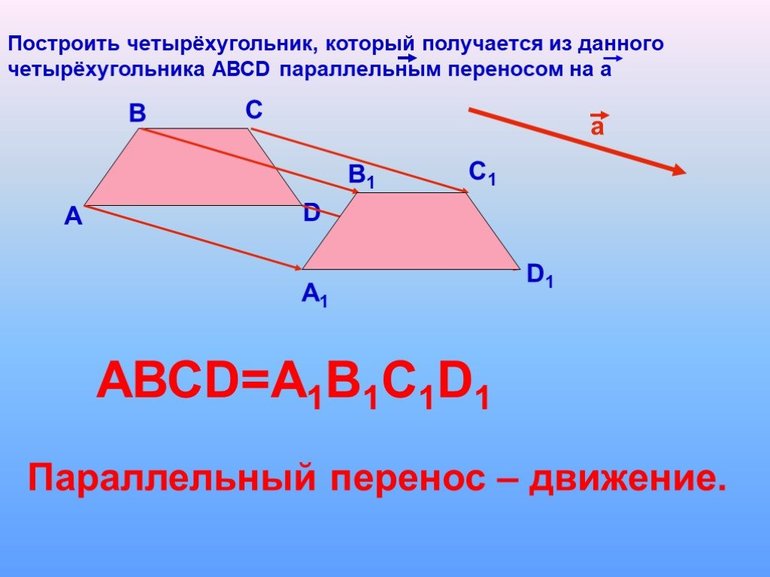
Координаты направленного отрезка на плоскости определяются так же, как и для точки, набором из двух чисел. Чтобы построить такой вектор в системе координат, необходимо его начало расположить в точке (0, 0), а конец со стрелкой будет располагаться в точке (x2-x1, y2-y1). Из этой геометрической интерпретации следует, что существует бесконечное множество направленных отрезков, которые эквивалентны между собой. Получаются они друг из друга с помощью параллельного переноса по всей плоскости координат.

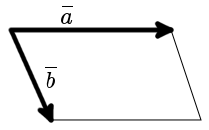
Как и числа, направленные отрезки также можно складывать между собой, вычитать и умножать. Рассматривая вопрос построение параллелограмма на векторах и нахождения его площади, необходимо изучить свойства векторного произведения. Оно представляет собой вектор, перпендикулярный плоскости, в которой лежат исходные направленные отрезки. Пусть a- и b- необходимо умножить векторно. Результатом произведения будет следующий вектор c-:

c- = [a-*b-] = |a-|*|b-|*sin (alfa).

Здесь alfa — угол между a- и b-, а |a-| и |b-| – длины соответствующих направленных отрезков.

Направление c- принято определять с помощью правила правой руки. Оно гласит: если четыре пальца ладони направить от конца первого умножаемого вектора к концу второго, то оттопыренный большой палец укажет направление результирующего векторного умножения.

Координаты вектора c- можно вычислить также, если воспользоваться понятием определителя матрицы. Пусть a- имеет координаты (a1, a2), а b- = (b1, b2), тогда формула для определения c- запишется в следующем виде:

c- = (0, 0, (a1*b2-b1*a2)).

Вектор c- имеет первые две нулевые координаты, поскольку он перпендикулярен плоскости, в которой находятся a- и b-.

Формула площади из геометрии

Чтобы получить формулу площади параллелограмма на векторах, необходимо вспомнить, как рассчитывается эта величина для треугольника. Если известна одна сторона (основание a) и высота, которая на нее опущена (h), то получается простое выражение:

Где S3 — площадь треугольника. Поскольку две таких плоских фигуры, которые соединены одной из своих сторон, образуют четырехугольник-паралелограм, то для него рассмотренную величину можно вычислить по формуле:

Пусть вторая сторона параллелограмма равна b, тогда с высотой h она связана через определение тригонометрической функции синус:

sin (alfa) = h/b => h = b*sin (alfa).

Если подставить это равенство в выражение для S4, то нахождение площади фигуры сведется к расчету произведения двух его смежных сторон и синуса угла между ними:

Поскольку угол alfa изменяется от 0 до 180 градусов, то функция синус всегда имеет положительное значение. Этой формулой часто пользуются на практике. Распространение инженерных калькуляторов позволяет быстро и с высокой точностью вычислять синусы любых углов.

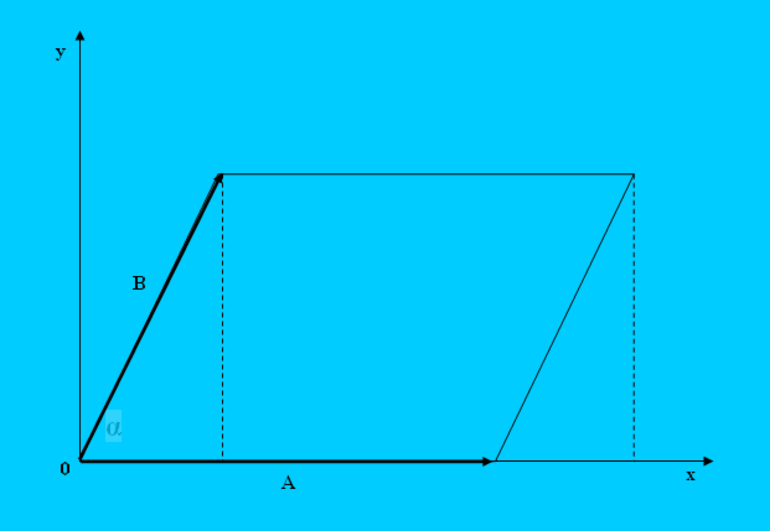
Построение параллелограмма

Определить площадь четырехугольника с попарно параллельными сторонами можно не только через длины его сторон. Если внимательно посмотреть на формулу для S4, то можно заметить, что она идентична по виду векторному произведению направленных отрезков.

Пусть имеется два вектора a- и b-. Угол между ними равен alfa. Если их начала совместить в одной точке на плоскости, затем, от конца a- продолжить вектор b-, а из b- начертить a-, то получится параллелограмм, побудованый на a- и b-. Очевидно, что модуль векторного произведения этих направленных отрезков будет равен площади полученной фигуры:

S4 = a*b*sin (alfa) = |[a-*b-]|.

Применяя координатное выражение этого произведения, можно записать следующую формулу для площади:

Где a- = (a1,a2) и b-=(b1,b2). Знак модуля необходим потому, что по правилу правой руки могут получаться отрицательные векторы. Площадь же является всегда величиной положительной.

Преимущество последней записанной формулы для S4 по сравнению с выражением, где необходимо знать длины и углы, заключается в том, что ее использование не требует никаких предварительных вычислений. Достаточно лишь знать координаты конца и начала образующих параллелограмм векторов.

Задача с тремя точками

Чтобы научиться пользоваться записанной простой формулой, следует решить простую задачу. Имеется три точки, координаты которых следующие:

На вершинах этих точек следует построить параллелограмм, а затем, рассчитать его площадь S4.

Задачу проще всего решать через использование векторов. Выберем произвольную точку из трех заданных. Пусть это будет A. Из нее выходит два вектора: AB- и AC-. Их координаты определяются таким образом:

AB- = (2−1, 0-(-1)) = (1, 1); AC- = (-4−1, 3- (-1)) = (-5, 4).

Чтобы определить площадь параллелограмма на этих векторах, следует применить формулу для их векторного произведения. Порядок умножения направленных отрезков не имеет значения. Получается следующий результат:

S4 = [AB-*AC-] = 1*4 — (-5)*1 = 9.

Результат получен в единицах квадратных соответствующей двумерной системы координат.

Если была выбрана в качестве исходной не точка A, а B или C, то получился бы тот же результат, что можно доказать, проделав аналогичные вычисления.

Диагонали фигуры

Некоторые задачи по геометрии параллелограммов в качестве начального условия предлагают знание одной или двух его диагоналей. По этим данным необходимо вычислить характеристики всей фигуры, включая ее площадь. Решать такие задачи также удобно с использованием понятия векторов.

Если дана диагональ, выраженная вектором f- и основание, представленное направленным отрезком a-, то формула для площади параллелограмма имеет вид:

Где beta — угол между a- и f-. Видно, что это выражение не отличается от предыдущих для S4. Доказать его справедливость несложно, если рассмотреть построенные на указанных векторах треугольники и использовать признаки их подобия.

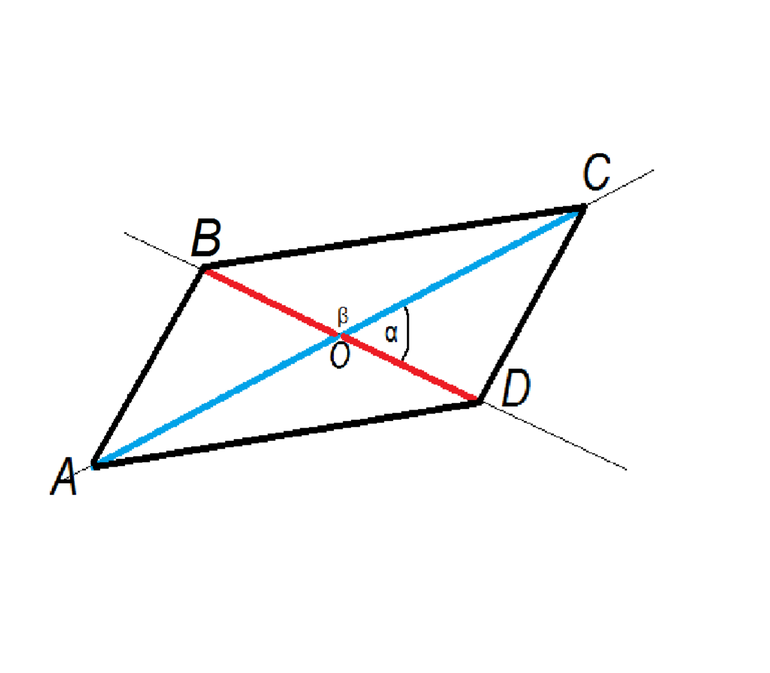
Другой случай, когда даны обе диагонали параллелограмма f- и e-. Воспользовавшись геометрическими построениями на плоскать, можно показать справедливость следующего выражения:

Здесь teta — это угол пересечения e- и f-. Таким образом, чтобы вычислить площадь параллелограмма, диагоналями которого служат вектора, следует вычислить половину модуля их векторного произведения.

Пример решения

Все разнообразие задач на определение площади параллелограмма сводится к знанию единственной формулы векторного произведения. Пусть известны две диагонали фигуры. Они имеют координаты:

Чтобы определить величину S4, достаточно без промежуточных вычислений воспользоваться формулой векторного произведения заданных направленных отрезков:

В связи с развитием интернета, всегда можно использовать калькулятор-онлайн для расчета величины S4. Соответствующий электронный ресурс можно знайти, воспользовавшись любой поисковой системой в браузере.

Трехмерное пространство

В пространственной системе координат каждый вектор задается тремя числами, поэтому их векторное произведение c- также будет представлять набор трех цифр. Построенный в пространстве параллелограмм на двух векторах будет иметь площадь, равную длине направленного отрезка c-. Для расчета его модуля следует использовать известное выражение: сумма квадратов трех координат под корнем.

Таким образом, площадь параллелограмма проще всего вычислять, используя операцию умножения векторов. Этот метод является универсальным не только для задач на плоскости, но и для решения проблем в трехмерной системе координат.

[spoiler title=”источники:”]

http://nauka.club/matematika/geometriya/ploshchad-parallelogramma-postroennogo-na-vektorakh.html

[/spoiler]

Задача 1 Разложить вектор По векторам и .

Пусть , т. е. ;

След., вектор .

Задача 2 Найти длину диагонали параллелограмма, построенного на векторах , если

Рассм. диагонали параллелограмма ;

Вычислим ;

;

Задача 3 Показать, что точки Являются вершинами параллелограмма и найти проекцию одной из диагоналей на большую сторону параллелограмма.

Рассм.

, след. – параллелограмм (так как две противоположные стороны параллельны и равны);

Рассм. Рассм. ; ,

След. – большая сторона параллелограмма ; рассм. диагональ ;

Вычислим Вычислим ;

.

Задача 4 Длина гипотенузы прямоугольного треугольника равна . Вычислить

Задача 5 Найти момент силы, приложенной в точке относительно точки, а также модуль и направляющие косинусы вектора силы

1) , где ; ;

;

2) ;

Направл. косинусы вектора : ; ; .

Задача 6 Треугольник построен на векторах Найти длину высоты , если векторы взаимно перпендикулярны и по модулю равны

Рассм. векторы рассм. ;

;

;

;

Задача 7 Найти координаты вершины тетраэдра, если известно, что она лежит на оси , объём тетраэдра равен , .

Пусть искомая вершина тетраэдра (т. к. т. );

Рассм. в-ры: ;

Рассм. смешанное произв-е:

Рассм. объём тетраэдра : ; ; ;

; ; ; след., возможные положения искомой т.: ; .

Задача 8 В треугольнике известны координаты двух вершин: И точки пересечения медиан . Составить уравнение высоты треугольника, проведённой из вершины .

1) Определим координаты точки Как середины отрезка :;

2) Определим координаты вершины , используя равенство , где ;

Рассм.

;

3) составим ур-е высоты : рассм. в-р ;

Рассм. т. И рассм. в-р ; тогда по условию задачи и и, след., ур-е прямой , проходящей через Перпендикулярно в-ру , можно записать в виде: т. е. .

Задача 9 В параллелограмме известны уравнения сторон и координаты точки пересечения диагоналей Составить уравнения двух других сторон и диагоналей параллелограмма.

1) определим координаты точки как точки пересечения прямых :

;

2) определим координаты точки из условия, что т. – середина отрезка :

;

3) составим уравнение диагонали как прямой, проходящей через точки : ;

4) составим уравнение стороны как прямой, проходящей через точку параллельно

Прямой ;

5) составим уравнение стороны как прямой, проходящей через точку Параллельно

Прямой ;

6) определим координаты точки как точки пересечения прямых :

;

7) составим уравнение диагонали как прямой, проходящей через точки : .

Задача 10 Составить уравнение плоскости, проходящей через точки

Пусть – искомая плоскость; рассм. векторы ;

Рассм. норм. вектор ;

Рассм. произв. т. и рассм. вектор ;

, т. е. ;

Задача 11 Составить уравнение прямой , которая, проходит через точку и пересекает две прямые и .

Рассм. направл. векторы прямых ;

Рассм. т.; рассм. векторы ;

Пусть – плоскость, в которой лежат прямые ; пусть – плоскость, в которой лежат прямые ; тогда искомая прямая есть линия пересечения плоскостей ;

;

;

В качестве направл. вектора прямой можно взять вектор ; выберем ;

Запишем канонические ур-я прямой Как ур-я прямой, проходящей через т. А параллельно

Вектору : ; параметрические ур-я прямой :

Задача 12 Составить уравнение геометрического места всех прямых, проходящих через точку перпендикулярно прямой .

Запишем канонич. уравнения прямой в виде: ; её направл. вектор ;

Рассм. произв. прямую , удовлетв. условию задачи; рассм. произв. точку и её направл. вектор ; , т. е. ;

Плоскость и есть искомое геометрическое место.

Задача 13 Вычислить определитель третьего порядка, пользуясь определением; результат проверить разложением

Определителя по первой строке.

1) Непосредственное вычисление:

2) Разложение по 1-й строке:

Задача 14 Решить систему линейных уравнений по правилу Крамера и с помощью обратной матрицы:

Запишем данную систему уравнений в матричной форме: , (1) , где ; ; ;

Рассм. опред-ль матрицы : ,

След., матр. – невырожденная и можно применять формулы Крамера и вычислять обратную матр. ;

1) решим с – му ур – й (1) по правилу Крамера, т. е. с помощью формул: , , , где ;

;

;

; , , ;

реш–е с–мы ур–й (1) в коорд. форме: вектор–решение с-мы (1): ;

2) получим реш–е с–мы ур–й (1) с помощью обратной матр. :

, след., матр.– невырожденная и существует обратная матр. ;

Умножим рав-во (1) слева на матрицу : , ; вычислим обратную матр. :

Находим алгебр. дополнения для всех эл-тов матрицы и составим из них м-цу :

Транспонируем м-цу и получим «присоединённую» м-цу

Разделим все эл-ты присоедин. м-цы на опр-ль и получим обратную матр. :

Находим теперь вектор-решение :

Задача 15 Установить, являются ли векторы линейно зависимыми.

Вычислим ранг системы векторов методом Гаусса, т. е. выпишем матрицу их координат и приведём её к ступенчатому виду:

ранг матрицы , след. данная система векторов линейно независима.

Задача 16 Исследовать систему линейных уравнений на совместность и в случае совместности найти её решение методом Гаусса.

Выпишем расширенную матрицу данной системы ур-й и приведём её к ступенчатому виду:

имеем ;

Так как , то по теореме Кронекера – Капелли данная система уравнений совместна, а так как , то система имеет бесконечное множество решений; объявим свободной переменной и выпишем общее решение системы в координатной форме:

общее решение системы имеет вид:

Задача 17 Найти матрицу преобразования, выражающего Через , если

Запишем данные преобразования в матричной форме: , где матрицы и

Вектор – столбцы имеют вид:

Рассм. ;

Вычислим матрицу .

Задача 18 Найти собственные числа и собственные векторы линейного преобразования, заданного матрицей

1) Находим собств. значения линейного преобразования , т. е. корни характеристического уравнения :

Рассм.

– собств. значения (действ.) лин. преобр-я ;

2) находим собств. векторы линейного преобразования , соотв. собств. значениям :

А) рассм.

Рассм. Пусть , тогда вектор ;

Б) рассм.

Рассм.

Пусть , тогда , вектор ;

Пусть , тогда , вектор ;

След. собств. векторы линейного преобразования суть:

; ; .

< Предыдущая

Комментарии преподавателя

 По­вто­ре­ние тео­рии. За­да­чи

 1. Основные определения

На­пом­ним, что су­ще­ству­ют такие фи­зи­че­ские ве­ли­чи­ны, для ко­то­рых важна не толь­ко ве­ли­чи­на, но и на­прав­ле­ние. Такие ве­ли­чи­ны на­зы­ва­ют­ся век­тор­ны­ми, или век­то­ра­ми, и обо­зна­ча­ют­ся они на­прав­лен­ным от­рез­ком, то есть таким от­рез­ком, у ко­то­ро­го от­ме­че­ны на­ча­ло и конец. Вве­де­но было по­ня­тие кол­ли­не­ар­ных век­то­ров, то есть таких, ко­то­рые лежат либо на одной пря­мой, либо на па­рал­лель­ных пря­мых.

Мы рас­смат­ри­ва­ем век­тор, ко­то­рый можно от­ло­жить от любой точки, за­дан­ный век­тор от про­из­воль­но вы­бран­ной точки можно от­ло­жить един­ствен­ным об­ра­зом.

Было вве­де­но по­ня­тие рав­ных век­то­ров – это такие со­на­прав­лен­ные век­то­ры, длины ко­то­рых равны. Со­на­прав­лен­ны­ми на­зы­ва­ют­ся кол­ли­не­ар­ные век­то­ры, на­прав­лен­ные в одну сто­ро­ну.

Были вве­де­ны пра­ви­ла тре­уголь­ни­ка и па­рал­ле­ло­грам­ма – пра­ви­ла сло­же­ния век­то­ров.

За­да­ны два век­то­ра – век­то­ры  и . Най­дем сумму этих двух век­то­ров . Для этого от­ло­жим из неко­то­рой точки А век­тор .  – на­прав­лен­ный от­ре­зок, точка А – его на­ча­ло, а точка В – конец. Из точки В от­ло­жим век­тор . Тогда век­тор  на­зы­ва­ют сум­мой за­дан­ных век­то­ров:  – пра­ви­ло тре­уголь­ни­ка (см. Рис. 1).

Рис. 1

За­да­но два век­то­ра – век­то­ры  и . Най­дем сумму этих двух век­то­ров  по пра­ви­лу па­рал­ле­ло­грам­ма.

От­кла­ды­ва­ем из точки А век­тор  и век­тор  (см. Рис. 2). На от­ло­жен­ных век­то­рах можно по­стро­ить па­рал­ле­ло­грамм. Из точки В от­кла­ды­ва­ем век­тор , век­то­ры  и  равны, сто­ро­ны ВС и

Рис. 2

АВ1 па­рал­лель­ны. Ана­ло­гич­но па­рал­лель­ны и сто­ро­ны АВ и В1С, таким об­ра­зом, мы по­лу­чи­ли па­рал­ле­ло­грамм. АС – диа­го­наль па­рал­ле­ло­грам­ма. 

 2. Правила сложения векторов

Для сло­же­ния несколь­ких век­то­ров при­ме­ня­ют пра­ви­ло мно­го­уголь­ни­ка (см. Рис. 3). Нужно из про­из­воль­ной точки от­ло­жить пер­вый век­тор, из его конца от­ло­жить вто­рой век­тор, из конца вто­ро­го век­то­ра от­ло­жить тре­тий и так далее, когда все век­то­ры от­ло­же­ны – со­еди­нить на­чаль­ную точку с кон­цом по­след­не­го век­то­ра, в итоге по­лу­чит­ся сумма несколь­ких век­то­ров.

Рис. 3

Кроме того, мы рас­смот­ре­ли по­ня­тие об­рат­но­го век­то­ра – век­то­ра, име­ю­ще­го такую же длину, как за­дан­ный, но ему про­ти­во­на­прав­лен­но­го.

 3. Решение примеров

При­мер 1 – за­да­ча 747: вы­пи­ши­те пары кол­ли­не­ар­ных со­на­прав­лен­ных век­то­ров, ко­то­рые опре­де­ля­ют­ся сто­ро­на­ми па­рал­ле­ло­грам­ма; ука­жи­те про­ти­во­по­лож­но на­прав­лен­ные век­то­ры;

Задан па­рал­ле­ло­грамм MNPQ (см. Рис. 4). Вы­пи­шем пары кол­ли­не­ар­ных век­то­ров. В первую оче­редь это век­то­ры  и . Они не толь­ко кол­ли­не­ар­ные, но и рав­ные, т.к. они со­на­прав­ле­ны, и длины их равны по свой­ству па­рал­ле­ло­грам­ма (в па­рал­ле­ло­грам­ме про­ти­во­по­лож­ные сто­ро­ны равны). Сле­ду­ю­щая пара . Ана­ло­гич­но

Рис. 4

вы­пи­шем кол­ли­не­ар­ные век­то­ры вто­рой пары сто­рон: ; .

Про­ти­во­по­лож­но на­прав­лен­ные век­то­ры: , , , .

При­мер 2 – за­да­ча 756: на­чер­ти­те по­пар­но некол­ли­не­ар­ные век­то­ры ,  и . По­строй­те век­то­ры ;; ;.

Для вы­пол­не­ния дан­но­го за­да­ния можем поль­зо­вать­ся пра­ви­лом тре­уголь­ни­ка или па­рал­ле­ло­грам­ма.

Спо­соб 1 – с по­мо­щью пра­ви­ла тре­уголь­ни­ка (см. Рис. 5):

Рис. 5

Спо­соб 2 – с по­мо­щью пра­ви­ла па­рал­ле­ло­грам­ма (см. Рис. 6):

Рис. 6

Ком­мен­та­рий: мы при­ме­ня­ли в пер­вом спо­со­бе пра­ви­ло тре­уголь­ни­ка – от­кла­ды­ва­ли из про­из­воль­но вы­бран­ной точки А пер­вый век­тор, из его конца – век­тор, про­ти­во­по­лож­ный вто­ро­му, со­еди­ня­ли на­ча­ло пер­во­го с кон­цом вто­ро­го, и таким об­ра­зом по­лу­ча­ли ре­зуль­тат вы­чи­та­ния век­то­ров. Во вто­ром спо­со­бе мы при­ме­ни­ли пра­ви­ло па­рал­ле­ло­грам­ма – по­стро­и­ли на нуж­ных век­то­рах па­рал­ле­ло­грамм и его диа­го­наль – ис­ко­мую раз­ность, помня тот факт, что одна из диа­го­на­лей – это сумма век­то­ров, а вто­рая – раз­ность.

При­мер 3 – за­да­ча 750: до­ка­жи­те, что если век­то­ры  и  равны, то се­ре­ди­ны от­рез­ков AD и BC сов­па­да­ют. До­ка­жи­те об­рат­ное утвер­жде­ние: если се­ре­ди­ны от­рез­ков AD и BC сов­па­да­ют, то век­то­ры  и  равны (см. Рис. 7).

Из ра­вен­ства век­то­ров  и  сле­ду­ет, что пря­мые АВ и CD па­рал­лель­ны, и что от­рез­ки АВ и CD равны. Вспом­ним при­знак па­рал­ле­ло­грам­ма: если у че­ты­рех­уголь­ни­ка пара про­ти­во­по­лож­ных сто­рон лежит на па­рал­лель­ных пря­мых, и их длины равны, то дан­ный че­ты­рех­уголь­ник – па­рал­ле­ло­грамм.

Рис. 7

Таким об­ра­зом, че­ты­рех­уголь­ник ABCD, по­стро­ен­ный на за­дан­ных век­то­рах, – па­рал­ле­ло­грамм. От­рез­ки AD и BC яв­ля­ют­ся диа­го­на­ля­ми па­рал­ле­ло­грам­ма, одно из свойств ко­то­ро­го: диа­го­на­ли па­рал­ле­ло­грам­ма пе­ре­се­ка­ют­ся и в точке пе­ре­се­че­ния де­лят­ся по­по­лам. Таким об­ра­зом, до­ка­за­но, что се­ре­ди­ны от­рез­ков AD и BC сов­па­да­ют.

До­ка­жем об­рат­ное утвер­жде­ние. Для этого вос­поль­зу­ем­ся дру­гим при­зна­ком па­рал­ле­ло­грам­ма: если в неко­то­ром че­ты­рех­уголь­ни­ке диа­го­на­ли пе­ре­се­ка­ют­ся и точ­кой пе­ре­се­че­ния де­лят­ся по­по­лам, то этот че­ты­рех­уголь­ник – па­рал­ле­ло­грамм. От­сю­да че­ты­рех­уголь­ник ABCD – па­рал­ле­ло­грамм, и его про­ти­во­по­лож­ные сто­ро­ны па­рал­лель­ны и равны, таким об­ра­зом, век­то­ры  и  кол­ли­не­ар­ны, оче­вид­но, что они со­на­прав­ле­ны, и мо­ду­ли их равны, от­сю­да век­то­ры  и  равны, что и тре­бо­ва­лось до­ка­зать.

При­мер 4 – за­да­ча 760: до­ка­жи­те, что для любых некол­ли­не­ар­ных век­то­ров  и  спра­вед­ли­во нера­вен­ство  (см. Рис. 8)

От­ло­жим из про­из­воль­ной точки А век­тор , по­лу­чим точку В, из нее от­ло­жим некол­ли­не­ар­ный ему век­тор . По пра­ви­лу па­рал­ле­ло­грам­ма или тре­уголь­ни­ка по­лу­чим сумму век­то­ров  – век­тор . Имеем тре­уголь­ник .

Длина суммы век­то­ров со­от­вет­ству­ет длине сто­ро­ны АС тре­уголь­ни­ка. По нера­вен­ству тре­уголь­ни­ка длина сто­ро­ны АС мень­ше, чем сумма длин двух дру­гих сто­рон АВ и ВС, что и тре­бо­ва­лось до­ка­зать.

Рис. 8

При­ме­не­ние век­то­ров к ре­ше­нию задач

 4. Выражение вектора через два неколлинеарных

На­пом­ним, что мы уже изу­чи­ли неко­то­рые факты о век­то­рах, и те­перь умеем опре­де­лять рав­ные век­то­ры, кол­ли­не­ар­ные век­то­ры, со­на­прав­лен­ные и про­ти­во­по­лож­но на­прав­лен­ные. Также мы умеем скла­ды­вать век­то­ры по пра­ви­лу тре­уголь­ни­ка и па­рал­ле­ло­грам­ма, скла­ды­вать несколь­ко век­то­ров по пра­ви­лу мно­го­уголь­ни­ка, умеем умно­жать век­тор на число. Ре­ше­ние задач с век­то­ра­ми ис­поль­зу­ет все эти зна­ния. Пе­рей­дем к ре­ше­нию неко­то­рых при­ме­ров.

При­мер 1 – за­да­ча 769: от­ре­зок ВВ1 – ме­ди­а­на тре­уголь­ни­ка . Вы­ра­зи­те через век­то­ры  и  век­то­ры , ,  и .

От­ме­тим, что век­то­ры  и  некол­ли­не­ар­ны, то есть пря­мые АВ и АС не па­рал­лель­ны.

В даль­ней­шем мы узна­ем, что любой век­тор может быть вы­ра­жен через два некол­ли­не­ар­ных век­то­ра.

Вы­ра­зим пер­вый век­тор (см. Рис. 1): , т. к. по усло­вию ВВ1 – ме­ди­а­на тре­уголь­ни­ка, зна­чит, век­то­ры  и  имеют рав­ные мо­ду­ли, кроме того, оче­вид­но, что они кол­ли­не­ар­ны и при этом со­на­прав­ле­ны, зна­чит, дан­ные век­то­ра равны.

Рис. 1

Для вы­ра­же­ния сле­ду­ю­ще­го век­то­ра вос­поль­зу­ем­ся пра­ви­лом па­рал­ле­ло­грам­ма для вы­чи­та­ния. Мы пом­ним, что одна из диа­го­на­лей па­рал­ле­ло­грам­ма, по­стро­ен­но­го на двух век­то­рах, со­от­вет­ству­ет сумме этих век­то­ров, а вто­рая – их раз­но­сти. Диа­го­наль, со­от­вет­ству­ю­щая раз­но­сти век­то­ров, сле­ду­ет от конца к на­ча­лу, таким об­ра­зом, если по­стро­ить на за­дан­ных век­то­рах  и  па­рал­ле­ло­грамм, то его диа­го­наль  будет со­от­вет­ство­вать раз­но­сти .

Век­тор  яв­ля­ет­ся про­ти­во­по­лож­ным к за­дан­но­му век­то­ру , от­сю­да .

Век­тор  ана­ло­гич­но век­то­ру  можно пред­ста­вить в виде раз­но­сти век­то­ров . При вы­ра­же­нии сле­ду­ет учесть тот факт, что точка В1 яв­ля­ет­ся се­ре­ди­ной от­рез­ка АС, зна­чит, век­то­ры  и  равны, зна­чит, век­тор  можно пред­ста­вить как удво­ен­ное про­из­ве­де­ние век­то­ра .

Перед ре­ше­ни­ем за­да­чи мы ска­за­ли, что через за­дан­ные два некол­ли­не­ар­ных век­то­ра можно вы­ра­зить любой век­тор. Вы­ра­зим, на­при­мер, ме­ди­а­ну АА1 (см. Рис. 2).

По­лу­чи­ли си­сте­му урав­не­ний, вы­пол­ним их сло­же­ние:

Век­то­ры  в сумме со­став­ля­ют ну­ле­вой век­тор, так как они кол­ли­не­ар­ны и про­ти­во­на­прав­ле­ны, а мо­ду­ли их равны, таким об­ра­зом по­лу­ча­ем:

Рис. 2

По­де­лим обе части урав­не­ния на два, по­лу­чим: 

Из дан­ной за­да­чи можно сде­лать вывод, что если за­да­ны два некол­ли­не­ар­ных век­то­ра, то любой тре­тий век­тор на плос­ко­сти можно од­но­знач­но вы­ра­зить через эти два век­то­ра. Для этого необ­хо­ди­мо при­ме­нить пра­ви­ло сло­же­ния век­то­ров, либо ме­то­дом тре­уголь­ни­ка, либо па­рал­ле­ло­грам­ма, и пра­ви­ло умно­же­ния век­то­ра на число.

 5. Свойство средней линии треугольника

При­мер 2: до­ка­зать с по­мо­щью век­то­ров свой­ство сред­ней линии тре­уголь­ни­ка (см. Рис. 3).

Задан про­из­воль­ный тре­уголь­ник , точки M и N – се­ре­ди­ны сто­рон АВ и АС со­от­вет­ствен­но, MN – сред­няя линия тре­уголь­ни­ка. Свой­ство сред­ней линии: сред­няя линия па­рал­лель­на ос­но­ва­нию тре­уголь­ни­ка и равна его по­ло­вине.

До­ка­за­тель­ство дан­но­го свой­ства ана­ло­гич­но для тре­уголь­ни­ка и тра­пе­ции.

Рис. 3

Вы­ра­зим век­тор  двумя спо­со­ба­ми:

По­лу­чи­ли си­сте­му урав­не­ний:

          Вы­пол­ним сло­же­ние урав­не­ний си­сте­мы:

Сумма век­то­ров  – это ну­ле­вой век­тор, длины этих век­то­ров равны по усло­вию, кроме того, они оче­вид­но кол­ли­не­ар­ны и про­ти­во­на­прав­ле­ны. Ана­ло­гич­но сум­мой век­то­ров  будет ну­ле­вой век­тор. По­лу­ча­ем:

По­де­лим обе части урав­не­ния на два:

Таким об­ра­зом, мы по­лу­чи­ли, что сред­няя линия тре­уголь­ни­ка равна по­ло­вине его ос­но­ва­ния. Кроме того, из ра­вен­ства век­то­ра  по­ло­вине век­то­ра  сле­ду­ет, что эти век­то­ры кол­ли­не­ар­ны и со­на­прав­ле­ны, а зна­чит, пря­мые MN и ВС па­рал­лель­ны.

Таким об­ра­зом, мы до­ка­за­ли свой­ство сред­ней линии тра­пе­ции при по­мо­щи век­то­ров.

 6. Свойство точки пересечения медиан треугольника

При­мер 3: задан про­из­воль­ный тре­уголь­ник  (см. Рис. 4). В нем про­ве­де­ны ме­ди­а­ны АА1, ВВ1, СС1. Точка пе­ре­се­че­ния ме­ди­ан – М. Век­тор  со­от­вет­ству­ет силе ,  – силе ,  – силе . До­ка­зать, что .

На­пом­ним, что ме­ди­а­ны тре­уголь­ни­ка пе­ре­се­ка­ют­ся в одной точке и этой точ­кой де­лят­ся в от­но­ше­нии 2:1, счи­тая от вер­ши­ны.

Ино­гда точку пе­ре­се­че­ния ме­ди­ан на­зы­ва­ют цен­тром тя­же­сти тре­уголь­ни­ка.

Вы­пол­ним сло­же­ние век­то­ров , вос­поль­зу­ем­ся для этого пра­ви­лом па­рал­ле­ло­грам­ма (см. Рис. 5).

Рис. 4

По­лу­ча­ем: 

С дру­гой сто­ро­ны, , так как BMCD – па­рал­ле­ло­грамм, диа­го­на­ли па­рал­ле­ло­грам­ма точ­кой пе­ре­се­че­ния де­лят­ся по­по­лам, А1 – точка пе­ре­се­че­ния диа­го­на­лей па­рал­ле­ло­грам­ма, зна­чит, от­рез­ки МА1 и А1D равны, от­сю­да, по свой­ству точки пе­ре­се­че­ния ме­ди­ан, длины век­то­ров  и  равны, но дан­ные век­то­ры про­ти­во­на­прав­ле­ны, а зна­чит, их сумма

Рис. 5

равна ну­ле­во­му век­то­ру. Мы пом­ним, что век­тор , а век­тор , таким об­ра­зом, , что и тре­бо­ва­лось до­ка­зать.

 7. Неравенство треугольника

При­мер 4 – за­да­ча 773: до­ка­жи­те, что для любых век­то­ров  и  спра­вед­ли­во сле­ду­ю­щее нера­вен­ство: 

Ре­ше­ние: пред­ста­вим раз­ность век­то­ров в виде суммы: . Также об­ра­тим вни­ма­ние на тот факт, что длины про­ти­во­на­прав­лен­ных век­то­ров  и  равны: . Таким об­ра­зом, можно пе­ре­пи­сать ис­ход­ное вы­ра­же­ние:

Для удоб­ства вве­дем новую пе­ре­мен­ную:  и пе­ре­пи­шем вы­ра­же­ние:

. А дан­ное нера­вен­ство – нера­вен­ство тре­уголь­ни­ка – было до­ка­за­но в преды­ду­щем уроке. От­ме­тим, что ра­вен­ство на­блю­да­ет­ся в том слу­чае, когда тре­уголь­ник вы­рож­да­ет­ся в от­ре­зок.

Итак, мы вспом­ни­ли все ос­нов­ные опре­де­ле­ния и свой­ства век­то­ров, вспом­ни­ли ос­нов­ные опе­ра­ции над век­то­ра­ми, рас­смот­ре­ли при­ме­не­ние век­то­ров при ре­ше­нии раз­лич­ных задач, до­ка­за­ли неко­то­рые свой­ства фигур и ре­ши­ли наи­бо­лее рас­про­стра­нен­ные типы задач.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/vektory/vektory-povtorenie-teorii-zadachi

http://interneturok.ru/ru/school/geometry/8-klass/vektory/primenenie-vektorov-k-resheniyu-zadach

http://metodbook.ru/index.php/matematika/9-testy-po-geometrii-9-klass/8-itogovyj-test-po-teme-vektory-variant-1.html

http://metodbook.ru/index.php/matematika/9-testy-po-geometrii-9-klass/9-itogovyj-test-po-teme-vektory-variant-2.html

http://uslide.ru/images/22/28455/960/img5.jpg

http://www.studfiles.ru/html/2706/538/html_OqWQ3sDQeV.5bGa/htmlconvd-WBhq8w_html_73af1ab4.png

http://uchkollektor39.ru/uploads/images/items/29cc1d8d90989d9f0e3df70c3d95a9ee.jpg

http://rushkolnik.ru/tw_files2/urls_3/891/d-890061/890061_html_m5ff065f.jpg

http://cs1-48v4.vk-cdn.net/p24/3551abddfac0c8.mp3?extra=amJxaBk9gfTT0lPmsOEwb8Rn_T2twbNJH1OUazYT-T9cSSu4_1787ibMzOu6ytv1rZKrpdEq7XnWZN1f-bjAuKyWIFf7mzw

http://matssir.ucoz.ru/_ld/0/33_G8p84-85.pptx

http://nsportal.ru/sites/default/files/2014/05/11/vektory._dokazatelstvo.pptx

http://v.5klass.net/zip/b66d124d0243f848a0bf454b75404034.zip

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---