Как найти точку пересечения диагоналей равнобедренной трапеции

3. Геометрия на плоскости (планиметрия). Часть I

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

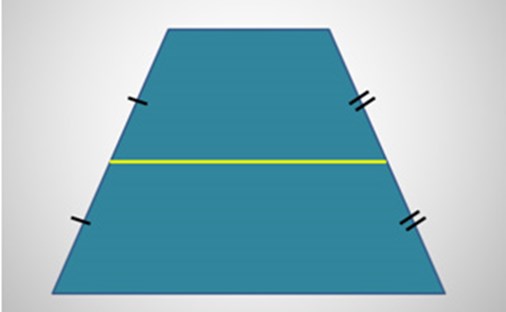
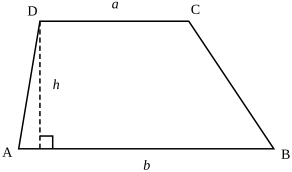
Признаки и свойства равнобедренной трапеции

(blacktriangleright) Равнобедренная трапеция – трапеция, у которой боковые стороны равны.

Свойства равнобедренной трапеции:

(blacktriangleright) Углы при каждом основании равны;

(blacktriangleright) Диагонали равны;

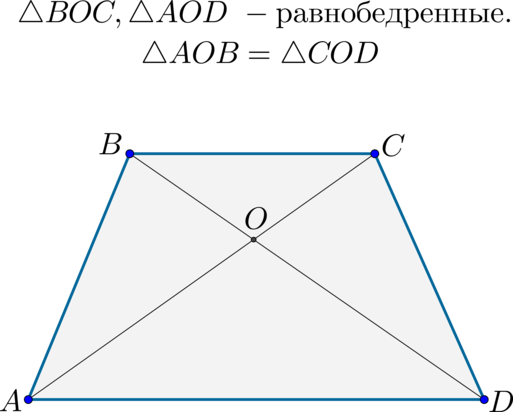
(blacktriangleright) Два треугольника, образованные диагоналями и одним из оснований, являются равнобедренными;

(blacktriangleright) Два треугольника, образованные диагоналями и боковой стороной, равны.

Задание
1

#296

Уровень задания: Равен ЕГЭ

В трапеции (ABCD): (AB = CD), (angle C – angle A = 80^{circ}). Найдите (angle D + angle B – angle C). Ответ дайте в градусах.

У равнобедренной трапеции углы при одном основании равны, тогда (angle B = angle C) и, следовательно, (angle D + angle B – angle C = angle D = angle A).

У равнобедренной трапеции сумма противоположных углов равна (180^{circ}) (так как (angle C = angle B), а (angle A + angle B = 180^{circ}), как сумма односторонних при параллельных прямых и секущей).

(angle A + angle C = 180^{circ}),

(angle C – angle A = 80^{circ})
тогда, вычитая из верхнего равенства нижнее, получаем (2cdot angle A = 100^{circ}). В итоге имеем: (angle D + angle B – angle C = angle A = 50^{circ}).

Ответ: 50

Задание
2

#1699

Уровень задания: Равен ЕГЭ

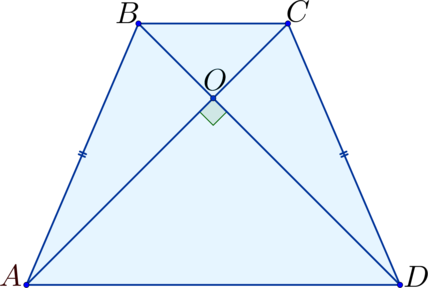
Диагонали в равнобедренной трапеции (ABCD) перпендикулярны. Найдите площадь трапеции, если диагональ (AC) равна (2).

В равнобедренной трапеции диагонали равны, поэтому (AC = BD = 2). Пускай (O) – точка пересечения диагоналей.

[begin{gathered}
S_{ABCD} = S_{triangle ABC} + S_{triangle CDA} = frac{1}{2}cdot AC cdot BO + frac{1}{2}cdot AC cdot OD =\ =frac{1}{2}cdot AC cdot(BO + OD) = frac{1}{2}cdot AC cdot BD = frac{1}{2} cdot 2 cdot 2 = 2end{gathered}]

Ответ: 2

Задание
3

#1789

Уровень задания: Равен ЕГЭ

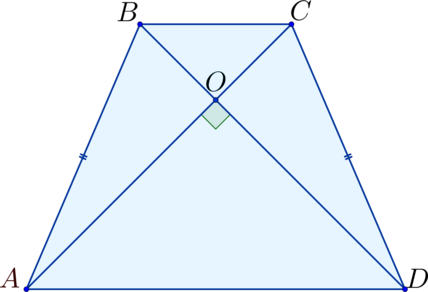
Найдите диагонали равнобедренной трапеции, если они перпендикулярны, а площадь трапеции равна (8).

Пусть (ABCD) — трапеция с диагоналями (AC) и (BD), (O) – точка их пересечения, тогда
(S_{ABCD} = S_{triangle ABC} + S_{triangle CDA} = frac{1}{2}cdot AC cdot BO + frac{1}{2}cdot AC cdot OD = )
(frac{1}{2}cdot AC cdot(BO + OD) = frac{1}{2}cdot AC cdot BD =
frac{1}{2}cdot AC^2 = 8) (Rightarrow) (AC = 4).

Ответ: 4

Задание
4

#1704

Уровень задания: Равен ЕГЭ

В равнобедренной трапеции (ABCD) основание (AD) вдвое длиннее основания (BC) и боковой стороны. Найдите острый угол трапеции.

Если опустить высоты (BH) и (CK) на основание (AD), то они отсекут равные отрезки (AH) и (KD), причем (AB = BC = HK) (Rightarrow) (AH = frac{AD – HK}{2} = frac{HK}{2} = frac{AB}{2}) (Rightarrow) (angle ABH = 30^circ), как угол в прямоугольном треугольнике, противолежащий катету, равному половине гипотенузы (Rightarrow) (angle BAK = 90^circ – 30^circ = 60^circ).

Ответ: 60

Задание
5

#295

Уровень задания: Равен ЕГЭ

(ABCD) – трапеция с основаниями (AD) и (BC). При этом (AB = CD = 6), (BC = 4), один из углов трапеции (ABCD) равен (60^{circ}). Найдите (AD).

Пусть (angle A = 60^{circ}), (BE) – высота в треугольнике (ABD). (angle ABE = 90^{circ} – 60^{circ} = 30^{circ}). Катет, лежащий против угла в (30^{circ}), равен половине гипотенузы, тогда (AE = 0,5cdot 6 = 3).

У равнобедренной трапеции углы при одном основании равны, тогда (angle D = 60^{circ}). Пусть (CF) – высота в треугольнике (ACD), тогда аналогично тому, как находили (AE), находим, что (FD = 3). (EF = BC), так как (BCFE) – прямоугольник. Тогда (AD = AE + EF + FD = 3 + 4 + 3 = 10).

Ответ: 10

Задание
6

#1700

Уровень задания: Равен ЕГЭ

Диагонали в равнобедренной трапеции (ABCD) перпендикулярны. (O) – точка пересечения диагоналей, причем (AO:OC = 7:1). Найдите периметр трапеции, если меньшее основание равно (1).

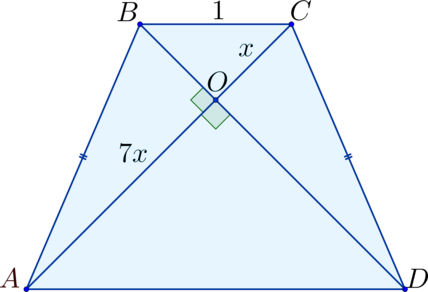
(BC) – меньшее основание, треугольники (triangle BOC) и (triangle AOD) подобны и их стороны относятся как (1:7) (Rightarrow) (BC:AD = 1:7) (Rightarrow) (AD = 7); (OB = OC), (OB^2 + OC^2 = 1^2) (Rightarrow) (OB = OC = frac{1}{sqrt2}) (Rightarrow) (AO = frac{7}{sqrt2}). В (triangle ABO): (AO^2 + OB^2 = AB^2) (Rightarrow) (AB = 5). Тогда (P_{ABCD} = AB + BC + CD + AD = 1 + 7 + 5 + 5 = 18).

Ответ: 18

Задание
7

#1702

Уровень задания: Равен ЕГЭ

В равнобедренной трапеции (ABCD) биссектриса (angle ABC) параллельна боковой стороне (CD) и пересекает основание (AD) в точке (K), которая делит (AD) в отношении (AK:KD = 1:2). Найдите периметр трапеции, если меньшее основание равно (4).

(BCDK) – параллелограмм, т.к. противоположные стороны попарно параллельны; (angle AKB = angle KBC), т.к. накрест лежащие при параллельных (BC) и (AD); (angle BAK = angle CDK = angle KBC) (Rightarrow) (triangle ABK) – равносторонний треугольник. (BC = KD = 4) (Rightarrow) (AK = 2 = AB = CD) (Rightarrow) (P_{ABCD} = AB + BC + CD + KD + AK = 2 + 4 + 2 + 4 + 2 = 14).

Ответ: 14

Учащимся старших классов, которые готовятся сдавать ЕГЭ по математике, в обязательном порядке стоит повторить тему «Равнобедренная трапеция» и освежить в памяти ее основные свойства и признаки. Многолетняя практика показывает, что подобные задания ежегодно встречаются в программе аттестационного испытания. Поэтому, если вы хотите успешно решить задачи ЕГЭ на применение основных свойств диагоналей или углов равнобедренной трапеции, вам непременно стоит разобраться в этой теме.

Образовательный портал «Школково» предлагает новый подход к подготовке к аттестационному испытанию. Наш ресурс позволяет учащимся определить наиболее сложные темы и ликвидировать имеющиеся пробелы в знаниях. Специалисты «Школково» подготовили и изложили весь материал в максимально доступной форме.

Чтобы выпускники могли успешно справляться с геометрическими задачами, мы рекомендуем вспомнить определение равнобедренной трапеции, свойства ее сторон, углов и диагоналей, а также формулу для вычисления площади. Эта информация представлена в разделе «Теоретическая справка».

Вспомнив основные свойства углов, диагоналей и сторон равнобедренной трапеции, учащиеся имеют возможность закрепить усвоенный материал, выполнив практические задания. Упражнения различного уровня сложности представлены в разделе «Каталог». В каждом из них вы найдете подробный алгоритм решения и правильный ответ.

Практиковаться в выполнении заданий по теме «Трапеция» при подготовке к ЕГЭ выпускники могут в режиме онлайн, находясь не только в Москве, но и в любом другом городе России. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.

УСТАЛ? Просто отдохни

Источник

25
Июл 2013

Категория: Справочные материалы

Трапеция. Свойства трапеции

2013-07-25
2016-06-15

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
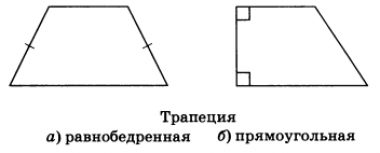
Если боковые стороны равны, трапеция называется равнобедренной.

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия – $k=frac{AD}{BC}.$

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

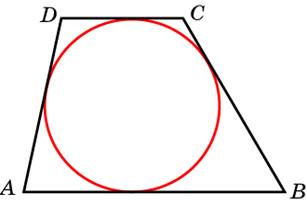
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

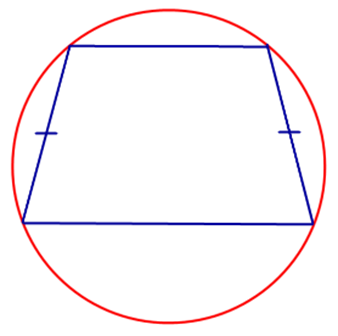
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Площадь

$S=frac{a+b}{2}cdot h$ или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Смотрите также площадь трапеции.

Автор: egeMax |

комментарий 431

Печать страницы

Источник

Трапеция и ее свойства

Т. А. Унегова

Определения:

Трапеция — это называется четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.

Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами трапеции.

Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

Если боковые стороны равны, трапеция называется равнобедренной.

Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание.

Трапеция называется вписанной в окружность, если каждая ее вершина принадлежит окружности.

Трапеция называется описанной вокруг окружности, если каждая ее сторона касается окружности.

Трапеция называется равнобедренной (равнобокой, равнобочной), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Теоремы о средней линии и диагоналях трапеции

Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме: $m=displaystyle frac{a+b}{2}$ .

Теорема 2. Диагонали трапеции делят среднюю линию трапеции на три отрезка. Средний из них равен полуразности оснований, а два крайних равны между собой: $EF=GH, ; FG=displaystyle frac{a-b}{2}$ .

Теорема 3. Средняя линия треугольника, составленного из диагоналей и суммы оснований трапеции, равна средней линии трапеции: PQ=MN .

Теорема 4. Четыре точки: середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон — лежат на одной прямой.

Эта теорема называется также «Замечательное свойство трапеции».

Теорема 5. Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.

Теоремы о площади трапеции

Теорема 6. Площадь трапеции равна произведению полусуммы ее оснований на высоту: $S=displaystyle frac{a+b}{2}cdot h$ .

Теорема 7. Площадь трапеции равна произведению ее средней линии на высоту: S=mh .

Теорема 8. Площадь трапеции (как и всякого выпуклого четырехугольника) равна половине произведения ее диагоналей на синус угла между ними: $S=displaystyle frac{1}{2}d_1d_2{sin alpha }$ , где d_1=AC, d_2=BD, (Вместо можно брать

Теорема 9. Если в трапецию можно вписать окружность, то (как и для всякого описанного многоугольника) площадь трапеции равна произведению ее полупериметра на радиус вписанной окружности: S=pr . Таким образом, $S=displaystyle frac{a+b+c+d}{2}cdot r$ .

Теорема 10. Площадь трапеции равна площади треугольника, составленного из диагоналей и суммы оснований этой трапеции. (Сравни эту теорему и теорему 3.)

Теоремы о вписанных и описанных трапециях

Теорема 11. Если трапеция вписана в окружность, то она равнобедренная. И наоборот, если трапеция равнобедренная, то около нее можно описать окружность.

Теорема 12. Если трапеция описана около окружности, то сумма оснований трапеции равна сумме ее боковых сторон.

Задачи ЕГЭ и ОГЭ по теме: Трапеция

Задача 1.

Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны sqrt{2} .

Решение:

Высота трапеции— это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины . Так как сторона квадратной клетки равна sqrt{2} , то по теореме Пифагора получаем, что h=2 .

Ответ: 2.

Задача 2.

Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол ${150}^{{}^circ }$ . Найдите площадь трапеции.

Решение:

Углы angle ABC и angle BAH — односторонние, их сумма равна ${180}^{{}^circ }$ , и тогда angle BAH $=30{}^circ .$

Из ABH найдем высоту BH. Катет, лежащий против угла в ${30}^{{}^circ }$ , равен половине гипотенузы. Получаем, что BH = 3,5.

Площадь трапеции равна $S=displaystyle frac{6+18}{2}cdot 3,5=42$ .

Ответ: 42.

Задача 3.

Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.

Решение:

Что можно увидеть на чертеже? Можно сказать, что изображена трапеция ABCD, и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, ABC и ACD, в которых проведены средние линии.

Напомним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны. Из ACD находим, что x=5.

Ответ: 5.

Задача 4.

Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Решение:

Проведем PQ — среднюю линию трапеции, PQ = 2,5 и . Отсюда получаем, что середина отрезка AC, то есть PM — средняя линия треугольника ABC и PM = 1. Аналогично, NQ = 1.

Ответ: 0,5.

Задача 5.

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Решение:

Периметр треугольника равен сумме его сторон, то есть

Периметр трапеции равен

Ответ: 23.

Задача 6.

В равнобедренной трапеции ABCD диагональ AC является биссектрисой острого угла трапеции и образует со стороной CD угол $63{}^circ$ . Найдите углы трапеции.

Решение:

Пусть angle CAD =alpha , тогда angle CAB =alpha и angle BAD =2alpha , так как трапеция равнобедренная.

Сумма углов $vartriangle ACD=3alpha +63{}^circ =180{}^circ$ , откуда
$alpha =39{}^circ .$
Итак, $angle D=78{}^circ$ , а $angle BCD=180{}^circ -78{}^circ =102{}^circ$ .

Ответ: $78{}^circ , 102{}^circ$ .

Задача 7.

В равнобедренной трапеции основания равны 10 м и 24 м, боковая сторона 25 м. Найдите высоту трапеции.

Решение:

В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и $h^2={25}^2-7^2=left(25-7right)left(25+7right)=18cdot 32.$ Отсюда,

Ответ: 24.

Задача 8.

Тупой угол равнобедренной трапеции равен ${135}^circ$ , а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.

Решение:

Проведем две высоты. Они разделят трапецию на три части: прямоугольник и два равных прямоугольных треугольника с острым углом $45{}^circ$ .

Каждый треугольник равнобедренный, поэтому h = 1,4.

Нетрудно видеть, что верхнее основание трапеции равно 2, а нижнее — 4,8. Отсюда площадь трапеции равна $displaystyle frac{2+4,8}{2}cdot 1,4=4,76$ .

Ответ: 4,76.

Задача 9.

Площадь трапеции равна 60м ^2, а основания 8 м и 12 м. Найдите высоту трапеции.

Решение:

Так как площадь трапеции $S=displaystyle frac{a+b}{2}cdot h$ , то $60=displaystyle frac{8+12}{2}cdot h$ , откуда h = 6.

Ответ: 6.

Задача 10.

В равнобедренной трапеции диагонали перпендикулярны и равны Найдите площадь трапеции.

Решение:

Проведем CE BD и DE — продолжение AD.

Так как BCDE — параллелограмм, то CE = a.

По теореме 10 получим, что $S_{ABCD}=S_{ACE}=displaystyle frac{1}{2}a^2$ .

Ответ: $displaystyle frac{1}{2}a^2$

Задач 11.

В трапеции ABCD с большим основанием AD диагональ AC перпендикулярна к боковой стороне CD и является биссектрисой угла A.

Найдите AD, если периметр трапеции равен 20, а угол D равен $60{}^circ$ .

Решение:

По условию задачи в прямоугольном ACD

angle D $=60{}^circ$ , следовательно, angle CAD $=30{}^circ$ .

Так как AC — биссектриса, то angle CAB $=30{}^circ$ , откуда angle DAB $=60{}^circ$ , то есть, трапеция равнобедренная. angle BCA =angle CAD $=30{}^circ$ как накрест лежащие, поэтому ABC — равнобедренный.

Обозначим длины боковых сторон ABC буквой x.

Тогда AB = BC = CD = x, и AD = 2x, так как в прямоугольном ACD против угла в $30{}^circ$ лежит катет, равный половине гипотенузы.

Таким образом, периметр трапеции, равный 20, составляет 5x, отсюда

x = 4 и AD = 8.

Ответ: 8.

Задача 12.

В равнобедренной трапеции ABCD с острым углом $60{}^circ$ меньшее основание BC равно 2, а боковая сторона AB равна 10. Продолжения боковых сторон трапеции пересекаются в точке M. Во сколько раз площадь трапеции больше площади треугольника BCM?

Решение:

Нетрудно видеть, что BCM равносторонний и BM = 2, тогда AM = 12 и BCM подобен ADM c коэффициентом .

Пусть $S_{BCM}$ =S_1 , $S_{ADM}=S_2$ , тогда

$S_2=k^2cdot S_1=36{cdot S}_1.$

Площадь трапеции будет равна

$S_{ABCD}=S_2-S_1=36 S_1-S_1=35 S_1=35 S_{BCM}.$

Ответ: 35.

Задача 13.

Сумма углов при одном из оснований трапеции равна $90{}^circ$ . Найдите длину отрезка, соединяющего середины оснований, если основания равны 6 и 10.

Решение:

Продолжим боковые стороны до пересечения в точке E и отметим точки F и G — середины оснований трапеции.

Так как сумма углов при основании трапеции равна $90{}^circ$ , то $angle BEC=90{}^circ$ , поэтому EF и EG — медианы в прямоугольных треугольниках BEC и AED соответственно.

Известно, что медиана, проведенная к гипотенузе, равна ее половине, значит

Ответ: 2.

Задача 14.

Найдите радиус окружности, вписанной в равнобочную трапецию, если средняя линия трапеции равна 10, а ее площадь 24.

Решение:

Так как площадь трапеции равна S=mh , а высота трапеции равна диаметру вписанной окружности, то есть h=2r, то , откуда r=1,2 .

Ответ: 1,2.

Задача 15.

Периметр прямоугольной трапеции равен 32, а большая боковая сторона равна 10. Найдите радиус r вписанной в трапецию окружности.

Решение:

По свойствам описанной трапеции сумма ее боковых сторон равна сумме оснований, поэтому

откуда

Сторона AB равна диаметру окружности, поэтому r=3 .

Ответ: 3.

Задача 16.

Около окружности описана трапеция, сумма боковых сторон которой равна 40. Найдите длину ее средней линии.

Решение:

Длина средней линии трапеции равна полусумме оснований. Если трапеция описана вокруг окружности, то в ней сумма оснований равна сумме боковых сторон, поэтому

$m=displaystyle frac{a+b}{2}=displaystyle frac{c+d}{2}=displaystyle frac{40}{2}=20.$

Ответ: 20.

Задача 17.

В окружность вписана трапеция так, что диаметр окружности служит основанием трапеции, а вершины другого основания делят полуокружность на три равные части. Найдите тупые углы трапеции. Ответ выразите в градусах.

Решение:

Так как AD — диаметр окружности, то дуга ABCD равна $180{}^circ$ . Она делится на три равные части по $60{}^circ .$

Вписанный угол D опирается на дугу ABC, которая равна $120{}^circ$ , отсюда $angle ADC=60{}^circ$ и, стало быть, $angle C=120{}^circ =angle B.$

Ответ: 120.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Трапеция и ее свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 ноября 2022 года; проверки требуют 26 правок.

Трапе́ция (от др.-греч. τραπέζιον — «столик» от τράπεζα — «стол») — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны^[1]. Часто в определении трапеции опускают последнее условие (см. ниже). Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон.

Варианты определения[править | править код]

Существует и другое определение трапеции.

Трапеция — это выпуклый четырёхугольник, у которого две стороны параллельны^[2]^[3]. Согласно этому определению, параллелограмм и прямоугольник — частные случаи трапеции. Однако при использовании такого определения большинство признаков и свойств равнобедренной трапеции перестают быть верными (так как параллелограмм становится её частным случаем). Приведённые в разделе Общие свойства формулы верны для обоих определений трапеции.

Связанные определения[править | править код]

Элементы трапеции[править | править код]

Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой

Параллельные противоположные стороны называются основаниями трапеции.
Две другие стороны называются боковыми сторонами.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Углом при основании трапеции называется её внутренний угол, образованный основанием с боковой стороной.

Виды трапеций[править | править код]

Трапеция, у которой боковые стороны равны, называется равнобедренной трапецией (реже равнобокой^[4] или равнобочной^[5] трапецией).
Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.

Равнобедренная трапеция
Прямоугольная трапеция

Свойства[править | править код]

Основной источник: ^[6]

Сумма углов, прилежащих к боковой стороне трапеции, равна $180^{circ }$ (как сумма двух внутренних односторонних углов при параллельных прямых, содержащих основания трапеции, и секущей, содержащей боковую сторону).
Средняя линия трапеции параллельна основаниям и равна их полусумме.^[7]
Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.
Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен ${frac {2xy}{x+y}}$ среднему гармоническому длин оснований трапеции.
В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
Если сумма углов при одном из оснований трапеции равна 90°, то продолжения боковых сторон пересекаются под прямым углом, а отрезок, соединяющий середины оснований, равен полуразности оснований.
Диагонали трапеции делят её на 4 треугольника. Два из них, прилежащие к основаниям, подобны. Два других, прилежащие к боковым сторонам, являются равновеликими [имеют одинаковую площадь].
Если отношение оснований равно , то отношение площадей треугольников, прилежащих к основаниям, равно $K^{2}$ .
Высота трапеции определяется формулой:

$h={sqrt {c^{2}-{frac {1}{4}}left({frac {c^{2}-d^{2}}{b-a}}+b-aright)^{2}}}$

где

— большее основание,

— меньшее основание,

— боковые стороны.

$d_{1}^{2}+d_{2}^{2}=2ab+c^{2}+d^{2}$

Их можно выразить в явном виде:

$d_{1}=AC={sqrt {ab+d^{2}+{frac {b(c^{2}-d^{2})}{b-a}}}}$

$d_{2}=BD={sqrt {ab+c^{2}-{frac {b(c^{2}-d^{2})}{b-a}}}}$

Если, наоборот, известны боковые стороны и диагонали, то основания выражаются формулами:

${displaystyle a={sqrt {frac {(c^{2}-d_{1}^{2})^{2}-(d^{2}-d_{2}^{2})^{2}}{2(c^{2}-d^{2}+d_{1}^{2}-d_{2}^{2})}}}}$

${displaystyle b={sqrt {frac {(c^{2}-d_{2}^{2})^{2}-(d^{2}-d_{1}^{2})^{2}}{2(c^{2}-d^{2}-d_{1}^{2}+d_{2}^{2})}}}}$

а при известных основаниях и диагоналях боковые стороны следующие:

${displaystyle c={sqrt {frac {a(d_{2}^{2}-b^{2})+b(d_{1}^{2}-a^{2})}{a+b}}}}$

${displaystyle d={sqrt {frac {a(d_{1}^{2}-b^{2})+b(d_{2}^{2}-a^{2})}{a+b}}}}$

Если же известна высота

, то

$d_{1}={sqrt {b^{2}+d^{2}-2b{sqrt {d^{2}-h^{2}}}}}={sqrt {h^{2}+left(b-{sqrt {d^{2}-h^{2}}}right)^{2}}}$

$d_{2}={sqrt {b^{2}+c^{2}-2b{sqrt {c^{2}-h^{2}}}}}={sqrt {h^{2}+left(b-{sqrt {c^{2}-h^{2}}}right)^{2}}}$

Прямая Ньютона для трапеции совпадает с её средней линией.

Неравенства для отрезков в трапеции[править | править код]

Теорема о четырёх точках трапеции[править | править код]

Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой.

Равнобедренная трапеция[править | править код]

Трапеция является равнобедренной тогда и только тогда, когда выполнено любое из следующих эквивалентных условий:

прямая, которая проходит через середины оснований, перпендикулярна основаниям (то есть является осью симметрии трапеции)^[8];
высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований;
углы при любом основании равны;
сумма противоположных углов равна 180°;
длины диагоналей равны;
диагонали трапеции образовывали с одним и тем же основание равные углы;
из каждой вершины одного основания другое основание было видно под одним и тем же углом^[9];
вокруг этой трапеции можно описать окружность;
вершинами этой трапеции также являются вершины некоторого антипараллелограмма.

Кроме того

если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Если — равнобочная трапеция (, ), причём — диагональ трапеции, то ${displaystyle {mathcal {{AC}^{2}=ADcdot BC+{AB}^{2}}}}$ .^[10]

Вписанная и описанная окружность[править | править код]

Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
Если трапецию можно вписать в окружность — то она равнобедренная.
Радиус описанной окружности равнобедренной трапеции:^{[источник не указан 2871 день]}

$R={frac {bcd_{1}}{4{sqrt {p(p-b)(p-c)(p-d_{1})}}}}={sqrt {frac {ab+c^{2}}{4-left({frac {b-a}{c}}right)^{2}}}}$

где $p={frac {1}{2}}(b+c+d_{1}),,,c$

— боковая сторона,

— бо́льшее основание,

— меньшее основание, $d_{1}=d_{2}$

— диагонали равнобедренной трапеции.

Если , то в равнобедренную трапецию можно вписать окружность радиуса

${displaystyle r={dfrac {h}{2}}={dfrac {sqrt {ab}}{2}}={dfrac {sqrt {d^{2}-l^{2}}}{2}}}$

Площадь[править | править код]

Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.

${displaystyle S={dfrac {(a+b)}{2}}h}$

Примечание: Приведённые выше две формулы эквивалентны, так как полусумма оснований равняется средней линии трапеции:

${displaystyle m={dfrac {(a+b)}{2}}}$

${displaystyle S={dfrac {a+b}{4(b-a)}}{sqrt {(a+c+d-b)(a+d-b-c)(a+c-b-d)(b+c+d-a)}}.}$

или

${displaystyle S={dfrac {a+b}{2}}{sqrt {c^{2}-{frac {1}{4}}left({dfrac {c^{2}-d^{2}}{b-a}}+b-aright)^{2}}}}$

Средняя линия разбивает фигуру на две трапеции, площади которых соотносятся как^[11]

${displaystyle {dfrac {S_{1}}{S_{2}}}={dfrac {3a+b}{a+3b}}}$

${displaystyle S={left({sqrt {S_{bigtriangleup AHD}}}+{sqrt {S_{bigtriangleup BHC}}}right)}^{2}.}$

Площадь трапеции равна произведению одной из боковых сторон на длину перпендикуляра, проведённого из середины другой боковой стороны к прямой, содержащей первую боковую сторону.

Формулы площади равнобедренной трапеции[править | править код]

${displaystyle S={dfrac {4r^{2}}{sin {alpha }}}}$

${displaystyle S={dfrac {d^{2}-l^{2}}{sin {alpha }}}}$

Площадь равнобедренной трапеции:

S=(b-ccos {gamma })csin {gamma }=(a+ccos {gamma })csin {gamma }

где

— боковая сторона,

— бо́льшее основание,

— меньшее основание, gamma

— угол между бо́льшим основанием и боковой стороной^[12].

Площадь равнобедренной трапеции через её стороны

$S={frac {a+b}{2}}{sqrt {c^{2}-{frac {1}{4}}(b-a)^{2}}}$

Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты:

${displaystyle S=h^{2}.}$

В этом случае средняя линия совпадает по длине с высотой трапеции, т. е. m=h .

История[править | править код]

Слово «трапеция» происходит от греческого слова др.-греч. τραπέζιον «столик» (уменьш. от τράπεζα «стол»), означающего стол. В русском языке от этого слова происходит слово «трапеза» (еда).

Примечания[править | править код]

↑ Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 587.
↑ Вся элементарная математика. Дата обращения: 6 июля 2015. Архивировано 9 июля 2015 года.
↑ Wolfram MathWorld. Дата обращения: 6 июля 2015. Архивировано 19 апреля 2015 года.
↑ Коллектив авторов. Современный справочник школьника. 5-11 классы. Все предметы. — Litres, 2015-09-03. — С. 82. — 482 с. — ISBN 9785457410022.
↑ М. И. Сканави. Элементарная математика. — 2013. — С. 437. — 611 с. — ISBN 9785458254489.
↑ Четырёхугольники. Архивная копия от 16 сентября 2015 на Wayback Machine
↑ Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 99.
↑ Эквивалентная формулировка: отрезки, соединяющие середины противоположных сторон трапеции, были взаимно перпендикулярны.
↑ Следствие. В случае перпендикулярности диагоналей боковым сторонам трапеция является равнобедренной.
↑ Комарова В. В. Экзаменационные вопросы и ответы. Геометрия: 9 и 11 выпускные классы. — М.: АСТ-ПРЕСС, 2000. — 448 с. — ISBN 5-7805-0416-4.
↑ Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. 2-е изд., перераб. и доп. — М.: Наука, 1974. — 592 с.
↑ Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов 1986. С. 184

Источник

В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.

Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.

Трапеция и все-все-все

Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.

Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.

В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.

Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.

Свойства диагоналей трапеции

Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.

Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2.
Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k².
Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т.
Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ.
А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b).

Свойства средней линии трапеции

Среднюю линию проведите в трапеции параллельно ее основаниям.

Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2.
Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.

Свойство биссектрисы трапеции

Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.

Свойства углов трапеции

Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180⁰: α + β = 180⁰ и γ + δ = 180⁰.
Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90⁰, длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2.
Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.

Свойства равнобедренной (равнобокой) трапеции

В равнобедренной трапеции равны углы при любом из оснований.
Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180⁰ – обязательное условие для этого.
Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2.
Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2.

Свойства трапеции, вписанной в окружность

Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.

Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ.
Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S_АМЕ.

Свойства трапеции, описанной около окружности

Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.

Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2.
У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ.
Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab.
И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.

Свойства прямоугольной трапеции

Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.

У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.

Доказательства некоторых свойств трапеции

Равенство углов при основании равнобедренной трапеции:

Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.

АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.

Откуда АКМ = 180⁰– МЕТ = 180⁰– КАЕ = КМЕ.

Что и требовалось доказать.

Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной:

Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.

МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.

У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.

Задача для повторения

Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150⁰ с меньшим основанием. Требуется найти площадь трапеции.

Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.

Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180⁰. Поэтому КАН = 30⁰ (на основании свойства углов трапеции).

Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30⁰. Поэтому КН = ½АВ = 4 см.

Площадь трапеции находим по формуле: S_АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см².

Послесловие

Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.

Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.

Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!

Источник

Признаки и свойства равнобедренной трапеции

Трапеция. Свойства трапеции

Свойства трапеции

Свойства и признаки равнобедренной трапеции

Вписанная окружность

Площадь

Трапеция и ее свойства

Теоремы о средней линии и диагоналях трапеции

Теоремы о площади трапеции

Теоремы о вписанных и описанных трапециях

Задачи ЕГЭ и ОГЭ по теме: Трапеция

Варианты определения[править | править код]

Связанные определения[править | править код]

Элементы трапеции[править | править код]

Виды трапеций[править | править код]

Свойства[править | править код]

Неравенства для отрезков в трапеции[править | править код]

Теорема о четырёх точках трапеции[править | править код]

Равнобедренная трапеция[править | править код]

Вписанная и описанная окружность[править | править код]

Площадь[править | править код]

Формулы площади равнобедренной трапеции[править | править код]

История[править | править код]

Примечания[править | править код]

Трапеция и все-все-все

Свойства диагоналей трапеции

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://blog.tutoronline.ru/media/521509/_________5.jpg?width=506px&amp;height=312px" width="506" height="312" alt="Трапеция 2" />

Свойства средней линии трапеции

Свойство биссектрисы трапеции

Свойства углов трапеции

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://blog.tutoronline.ru/media/521514/_________2.png" width="380" height="153" alt="Трапеция 2" />

Свойства равнобедренной (равнобокой) трапеции

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://blog.tutoronline.ru/media/521519/_________4.png?width=338px&amp;height=336px" width="338" height="336" alt="Трапеция 4" />

Свойства трапеции, вписанной в окружность

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://blog.tutoronline.ru/media/521524/_________6.jpg" width="307" height="205" alt="Трапеция 6" />

Свойства трапеции, описанной около окружности

Свойства прямоугольной трапеции

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://blog.tutoronline.ru/media/521529/_________3.gif" width="254" height="148" alt="Трапеция 3" />

Доказательства некоторых свойств трапеции

Задача для повторения

Послесловие

Вам также может понравиться

Как найти мини трактора

Как найти эффекты в adobe premiere

Как найти ширину брюк

Добавить комментарий Отменить ответ