Данная глава рассказывает о том, как найти координаты точки пересечения прямой с плоскостью при заданных уравнениях, определяющих эту плоскость. Будет рассмотрено понятие точки пересечения прямой с плоскостью, два способа нахождения координат точки пересечения прямой с плоскостью.
Точка пересечения прямой и плоскости – определение
Для углубленного изучения теории необходимо начать рассмотрение с понятия точки, прямой, плоскости. Понятие о точке, прямой линии рассматривается как на плоскости, так и в пространстве. Для детального рассмотрения необходимо обратиться к теме о прямой и плоскости в пространстве.
Существует несколько вариаций расположения прямой относительно плоскости и пространства:
- прямая лежит в плоскости;
- прямая параллельна плоскости;
- прямая пересекает плоскость.
Если рассмотреть третий случай, то отчетливо видно, что прямая с плоскостью при пересечении образуют общую точку, которую называют точкой пересечения прямой и плоскости. рассмотрим данный случай на примере.
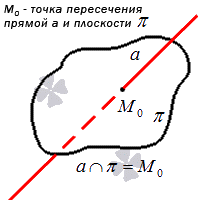
Нахождение координат точки пересечения прямой и плоскости
Была введена прямоугольная система координат Охуz трехмерного пространства. Каждая прямая имеет свое собственное уравнение, а каждая плоскость соответствует своему заданному уравнению, каждая точка имеет определенное количество действительных чисел – координат.
Чтобы подробно разобраться в теме координат пересечения, необходимо знать все виды уравнения прямой в пространстве и уравнений плоскости. в данном случае пригодятся знания о переходе от одного вида уравнения к другому.
Рассмотрим задачу, которая основывается на заданном пересечении прямой и плоскости. она сводится к нахождению координат пересечений.
Вычислить, может ли точка М0 с координатами -2, 3, -5 являться точкой пересечения прямой x+3-1=y-3=z+23 с плоскостью x-2y-z+3=0.
Решение
Когда точка принадлежит некоторой прямой, координаты точки пересечения являются решением обоих уравнения. Из определения имеем, что при пересечении образуется общая точка. Для решения задания необходимо подставить в оба уравнения координаты точки М0 и вычислить. Если она является точкой пересечения, то оба уравнения будут соответствовать.
Представим координаты точки -2, 3, -5 и получим:
-2+3-1=3-3=-5+23⇔-1=-1=-1-2-2·3-(-5)+3=0⇔0=0
Так как получаем верные равенства, делаем вывод, что точка М0 – точка пересечения заданной прямой с плоскостью.
Ответ: заданная точка с координатами является точкой пересечения.
Если координаты точки пересечения являются решением обоих уравнений, то они пересекаются.
Первый способ нахождения координат пересечения прямой и плоскости.
Когда задается прямая a с плоскостью α прямоугольной системы координат, известно, что они пересекаются в точке М0. Для начала займемся поиском координат заданной точки пересечения при заданном уравнении плоскости, имеющего вид Ax+By+Cz+D=0 с прямой линией a, являющейся пересечением плоскостей A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0. Данный способ задания прямой в пространстве рассматривается в статье уравнения прямой и уравнения двух пересекающихся плоскостей.
Необходимые нам координаты прямой a и плоскости α должны удовлетворять обоим уравнениям. Таким образом задается система линейных уравнений, имеющая вид
Ax+By+Cz+D=0A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0
Решение системы подразумевает обращение каждого тождества в верное равенство. Следует отметить, что при таком решении мы определяем координаты пересечения 3 плоскостей вида Ax+By+Cz+D=0, A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0. Для закрепления материала рассмотрим решение данных задач.
Прямая задана уравнением двух пересекающихся плоскостей x-y+3=05x+2z+8=0, причем пересекает еще одну 3x-z+7=0. Необходимо найти координаты точки пересечения.
Решение
Необходимые координаты получим при составлении и решении системы, имеющей вид x-y+3=05x+2z+8=03x-z+7=0.
Следует обратить внимание на тему решения систем линейных уравнений.
Возьмем систему уравнений вида x-y=-35x+2z=-83x-z=-7 и произведем вычисления по определителю основной матрицы системы. Получаем, что
∆=1-1050230-1=1·0·(-1)+(-1)·2·3+0·5·0-0·0·3-1·2·0-(-1)·5·(-1)=-11
Так как определитель матрицы не равен нулю, система имеет только одно решение. Для этого мы применим метод Крамера. Он считается очень удобным и подходящим для данного случая.
∆x=-3-10-802-70-1=(-3)·0·(-1)+(-1)·2·(-7)+0·(-8)·0–0·0·(-7)-(-3)·2·0-(-1)·(-8)·(-1)=22⇒x=∆x∆=22-11=-2∆y=1-305-823-7-1=1·(-8)·(-1)+(-3)·2·3+0·5·(-7)–0·(-8)·3-1·2·(-7)-(-3)·5·(-1)=-11⇒y=∆y∆=-11-11=1∆z=1-1-350-830-7=1·0·(-7)+(-1)·(-8)·3+(-3)·5·0–(-3)·0·3-1·(-8)·0-(-1)·5·(-7)=-11⇒z=∆z∆=-11-11=1
Отсюда следует, что координаты точки пересечения заданной прямой и плоскости имеет значение (-2, 1, 1).
Ответ: (-2, 1, 1).
Система уравнений вида Ax+By+Cz+D=0A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 имеет одно единственное решение. Когда прямая a определена такими уравнениями, как A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0, а плоскость α задается уравнением Ax+By+Cz+D=0, то они пересекаются. Когда прямая лежит в плоскости, система выдает бесконечное множество решений. При их параллельности уравнение решений не имеет, так как нет общих точек пересечения.
Найти точку пересечения прямой z-1=02x-y-2=0 и плоскости 2x-y-3z+1=0.
Решение
Заданные уравнения необходимо преобразовать в систему z-1=02x-y-2=02x-y-3z+1=0. Когда она будет иметь единственное решение, то получим искомые координаты пересечения в точке. При условии, если нет решений, то они параллельны, либо прямая лежит в этой же плоскости.
Получим, что основная матрица системы – A=0012-102-1-3, расширенная – T=00112-1022-1-3-1. Нам необходимо определить ранг матрицы A и T методом Гаусса:
1=1≠0, 01-10=1≠0, 0012-102-1-3=0, 011-102-1-3-1=0
Тогда получим, что ранг основной матрицы равен рангу расширенной. Применим теорему Кронекера-Капелли, отсюда видно, что у системы есть бесконечное множество решений. Получим, что прямая z-1=02x-y-2=0 принадлежит плоскости 2x-y-3z+1=0, что говорит об их невозможности пересечения и наличии общей точки.
Ответ: нет координат точки пересечения.
Задано пересечение прямой x+z+1=02x+y-4=0 и плоскости x+4y-7z+2=0, найти координаты точки пересечения.
Решение
Необходимо собрать заданные уравнения в систему вида x+z+1=02x+y-4=0x+4y-7z+2=0. Для решения применяем метод Гаусса. С его помощью мы определим все имеющиеся решения коротким путем. Для этого запишем
x+z+1=02x+y-4x+4y-7z+2=0⇔x+z=-12x+y=4x+4y-7z=-2⇔⇔x+z=-1y-2z=64y-8z=-1⇔x+z=-1y-2z=60=-25
Применив метод Гауса, стало понятно, что равенство неверное, так как система уравнений решений не имеет.
Делаем вывод, что прямая x+z+1=02x+y-4=0 с плоскостью x+4y-7z+2=0 не имеют пересечений. Отсюда следует, что невозможно найти координаты точки, так как они не пересекаются.
Ответ: нет точек пересечения, так как прямая параллельна плоскости.
Когда прямая имеет задана параметрическим или каноническим уравнением, то отсюда можно найти уравнение пересекающихся плоскостей, которые определяют прямую a, после чего искать необходимые координаты точки пересечений. Имеется еще один метод, который применяется для нахождения координат точки пересечения прямой и плоскости.
Второй способ нахождения точки начинается с задания прямой a, пересекающей плоскость α в точке М0. Необходимо найти координаты заданной точки пересечения при заданном уравнении плоскости Ax+By+Cz+D=0. Прямую а определяем параметрическими уравнениями, имеющими вид x=x1+ax·λy=y1+ay·λz=z1+az·λ , λ∈R.
Когда в уравнение Ax+By+Cz+D=0 производится подстановка x=x1+ax·λ, y=y1+ay·λ, z=z1+az·λ, выражение примет вид уравнения с неизвестной λ. Необходимо разрешить его относительноλ, тогда получим λ=λ0, которое соответствует координатам точки, в которой они пересекаются. Вычисление координат точки производится из x=x1+ax·λ0y=y1+ay·λ0z=z1+az·λ0.
Подробнее этот способ будет рассмотрен на примерах, приведенных ниже.
Найти координаты точки пересечения прямой x=-1+4·λy=7-7·λz=2-3·λ, λ∈R с плоскостью x+4y+z-2=0.
Решение
Для решения системы, необходимо произвести подстановку. Тогда получаем, что
-1+4·λ+4·7-7·λ+2-3·λ-2=0⇔-27·λ+27=0⇔λ=1
Найдем координаты точки пересечения плоскости с прямой, используя параметрические уравнения, со значением λ=1.
Получим :
x=-1+4·1y=7-7·1z=2-3·1⇔x=3y=0z=-1
Ответ: (3, 0, -1).
Когда прямая вида x=x1+ax·λy=y1+ay·λz=z1+az·λ, λ∈R принадлежит плоскости Ax+By+Cz+D=0, тогда необходимо подставить туда уравнение плоскости выражения x=x1+ax·λ, y=y1+ay·λ, z=z1+az·λ, тогда получим тождество такого вида 0≡0. При параллельности плоскости и прямой получаем неверное равенство, так как нет точек пересечения.
Если прямая задана каноническим уравнением, имеющим вид x-x1ax=y-y1ay=z-z1az, тогда необходимо переходить от канонических к параметрическим при поиске координат точки пересечения прямой с плоскостью Ax+By+Cz+D=0, то есть получим x-x1ax=y-y1ay=z-z1az⇔x=x1+ax·λy=y1+ay·λz=z1+az·λ и применим необходимы способ для нахождения координат точки пересечения заданной прямой и плоскости в пространстве.
§ 7. Первая позиционная задача. Построение точки пересечения прямой линии с плоскостью
Задача 7.1. Построить точку пересечения прямой п с плоскостью треугольника АВС. Определить видимость прямой п. (Рисунок 101)
Решение.
Задачи данного типа решаются в три этапа:
1. Проведение через заданную прямую вспомогательной проецирующей плоскости и нахождение линии пересечения этой вспомогательной плоскости с заданной плоскостью.
2. Построение точки пересечения прямой и плоскости, опираясь на результат этапа 1..
3. Определение видимости прямой.
1. Для решения задачи применяют проецирующую плоскость, проходящую через заданную прямую. Заключим прямую п в горизонтально проецирующую плоскость. Данная плоскость перпендикулярна горизонтальной плоскости проекций, на которой она отобразится в виде прямой, совпадающей с проекцией п1 . Обозначим ее утолщенной линией и буквами ГП1 (рисунок 102).
ГП пересекает стороны ΔАВС в точках 1 и 2: в точке 1 – со стороной АВ, а в точке 2 – со стороной ВС. Покажем проекции этих точек на эпюре (см. рис. 102).
Можно утверждать, что ГП, проведенная через прямую п пересекает плоскость треугольника АВС по прямой, проходящей через точки 1 и 2. На горизонтальной проекции эта прямая совпадает с прямой п (как и все другие прямые, лежащие в плоскости ГП), а на фронтальной проекции мы получаем эту прямую, соединив точки 12 и 22.
2. На пересечении проекций прямых п2 и (12 – 22) построим точку К2, которая является фронтальной проекцией точки К – точки пересечения прямой п и прямой, проходящей через точки 1 и 2. Найдем проекцию К1, проведя линию связи с фронтальной проекции на горизонтальную до пересечения с проекцией прямой п1 (рисунок 103).
3. Чтобы определить видимость прямой п, рассмотрим конкурирующие точки (рисунок 104)
Конкурирующими называются две точки, одна из проекций которых совпадает. На горизонтальной проекции рассмотрим конкурирующие точки, лежащие на стороне АВ (проекция А1В1) и прямой п (проекция п1). Их горизонтальная проекция совпадает – это точка 11. Если мы посмотрим на фронтальную проекцию эпюра, направив взгляд по проекционной линии связи, то увидим, что Прямая АВ лежит выше, чем прямая п, а это значит, что на горизонтальной проекции сторона А1В1 перекрывает прямую п1 , которая после пересечения с А1В1 становится невидимой. Далее, в точке К1 прямая как бы «протыкает» плоскость треугольника и становится видимой.
На фронтальной проекции также рассмотрим конкурирующие точки на прямой АВ (проекция А2В2) и прямой п (проекция п2). Направляем взгляд по стрелке вниз (рис. 104) и видим, что точка, расположенная на прямой п ближе к нам (ниже на эпюре), поэтому прямая п2 в месте пересечения со стороной А2В2 видимая, а после прохождения точки К2 становится невидимой.
Окончательно решение задачи выглядит так, как показано на рисунке 105.
Задача 7. 2. Построить точку пересечения прямой а с плоскостью, заданной параллельными прямыми m и n. Определить видимость прямой а. (Рисунок 106).
Решение:
Данную задачу решаем аналогично задаче 1.Для разнообразия вместо горизонтально проецирующей плоскости проведем фронтально проецирующую – результат решения от этого не изменится. Заключим прямую а в фронтально-проецирующую плоскость ФП, обозначив ее на эпюре как ФП2.
Плоскость ФП, проведенная через прямую а пересекает заданную плоскость по прямой, проходящей через точки 1 и 2. фронтальной проекции эта прямая совпадает с прямой п, а на горизонтальной проекции мы получаем эту прямую, соединив точки 12 и 21. Получив на эпюре точку N1 от пересечения прямой (11-21) и а1, «поднимаем» от нее линию связи на фронтальную проекцию и получаем на проекции а2 точку N2.
Видимость прямой определяем методом конкурирующих точек. Решение задачи представлено на рисунке 107.
Задача 7.3. Построить точку пересечения прямой l с плоскостью α, заданной следами . Определить видимость прямой l. (Рисунок 108).
Решение.
Заключим прямую l в горизонтально-проецирующую плоскость ГП и найдем точки пересечения этой плоскости со следами заданной плоскости α. Точка 1 – это точка пересечения ГП с горизонтальным следом α1, а точка 2 – это точка пересечения ГП с фронтальным следом α2 (рисунок 109).
Поскольку следы плоскости – это прямые, принадлежащие плоскостям проекций и самой плоскости, то нахождение проекций точек пересечения их с вспомогательной плоскостью ГП не представляет затруднений (см. рис. 109).
Также как и в двух предыдущих задачах, проведем прямую (1-2), являющуюся результатом пересечения ГП и плоскости α. Фронтальная проекция этой прямой представлена отрезком [12-22], а ее горизонтальная проекция совпадает с проекцией l1. Теперь мы можем получить проекцию М2, и «опустив» ее на плоскость Н получаем проекцию М1. Точка пересечения Прямой l и плоскости α найдена.
Видимость в данном случае легко определить интуитивно, поскольку плоскость задана следами. Применение метода конкурирующих точек также дает верное решение.
Упражнение 7.
Построить точку пересечения прямой l с плоскостью, заданной пересекающимися прямыми а и b. Определить видимость прямой l. (Рисунок 110)
Определение точки пересечения прямой с плоскостью
Для
определения точки пересечения прямой
с плоскостью пользуемся следующим
алгоритмом: прямую заключаем во
вспомогательную плоскость, находим
линию пересечения этих двух плоскостей
(заданной и вспомогательной), и линия
пересечения плоскостей в пересечении
с заданной прямой даст искомую точку.
Последним этапом в построении является
определение видимости прямой при помощи
конкурирующих точек.
Пример1.
Плоскость задана следами (рис.70)
Рис.70
1.
Для построения точки пересечения прямой
l
с плоскостью необходимо через прямую
провести вспомогательную плоскость
частного положения, например,
фронтально-проецирующую β
π2,
l”
fоβ,
fоβ
– собирающий след, hоβ
х
(рис.71).
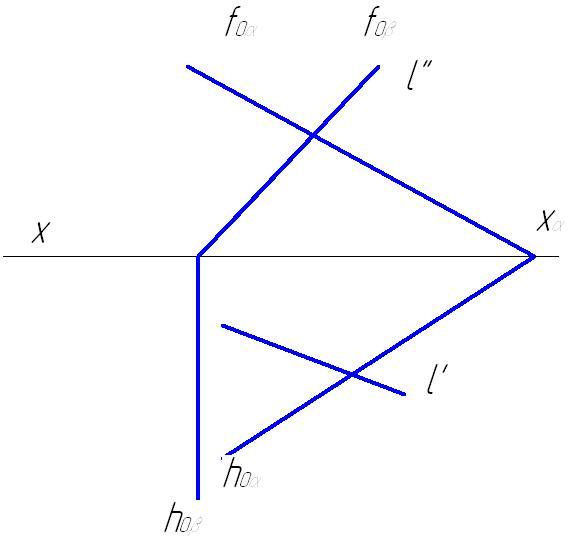Рис.71
2.
Строим линию пересечения MN
заданной и вспомогательной плоскости
М’=hоα∩
hоβ,
N”=
fоβ∩
fоα
(рис.72).
Рис.72
3.
Определяем точку пересечения К
заданной прямой l
с линией пересечения MN.
К’=М’N’∩l ‘, К”
– в пересечении линии проекционной
связи, проведенной из К’
и l ”.
4.
Видимость прямой l
в случае задания плоскости следами не
определяем.
Пример
2. Пересечение прямой с проецирующей
плоскостью (рис.73).
При
построении точки пересечения прямой с
проецирующей плоскостью задача
упрощается, т.к. одна из проекций искомой
точки будет лежать на собирающем следе.
На рис.73 дана горизонтально-проецирующая
плоскость. Искомая точка К
будет одновременно принадлежать
плоскости α и прямой а.
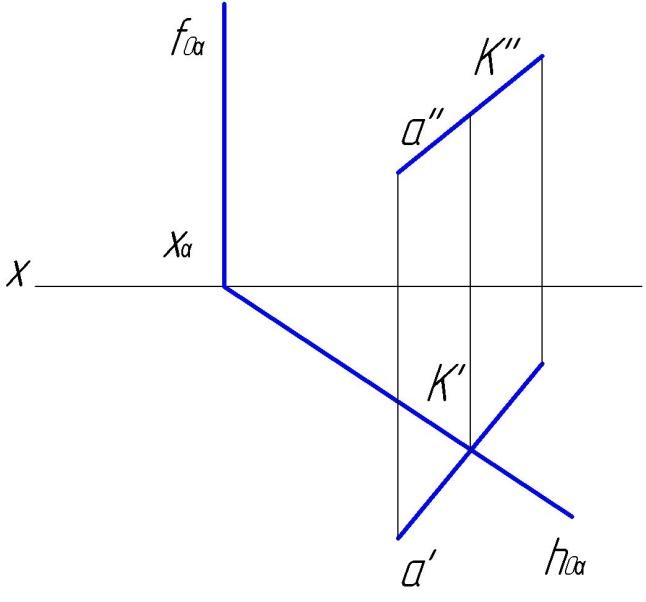Рис.73
Пример
3.
Плоскость
задана плоской фигурой (рис.74).
Рис.74
Через
прямую
l
проводим вспомогательную плоскость
частного положения, например,
горизонтально-проецирующую β
π1.l‘
hоβ,
hоβ
– собирающий след, fоβ
х
(рис.75).
Рис.75
2.
Строим линию пересечения MN
заданной и вспомогательной плоскостей.
М’=А’С’∩
hоβ М”
А”С”
и N’=В’С’∩ hоβ N”
”є
(рис. 76).
3.
Строим точку пересечения К
заданной прямой l
с линией пересечения МN.
К”= М”N”∩l”. К’
находится в пересечении линии проекционной
связи, проведенной из К”
и М’N’.
4.
Определяем видимость прямой относительно
ΔАВС
с помощью конкурирующих точек.
Определяем
видимость относительно плоскости π2
.Отметим фронтальную проекцию 1”
совпадающую с 2”.
Горизонтальную проекцию 2′
отметим на А’С’,
а 1′
на l’.
Горизонтальная проекция 1′
лежит перед 2′,
следовательно, фронтальная проекция
2”
не видима относительно π2.
Точка 1
лежит на прямой l, она видима на π2,
следовательно, фронтальная проекция
l”
от 1″2” до К”
видима, в точке К”
видимость меняется на противоположную.
Определим
видимость прямой l
относительно плоскости π1.
Отметим горизонтальную проекцию 3′,
совпадающую с горизонтальной проекцией
М’.
М”
А”С”
уже отмечена, 3”
l’‘.
Фронтальная проекция М”
лежит выше фронтальной проекции 3”,
следовательно, точка М
видима относительно π1.
Точка 3
лежит на l,
следовательно, от М’≡3′
до
К’,
горизонтальная проекция l’
невидима. В горизонтальной проекции К’
видимость
меняется на противоположную. За границами
ΔАВС
прямая l
везде
видима.
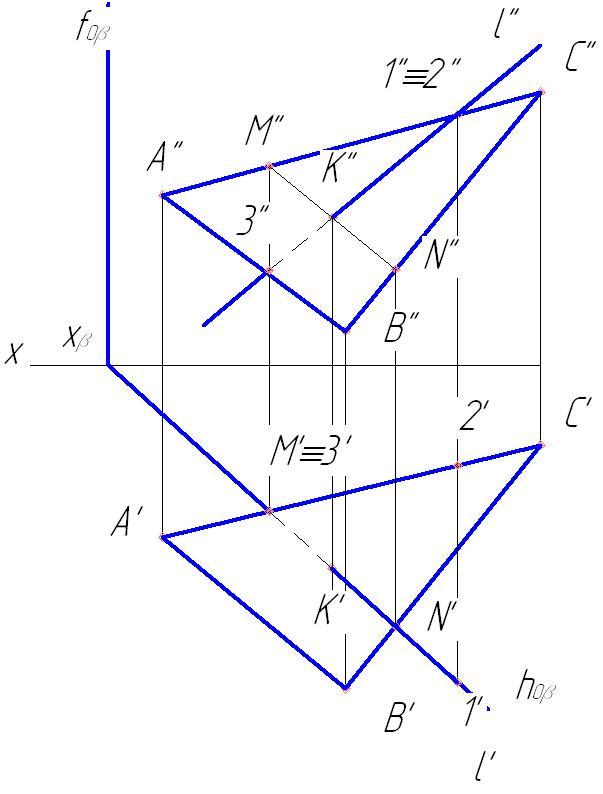Рис.76
Взаимное расположение прямых линий и плоскостей
Прямые
и плоскости могут быть параллельны или
перпендикулярны друг другу.
Параллельность
прямой и плоскости.
Прямая
параллельна плоскости, если она
параллельна прямой, лежащей в этой
плоскости.
Плоскость
задана ΔАВС.
Через (∙)D
провели прямую l
. Прямая l
|| ВС
(рис.77).
Рис.77
Параллельность
плоскостей
Две
плоскости параллельны между собой, если
две пересекающиеся прямые одной плоскости
параллельны двум пересекающимся прямым
другой плоскости.
Плоскость
задана двумя параллельными прямыми а
и b.
В этой плоскости проведем прямую 12.
Через
(∙)К
проведем две пересекающиеся прямые l
и n.
Прямая а
|| l,
прямая 12
|| n.
Эти две плоскости параллельны (рис.78).
Рис.78
Перпендикулярность
прямой и плоскости.
Прямая
перпендикулярна плоскости, если она
перпендикулярна двум пересекающимся
прямым, лежащим в этой плоскости. А так
как прямой угол, у которого одна из
сторон параллельна плоскости проекций,
проецируется ортогонально на эту
плоскость в прямой угол, то, следовательно,
горизонтальная проекция перпендикуляра
к плоскости перпендикулярна к
горизонтальной проекции горизонтали,
а фронтальная проекция – к фронтальной
проекции фронтали.
На
рис.79 показано построение прямой,
проведенной из точки D
(D’, D”)
перпендикулярно плоскости ΔАВС.
Прямая l перпендикулярна плоскости α,
если l’
┴ h ‘(h0α),
l”┴ f” (f0α).
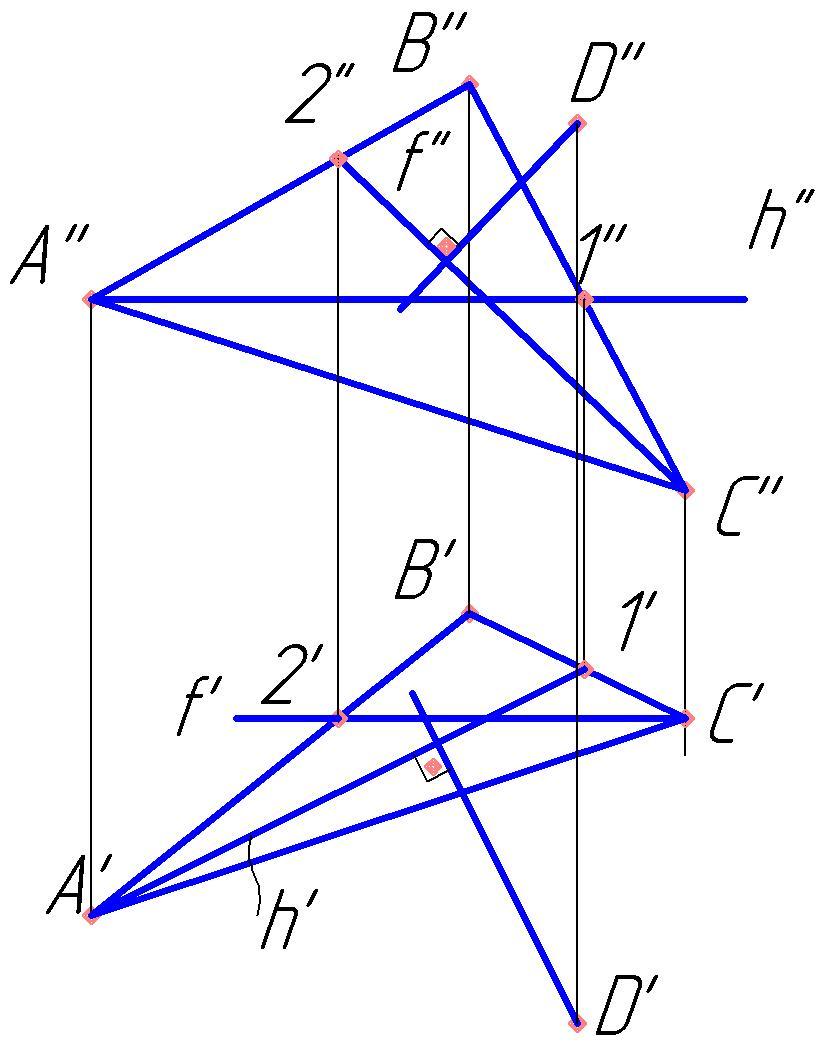Рис.79
На
рис.80 показано построение ┴ из (•) D
к плоскости, заданной следами.
Рис.80
Соседние файлы в папке Компьютерная графика
- #
- #
15.03.20153.99 Mб11Геометрическое черчение учебно-методическое пособие.wbk
- #
Построение точки пересечения прямой и плоскости
Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h0α, f0α.
Алгоритм
- Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h0γ, f0γ.
- Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B’ = h0α ∩ h0γ, A” = f0α ∩ f0γ. Точки A’ и B” лежат на оси x, их положение определяется по линиям связи.
- Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K’ = a’ ∩ A’B’. Фронтальная проекция K” лежит на прямой a”.
Алгоритм решения останется тем же, если пл. α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими возможными способами.
Видимость прямой a относительно плоскости α. Метод конкурирующих точек
- Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A” и С” совпадают, но при этом т. A и С удалены от плоскости проекций П2 на разное расстояние.
- Найдем горизонтальные проекции A’ и C’. Как видно на рисунке, точка C’ удалена от плоскости П2 на большее расстояние, чем т. A’, принадлежащая пл. α. Следовательно, участок прямой а”, расположенный левее точки K”, будет видимым. Участок a” правее K” является невидимым. Отмечаем его штриховой линией.
- Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D’ и E’ совпадают, но при этом т. D и E удалены от плоскости П1 на разное расстояние.
- Определим положение фронтальных проекций D” и E”. Как видно на рисунке, точка D”, находящаяся в пл. α, удалена от плоскости П1 на большее расстояние, чем т. E”, принадлежащая прямой a. Следовательно, участок а’, расположенный правее точки K’, будет невидимым. Отмечаем его штриховой линией. Участок a’ левее K’ является видимым.
Дополнительные материалы:
- Построение линии пересечения двух плоскостей
- Способы задания плоскости на чертеже
Пересечение прямой линии с поверхностью:
Для построения точки пересечения прямой с поверхностью через прямую следует провести вспомогательную плоскость и найти линию пересечения этой плоскости с поверхностью. Точка пересечения (или точка встречи заданной прямой и построенной линии или фигуры сечения) на поверхности и будет искомой точкой пересечения прямой с поверхностью. Сложность решения задачи зависит от трудоемкости нахождения линии пересечения, которая определяется следами поверхности и расположением прямой относительно как поверхности, так и плоскости проекций. Чтобы получить рациональное решение, следует пользоваться наиболее простым способом определения линии пересечения. Этого можно достичь двумя путями:
- выбором положения вспомогательной секущей плоскости;
- переводом секущей прямой в частное положение.
Вспомогательная секущая плоскость -проецирующая
Задание: определить точки пересечения прямой m с поверхностью пирамиды SABC (рис. 12.1).
Решение: для решения задачи прямую m заключают во фронтально проецирующую плоскость Σ (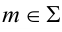
Задание: определить точки пересечения прямой m с поверхностью прямого кругового цилиндра (рис. 12.2).
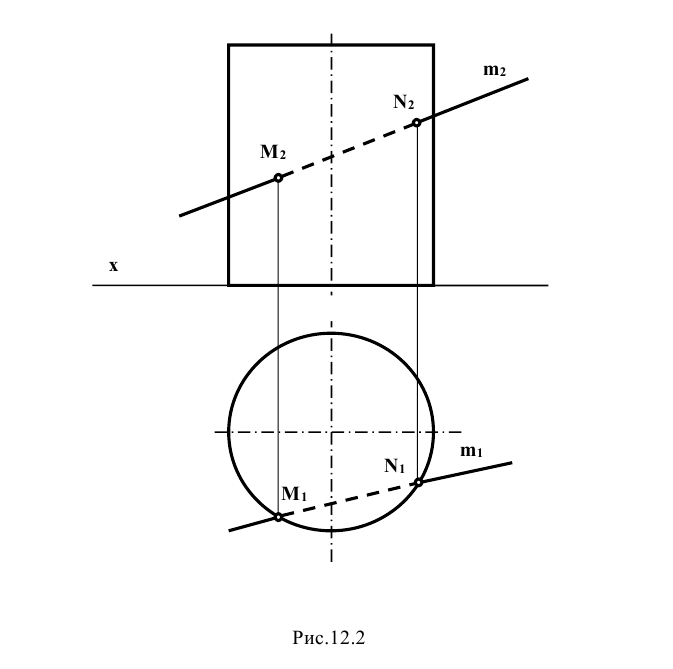
Решение: при решении задачи выделим проекции точек пересечения М и N прямой m с поверхностью цилиндра на горизонтальной проекции – точки 
. Так как образующие прямого кругового цилиндра являются горизонтально проецирующими прямыми, фронтальные проекции точек пересечения прямой m с поверхностью цилиндра 
и 
находят с помощью линий проекционной связи, как это показано на рисунке.
Вспомогательная секущая плоскость общего положения
Вспомогательную секущую плоскость, проводимую через прямую, при пересечении ею какой-либо поверхности, следует выбирать так, чтобы в результате получилось простейшее сечение. Например, при пересечении конической поверхности прямой линией такой плоскостью является плоскость, проходящая через вершину и пересекающая эту поверхность по прямым линиям (образующим).
При пересечении цилиндрической поверхности прямой линией вспомогательную плоскость целесообразно проводить через заданную прямую параллельно образующим цилиндра.
Задание: определить точки пересечения прямой m с поверхностью прямого кругового конуса (рис. 12.3).
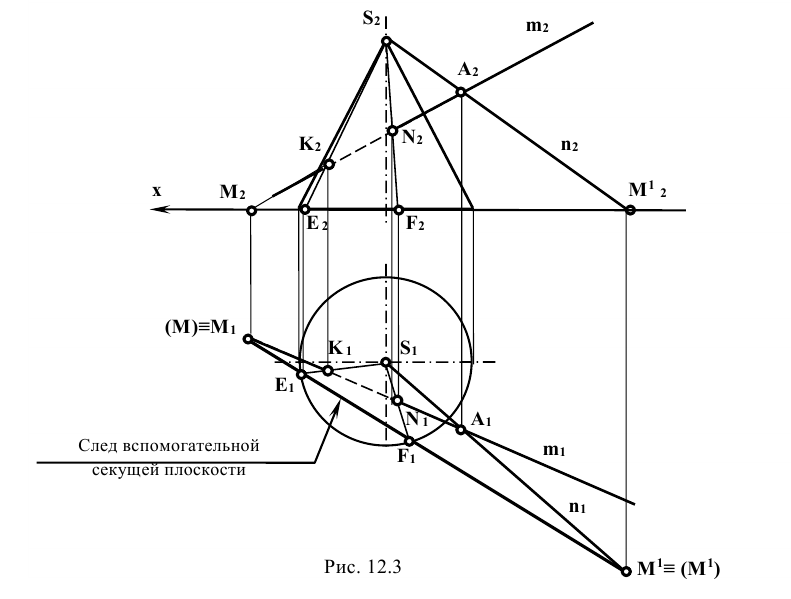
Решение: прямую m заключают в плоскость Р, проходящую через вершину конической поверхности S. Плоскость Р задана пересекающимися прямыми m и n, проходящими через точку А, которая выбирается произвольно на заданной прямой m.
Для определения горизонтального следа плоскости Р находят горизонтальные следы прямых m и n. Следы отмечают точками, например,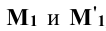 
, в которых горизонтальный след 
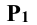плоскости Р пересекает основание конической поверхности. Проекции 
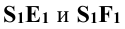– образующие поверхности конуса, по которым она пересекается плоскостью Р.
Точки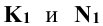 
– горизонтальные проекции искомых точек пересечения. Зная положение 
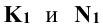определяют фронтальные проекции 
.
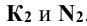Перевод прямой общего положения, пересекающей заданную поверхность в частное положение
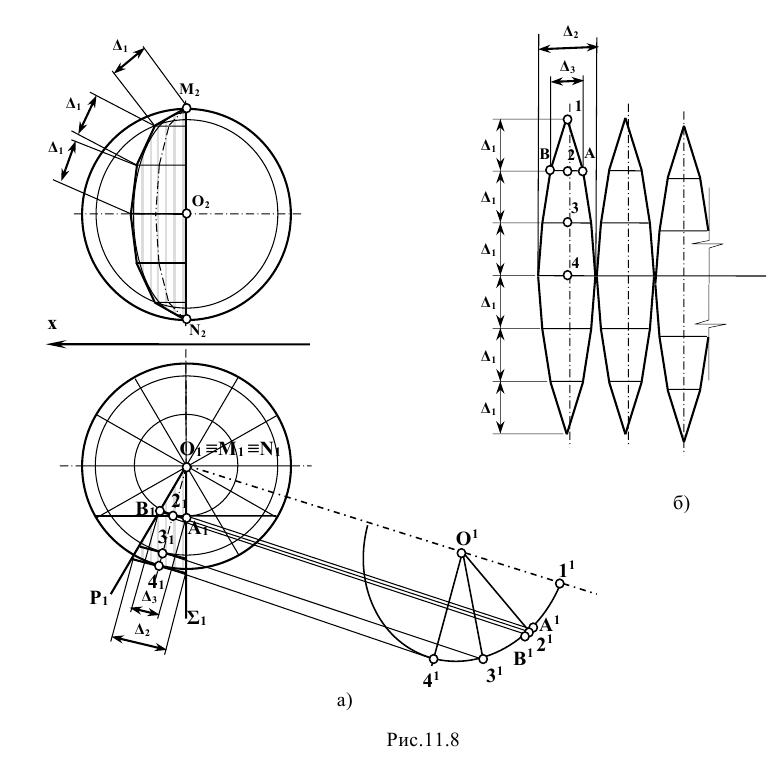
При пересечении поверхности сферы плоскостью в сечении получается окружность, которая проецируется на плоскости проекции в виде эллипсов или прямой и эллипса (если секущая плоскость – проецирующая). В случае, когда секущая плоскость параллельна плоскости проекции, окружность проецируется на эту плоскость проекции без искажения. Поэтому для упрощения решения задачи следует произвольно расположенную прямую перевести в положение, параллельное какой-либо плоскости проекции. Тогда прямую можно заключить в плоскость, параллельную плоскости проекции.
- Заказать чертежи
Задание: определить точки встречи прямой m, заданной отрезком АВ, с поверхностью сферы (рис. 12.4).
Решение: при решении этой задачи переводят прямую m общего положения в положение, параллельное плоскости проекции. Для этого вводят новую систему плоскостей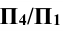 
в которой 
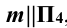, и переходят от системы 
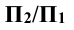к системе
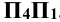. Новую ось проекций 
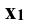проводят параллельно горизонтальной проекции прямой 
.
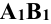Далее от концов горизонтальной проекции прямой, точек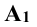 
и 
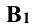проводят линии проекционной связи, перпендикулярные к новой оси проекций, и на них на плоскости 
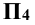откладывают координаты 
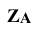и 
т.е. расстояния от оси проекций х до фронтальных проекций точек 
. Новая проекция 
будет натуральной длиной отрезка прямой АВ.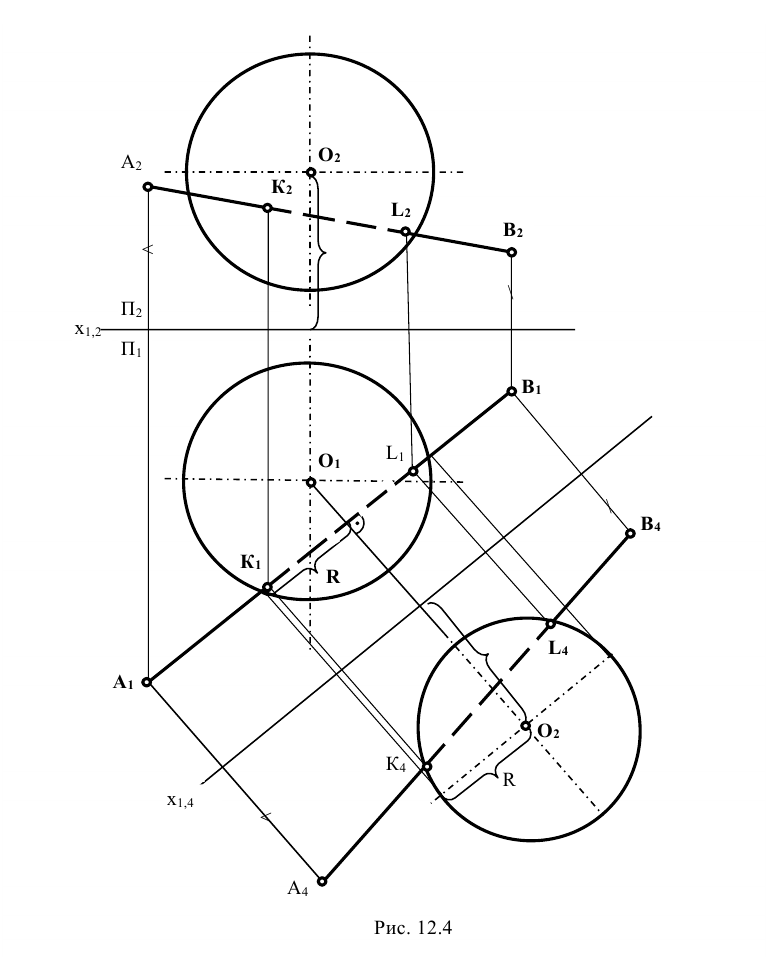 
Аналогично находят и центр сферы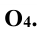
В новой системе горизонтально проецирующая плоскость Р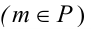 
пересечет поверхность сферы по окружности радиусом R, которая спроецируется на плоскость 
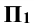в отрезок (1-2), а на плоскость 
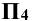в окружность тем же радиусом R. Точки 
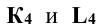– вспомогательные проекции точек пересечения, по которым определяют проекции точек 
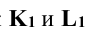а затем 
.
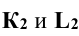Плоскость, касательная к поверхности
Плоскость, касательная к поверхности в заданной на поверхности точке, есть множество всех прямых — касательных, проведенных к поверхности через заданную точку.
Для задания плоскости, касательной к поверхности в заданной точке, достаточно провести через эту точку две произвольные линии, принадлежащие поверхности (желательно простые по форме) и к каждой их них построить касательные в точке пересечения этих линий. Построенные прямые (касательные) определяют касательную плоскость.
Задание: построить плоскость Р, касательную к поверхности сферы и проходящую через точку К (рис. 12.5).
Решение: плоскость, касательная к сфере, перпендикулярна к радиусу, проведенному в точку касания. Поэтому, проведя радиус ОК, строят плоскость, задавая ее горизонталью КВ и фронталью КС.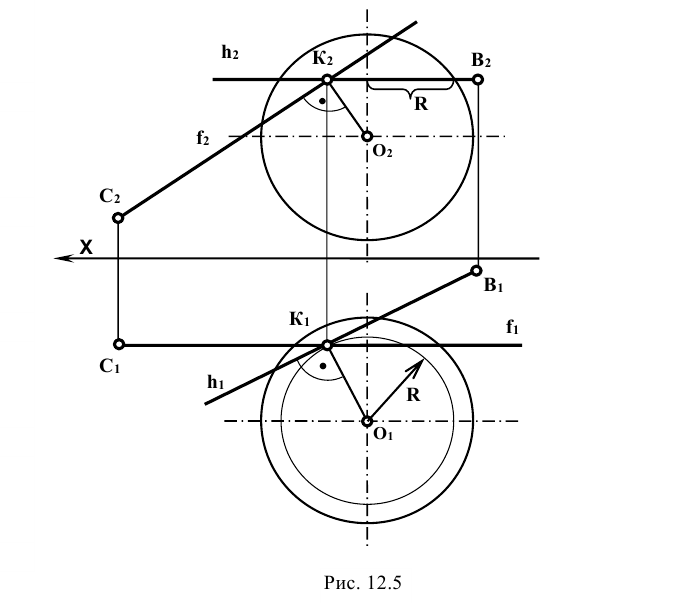 
При этом горизонтальная проекция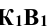 
перпендикулярна к 
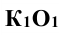, а фронтальная проекция 
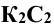перпендикулярна к 
.
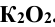- Построение линии пересечения поверхностей
- Проецирование прямой
- Взаимное положение плоскостей, прямой линии и плоскости
- Взаимное расположение точки, прямых и плоскостей
- Проецирование точки
- Прямая в пространстве и ее изображение на чертеже
- Многогранники
- Поверхности вращения
