Как найти точку пересечения медиан треугольника, зная координаты его вершин?
1 способ
Поскольку все медианы треугольника пересекаются в одной точке, достаточно составить уравнения двух медиан и найти координаты их точки пересечения.
Пример.
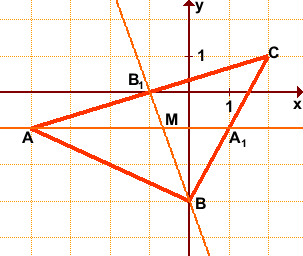
Найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1).
Решение:
Обозначим середины сторон BC и AC через A1 и B1 соответственно. По формулам координат середины отрезка
![]()
![]()
![]()
![]()
Составим уравнения медиан AA1 и BB1.
Уравнение медианы AA1 можно найти как уравнение прямой, проходящей через две точки A(-4;-1) и A1(1;-1).
![]()
то есть уравнение прямой AA1 y= -1.
B(0;-3), B1(-1;0). Найдём уравнение медианы BB1.
![]()
откуда уравнение прямой BB1 y= -3x-3.
Координаты точки пересечения прямых AA1 и BB1 ищем как решение системы уравнений
![]()
Ответ:
![]()
2 способ
Поскольку все медианы медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины, можно найти координаты концов любой медианы, а затем точку, которая делит медиану в отношении 2:1, начиная отсчёт от точки, которая является вершиной треугольника.
Например, в условиях предыдущей задачи — найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1), —
зная координаты A1(1;-1), найдём координаты точки M. Точка M пересечения медиан треугольника делит отрезок AA1 в отношении 2:1, считая от точки A.
По формулам деления отрезка в данном отношении
![]()
![]()
![]()
Пересечение меридиан в треугольнике
Точка пересечения медиан треугольника
Как найти точку пересечения медиан треугольника, зная координаты его вершин?
Поскольку все медианы треугольника пересекаются в одной точке, достаточно составить уравнения двух медиан и найти координаты их точки пересечения.
Найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1).
Обозначим середины сторон BC и AC через A1 и B1 соответственно. По формулам координат середины отрезка
Составим уравнения медиан AA1 и BB1.
Уравнение медианы AA1 можно найти как уравнение прямой, проходящей через две точки A(-4;-1) и A1(1;-1).
то есть уравнение прямой AA1 y= -1.
B(0;-3), B1(-1;0). Найдём уравнение медианы BB1.
откуда уравнение прямой BB1 y= -3x-3.
Координаты точки пересечения прямых AA1 и BB1 ищем как решение системы уравнений
Поскольку все медианы медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины, можно найти координаты концов любой медианы, а затем точку, которая делит медиану в отношении 2:1, начиная отсчёт от точки, которая является вершиной треугольника.
Например, в условиях предыдущей задачи — найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1), —
зная координаты A1(1;-1), найдём координаты точки M. Точка M пересечения медиан треугольника делит отрезок AA1 в отношении 2:1, считая от точки A.
Определение и свойства медианы треугольника
В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.
Определение медианы треугольника
Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).
Свойства медианы
Свойство 1 (основное)
Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:
Свойство 2
Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3
Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4
Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

- AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
- AB – самая короткая сторона, следовательно, медиана CD – самая длинная.
Свойство 5
Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы ma, проведенную к стороне a, можно найти по формуле:

Примеры задач
Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.
Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S△ = 5 см 2 ⋅ 6 = 30 см 2 .
Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.
Решение
Воспользуемся формулой, приведенной в свойстве 5:
Точка пересечения медиан треугольника


Средняя оценка: 4.1
Всего получено оценок: 211.
Средняя оценка: 4.1
Всего получено оценок: 211.
Медиана – это один из уникальных отрезков треугольника. Медиана имеет ряд свойств, полезных для решения задач, а точка пересечения медиан еще больше расширяет список этих свойств. О точке пересечения медиан, ее свойствах и пойдет речь сегодня.

Медиана
Медиана – это отрезок, соединяющий вершину треугольника с серединой отрезка противоположной стороны. Три медианы треугольника пересекаются в одной точке, которая зовется точкой пересечения медиан.
Медианы, в отличие от высот, всегда лежат внутри треугольника. Это логично, ведь отрезок медианы соединяет вершину и середину стороны. А середина стороны всегда лежит внутри треугольника.
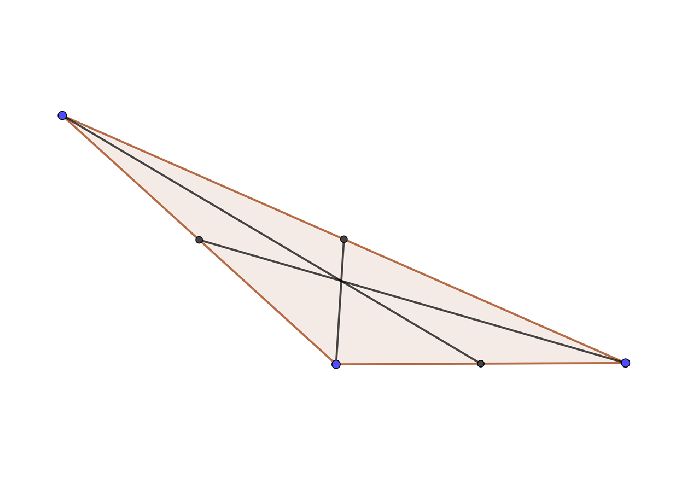 Рис. 1. Медианы в тупоугольном треугольнике.
Рис. 1. Медианы в тупоугольном треугольнике.
Если соединить два любых основания медиан отрезком, то получится средняя линия треугольника. Три средние линии треугольника образуют треугольник, подобный изначальному с коэффициентом подобия 1:2
Есть еще одно любопытное свойство медиан, которое позволит не запутаться при построении золотого сечения треугольника. Медиана в треугольнике всегда располагается между высотой и биссектрисой (исключение – равнобедренный и равносторонний треугольники).
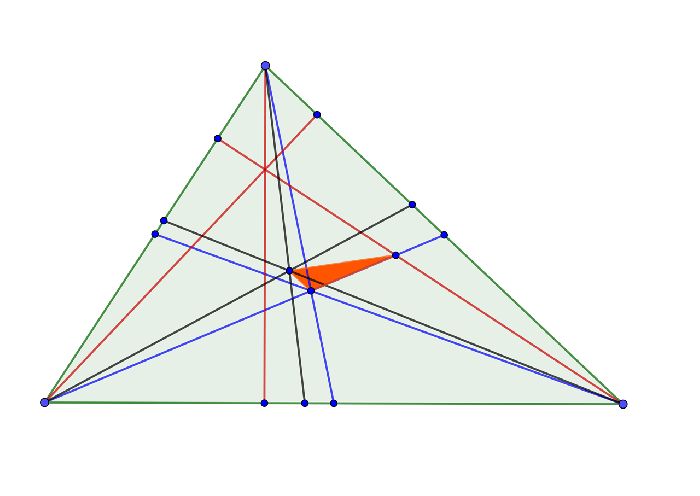 Рис. 2. Золотое сечение произвольного треугольника.
Рис. 2. Золотое сечение произвольного треугольника.
Приведем формулу вычисления длины медианы по трем сторонам. Эта формула часто используется при решении задач, и потому ее желательно запомнить.
Зачастую ученикам проще запомнить словесную формулировку, а не заучивать формулу. Чтобы найти медиану по трем сторонам, нужно взять корень из сумм удвоенных квадратов сторон минус квадрат стороны, к которой проведена медиана. Полученный корень нужно поделить пополам.
Точка пересечения медиан
Точка пересечения медиан является одной из 3 замечательных точек треугольника, которые составляют золотое сечение треугольника.
Точка пересечения медиан треугольника имеет ряд свойств, полезных при решении задач:
- Медиана точкой пересечения делится на отрезки в отношении 2:1 считая от вершины.
- Три медианы, проведенные в треугольнике, делят его на 6 равновеликих треугольников. Равновеликими называют треугольники с равной площадью. Сами по себе эти фигуры имеют мало общего, но численная характеристика площади у них совпадает.
- Точка пересечения медиан в треугольнике называется центроидом и является центром тяжести треугольника.
Точка пересечения медиан единственная из золотого сечения треугольника, имеет реальный физический смысл. Если из картона вырезать треугольник, тонким карандашом провести в нем медианы, то точка их пересечения будет центром тяжести плоской фигуры.
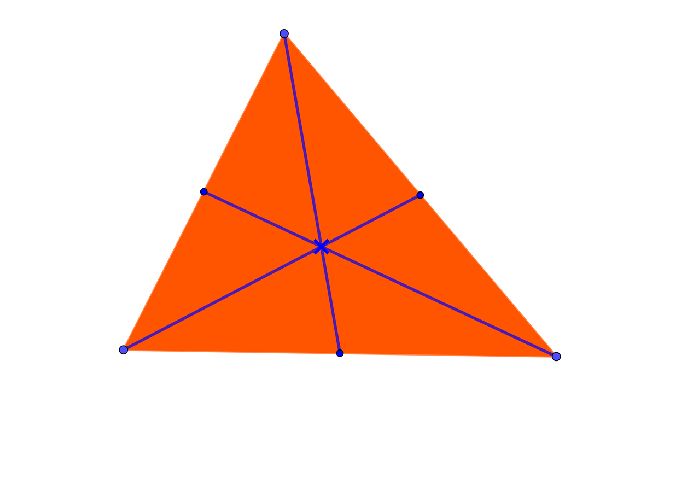 Рис. 3. Центр тяжести треугольника.
Рис. 3. Центр тяжести треугольника.
Это значит, что если установить иголку в эту точку, то фигура будет держаться на ней без прокола, исключительно за счет равновесия.

Что мы узнали?
Мы привели формулу вычисления медианы по 3 сторонам треугольника. Привели несколько свойств точки пересечения медиан в треугольнике. Поговорили о реальном физическом значение центроида треугольника.
Определение и свойства медианы в равнобедренном треугольнике
В данной статье мы рассмотрим определение и свойства медиан, проведенных к основанию и боковым сторонам равнобедренного треугольника, а также разберем пример решения задачи для закрепления теоретического материала.
Определение медианы
Медианой называется отрезок в треугольнике, который соединяет вершину и середину противоположной стороны.

Треугольник является равнобедренным, если две его стороны равны (боковые), а третья сторона – это основание фигуры.
- AB = BC – боковые стороны;
- AC – основание.
Свойства медианы в равнобедренном треугольнике
Свойство 1
Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она проведена.

- BD – медиана и высота, опущенная на основание AC, а также биссектриса угла ABC.
- ∠ABD = ∠CBD
Свойство 2
В равнобедренном треугольнике медианы пресекаются в одной точке (центр тяжести) и делятся в этой точке в отношении 2:1.

Свойство 3
Медиана делит равнобедренный треугольник на 2 равных по площади (равновеликих) треугольника. Следовательно, S1 = S2.

Свойство 4
Если провести три медианы в равнобедренном треугольнике, образуются 6 равновеликих треугольников (S1 = S2 = S3 = S4 = S5 = S6).

Свойство 5
Длину медианы в равнобедренном треугольнике, проведенную к основанию, можно найти по следующей формуле:

Свойство 6
Данной свойство, в отличие от перечисленных выше, не относится к медиане, опущенной на основание фигуры. Оно гласит:
Медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.

AF = CE, следовательно, AE = EB = BF = FC.
Пример задачи
Основание равнобедренного треугольника равняется 7 см, а боковая сторона – 12 см. Найдите длину медианы, проведенной к основанию фигуры.
Решение
Воспользуемся формулой, представленной в Свойстве 5, подставив в нее известные нам по условиям задачи значения:
Элементы треугольника. Медиана
Определение
Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны
Свойства
1. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины . Эта точка называется центром тяжести треугольника.
2. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника)
3. Медианы треугольника делят треугольник на 6 равновеликих треугольников
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы
5. Длина медианы треугольника вычисляется по формуле:
, где где — медиана к стороне ; — стороны треугольника
6. Длина стороны треугольника через медианы вычисляется по формуле:
, где – медианы к соответствующим сторонам треугольника, — стороны треугольника.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
[spoiler title=”источники:”]
[/spoiler]
В данной статье мы рассмотрим определение и свойства медиан, проведенных к основанию и боковым сторонам равнобедренного треугольника, а также разберем пример решения задачи для закрепления теоретического материала.
- Определение медианы
-
Свойства медианы в равнобедренном треугольнике
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
-
Свойство 5
- Свойство 6
- Пример задачи
Определение медианы
Медианой называется отрезок в треугольнике, который соединяет вершину и середину противоположной стороны.

- BD – медиана △ABC;
- AD = DC.
Треугольник является равнобедренным, если две его стороны равны (боковые), а третья сторона – это основание фигуры.
- AB = BC – боковые стороны;
- AC – основание.
Свойства медианы в равнобедренном треугольнике
Свойство 1
Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она проведена.

- BD – медиана и высота, опущенная на основание AC, а также биссектриса угла ABC.
- ∠ABD = ∠CBD
Свойство 2
В равнобедренном треугольнике медианы пресекаются в одной точке (центр тяжести) и делятся в этой точке в отношении 2:1.

- O – центр тяжести или центроид треугольника;
- AO = 2OF;
- BO = 2OD;
- CO = 2OE.
Свойство 3
Медиана делит равнобедренный треугольник на 2 равных по площади (равновеликих) треугольника. Следовательно, S1 = S2.

Свойство 4
Если провести три медианы в равнобедренном треугольнике, образуются 6 равновеликих треугольников (S1 = S2 = S3 = S4 = S5 = S6).

Свойство 5
Длину медианы в равнобедренном треугольнике, проведенную к основанию, можно найти по следующей формуле:
![]()
- a – основание;
- b – боковая сторона.
Свойство 6
Данной свойство, в отличие от перечисленных выше, не относится к медиане, опущенной на основание фигуры. Оно гласит:
Медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.

AF = CE, следовательно, AE = EB = BF = FC.
Пример задачи
Основание равнобедренного треугольника равняется 7 см, а боковая сторона – 12 см. Найдите длину медианы, проведенной к основанию фигуры.
Решение
Воспользуемся формулой, представленной в Свойстве 5, подставив в нее известные нам по условиям задачи значения:
![]()
Точка пересечения медиан треугольника


4.1
Средняя оценка: 4.1
Всего получено оценок: 315.
4.1
Средняя оценка: 4.1
Всего получено оценок: 315.
Медиана – это один из уникальных отрезков треугольника. Медиана имеет ряд свойств, полезных для решения задач, а точка пересечения медиан еще больше расширяет список этих свойств. О точке пересечения медиан, ее свойствах и пойдет речь сегодня.

Опыт работы учителем математики – более 33 лет.
Медиана
Медиана – это отрезок, соединяющий вершину треугольника с серединой отрезка противоположной стороны. Три медианы треугольника пересекаются в одной точке, которая зовется точкой пересечения медиан.
Медианы, в отличие от высот, всегда лежат внутри треугольника. Это логично, ведь отрезок медианы соединяет вершину и середину стороны. А середина стороны всегда лежит внутри треугольника.

Если соединить два любых основания медиан отрезком, то получится средняя линия треугольника. Три средние линии треугольника образуют треугольник, подобный изначальному с коэффициентом подобия 1:2
Есть еще одно любопытное свойство медиан, которое позволит не запутаться при построении золотого сечения треугольника. Медиана в треугольнике всегда располагается между высотой и биссектрисой (исключение – равнобедренный и равносторонний треугольники).

Приведем формулу вычисления длины медианы по трем сторонам. Эта формула часто используется при решении задач, и потому ее желательно запомнить.
$$m_c={{sqrt{2a^2+2b^2-c^2}}over{2}}$$
Зачастую ученикам проще запомнить словесную формулировку, а не заучивать формулу. Чтобы найти медиану по трем сторонам, нужно взять корень из сумм удвоенных квадратов сторон минус квадрат стороны, к которой проведена медиана. Полученный корень нужно поделить пополам.
Точка пересечения медиан
Точка пересечения медиан является одной из 3 замечательных точек треугольника, которые составляют золотое сечение треугольника.
Точка пересечения медиан треугольника имеет ряд свойств, полезных при решении задач:
- Медиана точкой пересечения делится на отрезки в отношении 2:1 считая от вершины.
- Три медианы, проведенные в треугольнике, делят его на 6 равновеликих треугольников. Равновеликими называют треугольники с равной площадью. Сами по себе эти фигуры имеют мало общего, но численная характеристика площади у них совпадает.
- Точка пересечения медиан в треугольнике называется центроидом и является центром тяжести треугольника.
Точка пересечения медиан единственная из золотого сечения треугольника, имеет реальный физический смысл. Если из картона вырезать треугольник, тонким карандашом провести в нем медианы, то точка их пересечения будет центром тяжести плоской фигуры.

Это значит, что если установить иголку в эту точку, то фигура будет держаться на ней без прокола, исключительно за счет равновесия.

Что мы узнали?
Мы привели формулу вычисления медианы по 3 сторонам треугольника. Привели несколько свойств точки пересечения медиан в треугольнике. Поговорили о реальном физическом значение центроида треугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Ляна Комбарова
4/5
Оценка статьи
4.1
Средняя оценка: 4.1
Всего получено оценок: 315.
А какая ваша оценка?
У этого термина существуют и другие значения, см. Медиана.

Треугольник и его медианы.
Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок в треугольнике, соединяющий вершину треугольника с серединой стороны, противоположной этой вершине.
Иногда медианой называют также прямую, содержащую этот отрезок, а иногда длину этого отрезка.
Точка пересечения медианы со стороной треугольника называется основанием медианы.
Если 












Связанные определения[править | править код]
Точка пересечения медиан делит каждую медиану на два отрезка.
Отрезок от вершины до точки пересечения называется предмедианой, а отрезок от точки пересечения до противоположной стороны постмедианой[1].
В частности можно сказать, что в любом треугольнике отношение предмедианы к постмедиане равно двум.
Свойства[править | править код]
Основное свойство[править | править код]
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Свойства медиан равнобедренного треугольника[править | править код]
В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой. Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.
У равностороннего треугольника все три медианы равны.
Если медианы равнобедренного треугольника, проведённые к боковым сторонам, пересекаются под прямым углом, то косинусы углов при основании этого треугольника равны 

Свойства оснований медиан[править | править код]

- Теорема Эйлера для окружности девяти точек: основания трёх высот произвольного треугольника, середины трёх его сторон (основания его медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (так называемой окружности девяти точек).
- Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией. Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
- Следствие (теорема Фалеса о параллельных отрезках). Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.
- Теркем доказал теорему Теркема[2]. Она утверждает, что если окружность девяти точек пересекает стороны треугольника или их продолжения в 3 парах точек (в 3 основаниях соответственно высот и медиан), являющихся основаниями 3 пар чевиан, то, если 3 чевианы для 3 из этих оснований пересекаются в 1 точке (например 3 медианы пересекаются в 1 точке), то 3 чевианы для 3 других оснований также пересекаются в 1 точке (то есть 3 высоты также обязаны пересечься в 1 точке).
Другие свойства[править | править код]
- Если треугольник разносторонний (неравносторонний), то его биссектриса, проведённая из любой вершины, лежит между медианой и высотой, проведёнными из той же вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Медиана делит пополам любой отрезок, параллельный стороне, к которой проведена эта медиана.
- Треугольник делится тремя медианами на шесть равновеликих треугольников. Центры описанных окружностей этих шести треугольников лежат на одной окружности, которая называется окружностью Ламуна.
- Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Большей стороне треугольника соответствует меньшая медиана.
- Отрезок прямой, симметричный или изогонально сопряжённый внутренней медиане относительно внутренней биссектрисы, называется симедианой треугольника. Три симедианы проходят через одну точку — точку Лемуана.
- Медиана угла треугольника изотомически сопряжена самой себе.
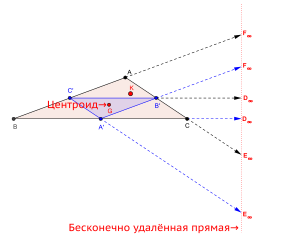
Бесконечно удаленная прямая — трилинейная поляра центроида
- Трилинейная поляра центроида (точки пересечения трех медиан) — бесконечно удаленная прямая (см. рис.).
Основные соотношения[править | править код]
Чтобы вычислить длину медианы, когда известны длины сторон треугольника, применяется теорема Аполлония (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):
- где
— медианы к сторонам треугольника
соответственно.
В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:
.
Обратно, можно выразить длину произвольной стороны треугольника через медианы:
- где
— медианы к соответствующим сторонам треугольника,
— стороны треугольника.
Площадь 
- где
— полусумма длин медиан.
Вариации и обобщение[править | править код]
- Чевиана — отрезок в треугольнике, соединяющий вершину треугольника с точкой на противоположной стороне.
См. также[править | править код]
- Биссектриса
- Высота треугольника
- Инцентр
- Симедиана
- Центроид
- Чевиана
Примечания[править | править код]
- ↑ Стариков В. Н. 10-е исследование по геометрии (§ До- (пред-)- и пост-чевианы)// Научный рецензируемый электронный журнал МГАУ «Наука и образование». 2020. № 1. 7 с.// http://opusmgau.ru/index.php/see/article/view/ 1604
- ↑ Дмитрий Ефремов. Новая геометрия треугольника Архивная копия от 25 февраля 2020 на Wayback Machine. — Одесса, 1902. — С. 16.
Литература[править | править код]
- Ефремов Дм. Новая геометрия треугольника, 1902 год.







