Загрузить PDF
Загрузить PDF
В алгебре прямоугольную систему координат на плоскости образуют две взаимно перпендикулярные оси – ось Х (горизонтальная ось) и ось Y (вертикальная ось). Точки пересечения – это точки, в которых графики функций пересекают оси координат. Точка пересечения с осью Y и точка пересечения с осью X лежат на соответствующих осях. В простых задачах точку пересечения с осью Х легко найти по графику функции. Также эту точку пересечения можно вычислить с помощью уравнения функции.
-

1
Найдите ось Х. Прямоугольная система координат образуется двумя осями – осью Х (горизонтальная ось, которая направлена слева направо) и осью Y (вертикальная ось, которая направлена снизу вверх).[1]
Чтобы найти точку пересечения с осью Х, посмотрите на эту ось. -

2
Найдите точку, в которой график пересекает ось Х. Это точка пересечения графика с осью Х.[2]
Если нужно найти точку пересечения с осью Х по графику, возможно, координатойэтой точки будет целое число, например, 4. Однако в большинстве случаев по графику удастся определить только приблизительную координату
, например, между 4 и 5.
-

3
Реклама
-

1
-

2
-

3
-

4
Реклама
-

1
Определите, записано ли уравнение в виде квадратного уравнения. Квадратное уравнение имеет вид
.[9]
Квадратное уравнение имеет два корня: график такого уравнения представляет собой параболу и пересекает ось Х в двух точках.[10]
- Например, уравнение
является квадратным уравнением, поэтому график пересечет ось Х в двух точках.
- Например, уравнение
-

2
Запишите формулу для решения квадратного уравнения. Формула:
, где
– коэффициент при переменной второго порядка (
),
– коэффициент при переменной первого порядка (
),
– свободный член.[11]
-

3
Подставьте соответствующие значения в формулу для решения квадратного уравнения. Убедитесь, что вместо каждой переменной подставляете правильное значение.
-

4
Упростите уравнение. Для начала перемножьте соответствующие значения. Убедитесь, что учли все знаки «плюс» и «минус».
-

5
Возведите соответствующее значение в квадрат. Сделайте это со значением переменной
. Затем результат прибавьте к другому числу, которое находится под знаком корня.
-

6
Выполните сложение. Так как в формуле присутствует знак
, придется выполнить одну операцию сложения и одну операцию вычитания. Выполните сложение, чтобы найти первое значение
.
-

7
Выполните вычитание. Так вы найдете второе значение
. Сначала извлеките квадратный корень, потом выполните вычитание в числителе и, наконец, результат разделите на 2.
-

8
Реклама
Советы
- Если дано линейное уравнение вида
, нужно знать угловой коэффициент (он равен значению коэффициента k) и координату «у» точки пересечения прямой с осью Y (она равна значению коэффициента b). Вместо «у» подставьте 0 и найдите «х». Вы получите координату «х» точки пересечения прямой с осью Х.
Реклама
Об этой статье
Эту страницу просматривали 75 702 раза.
Была ли эта статья полезной?
Еще один алгоритм определения пересечения двух отрезков
Время на прочтение
4 мин
Количество просмотров 26K
Недавно была публикация «Простой алгоритм определения пересечения двух отрезков». Я решил попробовать решить задачу пересечения двух отрезков немного по-другому, более геометрически.
Нахождение точки пересечения двух отрезков.
Имеем 2 отрезка {P0,P1} и {P2,P3}, где P0,P1,P2,P3 точки на плоскости. Будем обозначать x y координаты точки P как P.x и P.y
Имеем координаты 4 точек в массиве P(0..3) структуры point(x float, y float):
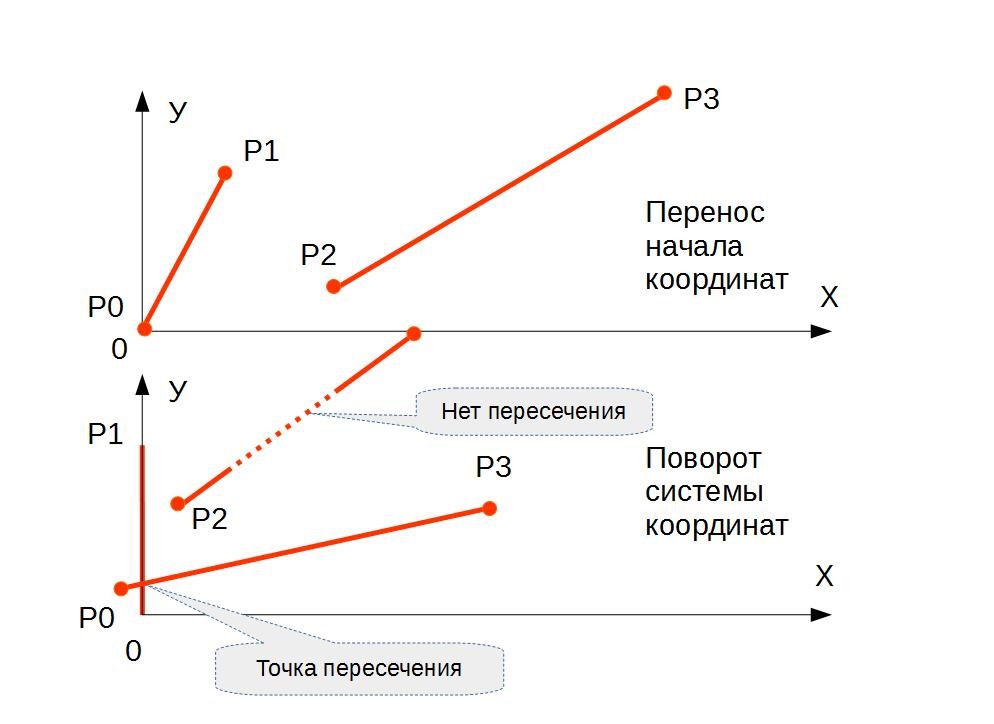
Шаг 1 — Перенос начала координат.
Запомним координаты точек P в дополнительном массиве P_copy. Перенесем начало системы координат в точку P0 и пересчитаем координаты точек:
P_copy = P
P(0).x = 0 ; P(0).y = 0
for ii = 1 to 3
P(ii).x = P(ii).x - P_copy(1).x ; P(ii).y = P(ii).y - P_copy(1).y
next
Шаг 2 — Поворот начала координат
Повернем систему координат так, чтобы отрезок {P0,P1} принял вертикальное положение (лег на ось Y). Вычислим длину отрезка {P0,P1} как:
L1 = SQRT ( (P(1).x)^2 + (P(1).y)^2 )
Синус и косинус угла alfa поворота осей координат:
если L1 > 0
sin_alf = sin(alfa) = P(1).x / L1
cos_alf = cos(alfa) = P(1).y / L1
если L1 = 0 // точку не поворачиваем
sin_alf = 0
cos_alf = 1
Cнова пересчитываем координаты точек P1,P2,P3:
P(0).x = 0 ; P(0).y = 0 // Точка P0 не поворачивается, она в начале координат
P(1).x = 0 ; P(1).y = L1
P(2).x = P(2).x * cos_alf - P(2).y * sin_alf
P(2).y = P(2).y * cos_alf + P(2).x * sin_alf
P(3).x = P(3).x * cos_alf - P(3).y * sin_alf
P(3).y = P(3).y * cos_alf + P(3).x * sin_alf
Шаг 3 — Поиск точки пересечения отрезков.
Запишем уравнение отрезка {P2,P3} и найдем точку его пересечения CR с осью Y:
P23X = P(2).x + ( P(3).x - P(2).x ) * beta
P23Y = P(2).y + ( P(3).y - P(2).y ) * beta
где 0 <= beta <= 1
В точке CR пересечения отрезка {P2,P3} с осью Y:
P(2).x + ( P(3).x - P(2).x ) * beta =0
Далее возможны 2 варианта в зависимости от значения P(3).x — P(2).x:
1 вариант:
если ( P(2).x - P(3).x ) <> 0 // отрезок {P2,P3} не вертикален
beta = P(2).x / ( P(2).x - P(3).x )
если beta >= 0 и beta <= 1 // отрезок {P2,P3} пересекает ось Y
CR.x = 0
CR.y = P(2).y + ( P(3).y - P(2).y ) * beta
//условие пересечения отрезков:
0 <= CR.y <= L1
2 вариант:
Если P(2).x = P(3).x, то это означает, что отрезок {P2,P3} вертикален и параллелен отрезку {P0,P1}. Пересечение отрезков возможно только если второй отрезок {P2,P3} тоже лежит на оси Y, и один из его концов лежит в первом отрезке {P0,P1} (или касается) или отрезок {P2,P3} накрывает {P0,P1}. Будем считать что для результата нам достаточно одной точки. Это будет одна из точек P0..P3.
Условия:
P(2).x = P(3).x = 0 // второй отрезок {P2,P3} вертикален b лежит на оси Y.
и // условие пересечения:
P(2).y >= 0 и P(2).y <= L1 // P2 внутри отрезка {P0,P1}
-> CR = P_copy(2) // результат выбираем вершину P2
или
P(3).y >= 0 и P(3).y <= L1 // P3 внутри отрезка {P0,P1}
-> CR = P_copy(3) // результат выбираем вершину P3
или
P(2).y < 0 и P(3).y > L1 // отрезок {P0,P1} внутри отрезка {P2,P3}
или
P(3).y < 0 и P(2).y > L1
-> CR = P_copy(0) // // результат выбираем вершину P0 (или P1)
)
Шаг 4
Если точка пересечения CR найдена по варианту 1 шага 3, то ее координаты пересчитываем для исходной системы координат. Используем переменные сохраненные на 1 и 2 шаге. Поворот на угол -alfa:
CR.x = CR.x * cos(-alfa) + CR.y * sin(-alfa) = CR.x * cos_alf + CR.y * sin_alf
CR.y = CR.y * cos(-alfa) - CR.x * sin(-alfa) = CR.y * cos_alf - CR.x * sin_alf
Перенос обратно:
CR.x = CR.x + P_copy(0).x
CR.y = CR.y + P_copy(0).y
Если точка пересечения CR найдена по условию 2 шага 3 пересчет координат не нужен. Пример кода на golang под катом. Golang ом я только балуюсь, поэтому к коду прошу быть снисходительным. Код можно запустить на golang.org:
код на golang
// line_cross project main.go
package main
import (
"fmt"
"math"
)
type point struct {
x float64
y float64
}
func main() {
var P [4]point
var P_copy [4]point
var L1, sin_alf, cos_alf, wsp1, wsp2, beta float64
var flag_cross bool
var CR point
// исходные данные x y координаты точек
P[0].x = 1.0
P[0].y = 2.0
P[1].x = 10.0
P[1].y = 20.0
P[2].x = 3.0
P[2].y = 9.0
P[3].x = 9.0
P[3].y = 3.0
// шаг 1
P_copy = P
fmt.Println("Исходные данные:")
for ii := 0; ii < 4; ii++ {
fmt.Println(" p", ii+1, " x", P_copy[ii].x, " y", P_copy[ii].y)
}
P[0].x = 0
P[0].y = 0
for ii := 1; ii < 4; ii++ {
P[ii].x = P[ii].x - P_copy[0].x
P[ii].y = P[ii].y - P_copy[0].y
}
// шаг 2
L1 = math.Sqrt(P[1].x*P[1].x + P[1].y*P[1].y)
if L1 > 0 {
sin_alf = P[1].x / L1
cos_alf = P[1].y / L1
} else {
sin_alf = 0
cos_alf = 0
}
P[1].x = 0
P[1].y = L1
for ii := 2; ii < 4; ii++ {
wsp1 = P[ii].x*cos_alf - P[ii].y*sin_alf
wsp2 = P[ii].y*cos_alf + P[ii].x*sin_alf
P[ii].x = wsp1
P[ii].y = wsp2
}
//шаг 3
flag_cross = false
if P[2].x-P[3].x == 0 { // отрезок {P3,P4) параллелен {P0,P1)
if P[2].x == 0 && P[3].x == 0 {
switch {
case P[2].y >= 0 && P[2].y <= L1:
flag_cross = true
CR = P_copy[2]
case P[3].y >= 0 && P[3].y <= L1:
flag_cross = true
CR = P_copy[3]
case (P[2].y < 0 && P[3].y > L1) || (P[3].y < 0 && P[2].y > L1):
flag_cross = true
CR = P_copy[0]
}
}
} else {
beta = P[2].x / (P[2].x - P[3].x)
if beta >= 0 && beta <= 1 {
CR.x = 0
CR.y = P[2].y + (P[3].y-P[2].y)*beta
if CR.y >= 0 && CR.y <= L1 {
//шаг 4
// пересчет координат
flag_cross = true
wsp1 = CR.x*cos_alf + CR.y*sin_alf
wsp2 = CR.y*cos_alf - CR.x*sin_alf
CR.x = wsp1
CR.y = wsp2
CR.x = CR.x + P_copy[0].x
CR.y = CR.y + P_copy[0].y
}
}
}
if flag_cross {
fmt.Println("Точка пересечения: х =", CR.x, " y=", CR.y)
} else {
fmt.Println("Отрезки не пересекаются !")
}
}
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png” style=”height: 600px;”>
0 и b > 0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png” style=”height: 600px;”>
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x – 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x – 2.
Как найти точку пересечения прямой с осью x по уравнению
При практическом построении прямой по ее уравнению наиболее точный график получится тогда, когда координаты взятых для ее построения двух точек – целые числа.
1. Если прямая определена общим уравнением Ax + By + C = 0 и , то для ее построения проще всего определить точки пересечения прямой с координатными осями.
Укажем, как определить координаты точек пересечения прямой с координатными осями. Координаты точки пересечения прямой с осью Ox находят из следующих соображений: ординаты всех точек, расположенных на оси Ox, равны нулю. В уравнении прямой полагают, что y равно нулю, и из полученного уравнения находят x. Найденное значение x и есть абсцисса точки пересечения прямой с осью Ox. Если окажется, что x = a, то координаты точки пересечения прямой с осью Ox будут (a, 0).
Чтобы определить координаты точки пересечения прямой с осью Oy, рассуждают так: абсциссы всех точек, расположенных на оси Oy, равны нулю. Взяв в уравнении прямой x равным нулю, из полученного уравнения определяют y. Найденное значение y и будет ординатой пересечения прямой с осью Oy. Если окажется, например, что y = b, то точка пересечения прямой с осью Oy имеет координаты (0, b).
Пример. Прямая 2x + y – 6 = 0 пересекает ось Ox в точке (3, 0). Действительно, взяв в этом уравнении y = 0, получим для определения x уравнение 2x – 6 = 0, откуда x = 3.
Чтобы определить точку пересечения этой прямой с осью Oy, положим в уравнении прямой x = 0. Получим уравнение y – 6 = 0, из которого следует, что y = 6. Таким образом, прямая пересекает координатные оси в точках (3, 0) и (0, 6).
Если же в общем уравнении прямой C = 0, то прямая, определяемая этим уравнением, проходит через начало координат. Таким образом, уже известна одна ее точка, и для построения прямой остается только найти еще одну ее точку. Абсциссу x этой точки задают произвольно, а ординату y находят из уравнения прямой.
Точка пересечения прямых в пространстве онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых (“канонический” или “параметрический” ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Точка пересечения прямых в пространстве − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в каноническом виде.
- 2. Точка пересечения прямых, заданных в параметрическом виде.
- 3. Точка пересечения прямых, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
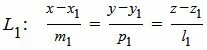 , , |
(1) |
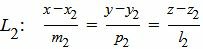 , , |
(2) |
Найти точку пересечения прямых L1 и L2 (Рис.1).
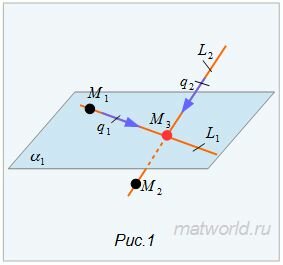
Запишем уравнение (1) в виде системы двух линейных уравнений:
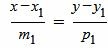 , , |
(3) |
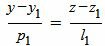 |
(4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Аналогичным образом преобразуем уравнение (2):
Запишем уравнение (2) в виде системы двух линейных уравнений:
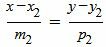 , , |
(7) |
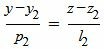 |
(8) |
Сделаем перекрестное умножение в уравнениях (7) и (8):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:
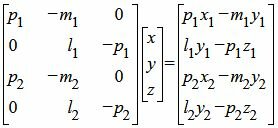 |
(11) |
Как решить систему линейных уравнений (11)(или (5), (6), (9), (10)) посмотрите на странице Метод Гаусса онлайн. Если система линейных уравнениий (11) несовместна, то прямые L1 и L2 не пересекаются. Если система (11) имеет множество решений, то прямые L1 и L2 совпадают. Единственное решение системы линейных уравнений (11) указывает на то, что это решение определяет координаты точки пересечения прямых L1 и L2 .
2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
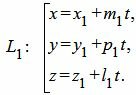 |
(12) |
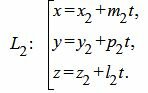 |
(13) |
Задачу нахождения нахождения точки пересечения прямых L1 и L2 можно решить разными методами.
Метод 1. Приведем уравнения прямых L1 и L2 к каноническому виду.
Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:
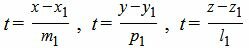 |
(14) |
Так как левые части уравнений (14) равны, то можем записать:
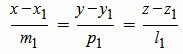 |
(15) |
Аналогичным образом приведем уравнение прямой L2 к каноническому виду:
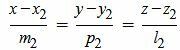 |
(16) |
Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямых L1 и L2 решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:
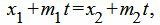 |
(17) |
 |
(18) |
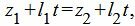 |
(19) |
Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).
3. Точка пересечения прямых в пространстве, заданных в разных видах.
Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.
4. Примеры нахождения точки пересечения прямых в пространстве.
Пример 1. Найти точку пересечения прямых L1 и L2:
 |
(20) |
 |
(21) |
Представим уравнение (20) в виде двух уравнений:
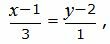 |
(22) |
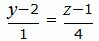 |
(23) |
Сделаем перекрестное умножение в уравнениях (22) и (23):
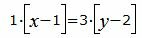
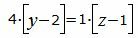
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
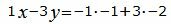
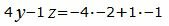
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
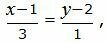 |
(26) |
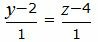 |
(27) |
Сделаем перекрестное умножение в уравнениях (7) и (8)
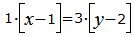
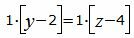
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
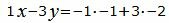
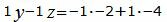
Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
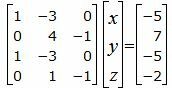 |
(30) |
Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
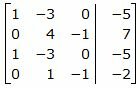
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1:
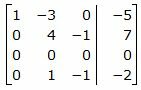
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:

Сделаем перестановку строк 3 и 4.
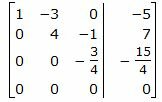
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:
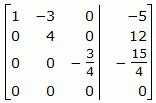
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:
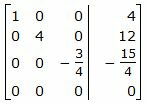
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
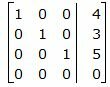
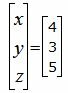
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
 |
(31) |
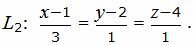 |
(32) |
Приведем параметрическое уравнение прямой L1 к каноническому виду. Выразим параметр t через остальные переменные:
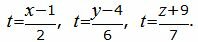
Из равентсв выше получим каноническое уравнение прямой:
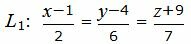 |
(33) |
Представим уравнение (33) в виде двух уравнений:
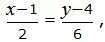 |
(34) |
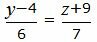 |
(35) |
Сделаем перекрестное умножение в уравнениях (34 и (35):

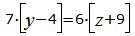
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

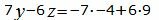
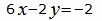 |
(36) |
 . . |
(37) |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
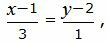 |
(38) |
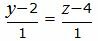 |
(39) |
Сделаем перекрестное умножение в уравнениях (38) и (39)
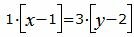
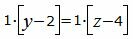
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
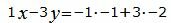
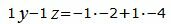
Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
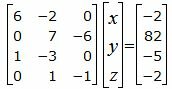 |
(42) |
Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:

Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:
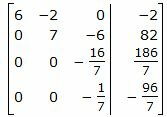
Исключим элементы 3-го столбца матрицы ниже элементаa33. Для этого сложим строку 4 со строкой 3, умноженной на -1/16:
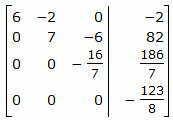
Из расширенной матрицы восстановим последнюю систему линейных уравнений:
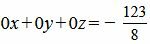 |
(43) |
Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L1 и L2 не пересекаются. То есть они или параллельны, или скрещиваются.
Прямая L1 имеет направляющий вектор q1=<2,6,7>, а прямая L2 имеет направляющий вектор q2=<3,1,1>. Эти векторы не коллинеарны. Следовательно прямые L1 и L2 скрещиваются .
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/grafik-linejnoj-funkcii
http://www.pm298.ru/reshenie/uravnpr4.php
http://matworld.ru/analytic-geometry/tochka-peresechenija-prjamyh-3d.php
[/spoiler]
Математика
6 класс
Урок № 79
Декартова система координат на плоскости
Перечень рассматриваемых вопросов:
- прямоугольная система координат;
- координатная плоскость;
- координатная ось, координата точки;
- изображение точек с действительными координатами на плоскости.
Тезаурус
Координатная плоскость. Зададим на плоскости две оси координат, расположив их под прямым углом. Координатные оси пересекаются в точке, являющейся началом отсчёта для каждой из них.
Ось х называют осью абсцисс – расположена горизонтально, направлена вправо. Ось у называют осью ординат – расположена вертикально, направлена вверх.
Оси координат разделяют плоскость на 4 угла, которые называются координатными четвертями.
Координаты точки М (х; у), где х – абсцисса, у – ордината точки.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Зададим на плоскости две оси координат, расположив их под прямым углом. Единичные отрезки осей возьмём равными друг другу.
Ось х называют осью абсцисс – расположена горизонтально, направлена вправо. Ось у называют осью ординат – расположена вертикально, направлена вверх.

Положительное направление на осях указывается стрелкой.
Точку пересечения осей называют началом координат.
Оси взаимно перпендикулярны, поэтому заданную таким образом систему координат называют прямоугольной.
Оси координат разделяют плоскость на 4 угла – координатные четверти. Обозначают римскими цифрами как показано на рисунке.

Одним из первых, кто начал широко использовать прямоугольную систему координат в своих исследованиях, был французский философ и математик Рене Декарт, поэтому её часто называют декартовой системой координат.
Пусть A – произвольная точка координатной плоскости. Проведём через точку A прямые, параллельные осям координат. Прямая, параллельная оси y, пересечёт ось x в точке A1, а прямая, параллельная оси x, пересечёт ось y в точке A2. Координату точки A1 на оси x называют абсциссой точки A. Координату точки A2 на оси y называют ординатой точки A. Абсциссу x и ординату y точки A называют координатами точки A.

Координаты точки, записывают в круглых скобках рядом с буквой, обозначающей эту точку: М (х; у).

Важно!
х – первая координата
у – вторая координата
Поменять местами х и у нельзя – получится другая точка.
Поэтому пару координат (x; y) точки A называют упорядоченной парой чисел.
Если на плоскости задана прямоугольная система координат хOу, то:
– каждой точке плоскости поставлена в соответствие упорядоченная пара чисел (координаты точки);
– разным точкам плоскости соответствуют разные упорядоченные пары чисел;
– каждая упорядоченная пара чисел соответствует одной точке плоскости.
То есть установлено взаимно однозначное соответствие между точками плоскости и упорядоченными парами чисел.
Алгоритм построения точки на координатной плоскости
Построим точку А(3; 6).
Введём прямоугольную систему координат.
На каждой оси откладываем заданные координаты х и у (x > 0 и y > 0, значит, точка A расположена в I координатной четверти).
Проводим перпендикуляры к оси х и оси у.
Точка их пересечения – искомая точка.

В(– 4; 5) – имеет отрицательную абсциссу и положительную ординату, значит, расположена во II четверти.
С(– 8; – 4) – имеет обе отрицательные координаты, значит, расположена в III четверти.
D(9; – 2) – имеет положительную абсциссу и отрицательную ординату, значит, расположена в IV четверти.
F(6; 0), E(– 5; 0) – точки лежат на оси абсцисс.
H(0; – 5) – точка лежит на оси ординат.
O(0; 0) – начальная точка системы координат.
В географии положение объектов на земной поверхности определяется двумя координатами: широтой и долготой.

В концертном зале своё кресло можно найти по номеру ряда и места.

В шахматах каждой клетке соответствует буква столбца и цифра ряда.

Разбор заданий тренировочного модуля
Тип 1. Ввод с клавиатуры пропущенных элементов в тексте
Построить прямую АВ, если А(3; 2), В(– 3; – 4).
Найти:
1) координаты точек пересечения прямой AB с осями;
2) координаты середины отрезка AB.

Шаг 1. Строим точки А и В по их координатам.
Шаг 2. Проводим прямую АВ.
Шаг 3. Находим точки пересечения с осями координат, обозначаем их буквами M и N. Определяем их координаты:
М (1; 0), N (0; – 1).
Шаг 4. Находим по графику середину отрезка АВ, это точка N (0; – 1).
Ответ: координаты точек пересечения прямой AB с осями: М (1; 0), N (0; – 1), координаты середины отрезка AB: N (0; – 1).
Тип 2. Нарисуйте фигуру, последовательно соединяя точки
(0; 4), (– 2; – 2), (3; 2), (– 3; 2), (2; – 4), (0; 4).

Оглавление
- Расположение отрезков на плоскости
- Параметрическое уравнение отрезка
- Найти точку пересечения двух отрезков
- Отрезки не пересекаются
- Метод SegmentSegment(…)
- Исходник приложения с классом Intersections
Расположение отрезков на плоскости
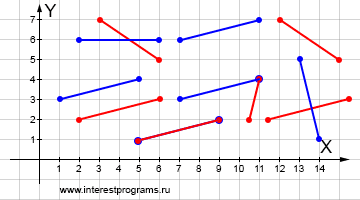
Два отрезка могут иметь различные положения на плоскости относительно друг друга. Поскольку отрезок ограниченная с двух сторон линия, данная геометрическая фигура предлагает больше вариантов расположения в сравнении с прямой и лучом.
Из вариантов пересечения или непересечения можно выделить несколько особых случаев, например: начала и концы отрезков совпадают, отрезки параллельны и не лежат друг на друге, начало или конец одного отрезка лежит на другом отрезке, совпадают только начальные или конечные точки.
Параметрическое уравнение отрезка
Расположение отрезка в координатной системе и его геометрия, также как прямой и луча, может описываться параметрическими уравнениями. Параметрическое уравнение отрезка(прямой, луча) представляет из себя выражение включающее координату начала, вектор направления и параметр задающий множество точек отрезка(прямой, луча).
Параметр может иметь ограничения или не иметь их.
система из параметрических уравнений: | x = x0 + vt | y = y0 + wt где v и w координаты (x, y) вектора направления v = x1 - x0 w = y1 + y0 при 0 ≤ t ≤ 1 - уравнения описывают отрезок, при 0 ≤ t < +∞ - уравнения описывают луч, при -∞ < t < +∞ - уравнения описывают прямую
Найти точку пересечения двух отрезков
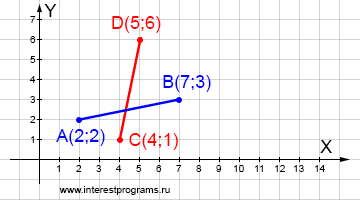
Система из 4-х параметрических уравнений позволяет найти точку пересечения двух отрезков. Нахождение точки пересечения отрезков аналогично описанному для двух лучей.
Дано: отрезок AB с координатами начальной и конечной точек – A(2;2) и B(7;3), отрезок CD с координатами – C(4;1) и D(5;6). Найти возможную точку пересечения отрезков AB и CD.
Отрезки имеют точку пересечения если оба параметра отрезков больше или равно нулю и меньше или равно единице.
| x = 2 + (7 - 2)tab | x = 2 + 5tab | y = 2 + (3 - 2)tab => | y = 2 + tab | x = 4 + (5 - 4)tcd | x = 4 + tcd | y = 1 + (6 - 1)tcd | y = 1 + 5tcd
Чтобы узнать есть ли точка пересечения отрезков AB и CD вычислим их параметры:
найдём соотношение параметров через возможно общую координату x 2 + 5tab = 4 + tcd => 5tab = 2 + tcd => tab = (2 + tcd)/5 (у.1) вычислим параметр tcd через возможно общую координату y 2 + tab = 1 + 5tcd => 2 + (2 + tcd)/5 = 1 + 5tcd => 10 + 2 + tcd = 5 + 25cd => tcd = 7/24 ≈ 0.292 вычислим параметр tab использую полученное соотношение (у.1) tab = (2 + 0.292)/5 ≈ 0.458
Оба параметра положительные и меньше единицы – отрезки пересекаются. Найдем точку пересечения используя уравнения из системы для двух отрезков:
x = 2 + 5tab => x = 2 + 5 * 0.458 = 4.29 y = 2 + tab => y = 2 + 0.458 = 2.458
Точка пересечения отрезков AB и CD имеет координаты (4.29; 2.458).
Отрезки не пересекаются
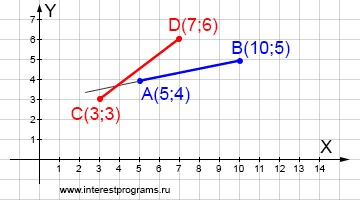
Отсутствие точки пересечения двух отрезков, безусловно, также подтверждается вычислением.
Дано: отрезок AB с координатами начальной и конечной точек – A(5;4) и B(10;5), отрезок CD с координатами – C(3;3) и D(7;6). Определить: отрезки пересекаются или не пересекаются. Если отрезки не пересекаются, найти мнимую точку пересечения.
Отрезки не пересекаются если хотя бы один из параметров отрицательный или больше единицы. Для вычисления используем систему из параметрических уравнений.
| x = 5 + (10 - 5)tab | x = 5 + 5tab | y = 4 + (5 - 4)tab => | y = 4 + tab | x = 3 + (7 - 3)tcd | x = 3 + 4tcd | y = 3 + (6 - 3)tcd | y = 3 + 3tcd
Чтобы узнать пересекаются отрезки или нет вычислим их параметры, вычисление будет происходит аналогично случаю пересечения описанному выше.
3 + 4tcd = 5 + 5tab => 4tcd = 2 + 5tab => tcd = (2 + 5tab)/4 3 + 3tcd = 4 + tab => 3 + 3(2 + 5tab)/4 = 4 + tab => 3 + (6 + 15tab)/4 = 4 + tab => 2 + 11tab = 0 => tab = -2/11 ≈ -0.182 параметр tab меньше нуля, значит отрезки не пересекаются tcd = (2 + 5tab)/4 => tcd = (2 + 5*-0.182)/4 ≈ 0.273 параметр tcd положительный и меньше единицы, значит мнимая точка лежит на отрезке CD
Найдем мнимую точку, расположенную на отрезке CD:
x = 5 + 5 * -0.182 = 4.09 y = 4 - 0.182 = 3.818
Метод SegmentSegment(…)
Метод вычисления точки пересечения отрезков инкапсулирован в классе Intersections. Метод статический, для вычисления точки пересечения не требуется создание экземпляра класса. Методы вычисляющие точки пересечения прямых и лучей описаны на страницах точка пересечения двух прямых на плоскости, пересечение луча и прямой, пересечение двух лучей.
В исходнике приложения, прикрепленного к странице происходит вычисление точки пересечения и создание параметрических уравнений каждого отрезка.
class Intersections
{
// Вычисление точки пересечения отрезков.
public static bool SegmentSegment(Point r1, Point r2, Point p1, Point p2, out Point pCross, out Info info)
{
// Параметрическое уравнение отрезка
// x = x0 + vt
// y = y0 + wt
// где v = x1 - x0
// w = y1 - y0
// при 0 <= t <= 1
// Оповещение о событиях пересечения или не пересечения.
info = new Info();
// Координаты направления вектора синего отрезка
double v = r2.X - r1.X;
double w = r2.Y - r1.Y;
// Координаты направления вектора красного отрезка
double v2 = p2.X - p1.X;
double w2 = p2.Y - p1.Y;
// ===== Частные случаи не пересечения =====
// Отрезки должны быть определены
if (v == 0 && w == 0 && v2 == 0 && w2 == 0)
{
info.Id = 10;
info.Message = "Отрезки неопределённы";
return false;
}
else if (v == 0 && w == 0)
{
info.Id = 11;
info.Message = "Синий отрезка неопределён";
return false;
}
else if (v2 == 0 && w2 == 0)
{
info.Id = 12;
info.Message = "Красный отрезка неопределён";
return false;
}
// Для вычисления параллельности отрезка
// необходимо сравнить направления их векторов.
// Вычисляем длины векторов
double lenBlue = Math.Sqrt(v * v + w * w);
double lenRed = Math.Sqrt(v2 * v2 + w2 * w2);
// Нормализация векторов - создание единичного вектора направления
double x = v / lenBlue;
double y = w / lenBlue;
double x2 = v2 / lenRed;
double y2 = w2 / lenRed;
// Точность совпадения величин double
double epsilon = 0.000001;
// Проверка на совпадение
if (r1.X == p1.X && r1.Y == p1.Y && r2.X == p2.X && r2.Y == p2.Y)
{
info.Id = 20;
info.Message = "Отрезки совпадают";
return false;
}
// Проверка на параллельность с определенной точностью.
if (Math.Abs(x - x2) < epsilon && Math.Abs(y - y2) < epsilon)
{
info.Id = 21;
info.Message = "Отрезки параллельны";
return false;
}
// ===== /Частные случаи не пересечения =====
// ===== Вычисление точки пересечения =====
// Проверка факта пересечения
// x = p1.X + v2t2
// y = p1.Y + w2t2
// r1.X + vt = p1.X + v2t2 => vt = p1.X - r1.X + v2t2 =>
// t = (p1.X - r1.X + v2t2) / v - (у.1) соотношение t-параметров
//
// Вычисление одного параметра с заменой соотношением другого
// r1.Y + wt = p1.Y + w2t2 => wt = p1.Y - r1.Y + w2t2 => t = (p1.Y - r1.Y + w2t2) / w
// (p1.X - r1.X + v2t2) / v = (p1.Y - r1.Y + w2t2) / w =>
// (p1.X - r1.X + v2t2) * w = (p1.Y - r1.Y + w2t2) * v =>
// w * p1.X - w * r1.X + w * v2t2 = v * p1.Y - v * r1.Y + v * w2t2 =>
// w * v2t2 - v * w2t2 = -w * p1.X + w * r1.X + v * p1.Y - v * r1.Y =>
// (w * v2 - v * w2) * t2 = -w * p1.X + w * r1.X + v * p1.Y - v * r1.Y =>
// t2 = (-w * p1.X + w * r1.X + v * p1.Y - v * r1.Y) / (w * v2 - v * w2) - (у.2)
double t2 = (-w * p1.X + w * r1.X + v * p1.Y - v * r1.Y) / (w * v2 - v * w2);
// t = (p1.X - r1.X + v2t2) / v - (у.1)
double t = (p1.X - r1.X + v2 * t2) / v;
// Если один из параметров меньше 0 и больше 1, значит пересечения нет.
if (t < 0 || t > 1 || t2 < 0 || t2 > 1)
{
info.Id = 20;
info.Message = "Пересечения нет";
return false;
}
// Координаты точки пересечения
pCross.X = p1.X + v2 * t2;
pCross.Y = p1.Y + w2 * t2;
info.Id = 0;
info.Message = "Пересечение есть";
return true;
// ===== /Вычисление точки пересечения =====
}
}
public class Info
{
// Для визуального сообщения.
public string Message;
// Для автоматических действий.
public int Id;
}
Исходник приложения с классом Intersections
К странице приложен исходник приложения на языке C#. Приложение демонстрирует вычисление точки пересечения двух отрезков. Графика приложения создает различные положения отрезков на плоскости окна. Управление начальными и конечными точками мышью и служебными клавишами.
Скачать исходник
WpfAppCrossSegmentSegment-vs17.zip
- Размер: 205 Кбайт
- Загрузки: 183
