Содержание:
Плоскость в пространстве
Общее уравнение плоскости
Определение: Уравнение вида 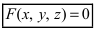
Определение: Порядок поверхности определяется по высшему показателю степени переменных х, у и z или по сумме показателей степени в произведении этих величин.
Определение: Уравнение вида Ax+By+Cz+D=O называется общим уравнением плоскости.
Рассмотрим частные случаи приведенного уравнения:
1. D = 0; Ах + By + Сz = 0. Из этого уравнения видно, что точка О(0; 0; 0) удов- летворяет этому уравнению, следовательно, это уравнение описывает плоскость, проходящую через начало координат (Рис. 36). 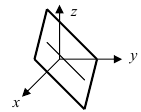
Рис. 36. Плоскость, проходящая через начало координат.
2. С = 0; Ах + Ву + D = 0. Этому уравнению удовлетворяет любое значение переменной z, поэтому данное уравнение описывает плоскость, которая параллельна оси аппликат (Oz) (Рис. 37). 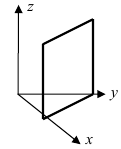
Рис. 37. Плоскость, проходящая параллельно оси аппликат.
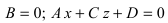 – плоскость параллельна оси ординат (Оу);
– плоскость параллельна оси ординат (Оу);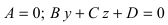 – плоскость параллельна оси абсцисс (Ох).
– плоскость параллельна оси абсцисс (Ох).
Замечание: При отсутствии в уравнении плоскости одной из переменных величин говорит о том, что плоскость параллельна соответствующей координатной оси.
3. С=0; D=0; Ах+ By=0 – плоскость проходит через начало отсчета параллельно оси аппликат (Рис. 38). 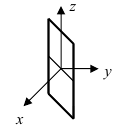
Рис. 38. Плоскость, проходящая через начало координат параллельно оси аппликат.
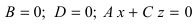 – плоскость проходит через начало координат параллельно оси ординат;
– плоскость проходит через начало координат параллельно оси ординат;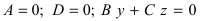 – плоскость проходит через начало координат параллельно оси абсцисс.
– плоскость проходит через начало координат параллельно оси абсцисс.
4. 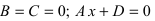 – плоскость проходит через точку
– плоскость проходит через точку 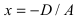 параллельно плоскости
параллельно плоскости 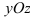 (Pис. 39).
(Pис. 39). 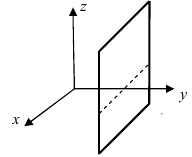
Рис. 39. Плоскость, проходящая параллельно координатной плоскости 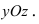
5. В = С = D = 0; Ах = 0=>х = 0 – уравнение описывает плоскость 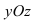 (Рис. 40).
(Рис. 40).
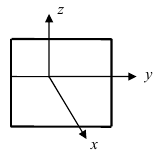
Рис. 40. Координатная плоскость 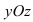 .
.
Другие уравнения плоскости
1. Уравнение плоскости в отрезках. Пусть в уравнении 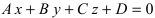 коэффициент
коэффициент 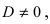 тогда выполним следующие преобразования
тогда выполним следующие преобразования
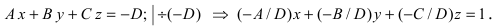
Введем следующие обозначения 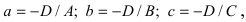 тогда уравнение примет вид
тогда уравнение примет вид 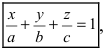 которое называется уравнением плоскости в отрезках. Найдем точки пересечения плоскости с координатными осями:
которое называется уравнением плоскости в отрезках. Найдем точки пересечения плоскости с координатными осями: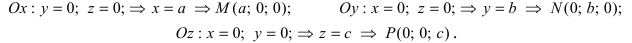
Откладывая на координатных осях точки М, N и Р, соединяя их прямыми лучим изображение данной плоскости (для определенности принято, что параметры а, b, с положительные) (Рис. 41): 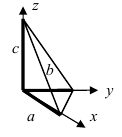
Рис. 41. Отрезки, отсекаемые плоскостью на координатных осях.
Из рисунка видно, что числа а, b, с показывают отрезки, отсекаемые плоскостью на координатных осях, считая от начала координат.
2. Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Пусть задана точка 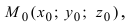 через которую проходит плоскость перпендикулярно к заданному вектору
через которую проходит плоскость перпендикулярно к заданному вектору 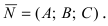 ОЗ. Вектор
ОЗ. Вектор 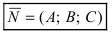 называется нормальным вектором плоскости, если он перпендикулярен любой паре неколлинеарных векторов, лежащих на плоскости.
называется нормальным вектором плоскости, если он перпендикулярен любой паре неколлинеарных векторов, лежащих на плоскости.
Возьмем на плоскости произвольную точку 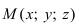 и образуем вектор
и образуем вектор 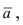 соединяющий точку
соединяющий точку 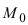 с точкой М (Рис. 42). Тогда
с точкой М (Рис. 42). Тогда 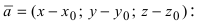
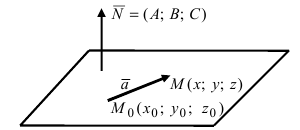
Рис. 42. Плоскость, проходящая через заданную точку перпендикулярно к нормальному вектору.
В силу того, вектор 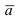 лежит в плоскости, то он перпендикулярен нормальному вектору
лежит в плоскости, то он перпендикулярен нормальному вектору 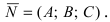 Используя условие перпендикулярности векторов
Используя условие перпендикулярности векторов 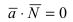 в проекциях перемножаемых векторов, получим уравнение плоскости, проходящая через заданную точку перпендикулярно к нормальному вектору:
в проекциях перемножаемых векторов, получим уравнение плоскости, проходящая через заданную точку перпендикулярно к нормальному вектору: 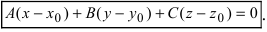
Пример:
Составить уравнение плоскости, проходящей через т. 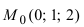 параллельно плоскости
параллельно плоскости 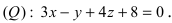
Решение:
Так как искомая плоскость параллельна плоскости (Q), то нормальный вектор этой плоскости 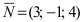 (см. коэффициенты при переменных величинах х, у и z в уравнении плоскости
(см. коэффициенты при переменных величинах х, у и z в уравнении плоскости 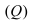 ) перпендикулярен к искомой плоскости и может быть взят в качестве нормального вектора этой плоскости. Используя уравнение плоскости, проходящей через заданную точку перпендикулярно к данному вектору, получаем:
) перпендикулярен к искомой плоскости и может быть взят в качестве нормального вектора этой плоскости. Используя уравнение плоскости, проходящей через заданную точку перпендикулярно к данному вектору, получаем: 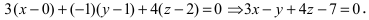
Пример:
Составить уравнение плоскости, проходящей через точки А(—1; 1 ;2) и В(0; —1; —1) параллельно вектору 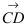 = (0; 0; -2):
= (0; 0; -2):
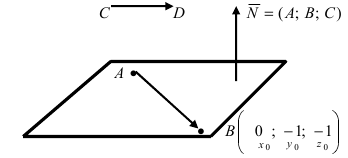
Решение:
Построим на искомой плоскости вектор 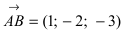 и вычислим нормальный вектор
и вычислим нормальный вектор 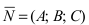 как векторное произведение векторов
как векторное произведение векторов 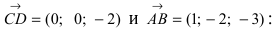
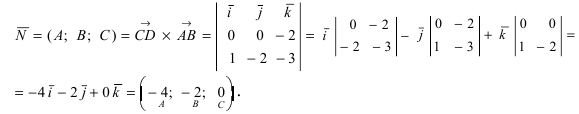
Уравнение плоскости, проходящей через заданную точку 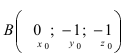 перпендикулярно к заданному вектору
перпендикулярно к заданному вектору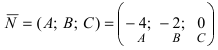 имеет вид:
имеет вид: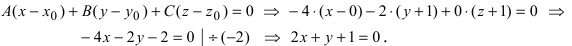
Отметим, что при выборе точки, через которую проходит искомая плоскость из точек 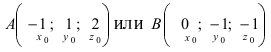 брать как точку, через которую проходит искомая плоскость.
брать как точку, через которую проходит искомая плоскость.
3. Уравнение плоскости, проходящей через три заданные точки. Пусть плоскость проходит через 3 известные точки 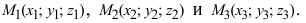 Возьмем произвольную точку плоскости М(х; у; z) и образуем векторы
Возьмем произвольную точку плоскости М(х; у; z) и образуем векторы 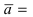
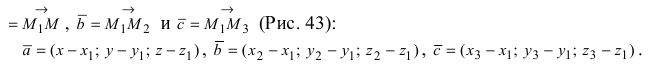
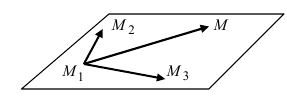
Рис. 43. Плоскость, проходящая через три заданные точки.
Вектора 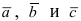 компланарные, используя условие компланарности векторов
компланарные, используя условие компланарности векторов 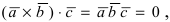 получим уравнение плоскости, проходящей через 3 известные точки:
получим уравнение плоскости, проходящей через 3 известные точки: 
Замечание: Полученный определитель третьего порядка раскрывается по элементам первой строки.
Пример:
Составить уравнение плоскости, проходящей через три заданные точки 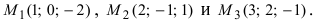
Решение:
Составим определитель третьего порядка 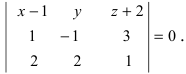 Раскроем определитель по элементам первой строки
Раскроем определитель по элементам первой строки 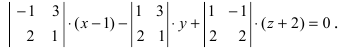 Вычислим определители второго порядка: -7(x-l) + 5y + 4(z + 2) = 0. Умножив уравнение на (-1) и раскрыв скобки, получим окончательный ответ:
Вычислим определители второго порядка: -7(x-l) + 5y + 4(z + 2) = 0. Умножив уравнение на (-1) и раскрыв скобки, получим окончательный ответ: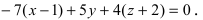
Основные задачи о плоскости в пространстве
1. Угол между пересекающимися плоскостями. Пусть даны две пересекающиеся плоскости 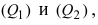 которые имеют нормальные векторы
которые имеют нормальные векторы
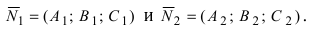
Пусть линия пересечения плоскостей определяется прямой (l). Из одной точки этой прямой проведем два перпендикулярных к прямой вектора 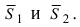 Меньший угол между этими векторами определяет угол между плоскостями (Рис.44):
Меньший угол между этими векторами определяет угол между плоскостями (Рис.44):
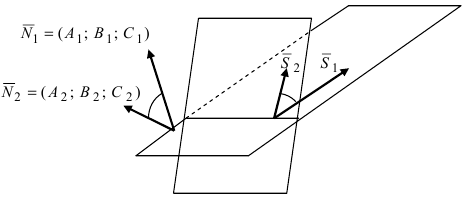
Рис.44. Угол между плоскостями.
В силу того, что 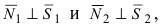 то угол между нормальными векторами равен углу между векторами
то угол между нормальными векторами равен углу между векторами 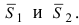 Из векторной алгебры известно, что угол между векторами определяется формулой:
Из векторной алгебры известно, что угол между векторами определяется формулой: 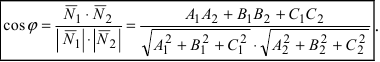
Следствие: Если плоскости перпендикулярны (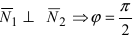 ), то условием перпендикулярности плоскостей является равенство:
), то условием перпендикулярности плоскостей является равенство: 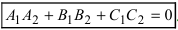 .
.
Следствие: Если плоскости параллельны, то нормальные вектора коллинеарны, следовательно, условие параллельности плоскостей: 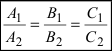
2. Расстояние от данной точки до заданной плоскости. Расстояние от данной точки 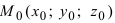 до заданной плоскости
до заданной плоскости 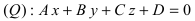 определяется по формуле:
определяется по формуле: 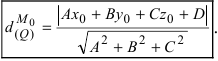
Пример:
На каком расстоянии от плоскости 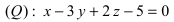 находится точка
находится точка 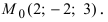
Решение:
Воспользуемся приведенной формулой: 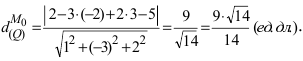
Прямая в пространстве
Общее уравнение прямой
Прямая в пространстве может быть задана как пересечение двух плоскостей: 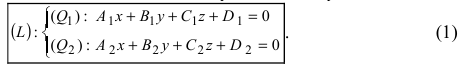
Определение: Геометрическое место точек пространства, удовлетворяющих системе уравнений (1), называется прямой в пространстве, а система уравнений (1) называется общим уравнением прямой.
Замечание: Для того чтобы система уравнений (1) определяла прямую в пространстве необходимо и достаточно, чтобы нормальные вектора плоскостей, определяющих прямую, 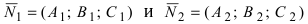 были неколлинеарными, т.е. выполняется одно из неравенств:
были неколлинеарными, т.е. выполняется одно из неравенств: 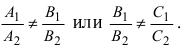
Пусть прямая проходит через точку 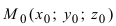 параллельно вектору
параллельно вектору 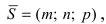 который называется направляющим вектором прямой (см. Лекцию Ле 7), тогда ее уравнение называется каноническим и имеет вид:
который называется направляющим вектором прямой (см. Лекцию Ле 7), тогда ее уравнение называется каноническим и имеет вид:

Замечание: Если в уравнении (2) одна из проекций направляющего вектора равна 0, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Пример:
Как расположена прямая 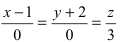 относительно координатных осей.
относительно координатных осей.
Решение:
Согласно замечанию эта прямая будет перпендикулярна осям абсцисс и ординат (параллельна оси аппликат) и будет проходить через точку 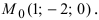 Приравняв каждую дробь уравнения (2) параметру t, получим параметрическое уравнение прямой:
Приравняв каждую дробь уравнения (2) параметру t, получим параметрическое уравнение прямой:
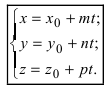
Пример:
Записать уравнение прямой 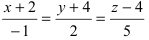 в параметрическом виде.
в параметрическом виде.
Решение:
Приравняем каждую дробь к параметру t: 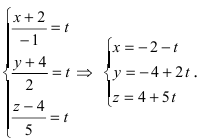 Если прямая проходит через две известные точки
Если прямая проходит через две известные точки 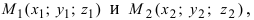 то ее уравнение имеет вид:
то ее уравнение имеет вид: 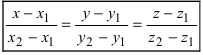 и называется уравнением прямой, проходящей через две заданные точки.
и называется уравнением прямой, проходящей через две заданные точки.
Пример:
Составить канонические и параметрические уравнения прямых, проходящих через точки А (— 1; 1; 2 ), В (0; -1; -1) И С (1; 0; -1), D (l; 0; 1 ).
Решение:
Составим каноническое уравнение прямой линии, проходящей через точки 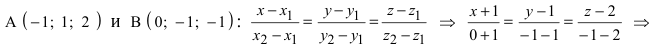
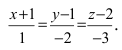 Перейдём к параметрическому уравнению
Перейдём к параметрическому уравнению 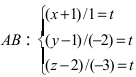 или
или 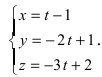 Составим каноническое уравнение прямой линии, проходящей через точки
Составим каноническое уравнение прямой линии, проходящей через точки 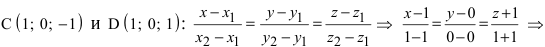
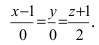 Перейдём к параметрическому уравнению прямой
Перейдём к параметрическому уравнению прямой 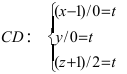
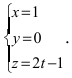
Основные задачи о прямой в пространстве
1. Переход от общего уравнения прямой к каноническому. Пусть прямая задана общим уравнением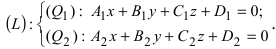 Для того, чтобы перейти от этого уравнения прямой к каноническому, поступают следующим образом:
Для того, чтобы перейти от этого уравнения прямой к каноническому, поступают следующим образом:
Пример:
Записать уравнение прямой 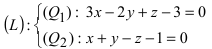 в каноническом и параметрическом виде.
в каноническом и параметрическом виде.
Решение:
Положив х = 0, получим СЛАУ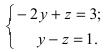 Складывая уравнения, найдем у = -4. Подставив это значение переменной у во второе уравнение системы, получим z = —5. Таким образом, прямая проходит через точку
Складывая уравнения, найдем у = -4. Подставив это значение переменной у во второе уравнение системы, получим z = —5. Таким образом, прямая проходит через точку 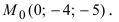 Найдем направляющий вектор прямой как векторное произведение нормальных векторов заданных плоскостей:
Найдем направляющий вектор прямой как векторное произведение нормальных векторов заданных плоскостей:
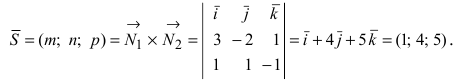
Запишем каноническое 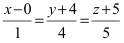 и параметрическое уравнения прямой:
и параметрическое уравнения прямой:
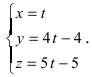
Угол между пересекающимися прямыми
Угол между двумя пересекающимися прямыми определяется как угол между их направляющими векторами. Если прямые 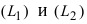 имеют направляющие вектора
имеют направляющие вектора
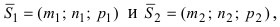
соответственно, то угол между прямыми определяется по формуле: 
Следствие: Если прямые перпендикулярны (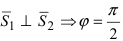 ), то условием перпендикулярности прямых является равенство:
), то условием перпендикулярности прямых является равенство: 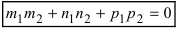
Следствие: Если прямые параллельны, то направляющие вектора коллинеарны, следовательно, условие параллельности прямых: 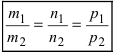
Координаты точки пересечения прямой и плоскости
Пусть прямая (L) задана общим уравнением 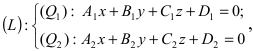 а плоскость (Q) уравнением Ax+By+Cz+D=0. Так как точка пересечения прямой и плоскости принадлежит одновременно обоим этим объектам, то ее координаты находят из системы уравнений:
а плоскость (Q) уравнением Ax+By+Cz+D=0. Так как точка пересечения прямой и плоскости принадлежит одновременно обоим этим объектам, то ее координаты находят из системы уравнений: 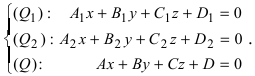 Если прямая (L) задана каноническим уравнением
Если прямая (L) задана каноническим уравнением 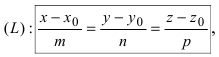 а плоскость (Q)
а плоскость (Q)
Рассмотрим возможные случаи:
- если выполняются условия
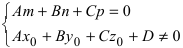 , то прямая не пересекает плоскость (прямая параллельна плоскости);
, то прямая не пересекает плоскость (прямая параллельна плоскости); - при условиях
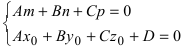 прямая лежит на плоскости;
прямая лежит на плоскости; - если
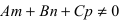 , прямая пересекает плоскость в одной точке.
, прямая пересекает плоскость в одной точке.
Пример:
Найти координаты точки пересечения прямой (L), заданной уравнением 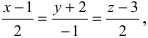 и плоскости (Q): 2x-y+3z-4=0.
и плоскости (Q): 2x-y+3z-4=0.
Решение:
Перепишем уравнение прямой (L) в параметрическом виде 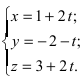 Подставим найденные величины в уравнение плоскости (Q)? получим
Подставим найденные величины в уравнение плоскости (Q)? получим
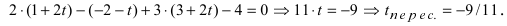
Найденное значение параметра 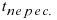 подставим в параметрическое уравнение прямой
подставим в параметрическое уравнение прямой 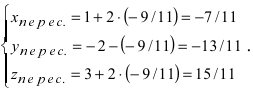 Таким образом, прямая пересекает заданную плоскость в точке
Таким образом, прямая пересекает заданную плоскость в точке 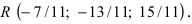
- Заказать решение задач по высшей математике
Угол между прямой и плоскостью
Пусть дана плоскость (Q) с нормальным вектором 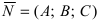 и пересекающая ее прямая (L) с направляющим вектором
и пересекающая ее прямая (L) с направляющим вектором 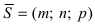 (Рис.45).
(Рис.45). 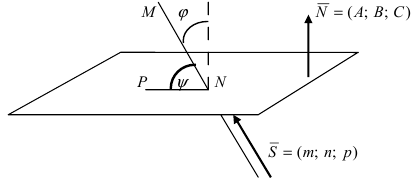
Рис. 45. Угол между прямой и плоскостью.
Угол 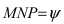 является углом между прямой (L) и плоскостью (Q). Угол между нормальным вектором плоскости и прямой обозначим через
является углом между прямой (L) и плоскостью (Q). Угол между нормальным вектором плоскости и прямой обозначим через 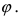 Из рисунка видно, что
Из рисунка видно, что 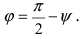 Следовательно,
Следовательно,
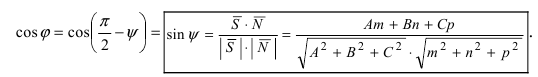
Следствие: Если прямая перпендикулярна плоскости (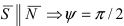 ), то условие перпендикулярности прямой и плоскости имеет вид:
), то условие перпендикулярности прямой и плоскости имеет вид: 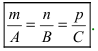
Следствие: Если прямая параллельна плоскости (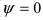 ), то направляющий вектор прямой и нормальный вектор плоскости перпендикулярны (
), то направляющий вектор прямой и нормальный вектор плоскости перпендикулярны (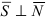 ), следовательно, условие параллельности прямой и плоскости:
), следовательно, условие параллельности прямой и плоскости: 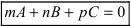 .
.
Плоскость и прямая в пространстве
Всякое уравнение первой степени относительно координат 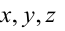
 задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.
задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.
Вектор 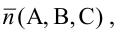 ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты А, В, С одновременно не равны 0.
ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты А, В, С одновременно не равны 0.
Особые случаи уравнения (3.1):
- D = 0, Ах + By + Cz = 0 – плоскость проходит через начало координат.
- С = 0, Ах + By + D = 0 – плоскость параллельна оси Oz.
- С = D = 0, Ах + By = 0 – плоскость проходит через ось Oz.
- С = В = 0, Ах + D = 0 – плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей: 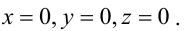
Прямая в пространстве может быть задана:
- как линия пересечения двух плоскостей, т.е. системой уравнений:
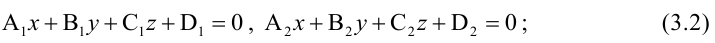
- двумя своими точками
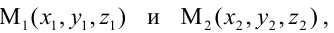 тогда прямая, через них проходящая, задается уравнениями:
тогда прямая, через них проходящая, задается уравнениями: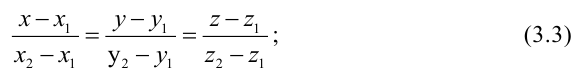
- точкой
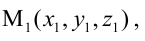 ей принадлежащей, и вектором
ей принадлежащей, и вектором 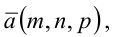 ей коллинеарным.
ей коллинеарным.
Тогда прямая определяется уравнениями: 
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор 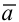 называется направляющим вектором прямой.
называется направляющим вектором прямой.
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: 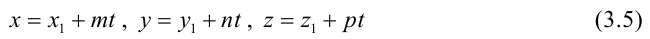 Решая систему (3.2) как систему линейных уравнений относительно неизвестных х и у, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой.
Решая систему (3.2) как систему линейных уравнений относительно неизвестных х и у, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой.
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения: 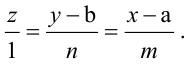
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор 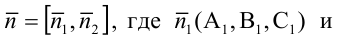
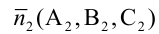 – нормальные векторы заданных плоскостей. Если один из знаменателей
– нормальные векторы заданных плоскостей. Если один из знаменателей 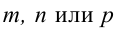 в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система
в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система 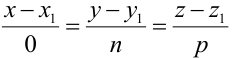 равносильна системе
равносильна системе 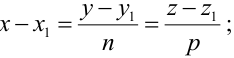 такая прямая перпендикулярна к оси Ох. Система
такая прямая перпендикулярна к оси Ох. Система 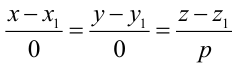 равносильна системе
равносильна системе 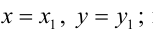 прямая параллельна оси Oz.
прямая параллельна оси Oz.
Пример:
Составьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение:
По условию задачи вектор 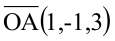 является нормальным вектором плоскости, тогда ее уравнение можно записать в виде
является нормальным вектором плоскости, тогда ее уравнение можно записать в виде 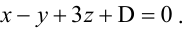 Подставив координаты точки А(1,-1,3), принадлежащей плоскости, найдем D:
Подставив координаты точки А(1,-1,3), принадлежащей плоскости, найдем D: 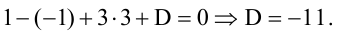 Итак,
Итак, 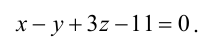
Пример:
Составьте уравнение плоскости, проходящей через ось Oz и образующей с плоскостью 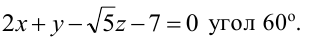
Решение:
Плоскость, проходящая через ось Oz, задается уравнением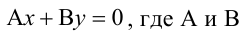 одновременно не обращаются в нуль. Пусть В не равно 0,
одновременно не обращаются в нуль. Пусть В не равно 0, 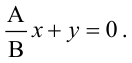 По формуле косинуса угла В между двумя плоскостями
По формуле косинуса угла В между двумя плоскостями 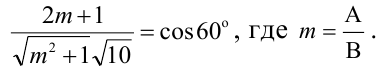
Решая квадратное уравнение 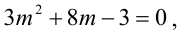 находим его корни
находим его корни 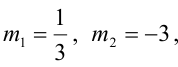 откуда получаем две плоскости
откуда получаем две плоскости 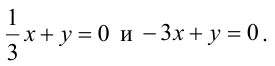
Пример:
Составьте канонические уравнения прямой: 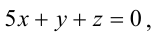
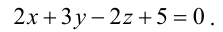
Решение:
Канонические уравнения прямой имеют вид:
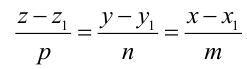 где
где 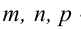 – координаты направляющего вектора прямой,
– координаты направляющего вектора прямой, 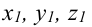 – координаты какой-либо точки, принадлежащей прямой. Прямая задана как линия пересечения двух плоскостей. Чтобы найти точку, принадлежащую прямой, фиксируют одну из координат (проще всего положить, например, х = 0) и полученную систему решают как систему линейных уравнений с двумя неизвестными. Итак, пусть х = 0, тогда у + z = 0, Зу-2z + 5 = 0 , откуда у = -l, z = l. Координаты точки
– координаты какой-либо точки, принадлежащей прямой. Прямая задана как линия пересечения двух плоскостей. Чтобы найти точку, принадлежащую прямой, фиксируют одну из координат (проще всего положить, например, х = 0) и полученную систему решают как систему линейных уравнений с двумя неизвестными. Итак, пусть х = 0, тогда у + z = 0, Зу-2z + 5 = 0 , откуда у = -l, z = l. Координаты точки 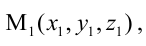 принадлежащей данной прямой, мы нашли: М(0,-1,1). Направляющий вектор прямой легко найти, зная нормальные векторы исходных плоскостей
принадлежащей данной прямой, мы нашли: М(0,-1,1). Направляющий вектор прямой легко найти, зная нормальные векторы исходных плоскостей 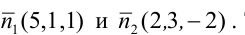 Тогда
Тогда
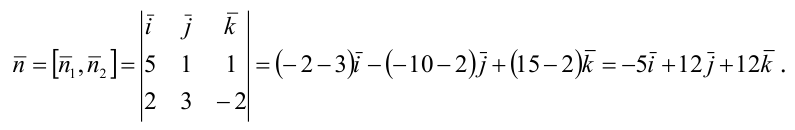 Канонические уравнения прямой имеют вид:
Канонические уравнения прямой имеют вид: 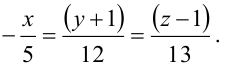
Пример:
В пучке, определяемом плоскостями 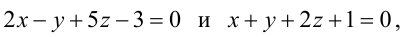 найти две перпендикулярные плоскости, одна из которых проходит через точку М (1,0,1).
найти две перпендикулярные плоскости, одна из которых проходит через точку М (1,0,1).
Решение:
Уравнение пучка, определяемого данными плоскостями, имеет вид 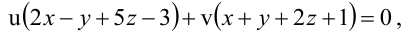 где
где 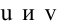 не обращаются в нуль одновременно. Перепишем уравнение пучка следующим образом:
не обращаются в нуль одновременно. Перепишем уравнение пучка следующим образом: 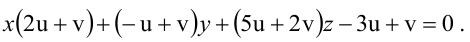
Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим: 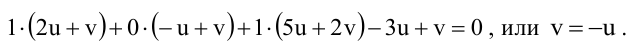
Тогда уравнение плоскости, содержащей М, найдем, подставив 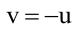 в уравнение пучка:
в уравнение пучка: 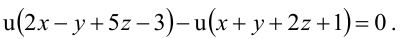
Т.к. и 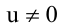 (иначе v=0, а это противоречит определению пучка), то имеем уравнение плоскости
(иначе v=0, а это противоречит определению пучка), то имеем уравнение плоскости 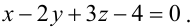 Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности плоскостей:
Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности плоскостей: 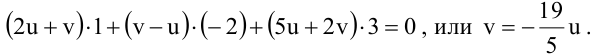
Значит, уравнение второй плоскости имеет вид: 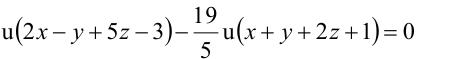 или
или 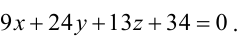
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
- Уравнения прямых и кривых на плоскости
1. Основные понятия.
Рассмотрим
прямоугольную систему координат Oxyz
в пространстве.
У равнением
равнением
поверхности
называется такое уравнение F(x,y,z)=0,
которому удовлетворяют координаты
каждой точки, лежащей на поверхности,
и не удовлетворяют координаты точек,
не лежащих на поверхности.
Например, сфера
– это геометрическое место точек,
равноудаленных от некоторой точки,
называемой центром сферы. Так все точки,
удовлетворяющие уравнению
![]() лежат на сфере с центром в точке О(0.0.0)
лежат на сфере с центром в точке О(0.0.0)
и радиусомR
(Рис.1).
Координаты любой
точки, не лежащей на данной сфере, не
удовлетворяют этому уравнению.
Линию в
пространстве
можно рассматривать как линию пересечения
двух поверхностей. Так на рисунке 1
пересечением сферы с плоскостью Oxy
является окружность с центром в точке
О и радиусом R.
Простейшей
поверхностью является плоскость,
простейшей линией в пространстве
является прямая.
2. Плоскость в пространстве.
2.1. Уравнение
плоскости по точке и нормальному вектору.
В системе
координат Oxyz
рассмотрим плоскость
![]() (Рис.2). Ее положение определяется заданием
(Рис.2). Ее положение определяется заданием
вектора![]() перпендикулярного этой плоскости, и
перпендикулярного этой плоскости, и
фиксированной точки![]() лежащей в этой плоскости. Вектор
лежащей в этой плоскости. Вектор![]()
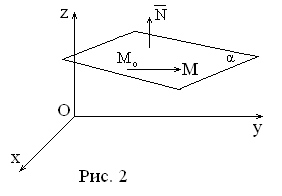 перпендикулярный плоскости
перпендикулярный плоскости![]() называетсянормальным
называетсянормальным
вектором
(вектором-нормалью). Рассмотрим
произвольную точку M(x,y,z)
плоскости
![]() .
.
Вектор![]() лежащий в плоскости
лежащий в плоскости![]() будет перпендикулярен вектору-нормали
будет перпендикулярен вектору-нормали![]() Используя условие ортогональности
Используя условие ортогональности
векторов![]() получим уравнение:
получим уравнение:![]() где
где
![]()
![]()
Уравнение
![]() (2.2.1)
(2.2.1)
называется
уравнением плоскости по точке и
нормальному вектору.
Если в уравнении
(2.1.1) раскроем скобки и перегруппируем
члены, то получим уравнение
![]() илиAx
илиAx
+ By
+ Cz
+ D
= 0, где
D
= ![]() .
.
2.2. Общее
уравнение плоскости.
Уравнение
![]() Ax
Ax
+ By
+ Cz
+D
= 0 (2.2.1)
называется общим
уравнением плоскости, где
![]() – нормальный вектор.
– нормальный вектор.
Рассмотрим
частные случаи этого уравнения.
1 ).D
).D
= 0. Уравнение имеет вид: Ax
+ By
+ Cz
= 0. Такая плоскость проходит через
начало координат. Ее нормальный вектор
![]()
2 ).
).
С = 0 :Ax
+ By
+ D
= 0
![]()
![]() плоскость
плоскость
параллельна оси oz
(Рис.3).
3). B
= 0 : Ax
+ Cz
+ D
= 0
![]()
![]()
плоскость параллельна оси oy
(Рис.4).

4). A
= 0 : By
+ Cz
+ D
= 0
![]()
![]()
плоскость параллельна оси ox
(Рис.5).

5). C
= D
= 0 : Ax
+ By
= 0
![]()
![]()
плоскость проходит через ось oz
(Рис.6).
6 ).B
).B
= D
= 0 : Ax
+ Cz
= 0
![]()
![]()
плоскость проходит через ось oy
(Рис.7).

7). A
= D
= 0 : By
+ Cz
= 0
![]()
![]()
плоскость проходит через ось ox
(Рис.8).
8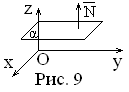 ).A
).A
= B
= 0 : Cz
+ D
= 0
![]()
![]() ||oz
||oz
![]() плоскость параллельна плоскостиOxy
плоскость параллельна плоскостиOxy
(Рис.9).
9). B
= C
= 0 : Ax
+ D
= 0
![]()
![]() ||ox
||ox
![]() плоскость
плоскость
п араллельна
араллельна
плоскостиOyz
(Рис.10).
1 0).A
0).A
= C
= 0 : By
+ D
= 0
![]()
![]() ||oy
||oy
![]() плоскость параллельна плоскостиOxz
плоскость параллельна плоскостиOxz
(Рис.11).
Пример 1.
Составить уравнение плоскости, проходящей
через точку
![]() перпендикулярно вектору
перпендикулярно вектору![]() Найти точки пересечения этой плоскости
Найти точки пересечения этой плоскости
с осями координат.
Решение.
По формуле (2.1.1) имеем
![]()
2x
– y
+ 3z
+ 3 = 0.
Для того, чтобы
найти пересечение этой плоскости с осью
ox,
подставим в полученное уравнение y
= 0, z
= 0. Имеем 2x
+ 3 = 0; x
= – 1,5.
Точка пересечения
искомой плоскости с осью ox
имеет координаты:
![]()
Найдем пересечение
плоскости с осью oy.
Для этого возьмем x
= 0; z
= 0. Имеем
– y
+ 3 = 0
![]()
y
= 3. Итак,
![]()
Для нахождения
точки пересечения с осью oz
возьмем x
= 0; y
= 0
![]() 3z
3z
+ 3 = 0
![]() z
z
= – 1. Итак,
![]()
Ответ:
2x
– y
+ 3z
+ 3 = 0, ![]() ,
,![]() ,
,![]() .
.
Пример 2.
Исследовать
плоскости, заданные уравнениями:
a).
3x
– y
+ 2z
= 0
б). 2x
+ z
– 1 = 0
в). – y
+ 5 = 0
г). x
= 0.
Решение.
а). Данная плоскость проходит через
начало координат (D
= 0) и имеет нормальный вектор
![]()
б). В уравнении
![]() коэффициентB
коэффициентB
= 0. Следовательно,
![]() Плоскость параллельна осиoy.
Плоскость параллельна осиoy.
в). В уравнении –
y
+ 5 = 0 коэффициенты A
= 0, C
= 0. Значит
![]()
Плоскость параллельна
плоскости oxz.
г). Уравнение x
= 0 задает плоскость oyz,
так как при B
= 0, C
= 0 плоскость параллельна плоскости oyz,
а из условия D
= 0 следует, что плоскость проходит через
начало координат.
Пример 3.
Составить уравнение плоскости, проходящей
через точку A(2,3,1)
и перпендикулярной вектору
![]() гдеB(1,0,
гдеB(1,0,
–1), C(–2,2,0).
Решение. Найдем
вектор
![]()
Вектор
![]() является нормальным вектором искомой
является нормальным вектором искомой
плоскости, проходящей через точкуA(2,3,1).
По формуле (2.1.1) имеем:
![]()
– 3x
+ 2y
+ z
+ 6 – 6 – 1 = 0![]()
![]() –
–
3x
+ 2y
+ z
– 1 = 0
![]()
3x
– 2y
– z
+ 1 = 0.
Ответ: 3x
– 2y
– z
+ 1 = 0.
2.3. Уравнение
плоскости, проходящей через три точки.
 Три точки, не
Три точки, не
лежащие на одной прямой, определяют
единственную плоскость (см. рис. 12). Пусть
точки
![]() не лежат на одной прямой. Чтобы составить
не лежат на одной прямой. Чтобы составить
уравнение плоскости, нужно знать одну
точку плоскости и нормальный вектор.
Точки, лежащие на плоскости, известны:
![]()
Можно взять любую. Для нахождения
нормального вектора воспользуемся
определением векторного произведения
векторов. Пусть
![]() Тогда
Тогда![]() следовательно,
следовательно,![]() Зная координаты точки
Зная координаты точки![]() и нормального вектора
и нормального вектора![]() найдем уравнение плоскости, применяя
найдем уравнение плоскости, применяя
формулу (2.1.1).
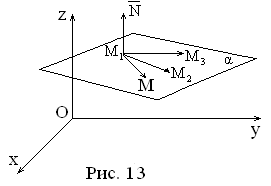 Другим способом
Другим способом
уравнение плоскости, проходящей через
три заданные точки, можно получить,
используя условие компланарности трех
векторов. Действительно, векторы ![]() где M(x,y,z)
где M(x,y,z)
– произвольная точка искомой плоскости,
компланарны (см. рис.13). Следовательно,
их смешанное произведение равно 0:
![]()
![]()
![]()
![]()
![]() .
.
Применив формулу
смешанного произведения в координатной
форме, получим:
 (2.3.1)
(2.3.1)
Пример 1.
Составить
уравнение плоскости, проходящей через
точки
![]()
Решение.
По формуле (2.3.1) имеем
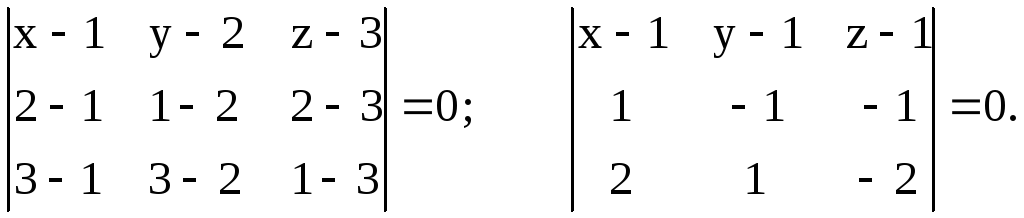
Раскрыв определитель,
получим:
![]()
![]()
![]()
![]()
![]()
Полученная плоскость
параллельна оси oy.
Ее нормальный вектор
![]()
Ответ:
x
+ z – 4 = 0.
2.4.
Угол между
двумя прямыми.
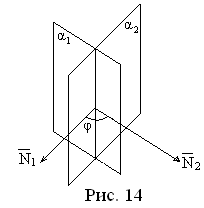 Две плоскости,
Две плоскости,
пересекаясь, образуют четыре двугранных
угла, равных попарно (см. рис. 14). Один из
двугранных углов равен углу между
нормальными векторами этих плоскостей.
Пусть даны
плоскости:
![]() и
и ![]()
Их нормальные
векторы имеют координаты:
![]()
Из векторной
алгебры известно, что
![]() или
или
![]() (2.4.1)
(2.4.1)
Пример: Найти
угол между плоскостями:
![]()
![]()
Решение:
Найдем
координаты нормальных векторов:
![]() По формуле (2.4.1) имеем:
По формуле (2.4.1) имеем:
![]()
![]()
Один из двугранных
углов, полученных при пересечении данных
плоскостей, равен
![]() Можно найти и второй угол:
Можно найти и второй угол:![]()
Ответ:
![]()
2.5.
Условие
параллельности двух плоскостей.
Пусть даны две
плоскости:

![]() и
и ![]()
Если эти плоскости
параллельны, то их нормальные векторы
![]() коллинеарны (см.
коллинеарны (см.
рис.15).
Если векторы
коллинеарны, то их соответствующие
координаты пропорциональны:
![]()
![]() (2.5.1)
(2.5.1)
Верно и обратное
утверждение: если нормальные векторы
плоскостей коллинеарны, то плоскости
параллельны.
Пример 1.
Какие из
указанных плоскостей
параллельны:
а).
![]() ,
,
б).
![]() ?
?
Решение:
а). Выпишем координаты нормальных
векторов.
![]() Проверим их
Проверим их
коллинеарность:
![]()
Отсюда следует,
что
![]()
б). Выпишем
координаты
![]()
Проверим
коллинеарность:
![]()
Векторы ![]() не коллинеарны,
не коллинеарны,
плоскости
![]() не параллельны.
не параллельны.
Пример 2.
Составить
уравнение плоскости, проходящей через
точку
M(2,
3, –2)
параллельно
плоскости
![]()
Решение:
Искомая плоскость параллельна данной
плоскости. Поэтому нормальный вектор
плоскости
![]() можно взять за нормальный вектор искомой
можно взять за нормальный вектор искомой
плоскости.![]() Применяя уравнение
Применяя уравнение
(2.1.1), получим:
![]()
Ответ: ![]() .
.
Пример 3.
Определить
при каких a
и b
плоскости параллельны:
![]()
Решение:
Выпишем координаты нормальных векторов:
![]() Так как плоскости
Так как плоскости
параллельны, то векторы ![]() коллинеарны.По условию (2.5.1)
коллинеарны.По условию (2.5.1)![]() Отсюда b
Отсюда b
= – 2 ; a
= 3.
Ответ: a
= 3; b
= –2.
2.6. Условие
перпендикулярности двух плоскостей.
Если плоскости
![]() перпендикулярны, то их нормальные
перпендикулярны, то их нормальные
векторы![]()
 тоже перпендикулярны
тоже перпендикулярны
(см. рис.16)..
Отсюда следует, что их скалярное
произведение равно нулю, т.е. ![]() или в координатах:
или в координатах:
![]()
![]()
![]()
![]() (2.6.1)
(2.6.1)
Это условие
перпендикулярности двух плоскостей.
Обратное утверждение также верно, то
есть, если выполняется условие (2.6.1), то
векторы ![]() следовательно,
следовательно,
![]()
Пример 1.
Какие из указанных плоскостей
перпендикулярны:
а).
![]() ,
,
б).
![]()
Решение: а).
Запишем координаты нормальных векторов:
![]() Проверим их
Проверим их
ортогональность:
![]()
Отсюда следует,
что ![]()
б). Запишем
координаты нормальных векторов:
![]()
Найдем их скалярное
произведение:
![]() то есть плоскости
то есть плоскости
![]() неперпендикулярны.
неперпендикулярны.
Пример 2.
При каком значении m
плоскости перпендикулярны
![]()
Решение:
Запишем
координаты нормальных векторов:
![]()
Найдем их скалярное
произведение:
![]()
Так как плоскости
перпендикулярны, то ![]()
Следовательно, 4 – 2m
= 0;
m
= 2.
Ответ:
m
= 2.
2.7. Расстояние
от точки до плоскости.
 Пусть дана точка
Пусть дана точка
![]() и плоскость
и плоскость![]()
Расстояние от
точки
![]() (см. рис.17) находим по формуле:
(см. рис.17) находим по формуле:
![]() (2.7.1)
(2.7.1)
Пример: Найти
расстояние от точки M(3,
9, 1) до плоскости
![]()
Решение:
Применяем формулу (2.7.1), где A
= 1, B
= – 2, C
= 2, D
= –3,
![]()
![]()
![]()
Ответ:
![]()
![]()
Соседние файлы в предмете Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.20154.96 Кб8Содержание OneNote.onetoc2
- #
|
4x+6y-5z-60=04x+6y-5z=604x/60+6y/60-5z/60=1x/15+y/10+z/(-12)=1 — ответ |
Плоскость.
1. Всякая плоскость в координатном пространстве OXYZ имеет векторное уравнение следующего вида: r ¦ п = p. Здесь
r = xi + yj + zk — радиус-вектор текущей точки плоскости
M(x, у, z); п = i cosa + j cos b + k cosg — единичный вектор, имеющий направление перпендикуляра, опущенного на плоскость из начала координат, a, b, g — углы, образованные этим перпендикуляром с осями координат OX, OY, OZ, и р — длина этого перпендикуляра.
При переходе к координатам это уравнение принимает вид xcos a + ycos b + zcos g – p = 0 (нормальное уравнение плоскости).
2. Уравнение всякой плоскости может быть записано также в виде Ах + Ву +Cz + D = 0 (общее уравнение). Здесь А, B, C можно рассматривать как координаты некоторого вектора
N = Ai + Bj + Ck, перпендикулярного к плоскости. Для приведения общего уравнения плоскости к нормальному виду все члены уравнения надо умножить на нормирующий множитель
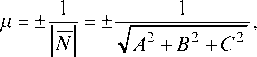
где знак перед радикалом противоположен знаку свободного члена D в общем уравнении плоскости.
3. Частные случаи расположения плоскости, определяемой уравнением Ах + Ву +Cz + D = 0:
А = 0; плоскость параллельна оси ОХ;
В = 0; плоскость параллельна оси О^
C = 0; плоскость параллельна оси ОZ;
D = 0; плоскость проходит через начало координат;
А = В = 0; плоскость перпендикулярна оси ОZ (параллельна плоскости ХОY);
А = C = 0; плоскость перпендикулярна оси ОY (параллельна плоскости ХОZ);
В = C = 0; плоскость перпендикулярна оси ОХ (параллельна плоскости YОZ);
А = D = 0; плоскость проходит через ось ОХ;
В = D = 0; плоскость проходит через ось OY;
C = D = 0; плоскость проходит через ось OZ;
А = В = D = 0; плоскость совпадает с плоскостью XOY (z = 0);
А = C = D = 0; плоскость совпадает с плоскостью XOZ (у = 0);
B = C = D = 0; плоскость совпадает с плоскостью YOZ (х = 0).
Если в общем уравнении Ах + By +Cz + D = 0 коэффициент D ф 0, то, разделив все члены уравнения на – D, можно уравнение
плоскости привести к виду ^ здесь
^ здесь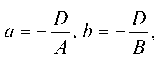
. Это уравнение плоскости называется уравнением в отрезках: в нем а — абсцисса точки пересечения плоскости с осью OX, b и с — соответственно ордината и аппликата точек пересечения плоскости с осями OY и OZ.
4. Угол j между плоскостями А1х + В1У + Qz + D1 = 0 и А2х + В2У +C2z + D2 = 0 определяется по формуле

Условие параллельности плоскостей:

Условие перпендикулярности плоскостей:

5. Расстояние от точки М0(х0; у0; z0) до плоскости, определяемой уравнением Находится по формуле
Находится по формуле


Оно равно взятому по абсолютной величине результату подстановки координат точки в нормальное уравнение плоскости; знак результата этой подстановки характеризует взаимное расположение точки M0 и начала координат относительно данной плоскости: этот знак положителен, если точка M0 и начало координат расположены по разные стороны от плоскости, и отрицателен, если они расположены по одну сторону от плоскости.
6. Уравнение плоскости, проходящей через точку М0(х0; у0; z0)
и перпендикулярной к вектору N = Ai + Bj + Ck, имеет вид А(х – х0) + B(y – у0) + C(z – z0) = 0. При произвольных А, В и C последнее уравнение определяет некоторую плоскость, принадлежащую к связке плоскостей, проходящих через точку М0. Его часто поэтому называют уравнением связки плоскостей.
7. Уравнение А1х + B1y +C1z + D1 + А(А2х + B^y +C2z + D2) = 0 при произвольном I определяет некоторую плоскость, проходящую через прямую, по которой пересекаются плоскости, определяемые уравнениями


и
некоторую плоскость, принадлежащую пучку плоскостей, проходящих через эту прямую (в силу чего такое уравнение часто называют уравнением пучка плоскостей). Если плоскости, определяемые уравнениями I и II, параллельны, то пучок плоскостей превращается в совокупность плоскостей, параллельных этим плоскостям.
8. Уравнение плоскости, проходящей через три заданные точки M1(r 1Х M1(Jj), M3(r 3) (Л = x1i + yd + z1k; r2 = x2i + У2 j + z2k; r3 = x3i + y3 j + z3 к), проще всего найти из условия компланарности векторов r – T1, r2 – rl, r3 – rl, где r = xi + yj+zk — радиус-вектор текущей точки искомой плоскости M:
или в координатной форме:


Пример 1.21. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + у + 5z – 1 = 0, 2x + 3у – z + 2 = 0 и через точку М(3, 2, 1).
Решение. Воспользуемся уравнением пучка плоскостей

Значение I определяем из условия, что координаты точки М должны удовлетворять этому уравнению:

Получаем искомое уравнение в виде:
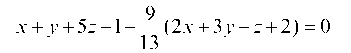
или, умножая на 13 и приводя подобные члены, в виде:

Пример 1.22. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + 3у + 5z – 4 = 0 и X – у – 2z + 7 = 0 и параллельной оси оу.
Решение. Воспользуемся уравнением пучка x + 3у + 5z – 4 + + l(x – у – 2z + 7) = 0, преобразуем уравнение к виду (1 + Х)х + (3 -1)у + (5 – 2l)z + (71 – 4) = 0.
Так как искомая плоскость параллельна оси ординат, то коэффициент при у должен равняться нулю, т. е. 3 – l = 0, I = 3. Подставив значение I в уравнение пучка, получаем

Пример 1.23. Найти уравнение плоскости, проходящей через точки М (2; -1; 4) и N(3; 2; -1) перпендикулярно к плоскости X + у + z – 3 = 0.
Решение. Воспользуемся уравнением плоскости, проходящей через первую из данных точек:

Условие прохождения этой плоскости через вторую точку и условие перпендикулярности определяются равенствами:

Исключая коэффициенты А, В и C из системы уравнений

получаем искомое уравнение в виде:


или
Пример 1.24. Из точки P(2; 3; -5) на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.
Решение. Основаниями перпендикуляров, опущенных на координатные плоскости, будут следующие точки М1(2; 3; 0), М2(2; 0; -5), М3(0; 3; -5). Напишем уравнение плоскости, проходящей через точки М1, М2, М3, для чего воспользуемся уравнением

находим

или

Пример 1.25. Составить уравнение плоскости, проходящей через точку M (2; 3; 5) и перпендикулярной к вектору
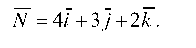
Решение. Достаточно воспользоваться уравнением плоскости, проходящей через данную точку и перпендикулярной к данному вектору:

Прямая.
1. Прямая может быть задана уравнениями 2-х плоскостей

пересекающихся по этой прямой.
2. Исключив поочередно х и у из предыдущих уравнений, получим уравнения х = аz + с, у = bz + d. Здесь прямая определена двумя плоскостями, проектирующими ее на плоскости хoz и yoz.
3. Если даны две точки M(x1, у1, z1) и N(x2, у2, z2), то уравнения прямой, проходящей через них, будут иметь вид:

4. Так называемые канонические уравнения
определяют прямую, проходящую через точку M(x1, у1, z1)
и параллельную вектору S = li + mj + nk. В частности, эти уравнения могут быть записаны в виде:


где a, b и g — углы, образованные прямой с осями координат.

5. От канонических уравнений прямой, вводя параметр t, нетрудно перейти к параметрическим уравнениям прямой:

6. Угол между двумя прямыми, заданными их каноническими
уравнениями


опре-
деляется по формуле
перпендикулярности двух прямых:


условие параллельности двух прямых:

7. Необходимое и достаточное условие расположения двух прямых, заданных их каноническими уравнениями, в одной плоскости (условие компланарности двух прямых):

Если величины /1, т, П1 непропорциональны величинам /2, m2, «2, то указанное соотношение является необходимым и достаточным условием пересечения двух прямых в пространстве.
условие параллельности прямой и плоскости: 

 условие перпендикулярности прямой и плоскости:
условие перпендикулярности прямой и плоскости:


 Определяется по формуле
Определяется по формуле

9. Для определения точки пересечения прямой
 С плоскостью Ах + Ву + Cz + D = 0 нужно решить совместно их уравнения, для чего следует воспользоваться параметрическими уравнениями прямой x = /t + X0, у = mt + у0, z = nt + z0:
С плоскостью Ах + Ву + Cz + D = 0 нужно решить совместно их уравнения, для чего следует воспользоваться параметрическими уравнениями прямой x = /t + X0, у = mt + у0, z = nt + z0:
а) если А/ + Вт + Cn ф 0, то прямая пересекает плоскость в одной точке;
б) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D ф 0, то прямая параллельна плоскости;
в) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D = 0, то прямая лежит в плоскости.
Пример 1.26. Привести к каноническому виду уравнения прямой 2х – у + 3z – 1 = 0 и 5х + 4у – z – 7 = 0.
Решение. Исключив вначале у, а затем z, получим:
Если разрешим каждое из уравнений относительно х, то будем иметь:
отсюда
Второй способ: найдем вектор S = li + mj + nk, параллельный искомой прямой. Так как он должен быть перпендикулярен к нормальным векторам заданных плоскостей N1 = 2i – j + 3k и N2= 5i + 4 j – k, то за него можно принять векторное произведение векторов N1 и N2.

Таким образом, l = -11; m = 17; n = 13.
За точку M1(x1, у1, z1), через которую проходит искомая прямая, можно принять точку пересечения ее с любой из координатных плоскостей, например с плоскостью yoz. Т ак как при этом x1 = 0, то координаты y1 и z1 этой точки определятся из системы уравнений заданных плоскостей, если в них положить х = 0:
Решая эту систему, находим у1 = 2; z1 = 1.
Итак, искомая прямая определяется уравнениями:

Мы получили прежний ответ.
Пример 1.27. Построить прямую



Решение. Искомую прямую можно построить как линию пересечения плоскостей. Для этого напишем уравнения плоскостей, которыми определена прямая, в отрезках на осях:

Пример 1.28. Из начала координат опустить перпендикуляр на прямую

Решение. Составим уравнение плоскости, проходящей через начало координат и перпендикулярной заданной прямой: 2х + 3у + z = 0. (Для этой плоскости можно принять А = l; B = m; C = n; D = 0; использовано условие перпендикулярности прямой и плоскости, см. п. 8 введения к настоящему разделу).
Найдем точку пересечения этой плоскости и данной прямой. Параметрические уравнения прямой имеют вид:

Построив данные плоскости, мы получим искомую прямую как линию пересечения этих плоскостей (рис. 20).
Для определения t имеем уравнение:


Остается составить уравнения прямой, проходящей через начало координат и через точку М (см. п. 3 введения к настоящему разделу):

Пример 1.29. В уравнениях прямой Определить
Определить
параметр n так, чтобы эта прямая пересекалась с прямой
 , и найти точку их пересечения.
, и найти точку их пересечения.
Решение. Для нахождения параметра n используем условие пересечения 2-х прямых:

Отсюда следует:

или

Следовательно, уравнения пересекающихся прямых таковы: искомой:

заданной:

Для вычисления координат точки пересечения этих прямых выразим из первого уравнения х и у через z: х = 2z, у = -3z. Подставляя их значения в равенство Имеем
Имеем ,
,
отсюда z = 1. Зная z, находим х и у: х = 2z = 2, у = -3z = -3. Следовательно M(2; -3; 1).
Пример 1.30. Прямая задана каноническими уравнениями

Составить общие уравнения этой прямой.
Решение. Канонические уравнения прямой можно записать в виде системы двух независимых уравнений:

Получили общие уравнения прямой, которая теперь задана пересечением 2-х плоскостей, одна из которых 5х – 3у – 13 = 0 параллельна оси Oz, а другая х + 3z – 11 = 0 параллельна оси Oy.
Пример 1.31. Найти координаты точки M, делящей попалам отрезок прямой

заключенный между плоскостями хoz и xoy.
Решение. Найдем точку А пересечения прямой с плоскостью хoz, полагая в уравнениях прямой у = 0. Тогда получим:
отсюда x = 2,6; z = 2,8. Тогда А(2,6; 0; 2,8).


отсюда X = 11, у = 14, или В(11; 14; 0).
Определяем координаты точки М, делящей отрезок АВ пополам:

Следовательно, координаты искомой точки М будут: М(6,8; 7; 1,4).
Пример 1.32. Составить уравнение плоскости, проходящей через прямую

параллельной прямой

Решение. Составим уравнение пучка плоскостей, проходящих через первую из данных прямых:

которое делим на а ф 0, и пусть b /а = I:

Аналогично, полагая в уравнениях прямой z = 0, найдем координаты точки В пересечения прямой с плоскостью хоу:
69
В этом пучке нужно выбрать плоскость, параллельную 2-й данной прямой. Из условия параллельности плоскости и прямой, имеем:




Отсюда l = 1.
Подставляя I = 1 в уравнение пучка плоскостей, получим:  Тогда искомое уравнение плоскости будет:
Тогда искомое уравнение плоскости будет:

Пример 1.33. Дана прямая  Найти ее проекцию на плоскость
Найти ее проекцию на плоскость
Решение. Нужно найти плоскость, которая проходит через данную прямую перпендикулярно к данной плоскости; тогда искомая проекция определится как пересечение этой плоскости с данной.
Составим уравнение пучка плоскостей, проходящих через данную прямую:
Эта плоскость должна быть перпендикулярной к данной плоскости, что можно записать как:
отсюда I = 1.
70
Тогда уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости, будет:
или
Проекция данной прямой на данную плоскость определяется как прямая пересечения плоскостей:

Запишем эту прямую в каноническом виде. Найдем на прямой какую-либо точку. Для этого положим, например х0 = 1, и система запишется в виде:

Отсюда, у0 = 1, z0 = 0, т. е. точка M(1; 1; 0) принадлежит искомой прямой.
Направляющий вектор прямой S = (l; m; n) найдем из того условия, что он перпендикулярен нормальным векторам
N1 = (2; -3; -2) и N2 = (5; 2; 2) плоскостей, определяющих искомую прямую.
В качестве S берем векторное произведение векторов N1 и N2 , т. е.

Тогда искомое уравнение в каноническом виде будет:


Раздел 2
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
| < Предыдущая | Следующая > |
|---|
