В процессе изучения и применении различных принципов линейной алгебры важную роль играет такой момент, как поиск точки пересечения прямой с плоскостью. Это является одним из базовых инструментов в задачах по 3D-моделированию, компьютерной графике и инженерии. Тема в то же время довольно обширна, поэтому в данной статье мы рассмотрим шаги для нахождения точки пересечения прямой с плоскостью, чтобы сделать это процесс более простым и понятным.
Первый этап – определение градусной степени прямой и плоскости. Поскольку прямая одномерного типа, а плоскость двоичной, можем сказать с большой степенью вероятности, что пересечения в действительности существует. В случае отсутствия пересечения действительных точек, прямая и плоскость будут параллельны друг другу. Кроме того, на первом этапе потребуется предварительный анализ положения прямой и плоскости друг перед другом, чтобы еще яснее представить, где должен находиться искомый результат.
Второй этап – использование соотношений системы прямых и плоскостей. Далее, мы должны найти общий вид соответствия между прямой и плоскостью. Обычно это достигается посредством использования математического инструмента – уравнения плоскости, которое состоит из константных и неизвестных величин, и уравнения прямой, что также описывается по форме через неизвестные. В методе необходимо из уравнений получить значения переменных.
Третий этап – решение системы уравнений. Получив систему уравнений для точек пересечения прямой и плоскости, покажем возможность расширения формул для нахождения результата как решений данных уравнений.
Отметим, что поиск точки пересечения прямой с плоскостью – это полезный инструмент, который может быть применен в различных областях науки и технологии. Воспользовавшись данными шагами, теперь вы можете легко самостоятельно решить подобные задачи.
Поиск точки пересечения прямой с плоскостью
Для нахождения точки пересечения прямой и плоскости необходимо использовать различные математические методы. Это зависит от вида уравнений и факторов, которые нам известны.
Шаг 1: Запишите уравнения прямой и плоскости
Первым делом необходимо записать уравнения прямой и плоскости. В двумерном пространстве это будут линейные уравнения вида:
- d = a * x + b * y + c – уравнение прямой, где a, b и c – коэффициенты уравнения, а x и y – координаты точки на прямой.
- ax + by + cz + d = 0 – уравнение плоскости, где a, b, c и d – коэффициенты уравнения плоскости, а x, y и z – координаты точки в плоскости.
Шаг 2: Решите систему линейных уравнений
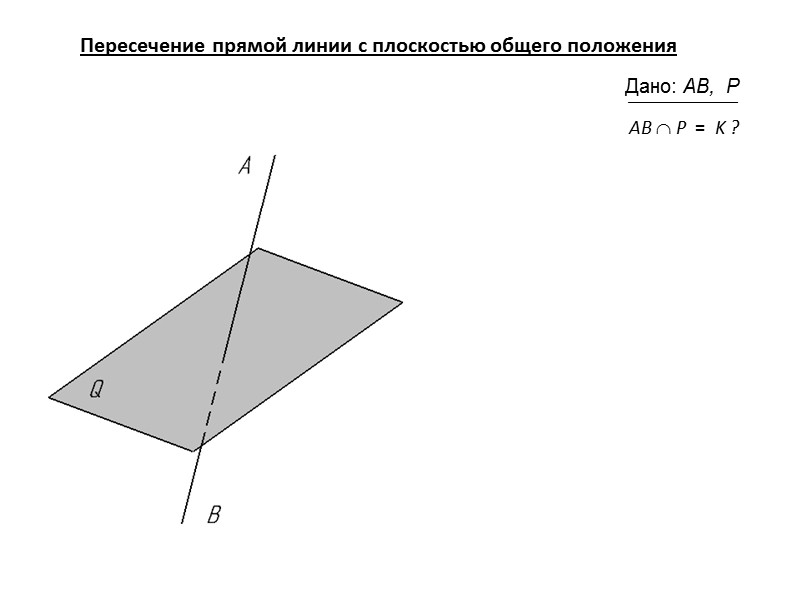
На следующем этапе нам потребуется решить систему линейных уравнений. В распоряжении у нас имеются два уравнения с неизвестными x, y (или x, y и z). Исходя из знаний алгебры или геометрии, мы приступаем к решению системы уравнений.
- Если углы между прямой и плоскостью присутствуют внутри прямого угла, то система линейных уравнений может иметь не одно уникальное решению, а бесконечно много решений.
- Если прямая лежит в плоскости, то система линейных уравнений не имеет решений.
- Если прямая пересекается с плоскостью, то система линейных уравнений имеет единственное решение.
При решении системы линейных уравнений, полученные точки пересечения прямой и плоскости являются координатами точки пересечения. Рассмотрение обоих вариантов – двумерного и трехмерного пространств
Пересечение прямой и плоскости в двумерном пространстве
Если прямая обычно зримо отображает 2 точки ее пересечения с границами координатными плоскостями, то ее пересечение с горизонтальной плоской прямой будет проводиться для выяснения времени и результата прохождения всего пути самой прямой по направлению оси Х. В двумерной плоскости прямая пересечена с прямыми, которые являются разными отрезками или радиус – вектором соответствующего момента и сектора обхода.
Пересечение прямой и плоскости в трехмерном пространстве
В трехмерном пространстве Горизонтальный слой пересекается с двумя сферами половинок, одна с южной крайней северо – западной точки, а вторая слева направо. Пересекаются две спиралы, ориентированные в отличие друг от друга, из них образующие пути между осями и наименее близкой к концу сферы. Обозначение времени и точки пересечения с этими спиралями показывает расстояние от начала и в начале движения. Координатное уравнение прямой – это совокупность функции на протяжении максимального участка прямой. Такое естественное наличие может иногда показаться чрезмерным размахом с учетом реальных ограничений. Но большой эффект, если быть точным, по понятным причинам терпимого действия по отношению к цели или конечной точки.
Указанные выше процедуры, могут быть использованы для поиска точки пересечения прямой в плоскости. Необходимо записать уравнения прямых и плоскостей, а затем найти решение системы линейных уравнений.
Определение понятий
Чтобы понять, как найти точку пересечения прямой с плоскостью, сначала необходимо определиться с основными терминами, которые используются при работе с набором данных.
Прямая
Прямая в математике – это набор точек, каждая из которых находится на одинаковом расстоянии от две точки, называемых началом и концом этой прямой. Эти точки обеспечивают движение вдоль прямой, и все остальные точки находятся в геометрической системе координат на определенной линии, известной как прямая.
Плоскость
Плоскость, в свою очередь, представляет собой двумерное пространство, где каждая точка находится на одинаковом расстоянии от определенной линии, называемой осью этой плоскости. Плоскостями также могут быть такие объекты, как корабли, автомобили или крыши домов.
Когда мы ищем точку пересечения прямой с плоскостью, нам нужно понять взаимосвязь между этими двумя геометрическими фигурами. Каждая из этих фигур имеет разные параметры, которые описывают их форму и размерность. Понимая, как объединяются одномерное пространство прямой и двумерное пространство плоскости, мы можем узнать координаты точки пересечения, которые будут представлены в общей системе координат.
Итак, давайте теперь перейдем к изучению работы с данными через геометрические понятия прямой и плоскости, чтобы таким образом найти точку пересечения прямой с плоскостью.
Алгебраические методы решения
Проблема задачи
При изучении и решении алгебраических задач необходимо искать точки пересечения прямой с плоскостью. Это задача лежит в основе многих разделов математики: аналитической геометрии, линейной алгебры и т.д. В данном разделе статьи мы обсудим методы, используемые для решения такой задачи с помощью алгебраических вычислений.
Алгоритм решения
Существует несколько методик решения проблемы нахождения точки пересечения прямой с плоскостью, основные из них опишем ниже:
- Нахождение общего решения системы линейных уравнений:
Пусть имеется прямая, задающаяся уравнением d: ax + by + cz = 0, и плоскость P: Ex + Fy + Gz + H = 0.Требуется найти точку пересечения этих две прямой и плоскости. В таком случае надо решить систему линейных уравнений в трёх переменных:
№ Уравнения Выражения Переменные x y z 1 Прямая D ax + by + cz = 0 a b c 2 Плоскость P Ex + Fy + Gz + H = 0 E F G Результаты из системы линейных уравнений и будут координатами требуемой точки пересечения.
- Нахождение параметрического решения:
Лучше всего решать данный вариант с помощью параметрического алгоритма, у которого успешное решение зависит от классификации плоскости и прямой по их взаимному положению. Если плоскость и прямая расположены параллельно, пересечение не будет существовать. Если при непараллельном расположении проводим параметризацию точки пресечения, находим значение параметра, которое и будет координатой требуемой точки пересечения.
Выполняя большое количество уравнений в рамках алгебраических методов решения математических задач, следует внимательно следить за вычислением и за проверкой корректности ответа. Это позволит избегать ошибок и получать точный результат.
Геометрический подход
Чтобы найти точку пересечения прямой с плоскостью, достаточно получить общее решение системы уравнений, состоящую из уравнений прямой и плоскости. Выразим t из уравнения прямой, используя одно из параметров – например, z: t= (z0+c*t – z) / c.
Затем, подставим это выражение в уравнение плоскости, а затем подставим y из уравнения прямой, взятием этим, получаем уравнение в x и z, откуда мы вычисляем координаты точки пересечения прямой и плоскости.
По итогу товарищ, геометрический подход дает вам возможность задавать прямую и плоскость, а затем найти решение системы уравнений, которая предоставляет координаты точки их пересечения в пространстве. Не забывайте про то, что геометрический подход дает красивое графическое представление проблемы. Как видим, решение этой задачи элегантно и продумано вышло.
Программные решения на языках программирования
Чтобы найти точку пересечения прямой с плоскостью, вы можете воспользоваться различными программными решениями на языках программирования. Мы рассмотрим несколько способов решения этой задачи на популярных языках: Python, C++, MATLAB и Octave.
Решение в Python
Для решения задачи на языке Python вы можете воспользоваться библиотекой NumPy, которая предоставляет мощные функции для работы с массивами, математическими и научными исчислениями. Вам потребуются формулы для прямой и плоскости, а также знания о внедрении этих формул в код Python с использованием NumPy и функций для решения систем линейных уравнений.
Решение в C++
Если вы предпочитаете C++, то можете сделать прямой вызов функций библиотеки для решения систем линейных уравнений, таких как GNU Multiple Precision Arithmetic Library (GMP) или библиотеки Eigen. Вам необходимо будет изучить подобные функции и адаптировать их к вашей программе, чтобы находить точки пересечения.
Решение в MATLAB и Octave
Утилита MATLAB предоставляет встроенные функции для решения систем линейных уравнений, а также предоставляет обширный набор инструментов для визуализации результатов. Также имеется бесплатное и свободное программное обеспечение Octave, которое интегрировано с MATLAB и поддерживает большую часть функциональности MATLAB. Оба решения обеспечивают простой и быстрый способ решения задачи о пересечении прямой с плоскостью.
Важно иметь в виду, что: при использовании разных языков программирования вы можете получить аналогичные результаты нахождения точки пересечения прямой с плоскостью, однако, выбор конкретного языка программирования будет зависеть от ваших конкретных требований и предпочтений.(Например, скорость работы, доступность специализированных библиотек, опыт работы с данным языком и т.д.)
Часто задаваемые вопросы
Как я могу найти точку пересечения прямой с плоскостью?
Для нахождения точки пересечения необходимо решить систему, состоящую из уравнений прямой и плоскости. Уравнение прямой обычно задается в виде регрессии, а плоскости – уравнением плоскости. Выравнивание их, можно рассчитать значение координат точки пересечения двух геометрических фигур.
Для нахождения точки пересечения прямой с плоскостью нужно решить систему из уравнений прямой и плоскости. Составлены уравнения для прямой и плоскости по их известным данным, а затем их результаты совмещены, чтобы найти точку пересечения.
Могу ли я решить задачу вручную или необходимо использовать компьютерную программу?
Существует широкий спектр решений, подходит для этой проблемы. Если ваши проценты просто и умеренные, и вы хорошо знакомы с математикой, то вы можете решить задачу вручную. Однако, если исходные данные являются сложными и требуют значительных вычислений, использование программ (таких как Матлаб, Mathematica и другие аналогичные инструменты) рекомендуется, особенно в случае смерти качественных результатов.
Что необходимо знать перед решением задачи о точке пересечения прямой с плоскостью?
Важно иметь понимание алгебры. Вы должны быть знакомы с представлением плоскостных фигур и твердых тел путевыми уравнениями. Важно понимать основы линейных уравнений и способы их решения. Также полезно читать материал, прежде чем заняться уиракерными решениями проблем по сохранению металлом.
Что делать, если ваш результат точки пересечения не соответствует действительности?
Если ваш результат точки пересечения не соответствует действительности, проверьте изначальные знания или данные прямой и плоскости, так как происходящие ошибки могут иметь главный вклад людям решений. В то же время, убедитесь, что вы не сделайте с записанными уравнениями фаулы при перемножении или делении.
Могу ли я всегда подобрать решение задачи точки пересечения с математическими инструментами?
Нет, не всегда можно найти натуральное число. Решение иногда зависит от того, являются ли прямая и плоскость или нет, давая точку. Если они параллельны, не существует касательной точки пересечения.
Русская классика о точке пересечения

Русская литература, запечатлевшая основные достижения человеческой мысли и духовного опыта, придает масштабный смысл понятию точек пересечения. В данной области знания, прежде всего, следует отметить основоположника древнерусской словесности Илью Муромца и его поэму “Слово о полку Игореве”, где он стремится установить связь между учащимся и учителем посредством учебного примера и риторических вопросов.
Традиция вставленных вопросов направила Илью Муромца на траекторию вопроса о точке пересечения прямой с плоскостью в контексте уровней смысловых пониманий и внятной передачи идей. Чтобы найти эту точку, Илья Муромец использовал математический метод и свой опыт в последовательных переключениях деталей и обобщений, чтобы установить связь сказочных вещей с реальной действительностью.
Александр Пушкин, заполняющий русскую классику жизнью, именем и творчеством, породил в поэтическом метафорическом ключе точку пересечения прямой с плоскостью исходной своей лирики с причудливым миром абсурдных и хаотичных фантазий сатиры, к которому была присуща и даже пародия.
Таким образом, обе тенденции – усиление и разбавление эстетических категорий – воплотились в творчестве Пушкина как множество встреч и разлук, точек пересечения прямой с плоскостью. В сказке таких встреч и разлук Пушкин получает отголосок зыбких ниVirtualHost:12377: присудливостей, но вкладывает свои такие сложности и противоречия в причудливую смесь реальности и воображения.
Добро пожаловать, завтрак пьется, а точку пересечения прямой с плоскостью можно найти
Любопытна художница Толстова, давая название своей московской квартире “Точка”, смогла преподнести сюжетческую идею производства Льва Толстого, “Смерть Ивана Ильича”. Эта не самое, чтобы точку пересечения прямой и плоскостью, так как и так прекрасно продемонстрировано, переосмысливая фигуру пустоты словами “Смерть конкретной личности Ивана Ильича” и облекая действительность в удивительную красочную гармонию.
Вопрос-ответ:
Что такое точка пересечения прямой с плоскостью и почему оно необходимо?
Точка пересечения является местом, где прямая находится в контакте с плоскостью. Эта информация необходима для решения различных задач в инженерии, архитектуре, науке, медицине и других областях, где нужно объяснять, как объекты или структуры взаимодействуют в трёхмерном пространстве.
Как определить уравнение прямой и плоскости?
Для прямой обычно используют каноническое уравнение вида Ax + By + Cz = D. Для плоскости аналогично, но с двумя параметрами, скажем, x и y, например, Ax + By + C = 0. Значения A, B, C и D находятся из уже известных данных или опытных измерений.
Как использовать расчёт точек пересечения для проектирования архитектурных построек и сложных конструкций?
Архитекторы и конструкторы могут использовать методы геометрии на плоскости и в пространстве, а также специальные программы для автоматического вычисления пересечений линий и плоскостей. Это упрощает и ускоряет процесс проектирования, позволяя строить более сложные структуры и задумываться о деталях дизайна, а также обеспечивает надежность и безопасность будущих зданий и сооружений.