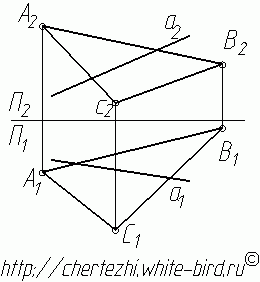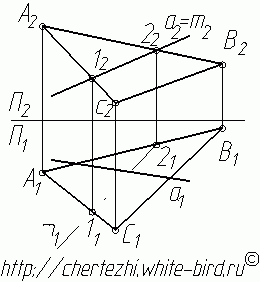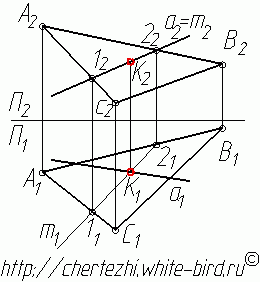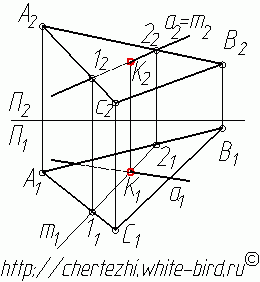
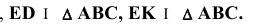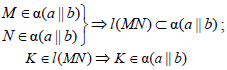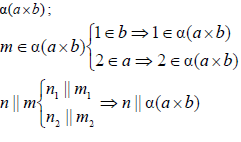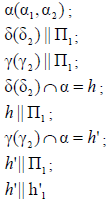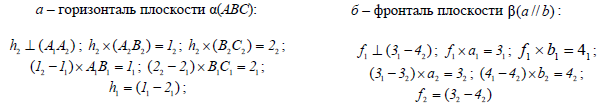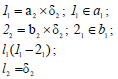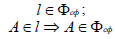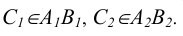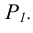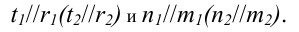Построение точки пересечения прямой и плоскости
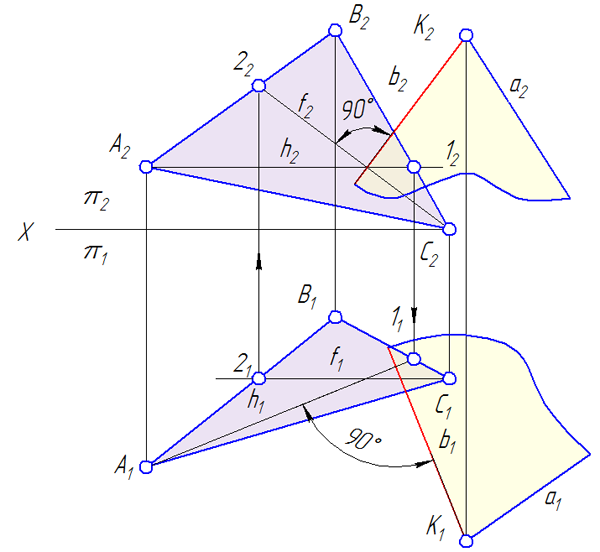
Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h0α, f0α.
Алгоритм
- Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h0γ, f0γ.
- Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B’ = h0α ∩ h0γ, A” = f0α ∩ f0γ. Точки A’ и B” лежат на оси x, их положение определяется по линиям связи.
- Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K’ = a’ ∩ A’B’. Фронтальная проекция K” лежит на прямой a”.
Алгоритм решения останется тем же, если пл. α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими возможными способами.
Видимость прямой a относительно плоскости α. Метод конкурирующих точек
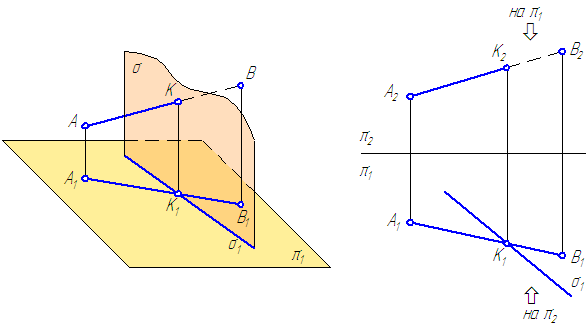
- Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A” и С” совпадают, но при этом т. A и С удалены от плоскости проекций П2 на разное расстояние.
- Найдем горизонтальные проекции A’ и C’. Как видно на рисунке, точка C’ удалена от плоскости П2 на большее расстояние, чем т. A’, принадлежащая пл. α. Следовательно, участок прямой а”, расположенный левее точки K”, будет видимым. Участок a” правее K” является невидимым. Отмечаем его штриховой линией.
- Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D’ и E’ совпадают, но при этом т. D и E удалены от плоскости П1 на разное расстояние.
- Определим положение фронтальных проекций D” и E”. Как видно на рисунке, точка D”, находящаяся в пл. α, удалена от плоскости П1 на большее расстояние, чем т. E”, принадлежащая прямой a. Следовательно, участок а’, расположенный правее точки K’, будет невидимым. Отмечаем его штриховой линией. Участок a’ левее K’ является видимым.
Дополнительные материалы:
- Построение линии пересечения двух плоскостей
- Способы задания плоскости на чертеже
Содержание:
Позиционными задачами называются задачи на построение элементов, общих для взаимодействующих объектов, и задачи на взаимное положение геометрических объектов. Первая группа задач включает задачи на принадлежность и задачи на пересечение. Ко второй группе задач относятся задачи на параллельность геометрических объектов.
Задачи на перпендикулярность объектов относят к метрическим задачам, которые будут рассмотрены в следующем разделе. Позиционные задачи, в которых участвуют поверхности, будут рассмотрены в главе “Поверхности”.
Классификация позиционных задач, относящихся к элементарным геометрическим объектам (точка, прямая, плоскость), представлена на рисунке 4.1.
Позиционные задачи
Задачи, связанные с определением взаимного расположения геометрических объектов в пространстве, традиционно называют позиционными.
Поскольку Начертательная геометрия изучает объекты расширенного Евклидова пространства
В линейной алгебре утверждается, что для всех объектов пространства справедливо выражение (в соответствии с рисунком 4.1)
где N— размерность рассматриваемого пространства,
Очевидно, все позиционные задачи, с точки зрения линейной алгебры, можно свести к определению вида и размерности пересечения.
Полагая, что рассматриваемое
пространство трехмерно, при вычислении размерности пересечения исходное выражение примет вид
Заметим, что этот подход позволяет определить только и только размерность
Рассмотрим вопрос о принадлежности точки прямой, точки и прямой -плоскости. Особенность решения этих вопросов заключается в том, что прямая и точка на чертеже задаются проекциями, а плоскость – соответствием трех пар точек.
Задачи на принадлежность
Эта группа задач содержит три типовые задачи – точка принадлежит прямой, точка принадлежит плоскости, прямая принадлежит плоскости, суть решения которых основана на свойствах проецирования. Если точка принадлежит прямой, то проекции этой точки принадлежат одноименным проекциям прямой.
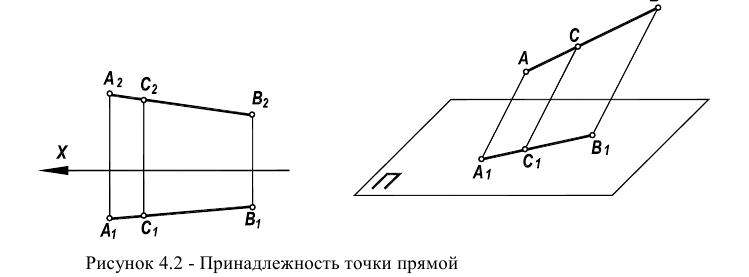
Точка принадлежит плоскости, если она принадлежит прямой, находящейся в этой плоскости (рисунок 4.2а). Прямая принадлежит плоскости, если она проходит через две точки, принадлежащих плоскости. Поэтому для того, чтобы указать в плоскости какую-либо точку, необходимо сначала указать в плоскости прямую, а затем на этой прямой указать положение точки.
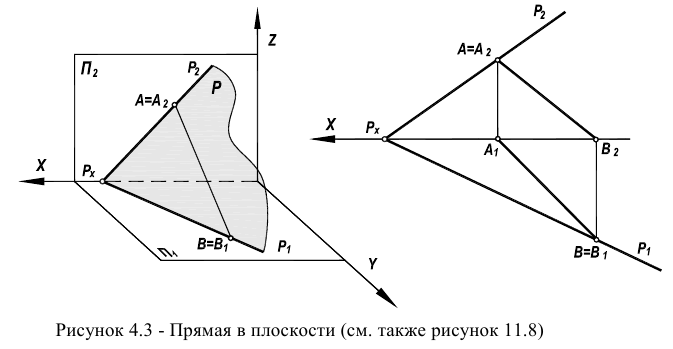
На рисунках 4.3 показано построение прямой в плоскостях, заданных треугольником и следами. Если плоскость задана треугольником, то целесообразно упомянутые точки взять на сторонах треугольника. Если плоскость задана следами, то в качестве двух точек целесообразно взять следы прямой. Это основано на следующем свойстве: если плоскость задана следами и в ней находится прямая, то следы прямой лежат на одноименных следах плоскости.
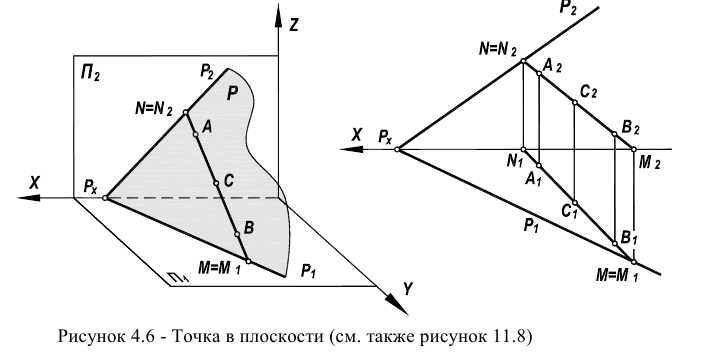
На рисунке 4.4 представлено построение точек в плоскости, заданной следами и точки в плоскости, заданной треугольником. В первом случае точка А построена с помощью горизонтали. На этом же рисунке показано построение точек (К и L), находящихся на следах плоскости. Во втором случае точка К построена с помощью прямой 1-2.
С рассматриваемым вопросом тесно связан вопрос о проведении плоскости частного положения (например, проецирующих плоскостей) через прямую.
Если прямая принадлежит плоскости частного положения и плоскость задается следами, то одна из проекций прямой будет совпадать с собирательным следом плоскости в соответствие с рисунком 4.5.
На рисунке 4.6 в эпюрной форме показано проведение через прямую фронтально проецирующей плоскости а и горизонтально проецирующей плоскости
Задачи на пересечение
Задача на пересечение двух прямых рассмотрена ранее в разделе “Пересекающиеся прямые”.
Наиболее важной позиционной задачей является задача о пересечении прямой с плоскостью. При решении задачи могут встретиться следующие случаи пересечения:
- Прямая общего положения пересекается с плоскостью частного положения;
- Прямая частного положения (например, проецирующая) пересекается с плоскостью общего положения;
- Прямая общего положения пересекается с плоскостью общего положения.
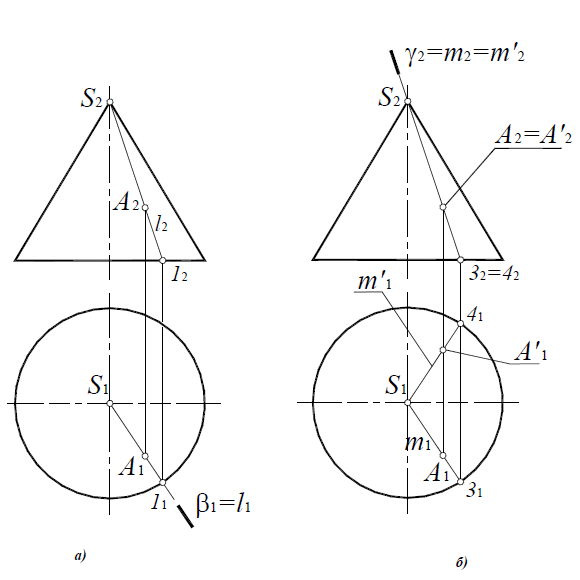
Решение первых двух задач не представляет особых трудностей (рисунок 4.7). На рисунке 4.7а дано построение точки встречи прямой общего положения с горизонтально-проецирующей плоскостью, а на рисунке 4.76 – горизонтально-проецирующей прямой с плоскостью общего положения. Последняя задача решена с помощью вспомогательной прямой 1-2.
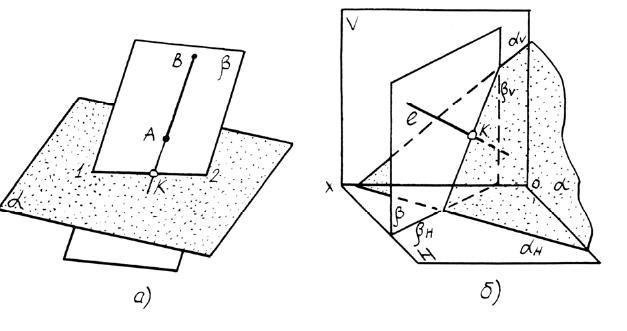
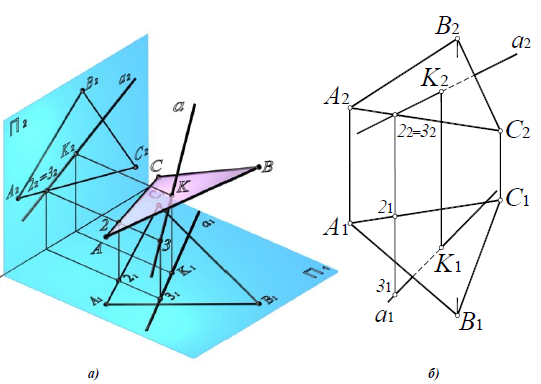
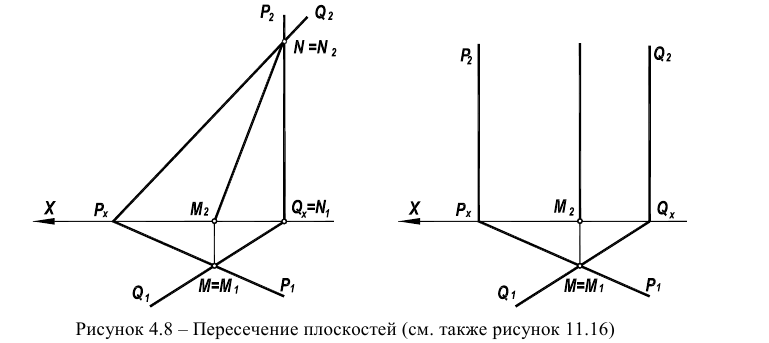
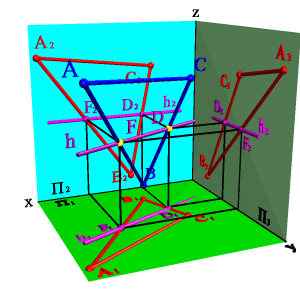
Для решения задачи о пересечении прямой с плоскостью в общем положении разработана следующая методика (рисунок 4.8а):
- Через прямую проводят вспомогательную плоскость частного положения
(чаще всего проецирующую плоскость, заданную следами);
- Находят линию пересечения заданной а и вспомогательной плоскостей
(линия 1-2);
- Находят точку пересечения заданной прямой и найденной линии пересечения плоскостей. Полученная точка К – искомая.
Рисунок 4.8 – Пересечение прямой общего положения с плоскостью общего положения
На рисунке 4.86 дана пространственная схема решения задачи, в которой прямая пересекается с плоскостью, заданной следами. В качестве вспомогательной плоскости взята горизонтально-проецирующая плоскость.
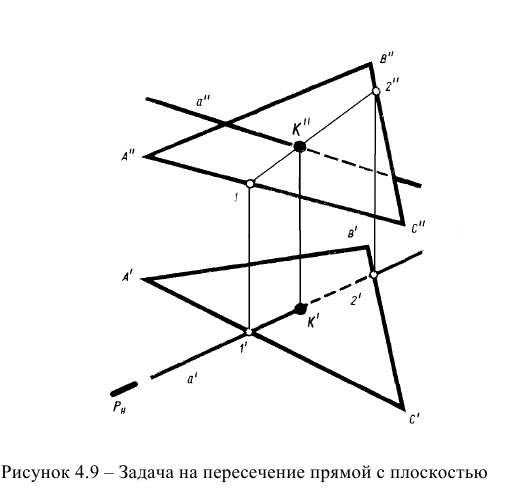
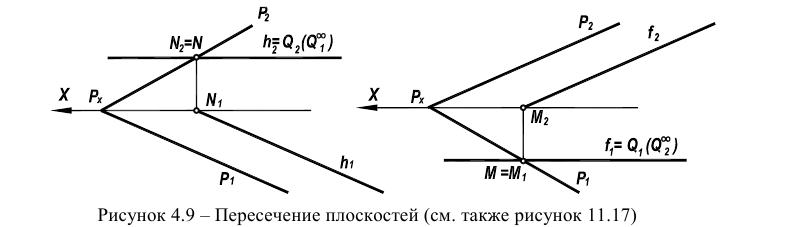
На рисунке 4.9 дано решение задачи на пересечение прямой общего положения с плоскостью общего положения, заданной треугольником. В качестве вспомогательной плоскости использована горизонтально-проецирующая плоскость.
Видимость проекций определена методом конкурирующих точек (прямых).
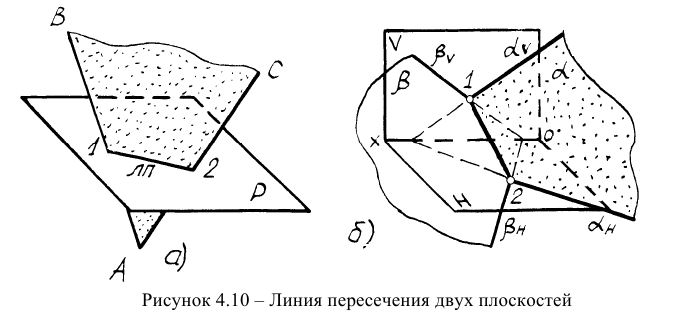
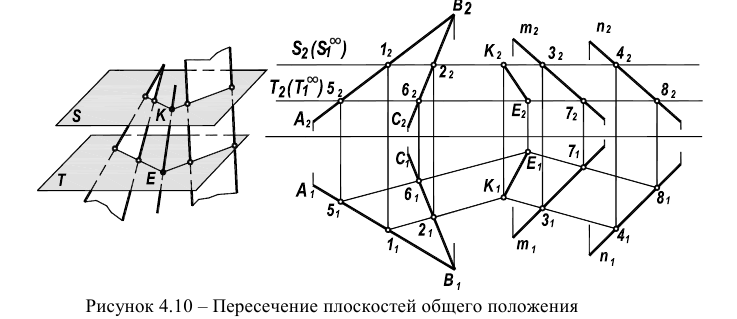
К главным задачам на пересечение относится также задача о пересечении двух плоскостей. Линия пересечения двух плоскостей – это прямая, принадлежащая как одной, так и другой плоскости. Следовательно, для построения линии пересечения двух плоскостей надо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям (рисунок 4.10).
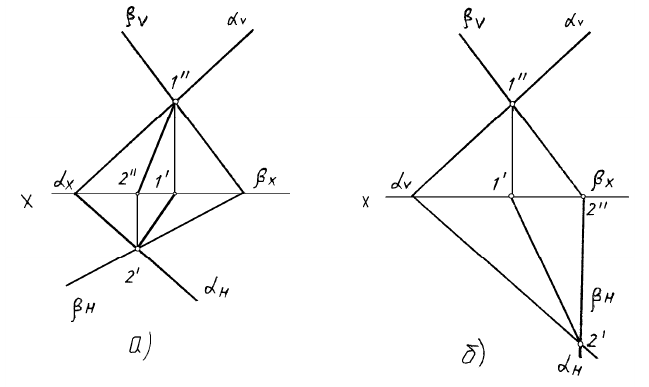
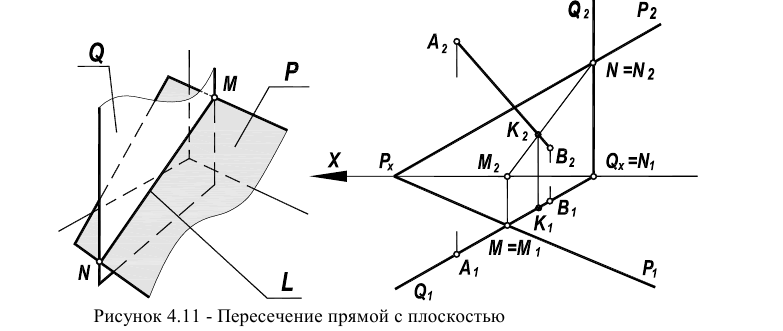
Если плоскости заданы следами, то исходя из рисунка 4.106 линия пересечения таких плоскостей определяется точками пересечения одноименных следов. На рисунке 4.11 представлены решения задач о пересечении двух плоскостей, заданных следами. Во втором случае одна из плоскостей является плоскостью общего положения, а другая -фронтально-проецирующей.
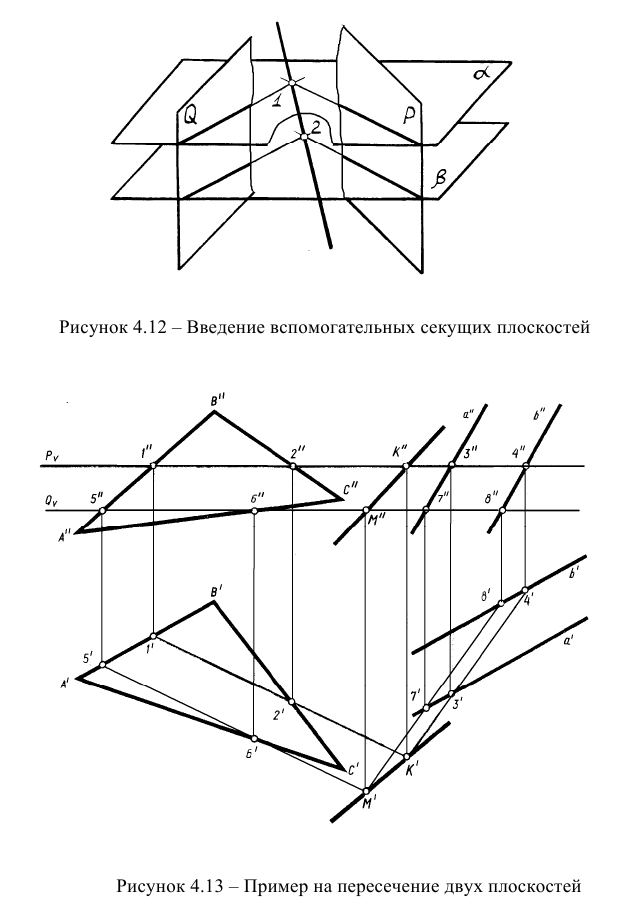
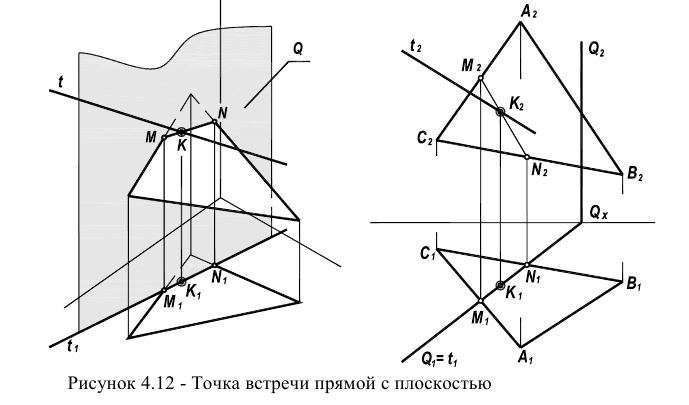
Рисунок 4.11 – Пересечение плоскостей, заданных следами В случаях, если плоскости заданы разными способами, применяют общий метод построения линии пересечения, основанный на введении вспомогательных плоскостей (рисунок 4.12).
Сущность метода заключается в том, что заданные плоскости Q и Р дважды пересекают вспомогательными плоскостями а и 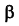
Если пересекающиеся плоскости являются плоскостями частного положения, или если одна из пересекающихся плоскостей является плоскостью частного положения, то задача упрощается. На рисунке 4.14 представлены примеры решения задач на пересечение упомянутых плоскостей. И более трудоемкой задачей является задача на пересечение двух плоскостей общего положения, заданных плоскими фигурами, например, треугольниками, многоугольниками и т.д.
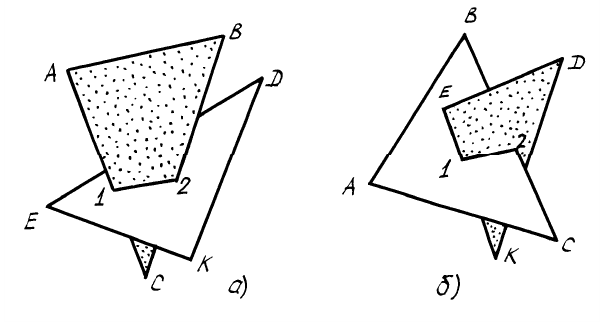
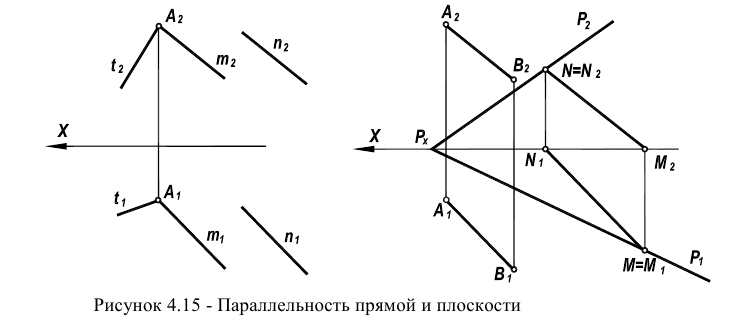
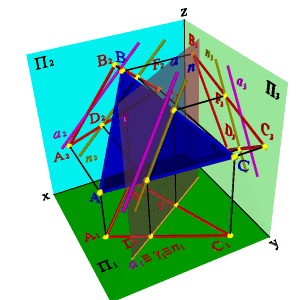
При пересечении плоских фигур возможны два случая пересечения (рисунок 4.15): полное пересечение (а) и неполное пересечение (б).
Рисунок 4.15 – Полное и неполное пересечение плоских фигур
В обоих случаях линия пересечения треугольников определяется двумя точками 1 и 2, каждая из которых определяется как точка пересечения стороны одного треугольника с плоскостью другого. Отсюда следует вывод: для того, чтобы построить линию пересечения
треугольников, необходимо дважды решить задачу о пересечении стороны одного треугольника с плоскостью другого треугольника (типовая задача о пересечении прямой с плоскостью). При этом пару пересекающихся объектов можно подбирать произвольно. В любом случае линия пересечения будет построена.
Задачи на параллельность
Задача на параллельность двух прямых была рассмотрена ранее в разделе “Параллельные прямые”.
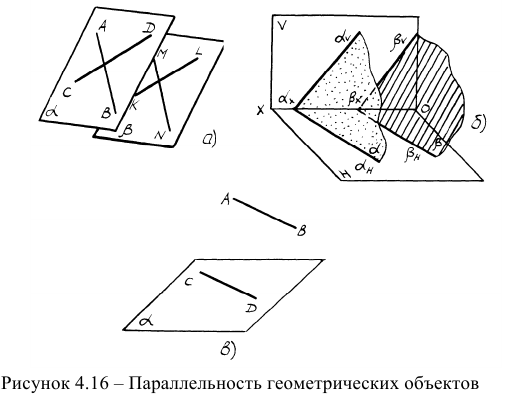
Задачи на параллельность плоскостей основываются на положениях элементарной геометрии. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости взаимно параллельны двум пересекающимся прямым другой плоскости (рисунок 4.16а).
Если две параллельные плоскости заданы следами, то одноименные следы таких плоскостей параллельны друг другу (рисунок 4.166).
Прямая будет параллельна плоскости в том случае, если она параллельна любой прямой, находящейся в этой плоскости.
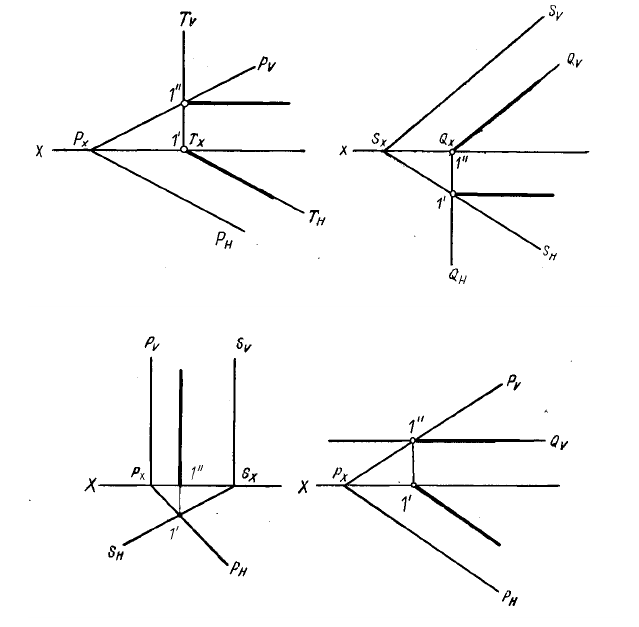
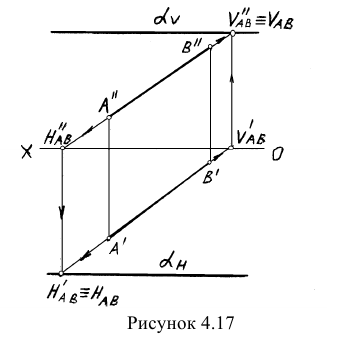
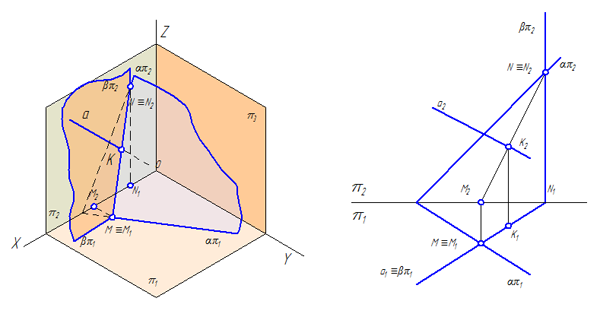
Пример: Через прямую АВ провести профильно-проецирующую плоскость (рисунок 4.17).
Решение: Как было показано ранее горизонтальный и фронтальный следы профильно-проецирующей плоскости располагаются параллельно оси ОХ. Было также показано, что если прямая принадлежит плоскости, заданной следами, то следы прямой находятся на одноименных следах плоскости. Сказанное позволяет разработать план решения задачи:
- Найдем горизонтальный и фронтальный следы прямой;
- Через найденные следы прямой проведем одноименные следы плоскости.
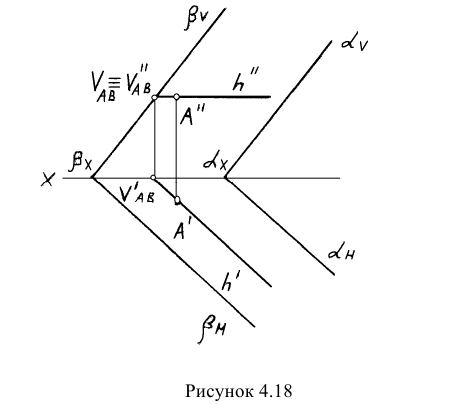
Пример: Через точку провести плоскость, параллельную заданной (рисунок 4.18).
Решение: Плоскость задана следами. Искомую плоскость целесообразно тоже задать следами. Чтобы обеспечить параллельность плоскостей, необходимо следы искомой плоскости провести параллельно одноименным следам заданной плоскости.
Для того чтобы искомая плоскость проходила через заданную точку, необходимо через точку провести прямую (например, горизонталь), которая принадлежала бы искомой плоскости. Исходя из изложенного, определяется следующий план решения задачи:
- Проводим через заданную точку горизонталь h;
- Через фронтальный след горизонтали проводим фронтальный след искомой плоскости параллельно фронтальному следу заданной плоскости;
- Горизонтальный след искомой плоскости проводим параллельно горизонтальному следу заданной плоскости.
- Через фронтальный след горизонтали проводим фронтальный след искомой плоскости параллельно фронтальному следу заданной плоскости;
- Горизонтальный след искомой плоскости проводим параллельно горизонтальному следу заданной плоскости.
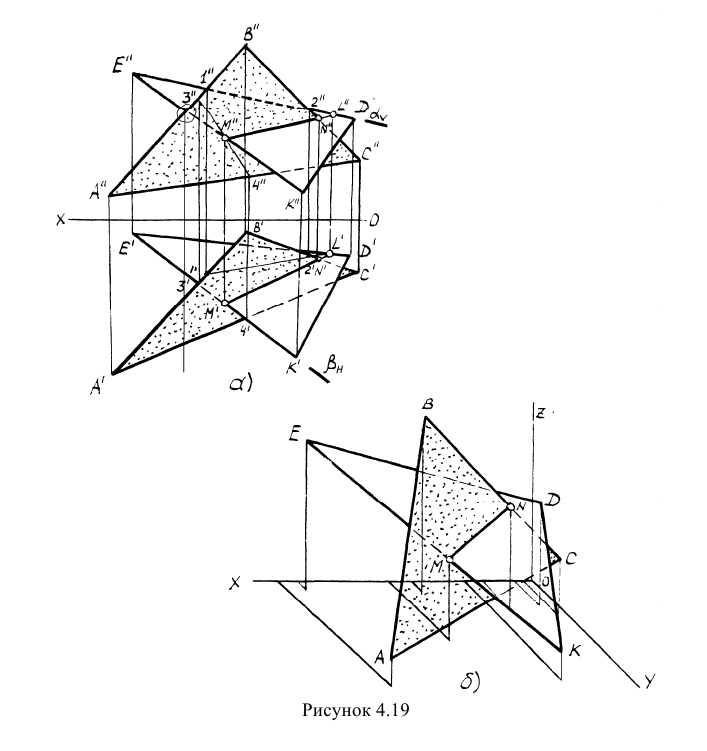
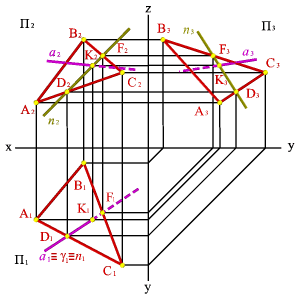
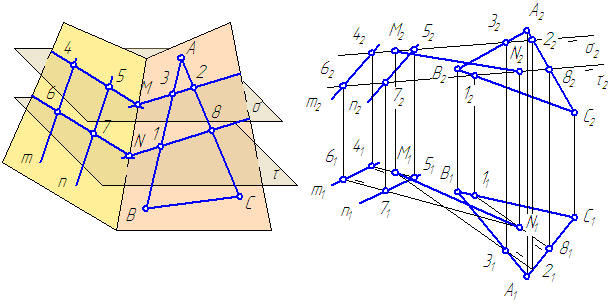
Пример: Построить линию пересечения треугольников АВС и EDK, определить видимость проекций (рисунок 4.19).
Построить линию пересечения треугольников АВС и EDK, определить видимость проекций (рисунок 4.19).
Решение: Предварительно намечаем две произвольные задачи на пересечение стороны одного треугольника с плоскостью другого (произвольно). Например,
Решаем первую задачу. Через ED проводим вспомогательную фронтально-проецирующую плоскость а (след плоскости 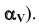
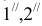
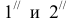
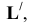
Аналогично решаем вторую задачу. В качестве вспомогательной плоскости берем горизонтально-проецирующую плоскость 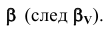
Далее соединяем полученные точки L и М. Однако не вся эта линия будет являться линией пересечения треугольников, а лишь участок MN, который принадлежит обоим треугольникам. Таким образом, в результате решения двух произвольно выбранных задач получили линию MN пересечения заданных треугольников.
Определяем видимость проекций треугольников. При определении видимости проекций методом конкурирующих точек (прямых) необходимо учитывать следующие особенности:
- Плоскости треугольников считаются геометрически непрозрачными;
- В точках М и N линии пересечения видимость сторон треугольников меняется;
- Если при вершине какого-либо треугольника одна сторона видна (не видна), то и другая сторона будет видна (не видна).
Учет перечисленных особенностей позволяет определить видимость проекций треугольников по анализу одного конкурирующего места на каждой проекции, что значительно ускоряет решение задачи.
Отметим на фронтальной проекции любое конкурирующее место из шести (отмечено кружочком). Проведем через него линию связи и вдоль линии связи сравним ординаты конкурирующих прямых ЕК и АВ. Наибольшую ординату имеет прямая АВ. Она и будет видна на рассматриваемой фронтальной проекции. Видимость остальных сторон треугольников определяется с учетом особенностей, отмеченных выше.
На горизонтальной проекции отметим конкурирующее место, в котором конкурируют прямые АВ и ED. Аналогично описанному определяем, что на горизонтальной проекции будет видна прямая АВ, так как у ней наибольшая аппликата. Видимость остальных сторон треугольников определим аналогично рассмотренному выше.
Для усиления эффекта видимости треугольников на проекциях целесообразно один их треугольников заштриховать с учетом видимости или раскрасить оба треугольника.
На рисунке 4.196 представлено наглядное аксонометрическое изображение пересекающихся треугольников в косоугольной фронтальной изометрии. Вершины треугольников строятся по заданным координатам точек, линия пересечения MN – по координатам, взятым с проекционного чертежа.
Относительное положение прямой и плоскости
Прямая по отношению к плоскости может занимать три различных
положения:
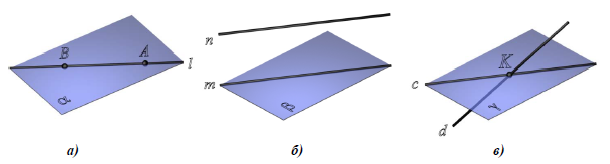
- • прямая l лежит в плоскости (рис. 8.1,а);
- • прямая n параллельна плоскости (рис. 8.1, б);
- • прямая d пересекается с плоскостью (рис. 8.1,в).
Рис. 8.1. Относительное положение прямой и плоскости:
а – l ⊂ α ; б – n || β ; в – d х γ
Принадлежность точки и прямой линии плоскости
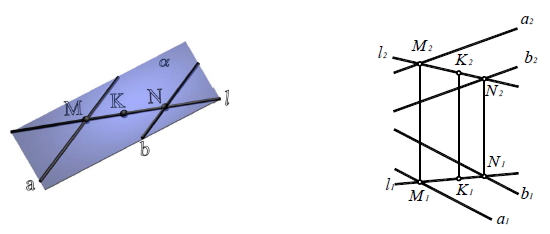
Прямая линия принадлежит плоскости, если две точки этой прямой принадлежат плоскости (рис. 8.2).
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости (см. рис. 8.2).
Рис. 8.2. Принадлежность точки и прямой линии плоскости:
Параллельность прямой и плоскости
Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости (рис. 8.3).
Рис. 8.3. Параллельность прямой и плоскости:
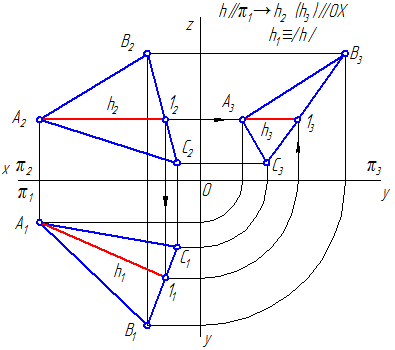
Линии уровня плоскости
Прямые, лежащие в данной плоскости и параллельные одной из плоскостей проекций, называются линиями уровня плоскости.
Прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций П1, называется горизонталью плоскости (рис. 8.4). Все горизонтали плоскости параллельны между собой, поскольку каждая из них может быть получена как линия пересечения данной плоскости общего положения и горизонтальной плоскости уровня.
Рис. 8.4. Горизонтали плоскости:
Рассмотрим построение горизонтали плоскости общего положения α(ABC) (рис. 8.5,а).
Рис. 8.5. Линии уровня плоскости:
Фронтальная проекция любой горизонтали всегда перпендикулярна линиям связи, поэтому построение горизонтали начинается с построения ее фронтальной проекции h2 
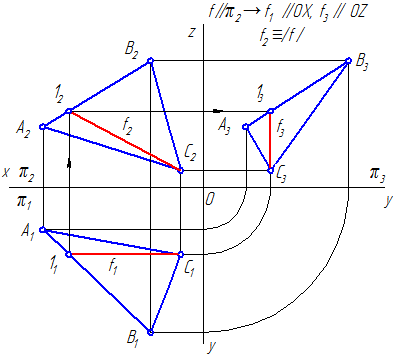
Фронталь плоскости β( a||b )строится аналогично, но построение фронтали начинается с построения ее горизонтальной проекции (рис. 8.5,б). Все фронтали плоскости также параллельны между собой, поскольку каждая из них может быть получена как линия пересечения данной плоскости общего положения и фронтальной плоскости уровня.
Таким образом, любую плоскость общего положения можно представить как совокупность параллельных линий уровня – горизонталей, фронталей или профильных прямых. Иными словами, плоскость общего положения, заданную любым способом, можно также задать параллельными линиями уровня или пересекающимися горизонталью и фронталью. Такой способ задания плоскостей наиболее удобен для решения ряда метрических задач.
Пересечение прямой общего положения и плоскости частного положения
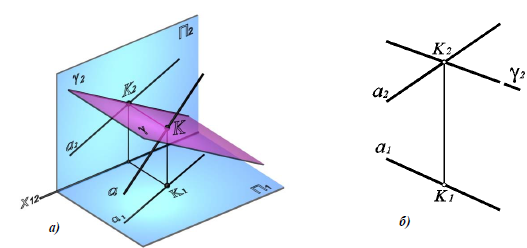
Рассмотрим построение точки пересечения K фронтально-проецирующей плоскости γ(γ2)
Рис. 8.6. Пересечение прямой общего положения и плоскости частного положения:
а- наглядное изображение;
б – комплексный чертеж
Поскольку K ⊂ γ(γ2), K2 ⊂ γ2, но одновременно к ⊂ a, следовательно, K 2 = γ 2 × a 2, а K 1 = (K 2 K 1) × a1.
Пересечение двух плоскостей частного положения
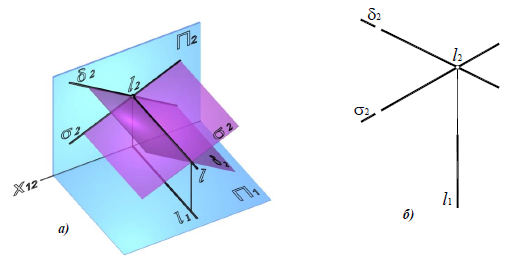
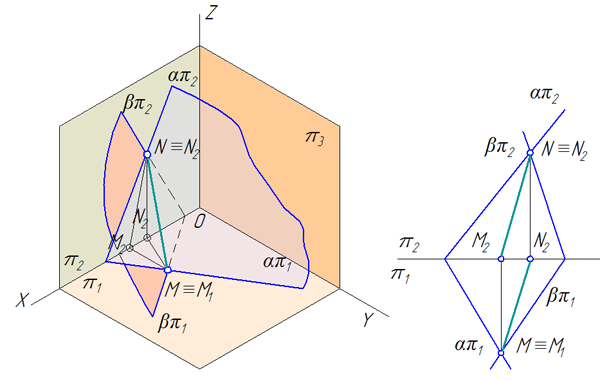
Линией пересечения двух фронтально-проецирующих плоскостей δ(δ2) и σ(σ2) является фронтально-проецирующая прямая l (рис. 8.7).
Рис. 8.7. Пересечение плоскостей частного положения:
а-наглядное изображение; б – комплексная проекция
линии пересечения двух фронтально-проецирующих плоскостей δ(δ2)и σ(σ2)определяется как точка пересечения фронтальных следов плоскостей δ2 и σ2: l2=δ2×σ2, а горизонтальная проекция строится по линии связи, перпендикулярно направлению оси x12.
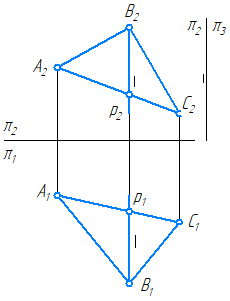
Пересечение плоскости общего положения и плоскости частного положения
Линией пересечения двух плоскостей (рис. 8.8) является прямая, для построения которой достаточно определить две точки, принадлежащие обеим плоскостям одновременно.
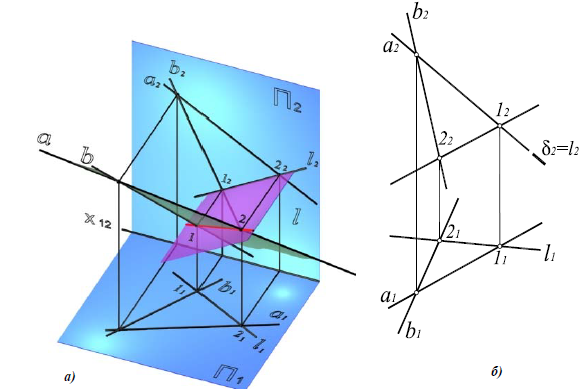
Рис. 8.8. Пересечение плоскости общего положения с проецирующей плоскостью
а – наглядное изображение; б – комплексный чертеж
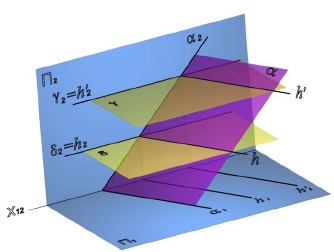
Рассмотрим построение линии пересечения l плоскости общего положения α(a×b) и фронтально-проецирующей плоскости δ(δ2)(рис. 8.8, б). Линия, по которой пересекаются две плоскости, принадлежит обеим плоскостям одновременно, следовательно, для ее построения достаточно определить две точки, общие для пересекающихся плоскостей, или одну точку и направление линии пересечения.
В данном случае, достаточно определить точки пересечения прямых а и b с плоскостью δ(δ2). Они однозначно определят линию пересечения l.
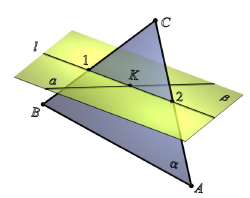
Пересечение прямой общего положения и плоскости общего положения. Первая позиционная задача
Задача об определении точки пересечения прямой общего положения с плоскостью общего положения называется первой позиционной задачей. На рис. 8.9 представлено наглядное изображение решения первой позиционной задачи.
Рис. 8.9. Пересечение прямой общего положения и плоскости общего положения
Дано: а(ABC) – плоскость общего положения;
a (a 1, a2) – прямая общего положения.
Определить: K=a×α(ABC).
Решение:
1. Прямую заключить во вспомогательную плоскость частного положения: αeβ.
2. Определить линию l как линию пересечения вспомогательной и заданной плоскостей l=α (ABC) 
3. Определить взаимное положение заданной прямой a и полученной прямой l.
Поскольку прямые a и l лежат в одной плоскости, они могут пересекаться или быть параллельными. Точка пересечения K=a×l и является искомой точкой пересечения прямой а с плоскостью α(ABC). Если прямые a и l параллельны, то прямая а параллельна плоскости α(ABC).
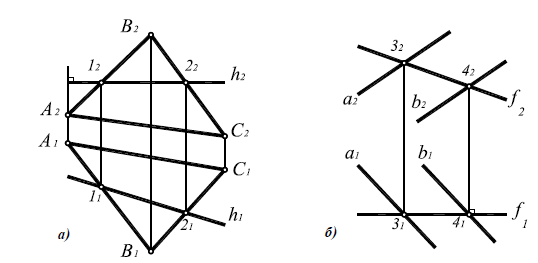
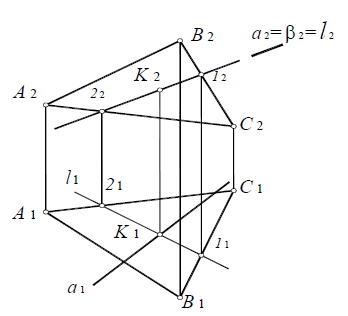
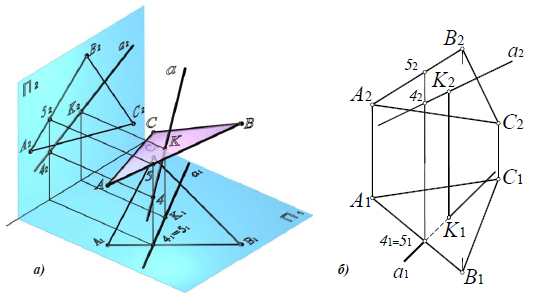
Определение точки пересечения прямой a(a1,a2) и плоскости α(ABC) на комплексном чертеже:
1. Заключить прямую a(a 1 ,а 2) во вспомогательную проецирующую плоскость β(β2) (рис. 8.10).
2. Определить линию пересечения l(1-2) вспомогательной плоскости β(β2) и заданной плоскости α(ABC):
l = α(ABC)
Рис. 8.10. Пересечение прямой a(a1,a2 )и плоскости α( ABC)
3. Определить взаимное положение заданной прямой a и полученной прямой l. В данном случае, прямые а и lпересекаются в точке K, которая и является искомой точкой пересечения прямой a(a1,a2) и плоскости α(ABC):
11×a 1=K1; K2∈a2; K= a(a1,a2)×α(ABC).
4. Считая плоскость непрозрачной, определить видимость прямой a(a1 ,a2) относительно плоскости α(ABC)
Рис. 8.11. Определение видимости относительно горизонтальной плоскости проекций:
а – наглядное изображение;
б – комплексный чертеж
Для определения видимости относительно горизонтальной плоскости проекций необходимо найти конкурирующие точки – точки, горизонтальные проекции которых совпадают.
Прямые a и (AB) в пространстве являются скрещивающимися (точки пересечения проекций не лежат на одной линии связи), поэтому для определения видимости прямой относительно плоскости достаточно определить видимость прямой a относительно прямой (AB) (8.11). Для этого рассмотрим две конкурирующие точки: 4 – на прямой a и 5 – на прямой (AB). Высота точки 5 больше, следовательно, на П1 видима прямая (AB), то есть плоскость, а прямая a – невидима.
Рис. 8.12. Определение видимости относительно фронтальной плоскости проекций:
а – наглядное изображение; б – комплексный чертеж
Видимость прямой а по отношению к плоскости α(ABC) на фронтальной плоскости проекций (рис. 8.12) определяется с помощью конкурирующих точек 2на прямой (AC) и 3-на прямой а. Глубина точки 3 больше, следовательно, видима будет прямая а.
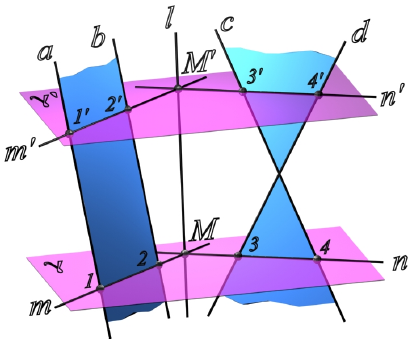
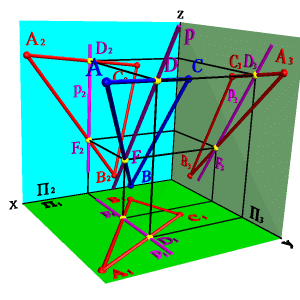
Пересечение двух плоскостей общего положения. Вторая основная позиционная задача
Вторая позиционная задача – это задача об определении линии пересечения двух плоскостей. Наглядное изображение решения второй позиционной задачи показано на рис. 8.13.
Рис. 8.13. Пересечение двух плоскостей общего положения
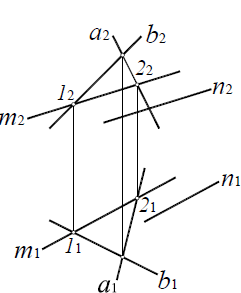
Алгоритм решения второй позиционной задачи состоит в следующем:
1. Заданные плоскости α(a||b) и β(c×d) пересечь вспомогательной плоскостью частного положения γ.
2. Определить линии пересечения m и n вспомогательной плоскости с каждой из заданных плоскостей:
γ 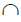
γ 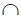
3. Определить точку M пересечения линий m и n. Точка M принадлежит прямой m, а, следовательно, и плоскости α (a||b). Точка M принадлежит прямой n, следовательно, и плоскости β(c×d). Таким образом, точка M принадлежит обеим плоскостям, то есть является одной из точек линии пересечения.
4. Вторую точку линии пересечения определяют аналогично, рассекая плоскости α(a||b) и β(c×d) вспомогательной плоскостью частного положения γ’.
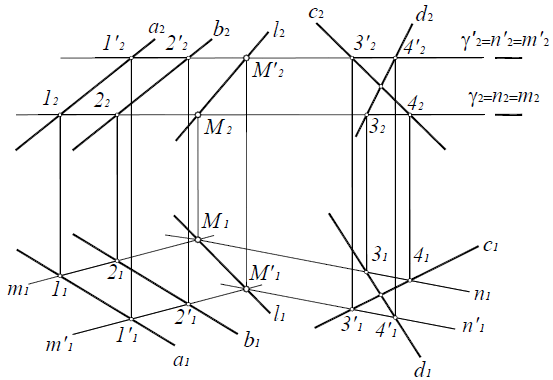
Определение линии пересечения двух плоскостей общего положения α(a||b) и β(c×d) на комплексном чертеже:
1. Пересечь данные плоскости вспомогательной фронтально-проецирующей плоскостью γ(γ2)
2. Определить линии пересечения вспомогательной плоскости с каждой из заданных плоскостей:
m =γ(γ2)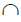
n =γ(γ2)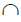
3. Определить точку пересечения прямых n и m:M=n× m.
4. Точка M ⊂ m 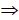
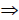
5. Точка M’ определяется аналогично, вспомогательной плоскости γ/(γ/2).
Рис. 8.14. Вторая позиционная задача
6. Через полученные точки M и M’ провести прямую l. Прямая l -искомая линия пересечения плоскостей α( a || b) и β( c × d).
- Заказать чертежи
Сечение поверхности плоскостью
В сечении поверхности плоскостью получается плоская кривая линия, которую строят по отдельным точкам. Сначала строят опорные точки – точки смены видимости и экстремальные (крайние). Точки смены видимости принадлежат очерковым образующим поверхности. Экстремальными точками являются: самая близкая и самая удаленная, высшая и низшая и т. д. относительно плоскостей проекций.
Если проекция линии пересечения этими точками не определяется полностью, то строят дополнительные, промежуточные между опорными, точки. При построении сечений секущая плоскость обычно считается прозрачной и определяется только видимость поверхности и линии сечения.
Точка на поверхности
Точка принадлежит поверхности, если она принадлежит какой-либо линии на этой поверхности. Для построения точек на поверхности или определения недостающих проекций строится сечение поверхности вспомогательной плоскостью. Вспомогательная плоскость выбирается таким образом, чтобы в сечении получались простые линии – прямые или окружности. Кроме того, окружность в сечении должна проецироваться на одну из плоскостей проекций без искажения.
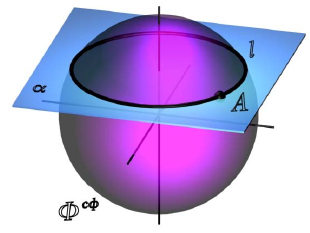
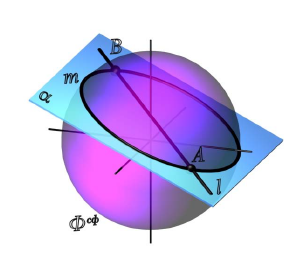
Рис. 8.15. Точка на поверхности сферы:
Любая плоскость рассекает поверхность сферы по окружности (рис. 8.15), но без искажения на соответствующую плоскость проекций проецируются только окружности, лежащие в плоскостях уровня. Таким образом, для построения точки на поверхности сферы в качестве вспомогательных плоскостей используются только плоскости уровня.
На поверхности конуса можно получить как окружности, так и прямые линии.
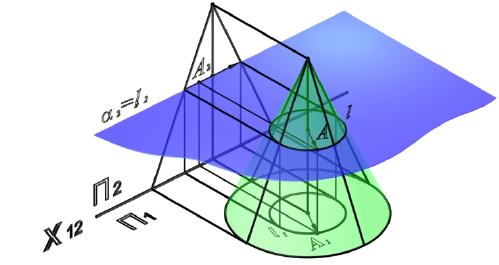
Для построения горизонтальной проекции точки A на поверхности конуса (рис. 8.16, 8.17), конус рассекается горизонтальной плоскостью уровня α(α2), проходящей через точку A.
В сечении конуса получается окружность радиуса r, которая проецируется на П1 без искажения – как окружность 11 с центром в точке 01 радиусом r1=r. Фронтальная проекция окружности -12 представляет собой отрезок [ 11 2 1].
Рис. 8.16. Точка на поверхности конуса
Рис. 8.17. Построение точки на поверхности конуса
Горизонтальная проекция точки A строится на пересечении вертикальной линии связи (A2A1) и окружности l1. При этом фронтальной проекции A2 могут соответствовать две точки – A и A’.
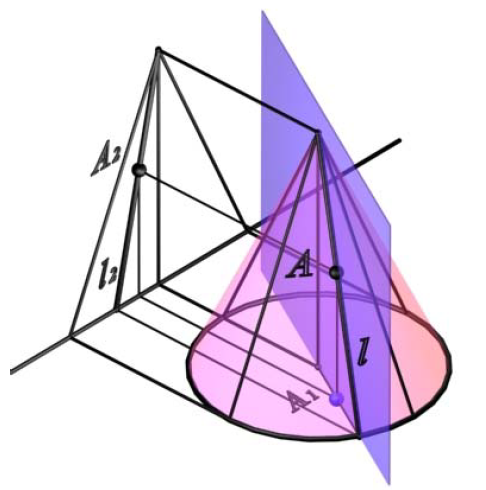
Поскольку любая плоскость, проходящая через вершину конуса, рассекает его по двум пересекающимся прямым, вспомогательную плоскость можно задать точкой A и осью вращения конуса (рис. 8.18).
Рис. 8.18. Точка на поверхности конуса
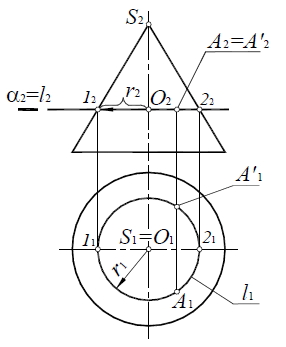
Если необходимо определить фронтальную проекцию точки A, принадлежащей поверхности конуса (рис. 8.19,а), конус рассекается вспомогательной горизонтально-проецирующей плоскостью β(A, i), проходящей через ось вращения конуса и искомую точку. Плоскость β(A, i) пересекает основание конуса в точке 1. Вершина конуса S и точка 1 определят образующую конуса l, проходящую через точку A:
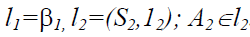
Рис. 8.19. Построение точки на поверхности конуса:
а – определение фронтальной проекции;
б – определение горизонтальной проекции
Если необходимо определить горизонтальную проекцию точки A, принадлежащей поверхности конуса (рис. 8.19,б), конус рассекается вспомогательной фронтально-проецирующей плоскостью γ(γ2) eS. Плоскость γ(γ2) пересекает основание конуса в точках 3 и 4. Вершина конуса S и точка 3 определят образующую конуса m, проходящую через точку A:
m2= γ2, m1=(S1,31); A1 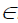
m’2=γ2, m’1=(S1,31); A’1βm,1.
Таким образом, данной фронтальной проекции точки A2 могут соответствовать две точки – A и A/.
Сечение поверхности вращения плоскостью частного положения
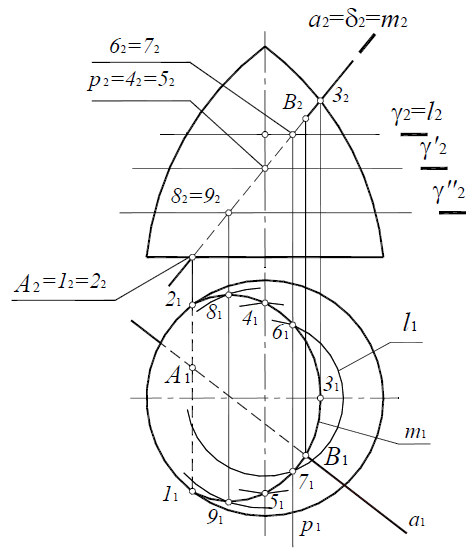
Рассмотрим построение линии пересечения поверхности закрытого тора с фронтально-проецирующей плоскостью μ(μ2) (рис. 8.20). Сначала определяются опорные точки: 1 и 2 – точки пересечения плоскости μ(μ2) с плоскостью основания тора, точка 3 – точка пересечения плоскости μ(μ2) с очерковой образующей тора.
Промежуточные точки 4 и 5 строятся при помощи вспомогательной плоскости уровня γ(γ2), которая рассекает поверхность тора по линии:
l=Фm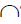
P=μ(μ2)nγ(γ2); p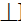
Точки 4 и 5 пересечения полученных линий принадлежат секущей плоскости μ(μ2) и линии l поверхности тора, то есть принадлежат плоскости и поверхности одновременно, а следовательно, являются точками искомой линии пересечения m.
Точки 6, 7, 8 и 9 определяются аналогично. Полученные точки соединяют плавной лекальной кривой и определяют видимость линии пересечения m относительно поверхности.
Рис. 8.20. Сечение поверхности вращения плоскостью частного положения
При построении сечений поверхности плоскостью общего положения выполняют такое преобразование комплексного чертежа, при котором плоскость займет частное положение.
Цилиндрические сечения
В сечении цилиндрической поверхности вращения плоскостью могут быть получены следующие линии:
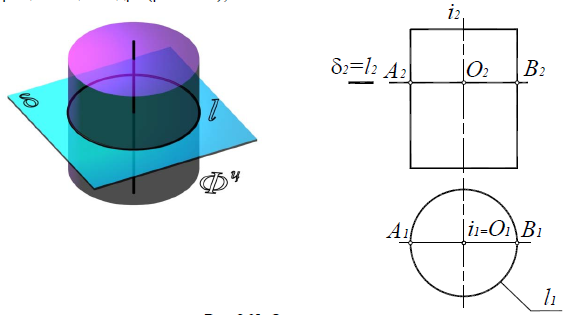
Окружность, если секущая плоскость δ(δ2) перпендикулярна оси вращения цилиндра (рис. 8.21);
Рис. 8.21. Окружность
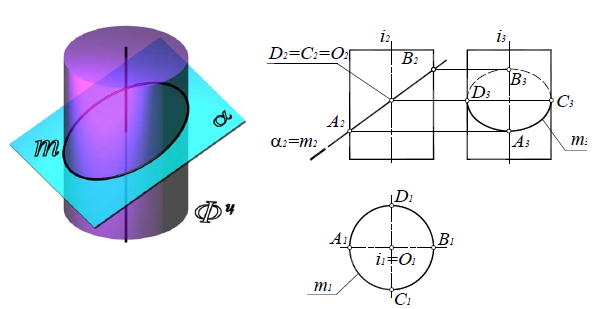
Эллипс, если секущая плоскость α(α2) наклонена под произвольным углом к оси цилиндра (рис. 8.22);
Рис. 8.22. Эллипс
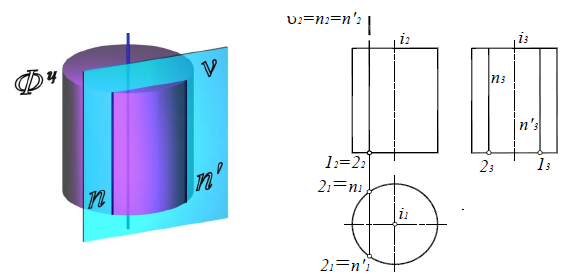
Две параллельные прямые (образующие), если секущая плоскость ν(ν2)
параллельна оси цилиндра (рис. 8.23)
Рис. 8.23. Параллельные прямые
На плоскость, перпендикулярную оси вращения поверхности, окружность и эллипс на поверхности цилиндра проецируются в окружность, совпадающую с проекцией всей поверхности.
Конические сечения
Кривые линии, которые получаются в сечении прямого кругового конуса плоскостью, называются коническими сечениями. В зависимости от положения секущей плоскости по отношению к конической поверхности образуются
следующие линии:
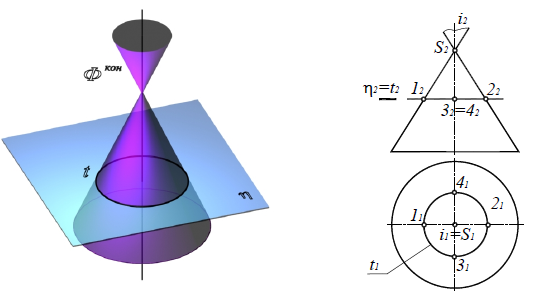
Окружность, если секущая плоскость η(η2) перпендикулярна оси вращения конуса i (рис. 8.24).
Рис. 8.24. Окружность
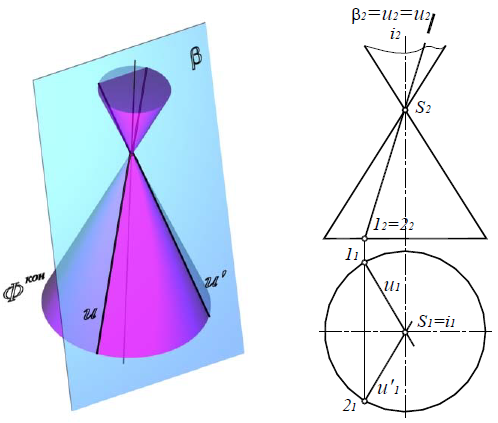
Две пересекающиеся прямые, если секущая плоскость β(β2) проходит через вершину поверхности конуса (рис. 8.25).
Рис. 8.25. Пересекающиеся прямые
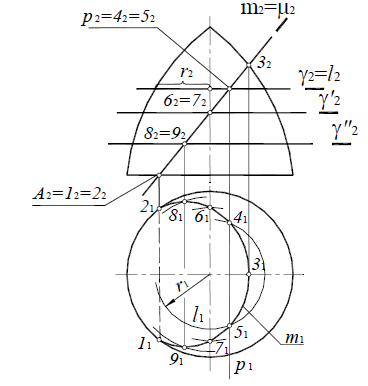
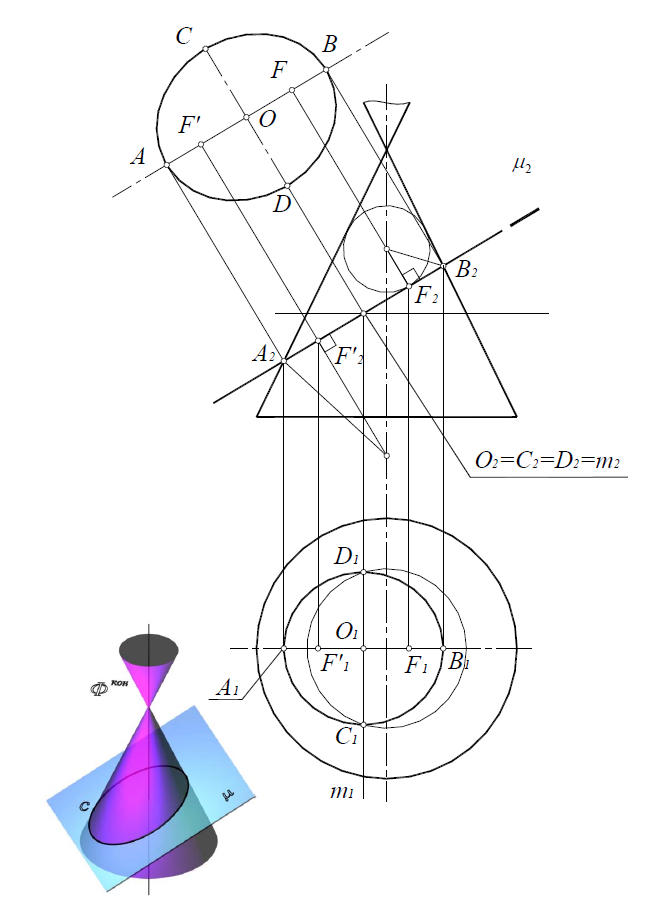
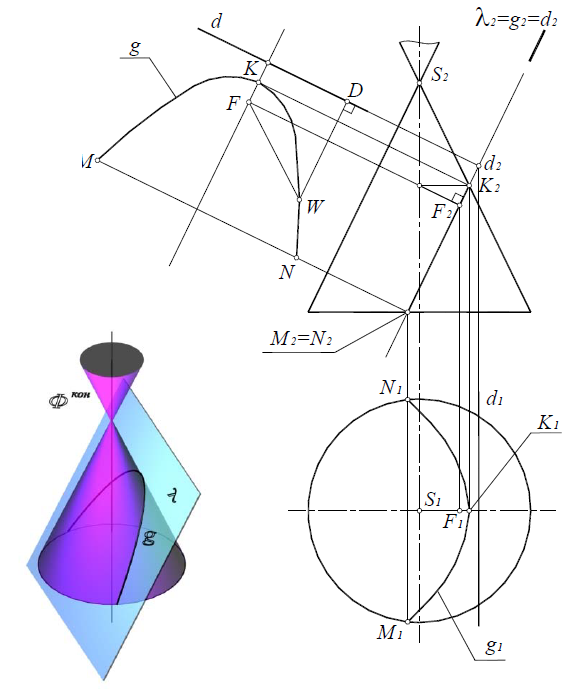
Эллипс (рис. 8.26), если секущая плоскость μ(μ2) пересекает все образующие, расположенные по одну сторону от вершины конуса.
Точки A и B являются опорными и не требуют дополнительных построений (см. рис. 95.). Отрезок [AB] определяет большую ось эллипса. Для определения малой оси отрезок [A2B2] делят пополам. Так получается центр эллипса – точка O. Затем через точку O проводят вспомогательную плоскость σ(σ2), которая пересекает поверхность конуса по окружности:
σ(σ2)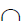
σ(σ2)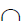
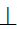
m1×l1=C1D1; [C1D1] – малая ось эллипса.
Для построения фокуса проводят биссектрису угла 
Свойство эллипса: сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равна большой оси эллипса АВ=FP+F’P.
Рис. 8.26. Эллипс
Парабола (рис. 8.27), если секущая плоскость λ(λ2) параллельна одной из образующих поверхности конуса.
Рис. 8.27. Парабола
Точка К – вершина параболы (см. рис. 96). Точки N и Mлежат на основании. Фокус параболы строится при проведении биссектрисы угла 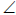

Свойство параболы: расстояние от любой точки параболы до ее фокуса равно расстоянию от этой точки до директрисы WD=WF.
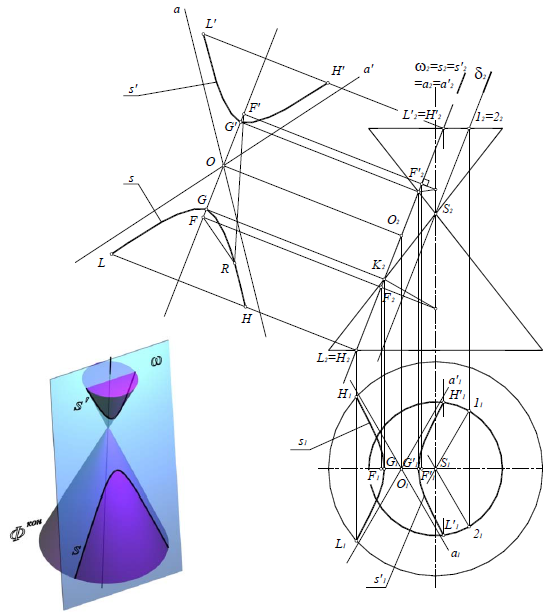
Гипербола (рис. 8.28), если секущая плоскость ω(ω2) пересекает обе половины поверхности конуса.
Рис. 8.28. Гипербола
При пересечении конуса образуются две части гиперболы 5 и 5′. G и G’ -вершины гиперболы, F(F 1, F2) и F'(F 1‘, F2) – фокусы гиперболы, O(O 1, O2) -центр гиперболы, а и a′ – асимптоты гиперболы, получающиеся как прямые, параллельные образующим конуса S1 и S2, полученным при рассечении его плоскостью δ(δ2),параллельной плоскостиω(ω2).
Свойство гиперболы: разность расстояний от любой точки гиперболы до ее фокусов есть величина постоянная, равная расстоянию между вершинами гиперболы RF-RF’=GG’.
Пересечение прямой с поверхностью
Прямая по отношению к поверхности может занимать следующие положения:
- прямая касается поверхности (одна общая точка);
- прямая пересекает поверхность (две и более общих точек);
- прямая не пересекает и не касается поверхности (общих точек нет).
Алгоритм решения задач об определении взаимного положения поверхности и прямой аналогичен решению первой позиционной задачи (рис. 8.29):
- Прямая заключается во вспомогательную плоскость частного положения.
- Определяется линия пересечения вспомогательной плоскости и заданной поверхности, то есть, строится сечение поверхности вспомогательной плоскостью.
- Определяется взаимное положение полученной линии (сечения) и заданной прямой. Точки пересечения являются искомыми точками пересечения прямой с поверхностью.
- Определяется видимость прямой относительно поверхности.
Рис. 8.29. Пересечение прямой с поверхностью
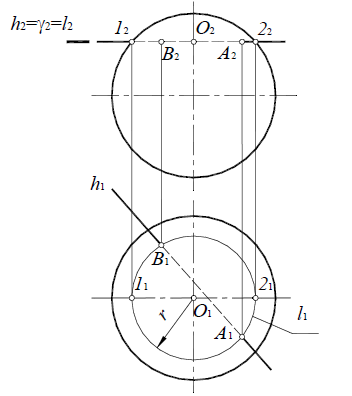
Для построения точки пересечения поверхности сферы с горизонталью (рис. 8.30), горизонталь заключают во вспомогательную горизонтальную плоскость уровня γ(γ2).
Сечение сферы горизонтальной плоскостью уровня представляет собой окружность l с центром в точке O2 и радиусом r=O2l2, которая проецируется на П1 без искажения. Затем определяются точки пересечения окружности l1 и заданной горизонтали h1 :
h 1×11=A1, B1; A2, B2∈h2.
Далее следует определить видимость прямой: между точками A и B прямая невидима на обеих проекциях, поскольку находится внутри сферы, фронтальная проекция горизонтали находится выше фронтальной проекции очерковой образующей сферы, поэтому горизонталь на П1 видима; точка A имеет большую глубину, чем очерковая образующая сферы, поэтому на фронтальной проекции горизонталь видима до точки A, а за точкой B – невидима.
Рис. 8.30. Пересечение прямой с поверхностью сферы
Для построения точки пересечения поверхности закрытого тора с прямой общего положения (рис. 8.31), прямую заключают во вспомогательную фронтально-проецирующую плоскость δ(δ2). Далее строится сечение тора плоскостью δ(δ2):
Точки 1 и 2 – точки пересечения с основанием и точка 3 – опорные точки на очерковой образующей определяются без дополнительных построений;
Точки 4 и 5 также опорные (лежат на образующих, проекции которых совпадают с осью тора). Точки 4 и 5 определяются как точки на поверхности тора с помощью вспомогательной плоскости γ’.
Промежуточные точки 6,7,8,9 определяются аналогично.
Полученные точки соединяются плавной лекальной кривой m. Линия m -сечение тора плоскостью δ(δ2). Затем определяют точки A и B пересечения полученной линии m с прямой a и определяют видимость. Точки A и B -искомые точки пересечения прямой с поверхностью тора.
Рис. 8.31. Пересечение прямой общего положения с поверхностью тора
1. a(a1, a2) ∈ δ(δ2);
2. m = δ(δ2)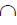
γ(γ2) – вспомогательная плоскость;
γ(γ2) 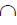
γ(γ2) 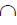
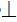
l×p = 6, 7 – промежуточные точки сечения m;
m×a = A, B – искомые точки пересечения прямой с поверхностью тора;
3. Определить видимость прямой относительно поверхности тора.
Принадлежность точки и прямой
Вопрос о принадлежности точки прямой решается на основе свойств (особенностей) метода проецирования. Точка С лежит на прямой АВ, если ее проекции, в соответствии с рисунком 4.2, лежат на одноименных проекциях Прямой
В геометрии принято считать, что прямая принадлежит плоскости, если две ее точки (действительные или несобственные) принадлежат этой плоскости (рисунки 4.3, 11.8)
В соответствии с рисунком 4.3 прямая AВ лежит в плоскости Р. Это обуславливается тем, что точка A лежит на следе 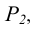
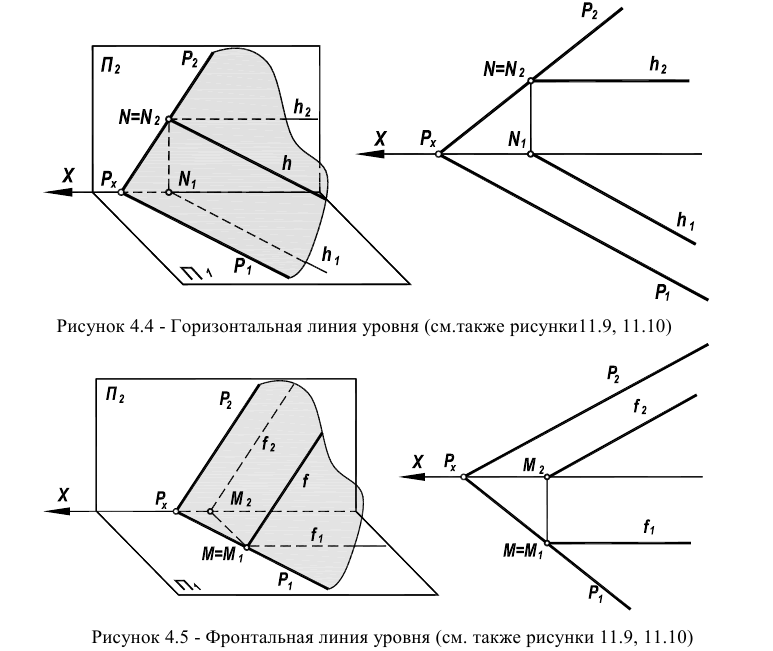
При условии, что одна из точек плоскости, через которые проходит прямая, лежит на следе и является несобственной (в соответствии с рисунками 4.4 и 4.5), прямая общего положения переходит в прямую частного положения (линию уровня).
В плоскости различают горизонтальную линию уровня h (рисунки 4.4, 11.9) и фронтальную линию уровня 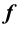
В силу специального расположения следов 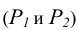
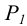
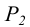
Фронтали и горизонтали плоскости получили название главных линии плоскости.
Вопрос о принадлежности точки плоскости можно свести к предыдущей задаче. Достаточно добиться того, чтобы точка лежала на одной из прямых плоскости (рисунки 4.6, 11.8)
Точка С лежит на прямой АВ (ее проекции, в соответствии с рисунком 4.2, лежат на одноименных проекциях прямой 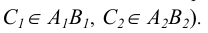
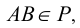
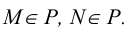
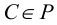
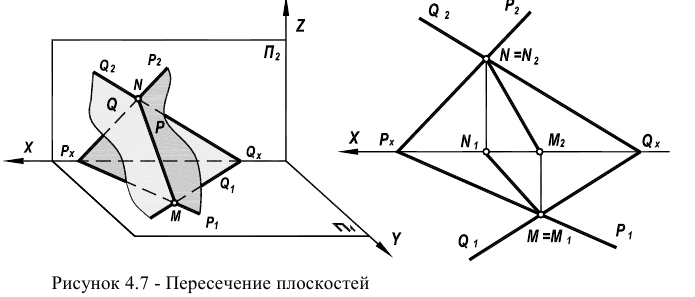
Пересечение плоскостей
В соответствии с формулой р=2+2-3=1 пересечение двух плоскостей должно привести к появлению одномерного объекта, т.е. прямой линии. Для построения линии пересечения двух плоскостей общего положения (Р и 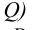
Пересечение горизонтальных следов 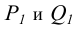
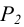
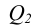
Если одна из плоскостей проецирующая (например, горизонтально-проецирующая, в соответствии с рисунком 4.8, 4.12), то линия пересечения 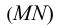
При пересечении плоскости общего положения плоскостью уровня в сечении получается соответствующая линия уровня (рисунок 4.9).
Определение линии пересечения двух плоскостей для других случаев, например, при задании плоскостей треугольником (симплексом) и параллельными прямыми, базируется на следующей идее. Три плоскости всегда пересекаются в одной точке. Следовательно, введение дополнительной плоскости к двум, уже имеющимся, позволит определить точку, одновременно принадлежащую заданным плоскостям. Проиллюстрируем это на рисунке 4.10.
Две плоскости, заданные параллельными и пересекающимися прямыми, пересекаются по прямой ЕК, найденной с помощью секущих плоскостей уровня S и Т. Плоскость S пересекает 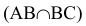
Пересечение прямой и плоскости
Пересечением прямой и плоскости в пространстве является точка, что подтверждается и вычислением по формуле р=1 +2-3=0.
Прямая L в пространстве (в соответствии с рисунком 4.11) может рассматриваться как результат пересечения проецирующих плоскостей 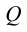
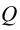
Восстановление одной из проецирующих плоскостей, например 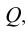
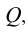
Аналогичное решение этой задачи и в случае задания плоскости Р треугольником (симплексом). Восстановление одной из проецирующих плоскостей (например, 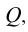
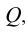
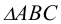
Параллельность
Частным случаем пересечения прямых и плоскостей является взаимная параллельность. В трехмерном пространстве отсутствует полная параллельность. Понятие параллельности вводится с помощью признаков (условий).
При параллельности пересечением является несобственный элемент.
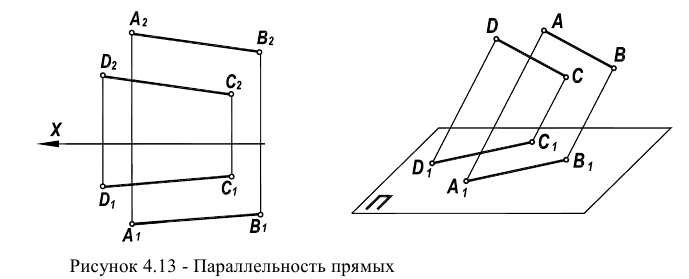
Признак параллельности прямых следует непосредственно из определения пересечения прямых (раздел 2.1). В соответствии с рисунком 4.13 одноименные проекции параллельных прямых попарно параллельны (параллельные прямые пересекаются в несобственной точке).
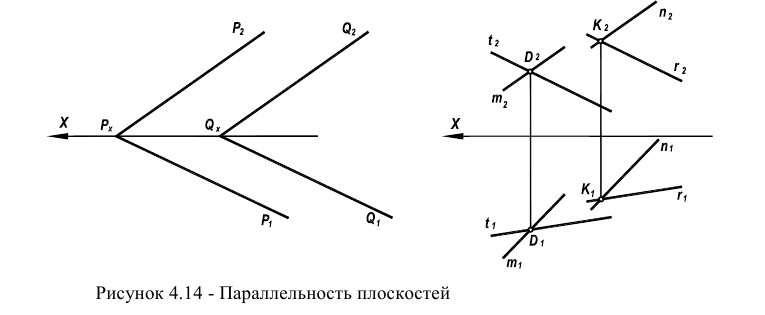
Признаком параллельности плоскостей является то, что две пересекающиеся прямые одной плоскости должны быть параллельны двум пересекающимся прямым другой плоскости (рисунок 4.14).
Такими прямыми могут быть следы. В этом случае одноименные следы должны быть параллельны между собой
В любом другом случае (в соответствии с рисунком 4.14) должна соблюдаться параллельность пересекающихся прямых, образующих плоскости,
Параллельность прямой и плоскости должны отвечать следующему условию: прямая параллельна плоскости, если она параллельна одной из прямых этой плоскости. В соответствии с вышесказанным и рисунком 4.15 проекции
пространственной прямой должны быть параллельны соответствующим проекциям прямой, лежащей в плоскости.
Прямая n параллельна прямой m, лежащей в плоскости 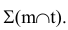
- Методы преобразования эпюра Монжа
- Касательные плоскости
- Пересечение поверхностей вращения плоскостью
- Виды, разрезы, сечения
- Метод замены плоскостей проекций
- Проецирование прямой линии
- Проецирование плоскости
- Плоскость на эпюре Монжа
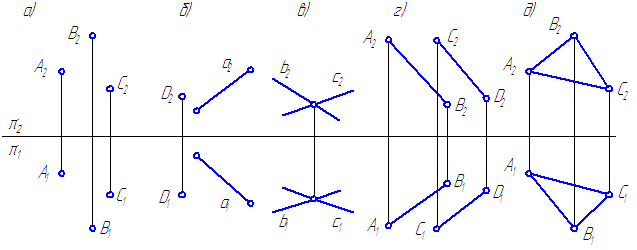
Пересекающимисяназываются две прямые лежащие в одной
плоскости и имеющие одну общую точку.
Если
прямые пересекаются, то точки пересечения
их одноименных проекций находится на
одной линии связи(рис.
3.21).
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 3.21. Пересекающиеся прямые |
В общем случае справедливо и обратное
утверждение, но есть два частных случая:
1. Если одна из прямых параллельна
какой-либо из плоскостей проекций,
например профильной плоскости проекций
(рис. 3.22), по двум проекциям невозможно
судить об их взаимном расположении. Так
горизонтальная и фронтальная проекции
отрезков АВиСДпересекаются, причем точка пересечения
проекций лежит на одной линии связи,
профильные проекции этих отрезков тоже
пересекаются, однако точка их пересечения
не лежит на одной линии связи с точками
пересечения горизонтальной и фронтальной
проекций отрезков, следовательно, не
пересекаются и сами отрезки.
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 3.22.Одна из прямых параллельна |
2. Пересекающие
прямые расположены в общей для них
проекционной плоскости, например
перпендикулярной фронтальной плоскости
проекций (рис. 3.23). О взаимном расположении
прямых, лежащих в этой плоскости, можно
судить по одной проекции, например, на
горизонтальную плоскость проекций
(А1В1∩С1D1ÞАВ∩СD)
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 3.23. Пересекающиеся прямые |
3. Скрещивающиеся прямые
Скрещивающимисяназываются две прямые не лежащие в одной
плоскости.
Если прямые не пересекаются
и не параллельны между собой, то точка
пересечения их одноименных проекций
не лежит на одной линии связи.
Точке пересечения фронтальных проекций
прямых (рис. 3.24) соответствуют две точки
АиВ, из которых одна
принадлежит прямойа,другаяв . Их фронтальные проекции
совпадают лишь потому, что в пространстве
обе точкиАиВнаходятся
на общем перпендикуляре к фронтальной
плоскости проекций. Горизонтальная
проекция этого перпендикуляра,
обозначенная стрелкой, позволяет
установить, какая из двух точек ближе
к наблюдателю. На предложенном примере
ближе точкаВлежащая на прямойв, следовательно, прямаяв
проходит в этом месте ближе прямойаи фронтальная проекция точкиВзакрывает проекцию точкиА. (Для
точекСиДрешение
аналогично).
Этот способ определения видимости по
конкурентным точкам. В
данном случае точкиАиВ-
фронтально
конкурирующие,
а С
и Д
–горизонтально
конкурирующие.
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 3.24. Скрещивающиеся |
Лекция №3-6 Проекции плоских углов.
Угол– геометрическая
фигура, состоящая из двух различных
лучей, выходящих из одной точки.Углом
между прямыми называется меньший
из двух углов между лучами, параллельными
этим прямым.Углом между
плоскостью и не перпендикулярной ей
прямой называется угол между
прямой и её проекцией на данную плоскость.
Рассмотрим ряд свойств ортогональных
проекций плоских углов:
1. Если хотя бы одна из сторон прямого
угла параллельна плоскости проекций,
а другая не перпендикулярна ей, то на
эту плоскость прямой угол проецируется
без искажения (Теорема
о проецировании прямого угла)
|
|
|
|
Рисунок 3.25. Теорема |
Рисунок 3.26. Обратная |
Дано: ÐАВС
=
90о; [ВС]
// П1;
[АС]
#
П1.
Для доказательства теоремы продлим
отрезок АС до
пересечения с плоскостью П1
(рис. 3.25) получим горизонтальный след
прямой – точку М
º
М1, одновременно
принадлежащую прямой и ее проекции. Из
свойства ортогонального проецирования
следует, что [ВС]
// [В1С1].
Если через точку М
проведем прямую МD
параллельную С1В1
, то она будет параллельна и СВ,
а следовательно ÐСМD=
90о.
Согласно теореме о трех
перпендикулярах ÐС1МD=90о.Таким образом,MDА1С1 иMD//В1С1,
следовательно,А1С1В1 90о,
что и требовалось доказать. В
случае когда [АС^]П1
проекцией угла, согласно свойствам
ортогонального проецирования, будет
прямая линия.
2. Если проекция угла представляет
угол 900, то проецируемый
угол будет прямым лишь при условии, что
одна из сторон этого угла параллельна
плоскости проекций (рис. 3.26).
3. Если обе стороны любого угла параллельны
плоскости проекций, то его проекция
равна по величине проецируемому углу.
4. Если стороны угла параллельны
плоскости проекций или одинаково
наклонены к ней, то деление проекции
угла на этой плоскости пополам
соответствует делению пополам и самого
угла в пространстве.
5. Если стороны угла не параллельны
плоскости проекций, то угол на эту
плоскость проецируется с искажением.
Лекция
№4
|
типы |
Решение многих задач способами
начертательной геометрии, в конечном
счете, сводится к определению позиционных
и метрических характеристик геометрических
объектов. В связи с этим все многообразие
задач может быть отнесено к двум группам:
1.Задачи позиционные– решение, которых должно давать ответ
на вопрос о взаимном расположении
геометрических объектов (в частном
случае, выяснить их взаимную принадлежность)
как по отношению друг к другу, так и
относительно системы координатных
плоскостей проекций.
2.Задачи метрические– при решении задач этой группы появляется
возможность ответить на вопросы,
касающиеся как внутренней метрики
заданных геометрических объектов
(определение расстояния между различными
точками объекта и нахождения углов
между линиями и поверхностями,
принадлежащими этому объекту), так и
определение расстояний между точками
и величин углов между линиями и
поверхностями, принадлежащими различным
объектам.
В начертательной геометрии задачи
решаются графически. Количество и
характер геометрических построений
при этом определяются не только сложностью
задачи, но и в значительной степени
зависит от того, с какими проекциями
(удобными или неудобными) приходится
иметь дело. При этом наиболее выгодным
частным положением геометрического
объекта следует считать:
Положение, перпендикулярноек плоскости проекций (для решения
позиционных, а в ряде случаев, и метрических
задач);
Положение, параллельноепо
отношению к плоскости проекций (при
решении метрических задач).
При решении метрических задач, связанных
с определением истинных размеров
изображенных на эпюре фигур, могут
встретиться значительные трудности,
если заданные проекции не подвергнуть
специальным преобразованиям.
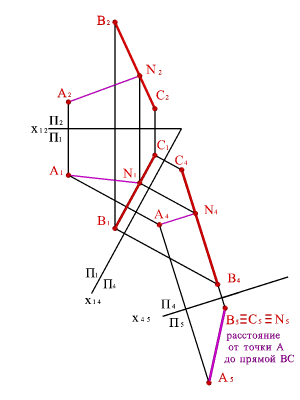
Рассмотрим на примере: Определить
расстояние от точкиАдо прямойm. Расстояние от точки
до прямой – это натуральная величина
перпендикуляра восстановленного из
точки к прямой линии. Простейшим условием
такой задачи является случай, когда
прямая является проецирующей. Определим
расстояние от точкиАдо прямойm, когда прямая является
горизонтально проецирующей линией
(рис. 4.1), т.е.m^П1,
m \ П2,
m \ П3.
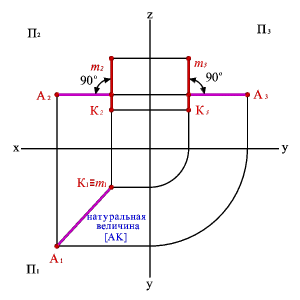
Согласно, теореме о проецировании
прямого угла, перпендикуляр из проекций
точкиАможно проводить к
фронтальной и профильной проекции
прямойm, при этом
полученный отрезокАК– горизонталь,
т.е. параллелен горизонтальной плоскости
проекций и на эту плоскость проецируется
в натуральную величину.
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 4.1. Расстояние от точки до |
|
Методы преобразования |
Если прямая параллельна одной из
плоскостей проекций т.е. является прямой
уровня, то без преобразования ортогональных
проекций можно только найти проекции
перпендикуляра. Пусть прямая f
фронталь, т.е.f \
П2значит перпендикуляр
можно проводить из проекцийА2к фронтальной проекции прямойm2,
на эту плоскость угол будет проецироваться
без искажения (рис. 4.2). Однако полученные
проекции отрезкаАК не
отражают истинной величины отрезка
потому, чтоАК – отрезок прямой
общего положения.
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 4.2. Расстояние от точки до |
Общий случай подобной задачи, когда
требуется найти расстояние от точки до
прямой общего положения, то даже
построение проекции искомого отрезка
без преобразования проекций не
представляется возможным.
Сопоставление приведенных чертежей
показывает, что трудности решения одной
и той же задачи существенно зависят от
положения геометрических объектов
относительно плоскостей проекций.
В связи с этим, естественно, возникает
вопрос, каким путем можно получить
удобные проекции для решения поставленной
задачи по заданным неудобным ортогональным
проекциям.
Переход от общего положения геометрической
фигуры к частному можно осуществлять
за счет изменения взаимного положения
проецируемой фигуры и плоскостей
проекций.
При ортогональном проецировании это
достигается двумя путями:
1. Перемещение в пространстве проецируемой
фигуры так, чтобы она заняла частное
положение относительно плоскостей
проекций, которые при этом не меняют
своего положения в пространстве – метод
плоскопараллельного перемещения.
2. Перемещением плоскостей проекций в
новое положение по отношению, к которому
проецируемая фигура (которая не меняет
положения в пространстве) окажется в
частном положении – метод замены
плоскостей проекций.
Лекция
№4
|
Метод плоскопараллельного |
Изменение взаимного положения
проецируемого объекта и плоскостей
проекций методом плоскопараллельного
перемещения осуществляется путем
изменения положения геометрического
объекта так, чтобы траектория движения
её точек находилась в параллельных
плоскостях. Плоскости носители траекторий
перемещения точек параллельны какой-либо
плоскости проекций (рис. 4.3). Траектория
произвольная линия. При параллельном
переносе геометрического объекта
относительно плоскостей проекций,
проекция фигуры хотя и меняет свое
положение, но остается конгруэнтной
проекции фигуры в ее исходном положении.
|
|
|
|
|
а)модель |
б) эпюр |
|
|
Рисунок 4.3. Определение натуральной |
Свойства плоскопараллельного перемещения:
1. При всяком перемещении точек в плоскости
параллельной плоскости П1,
её фронтальная проекция перемещается
по прямой линии, параллельной осих.
2. В случае произвольного перемещения
точки в плоскости параллельной П2,
её горизонтальная проекция перемещается
по прямой параллельной осих.
В зависимости от положения этих
плоскостей по отношению к плоскостям
проекций и вида кривой линии – определяющей
траекторию перемещения точек, метод
плоскопараллельного проецирования
имеет следующие частные случаи:
1. Метод вращения вокруг оси, перпендикулярной
плоскости проекций;
2. Метод вращения вокруг оси,
параллельной плоскости проекций;
3. Метод вращения вокруг оси, принадлежащей
плоскости проекций (вращение вокруг
следа плоскости)- способ совмещения.
Рассмотрим некоторые из этих способов.
|
Метод вращения вокруг |
Плоскости носитель траекторий перемещения
точек параллельны плоскости проекций.
Траектория – дуга окружности, центр
которой находится на оси перпендикулярной
плоскости проекций. Для определения
натуральной величины отрезка прямой
общего положения АВ(рис. 4.4),
выберем ось вращения перпендикулярную
горизонтальной плоскости проекций и
проходящую черезВ1.
Повернем отрезок так, чтобы он стал
параллелен фронтальной плоскости
проекций (горизонтальная проекция
отрезка параллельна осиx). При этом
точкаА1переместиться
вА*1, а точкаВне изменит своего положения. Положение
точкиА*2находится на
пересечении фронтальной проекции
траектории перемещения точкиА(прямая линия параллельная осиx) и
линии связи проведенной изА*1.
Полученная проекцияВ2
А*2определяет действительные
размеры самого отрезка.
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 4.4. Определение натуральной |
|
Метод вращения вокруг |
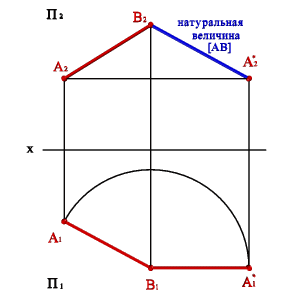
Рассмотрим этот способ на примере
определения угла между пересекающимися
прямыми (рис.4.5). Рассмотрим две проекции
пересекающихся прямых а ив которые пересекаются в
точкеК. Для то чтобы определить
натуральную величину угла между этими
прямыми необходимо произвести
преобразование ортогональных проекций
так, чтобы прямые стали параллельны
плоскости проекций. Воспользуемся
способом вращения вокруг линии уровня
– горизонтали. Проведем произвольно
фронтальную проекцию горизонталиh2параллельно осиОх, которая
пересекает прямые в точкахА2иВ2. Определив проекцииА1иВ1,
построим горизонтальную проекцию
горизонталиh1
. Траектория движения всех точек при
вращении вокруг горизонтали – окружность,
которая проецируется на плоскость П1
в виде прямой линии перпендикулярной
горизонтальной проекции горизонтали.
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок 4.5. Определение угла между |
Таким образом, траектория движения
точки К1определена
прямойК1О1,
точкаО-центр окружности –
траектории движения точкиК.
Чтобы найти радиус этой окружности
найдем методом треугольника натуральную
величину отрезкаКО.Продолжим
прямуюК1О1так чтобы|КО|=|О1К*1|
. Точка К*1
соответствует точке К
, когда прямые а
и в
лежат в
плоскости параллельной П1
и проведенной через горизонталь – ось
вращения. С учетом этого через точку
К*1
и точки А1
и В1
проведем прямые, которые лежат теперь
в плоскости параллельной П1,
а следовательно и угол j
– натуральная величина угла между прямыми
а
и в.
|
Метод замены плоскостей |
Изменение взаимного положения проецируемой
фигуры и плоскостей проекций методом
перемены плоскостей проекций, достигается
путем замены плоскостей П1иП2новыми плоскостямиП4(рис. 4.6). Новые
плоскости выбираются перпендикулярно
старым. Некоторые преобразования
проекций требуют двойной замены
плоскостей проекций (рис. 4.7). Последовательный
переход от одной системы плоскостей
проекций другой необходимо осуществлять,
выполняя следующее правило:
расстояние
от новой проекции точки до новой оси
должно равняться расстоянию от заменяемой
проекции точки до заменяемой оси.
Задача 1: Определить натуральную величину
отрезка АВпрямой общего положений
(рис. 4.6). Из свойства параллельного
проецирования известно, что отрезок
проецируется на плоскость в натуральную
величину, если он параллелен этой
плоскости.
Выберем новую плоскость проекций П4,
параллельно отрезкуАВи
перпендикулярно плоскостиП1.
Введением новой плоскости, переходим
из системы плоскостейП1П2в системуП1П4, причем в новой системе плоскостей
проекция отрезкаА4
В4будет натуральной
величиной отрезкаАВ.
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок 4.6. Определение натуральной |
Задача 2: Определить расстояние от точки
Адо прямой общего положения,
заданной отрезкомАВ(рис._4.7).
|
|
|
||
|
а) модель |
б)эпюр |
||
|
Рисунок 4.7. Определение расстояния от |
Лекция
№5-1
|
Плоскость |
Плоскость–
одно из основных понятий геометрии. При
систематическом изложении геометрии
понятие плоскость обычно принимается
за одно из исходных понятий, которое
лишь косвенным образом определяется
аксиомами геометрии. Некоторые
характеристические свойства плоскости:
1. Плоскость есть поверхность, содержащая
полностью каждую прямую, соединяющую
любые ее точки;
2. Плоскость есть множество точек,
равноотстоящих от двух заданных точек.
Плоскость в линейной алгебре – поверхность
первого порядка: в декартовой системе
координат плоскость может быть задана
уравнением 1-ой степени. Общее уравнение
плоскости:
Ax+By+Cz+D=0,
где А, В, С, иD– постоянные,
причемА, ВиСодновременно
не равны нулю.
|
Способы |
Положение плоскости в пространстве
можно определить:
1. Тремя точками, не лежащими на одной
прямой линии (рис.5.1);
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 5.1. Плоскость заданная тремя |
2. Прямой линией и точкой, не принадлежащей
этой прямой (рис.5.2);
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 5.2. Плоскость заданная прямой |
3. Двумя пересекающимися прямыми
(рис.5.3);
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 5.3. Плоскость заданная двумя |
4. Двумя параллельными прямыми (рис.5.4);
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 5.4. Плоскость заданная двумя |
Лекция
№5-2
|
Различное |
В зависимости от положения плоскости
по отношению к плоскостям проекций она
может занимать как общее, так и частные
положения.
1. Плоскость не перпендикулярная ни
одной плоскости проекций называется
плоскостью
общего положения. Такая
плоскость пересекает все плоскости
проекций (имеет три следа: – горизонтальныйaП1; –
фронтальныйaП2;
– профильныйaП3).
Следы плоскости общего положения
пересекаются попарно на осях в точках
ax,ay,az.
Эти точки называются точками схода
следов, их можно рассматривать как
вершины трехгранных углов, образованных
данной плоскостью с двумя из трех
плоскостей проекций.
Каждый из следов плоскости совпадает
со своей одноименной проекцией, а две
другие разноименные проекции лежат на
осях (рис.5.5).
2.Плоскости перпендикулярные плоскостям
проекций – занимают частное положение
в пространстве и называются проецирующими.
В зависимости от того, какой плоскости
проекций перпендикулярна заданная
плоскость, различают:
2.1. Плоскость перпендикулярная
горизонтальной плоскости проекций
(^aP1),
называетсягоризонтально
проецирующей плоскостью.
Горизонтальная проекция такой плоскости
представляет собой прямую линию, которая
одновременно является её горизонтальным
следом. Горизонтальные проекции всех
точек любых фигур в этой плоскости
совпадают с горизонтальным следом
(рис.5.6).
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 5.6. Горизонтально проецирующая |
2.2. Плоскость перпендикулярная фронтальной
плоскости проекций (a^П2)-фронтально проецирующая
плоскость. Фронтальной проекцией
плоскостиaявляется прямая линия, совпадающая со
следомaП2(рис.5.7).
|
|
|
|
|
а)модель |
б) эпюр |
|
|
Рисунок 5.7. Фронтально проецирующая |
2.3. Плоскость перпендикулярная профильной
плоскости ( ^aП3)
–профильно проецирующая
плоскость. Частным случаем
такой плоскости являетсябиссекторная
плоскость(рис.5.8).
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 5.8. Биссекторная плоскость |
3. Плоскости параллельные плоскостям
проекций – занимают частное положение
в пространстве и называютсяплоскостями
уровня.В
зависимости от того, какой плоскости
параллельны исследуемая плоскость,
различают:
3.1. Горизонтальная
плоскость – плоскость параллельная
горизонтальной плоскости проекций
(a//П1)
– (^aП2,^aП3).
Любая фигура в этой плоскости проецируется
на плоскостьП1без
искажения, а на плоскостиП2иП3в прямые – следы
плоскостиaП2иaП3(рис.5.9).
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 5.9. Горизонтальная плоскость |
3.2. Фронтальная
плоскость – плоскость
параллельная фронтальной плоскости
проекций (a//П2),
(a^П1,
a^П3).
Любая фигура в этой плоскости
проецируется на плоскостьП2без искажения, а на плоскостиП1иП3в прямые – следы
плоскостиaП1иaП3(рис.5.10).
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 5.10. Фронтальная плоскость |
3.3. Профильная
плоскость – плоскость
параллельная профильной плоскости
проекций (a//П3),
(a^П1,
a^П2).
Любая фигура в этой плоскости
проецируется на плоскостьП3без искажения, а на плоскостиП1иП2в прямые – следы
плоскостиaП1иaП2(рис.5.11).
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 5.11. Профильная плоскость |
Лекция
№5-3
|
Следы плоскости |
Следом плоскостиназывается линия пересечения плоскости
с плоскостями проекций. В зависимости
от того с какой из плоскостей проекций
пересекается данная, различают:горизонтальный,фронтальныйипрофильныйследы
плоскости.
Каждый след плоскости является прямой
линией, для построения которых необходимо
знать две точки, либо одну точку и
направление прямой( как для построения
любой прямой). На рисунке 5.12 показано
нахождение следов плоскости α(АВС).
Фронтальный след плоскости
αП2, построен,
как прямая соединяющая две точки N(АС)
и N(АВ), являющиеся
фронтальными следами соответствующих
прямых, принадлежащих плоскости α.Горизонтальный след αП1
– прямая, проходящая через горизонтальные
следы прямых ВС и
АВ. Профильный след
αП3 – прямая соединяющая
точки (αy и αz)
пересечения горизонтального и фронтального
следов с осями.
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок |
|
Взаимное |
Определение взаимного положения прямой
и плоскости – позиционная задача, для
решения которой применяетсяметод
вспомогательных секущих плоскостей.
Сущность метода заключается в
следующем: через прямую проведем
вспомогательную секущую плоскостьg
и установим относительное положение
двух прямыхаив,
последняя из которых является линией
пересечения вспомогательной секущей
плоскостиgи
данной плоскостиa(рис.5.13).
|
|
Каждому из трех возможных случаев
Таким образом возможны три случая
Рассмотрим каждый случай. |
|
Рисунок 5.13. Метод вспомогательных |
|
Прямая |
Аксиома 1. Прямая
принадлежит плоскости, если две её точки
принадлежат той же плоскости (рис.5.14).
Задача. Дана плоскость (n,k)
и одна проекция прямой m2.
Требуется найти недостающие проекции
прямой mесли известно, что она
принадлежит плоскости, заданной
пересекающимися прямымиnиk.
Проекция прямой m2пересекает прямыеnиkв точкахВ2иС2,
для нахождения недостающих проекций
прямой необходимо найти недостающие
проекции точек ВиСкак
точек лежащих на прямых соответственноnиk.
Таким образом точки ВиСпринадлежат плоскости заданной
пересекающимися прямымиnиk,
а прямаяmпроходит через эти
точки, значит согласно аксиоме прямая
принадлежит этой плоскости.
|
|
|
||||
|
а) модель |
б) эпюр |
||||
|
Рисунок 5.14. Прямая и плоскость имеют |
Аксиома 2.
Прямая принадлежит плоскости, если
имеет с плоскостью одну общую точку и
параллельна какой-либо прямой расположенной
в этой плоскости (рис.5.15).
Задача.
Через точку Впровести прямуюmесли известно, что она принадлежит
плоскости заданной пересекающимися
прямымиnиk.
Пусть В принадлежит прямойn
лежащей в плоскости заданной
пересекающимися прямымиnиk.
Через проекциюВ2проведем проекцию прямойm2параллельно прямойk2,
для нахождения недостающих проекций
прямой необходимо построить проекцию
точки В1,как точки лежащей на проекции прямойn1и через неё
провести проекцию прямойm1параллельно проекцииk1.
Таким образом точки Впринадлежат
плоскости заданной пересекающимися
прямымиnиk, а прямаяmпроходит через эту точку и параллельна
прямойk, значит
согласно аксиоме прямая принадлежит
этой плоскости.
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок 5.15. Прямая имеет с плоскостью |
|
Главные |
Среди прямых линий, принадлежащих
плоскости, особое место занимают прямые,
занимающие частное положение в
пространстве:
1. Горизонтали
h– прямые, лежащие
в данной плоскости и параллельные
горизонтальной плоскости проекций(hÎСВА,
h//P1,
h2//Ох,h3//Оy)(рис.5.16).
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок |
2. Фронталиf– прямые, расположенные в плоскости и
параллельные фронтальной плоскости
проекций(fÎСВА,
f//P2,
f1//Ох,
f3//Оz)(рис.5.17).
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок |
3. Профильные прямыер– прямые, которые находятся в данной
плоскости и параллельны профильной
плоскости проекций(рÎСВА,
р//P3,
р1^Ох,
р2^Ох)
(рис.5.18).
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок |
Следует заметить, что следы плоскости
можно отнести тоже к главным линиям.
Горизонтальный след – это горизонталь
плоскости, фронтальный – фронталь и
профильный – профильная линия плоскости.
4. Линия наибольшего
скатаи её горизонтальная
проекция образуют линейный уголj, которым измеряется двугранный угол,
составленный данной плоскостью и
горизонтальной плоскостью проекций
(рис.5.19).
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок 5.19. |
Очевидно, что если прямая не имеет двух
общих точек с плоскостью, то она или
параллельна плоскости, или пересекает
ее.
|
Прямая |
При решении вопроса о параллельности
прямой линии и плоскости необходимо
опираться на известное положение
стереометрии: прямая
параллельна плоскости, если она
параллельна одной из прямых, лежащих в
этой плоскостии
не принадлежит этой плоскости.
Задача.Дано: проекции плоскости
общего положенияABCи прямой общего положенияа.
Требуется оценить их взаимное положение
(рис.5.20).
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок 5.20. Прямая |
Для этого через прямую апроведем
вспомогательную секущую плоскостьg– в данном случае горизонтально
проецирующая плоскость. Найдем линию
пересечения плоскостей gиАВС– прямуюп(DF). Проекция прямойпна
горизонтальную плоскость проекций
совпадает с проекциейа1и со следом плоскостиg.
Проекция прямойп2параллельнаа2, п3параллельнаа3, следовательно,
прямаяапараллельна плоскостиAВС.
|
Прямая |
Нахождение точки пересечения прямой
линии и плоскости – основная задача
начертательной геометрии.
Задача. Дано: плоскостьAВС
и прямаяа.
Требуется найти точку пересечения
прямой с плоскостью и определить
видимость прямой по отношению к плоскости.
Для решения задачи:
-
Через горизонтальную проекцию прямой
а1проведем вспомогательную
горизонтально проецирующую плоскостьg(таким образом
а g Î). -
Горизонтальный след плоскости g1пересекает проекцию плоскостиA1В1С1в точкахD1 иF1,
которые определяют положение
горизонтальной проекциип1–
линии пересечения плоскостейgиAВС. Для нахождения фронтальной
и профильной проекциипспроецируем точкиDиFна фронтальную и профильную плоскости
проекций. -
На фронтальной и профильной проекциях
линия пересечения плоскостей ппересекает проекцииав точкеК, которая и является проекцией
точки пересечения прямойас
плоскостью AВС, по линии
связи находим горизонтальную проекциюК1. -
Методом конкурирующих точек определяем
видимость прямой апо отношению к
плоскостиAВС.
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок 5.21. Нахождение точки пересечения |
Таким образом алгоритм решения задачи
состоит из следующей последовательности
действий (рис.5.21):
1. Построение вспомогательной секущей
плоскости g (горизонтально – проецирующая плоскость
), которую проводят через прямуюа
(а)gÎ;
2. Построение линии пересечения
вспомогательной плоскости gи заданной плоскостиa
(п)gÇa=;
3. Определение искомой точки К,
как точки пересечения двух прямых,
заданной –аи полученной в
результате пересечения плоскостей –п (К=а
Ç п).
В качестве вспомогательной плоскостиgрекомендуется
брать одну из проецирующих плоскостей.
4. Определение видимости прямой а
относительно плоскостиa.
|
Прямая |
Докажем следующую теорему о перпендикуляре
к плоскости: Если прямая
перпендикулярна плоскости, то
горизонтальная проекция этой прямой
перпендикулярна горизонтальной проекции
горизонтали плоскости, а фронтальная
проекция – фронтальной проекции фронтали
плоскости.
Пусть прямая n, перпендикулярная
плоскости,пересекает плоскостьBCDв точкеN, тогда по
условиюn перпендикулярна
любой прямой плоскости. Проведем в
плоскостиBCD горизонталь
h, а на основании теоремы о проецировании
прямого угла можно утверждать, что на
горизонтальную плоскость проекций они
проецируются под прямым углом, т.е.n1
h1.
Аналогично для фронтали –f
n
f2
n2.
Справедлива и обратная теорема: Если
проекции прямой перпендикулярны
одноименным проекциям соответствующих
главных линий плоскости (горизонтали
и фронтали), то такая прямая перпендикулярна
плоскости.
Доказательство следует из теоремы о
проецировании прямого угла.
Исходя из рассмотренных теорем, можно
решить задачу о построении перпендикуляра
к плоскости из точки А(рис.5.22).
Задача. Дано: плоскостьВСD
и точкаА.
Требуется построить прямую линиюnпроходящую через точкуАи перпендикулярную плоскостиВСD.
В плоскости ВСDпостроим
фронтальfи горизонтальh. В
горизонтальной плоскости проекций
проведем через точкуА1прямуюn1перпендикулярно
горизонтальной проекции горизонталиh1, а на фронтальной плоскости
проекций через точкуА2прямуюn2перпендикулярно
фронтальной проекции фронталиf2,
согласно выше сказанному полученная
прямаяnбудет перпендикулярна
плоскостиВСD.
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок 5.22. Построение прямой, |
|
Взаимное |
Возможны два варианта взаимного
расположения точки и плоскости: либо
точка принадлежит плоскости, либо нет.
Если точка принадлежит плоскости то из
трех проекций, определяющих положение
точки в пространстве, произвольно задать
можно только одну.
Рассмотрим пример (рис.5.23): Построение
проекции точки Апринадлежащей
плоскости общего положения заданной
двумя параллельными прямымиa(a//b).
Задача. Дано: плоскость(а,в)
и проекция точкиА2.
Требуется построить проекциюА1если известно, что точкаАлежит
в плоскостив,а.
Через точку А2
проведем проекцию прямойm2,
пересекающую проекции прямыхa2
иb2в точкахС2иВ2(С,aÎ
BaÎ
Þ maÎ).Построив проекции точекС1иВ1, определяющие
положениеm1,
находим горизонтальную проекцию точкиА(А1Î
m1,
maÎ
Þ АaÎ).
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок 5.23. Точка,принадлежащая плоскости |
Через точку А2
проведем проекцию прямойm2,
пересекающую проекции прямыхa2
иb2в точкахС2иВ2(СÎ,aBÞaÎmaÎ).Построив проекции точекС1иВ1, определяющие
положениеm1,
находим горизонтальную проекцию точкиА(А1Î
m1,
m ÞaÎ
АaÎ).
Лекция
№5_5
|
|
Возможны два варианта взаимного
расположения точки и плоскости: либо
точка принадлежит плоскости, либо нет.
Если точка принадлежит плоскости то из
трех проекций, определяющих положение
точки в пространстве, произвольно задать
можно только одну.
Рассмотрим пример (рис.5.23): Построение
проекции точки Апринадлежащей
плоскости общего положения заданной
двумя параллельными прямымиa(a//b).
Задача. Дано: плоскость(а,в)
и проекция точкиА2.
Требуется построить проекциюА1если известно, что точкаАлежит
в плоскостив,а.
Через точку А2
проведем проекцию прямойm2,
пересекающую проекции прямыхa2
иb2в точкахС2иВ2(С,aÎ
BaÎ
Þ maÎ).Построив проекции точекС1иВ1, определяющие
положениеm1,
находим горизонтальную проекцию точкиА(А1Î
m1,
maÎ
Þ АaÎ).
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок 5.23. Точка,принадлежащая плоскости |
Через точку А2
проведем проекцию прямойm2,
пересекающую проекции прямыхa2
иb2в точкахС2иВ2(СÎ,aBÞaÎmaÎ).Построив проекции точекС1иВ1, определяющие
положениеm1,
находим горизонтальную проекцию точкиА(А1Î
m1,
m ÞaÎ
АaÎ).
|
Взаимное |
Две плоскости в пространстве могут быть
либо взаимно параллельны, в частном
случае совпадая друг с другом, либо
пересекаться. Взаимно перпендикулярные
плоскости представляют собой частный
случай пересекающихся плоскостей.
1.Параллельные плоскости.
Плоскости параллельны, если две
пересекающиеся прямые одной плоскости
соответственно параллельны двум
пересекающимся прямым другой плоскости.
Это определение хорошо иллюстрируется
задачей, через точку Впровести
плоскость параллельную плоскости,
заданной двумя пересекающимися прямыми
ab(рис.5.24).
Задача.Дано: плоскость общего
положения, заданную двумя пересекающимися
прямымиabи точкаВ.
Требуется через точку Впровести
плоскость, параллельную плоскостиab
и задать её двумя пересекающимися
прямымиc иd.
Согласно определения если две
пересекающиеся прямые одной плоскости
соответственно параллельны двум
пересекающимся прямым другой плоскости
то эти плоскости параллельны между
собой.
Для того чтобы провести на эпюре
параллельные прямые необходимо
воспользоваться свойством параллельного
проецирования – проекции параллельных
прямых – параллельны между собой
d//a,с//b
Þ
d1//a1,с1//b1;d2//a2,с2//b2;d3//a3,с3//b3.
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок 5.24. Параллельные плоскости |
2.Пересекающиеся
плоскости, частный случай –
взаимно перпендикулярные плоскости.
Линия пересечения двух плоскостей
является прямая, для построения которой
достаточно определить две её точки,
общие обеим плоскостям, либо одну точку
и направление линии пересечения
плоскостей.
Рассмотрим построение линии пересечения
двух плоскостей, когда одна из них
проецирующая (рис.5.25).
Задача. Дано: плоскость общего
положения задана треугольникомАВС,
а вторая плоскость – горизонтально
проецирующаяa.
Требуется построить линию пересечения
плоскостей.
Решение задачи заключается в нахождении
двух точек общих для данных плоскостей,
через которые можно провести прямую
линию. Плоскость, заданная треугольником
АВСможно представить, как
прямые линии (АВ), (АС),
(ВС). Точка пересечения прямой
(АВ) с плоскостьюa– точкаD, прямой (AС) –F.
Отрезок[DF]определяет линию пересечения плоскостей.
Так как–
горизонтально проецирующая плоскость,
то проекцияD1F1совпадает со следом плоскостиП1
таким образом остается только построить
недостающие проекцииDFнаП2иП3.
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок 6.25. Пересечение плоскости |
Перейдем к общему случаю. Пусть в
пространстве заданы две плоскости
общего положения a(n,m)иb(ABC)
(рис.5.26).
|
|
|
||
|
а) модель |
б) эпюр |
||
|
Рисунок 5.26. Пересечение плоскостей |
Рассмотрим последовательность построения
линии пересечения плоскостей a(m//n)иb(АВС).
По аналогии с предыдущей задачей для
нахождения линии пересечения данных
плоскостей проведем вспомогательные
секущие плоскостиgиd. Найдем линии
пересечения этих плоскостей с
рассматриваемыми плоскостями. Плоскостьgпересекает
плоскостьaпо
прямой (12), а плоскостьb– по прямой (34). ТочкаК–
точка пересечения этих прямых одновременно
принадлежит трем плоскостямa,
bиg,
являясь таким образом точкой принадлежащей
линии пересечения плоскостейaиb. Плоскостьdпересекает плоскостиaиbпо прямым (56)
и (7C) соответственно, точка их
пересеченияМрасположена
одновременно в трех плоскостяхa,
b, dи принадлежит прямой линии пересечения
плоскостейaиb.
Таким образом найдены две точки
принадлежащие линии пересечения
плоскостейaиb– прямая (КМ).
Некоторого упрощения при построении
линии пересечения плоскостей можно
достичь, если вспомогательные секущие
плоскости проводить через прямые,
задающие плоскость.
Взаимно перпендикулярные
плоскости. Из стереометрии
известно, что две плоскости взаимно
перпендикулярны, если одна из них
проходит через перпендикуляр к другой.
Через точкуАможно провести
множество плоскостей перпендикулярных
данной плоскостиa(f,h).
Эти плоскости образуют в пространстве
пучок плоскостей, осью которого является
перпендикуляр опущенный из точкиАна плоскостьa. Для того чтобы из точкиАпровести плоскость перпендикулярную
плоскости заданной двумя пересекающимися
прямымиhf необходимо из точкиАпровести прямую n перпендикулярную
плоскостиhf(горизонтальная
проекция nперпендикулярна
горизонтальной проекции горизонталиh, фронтальная проекцияnперпендикулярна фронтальной проекции
фронталиf). Любая плоскость
проходящая через прямуюnбудет
перпендикулярна плоскостиhf,
поэтому для задания плоскости через
точки Апроводим произвольную
прямуюm. Плоскость заданная
двумя пересекающимися прямымиmnбудет перпендикулярна плоскостиhf
(рис.5.27).
|
|
|
|
|
а) модель |
б) эпюр |
|
|
Рисунок 5.27. Взаимно |
Лекция
№6-1
3.1. Способы задания плоскости на ортогональных чертежах
Положение плоскости в пространстве определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, взятой вне прямой;
- двумя пересекающимися прямыми;
- двумя параллельными прямыми;
- плоской фигурой.
В соответствии с этим на эпюре плоскость может быть задана:
- проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
- проекциями точки и прямой (Рисунок 3.1,б);
- проекциями двух пересекающихся прямых (Рисунок 3.1,в);
- проекциями двух параллельных прямых (Рисунок 3.1,г);
- плоской фигурой (Рисунок 3.1,д);
- следами плоскости;
- линией наибольшего ската плоскости.
Рисунок 3.1 – Способы задания плоскостей
Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.
Плоскость общего положения может иметь три следа: горизонтальный – απ1, фронтальный – απ2 и профильный – απ3, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π1, фронтальной π2 и профильной π3 (Рисунок 3.2).
Рисунок 3.2 – Следы плоскости общего положения
3.2. Плоскости частного положения
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости: все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).
Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).
Рисунок 3.4 – Эпюры плоскостей частного положения
3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).
Рисунок 3.5 – Принадлежность точки плоскости
α = m // n D ∈ n ⇒ D ∈ α
Рисунок 3.6 – Принадлежность прямой плоскости
left.begin{array}{l}alpha=mparallel n,\Dinalpha\Cinalpha\end{array}right} Longrightarrow CDinalpha
Упражнение
Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С.
Рисунок 3.7 – Решение задачи
Решение:
- ABCD – плоский четырехугольник, задающий плоскость.
- Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
- Согласно признаку пересекающихся прямых, построим фронтальную проекцию точки пересечения этих прямых — K: A2C2 ∩ B2D2=K2.
- Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD: на проекции диагонали B1D1 строим К1.
- Через А1К1 проводим проекцию диагонали А1С1.
- Точку С1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А1К1.
3.4. Главные линии плоскости
В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).
Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π1) (Рисунок 3.8, а; 3.9).
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π2) (Рисунок 3.8, б; 3.10).
Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π3) (Рисунок 3.8, в; 3.11).
Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником
Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником
Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником
Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами
Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами
Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами
3.5. Взаимное положение прямой и плоскости
Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.
3.5.1. Параллельность прямой плоскости
Признак параллельности прямой плоскости: прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).
alpha=mcap n\left.begin{array}{l}a_2parallel m_2\a_1parallel m_1\end{array}right} Rightarrow aparallelalpha
Рисунок 3.12 – Параллельность прямой плоскости
3.5.2. Пересечение прямой с плоскостью
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:
- Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
- Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
- Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.
Рисунок 3.13 – Построение точки встречи прямой с плоскостью
Упражнение
Заданы: прямая АВ общего положения, плоскость σ⊥π1. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.
Решение:
-
- Точка К должна принадлежать прямой АВ ⇒ К1∈А1В и заданной плоскости σ ⇒ К1∈σ, следовательно, К1 находится в точке пересечения проекций А1В1 и σ1;
- Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ1 (горизонтальный след плоскости);
- Фронтальную проекцию точки К находим посредством линии проекционной связи: К2∈А2В2.
Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения
Упражнение
Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).
Требуется построить точку пересечения прямой EF с плоскостью σ.
Рисунок 3.15 – Пересечение прямой с плоскостью
Решение:
- Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
- Если α⊥π1, то на плоскость проекций π1 плоскость α проецируется в прямую (горизонтальный след плоскости απ1 или α1), совпадающую с E1F1;
- Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено ниже);
- Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K.
Алгоритм решения задачи (Рисунок 3.15, б): Через EF проведем вспомогательную плоскость α:
- left.begin{array}{l}alpha perp pi_1\alphain EF\end{array}right} Longrightarrow alpha_1in E_1F_1
- alphacapsigma=(1-2)left.begin{array}{l}|alpha_1cap A_1C_1=1_1longrightarrow 1_2\|alpha_1cap A_1B_1=2_1longrightarrow 2_2\end{array}right.
- (1_2-2_2)cap E_2F_2=K_2\left.begin{array}{l}Kin EF\Kin (1-2)Rightarrow Kinsigma\end{array}right}Longrightarrow K=EFcap (sigma =triangle ABC)
3.6. Определение видимости методом конкурирующих точек
При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π1 или π2.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π2 (рис. 3.15)
Выберем точки, конкурирующие на π2 – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π2.
Направление взгляда на π2 показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π2, видно, что точка 41 располагается ближе к наблюдателю, чем 31.
41∈E1F1 ⇒ 4∈EF ⇒ на π2 будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π1.
Для определения видимости выберем точки, конкурирующие на π1 – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π1.
Направление взгляда на π1 показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π1, видно, что точка 22 располагается ближе к наблюдателю, чем 52.
22∈А2В2 ⇒ 2∈АВ ⇒ на π1 будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.
3.7. Перпендикулярность прямой плоскости
Признак перпендикулярности прямой плоскости: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.
Рисунок 3.16 – Задание прямой, перпендикулярной плоскости
Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)
Теорема доказывается через теорему о проецировании прямого угла в частном случае.
Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).
Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.
- Построим горизонталь и фронталь в плоскости σ=ΔАВС : σ=ΔАВС : A-1∈σ; A-1//π1; С-2∈σ; С-2//π2.
- Восстановим из точки K перпендикуляр к заданной плоскости: p1⊥h1 и p2⊥f2, или p1⊥απ1 и p2⊥απ2.
3.8. Взаимное положение двух плоскостей
3.8.1. Параллельность плоскостей
Две плоскости могут быть параллельными и пересекающимися между собой.
Признак параллельности двух плоскостей: две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Упражнение
Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).
Через точку F провести плоскость β, параллельную плоскости α.
Рисунок 3.17 – Построение плоскости, параллельной заданной
Решение: В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.
- Через точку F проводим прямую m, параллельную, например, АВ.
- Через точку F, или же через любую точку, принадлежащую m, проводим прямую n, параллельную, например, ВС, причём m∩n=F.
- β = m∩n и β//α по определению.
3.8.2. Пересечение плоскостей
Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.
Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.
Упражнение
Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей.
Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами
Порядок построения линии пересечения плоскостей:
- Найти точку пересечения горизонтальных следов — это точка М (её проекции М1 и М2, при этом М1=М, т.к. М – точка частного положения, принадлежащая плоскости π1).
- Найти точку пересечения фронтальных следов — это точка N (её проекции N1 и N2, при этом N2=N, т.к. N – точка частного положения, принадлежащая плоскости π2).
- Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М1N1 и М2N2.
МN – линия пересечения плоскостей.
Упражнение
Задана плоскость σ = ΔАВС, плоскость α – горизонтально- проецирующая (α⊥π1) ⇒α1 – горизонтальный след плоскости (Рисунок 3.19). Построить линию пересечения этих плоскостей.
Решение:
Так как плоскость α пересекает стороны АВ и АС треугольника АВС, то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.
Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L, то есть K1 и L1 , на пересечении горизонтального следа (α1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС: А1В1 и A1C1. После чего посредством линий проекционной связи находим фронтальные проекции этих точек K2 и L2 на фронтальных проекциях прямых АВ и АС. Соединим одноимённые проекции: K1 и L1; K2 и L2. Линия пересечения заданных плоскостей построена.
Алгоритм решения задачи:
left.begin{array}{l}ABcapsigma=K\ACcapsigma=L\end{array}right} left.begin{array}{l}Rightarrow A_1B_1capsigma_1=K_1 rightarrow K_2\Rightarrow A_1C_1cap sigma_1=L_1 rightarrow L_2\end{array}right.
KL – линия пересечения ΔАВС и σ (α∩σ = KL).
Рисунок 3.19 – Пересечение плоскостей общего и частного положения
Упражнение
Заданы плоскости α = m//n и плоскость σ = ΔАВС (Рисунок 3.20). Построить линию пересечения заданных плоскостей. Решение:
- Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
- В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π2; τ⊥π2.
- Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:
— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7); — результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).
- Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях σ и β, то есть на прямой пересечения этих плоскостей;
- Аналогично находим точку N, общую для плоскостей σ и β.
- Соединив точки M и N, построим прямую пересечения плоскостей σ и β.
Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)
Алгоритм решения задачи:
left.begin{array}{l}alphacapsigma=(4-5)\betacapsigma=(3-2)\end{array}right}\left.begin{array}{l}alphacaptau=(6-7)\betacaptau=(1-8)\end{array}right}left.begin{array}{l}(4_1-5_1)cap(3_1-2_1)=M_1rightarrow M_2\(6_1-7_1)cap(1_1-8_1)=N_1rightarrow N_2\end{array}right}rightarrow\left.begin{array}{l}M_1N_1\M_2N_2\end{array}right}Rightarrowalphacapbeta=MN
Упражнение
Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).
Рисунок 3.21 Решение задачи на пересечение плоскостей
Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π2, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π2 (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.
3.8.3. Взаимно перпендикулярные плоскости
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Упражнение
Задана плоскость σ⊥π2 и прямая общего положения – DE (Рисунок 3.22)
Требуется построить через DE плоскость τ⊥σ.
Решение.
Проведём перпендикуляр CD к плоскости σ – C2D2⊥σ2 (на основании теоремы о проецировании прямого угла).
Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости
По теореме о проецировании прямого угла C1D1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.
Упражнение
Задана плоскость α = ΔАВС и точка K вне плоскости α. Требуется построить плоскость β⊥α, проходящую через точку K. Алгоритм решения (Рисунок 3.23):
- Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС;
- Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости: если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b2⊥f2; b1⊥h1;
- Задаём плоскость β любым способом, например, β = a∩b, таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.
Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС
3.9. Задачи для самостоятельного решения
1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.
Постройте фронтальную проекцию точки К.
Рисунок 3.24
2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).
Рисунок 3.25
3. Постройте проекции квадрата, принадлежащего плоскости α⊥π2, если его диагональ MN //π2 (Рисунок 3.26).
Рисунок 3.26
4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).
Рисунок 3.27
5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.
Рисунок 3.28
6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π1.
7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π1.
|
Разделы Уроки по теме Рекомендуем |

Точка пересечения прямой и плоскости Автор: Moroz Дата: 2010-09-30
Рассмотрим пошаговую инструкцию построения точки пересечения прямой общего положения с плоскостью общего положения.Отметим, что построение точки пересечения прямой и плоскости – это одна из основ решения задач по предмету начертательная геометрия, не освоив которую дальнейшее понимание предмета будет достаточно трудным. Порядок построения точки пересечения прямой и плоскости1. Заключим прямую а во вспомогательную фронтально-проецирующую плоскость (плоскость перпендикулярную фронтальной плоскости проекции). На фронтальной проекции она сольется с прямой а. Очевидно, что линия m пересечения этой плоскости с плоскостью треугольника АВС на фронтальной проекции так же будет сливаться с прямой а (а=m). 2. Определим фронтальные проекции двух точек этой линии m: точки 1 и 2. 3. Найдем их горизонтальные проекции. 4. Соединим горизонтальные проекции точек 1 и 2 – получим горизонтальную проекцию прямой m (которая является линией пересечения вспомогательной плоскости с плоскостью треугольника АВС, и соответственно принадлежит обеим плоскостям). Так как прямая а принадлежит вспомогательной плоскости, и прямая m принадлежит ей же, то точка пересечения этих прямых К и есть точка пересечения прямой а с плоскостью треугольника АВС. 5. С помощью линии связи найдем фронтальную проекцию точки пересечения К. 6. Осталось только определить видимость прямой а. Это можно сделать с помощью метода конкурирующих точек. Обратите внимание, что мы начали поиск точки пересечения прямой с плоскостью с того, что заключили прямую а во вспомогательную фронтально-проецирующую плоскость. Точно таким же образом можно было заключить прямую а в горизонтально-проецирующую плоскость, и тогда бы построения начались как бы “снизу вверх”, но смысл остался бы точно таким же, как и конечное решение – точка пересечения прямой с плоскостью. Внимание! Для этой темы есть видеоурок. Просмотров: 231459 Вы можете сказать “спасибо!” автору статьи: пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект “White Bird. Чертежи Студентам” или или запишите наш телефон и расскажите о нас своим друзьям – кто-то наверняка ищет способ выполнить чертежи или создайте у себя на страничке или в блоге заметку про наши уроки – и кто-то еще сможет освоить черчение.
А вот это – не реклама. Это напоминание, что каждый из нас может сделать. Если хотите – это просьба. Мы действительно им нужны: Комментарии: Очень легко и понятно вы описали как найти точку пересечения прямой и плоскости, мегареспект! Сделайте нормальные чертежи!!! Без анимации пошаговые. А вот нечего торопиться. Надо покушать как следует, сесть и всмотреться в гифку. Тогда и познаешь дзен. 🙂
Помогите пожалуста!!!!!!у меня плоскость перпендикулярна фронтальной плоскости проекции и задана следами, а прямая горизонтальна горизонтальной плоскости проекций Это простооо кул,все понятно,мегареспект вам!! 4. Соединим горизонтальные проекции точек 1 и 2 – получим горизонтальную проекцию прямой m (которая является точкой пересечения вспомогательной плоскости с плоскостью треугольника АВС… Я всё равно ничего не понял. Хоть на первый взгляд это более толковое объяснение решения, чем пишут в книгах – там ваще мрак. Высший класс! Ключевое предложение для понимания сути: “Заключим прямую а во вспомогательную фронтально-проецирующую плоскость …” Эмм… Это сарказм? 🙂 Спасибо огромное.Всё доходчиво и ясно! Как быть если прямая на П2 перпендикулярна Ох, а на П1 в точку проэцируется? Добавьте свой комментарий: |
Последние уроки Как построить диметрию детали? Построение наклонного сечения, заданного на виде слева Определение линии пересечения двух плоскостей. Метод вспомогательных секущих плоскостей. Наша почта: zakaz@trivida.ru Наша страница в ВК: Случайный комментарий Валерий: Антон, у вас офис только в Москве? или в других городах тоже есть? Валерий, в настоящее время мы не имеем региональных представительств. Хорошо это или нет – не знаю. Сейчас для удаленных пользователей доступны только услуги по выполнению чертежей в электронном виде |



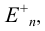
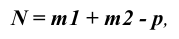
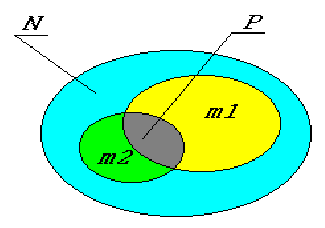
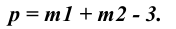
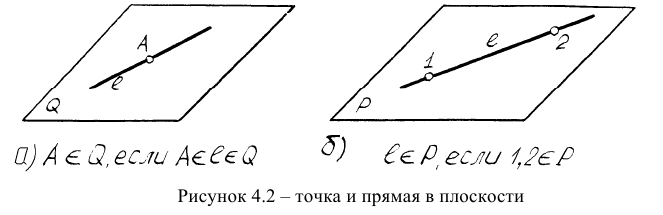
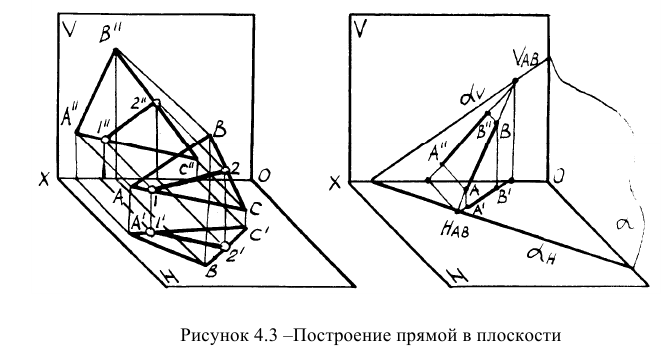
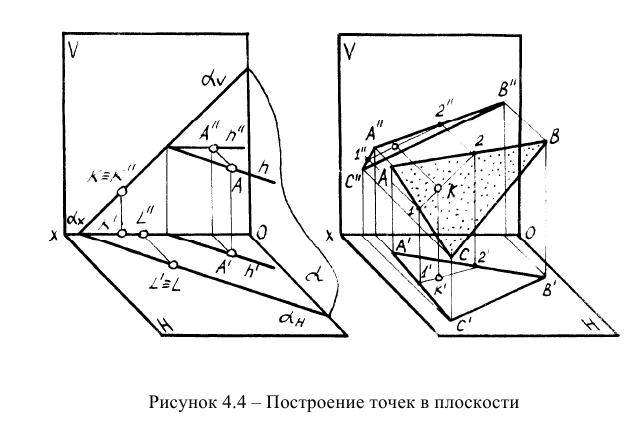
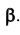
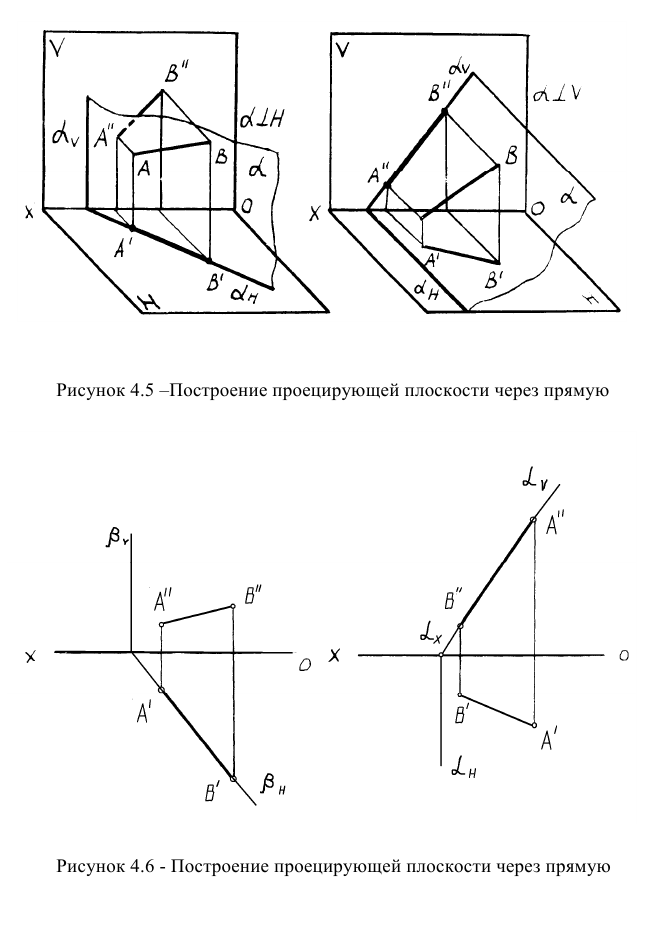
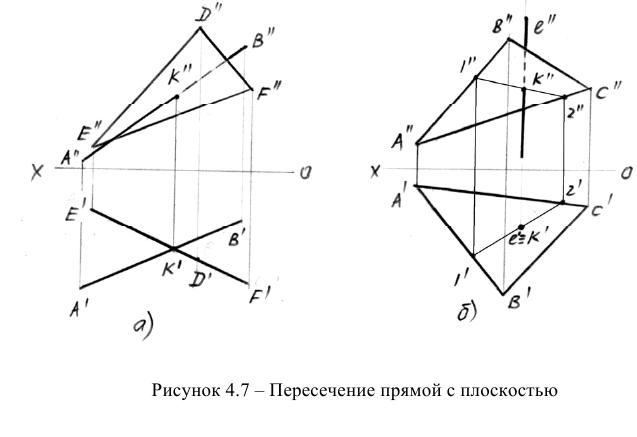
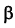 (чаще всего проецирующую плоскость, заданную следами);
(чаще всего проецирующую плоскость, заданную следами);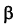 (линия 1-2);
(линия 1-2);