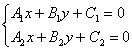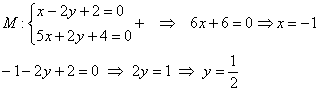Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне
просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так
и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом
их описывают.
Запомните!
Точка — элементарная фигура, не
имеющая частей.
Прямая состоит из множества
точек и простирается бесконечно
в обе стороны.
На рисунке изображена прямая a и точки D, F, G и
H. Точки F и G
лежат на прямой a.
Точки D и H
не
лежат на прямой a.
В тексте точку обозначают символом «(·)».
Принадлежность и непринадлежность точки
прямой обозначают символами «∈» и «∉». Знак принадлежности можно запомнить как
зеркальное отображение буквы «Э» или как знак евро «€» .
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
- (·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a);
- (·)G ∈ a — точка G принадлежит прямой a;
- (·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a);
- (·)H ∉ a — точка H не принадлежит прямой a.
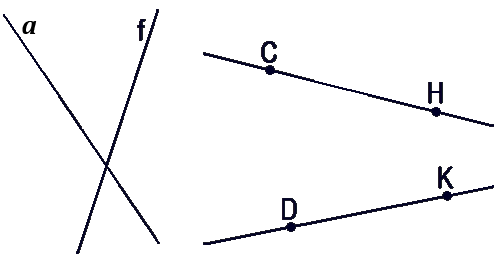
Как обозначить прямую
Прямую обычно обозначают одной
маленькой латинской буквой.
Прямую, на которой отмечены
две точки, иногда обозначают
по названиям этих точек большими латинскими точками.
- На рисунке изображены:
- Прямая a
- Прямая f
- Прямая CH
- Прямая DK
Точки D, E и F — лежат на одной прямой, поэтому:
прямая DE,
прямая EF и
прямая DF —
это три разных имени одной и той же прямой.
Разбор примера
Проведите прямую, обозначьте её буквой a и
отметьте точки A и B, лежащие на этой прямой, и
точки P, Q и R, не лежащие на ней. Опишите
взаимное расположение точек A, B, P, Q, R и
прямой a, используя символы ∈ и ∉.
Решение задачи
Проведём прямую.
Обозначим её буквой a.
Отметим точки (·)A и (·)B, лежащие на прямой a.
Отметим точки (·)P, (·)Q и (·)R, не лежащие на прямой a.
Опишем взаимное расположение точек и прямой.
- (·)A ∈ a
- (·)B ∈ a
- (·)P ∉ a
- (·)Q ∉ a
- (·)R ∉ a
Задача решена.
Как обозначается пересечение прямых
На рисунке прямые a и b
не пересекаются.
Прямые b и
c пересекаются.
Хотя на чертеже не видно, но прямые a и
c тоже пересекаются (это становится ясно, если мысленно
продолжить вниз прямые a и с).
В тексте пересечение прямых обозначают
символом ∩. Информацию на рисунке выше можно записать следующим образом:
- b ∩ c — прямые b и с пересекаются;
- a ∩ c — прямые a и с пересекаются.
Прямые e и g имеют общую точку M.
Другими словами, прямые пересекаются в точке M. Геометрическими обозначениями
пересечение прямых в точке записывается так:
e ∩ g = (·)M
Прямые e и f не имеют общей точки — т.е. они не
пересекаются.
Взаимное расположение прямой и точек
Запомните!
Через любые две точки можно
провести прямую, и притом
только одну.
Через одну точку (·)A можно провести
сколько угодно прямых.
Через две точки
(·)A и (·)B можно провести
только одну прямую.
Сколько общих точек имеют две прямые
Запомните!
Две прямые либо имеют только
одну общую точку, либо не имеют
общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e
нет общих точек, т.к. эти
прямые не пересекаются.
Второй случай расположения прямых
Возможен вариант, что прямые f и e
пересекаются и, значит, имеют одну общую точку (·)M.
Третий случай расположения прямых
Предположим, что прямые
f и e имеют две или больше общих точек.
Например, точки (·)A и (·)B.
Но мы знаем, что через две
точки можно провести только одну прямую. Значит,
прямые f и e совпадают и наше предположение, что
у двух прямых может быть две или более общих точек неверно.
Вывод: две прямые либо имеют только
одну общую точку, либо не имеют
общих точек.
Разбор примера
Проведите три прямые так, чтобы каждые две из
них пересекались. Обозначьте все точки
пересечения этих прямых. Сколько получилось
точек? Рассмотрите все возможные случаи.
Решение задачи
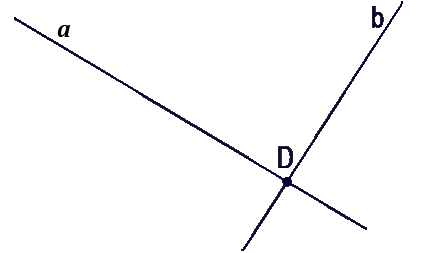
Проведём две прямые a и b так, чтобы эти две
прямые пересекались, и обозначим точку
пересечения.
Как мы видим, точка пересечения только одна. Мы
можем провести третью прямую так, чтобы она
тоже проходила через эту точку пересечения.
Теперь прямая a пересекается
с прямой b,
прямая b пересекается с прямой c и
прямая c пересекается с прямой a.
В этом случае
у нас только одна точка
пересечения всех прямых — точка (·)D.
Но возможен и другой вариант. Мы можем провести третью прямую c так,
чтобы она не проходила через точку (·)D. Тогда
получится
три точки пересечения — (·)D, (·)E и (·)F.
Прямая a пересекается
с прямой b
в точке (·)D,
прямая b пересекается с прямой c в точке (·)F и
прямая c пересекается с прямой a
в точке (·)E. Условие задачи выполнено.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или
три.
Что такое отрезок
Запомните!
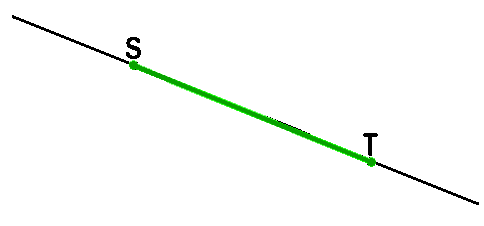
Отрезок —
часть прямой, ограниченная
двумя точками.
Две точки, ограничивающие отрезок, называются
концами отрезка. У отрезка на рисунке выше концы
называются S и
T.
Сам отрезок можно назвать ST
или TS. Когда изображают отрезок, оставшиеся от
прямой хвосты можно не рисовать.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
11 июля 2018 в 19:19
Тимофей Программист
Профиль
Благодарили: 0
Сообщений: 1
Тимофей Программист
Профиль
Благодарили: 0
Сообщений: 1
Диагональ AC параллелограмма ABCD является диаметром окружности, которая делит отрезки AD и CD в точках E и F соответственно. CF = 11. FD = 5. AE:ED = 1:4. Найти площадь данного параллелограмма.
0
Спасибо
Ответить
13 июля 2018 в 1:01
Ответ для Тимофей Программист
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
S = 80√15
0
Спасибо
Ответить
3 октября 2016 в 20:57
Ольга Смирнова
Профиль
Благодарили: 0
Сообщений: 1
Ольга Смирнова
Профиль
Благодарили: 0
Сообщений: 1
На плоскости проведены четыре прямые и отмечены точки, в которых эти прямые попарно пересекаются. Какое наибольшее число таких точек могло получиться?
0
Спасибо
Ответить
5 октября 2016 в 19:08
Ответ для Ольга Смирнова
Никита Фролов
Профиль
Благодарили: 0
Сообщений: 1
Никита Фролов
Профиль
Благодарили: 0
Сообщений: 1
наибольшее число точек пересечения-5
0
Спасибо
Ответить
7 октября 2016 в 19:14
Ответ для Ольга Смирнова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Максимум 6 точек.
Вообще, для N прямых наибольшее число точек пересечения равно .
Никита не прав.
0
Спасибо
Ответить
7 октября 2016 в 19:15
Ответ для Ольга Смирнова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Это не верно.
0
Спасибо
Ответить
6 июля 2016 в 18:28
Ирина Поджарова
Профиль
Благодарили: 0
Сообщений: 2
Ирина Поджарова
Профиль
Благодарили: 0
Сообщений: 2
В равнобедренном треугольнике высота равна 45 см, а основание относится к боковой стороне как 4:3. Найти радиус вписанного круга.
0
Спасибо
Ответить
7 июля 2016 в 8:45
Ответ для Ирина Поджарова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Для решения задачи воспользуемся формулой радиуса окружности вписанной в равнобедренный треугольник:
r= · ?
0
Спасибо
Ответить
7 июля 2016 в 8:53
Ответ для Ирина Поджарова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
, где a — сторона треугольника, b-основание.
Необходимо найти a и b.
Высота в равнобедренном треугольнике вычисляется по формуле:
h=?(a2 — ). из условия видно, что b=
0
Спасибо
Ответить
7 июля 2016 в 8:55
Ответ для Ирина Поджарова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
b=4a/3. Знаем, что h=45, можем вычислить длину основания. Зная длину основания можем вычислить длину стороны. Сзная длину стороны и основания можем вычислить радиус вписанной окружности. Дальше-дело техники. Удачи.
P.S. Прошу прощения, что много сообщений, какие то проблемы с браузером.
0
Спасибо
Ответить
9 июля 2016 в 7:28
Ответ для Ирина Поджарова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
(3x)2 = (2x)2 + 452
x2 = 405.
(45 ? r)2 = r2 + x2
r = 18.
0
Спасибо
Ответить
19 мая 2016 в 23:29
Иван Черновалов
Профиль
Благодарили: 0
Сообщений: 1
Иван Черновалов
Профиль
Благодарили: 0
Сообщений: 1
Провести касательные к элипсу
+
= 1 которые параллельны прямой 2x-y+17=0 (ответ 12x-13y+-169=0)
0
Спасибо
Ответить
7 июня 2016 в 2:23
Ответ для Иван Черновалов
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Касательные имеют вид 2x — y + c = o.
Параметр с находим из условия, что уравнение
+ = 1 имеет 1 корень.
0
Спасибо
Ответить
26 января 2016 в 19:47
Ян Кифа
Профиль
Благодарили: 0
Сообщений: 1
Ян Кифа
Профиль
Благодарили: 0
Сообщений: 1
незнайка начертил 3 прямые линии на каждой из них поставил 3 точки всего он поставил 6 точек начерти как он это зделал
0
Спасибо
Ответить
31 января 2016 в 18:36
Ответ для Ян Кифа
Roma Bobrov
Профиль
Благодарили: 0
Сообщений: 1
Roma Bobrov
Профиль
Благодарили: 0
Сообщений: 1
.—–.
.—–.
.—–.
0
Спасибо
Ответить
19 сентября 2016 в 10:53
Ответ для Ян Кифа
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Две линии просто пересекаются. третья линия пересекает две линии вертикально. Точки стоят на пересечениях и по одной на каждой линии.
0
Спасибо
Ответить
19 ноября 2015 в 18:19
Анна Вопилова
Профиль
Благодарили: 0
Сообщений: 1
Анна Вопилова
Профиль
Благодарили: 0
Сообщений: 1
При каком значении высоты прямоугольная трапеция с острым углом 45 и периметром P = 4(1 + ? 2) имеет наибольшую площадь?
0
Спасибо
Ответить
8 июня 2016 в 21:52
Ответ для Анна Вопилова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
2.
0
Спасибо
Ответить
22 августа 2015 в 15:21
Мария Кузнецова
Профиль
Благодарили: 0
Сообщений: 3
Мария Кузнецова
Профиль
Благодарили: 0
Сообщений: 3
Всем снова привет)
Еще не могу разобраться в такой задаче:
Длина одной стороны четырёхугольника составляет 3/11 его периметра, длина другой
— 4/11,
а сумма равна 28 см.
Найдите периметр четырёхугольника.
Это 1731 из виленкина 5 класс, если что!
0
Спасибо
Ответить
22 августа 2015 в 15:42
Ответ для Мария Кузнецова
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 27
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 27
Здравствуй, Мария.
Прежде чем приступить к решению задачи ВНИМАТЕЛЬНО прочитаем условие задачи и
подчеркнём в условии все важные данные.
В этой задаче важно заметить, что в условии говорится не
о прямоугольнике, а о четырёхугольнике.
Поэтому мы не можем пользоваться
формулой нахождения периметра прямоугольника:
P = 2(a + b)
Запишем условие задачи в краткой записи, где a,b — стороны четырёхугольника, P — периметр.
№ 1731
|
Дано: a = 3/11 · P P = ? |
Решение: Прежде всего вспомним, что если в условии записано «составляет от» чего-то, значит это |
Также находим b:
Подставим эти значения в выражение:
У нас получилось уравнение с одним неизвестным. Обе дроби с одинаковыми знаменателями,
поэтому сложить их для нас не составит труда. (Если вы не помните как правильно складывать дроби,
освежить свои знания можно в уроке: “Сложение дробей”.)
Чтобы найти «P» вспомним правило: «Чтобы найти неизвестный множитель надо произведение разделить на известный множитель.»
Разделим дроби по правилам деления дробей.
Ответ: периметр равен 44 см
Кратко оформить задачу можно следующим образом.
№ 1731
|
Дано: a = 3/11 · P P = ? |
Решение:
|
Ответ: P = 44 см
0
Спасибо
Ответить
13 июля 2015 в 14:25
Денис Кежватов
Профиль
Благодарили: 0
Сообщений: 1
Денис Кежватов
Профиль
Благодарили: 0
Сообщений: 1
Сколько равносторонних треугольников
умещается внутри окружности, если стороны треугольников равны радиусу окружности?
0
Спасибо
Ответить
31 августа 2016 в 10:15
Ответ для Денис Кежватов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Вспомним свойство равностороннего треугольника: углы при каждом из оснований равны между собой и равны 60°.
Окружность равна 360°. Значит 360°/60° = 6.
Ответ 6 равносторонних треугольников умещается внутри окружности, если стороны треугольников равны радиусу этой окружности.
Если нарисовать это на бумаге, становится гораздо понятнее и очевиднее.
0
Спасибо
Ответить
|
0 / 0 / 0 Регистрация: 04.10.2019 Сообщений: 38 |
|
|
1 |
|
Как найти точку пересечения трех прямых, проведенных через три заданные точки?08.10.2020, 16:26. Показов 1528. Ответов 3
Необходимо найти точку Е, угол наклона линии DE (какую то одну, их как я понимаю может быть множество) геометрическими построениями. Линия ВЕ должна быть проведена через точку В, линия FE через точку F, линия DE через точку D, при этом DE биссектриса ВЕ и FE. Миниатюры
0 |
|
8710 / 6313 / 3388 Регистрация: 14.01.2014 Сообщений: 14,486 |
|
|
08.10.2020, 18:00 |
2 |
|
РешениеПроведём окружность через точки B, D и F. Тогда большая дуга этой окружности (которая не содержит точки D) будет геометрическим местом точек Е, т.е. любая точка этой дуги является решением задачи.
0 |
|
8710 / 6313 / 3388 Регистрация: 14.01.2014 Сообщений: 14,486 |
|
|
08.10.2020, 18:28 |
3 |
|
Проверил Ваш рисунок один к одному, Ваша точка Е действительно лежит на указанной дуге окружности. Понятно, что в качестве этой точки можно взять даже концы В и F этой дуги. Миниатюры
1 |
|
0 / 0 / 0 Регистрация: 04.10.2019 Сообщений: 38 |
|
|
09.10.2020, 07:44 [ТС] |
4 |
|
А как это доказать? Обозначим точку пересечения линий BF и CD точкой О, тогда ВО = OF, DO общая, углы при точке O равны, следовательно треугольники BDO и FDO равны и равны их стороны BD и FD. Если предположить, что они лежат на окружности, тогда длины дуг BD и FD равны, так как равны эти хорды и следовательно равны и вписанные углы проходящие через эти точки? Центр окружности лежит на линии DC.
0 |
2.5.3. Как найти точку пересечения прямых?
Если прямые пересекаются в точке
, то её координаты являются решением системы линейных уравнений
Как найти точку пересечения прямых? Решить систему.
И вот вам, кстати, геометрический смысл системы двух линейных уравнений с двумя неизвестными – это две пересекающиеся (чаще
всего) прямые. И реже:
– если система несовместна (без решений), то прямые параллельны;
– если , то прямые
совпадают, то есть, фактически нам дано не два, а одно уравнение.
Задача 77
Найти точку пересечения прямых
Существуют два способа решения – графический и аналитический.
Графический способ состоит в том, чтобы просто начертить данные прямые и узнать точку пересечения непосредственно из чертежа:

.
Для проверки следует подставить её координаты в уравнение каждой прямой, они должны подойти и там,
и там. Графический способ, конечно, неплох, но существует и заметные минусы. Нет, дело не в том, что так решают семиклассники, дело в том, что на
правильный и ТОЧНЫЙ чертёж уйдёт время. Кроме того, некоторые прямые построить не так-то просто, да и сама точка пересечения может находиться
где-нибудь в тридесятом царстве за пределами тетрадного листа.
Поэтому точку пересечения целесообразнее искать аналитическим
методом. Решим систему, уравнения проще всего сложить
почленно:
Ответ:
Проверка тривиальна – координаты точки пересечения должны удовлетворять каждому уравнению системы. К слову, этой задачей мы
заодно рассмотрели графический способ решения системы двух линейных уравнений с двумя неизвестными.
Задача 78
Найти точку пересечения прямых , если известны координаты точек
Это задача для самостоятельного решения, которое удобно разбить на несколько этапов. Анализ условия подсказывает, что нужно:
1) составить уравнение прямой ;
2) составить уравнение прямой ;
3) выяснить взаимное расположение прямых ;
4) если прямые пересекаются, то найти точку пересечения.
Разработка алгоритма действий типична для геометрических задач, и я на этом буду неоднократно заострять внимание.
В первой части параграфа мы узнали, как построить прямую, параллельную данной, и сейчас
избушка на курьих ножках разворачивается на 90 градусов:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Переменные комплексные — см. Комплексные переменные Перемещение силы параллельное 365 Перемещения возможные — Принцип 377 —— звеньев механизма — Измерения 433 Переносная скорость 384 Переносное ускорение 384 Пересечение трех прямых — Условия 242 [c.580]
Пересечение трех прямых — Условия 242 [c.558]
Условие пересечения трех прямых. 4,х + Biy+ i = 0 Л.2Х + В / +С.2 = 0 и. 1.x – B y + s = 0. В одной точке [c.16]
Для графического проектирования вычерчиваем механизм крана в трех положениях. Точку О найдем как центр окружности, проведенной через точки А,, А2 и A3. Построение удобнее вести методом, несколько отличающимся от метода, описанного в учебнике геометрии А. П. Киселева. Для этого радиусом, близким к /о, делаем засечки из центров Ai, Л2 и А . Получается криволинейный треугольник. Нетрудно заметить, что центр О располагается со стороны основания этого треугольника. Зная это, следует так изменить радиус засечки, чтобы другой криволинейный треугольник расположился по другую сторону точки О. После этого точку О найдем в точке пересечения трех прямых, соединяющих сходственные вершины криволинейных треугольников. [c.291]
Пересечение трех прямых 1 — 242 Перестановки 1 — 79, 115 Периметры плоских фигур — Вычисление [c.451]
С проведением взаимно перпендикулярных прямых связано построение ортоцентра — точки пересечения трех высот треугольника и центра описанной окружности— точки пересечения перпендикуляров, восставленных из середин сторон треугольника. [c.49]
Характеристики алгебраических кривых. Одна из основных характеристик — порядок кривой — определяется графически количеством точек пересечения с прямой, если она плоская, или с плоскостью, если она пространственная. При этом надо иметь в виду, что в число точек входят как действительные, так и мнимые точки. Например, на рис. 84 приведена кривая третьего порядка т, которую прямая а пересекает в трех различных действительных точках, прямая Ь — в двух совпавших (касается здесь) и одной отличной от них точках, а прямая с — в одной действительной и в двух мнимых точках. [c.65]
Геометрический способ. Поскольку точка Mj находится в равновесии под действием трех сил, то силовой треугольник, построенный на этих силах, должен быть замкнутым (рис. 1, б). Построение силового треугольника следует начинать с заданной силы Р. Изобразив вектор Р, проводим че з ег начало и конец прямые, параллельные направлениям сил и Т . Точка пересечения этих прямых определит третью вершину силового треугольника. Ориентация всех векторов должна быть такова, чтобы силовой треугольник был замкнутым. Это дает возможность проверить правильность направления неизвестных реакций. [c.8]
В системе на рис. 1 отрезки 1 ,. . соединяют не лежащие на одной прямой точки А, В ш D базы 1 с тремя не лежащими на одной прямой точками а, Ъ, d тела 2 так, что в каждой из указанных точек базы и тела сходятся два отрезка. Положение тела 2 относительно базы 1 характеризуется совокупностью значений Zj,. . ., Zg, так как все они являются сторонами геометрически неизменяемых (при данных значениях Z ,. . ., фигур — треугольников Aad, АВа, Bab, BDb, Dbd, ADd. При этом положение точек А, В, D на базе и точек а, Ь, d на теле должно быть определено. Структуры Z-координат характеризуются способом соединения базы и тела отрезками Z ,. . ., Z и могут быть различными. Общие требования к структурам Z-координат необходимость наличия не менее шести отрезков, соединяющих базу с телом так, чтобы была обеспечена геометрическая неизменяемость структуры, причем на базе и теле должно быть не менее трех расположенных не на одной прямой точек. При этом недопустимо пересечение в одной точке более трех отрезков, параллельность трех отрезков п пересечение трех других в одной точке, расположение всех отрезков в двух плоскостях. [c.79]
Проведем характеристики из этой точки вниз до пересечения с прямой t = ti, получим точки a i,2 и х.2, . В уравнениях (3), записанных для этих характеристик, содержится шесть неизвестных параметров, которые можно определить с помощью интерполяции, используя полиномы Лагранжа. Эти полиномы записываем для параметров Рд, -Рп, г л и wn относительно любых трех фиксированных точек на прямой t — ti. Решаем полученную систему урав- [c.102]
Линия пересечения плоскостей является прямой, следовательно, она может быть определена двумя точками. С другой стороны, точка определяется пересечением трех плоскостей. [c.194]
При ответственной разметке применяется точный кернер (фиг. 72). Нижние концы ножек кернера запилены на клин с углом при вершине 55. Ребра ножек / и 2 лежат точно на одной прямой, а ребро ножки 3—перпендикулярно к ним. Рабочий конец кернера отшлифован на конус с углом при вершине 60 и ось его лежит в точке пересечения трех ребер перпендикулярно к плоскости, в которой эти ребра находятся. [c.109]
Задача сводится к определению геометрического места точек, относительно которых результирующий момент векторов VI и —равен нулю. Таким геометрическим местом будет являться прямая, проходящая через точку пересечения линии действия векторов VI и —Vh, направление которых совпадает с направлением равнодействующего вектора для векторов скорости и —Рассматривая точки 1 и 2, найдем другую прямую. Точка пересечения этих прямых и будет искомой точкой, так как относительно нее равны по величине и по направлению моменты скоростей всех трех заданных точек. [c.121]
В декартовой системе координат поверхности д1 = х=С , Я2 = У= С2, 7з = 2 = Сз суть плоскости, параллельные координатным плоскостям, проходящим через начало координат. Пересечения координатных плоскостей определяют координатные линии— прямые, параллельные осям Ох, Оу, Ог. Каждая точка пространства определяется пересечением трех координатных плоскостей или трех координатных линий (осей). [c.91]
Последнее положение объясняется тем, что точка в пространстве определяется пересечением трех плоскостей, которые пересекаются по трем прямым линиям, сходящимся в этой точке. [c.48]
Для построения вспомогательных лучевых сечений поверхности на ней следует построить каркас линий-окружности 1,…, IV. Затем определяются точки пересечения лучевых прямых с построенными линиями сечений поверхности. Для каждого отрезка кривых линий контура тени необходимо построить не менее трех точек тени. [c.151]
ОРТОЦЕНТР. Точка пересечения трех высот плоского треугольника. В остроугольном треугольнике эта точка внутри него, в тупоугольном — вне треугольника, а в прямоугольном — в вершине прямого угла. [c.75]
Плоскости эллипсов попарного пересечения цилиндров изо5ражаются в виде трех прямых, пересекаюпщхся в одной точке 0. [c.29]
Теорема Дезарга для плоскости. Если два треугольника АВС и А В С расположены в одной плоскости так, что прямые, соединяющие соответственные вершины этих треугольников, пересекаются в одной точке 8, то три точки пересечения трех пар соответственных сторон треугольников (Ад=ВС X В С, Вд=СА X С А , Сд=АВ X А В ) лежат на одной прямой (рис. 14). [c.26]
При построении предельных кривых по разрушению на основе общего уравнения (10) для частных случаев, приведенных на рис. 23, получается пучок прямых, имеющих общую точку пересечения D. В точке D пересекаются также прямая предельных напряжений образцов без концентратора и прямая, характеризующая цикл с R =—оо. Физическое значение имеют отрезки прямых предельных напряжений по разрушению только в диапазоне между точками С и R = RfKoT. Таким образом получено, что предельная кривая по разрушению деталей с концентратором состоит из трех прямых, определяемых уравнениями (10), (22) и (14). [c.54]
Чтобы оправдать это утвержденпе, заметим, что всякое состояние плоского движения (имеющего мгновенный центр на конечном расстоянии) мож но рассматривать, как вращение вокруг некоторой прямой, перпендикулярной к плоскости движения. Вследствие этого, когда два п.тоские движения происходит совместно (с мгновенными центрами на конечном [ асстоянии), то составленное движение также имеет характер вращения (III, рубр. 27), ось которого ленгит в плоскости осей составляющих вра и,епий. Поэтому пересечения трех осей о плоскостью движения, т. е. мгновенные центры трех вращений, расположены на одной прямой. [c.238]
ОлРЕДЕЯЕНИЕ ЦЕНТРА ТЯЖЕСТИ НЕКОТОРЫХ ФИГУР. У фигур, имеющих центр (точка пересечения трех несовпадающих диаметральных плоскостей, если речь идет об объеме, и двух диаметральных прямых, если речь идет о плоской фигуре), центр тяжести совпадает с центром фигуры (п. 13). [c.34]
Из (3.9) следует, что многообразием уровня всех газодинамических величин явля ются прямые линии в пространстве xi, Ж2, жз, I, Действительно, из (3.9) получаем, что такое многообразие определяется пересечением трех гиперплоскостей ( = onst — уравнение одной из них). При этом прямые линии уровня при условиях G 0, I 0, вообще говоря, не проходят через одну фиксированную точку пространства xi, Ж2, жз, t, т. е. течение не является коническим. Таким образом, построенное решение является неконической вихревой тройной волной с прямолинейными образующими. [c.175]
Из (4.24) следует, что многообразиями уровня всех газодинамических величин, когда щ = = onst, 0 = 0 = onst, т. е. и = onst, являются прямые линии в пространстве xi, хо, жз, t. Действительно, из (4.24) следует, что такое многообразие определяется пересечением трех гиперплоскостей в пространстве xi, Х2, жз, t. Так как функции Gk 0 и G 0, то эти прямые, вообще говоря, не проходят через одну фиксированную точку пространства, т. е. течение не является коническим. [c.188]
Решение. Реакция цепи направлена по ВС реак1щя в шарнире не известна ни по модулю, ни по направлению. Сложим графически при помощи силового и веревочного многоугольников данные в задаче параллельные силы Р и Их равнодействующая В проходит через точку пересечения К сторон а и ш веревочного многоугольника. Продолжим линию действия силы Д до пересечения с прямой ВС в точке так как к балке теперь приложены три силы (сила Л, реакция шарнира и реакция цепи), то на основании теоремы о трех уравновешенных силах ) заключаем, что линия действия реакции шарнира А проходит через точку следовательно, она направлена по прямой АВ. Таким образом, направления обеих искомых сил теперь известны чтобы найти силы, достаточно построить силовой треугольник проводим вектор аЬ, равный силе Д пз точек а и 6 проводим прямые, параллельные ВС и АВ, до их пересечения в точке с векторы Ьс и са определяют искомую реакцию шарнира Дд и реакцию цепи Г, модуль которой и равен искомому натяжению цепи. [c.146]
Итак, пусть установлено перспективно-коллинеарное соответствие точек двух плоскостей и Я, при котором отрезку плоскости Я соответствует отрезок АВ плоскости Я. Центром проектирования при этом является точка 5 (рис. 389). Установим относительное положение проектирующих лучей АА и ВВ, после поворота плоскости Я на произвольный угол ф вокруг оси коллинеации 0,0,. Новое положение плоскости обозначено П . Прямая Л,В, после вращения плоскости займет положениеЛаВ , но по-прежнему будет пересекаться с прямой ЛВ в неподвижной точке Сд, лежащей на оси вращения 0,0,. Следовательно, прямые ЛВ и Л В расположены в одной плоскости. Той же плоскости принадлежат прямые АА и ВВ . Значит, эти прямые пересекаются в некоторой точке 5 . Приведенное рассуждение справедливо для любого положения вращающейся плоскости и для любой пары каких угодно трех прямых ЛЛ1, BB , СС , не лежащих в одной плоскости, но соединяющих соответственные точки. Если же из тргх прямых, не лежащих в одной плоскости, каждые две пересекаются, то все эти прямые имеют одну точку пересечения. Присоединяя к этим трем прямым любую другую, соединяющую соответственные точки, делаем вывод о том, что все прямые, соединяющие соответственные точки, при вращении плоскости П пресекаются в одной точке [c.277]
Действительно, в рассматриваемом соответствии родственными точками фигур будут перспективы А , В , и вторичные проекции Ад-, Ь , Ск одних и тех же точек пространства. Но известно, что перспектива точки и ее вторичная проекция всегда расположены на одном перпендикуляре к основанию картины. Следовательно, прямые, соединяющие каждую пару родственных точек, параллельны между собой (пересекаются в бесконечно удаленной точке). Применяя теорему Дезарга для плоскости, заключаем, что три точки Ьд, Мд, Л/д пересечения трех пар род- [c.284]
Построение точки пересечения трех высот треугольника ) и точки пересечения перпендикуляров к сторонам треугольника, проведенных через их середи-ны , связано с проведением взаимно перпендикулярных прямых. [c.76]
Действительно, в рассматриваемом соответствии родственными точками фигур будут перспективы А, В, С и вторичные проекции а, Ь, с одних и тех же точек пространства. Но известно, что перспектива точки и ее вторичная проекция всегда расположены на одном перпендикуляре к основанию картины. Следовательно, прямые, соединяющие каждую пару родственных точек, параллельны между собой (пересекаются в бесконечно удаленной точке). Применяя теорему Дезарга для плоскости, заключаем, что три точки L , М , пересечения трех пар родственных сторон треугольников АВС и ab лежат на одной прямой Oiu — оси родства. Эта прямая является перспективой линии пересечения предметной плоскости и плоскости, в которой расположен треугольник. [c.354]
Выражение (2) определяет зависи-МОСТЬ между переменными Х], Х2 и Хд которая устанавливается номограммой данного вида. Эта номограмма, как показывает вывод уравнения (2), дает воз . ожность очень просто определять значения одной из трех переменных Х], Х2 и если значения двух других даны. Действительно, если, например, даны значения и Хд и требуется определить значение хо, то достаточно соединить прямой линией те деления на первой и третьей шкалах, отметки которых отвечают данным значениям и х точка пересечения этой прямой со средней шкалой дает нам искомое значение Х2-Совершенно так же можно определять значения или Хд, если даны значения Хо и Хз или X и X-. Отсюда становится понятным название этого типа номограмм — ксмограм ы на выравненных точках. [c.548]
c.242
]
Справочник машиностроителя Том 1 Изд.2 (1956) — [
c.242
]
Точка пересечения прямых в пространстве онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых (“канонический” или “параметрический” ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Точка пересечения прямых в пространстве − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в каноническом виде.
- 2. Точка пересечения прямых, заданных в параметрическом виде.
- 3. Точка пересечения прямых, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
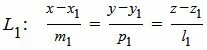 , , |
(1) |
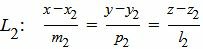 , , |
(2) |
где M1(x1, y1, z1) и M2(x2, y2, z2) − точки, лежащие на прямых L1 и L2, соответственно, а q1={m1, p1, l1} и q2={m2, p2, l2} − направляющие векторы прямых L1 и L2, соответственно.
Найти точку пересечения прямых L1 и L2 (Рис.1).
Запишем уравнение (1) в виде системы двух линейных уравнений:
Сделаем перекрестное умножение в уравнениях (3) и (4):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Аналогичным образом преобразуем уравнение (2):
Запишем уравнение (2) в виде системы двух линейных уравнений:
Сделаем перекрестное умножение в уравнениях (7) и (8):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:
Как решить систему линейных уравнений (11)(или (5), (6), (9), (10)) посмотрите на странице Метод Гаусса онлайн. Если система линейных уравнениий (11) несовместна, то прямые L1 и L2 не пересекаются. Если система (11) имеет множество решений, то прямые L1 и L2 совпадают. Единственное решение системы линейных уравнений (11) указывает на то, что это решение определяет координаты точки пересечения прямых L1 и L2 .
2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
где M1(x1, y1, z1) и M2(x2, y2, z2) − точки, лежащие на прямых L1 и L2, соответственно, а q1={m1, p1, l1} и q2={m2, p2, l2} − направляющие векторы прямых L1 и L2, соответственно.
Задачу нахождения нахождения точки пересечения прямых L1 и L2 можно решить разными методами.
Метод 1. Приведем уравнения прямых L1 и L2 к каноническому виду.
Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:
Так как левые части уравнений (14) равны, то можем записать:
Аналогичным образом приведем уравнение прямой L2 к каноническому виду:
Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямых L1 и L2 решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:
Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).
3. Точка пересечения прямых в пространстве, заданных в разных видах.
Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.
4. Примеры нахождения точки пересечения прямых в пространстве.
Пример 1. Найти точку пересечения прямых L1 и L2:
Представим уравнение (20) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (22) и (23):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Упростим:
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (7) и (8)
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Упростим:
Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1:
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:
Сделаем перестановку строк 3 и 4.
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
Запишем решение:
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
Приведем параметрическое уравнение прямой L1 к каноническому виду. Выразим параметр t через остальные переменные:
Из равентсв выше получим каноническое уравнение прямой:
Представим уравнение (33) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (34 и (35):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Упростим:
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (38) и (39)
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Упростим:
Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:
Исключим элементы 3-го столбца матрицы ниже элементаa33. Для этого сложим строку 4 со строкой 3, умноженной на -1/16:
Из расширенной матрицы восстановим последнюю систему линейных уравнений:
Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L1 и L2 не пересекаются. То есть они или параллельны, или скрещиваются.
Прямая L1 имеет направляющий вектор q1={2,6,7}, а прямая L2 имеет направляющий вектор q2={3,1,1}. Эти векторы не коллинеарны. Следовательно прямые L1 и L2 скрещиваются .
Ответ. Прямые L1 и L2 не пересекаются.







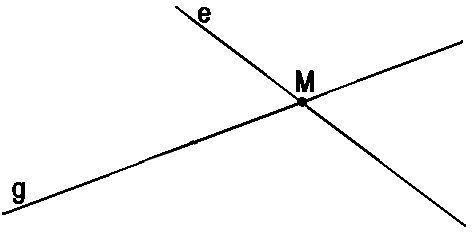
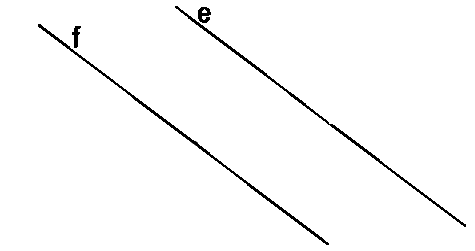
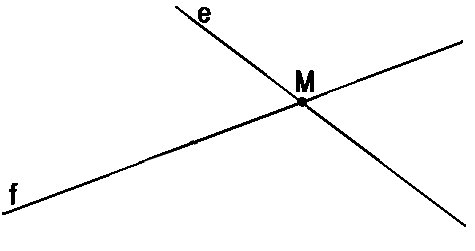

















.png)
.png)
.png)
.png)
.png)
.png)
.png)


 Сообщение было отмечено PSV_285 как решение
Сообщение было отмечено PSV_285 как решение