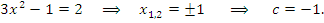Проведем хорду 






Значит, внутри отрезка нашлась точка с, в которой выполняется равенство

Это утверждение и составляет суть теоремы Лагранжа. Дадим строгое доказательство этой теоремы, не опирающееся на наглядность.
Теорема 3 (теорема Лагранжа). Пусть функция 




Доказательство. Пусть 



Рассмотрим функцию 

потому непрерывна на отрезке 





Итак, вспомогательная функция 


При 

откуда

Теорема доказана.
Заметим, что если 

Неудобно, что в формуле (1) фигурирует неизвестное число с. Тем не менее, как увидим позднее, это не является препятствием для многочисленных применений этой формулы в математическом анализе.
Пример 3. Проверим, применима ли теорема Лагранжа к функции 
Решение. Функция 


В данном случае


Рис. 38
Подставим полученные значения в формулу (2) Лагранжа:

Из этого уравнения находим 


Пример 4. Докажем неравенство 

Решение. Функция 





Так как 



Теорема
25.3 (Лагранж). Если
функция ƒ(х) непрерывна на отрезке [а;b],
дифференцируема на интервале (α;b), то
найдется хотя бы одна точка сє(a;b) такая,
что выполняется равенство
ƒ(b)-ƒ(a)=ƒ'(с)(b-a).
(25.2)
▼ Решение:
Теорему Лагранжа можно рассматривать
как частный случай теоремы Коши.
Действительно, положив φ(х)=х, находим
φ(b)-φ(a)=b-a, φ'(х)=1, φ'(с)=1.
Подставляя
эти значения в формулу
получаем
или
ƒ(b)-ƒ(a)=ƒ'(с)(b-a)
▲.
Полученную
формулу называют формулой
Лагранжа или формулой
о конечном приращении:
приращение дифференцируемой функции
на отрезке [a;b] равно приращению аргумента,
умноженному на значение производной
функции в некоторой внутренней точке
этого отрезка
Теорема
Лагранжа имеет простой геометрический
смысл. Запишем формулу (25.2) в виде
,
где
α<с<b. Отношение
есть
угловой коэффициент секущей АВ, а
величина ƒ'(с) — угловой коэффициент
касательной к кривой в точке с абсциссой
х=с.
Следовательно,
геометрический смысл теоремы Лагранжа
таков: на графике функции y=f(x) найдется
точка С(с;ƒ(с)) (см. рис. 142), в которой
касательная к графику функции параллельна
секущей АВ.
Следствие
25.1. Если производная функции равна нулю
на некотором промежутке, то функция
постоянна на этом промежутке.
Пусть
ƒ'(х)=0 для xє(α;b).
Возьмем произвольные x1 и
х2 из
(а;b) и пусть x1<х2.
Тогда по теореме Лагранжа сє(х1;х2)
такая, что ƒ(х2)-f(x1)=ƒ'(с)(х2-х1).
Но по условию ƒ'(х)=0, стало быть, ƒ'(с)=0,
где х1<с<х2.
Поэтому имеем ƒ(х2)-ƒ(х1)=0,
т. е. ƒ(х2)=f(x1).
А так как x1 и
х2 —
произвольные точки из интервала
(α;b),то x
є (а;b) имеем ƒ(х)≈с.
Следствие
25.2. Если две функции имеют равные
производные на некотором промежутке,
то они отличаются друг от друга на
постоянное слагаемое.
Пусть
f1‘ (x)=f2‘(x)
при хє(α;b). Тогда (f1(x)-f2(x))’=f1‘(x)-f2‘(x)=0.
Следовательно, согласно следствию 25.1,
функция f1(х)-f2(x)
есть постоянная, т. е. f1(x)-f2(x)=C
для xє(α;b).
<<
Пример 25.1
Доказать,
что arcsinx + arccosx = /2,
где х є [-1;1].

Решение:
Пусть ƒ(х)=arcsinx+arccosx. Тогда xє(-1;1)
имеем
Отсюда
следует, что ƒ(х)=С, т.е. arcsinx+arccosx=С. Положив
х=0, находим 0+ /2=С,
т. е. С= /2.
Поэтому arcsinx+arccosx= /2.
Это равенство выполняется и при х=±1
(проверьте!).
Аналогично
доказывается, что arctgх+arcctgх= /2.
Формуле
Лагранжа можно придать другой вид.
Применив теорему Лагранжа к отрезку
[х;х+∆х] (∆х>0), будем иметь
ƒ(х+∆х)-ƒ(х)=ƒ'(с)∆х.
(25.3)
Каждое
число сє(х;х+∆х) можно записать в виде
с=х+θ∆х, где 0<θ<1 (действительно,
х<с<х+∆х 0<с-х<∆х 0<
<1;
положим
=θ с=х+θ∆х).
Формула (25.3) примет вид
ƒ(х+∆х)-ƒ(х)=ƒ'(х+θ∆х)∆х,
где 0<θ<1.
Используя
теорему Лагранжа, можно оценить точность
приближенного равенства ∆у≈dy. Сделаем
это, считая, что функция ƒ(х) имеет
непрерывную вторую производную ƒ”(х):
∆у-dy=(ƒ(х+∆х)-ƒ(х))-ƒ'(х)∆х=ƒ'(с)∆х-ƒ'(х)∆х=(ƒ'(с)-ƒ'(х))∆х=ƒ”(c1)(c-х)∆х,
где
с1є(х;с)
(рис. 143).
Итак,
∆у-dy=f”(c1)(c-х)∆х.
Пусть
Так
как |с-х|<∆х, a ƒ”(c1)≤M,
то получаем оценку |∆у-dy|≤М|∆х|2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Условный экстремум
4 раздела
от теории до практики
2 примера
Примеры решения задач
видео
Примеры решения задач
-
Понятие условного экстремума.
Начать изучение
-
Прямой метод отыскания точек условного экстремума.
Начать изучение
-
Метод множителей Лагранжа.
Начать изучение
-
Несколько замечаний о методе множителей Лагранжа.
Начать изучение
Понятие условного экстремума.
Пусть на открытом множестве (G subset boldsymbol{R}^{n}) заданы функции (f_{0}(x)), (f_{1}(x), ldots, f_{m}(x)), причем (m < n), и пусть (E) — множество точек множества (G), удовлетворяющих системе уравнений
$$
f_{1}(x) = 0, ldots, f_{m}(x) = 0.label{ref1}
$$
Уравнения eqref{ref1} будем называть уравнениями связей (или просто связями).
Определение 1.
Точка (x^{0} = (x_{1}^{0}, ldots, x_{n}^{0}) in G) называется точкой условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}, если найдется такая окрестность (S_{delta}(x^{0})), что для всех (x in G cap S_{delta}(x^{0})) выполнено неравенство (f_{0}(x) geq f_{0}(x^{0})).
Определение 2.
Точка (x^{0} in G) называется точкой строгого условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}, если найдется такая окрестность (S_{delta}(x^{0})), что для всех (x in dot{S}_{delta}(x^{0}) cap G) выполнено неравенство (f_{0}(x) geq f_{0}(x^{0})).
Аналогично определяются точки условного максимума. Точки условного максимума и минимума называются точками условного экстремума.
Прямой метод отыскания точек условного экстремума.
Предположим, что из системы уравнений eqref{ref1} можно выразить какие-либо (m) переменных (x_{i}) через остальные переменные. Тогда, подставив вместо соответствующих переменных (x_{i}) их выражения через остальные (n-m) переменных в функцию (f_{0}(x)), получим функцию (F) от (n-m) переменных.
Задача о нахождении точек экстремума функции (f_{0}(x)) при наличии связей eqref{ref1} сведется к задаче нахождения обычного (безусловного) экстремума функции (F), зависящей от (n-m) переменных.
Пример 1.
Найти точки условного экстремума функции (z = 1-x^{2}-y^{2}), если (x+y = 1).
Решение.
(vartriangle) Уравнение связи (x+y = 1) легко разрешается относительно переменной (y), а именно (y = 1-x). Подставив это выражение для (y) в функцию (z = 1-x^{2}-y^{2}), получаем, что (z = 1-x^{2}-(1-x)^{2} = 2x-2x^{2}). Функция (2x-2x^{2}) имеет максимум при (x = frac{1}{2}). Точка ((frac{1}{2}, frac{1}{2})) является точкой условного максимума функции (z(x, y)) при наличии связи (x+y = 1), причем (z_{max} = displaystylefrac{1}{2}). (blacktriangle)
Замечание 1.
Прямой метод нахождения условного экстремума редко бывает эффективным ввиду трудности разрешения уравнений связей относительно какой-либо группы переменных.
Метод множителей Лагранжа.
Определение 3.
Рассмотрим функцию (n+m) переменных
$$
L(x, lambda) = f_{0}(x)+lambda_{1}f_{1}(x)+ldots+lambda_{m}f_{m}(x),nonumber
$$
где (x in G), а (lambda = (lambda_{1}, ldots, lambda_{m}) in boldsymbol{R}^{m}). Числа (lambda_{1}, ldots, lambda_{m}) называются множителями Лагранжа, а функция (L(x, lambda)) называется функцией Лагранжа.
Будем говорить, что ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа, если
$$
begin{array}{cc}
& displaystylefrac{partial L}{partial x_{1}} (x^{0}, lambda^{0}) = 0, ldots, frac{partial L}{partial x_{n}} (x^{0}, lambda^{0}) = 0\
&\
& displaystylefrac{partial L}{partial lambda_{1}} (x^{0}, lambda^{0}) = f_{1}(x^{0}) = 0, ldots, frac{partial L}{partial lambda_{m}} (x^{0}, lambda^{0}) = f_{m}(x^{0}) = 0.
end{array}label{ref2}
$$
Теорема 1.
(Теорема Лагранжа).
Пусть (x^{0}) — точка условного экстремума функции (f_{0}(x)) при наличии связей eqref{ref1}, и пусть функции (f_{i}(x)), (i = overline{0, m}), непрерывно дифференцируемы в окрестности точки (x^{0}), причем в точке (x^{0}) ранг матрицы Якоби
$$
A = begin{pmatrix}displaystylefrac{partial f_{1}}{partial x_{1}}(x)&ldots&displaystylefrac{partial f_{1}}{partial x_{n}}(x)\………&…..&…….\displaystylefrac{partial f_{m}}{partial x_{1}}(x)&ldots&displaystylefrac{partial f_{m}}{partial x_{n}}(x)end{pmatrix}label{ref3}
$$
равен (m).
Тогда найдутся такие множители Лагранжа (lambda_{1}^{0}, ldots, lambda_{m}^{0}), что ((x^0, lambda^0)) будет стационарной точкой функции Лагранжа.
Доказательство.
(circ) Так как (m < n), а ранг матрицы Якоби в точке (x^{0}) равен (m), то хотя бы один из миноров этой матрицы порядка (m) отличен от нуля.
Без ограничения общности можно считать, что
$$
begin{vmatrix}displaystylefrac{partial f_{1}}{partial x_{1}}(x^{0})&ldots&displaystylefrac{partial f_{1}}{partial x_{m}}(x^{0})\………&…..&…….\displaystylefrac{partial f_{m}}{partial x_{1}}(x^{0})&ldots&displaystylefrac{partial f_{m}}{partial x_{m}}(x^{0})end{vmatrix} neq 0,label{ref4}
$$
так как выполнения условия eqref{ref4} всегда можно добиться, перенумеровывая переменные и уравнения связей в нужном порядке.
Пусть (x^{0}) есть точка условного минимума функции (f_{0}(x)). Тогда существует окрестность (K'(x^{0}) = K’_{1}(x_{1}^{0}, ldots, x_{m}^{0}) times K’_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})) такая, что
$$
f_{0}(x)-f_{0}(x^{0}) geq 0 mbox{при всех} x in E cap K’ (x^{0}).label{ref5}
$$
В силу непрерывности частных производных и выполнения условия eqref{ref4} можно применить теорему о неявных функциях. В силу этой теоремы найдется такая окрестность
$$
K(x^{0}) = K_{1}(x_{1}^{0}, ldots, x_{m}^{0}) times K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0}) subset K'(x^{0}),nonumber
$$
в которой система уравнений связей eqref{ref1} определяет переменные (x_{1}, ldots, x_{m}) как неявные функции переменных (x_{m+1}, ldots, x_{m}). Это означает, что найдется единственный набор непрерывно дифференцируемых в окрестности (K’_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})) функций (varphi_{i}(x_{m+1}, ldots, x_{n})), (i = overline{1, m}), таких, что
$$
varphi_{i}(x_{m+1}^{0}, ldots, x_{m}^{0}) = x_{i}^{0}, i = overline{1, m};label{ref6}
$$
$$
f_{i}(varphi_{1}(x_{m+1}, ldots, x_{n}), ldots, varphi_{m}(x_{m+1}, ldots, x_{n}), x_{m+1}, ldots, x_{n}) equiv 0,label{ref7}
$$
$$
(varphi_{1}(x_{m+1}, ldots, x_{n}), ldots, varphi_{m}(x_{m+1}, ldots, x_{n})) in K_{1}(x_{1}^{0}, ldots, x_{m}^{0})nonumber
$$
при ((x_{m+1}, ldots, x_{n}) in K_{2}(x_{1}^{0}, ldots, x_{m}^{0})), (i = overline{1, m}).
Другими словами, множество (E cap K(x^{0})) можно задать следующим образом:
$$
begin{array}{cc}
& E cap K(x^{0}) = {x: x = (x_{1}, ldots, x_{n}), (x_{m+1}, ldots, x_{n}) in K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0}),\
& \
& x_{i} = varphi_{i}(x_{m+1}, ldots, x_{n}), i = overline{1, m}}.
end{array}label{ref8}
$$
Так как (K(x^{0}) subset K'(x^{0})), то из неравенства eqref{ref5} следует, что функция (f_{0}(x)) принимает на множестве (E cap K(x^{0})) наименьшее значение в точке (x^{0}). Если взять представление множества (E cap K(x^{0})) в виде eqref{ref8}, то сложная функция
$$
F(x_{m+1}, ldots, x_{n}) = f_{0}(varphi_{1}(x_{m+1}, ldots, x_{n}), ldots, varphi_{m}(x_{m+1}, ldots, x_{n}), x_{m+1}, ldots, x_{n})label{ref9}
$$
определена в окрестности (K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})) и принимает в этой окрестности наименьшее значение в точке ((x_{m+1}^{0}, ldots, x_{n}^{0})). Следовательно, в силу необходимых условий экстремума должно выполняться равенство (dF(x_{m+1}^{0}, ldots, x_{n}^{0}) = 0). Воспользовавшись инвариантностью формы первого дифференциала и равенством eqref{ref9}, получаем, что
$$
sum_{k=1}^{n} frac{partial f_{0}(x^{0})}{partial x_{k}} dx_{k} = 0.label{ref10}
$$
В равенстве eqref{ref10} (dx_{m+1}, ldots, dx_{n}) есть дифференциалы независимых переменных, a (dx_{1}, ldots, dx_{n}) — дифференциалы функций (varphi_{i}, ldots, varphi_{m}), зависящих от (x_{m+1}, ldots, x_{n}). Для краткости будем говорить о независимых и зависимых дифференциалах.
Найдем связи между зависимыми и независимыми дифференциалами. Дифференцируя тождества eqref{ref7} в точке ((x_{m+1}^{0}, ldots, x_{n}^{0})) и пользуясь инвариантностью формы первого дифференциала, получаем
$$
sum_{k=1}^{n} frac{partial f_{i}(x^{0})}{partial x_{k}} dx_{k} = 0, i = overline{1, m}.label{ref11}
$$
Умножая равенства eqref{ref11} на множители (lambda_{i}) и складывая полученные равенства с равенством eqref{ref10}, находим
$$
0 = sum_{k=1}^{n} left(frac{partial f_{0}}{partial x_{k}}+sum_{i=1}^{m} frac{partial f_{i}}{partial x_{k}} lambda_{i}right)_{x = x^{0}} dx_{k} = sum_{k=1}^{n} frac{partial L(x^{0}, lambda)}{partial x_{k}} dx_{k},label{ref12}
$$
где (L(x^{0}, lambda)) есть функция Лагранжа.
Подберем множители (lambda_{1}^{0}, ldots, lambda_{m}^{0}) так, чтобы коэффициенты при зависимых дифференциалах в равенстве eqref{ref12} обратились в нуль, то есть
$$
frac{partial L(x^{0}, lambda)}{partial x_{k}} = frac{partial f_{0}(x^{0})}{partial x_{k}}+sum_{i=1}^{m} lambda_{i}^{0} frac{partial f_{i}(x^0)}{partial x_{k}} = 0, k = overline{1, m}.label{ref13}
$$
Система уравнений eqref{ref13} единственным образом определяет множители (lambda_{1}^{0}, ldots, lambda_{m}^{0}), так как ее определитель eqref{ref4} отличен от нуля.
При выполнении условий eqref{ref13} уравнение eqref{ref12} примет вид
$$
sum_{k=m+1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} dx_{k} = 0.label{ref14}
$$
Так как дифференциалы независимых переменных (dx_{m+1}, ldots, dx_{n}), могут принимать любые значения, то из eqref{ref14} следует, что
$$
frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} = 0, k = m+1, ldots, n.label{ref15}
$$
Объединяя равенства eqref{ref13} и eqref{ref15}, получаем
$$
frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} = 0, k = overline{1, n}.nonumber
$$
Так как точка (x^{0} in E) и, следовательно, удовлетворяет уравнениям связей, то
$$
frac{partial L(x^{0}, lambda^{0})}{partial lambda_{j}} = f_{i}(x^{0}) = 0, j = overline{1, m}.nonumber
$$
Таким образом, ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа (L(x, lambda)). (bullet)
Второй дифференциал функции Лагранжа, вычисленный при фиксированных (lambda_{1}^{0}, ldots, lambda_{m}^{0}) по переменным ((x_{1}, ldots, x_{n})) в точке ((x_{1}^{0}, ldots, x_{n}^{0})), будем обозначать через (d_{xx}^{2}L(x^{0}, lambda^{0})).
Таким образом,
$$
d_{xx}^{2}L(x^{0}, lambda^{0}) = sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} L(x^{0}, lambda^{0})}{partial x_{k} partial x_{j}} dx_{k} dx_{j}.label{ref16}
$$
Иногда вместо (d_{xx}^{2}L(x^{0}, lambda^{0})) будем писать (d^{2}L(x^{0}, lambda^{0})).
Обозначим через (E_{T}) следующее линейное многообразие в (boldsymbol{R}^{n}):
$$
E_{T} = left{xi = (xi_{1}, ldots, xi_{n}) in boldsymbol{R}^{n}: sum_{k=1}^{n} frac{partial f_{i}(x^{0})}{partial x_{k}} xi_{k} = 0, i = overline{1, m}right}.label{ref17}
$$
Равенства eqref{ref11} означают, что (dx = (dx_{1}, ldots, dx_{n}) in E_{T}).
Теорема 2.
Пусть (x^{0}) есть точка условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}, и пусть функции (f_{i}(x)), (i = overline{1, m}), имеют непрерывные частные производные второго порядка в окрестности точки (x^{0}), причем в точке (x^{0}) ранг функциональной матрицы eqref{ref3} равен (m).
Тогда найдутся множители Лагранжа (lambda_{1}^{0}, ldots, lambda_{m}^{0}) такие, что ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа, a (d^{2}L(x^{0}, lambda^{0}) geq 0) при ((dx_{1}, ldots, dx_{n}) in E_{T}).
Доказательство.
(circ) Так как выполнены все условия теоремы 1, то найдутся множители Лагранжа (lambda_{1}^{0}, ldots, lambda_{m}^{0}) такие, что ((x^{0}, lambda^{0})) будет стационарной точкой функции Лагранжа, то есть выполняются условия eqref{ref2}. Повторяя рассуждения теоремы 1, рассмотрим сложную функцию eqref{ref9}, имеющую безусловный экстремум в точке ((x_{m+1}^{0}, ldots, x_{n}^{0})). Так как эта функция имеет непрерывные частные производные второго порядка, то, в силу теоремы о необходимом условии минимума должно быть выполнено условие (d^{2}F(x_{m+1}^{0}, ldots, x_{n}^{0}) geq 0).
Воспользовавшись правилом нахождения второго дифференциала сложной функции и формулой eqref{ref9}, находим, что
$$
sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} f_{0}(x^{0})}{partial x_{k} partial x_{j}} dx_{k} dx_{j}+sum_{k=1}^{n} frac{partial^{2} f_{0}}{partial x_{k}}(x^{0}) d^{2}x_{k} geq 0.label{ref18}
$$
Дифференцируя два раза в точке (x_{m+1}^{0}, ldots, x_{n}^{0}) тождества eqref{ref7}, получаем равенства
$$
sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} f_{i}(x^{0})}{partial x_{k} partial x_{j}} dx_{k} dx_{j}+sum_{k=1}^{n} frac{partial^{2} f_{i}}{partial x_{k}}(x^{0}) d^{2}x_{k} = 0.label{ref19}
$$
Если умножить каждое из равенств eqref{ref19} на соответствующий множитель Лагранжа (lambda_{i}^{0}) и сложить с неравенством eqref{ref18}, то получаем неравенство
$$
d_{xx}^{2}L(x^{0}, lambda^{0})+sum_{k=1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} d^{2}x_{k} geq 0.label{ref20}
$$
Последняя сумма в неравенстве eqref{ref20} равна нулю, так как ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа и в ней выполняются условия eqref{ref2}. Таким образом, (d_{xx}^{2}L(x^{0}, lambda^{0}) geq 0) при ((dx_{1}, ldots, dx_{n}) in E_{T}). (bullet)
Теорема 3.
(Достаточные условия условного экстремума).
Пусть функции (f_{i}(x)), (i = overline{0, m}), имеют непрерывные частные производные второго порядка в окрестности точки (x^{0} in boldsymbol{R}^{n}), причем в точке (x^{0}) ранг функциональной матрицы (3) равен (m), и пусть ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа (L(x, lambda)).
Тогда если (d_{xx}L(x^{0}, lambda^{0})) есть положительно определенная квадратичная форма при (dx in E_{T}), то (x^{0}) является точкой условного строгого минимума функции (f_{0}(x)) при наличии связей eqref{ref1}. Если (d_{xx}L(x^{0}, lambda^{0})) есть отрицательно определенная квадратичная форма при (dx in E_{T}), то (x^{0}) — точка условного строгого максимума. Если (d_{xx}L(x^{0}, lambda^{0})) есть неопределенная квадратичная форма при (dx in E_{T}), то (x^{0}) не есть точна условного экстремума функции (f_{0}(x)) при наличии связей eqref{ref1}.
Доказательство.
(circ) Пусть
$$
E = {x: f_{i}(x) = 0, i = overline{1, m}}.label{ref21}
$$
По условию теоремы функции (f_{i}(x)), (i = overline{0, m}), имеют непрерывные частные производные второго порядка, а ранг функциональной матрицы eqref{ref3} равен (m). Повторяя рассуждения теоремы 1, можем без ограничения общности считать, что выполнено условие eqref{ref4} и что найдется такая окрестность (K(x^{0}) = K_{1}(x_{1}^{0}, ldots, x_{m}^{0}) times K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})), что множество (E cap K(x^{0})) можно задать формулой eqref{ref8}. На (E cap K(x^{0})) функция (f_{0}(x)) становится функцией (n-m) переменных (F(x_{m+1}^{0}, ldots, x_{n}^{0})), определенной формулой eqref{ref9} и имеющей непрерывные частные производные второго порядка.
По условию теоремы ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа, то есть
$$
begin{array}{cc}
& displaystylefrac{partial L}{partial x_{k}} (x^{0}, lambda^{0}) = 0, k = overline{1, n};\
&\
& displaystylefrac{partial L}{partial lambda_{i}} (x^{0}, lambda^{0}) = f_{i}(x^{0}) = 0, i = overline{1, m}.
end{array}label{ref22}
$$
Из формул eqref{ref22} следует, что (x^{0} in E) и что
$$
d_{x}L(x^{0}, lambda^{0}) = sum_{k=1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} d^{2}x_{k} = 0.label{ref23}
$$
Рассмотрим функцию (L(x, lambda^{0})) на множестве (E cap K(x^{0})). Очевидно, что
$$
L(x, lambda^{0}) = f_{0}(x) = F(x_{m+1}, ldots, x_{n}) mbox{при} x in E cap K(x^{0}).label{ref24}
$$
В силу инвариантности формы первого дифференциала из формулы eqref{ref24} следует, что
$$
dF(x_{m+1}^{0}, ldots, x_{n}^{0}) = d_{x}L(x^{0}, lambda^{0}) = 0.label{ref25}
$$
Находя второй дифференциал от обеих частей равенства eqref{ref24} и используя равенства eqref{ref22}, получаем
$$
d^{2}F(x_{m+1}^{0}, ldots, x_{n}^{0}) = sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} L(x^{0}, lambda^{0})}{partial x_{j} partial x_{k}} dx_{j} dx_{k}+sum_{k=1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} d^{2}x_{k} = d_{xx}^{2}L(x^{0}, lambda^{0}).label{ref26}
$$
Пусть (d_{xx}^{2}L(x^{0}, lambda^{0}) > 0) при (dx in E_{T}), (dx neq 0). Так как множество (E cap K(x^{0})) можно задать в форме eqref{ref8}, то, выбирая (dx_{m+1}, ldots, dx_{n}) произвольным образом, получим, что дифференциалы (dx_{1},…, dx_{m}) зависят от ((dx_{m+1}, ldots, dx_{n})). Дифференцируя тождества eqref{ref7} в точке (x^{0}), получаем соотношения eqref{ref11}, которые означают, что (dx in E_{T}).
Из формулы eqref{ref26} тогда следует, что
$$
d^{2}F(x_{m+1}^{0}, ldots, x_{n}^{0}) > 0 mbox{при} dx_{m+1}^{2}+ldots+dx_{n}^{2} > 0.label{ref27}
$$
Из eqref{ref25} и eqref{ref27} получаем, что ((x_{m+1}^{0}, ldots, x_{n}^{0})) есть точка строгого минимума функции (F(x_{m+1}, ldots, x_{n})), то есть (x^{0}) есть точка строгого минимума функции (f_{0}(x)) на множестве (E cap K(x^{0})). Таким образом, (x^{0}) есть точка строгого условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}.
Аналогично рассматривается случай, когда (d_{xx}^{2}L(x^{0}, lambda^{0}) < 0), (dx in E_{T}), (dx neq 0). Если же (d_{xx}^{2}L(x^{0}, lambda^{0})) при (dx in E_{T}) есть неопределенная квадратичная форма, то не выполняется условие (d_{xx}^{2}L(x^{0}, lambda^{0}) geq 0) при (dx in E_{T}), являющееся, в силу теоремы 2, необходимым условием минимума. Поэтому (x^{0}) не есть точка условного минимума функции (f_{0}(x)) при связях eqref{ref1}. Аналогично доказывается, что (x^{0}) не может быть точкой условного минимума функции (-f_{0}(x)), а следовательно, и точкой условного максимума функции (f_{0}(x)) при связях eqref{ref1}. (bullet)
Замечание.
Если окажется, что (d_{xx}^{2}L(x^{0}, lambda^{0})) есть положительно определенная квадратичная форма на всем пространстве (boldsymbol{R}^{n}), то (d_{xx}^{2}L(x^{0}, lambda^{0}) > 0) при (dx in E_{T}), (dx neq 0). Поэтому в этом случае в квадратичной форме (d_{xx}^{2}L(x^{0}, lambda^{0})) не нужно исключать зависимые дифференциалы.
Пример 1.
Найти экстремумы функции (x-2y+2z = u) и на сфере (x^{2}+y^{2}+z^{2} = 1).
Решение.
(vartriangle) Строим функцию Лагранжа
$$
L(x, y, z, lambda) = x-2y+2z+lambda(x^{2}+y^{2}+x^{2}-1)nonumber
$$
Стационарные точки функции Лагранжа находим, решая систему уравнений
$$
frac{partial L}{partial x} = 1+2lambda x = 0,quad frac{partial L}{partial y} = -2+2lambda y = 0,quad frac{partial L}{partial z} = 2+2lambda z = 0,nonumber
$$
$$
frac{partial L}{partial lambda} = x^{2}+y^{2}+z^{2}-1 = 0.nonumber
$$
Исключая из этой системы (x, y, z), получаем (displaystyleleft(frac{1}{2lambda}right)^{2}+left(frac{1}{lambda}right)^{2}+left(frac{1}{lambda}right)^{2}-1 = 0), откуда (lambda_{1} = displaystylefrac{3}{2}), (lambda_{2} = -displaystylefrac{3}{2}).
У функции Лагранжа есть две стационарные точки,
$$
M_{1} = left(-frac{1}{3}, frac{2}{3}, -frac{2}{3}, frac{3}{2}right)quad mbox{и}quad M_{2} = left(frac{1}{3}, -frac{2}{3}, frac{2}{3}, -frac{3}{2}right).nonumber
$$
Так как (d^{2}L(M_{1}) = 3(dx^{2}+dy^{2}+dz^{2}) > 0), a (d^{2}L(M_{2}) = -3(dx^{2}+dy^{2}+dz^{2}) < 0) при (dx^{2}+dy^{2}+dz^{2} > 0), тo (displaystyleleft(-frac{1}{3}, frac{2}{3}, -frac{2}{3}, frac{3}{2}right)) — точка условного минимума, a (displaystyleleft(frac{1}{3}, -frac{2}{3}, frac{2}{3}, -frac{3}{2}right)) — точка условного максимума функции (u = x-2y+2x) при наличии ограничения (x^{2}+y^{2}+z^{2}-1 = 0), Причем (u_{min} = -3), (u_{max} = 3). (blacktriangle)
Пример 2.
Найти условные экстремумы функции (f_{0}(x, y) = e^{axy}), (a neq 0), при наличии ограничения (f_{i}(x, y) = x^{3}+y^{3}+x+y-4 = 0).
Решение.
(vartriangle) Построим функцию Лагранжа:
$$
L(x, y) = e^{axy}+lambda(x^{3}+y^{3}+x+y-4).nonumber
$$
Стационарные точки функции Лагранжа определяются из системы уравнений
$$
begin{array}{cc}
& displaystylefrac{partial L}{partial x} = aye^{axy}+lambda(3x^{2}+1) = 0,\
&\
& displaystylefrac{partial L}{partial y} = axe^{axy}+lambda(3y^{2}+1) = 0,\
&\
& displaystylefrac{partial L}{partial lambda} = x^{3}+y^{3}+x+y-4 = 0.
end{array}label{ref28}
$$
Умножая первое уравнение на (x), а второе на (y) и вычитая, получаем
$$
lambda(3x^{3}-3y^{3}+x-y) = lambda(x-y)(3x^{2}+3xy+3y^{2}+1) = 0.label{ref29}
$$
Если (lambda = 0), то из первых двух уравнений eqref{ref28} получаем (x = y = 0). Но (x = y = 0) не удовлетворяет уравнению связи. Итак, (lambda neq 0), поэтому из eqref{ref29} следует, что (x = y) (второй сомножитель всегда положителен: (3(x^{2}+xy+y^{2})+1 > 0)). Подставляя (x = y) в уравнение связи, получаем (x^{3}+x = 2), (x = y = 1). Первое из уравнений eqref{ref28} дает при (x = y = 1) значение (lambda = -displaystylefrac{a}{4} e^{a}).
Итак, ((1, 1, -displaystylefrac{a}{4} e^{a})) есть единственная стационарная точка функции Лагранжа.
Так как
$$
d(e^{axy}) = a(x dy+y dx) e^{axy},nonumber
$$
$$
d^{2}(e^{axy}) = a^{2}(x dy+y dx)^{2} e^{axy}+2a dx dy e^{axy},nonumber
$$
$$
d^{2}(x^{3}+y^{3}+x+y-4) = 6x dx^{2}+6y dy^{2},nonumber
$$
то для второго дифференциала функции Лагранжа при (lambda_{0} = -displaystylefrac{a}{4} e^{a}) и (x = y = 1) получается следующее выражение:
$$
d^{2}L(1, 1, lambda_{0}) = ae^{a}left[a(dx+dy)^{2}+2 dx dy-frac{3}{2}(dx^{2}+dy^{2})right].label{ref30}
$$
Дифференцируя уравнение связи при (x = y = 1), получаем, что (dy+dx = 0). Подставляя (dy = -dx) в уравнение eqref{ref30}, получаем равенство
$$
d^{2}L(1, 1, lambda_{0}) = -5ae^{a}dx^{2}.label{ref31}
$$
Поэтому при (a < 0) в точке (1,1) будет условный минимум, а при (a > 0) — условный максимум функции (f_{0}(x, y)) при наличии связи (x^{3}+y^{3}+x+y = 4), причем экстремальное значение функции равно (e^{a}). (blacktriangle)
Замечание.
Уравнение связи (x^{3}+y^{3}+x+y = 4) было бы затруднительно разрешить относительно одной из переменных. Метод Лагранжа для примера 2 более эффективен, чем прямой метод исключения зависимых переменных.
Несколько замечаний о методе множителей Лагранжа.
Задачи об отыскании экстремумов функций (как числовых, так и функций более общей природы) при наличии ограничений являются весьма распространенными. Теория экстремальных задач интенсивно развивается и находит широкий круг приложений. Здесь были рассмотрены ограничения типа равенств, задаваемые достаточно гладкими функциями (гладкие связи). Метод множителей Лагранжа имеет глубокие обобщения и на более общий случай, когда ограничения задаются системой равенств и неравенств при помощи недифференцируемых в обычном смысле функций.
В конкретных прикладных вопросах множители Лагранжа имеют содержательную интерпретацию. Так, в механике множители Лагранжа задают реакции связей, а в математической экономике — цены на продукты производства. Широко развиты приближенные методы решения экстремальных задач, использующие современную вычислительную технику.
Теорема Лагранжа
ТЕОРЕМА
Если функция (
y=f(x)
) непрерывна на отрезке (
[mathrm{a}, mathrm{b}]
), а также дифференцируема на интервале (
(mathrm{a}, mathrm{b})
), то на интервале (
(mathrm{a}, mathrm{b})
) найдется хотя бы одна точка c, для которой будет справедливо равенство:
(
frac{f(b)-f(a)}{b-a}=f^{prime}(c)
)
Геометрический смысл теоремы Лагранжа
На графике функции (
mathrm{y}=mathrm{f}(mathrm{x})
) найдется точка, касательная к которой параллельна отрезку, соединяющему точки графика с абсциссами (
mathrm{a}
) и (
b
) (рис. 1).
Примеры решения задач
ПРИМЕР 1
Учитывая, что функция (
f(x)=-x^{2}+2 x
)удовлетворяет условиям теоремы Лагранжа на промежутке (
[1,3]
), найти точку (
c in(1,3)
), в которой
(
f^{prime}(c)=frac{f(3)-f(1)}{2}
)
Вычислим значение заданной функции на концах отрезка (
[1,3]
). Получим
(
f(1)=-1^{2}+2 cdot 1=1
), (
f(3)=-3^{2}+2 cdot 3=-3
)
Тогда
(
frac{f(3)-f(1)}{2}=frac{-3-1}{2}=-2
)
Таким образом (
f^{prime}(c)=-2
). Найдем производную заданной функции (
f^{prime}(x)=-2 x+2
) . В точке (
mathbf{X}
) производная равна
(
f^{prime}(c)=-2 c+2=-2
)
Получили уравнение относительно (
mathrm{c}
). Решая его, получим, что (
mathrm{c}=2
). Эта точка принадлежит заданному интервалу (
(1,3)
).
mathrm{c}=2
)
ПРИМЕР 2
На дуге кривой (
f(x)=x^{3}-x
) между точками (
A(-2,-6)
) и (
mathrm{B}(1,0)
)найти точку (
C(c, f(c))
), касательная в которой параллельна хорде (
mathrm{AB}
).
Согласно геометрическому смыслу теоремы Лагранжа, абсцисса точки (
mathrm{C}
) удовлетворяет условию:
(
frac{f(b)-f(a)}{b-a}=f^{prime}(c)
)
Найдем значение правой части этого равенства:
(
frac{0-(-6)}{1-(-2)}=2
)
Тогда (
f^{prime}(c)=2
) .Вычислим производную заданной функции (
f^{prime}(x)=3 x^{2}-1
). В точке (
C(c, f(c))
), она будет иметь значение
(
f^{prime}(c)=3 c^{2}-1=2
)
Решая полученное уравнение относительно c, имеем
(
3 c^{2}=3 Rightarrow c^{2}=1 Rightarrow c=pm 1
)
По условию теоремы Лагранжа (
c in(-2,1)
), таким образом, подходит значение (
c=-1
). Найдем ординату точки (
mathrm{C}
)
(
f(c)=(-1)^{3}-(-1)=0
)
mathrm{C}(2,0)
)
–
 удовлетворяет условиям теоремы Лагранжа в промежутке [-2,1], найти точку
удовлетворяет условиям теоремы Лагранжа в промежутке [-2,1], найти точку 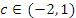 , в которой
, в которой

Решение. Очевидно, что

Тогда
Рис. 7. Функция