Физическим
маятником называют твердое тело,
способное совершать колебания вокруг
некоторой оси, не проходящей через его
центр масс.
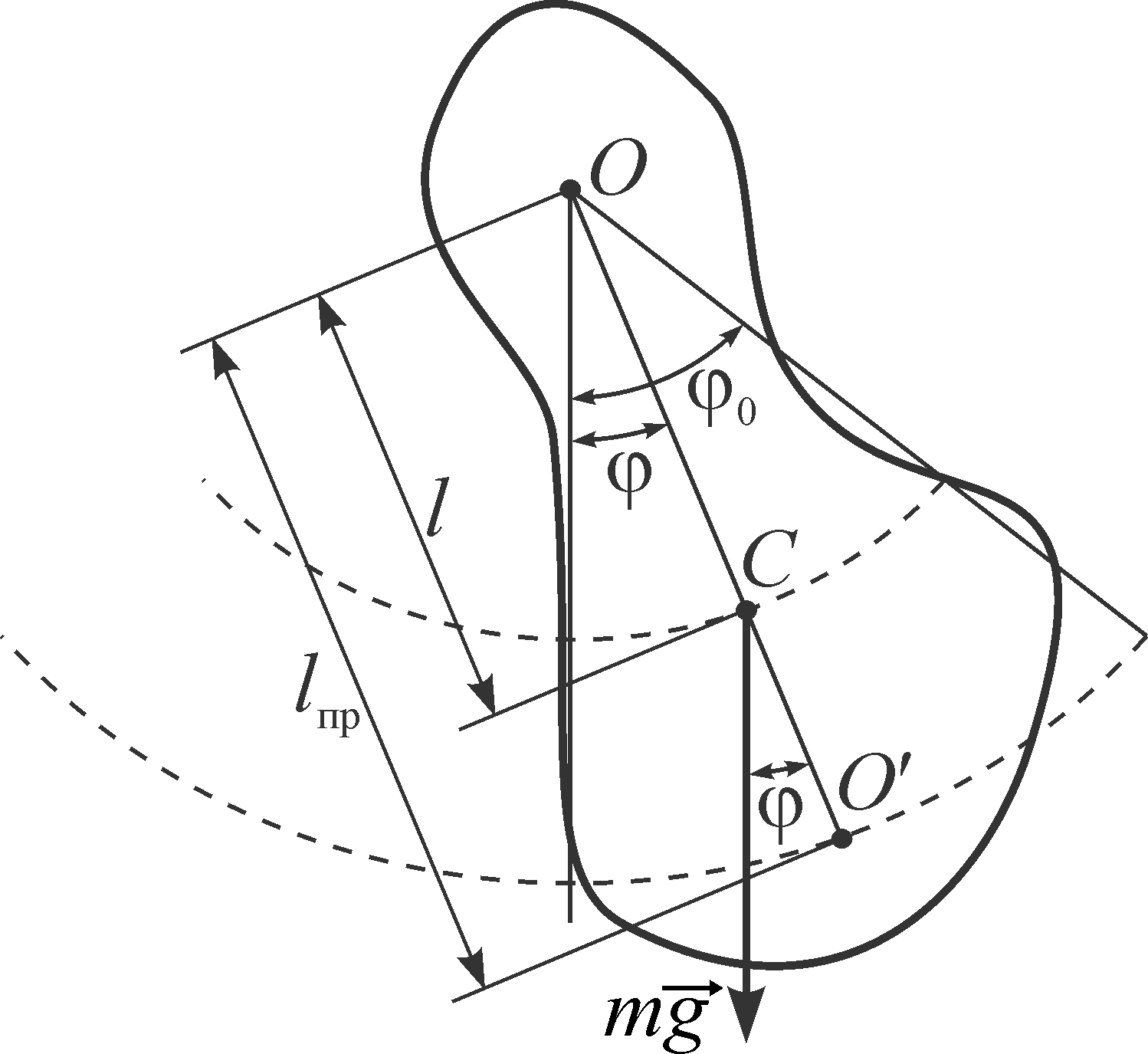
В положении равновесия центр масс
маятника (точка С)
находится с точкой подвеса маятника О
на одной вертикали (рис. 13).
Колебания
физического маятника, так же как и
математического происходят под действием
силы тяжести. При отклонении маятника
от положения равновесия на угол
возникает вращающий момент силы тяжести
относительно горизонтальной оси,
проходящей через точкуО,
равный
|
|
где
– радиус вектор, проведенный из точкиО
в точку приложения силы тяжести, т.е. до
центра масс тела (точка С).
|
|
|
Рис. |
Модуль момента
силы тяжести равен
,
(4)
где
l
– расстояние от точки подвеса до точки
приложения силы тяжести, т.е. до центра
масс тела.
Из
уравнения динамики вращательного
движения тела следует, что момент силы
тяжести равен произведению момента
инерции тела на его угловое ускорение,
т.е.
,
(5)
где
I
– момент инерции тела относительно оси
вращения,
– угловое ускорение. Знак минус означает,
что направление вектора момента силы
тяжести противоположно направлению
вектора углового ускорения.
Учитывая,
что
,
уравнение (5) с учетом (4) можно записать
в виде
|
|
Это
уравнение приводится к следующему виду:
|
|
Введем
обозначение
.
При малых углах отклонения можно считать,
что.
Тогда дифференциальное уравнение
колебания физического маятника (6)
запишется как
.
Решение
этого уравнения имеет вид
,
где
– максимальный угол отклонения маятника
от положения равновесия называемой
амплитудой гармонических колебаний,– начальная фаза колебаний;
– циклическая частота.
Поскольку
,
то период колебания физического маятника
равен
.
Для
математического маятника, момент инерции
которого равен
,
выражение
для периода колебаний будет следующим
.
Из
сопоставления последних двух формул
получается, что математический маятник
с длиной
|
|
(6) |
будет
иметь такой же период колебаний, как и
данный физический маятник. Эту величину
называют приведенной длиной физического
маятника.
Точку
на прямой, соединяющей точку подвеса с
центром масс, лежащую на расстоянии
приведенной длины от оси вращения,
называют центром качания физического
маятника (точка
на рис. 13). При переносе точки подвеса
в центр качания период колебания маятника
будет прежним. Точка подвеса и центр
качания обладают свойством взаимности:
при переносе точки подвеса в центр
качания прежняя точка подвеса становится
новым центром качания, и период колебаний
физического маятника не изменится.
Обозначим
момент инерции физического маятника
относительно оси проходящий через центр
масс за
.
Тогда, используя теорему Штейнера,
получим
|
|
(7) |
Подставив
в уравнение (6) момент инерции, определяемый
выражением (7) получим следующее выражение:
|
|
(8) |
Из
уравнения (8) видно, что приведенная
длина всегда больше l,
так что точка подвеса O
и центр качания лежат по разные стороны
от центра масс C.
Зная период колебания T,
массу маятника m
и приведенную длину, можно рассчитать
момент инерции I
физического маятника
|
|
(9) |
или
|
|
(10) |
где
l
– расстояние от точки подвеса до центра
масс.
Соседние файлы в папке 07-02-2013_14-00-36
- #
- #
- #
- #
- #
Центр тяжести (центр масс):
Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.
Центр тяжести – геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.
На каждую точку тела в поле сил тяжести действует сила, а на все тело – равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.
Центр масс (центр инерции) – точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе внешние силы.
При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.
Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.
При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, – параллельными.
Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.
Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.
Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.
Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.
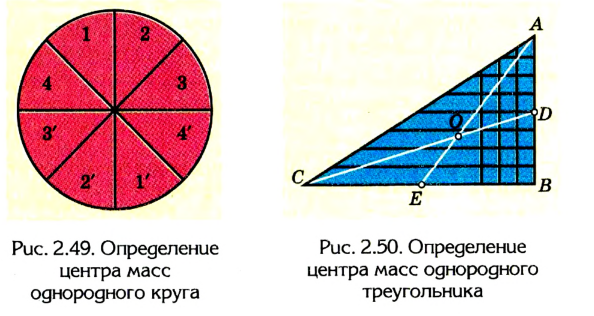
Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.
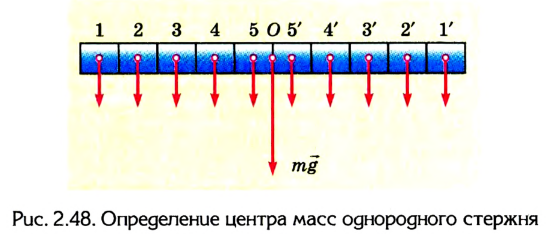
1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О – середине стержня.
Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.
Центр тяжести однородного стержня расположен в середине стержня.
2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).
Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.
Центр тяжести однородного круга совпадает с его центром.
Центр тяжести однородного треугольника находится в точке пересечения его медиан.
3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.
Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.
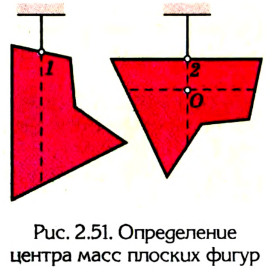
4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).
Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.
Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.
Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.
- Заказать решение задач по физике
Центр тяжести тела и центр масс тела
Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.
Рис. 151
Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.
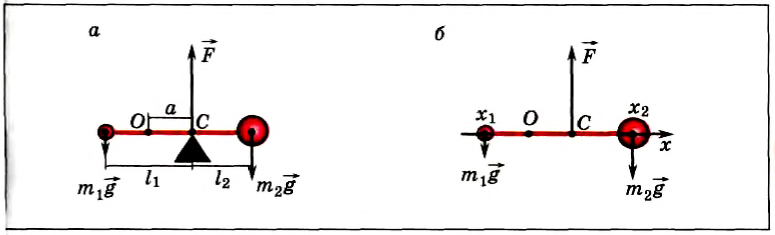
Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m1 и m2, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:
или
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:
Рис. 152
Поскольку F=(m1 + m2)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.
Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х1, хс и х2. Запишем условие моментов относительно точки О:
Отсюда
При выводе этой формулы было использовано значение силы F = (m1 + m2) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии хс, определенном формулой (2).
Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.
Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.
Если произвольное тело можно разбить на n элементов, массы которых m1, m2…, mn, и если известны координаты центров масс этих элементов x1, x2…, xn относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:
Естественно, что такие же соотношения можно записать и для ус и zc. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m1 = 2m2). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C1) и линейки (C2).
Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х1 = 0, y1 =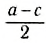
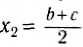
По формуле (3): .
Таким образом, центр масс угольника находится вне тела.
Главные выводы:
- Центр тяжести — точка, в которой приложена сила тяжести.
- Центр масс симметричных однородных тел находится в их геометрическом центре.
- Координаты центра масс тела можно вычислить по формуле (3).
- Импульс тела в физике
- Замкнутая система в физике
- Реактивное движение в физике
- Освоение космоса – история, этапы и достижения с фотографиями
- Международная система единиц СИ
- Математика – язык физики
- Законы Ньютона в физике
- Гравитационные силы в физике
Содержание
- Техническая механика
- Методы нахождения центра тяжести
- Метод симметрии
- Метод разбиения
- Метод отрицательных масс
- Практические методы определения центра тяжести тел
- Положение центра тяжести некоторых фигур
- Пример решения задачи на определение центра тяжести
- Лекция 8. Центр тяжести твердого тела
- 8.1. Понятие центра тяжести
- 8.2. Способы нахождения центра тяжести
- 8.3. Центры тяжести некоторых однородных тел
- 8.4. Пример расчета координат центра тяжести
- Вопросы для самоконтроля
- Задачи к лекции
Техническая механика
Методы нахождения центра тяжести
Наиболее часто для нахождения центра тяжести тела или фигуры применяют следующие методы:
- метод симметрии;
- метод разбиения;
- метод отрицательных масс.
Рассмотрим приемы, применяемые в каждом из перечисленных методов.
Метод симметрии
Представим себе однородное тело, которое имеет плоскость симметрии. Выберем такую систему координат, чтобы оси x и z лежали в плоскости симметрии (см. рисунок 1) .
В этом случае каждой элементарной частице силой тяжести Gi с абсциссой yi = +a соответствует такая же элементарная частица с абсциссой yi = -a , тогда:
Отсюда вывод: если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.
Аналогично можно доказать и следующие положения:
- Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси;
- Если однородное тело имеет две оси симметрии, то центр тяжести тела находится в точке их пересечения;
- Центр тяжести однородного тела вращения лежит на оси вращения.
Метод разбиения
Этот метод заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют приведенные ранее формулы для определения общего центра тяжести тела.
Допустим, что мы разбили тело силой тяжести G на три части G’ , G» , G»’ , абсциссы центров тяжести этих частей x’C, x»C, x»’C известны.
Формула для определения абсциссы центра тяжести всего тела:
Перепишем ее в следующем виде:
Последнее равенство запишем для каждой из трех частей тела отдельно:
Сложив левые и правые части этих трех равенств, получим:
Но правая часть последнего равенства представляет собой произведение GxC , так как
Следовательно, xC = (G’x’C + G»x»C + G»’x»’C)/G , что и требовалось доказать.
Аналогично определяются координаты центра тяжести на координатных осях y и z :
Полученные формулы аналогичны формулам для определения координат цента тяжести, выведенные выше. Поэтому в исходные формулы можно подставлять не силы тяжести элементарных частиц Gi , а силы тяжести конечных частей; под координатами xi , yi , zi понимают координаты центров тяжести частей, на которые разбито тело.
Метод отрицательных масс
Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.
Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.
Практические методы определения центра тяжести тел
На практике для определения центра тяжести плоских тел сложной формы часто применяют метод подвешивания , который заключается в том, что плоское тело подвешивают на нити за какую-нибудь точку. Прочерчивают вдоль нити линию, и тело подвешивают за другую точку, не находящуюся на полученной линии.
Затем вновь проводят линию вдоль нити.
Точка пересечения двух линий и будет являться центром тяжести плоского тела.
Еще один способ определения центра тяжести, применяемый на практике, называется метод взвешивания . Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т. п., которые имеют сложную объемную форму и точечную опору на грунт.
Метод заключается в применении условий равновесия, исходя из того, что сумма моментов всех сил, действующих на неподвижное тело равна нулю.
Практически это осуществляется взвешиванием одной из опор машины (задние или передние колеса устанавливаются на весы), при этом показания весов, по сути, являются реакцией опоры, которая учитывается при составлении уравнения равновесия относительно второй точки опоры (находящейся вне весов).
По известной массе (соответственно – весу) тела, показанию весов в одной из точек опоры, и расстоянию между точками опоры можно определить расстояние от одной из точек опоры до плоскости, в которой расположен центр тяжести.
Чтобы найти подобным образом линию (ось), на которой расположен центр тяжести машины, необходимо произвести два взвешивания по принципу, изложенному выше для метода подвешивания (см. рис. 1а) .
Положение центра тяжести некоторых фигур
Прямоугольник. Так как прямоугольник имеет две оси симметрии, то центр тяжести его площади находится в точке пересечения этих осей, иначе говоря, в точке пересечения диагоналей прямоугольника.
Треугольник. Пусть дан треугольник АBD (см. рисунок 2) .
Разобьем его на элементарные (бесконечно узкие) полоски, параллельные стороне AD . Центр тяжести каждой полоски будет лежать на медиане Bd (т. е. в середине каждой полоски) , следовательно, на этой медиане будет лежать и центр тяжести всей площади треугольника. Разбив треугольник на элементарные полоски, параллельные стороне AB , увидим, что искомый центр тяжести лежит и на медиане aD .
Проделав аналогичное действие с треугольником относительно стороны ВD , получим тот же результат – центр тяжести находится на соответствующей медиане.
Следовательно, центр тяжести всей площади треугольника лежит на точке пересечения его медиан, поскольку эта точка является единственной общей точкой для всех трех медиан данной геометрической фигуры.
Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в соотношении 1:2 от основания. Следовательно, центр тяжести треугольника расположен на расстоянии одной трети высоты от каждого основания.
Дуга окружности. Возьмем дугу окружности АВ радиусом R с центральным углом 2α (см. рисунок 3) . Систему координат выберем так, чтобы начало координат было в центре окружности, а ось x делила дугу пополам, тогда yC = 0 вследствие симметрии дуги относительно оси x . Определим координату центра тяжести xC .
Разобьем дугу АВ на элементарные части li , одна из которых изображена на рисунке. Тогда, согласно сделанным выше выводам,
Дугу li вследствие малости примем за отрезок прямой. Из подобия треугольника ODiCi и элементарного треугольника S (на рисунке заштрихован) получим:
поскольку RΣΔyi = AB , а Σli = l – длина дуги АВ . Но АВ = 2R sinα , а l = 2Rα , следовательно,
При α = π/2 рад (полуокружность) , xC = 2R/π .
Круговой сектор. Возьмем сектор радиусом R с центральным углом 2α (см. рисунок 3а) . Проведем оси координат, как показано на рисунке (ось x направлена вдоль оси симметрии сектора), тогда yC = 0 .
Определим xC , для чего разобьем сектор на ряд элементарных секторов, каждый из которых из-за малости дуги li можно принять за равнобедренный треугольник с высотой R . Тогда центр тяжести каждого элементарного сектора будет находиться на дуге радиуса 2R/3 и задача определения центра тяжести сектора сводится к определению центра тяжести этой дуги.
Очевидно, что
При α = π/2 рад (полукруг) : xC = 4R/(3π) .
Пример решения задачи на определение центра тяжести
Задача:
Определить положение центра тяжести сечения, составленного из двутавра № 22 и швеллера № 20, как показано на рисунке 4 .
Решение.
Из курса инженерной графики известно, что номер проката соответствует наибольшему габаритному размеру его сечения, выраженного в сантиметрах.
Так как сечение, составленное из двутавра и швеллера, представляет собой фигуру, симметричную относительно оси y , то центр тяжести такого сечения лежит на этой оси, т. е. xC = 0 .
По справочнику определим площади и координаты центров тяжести двутавра 1 и швеллера 2.
Для двутаврового сечения: А1 = 15,2 см 2 ; y1 = 22/2 = 11 см.
Для швеллерного сечения: А2 = 12 см 2 ; y2 = 22 + d – z0 = 22 + 0,32 – 1,25 = 21,07 см ,
где d – толщина стенки швеллера; z0 – размер, определяющий положение центра тяжести швеллера.
Применим формулу для определения координаты центра тяжести всего сечения:
Источник
Лекция 8. Центр тяжести твердого тела
8.1. Понятие центра тяжести
Частный случай распределенной нагрузки – сила притяжения, действующая на каждую точку тела со стороны Земли; говорят, что тело помещено в поле силы тяжести (или просто в поле тяжести).
Замечание. Силовым полем называют область пространства, в каждой точке которой на материальную частицу действует сила, зависящая от положения этой частицы. Например, поле, созданное с помощью магнита, действует на движущиеся заряженные частицы.
Если в поле тяжести помещена материальная точка, то действующая на нее сила тяжести численно равна mg и направлена вдоль прямой, соединяющей саму точку с центром Земли. Здесь m – масса точки, g – ускорение свободного падения.
Чтобы определить величину и направление силы тяжести, действующей на тело конечных размеров, разобьем его на мелкие части, каждую из которых можно считать материальной точкой. В принципе, силы, действующие на участки разбиения, образуют сходящуюся систему: они направлены к центру Земли (рис. 8.1 а). Но, как правило, радиус Земли во много раз больше размеров тела, а значит, эти силы можно считать сонаправленными (рис. 8.1 б).
Рис. 8.1. Распределенная нагрузка, действующая на тело со стороны Земли
Как известно, сила притяжения материальной точки к Земле зависит от расстояния до центра планеты и, как следствие, от высоты над ее поверхностью. Далее будем считать, что эта высота мала по сравнению с земным радиусом. Вместе с предположением о малых размерах самого тела это позволяет принять, что ускорение свободного падения для всех точек тела одинаково и равно ускорению на поверхности Земли.
Силовое поле называют однородным, если абсолютная величина и направление силы, действующей на помещенную в него материальную точку, не зависит от ее местоположения. Из вышесказанного следует, что если тело малых размеров находится вблизи поверхности Земли, то поле тяжести, в которое оно при этом попадает, можно считать однородным.
Замечание. Указанные предположения о малых размерах тела и малой высоте над поверхностью планеты – это не единственные сделанные нами упрощения. Строго говоря, Земля не имеет идеально шарообразной формы – она «сдавлена» у полюсов. Кроме того, на величину и направление силы тяжести влияет вращение Земли. В итоге ускорение свободного падения g зависит от географической широты: на полюсах оно максимально (9.832 м/с 2 ), на экваторе – минимально (9.780 м/с 2 ). В качестве стандартного (нормального) выбрано значение g на широте 45.5°, равное 9.80665 м/с 2 . Чаще всего в инженерных расчетах указанными поправками можно пренебречь и считать, что ускорение свободного падения равно 9.8 м/с 2 .
Пусть тело разбито на n участков, массы которых равны m1, m2. mn, соответственно. Складывая сонаправленные силы тяжести, приложенные к каждому из них, мы найдем суммарную силу тяжести, действующую на тело в целом: G = (m1 + m2 + . + mn)g. Учитывая, что m1 + m2 + . + mn = M – это масса всего тела, мы получим
Если тело однородно (имеет постоянную плотность), формула (8.1 а) принимает вид
где ρ – плотность тела, V – его объем (напомним, что плотностью тела называется масса, приходящаяся на единицу его объема).
Остается найти центр C параллельных сил, действующих на тело со стороны Земли. Он и называется центром тяжести тела. Для этого предположим, что силы тяжести, действующие на отдельные участки разбиения тела, приложены в точках с радиус-векторами (vec r_<1>,vec r_<2>,ldots,vec r_) относительно некоторого начала координат O (т.е. сами эти точки являются центрами тяжести участков разбиения). Тогда, подставив выражения для сил тяжести в (7.6) и сократив числитель и знаменатель на g, получим
| $$vec r_=fracvec r_<1>+m_<2>vec r_<2>+ldots+m_vec r_>.$$ | (8.2 а) |
Для однородных тел это соотношение после сокращения числителя и знаменателя на плотность ρ принимает вид
| $$vec r_=fracvec r_<1>+V_<2>vec r_<2>+ldots+V_vec r_>.$$ | (8.2 б) |
Здесь V1, V2. Vn – объемы отдельных участков, на которые разбито исходное тело, V1 + V2 + . + Vn = V. Если тело является плоским (например, представляет собой деталь, вырезанную из металлического листа малой толщины), объемы следует заменить на площади. Если тело составлено из отрезков линий (такой, к примеру, можно считать арматуру, поддерживающую железобетонные конструкции), вместо объемов в равенстве (8.2 б) должны фигурировать длины.
Соотношения (8.2 а) и (8.2 б) можно записать в координатной форме, аналогично (7.7):
| $$x_=fracx_<1>+V_<2>x_<2>+ldots+V_x_>,;y_=fracy_<1>+V_<2>y_<2>+ldots+V_y_>,; z_=fracz_<1>+V_<2>z_<2>+ldots+V_z_>.$$ | (8.3 а) |
Чтобы повысить точность вычислений, придется все более и более измельчать разбиение исходного тела. В конечном итоге это приведет к тому, что положение центра тяжести станет выражаться тройным интегралом по всему объему, занятому телом, подобно формуле (7.9). Например, для координаты x получится выражение
| $$x_=frac<1>iiint_xdV.$$ | (8.3 б) |
Замечание. Центр тяжести тела может и не принадлежать телу, если оно не является выпуклым. Напомним, что тело называют выпуклым, если отрезок, соединяющие две его любые точки, полностью принадлежит телу (рис. 8.2).
Рис. 8.2. а) – выпуклое тело; б), в) – невыпуклые тела
Например, с помощью метода разбиения легко показать, что центр тяжести фигуры, составленной из двух стержней одинаковй длины a и с равной погонной плотностью, расположенных под прямым углом, находится на растоянии a/4 от каждого из них и, тем самым, не принадлежит самой фигуре (рис. 8.3).
Помимо общих формул, существует несколько простых приемов, помогающих определить положение центра тяжести. Ниже будут изучены некоторые из них. При этом для простоты все изучаемые тела будут считаться однородными (хотя некоторые методы применимы и к неоднородным телам).
8.2. Способы нахождения центра тяжести
Метод симметрии. Этот способ основан на следующем факте: если однородное тело имеет некоторый элемент симметрии (зеркальную плоскость, ось или центр симметрии), то его центр тяжести должен лежать на этом элементе.
Действительно, пусть тело имеет плоскость симметрии π. Тогда на две его «половинки» действуют равные по модулю и сонаправленные силы тяжести (vec G_<1>) и (vec G_<2>), а точки C1 и C2 (центры тяжести «половинок») расположены симметрично относительно зеркальной плоскости (рис. 8.4).
Рис. 8.4. Положение центра тяжести зеркально-симметричного тела
Сила тяжести (vec G), действующая на тело в целом, является равнодействующей сил (vec G_<1>) и (vec G_<2>) и должна быть приложена вдоль линии, проходящей через середину отрезка C1C2 и принадлежащей плоскости π. Поэтому и центр тяжести тела, лежащий на линии действия (vec G), находится в этой же плоскости.
С помощью аналогичных рассуждений можно продемонстрировать, например, что центр тяжести осесимметричного тела лежит на этой оси.
Пример. Точка пересечения диагоналей паралеллограмма является его центром симметрии. Поэтому и центр тяжести однородного («сплошного») параллелограма находится в точке пересечения его диагоналей (рис. 8.5).
Рис. 8.5. Центр тяжести параллелограмма
Это утверждение в равной степени справедливо и для паралеллограмма, составленного из двух пар равных по длине стержней с одинаковой погонной плотностью.
Если однородное тело имеет несколько плоскостей или осей симметрии, то его центр тяжести находится на их пересечении. Это объясняется тем, что он должен принадлежать каждой из указанных плоскостей (осей).
Пример. Судно с нагруженным трюмом можно рассматривать как тело, разбитое на части: одной из них служит сам корпус судна, а другими – отдельные места груза. При дифферентовке (перемещении этих грузов) координаты их центров тяжести изменяются; согласно (8.3 а), меняться станет и положение центра тяжести всего нагруженного судна. Пользуясь этим, можно добиться максимальной остойчивости судна и предотвратить его переворот при сильной качке. Наоборот, неудачное закрепление грузов может привести к нежелательному смещению центра тяжести и перевороту судна.
Чтобы упростить вычисления, исследуемое тело стараются разбивать на небольшое количество участков возможно более простой формы.
Пример. Из квадрата KLMN со стороной 60 см вырезан квадрат MPQR со стороной 30 см (рис. 8.6 а). Найти центр тяжести полученного тела.
Разобьем исходное тело на два: прямоугольник KSPN и квадрат SLRQ. Пусть C1 и C2 – их центры тяжести. Введем систему координат с началом в точке K, ось x направим вдоль стороны KN, ось y – вдоль KL (рис. 8.6 б).
Исходя из сказанного выше, C1 есть точка пересечения диагоналей KSPN. В выбранной системе координат она имеет абсциссу x1 = 30 см и ординату y1 = 15 см. Аналогично, C2 (точка пересечения диагоналей квадрата SLRQ) находится на расстоянии SQ/2 = 15 см от оси y и на расстоянии KS + SL/2 = 45 см от оси x, а значит, имеет координаты x2 = 15 см, y2 = 45 см. Площади S1 и S2 участков KSPN и SLPQ равны, соответственно, 60·30 = 1800 см 2 и 30·30 = 900 см 2 . Пользуясь формулой (8.3 а), найдем координаты точки C – центра тяжести большого квадрата с вырезом:
xC = (1800·30 + 900·15)/(1800 + 900) = 25 см, yC = (1800·15 + 900·45)/(1800 + 900) = 25 см.
Таким образом, в данном случае абсцисса и ордината центра тяжести одинаковы. Этот результат легко объясним: полученное тело, несмотря на вырез, остается симметричным относительно диагонали KM, поэтому центр тяжести тела должен лежать на этой линии.
Рис. 8.7. Тело с вырезанной частью
Тогда центр тяжести C «тела с вырезом» имеет координаты
| $$x_=fracx_<1>-V_<2>x_<2>>-V_<2>>,;y_=fracy_<1>-V_<2>y_<2>>-V_<2>>,; z_=fracz_<1>-V_<2>z_<2>>-V_<2>>.$$ | (8.4) |
Это соотношение отличается от (8.3 а) лишь тем, что объем вырезаемого участка учитывается со знаком «–». Отсюда и присходит название метода (иногда вместо отрицательных объемов говорят о «методе отрицательных масс»).
Понятно, что центр тяжести объединенной системы, полученной из тела «с вырезом» и вырезанной части, должен находиться в исходной точке C1. Легко убедиться, что подстановка (8.4) в (8.3 а) дает правильный результат:
(остальные координаты вычисляются таким же образом). Изучаемый способ также называют способом дополнения, поскольку тело «с вырезом» дополняется до целого прибавлением объема V2.
Пример. Найти положение квадрата с вырезанной четвертью (см. предыдущий пример) методом отрицательных объемов.
Введем систему координат аналогично тому, как это было сделано ранее (рис. 8.8).
Центр тяжести C1 квадрата KLMN совпадает с точкой Q и имеет координаты x1 = 30 см, y1 = 30 см. Центр тяжести квадрата MPQR находится в точке C2(45; 45). Площади фигур равны 3600 см 2 и 900 см 2 , соответственно. Подставляя эти данные в формулу (8.4), найдем, что центр тяжести C фигуры KLRQPN имеет координаты
Как и следовало ожидать, результаты, найденные разными методами, совпадают.
Экспериментальный метод. Он основан на определении центра тяжести как центра параллельных сил: при одновременном их повороте (или, что то же самое, при повороте тела относительно линий действия этих сил) центр тяжести не меняет положения.
Представим, что тело подвешено за некоторую точку. Тогда на него действуют две силы: тяжести (vec G) и реакции в точке подвеса (рис. 8.9 а).
Рис. 8.9. Определение центра тяжести экспериментальным способом
Поскольку они уравновешены, линия действия силы (vec G), содержащая центр тяжести C, проходит через точку подвеса (см. первую аксиому статики). Поэтому можно отметить на теле линии действия силы тяжести при подвешивании его в нескольких разных точках (рис. 8.9 б), и искомый центр тяжести будет находиться на пересечении этих линий.
8.3. Центры тяжести некоторых однородных тел
Центр тяжести стержня располагается в его середине. Это следует из того, что стержень симметричен относительно указанной точки (рис. 8.10).
Рис. 8.10. Центр тяжести однородного стержня
Как уже было сказано ранее, центр тяжести параллелограмма располагается на пересечении его диагоналей. Аналогично, центр тяжести параллелепипеда (однородного либо «собранного» из плоских граней равной поверхностной плотности или ребер одинаковой погонной плотности) также располагается в точке пересечения его диагоналей (рис. 8.11).
Рис. 8.11. Центр тяжести однородного параллелепипеда
Центр тяжести площади треугольника располагается в точке пересечения его медиан (рис. 8.12).
Рис. 8.12. Центр тяжести однородного треугольника
Докажем это. Разрежем треугольник на полоски, паралелльные одной из его сторон. Сделаем полосы настолько тонкими, что каждую из них можно приближенно считать отрезком. В этом случае сила тяжести, действующая на треугольник в целом, станет эквивалентной системе сил, приложенных к серединам отрезков (рис. 8.13).
Эти середины заполняют собой медиану треугольника, проведенную к выбранной стороне. Следовательно, и искомый центр тяжести (точка приложения равнодействующей сил тяжести, действующих на все полоски) лежит на данной медиане.
Разрезая исходный треугольник на тонкие полоски, параллельные другой стороне, можно показать, что его центр тяжести принадлежит другой медиане. Но все медианы треугольника пересекаются в одной точке. Значит, именно в ней и находится искомый центр тяжести.
Далее найдем положение центра тяжести однородной дуги окружности с центральным углом 2α и радиусом R. Введем систему координат так, как показано на рис. 8.14.
Рис. 8.14. Определение центра тяжести однородной дуги окружности
Используя метод симметрии, легко получить, что искомая точка C лежит на оси Ox, т.е. yC = 0. Осталось найти координату xC. Для этого разобьем дугу на мелкие участки и соединим их концы с вершиной угла. Тогда он сам будет разбит на малые углы. Вследствие того, что длины участков разбиения дуги невелики, каждый из них можно считать прямолинейным отрезком длины dl = R dβ, где dβ – радианная мера соответствующего угла.
Пусть β – угол между осью Ox и отрезком, соединяющим точку O c серединой участка разбиения (см. рис. 8.14). Тогда абсцисса x центра тяжести этой дуги приближенно равна R cos β. Подставим это значение x в формулу (8.3 б). Вместо объема V в данном случае должна фигурировать длина дуги, равная R·2α, вместо множителя dV под интегралом – найденная ранее величина dl, причем угол β изменяется в пределах от –α до α:
Итак, центр тяжести однородной дуги лежит на ее оси симметрии на расстоянии (R sin α)/α от ее центра.
Замечание. Как видно, искомая точка не лежит на самой дуге. Это неудивительно, ибо дуга окружности не является выпуклой фигурой.
Выясним местоположение центра тяжести кругового сектора радиуса R и радианной меры 2α. Аналогично предыдущему случаю, можно утверждать, что искомая точка находится на оси симметрии фигуры.
Разобьем исходный центральный угол на меньшие углы Δα. Будем предполагать их настолько малыми, что соответствующие секторы можно приближенно считать равнобедренными треугольниками, боковые стороны которых равны R (рис. 8.15).
Рис. 8.15. Определение центра тяжести однородного кругового сектора
Центр тяжести каждого из таких треугольников лежит на его медиане, проведенной к основанию, и делит ее в отношении 2:1, считая от вершины (по свойству точки пересечения медиан). Поскольку в силу малости Δα длину каждой из таких медиан можно приближенно считать равной R, то центры тяжести треугольников, на которые разбит сектор, заполняют собой дугу окружности радиуса 2R/3 и той же радианной меры 2α, что и исходный сектор.
Таким образом, задача сводится к определению положения центра тяжести полученной дуги. Но из сказанного выше следует, что эта точка имеет абсциссу
Замечание 1. Правдоподобность полученных результатов можно проверить на простом частном случае. Если 2α = 2π, т.е. центральный угол является полным, то, как следует из полученных формул, центры тяжести дуги и сектора располагаются в точке с абсциссой xC = 0. Этот результат вполне предсказуем: при 2α = 2π дуга превращается в окружность, а сектор – в круг. Их центры тяжести должны лежать на элементе симметрии, т.е. в центре окружности или круга. Но у этой точки абсцисса xC заведомо равна нулю, что и требовалось.
Замечание 2. Легко видеть, что центр тяжести сектора располагается ближе к вершине центрального угла, чем центр тяжести дуги окружности того же радиуса и той же радианной меры. Этот факт нетрудно объяснить. Масса сектора распределена по его площади равномерно, а не сосредоточена вдоль криволинейной части его границы. Поэтому его центр тяжести и смещается в сторону от дуги, стягивающей центральный угол.
Центр тяжести объема конуса или пирамиды лежит на отрезке, соединяющем вершину с центром тяжести основания (рис. 8.16), и делит его в отношении 3:1, считая от этой вершины.
Рис. 8.16. Определение центра тяжести пирамиды или конуса
Тот факт, что искомый центр тяжести лежит на указанном отрезке, легко обосновать, рассуждая таким же образом, как и при поиске центра тяжести треугольника: достаточно разрезать конус на тонкие слои, параллельные основанию. Осталось найти отношение, в котором искомая точка делит отрезок OK = l (K – центр тяжести основания).
Каждая точка отрезка служит центром тяжести сечения конуса, проходящего через эту точку параллельно основанию. Значит, в произвольной точке L, лежащей на OK, сосредоточена сила, пропорциональная площади сечения, проходящего через L. Направим ось x вдоль OK; тогда K имеет абсциссу l. Рассечем изучаемое тело плоскостью OAK, проходящей через эту ось и одну из образующих конуса OA (см. рис. 8.16). Треугольники OBL и OAK подобны с коэффициентом k = x/l, где x – абсцисса L. Все сечения конуса, параллельные основанию, также подобны между собой, поэтому площадь сечения S, проходящего через L, равна k 2 S0, где S0 – площадь основания.
Для вычисления координаты центра тяжести воспользуемся формулой (7.9), в которой положим a = 0, b = l, p(x) = k 2 S0, k = x/l. После несложных вычислений получим, что xC = 3l/4. Тем самым, утверждение доказано.
Замечание. Можно воспользоваться и формулой (8.3 б), в которой тройной интеграл следует заменить интегралом по отрезку.
Как уже было сказано, рассуждения для конуса в пространстве аналогичны рассуждениям, проведенным для треугольника на плоскости. Различие состоит в отношении, в котором центр тяжести делит выбранный отрезок: на плоскости оно составляет 2:1, а в пространстве – 3:1.
Еще два результата приведем без доказательства. Пусть дан шаровой сектор радиуса R и высоты H и шаровой сегмент с теми же параметрами (рис. 8.17).
Рис. 8.17. Шаровые сектор и сегмент (сегмент выделен цветом)
Тогда центры тяжести объема сектора и площади сегмента расположены в точках с координатами
соответственно. Ось Ox является осью симметрии сектора (сегмента), начало отсчета располагается в центре шара.
Замечание. Объем шарового сектора и площадь сегмента (шарового свода) вычисляются по формулам V = 2/3 πR 2 H, S = 2πRH. При H = 2R эти равенства переходят в формулы для вычисления объема шара и площади сферы.
8.4. Пример расчета координат центра тяжести
Полусфера со срезанным верхом помещена на коробчатое основание в форме прямоугольного параллелепипеда, составленное из плоских граней. Срезанная часть заменена плоской «крышкой» в форме круга. Определить положение центра тяжести полученного тела, считая, что все его элементы однородны и имеют одинаковую поверхностную плотность. Размеры даны в см (рис. 8.18).
Изучаемое тело составлено из четырех других тел более простой формы: поверхностей параллелепипеда, круга и полусферы, от которой, в свою очередь, «отрезан» сегмент. Поскольку радиус полусферы R = 30 см, а высота полученной в итоге части равна 20 см, то высота срезанного сегмента составляет 10 см.
Введем систему координат с началом в центре полушара O, как показано на рис. 8.18. Ось Ox направим вдоль короткого горизонтального ребра параллелепипеда, ось Oy – вдоль длинного ребра, ось Oz – вертикально вверх. Поскольку тело симметрично относительно плоскости Oyz, то абсцисса центра тяжести C равна нулю. Требуется найти лишь ординату и аппликату этой точки. Используя методы разбиения и отрицательных объемов, получим, что эти координаты можно отыскать по формулам
| $$y_=fracy_<1>+S_<2>y_<2>+S_<3>y_<3>-S_<4>y_<4>>+S_<2>+S_<3>-S_<4>>,; z_=fracz_<1>+S_<2>z_<2>+S_<3>z_<3>-S_<4>z_<4>>+S_<2>+S_<3>-S_<4>>.$$ | (8.5) |
Индекс «1» относится к параллелепипеду, «2» – к полусфере, «3» – к кругу, а «4» – к срезанному сегменту (его площадь учитывается со знаком «–»). Поскольку конструкция составлена из поверхностных элементов, то в приведенных формулах фигурируют именно площади, а не объемы.
Поскольку второе по величине ребро параллелепипеда равно диаметру полушара, площадь его поверхности составляет S1 = 2·(100·60 + 100·10 + 60·10) = 15200 см 2 . Центр тяжести данной фигуры находится на расстоянии 100/2 = 50 см от ее левой грани и на расстоянии 20/2 = 10 см от ее верхней грани. Поскольку начало отсчета O лежит на верхней грани в 30 см от левого края параллелепипеда, координаты центра тяжести фигуры 1 таковы: y1 = 20 см, z1 = –5 см.
Фигура 2 представляет собой шаровой сегмент высоты H = R, с центром в точке O и осью симметрии Oz. Ее площадь S2 = 4π·30 2 /2 = 1800π см 2 , а координаты центра тяжести равны y2 = 0 см, z2 = 30 – 30/2 = 15 см.
Очевидно, что центр тяжести круга находится в точке (0; 0; 20). Радиус этого круга равен (sqrt<30^2-20^2>=sqrt<500>) см, поэтому его площадь S3 = 500π см 2 .
Площадь срезанного шарового свода равна S4 = 2π·30·10 = 600π см 2 . Ордината его центра тяжести y4 = 0 см, а аппликата z4 = 30 – 10/2 = 25 см.
Подставляя найденные параметры в (8.5), найдем, что yC ≈ 14.80 см, zC ≈ –0.34 см. Итак, C(0; 14.80; –0.34). Как и следовало ожидать, центр тяжести оказался смещен от начала координат вправо (за счет того, что фигура 1 несимметрична относительно Oz) и вниз (поскольку площадь поверхности, а значит, и вес параллелепипеда больше, чем у шарового сегмента).
Вопросы для самоконтроля
- Что такое центр тяжести? Является ли система сил тяжести, приложенных к телу, параллельной?
- В вершинах треугольника размещены материальные точки равной массы. Доказать, что центр тяжести этой системы находится в точке пересечения медиан треугольника.
- Как надо изменить расчетные формулы методов разбиения и отрицательных объемов, чтобы они оставались справедливыми и для неоднородных тел?
- На чем основан экспериментальный метод определения центра тяжести? Показать, что данный метод справедлив и для неоднородных тел.
- Как найти центр тяжести произвольного четырехугольника?
- Вывести формулу для определения координат центра тяжести однородного кругового сектора.
- Как определяется положение центра тяжести однородного конуса?
Задачи к лекции
- Вырезать из картона или плотной бумаги произвольный треугольник, определить положение его центра тяжести экспериментально. Провести в треугольнике медианы и сравнить положение их точки пересечения с положением центра тяжести.
От кругового сектора, радиус которого равен 10 см, а центральный угол – 60°, отделен сегмент (рис. 8.19). Найти положение его центра тяжести.
Найти координаты центра тяжести однородной плоской фигуры, изображенной на рис. 8.20.
Ответы. 2. Центр тяжести лежит на оси симметрии сегмента (сектора) на расстоянии около 9.2 см от вершины сектора. 3. Приближенное положение: C(4.50; 8.46).
Также рекомендуется решить задачи из §9 [2]; РГР С8 [3].
Источник
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 июля 2022 года; проверки требует 1 правка.
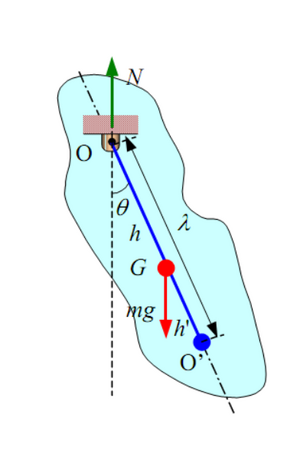
Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Дифференциальное уравнение движения физического маятника[править | править код]
Момент инерции относительно оси, проходящей через точку подвеса, по теореме Штейнера:
,
где 

Динамическое уравнение произвольного вращения твёрдого тела:
,
где 
,
где 

Момент, вызванный силой тяжести, зависит от угла отклонения тела от положения равновесия:
.
Если пренебречь сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести:
.
Если разделить обе части уравнения на 
,
получим:
.
Такое уравнение аналогично уравнению колебаний математического маятника длиной 

Центр качания физического маятника. Теорема Гюйгенса[править | править код]
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести, точку на расстоянии 
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром тяжести. Тогда момент инерции относительно оси подвеса будет равен 

Согласно теореме Гюйгенса,
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
Вычислим приведённую длину для нового маятника:
.
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
Период колебаний физического маятника[править | править код]
Наиболее общий случай[править | править код]
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания.
Для этого умножим левую 

.
Интегрируя это уравнение, получаем:
,
где 



Подставляем и преобразовываем получившееся уравнение:
Отделяем переменные и интегрируем это уравнение:
.
Удобно сделать замену переменной полагая 
Здесь 
Здесь 
Период малых колебаний физического маятника[править | править код]
Если 



Период колебания маятника в этом случае:
В иной формулировке: если амплитуда колебаний 
Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.
Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах отклонения до 1 радиана (≈57°):
См. также[править | править код]
- Математический маятник
- Маятник Дубошинского
Ссылки[править | править код]
- маятник — статья из Большой советской энциклопедии.
|
|
Макеты страниц
336. Приведение движения физического маятника к движению простого маятника.
Физическим маятником называют твердое телэ, находящееся под действием только
собственного веса и имеющее неподвижную горизонтальную ось, вокруг которой оно может свободно вращаться без трения.
Проведем через центр тяжести Г тела (фиг. 44) вертикальную плоскость, перпендикулярную к неподвижной оси и пересекающую эту ось в точке О. Примем точку О за начало координат. Проведем ось Oz вертикально в сторону действия тяжести и примем только что нами определенную вертикальную плоскость за плоскость 
Прямая ОГ будет двигаться в этой плоскости, и движение этой прямой позволит определить движение всего тела.

Фиг. 44
Обозначим через а расстояние ОГ, через 
Уравнение движения может быть выведено, как в предыдущем параграфе, из теоремы моментов, которая приводит к дифференциальному уравнению второго порядка. В данном случае, однако, удобнее применить теорему живых сил, которая непосредственно дает уравнение первого порядка. Живая сила в начальный момент по предположению равна нулю; поэтому ее приращение в момент t равно самой живой силе, т. е. 






Заменим 

тогда получим

Это уравнение может быть написано в виде

где постоянная I определяется уравнением

Уравнение (1), определяющее угол 


Отложим на прямой ОГ от точки О длину ОС, равную 
Длина О простого синхронного маятника называется также длиной физического маятника.
Все свойства, установленные для простого маятника, применимы поэтому и к физическому маятнику. Его движение является колебательным и периодическим. Бесконечно малые колебания изохронны, и период простого колебания (половина периода полного колебания) определяется асимптотической формулой:

337. Свойства центра колебаний и точки подвеса.
Точка подвеса О и центр колебаний С обладают замечательными свойствами, которые были открыты Гюйгенсом.
1°. Центр тяжести Г лежит между точкой подвеса а центром колебаний.
Чтобы это доказать, покажем, что 

Мы имеем (п° 319)

Разделим это равенство на 

2°. Точка подвеса и центр колебаний взаимны между собой.
Под этим понимают, что если заставить тело вращаться вокруг оси, проведенной в этом теле через точку С (ранее бывшую центром колебаний) параллельно прежней оси, проходившей через О, то точка О будет центром колебаний нового маятника.
Действительно, предыдущая формула дает

Множители а и 

Величина 
3°. Длина l маятника остается той же самой для всех осей подвеса, параллельных между собой и лежащих 
В самом деле, k и а имеют соответственно одни и те же значения для всех указанных случаев, и формула (3) дает поэтому одно и то же значение для l.
4°. Для всех осей подвеса, параллельных одному и тому же направлению, данному в теле, длина l маятника будет, наименьшей, когда ось находится на расстоянии 
Заметим, что k есть постоянная величина для этих параллельных между собой направлений, а потому l зависит только от а. Дифференцируя формулу (3) по а, получим

Эта производная переходит от отрицательных значений к положительным (вместе с множителем 


Таким образом, для осей подвеса, имеющих одно и то же направление в теле, длина маятника будет наименьшей, когда центр тяжести находится на равных расстояниях от центра колебаний и центра подвеса.
338. Маятник Борда.
Борда для измерения ускорения силы тяжести пользовался физическим маятником, представлявшим собой платиновый шар радиуса R, подвешенный к неподвижной точке О на очень тонкой металлической нити, масса которой была так мала, что можно было считать центр тяжести маятника совпадающим с центром шара О. Принимая во внимание, что расстояние 

где вместо величины 

В маятнике, применявшемся Борда, было 

339. Оборотный маятник Катера. Теорема Гюйгенса.
Гюйгенс доказал следующую теорему:
Если в плоскости, проходящей через центр тяжести твердого тела, возьмем две параллельные между собой оси подвеса, расположенные по ту и другую стороны от центра тяжести и на различных расстояниях от него, и если длина l простого синхронного маятника одна и та же в обоих случаях, то эта длина в точности равна расстоянию между осями.
Пусть 

Таким образом, а и 

Следовательно, на основании свойств корней квадратного уравнения, имеем а 

Фиг. 45
По этому принципу построен оборотный маятник Катера, который применяется в геодезии, так как его устройство позволяет легко получить заданную длину маятника.
Маятник Катера (фиг. 45) состоит из латунной линейки, имеющей две призмы С и С, ребра которых параллельны и расположены в плоскости симметрии линейки. Массивная чечевица, помещенная у одного из концов линейки, обеспечивает выполнение условия, чтобы центр тяжести не совпадал с серединой расстояния между ребрами призм. Две ползушки а и а, которые могут скользить по линейке и из которых одна перемещается посредством винта, соединенного с другой, позволяют легко изменять положение центра тяжести. Маятник заставляют колебаться попеременно около каждой из призм и, действуя ползушками, добиваются после ряда проб, чтобы периоды
колебаний в обоих случаях сделались одинаковыми. Длина синхронного маятника окажется при этом равной расстоянию между ребрами призм.
340. Наклонный маятник.
Если ось подвеса не горизонтальна, то маятник будет наклонным. Теория для этого случая не отличается от той, которая изложена выше. Движущей силой является постоянная проекция силы тяжести на плоскость, перпендикулярную к наклонной оси. Пусть а есть угол наклона оси подвеса к горизонтальной плоскости; проекция силы тяжести на плоскость, перпендикулярную к оси, равна 


Длина синхронного маятника с таким периодом будет 
Оглавление
- ЧАСТЬ ЧЕТВЕРТАЯ. ДИНАМИКА СИСТЕМ. ОБЩИЕ ТЕОРЕМЫ
- § 2. ТЕОРЕМА МОМЕНТОВ И ТЕОРЕМА ПЛОЩАДЕЙ
- § 3. ТЕОРЕМА ЖИВЫХ СИЛ
- § 4. ТЕОРЕМА ЭНЕРГИИ
- ГЛАВА XIII. ОБЩИЕ ТЕОРЕМЫ В ОТНОСИТЕЛЬНОМ ДВИЖЕНИИ ОКОЛО ЦЕНТРА ИНЕРЦИЙ
- § 1. КОЛИЧЕСТВО ДВИЖЕНИЯ И ЖИВАЯ СИЛА В ОТНОСИТЕЛЬНОМ ДВИЖЕНИИ
- § 2. ТЕОРЕМА МОМЕНТОВ И ТЕОРЕМА ПЛОЩАДЕЙ В ОТНОСИТЕЛЬНОМ ДВИЖЕНИИ ОКОЛО ЦЕНТРА ИНЕРЦИИ
- § 3. ТЕОРЕМЫ ЖИВЫХ СИЛ И ЭНЕРГИИ
- ГЛАВА XIV. ТЕОРИЯ УДАРА. ОБЩИЕ ТЕОРЕМЫ
- § 1. УДАРЫ, ПРИЛОЖЕННЫЕ К ТОЧКЕ
- § 2. УДАРЫ, ПРИЛОЖЕННЫЕ К МАТЕРИАЛЬНОЙ СИСТЕМЕ. ПРЕОБРАЗОВАНИЕ ОБЩИХ ТЕОРЕМ
- § 3. ИЗМЕНЕНИЕ ЖИВОЙ СИЛЫ В ТЕЧЕНИЕ УДАРА
- § 4. ПРИЛОЖЕНИЕ. УДАР ДВУХ ТЕЛ
- ЧАСТЬ ПЯТАЯ. ДИНАМИКА ТВЕРДОГО ТЕЛА
- § 1. ОПРЕДЕЛЕНИЯ, ЭЛЛИПСОИД ИНЕРЦИИ
- § 2. ПРИМЕРЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН, КОТОРЫЕ ВЫРАЖАЮТСЯ ЧЕРЕЗ МОМЕНТЫ ИНЕРЦИИ ИЛИ ЧЕРЕЗ ПРОИЗВЕДЕНИЯ ИНЕРЦИИ
- § 3. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СПЛОШНЫХ ТЕЛ
- ГЛАВА XVI. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ ДВИЖЕНИЯ И РЕАКЦИЙ
- § 2. ТЕОРИЯ ФИЗИЧЕСКОГО МАЯТНИКА
- § 3. УДАРЫ, ПРИЛОЖЕННЫЕ К ТВЕРДОМУ ТЕЛУ, ИМЕЮЩЕМУ НЕПОДВИЖНУЮ ОСЬ
- ГЛАВА XVII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ
- § 1. УРАВНЕНИЯ ЭЙЛЕРА
- § 2. СЛУЧАЙ, КОГДА ГЛАВНЫЙ МОМЕНТ ПРИЛОЖЕННЫХ СИЛ ОТНОСИТЕЛЬНО НЕПОДВИЖНОЙ ТОЧКИ РАВЕН НУЛЮ
- § 3. СЛУЧАЙ ИНТЕГРИРУЕМОСТИ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ В ДВИЖЕНИИ ПО ПУАНСО
- § 4. УДАРЫ, ПРИЛОЖЕННЫЕ К ТВЕРДОМУ ТЕЛУ, ИМЕЮЩЕМУ НЕПОДВИЖНУЮ ТОЧКУ
- ГЛАВА XVIII. ДВИЖЕНИЕ ТЯЖЕЛОГО ТЕЛА ВРАЩЕНИЯ, ЗАКРЕПЛЕННОГО В ОДНОЙ ИЗ ТОЧЕК ЕГО ОСИ
- § 1. НАЧАЛЬНОЕ ВРАЩЕНИЕ ПРОИСХОДИТ ВОКРУГ ОСИ ТЕЛА
- § 2. ДВИЖЕНИЕ ТЯЖЕЛОГО ТЕЛА ВРАЩЕНИЯ, ЗАКРЕПЛЕННОГО В ОДНОЙ ИЗ ТОЧЕК СВОЕЙ ОСИ, ПРИ ПРОИЗВОЛЬНЫХ НАЧАЛЬНЫХ УСЛОВИЯХ
- § 3. ОСОБЫЕ СЛУЧАИ ПРЕДЫДУЩЕЙ ЗАДАЧИ
- § 4. ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ В СЛУЧАЕ, КОГДА СОСТАВЛЯЮЩАЯ r0 НАЧАЛЬНОЙ УГЛОВОЙ СКОРОСТИ ОЧЕНЬ ВЕЛИКА
- § 5. СЛОЖНЫЙ СФЕРИЧЕСКИЙ МАЯТНИК
- ГЛАВА XIX. ГИРОСКОПИЧЕСКИЙ ЭФФЕКТ В ДВИЖЕНИИ ТВЕРДОГО ТЕЛА ВРАЩЕНИЯ ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ
- § 1. ГИРОСКОПИЧЕСКИЙ ЭФФЕКТ. СТРЕМЛЕНИЕ ОСЕЙ ВРАЩЕНИЯ К ПАРАЛЛЕЛЬНОСТИ
- § 2. ПРИМЕНЕНИЕ ОСЕЙ, ДВИЖУЩИХСЯ В ПРОСТРАНСТВЕ И В ТЕЛЕ
- § 3. ГИРОСКОПИЧЕСКИЙ ЭФФЕКТ В ОТНОСИТЕЛЬНОМ ДВИЖЕНИИ, КОГДА ПЕРЕНОСНОЕ ДВИЖЕНИЕ ЕСТЬ РАВНОМЕРНОЕ ВРАЩЕНИЕ
- § 4. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ОСИ ГИРОСКОПА В ПЛОСКОСТИ, СОВЕРШАЮЩЕЙ РАВНОМЕРНОЕ ВРАЩЕНИЕ
- § 5. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ГИРОСКОПА У ПОВЕРХНОСТИ ЗЕМЛИ
- ГЛАВА XX. ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 1. ОПРЕДЕЛЕНИЕ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 2. РАЗЛИЧНЫЕ ПРИМЕРЫ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 3. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ВРАЩЕНИЯ, ОПИРАЮЩЕГОСЯ НА ГОРИЗОНТАЛЬНУЮ ПЛОСКОСТЬ
- ЧАСТЬ ШЕСТАЯ. УРАВНЕНИЯ МЕХАНИКИ
- § 1. ТЕОРЕМА ДАЛАМБЕРА. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- § 2. УРАВНЕНИЯ ЛАГРАНЖА
- § 3. ПРИНЦИП ГАМИЛЬТОНА
- § 4. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
- ГЛАВА XXII. КАНОНИЧЕСКИЕ УРАВНЕНИЯ
- § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
- § 2. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ
- § 3. ПРИМЕНЕНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ К НЕКОТОРЫМ КЛАССИЧЕСКИМ ЗАДАЧАМ
- ЧАСТЬ СЕДЬМАЯ. МЕХАНИКА ЖИДКОСТЕЙ
- ГЛАВА XXIII. ГИДРОСТАТИКА
- § 2. ДАВЛЕНИЯ, ПРОИЗВОДИМЫЕ НА ТВЕРДОЕ ТЕЛО, НАХОДЯЩЕЕСЯ В ЖИДКОСТИ
- § 3. ОТНОСИТЕЛЬНОЕ РАВНОВЕСИЕ. РАВНОВЕСИЕ ЖИДКОСТИ, НАХОДЯЩЕЙСЯ В РАВНОМЕРНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- ГЛАВА XXIV. РАВНОВЕСИЕ ПЛАВАЮЩИХ ТЕЛ
- § 1. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА, ОПИРАЮЩЕГОСЯ НА ГОРИЗОНТАЛЬНУЮ ПЛОСКОСТЬ ОДНОЙ ТОЧКОЙ
- § 2. ТЕОРЕМЫ ДЮПЕНА
- § 3. РАВНОВЕСИЕ ПЛАВАЮЩЕГО ТЕЛА
- ГЛАВА XXV. ДИНАМИКА ЖИДКОСТЕЙ
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
- § 2. УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ
- § 3. КИНЕМАТИКА ЖИДКОЙ ЧАСТИЦЫ
- § 4. ОБЩИЕ СВОЙСТВА ДВИЖЕНИЯ ЖИДКОСТИ. ВИХРИ
- ДОБАВЛЕНИЯ. I. О ПРИНЦИПЕ НАИМЕНЬШЕГО ПРИНУЖДЕНИЯ
- II. О ПРИНЦИПЕ НАИМЕНЬШЕГО ДЕЙСТВИЯ
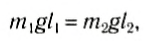
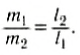
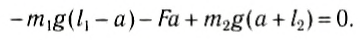
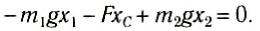
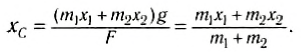
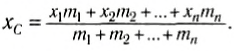
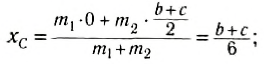
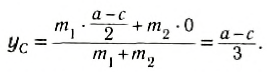








































![{displaystyle T=2pi {sqrt {frac {lambda }{g}}}left{1+left({frac {1}{2}}right)^{2}sin ^{2}left({frac {alpha }{2}}right)+left({frac {1cdot 3}{2cdot 4}}right)^{2}sin ^{4}left({frac {alpha }{2}}right)+dots +left[{frac {left(2n-1right)!!}{left(2nright)!!}}right]^{2}sin ^{2n}left({frac {alpha }{2}}right)+dots right}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aae1c69041f6957ab485b97bcbe5025dc688c47a)





