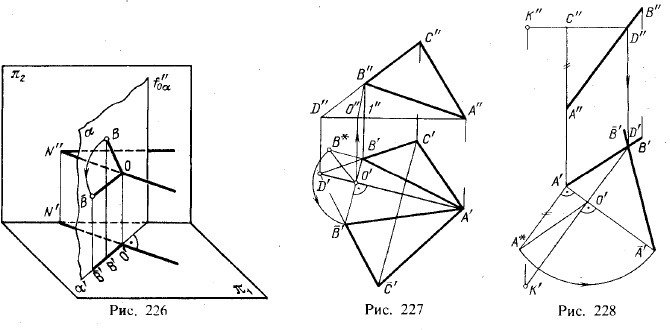
Поворот плоской фигуры вокруг ее горизонтали. Для определения формы и размеров плоской фигуры можно ее повернуть вокруг принадлежащей ей горизонтали так, чтобы в результате вращения фигура расположилась параллельно плоскости π1.
Рассмотрим сначала поворот точки (рис. 226). Точка В вращается вокруг некоторой горизонтально расположенной оси ON”, описывая дугу окружности, лежащую в пл. α. Эта плоскость перпендикулярна к оси вращения и, следовательно, является горизонтально-проецирующей; поэтому горизонтальная проекция окружности, описываемой точкой В, должна находиться на α’.
Если радиус ОВ займет положение, параллельное пл. π1 то проекция О’B‘ окажется равной ОВ, т. е. равной натуральной величине радиуса ОВ.
Теперь рассмотрим рис. 227. На нем показан поворот треугольника АВС. В качестве оси вращения взята горизонталь AD. Точка А, расположенная на оси
1) Получающаяся при этом проекция куба на пл. π2 (рис. 225) совпадает с изображением куба в прямоугольной изометрической проекции, изучаемой в курсе черчения средней школы.
вращения, останется на месте. Следовательно, для изображения горизонтальной проекции треугольника после поворота надо найти положение проекций других двух его вершин. Опуская из точки В’ перпендикуляр на A’D’, находим горизонтальную проекцию центра вращения — точку О’ и горизонтальную проекцию радиуса вращения точки В — отрезок О’В’, а затем фронтальную проекцию центра вращения — точку О” и фронтальную проекцию радиуса вращения точки В — отрезок 0″В”. Теперь надо определить натуральную величину радиуса вращения точки В. Для этого применен способ, указанный в § 13, т. е. построение прямоугольного треугольника. По катетам О’В’ и В’В* = В”1″ строим прямоугольный треугольник О’В’В*, гипотенуза его равна радиусу вращения точки В.
Теперь можно найти положение точки B‘, а затем точки С‘, причем не определять радиус вращения точки С, а найти положение точки С‘ в пересечении двух прямых, из которых одна является перпендикуляром, проведенным из точки С’ к прямой A’D’, а другая проходит через найденную точку B‘ и точку D’ (горю зонтальную проекцию точки D, принадлежащей стороне ВС и расположенной на оси вращения).
Проекция А’B‘С‘ выражает натуральную величину ΔАВС, так как после поворота плоскость треугольника параллельна пл. π1. Фронтальная же проекция треугольника совпадает с фронтальной проекцией горизонтали, т. е. представляет собой прямую линию.
На рис. 227 дано построение для случая, когда горизонталь проведена вне проекций треугольника. Это позволяет избежать наложения проекций одной на другую, но чертеж занимает большую площадь.
Если требуется повернуть плоскую фигуру до положения параллельного пл. π2, то за ось вращения надо выбрать фронталь.
Обратим внимание на то, что в построении, показанном на рис. 226, фронтальная проекция радиуса вращения точки В не участвует. Очевидно, поняв сущность построения, можно не строить этой проекции. Пример дан на рис. 228, где показан поворот плоскости, заданной точкой К и прямой АВ, до положения, параллельного пл. π1. Поворот совершен вокруг горизонтали KD. Горизонталь проведена через точку К, которая, следовательно, останется «неподвижной». Остается повернуть прямую АВ вокруг KD, точнее, повернуть, например, только точку А, так как точка D на прямой АВ также «неподвижна»: она принадлежит оси вращения. Проведя А’О’⊥ K’D’, т. е. наметив положение горизонтального следа той горизонтально-проецирующей плоскости, в которой находится и поворачивается точка А, получаем точку О’ — горизонтальную проекцию центра вращения точки А и О’А’ — горизонтальную проекцию радиуса вращения точки А. Теперь находим натуральную величину радиуса вращения RA как гипотенузу треугольника О’А’А*, в котором катет А’А*_= А”С”. Найдя точку А’ — горизонтальную проекцию точки А после поворота, проводим А’В’ — горизонтальную проекцию прямой АВ после поворота, пользуясь точкой D’. Итак, мы обошлись без фронтальных проекций центра вращения и радиуса вращения.
Поворот плоскости вокруг ее следа до совмещения с соответствующей плоскостью проекций 1). Если плоскость вращать вокруг ее следа до совмещения с плоскостью проекций, в которой расположен этот след, то отрезки линий и фигуры, расположенные в плоскости, изобразятся без искажения. Очевидно, это построение аналогично по своему содержанию повороту плоскости вокруг ее горизонтали или фронтали до параллельности соответствующей плоскости проекций: следы плоскости можно рассматривать — горизонтальный след как «нулевую» горизонталь плоскости, фронтальный — как «нулевую» фронталь.
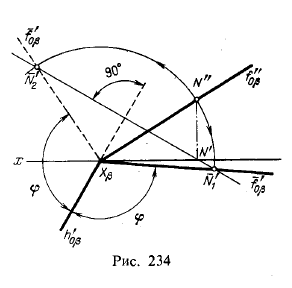
На рис. 229 показано совмещение плоскости общего положения α с плоскостью π1 причем поворот произведен вокруг h’0α в направлении от плоскости π2 к зрителю.
В положении совмещения с пл. π1 на пл. α окажутся две пересекающиеся прямые — след h’0α и прямая f“0α которая представляет собой след f”0α, совмещенный с пл. π1.
1) Этот случай известен также под названием «способ совмещения».
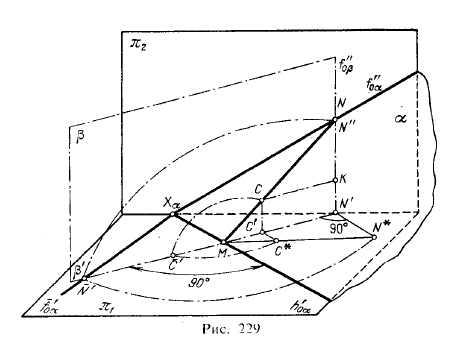
След h’0α как ось вращениπ1 не меняет своего положения; точка пересечения следов также не меняет своего положения, а потому, если бы требовалось указать совмещенное положение следа f”0α то достаточно было бы найти еще одну точку этого следа (кроме точки Xα) в положении совмещения в пл. π1. Найдем совмещенное положение какой-нибудь точки N, лежащей на следе f”0α. Эта точка опишет дугу окружности в пл. β, перпендикулярной к оси вращения; центр этой дуги лежит в точке М пересечения пл. β со следом h’0α. Описывая из точки М дугу радиусом MN в пл. β мы получаем в пересечении этой дуги с β’ точку N’ на пл. π1. Проведя через Xα, и N‘ прямую, получим f‘0α. Так как отрезок XαN не изменяет своей величины при вращении плоскости, то, очевидно, точку N‘ можно получить в пересечении β’ с дугой, описанной в пл. π1, из Хα радиусом XαN.
На чертеже (рис. 230) на следе f”0α выбрана произвольная точка N (она совпадает со своей проекцией N”); через ее проекцию N’ проведена прямая N’M, перпендикулярная к оси вращения — следу h’0α. На этой прямой должна лежать точка N после совмещения с пл. π1 на расстоянии от точки М, равном радиусу вращения точки N, или на расстоянии XαN” от точки Хα. Длину радиуса вращения можно определить как гипотенузу прямоугольного треугольника с катетами MN’ и N’N* (N’N* = N”N’). Проводя из точки М дугу радиуса MN* или из точки Xα дугу радиуса ХαN”, получаем на прямой N’M совмещенное с пл. π1 положение точки N — точку N’. Проведя через точки Хα и N‘ прямую, получим совмещенное положение следа f”0α – прямую f’0α.
Вернемся к рис. 229 и рассмотрим на нем совмещение точки С с пл. π1
Нахождение совмещенного положения точки С с пл. π1 показано на рис. 231 слева. Через точку С’ проведена прямая С’М, перпендикулярная к h’0α. Радиус вращения МС* найден как гипотенуза прямоугольного треугольника, у которого один катет СМ, а другой катет С’С* = С”1. Радиусом МС* проводим из точки М дугу и засекаем на продолжении прямой СМ точку С‘ — положение точки С в пл. π1.
Это построение можно выполнить и так, как показано на рис. 231 справа. Установив положение точки С в пл. α при помощи фронтали и проведя прямую С’М перпендикулярно к h’0α, засекаем эту прямую из точки L’, как из центра, дугой, радиус которой равен отрезку С”L”, т. е. натуральной величине отрезка CL в пл. α. В совмещении эта величина сохраняется: C‘L’ = СL
Если в плоскости дан отрезок прямой, то, найдя совмещенное положение концов этого отрезка, мы получаем натуральную величину отрезка.
Как известно, каждая горизонталь, взятая в пл. α, располагается параллельно h’0α, а фронталь — параллельно f”0α поэтому, если придется находить совмещенное положение горизонтали или фронтали, достаточно будет найти совмещенное положение их следа, через который и провести прямую, параллельную соответственно h’0α или f“0α (если пл. α совмещена с пл. π1)
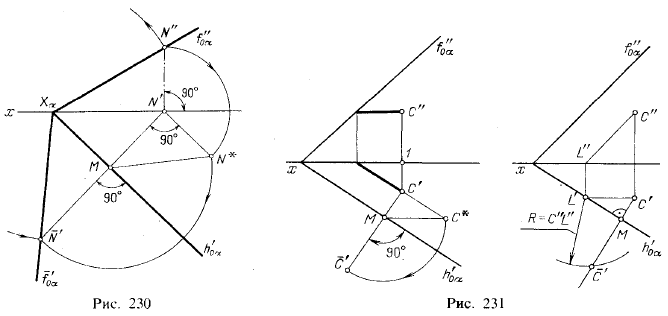
Этим мы воспользуемся для обратного построения. Пусть задана точка С‘ — совмещенное с пл. π1 положение точки С; требуется найти проекции точки С, если она должна_лежать в пл. α, заданной следами (см. также рис. 229).
Когда точку С‘ «поднимают в пространство», то горизонтальная ее проекция — точка С’ — перемещается по прямой СN’ (рис. 232), перпендикулярной к h’0α т. е.
по следу β’ плоскости вращения β. Точка С в пространстве должна лежать на линии пересечения плоскости α с плоскостью вращения (рис. 229) на расстоянии МС‘ от точки М.
Построим на пл. π1 прямоугольный треугольник MN’N*, у которого сторона N’N* = N”N’ (рис. 232) и который, следовательно, равен треугольнику MN’N” в пространстве.
Откладывая на гипотенузе MN* от точки М отрезок МС‘ (радиус вращения), получаем точку С*. Проведя через нее прямую, перпендикулярную к MN’, получим точку С’ — искомое положение горизонтальной проекции точки С.
Точка С” должна находиться на перпендикуляре, проведенном из точки С’ к оси х на расстоянии С”1, равном С’С*.
Если надо «поднять в пространство» отрезок прямой линии, то следует в общем случае поднять две его точки так, как это только что было указано, или использовать так называемую «неподвижную» точку. Это показано на рис. 233, где надо было «поднять в пространство» (т. е. на пл. α) отрезок АВ, заданный в совмещенном с пл. положении (A‘B‘). Построение несколько усложнено тем, что точка пересечения следов f”0α и h’0α считается недоступной.
Построена вспомогательная пл. β||α, и найден след f‘0β совмещении с пл. π1. Так как β||α то f‘0β определяет направление фронталей как пл. β, так и пл. α в совмещенном с пл. π1 положении. Поэтому, проведя B‘N’||f‘0β, получаем в совмещении с пл. π1 фронталь пл. α, на которой расположена в пространстве точка В. Построив проекции этой фронтали, находим на них проекции В’ и В”. Если же теперь продолжить прямую A‘B‘ до пересечения в точке М’ со следом h’0α, то на прямой, проходящей через эту «неподвижную» точку М’ и через построенную проекцию В’, расположится горизонтальная проекция А’В’. Проекция А”В” получится на прямой, проходящей через точки М” и В”.
Нами рассмотрено совмещение плоскости с горизонтальной плоскостью проекций, причем вращение плоскости производилось вокруг горизонтального следа. Если требуется совместить ее с фронтальной плоскостью проекций, то следует вращать плоскость вокруг ее фронтального следа.
Если горизонтально-проецирующую плоскость вращать вокруг ее фронтального следа до совмещения с пл. π2, то горизонтальный след плоскости после Совмещения расположится на оси проекций. Также, если фронтально-проецирующую плоскость вращать вокруг ее горизонтального следа до совмещения с пл. π1 то фронтальный след плоскости расположится на оси проекций.
На рис. 234 изображена плоскость с тупым углом между следами f”0β и h’0β в совмещении с пл. π1 при «вращении на зрителя» и при вращении в обратном направлении.
Вопросы к §§ 36-37
- Можно ли показать на чертеже поворот, например, прямой вокруг оси, перпендикулярной к пл. π1, или пл. π2, не изображая самой оси? На чем основан такой прием?
- Какое название встречается для вращения без изображения оси?
- Как располагается плоскость вращения точки, если ось вращения последней лишь параллельна пл. π1 или пл. π2, но не перпендикулярна ни к π1 ни к π2? Почему при этом приходится определять натуральную величину радиуса вращения?
- Что служит признаком достижения горизонтального положения плоскости, заданной горизонталью и точкой, при повороте вокруг этой горизонтали и где получается фронтальная проекция точки после поворота?
- Что понимается под названием «способ совмещения»?
- Что понимается под названием «подъем в пространство»?
Цели урока:
Образовательные
- ввести понятие поворота и доказать, что поворот
есть движение; - рассмотреть поворот отрезка, в зависимости от
центра поворота (центр поворота лежит вне
отрезка, на отрезке и является одним из концов
отрезка); - научить построению отрезка при повороте его на
данный угол; - проверить усвоение материала, изученного на
предыдущих уроках и материала, пройденного на
этом уроке.
Развивающие
- развивать умение анализировать условие задачи,
строить логическую цепочку при решении задач,
обоснованно делать выводы; - развивать мыслительный процесс, познавательный
интерес, математическую речь учащихся;
Воспитательные
- воспитывать внимательность, наблюдательность,
положительное отношение к обучению.
Содержание темы: урок по геометрии
разработан для учащихся 9 класса.
Тип урока: урок изучения нового
материала и промежуточного контроля усвоения
учащимися пройденного на этом уроке и изученного
ранее материала.
Организационные формы общения: коллективная,
индивидуальная, фронтальная, в парах.
Структура занятия:
- Мотивационная беседа с учащимися с последующей
постановкой целей; - Проверка домашнего задания;
- Актуализация опорных знаний;
- Обогащение знаний;
- Закрепление изученного материала;
- Проверка усвоения изученного материала
(тестирование с последующей взаимопроверкой); - Подведение итога занятия (рефлексия);
- Домашнее задание.
Оформление: мультимедийный
проектор, экран, ноутбук, компьютерная
презентация, сигнальные карточки.
Мотивационная беседа.
Без движения — жизнь только
летаргический сон.
Жан Жак Руссо
I. Сообщение темы, целей и хода урока.
(СЛАЙД 2)
– Ребята, Вы знаете какую важную роль имеет
движение в жизни человека, общества, науки.
Большую роль играет движение и в математике:
преобразование графиков, отображение точек,
фигур, плоскостей – всё это движение. На
предыдущих уроках мы с Вами рассмотрели
несколько видов движения. Сегодня мы
познакомимся ещё с одним видом движения:
поворотом. Тема урока: поворот.
И наш урок тоже является примером движения,
только движения не с физической точки зрения, а
движением в умственном развитии, познании нового
и приобретения новых знаний. В течение всего
урока Вы будете выполнять различные задачи,
тесты. Поэтому будьте активны, продвигайтесь в
своих знаниях вперёд на протяжении всего урока и
улучшайте свои результаты от одного этапа к
другому!
В течение всего урока, как мою речь, так и вашу
будет сопровождать презентация, которая поможет
проверить правильность выполнения Вами домашней
работы, предложенных тестов и самостоятельно
решённых задач.
II. Проверка домашнего задания.
С помощью СЛАЙДОВ 3-5 проверить решение № 1165.
III. Актуализация опорных знаний.
Тест №1. (СЛАЙДЫ 6-13)
Приложение 1
После выполнения теста ребята обмениваются
тетрадями и выполняют взаимопроверку.
IV. Изучение нового материала.
(обогащение знаний)
(СЛАЙД 14) Отметим на плоскости точку О
(неподвижная точка), и зададим угол a – угол
поворота. Поворотом плоскости вокруг точки О на
угол a называется отображение плоскости на
себя, при котором каждая точка M отображается в
такую точку M1, что OM =OM1 и угол MOM1
= a.
(СЛАЙД 15) При этом точка O остаётся на месте, т.е.
отображается сама в себя, а все остальные точки
поворачиваются вокруг точки O в одном и том же
направлении на угол a по часовой стрелки или
против часовой стрелки.
(СЛАЙД 16) Точка О называется центром поворота, a
– угол поворота. Обозначается Роa.
(СЛАЙД 17) Если поворот выполняется по часовой
стрелке, то угол поворота a считается
отрицательным. Если поворот выполняется против
часовой стрелки, то угол поворота –
положительный.
– Ребята, давайте вспомним понятие движения. Как
Вы думаете, является ли поворот движением?
(высказывают предположения)
– Поворот – является движением, т.е.
отображением плоскости на себя. Докажем это.
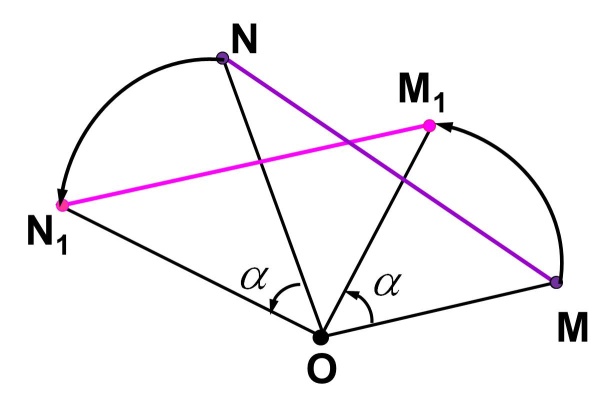
Рис.1
(СЛАЙД 18 или СЛАЙД 19)
(Доказательство может выполнить сильный ученик
по СЛАЙДУ 18. В этом случае можно сразу после
доказательства перейти к СЛАЙДУ 20.
Доказательство может выполнить учитель вместе с
классом по СЛАЙДУ 19, на котором отображаются
этапы доказательства.)
V. Закрепление изученного материала.
Задание. Построить точку M1,
которая получается из точки M поворотом на угол 60o.
Поэтапно с помощью слайда 20 прорабатывается
построение точки M1.
(СЛАЙД 20)
– Какие инструменты нам понадобятся для того,
чтобы выполнить поворот? (линейка, циркуль,
транспортир)
– Ребята, что сначала нужно отметить? (точку M и
центр поворота – точку O)
– Как задаём центр поворота? Отмечаем в
определённом месте? (нет, произвольно)
– Как будем выполнять поворот по часовой или
против часовой стрелки? Почему? (против, т.к. угол
положительный)
– Что нужно построить, чтобы отложить угол 60o?
(луч OM)
– Как найти на второй стороне угла точку M1?
(с помощью циркуля отложить отрезок OM1=OM)
– Рассмотрим, как выполняется поворот отрезка в
зависимости от расположения центра поворота.
– Рассмотрим случай, когда центр поворота лежит
вне отрезка. Решим № 1166 (а). (Если класс сильный, то
можно вместе с детьми составить план решения
задачи, дать задание решить № 1166 (а)
самостоятельно. Решение проверить с помощью
СЛАЙДА 21. Если ребята затрудняются с выполнением
задания, то решать коллективно, опираясь на СЛАЙД
21)
Работа в парах.
Задание. Построить фигуру, которая
получится при повороте отрезка AB на угол – 100o
вокруг точки А.
(наводящие вопросы)
– Какая точка является центром поворота? Что
можно о ней сказать? (это один из концов отрезка –
точка А, она будет неподвижной, оставаться на
месте)
– Как будем выполнять поворот по часовой
стрелки или против часовой? (по часовой, т.к. угол
отрицательный)
– Составьте план решения задачи.
Задание выполняют по парам. Проверяют решение с
помощью СЛАЙДА 22.
Индивидуальная работа.
Задание. Построить фигуру, в которую
переходит отрезок AB при повороте на угол – 100o
вокруг точки О – середины отрезка AB.
– Составьте план решения задачи. Задание
выполняют самостоятельно, решение проверяем с
помощью СЛАЙДА 23.
– Сегодня на уроке мы рассмотрели поворот
отрезка в зависимости от расположения центра
поворота. На следующих уроках мы рассмотрим
повороты других фигур. (продемонстрировать
СЛАЙДЫ 24-25)
VI. Проверка усвоения изученного материала.
Тест №2. (СЛАЙДЫ 26-30)
Приложение 2
Самопроверка.
VII. Подведение итога урока. (рефлексия)
– Ребята, давайте выделим тех, кто был лучшим на
каждом этапе. (подводится итог, выставляются
оценки)
– Поднимите руки, кому понравился урок.
Отметьте, что интересного было на уроке?
VII. Домашнее задание.
- № 1166 (б), № 1167 – для тех, кто получил оценку “3”.
- № 1167 (рассмотреть три случая расположения
центра поворота: центр – вершина А, центр
расположен вне треугольника, центр лежит на
стороне АВ треугольника) – для тех, кто получил
оценку “4” и “5”.
Содержание:
Геометрические преобразования:
В этой лекции вы узнаете, что такое преобразование фигуры. Ознакомитесь с такими видами преобразований, как параллельный перенос, центральная симметрия, осевая симметрия, поворот, гомотетия, подобие.
Вы научитесь применять свойства преобразований при решении задач и доказательстве теорем.
Движение (перемещение) фигуры. Параллельный перенос
Пример:
На рисунке 17.1 изображены отрезок 
Мы указали правило, с помощью которого каждой точке 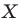 отрезка
отрезка 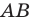 поставлена в соответствие единственная точка
поставлена в соответствие единственная точка 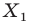 отрезка
отрезка 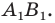 В этом случае говорят, что отрезок
В этом случае говорят, что отрезок 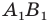 получен в результате преобразования отрезка
получен в результате преобразования отрезка 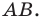
Пример:
На рисунке 17.2 изображены полуокружность 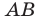 и прямая
и прямая 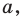 параллельная диаметру
параллельная диаметру 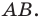 Каждой точке
Каждой точке 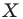 полуокружности поставим в соответствие точку
полуокружности поставим в соответствие точку 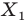 прямой а так, чтобы прямая
прямой а так, чтобы прямая 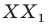 была перпендикулярна прямой
была перпендикулярна прямой 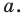 Понятно, что все такие точки
Понятно, что все такие точки 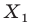 образуют отрезок
образуют отрезок 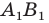 В этом случае говорят, что отрезок
В этом случае говорят, что отрезок 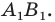 получен в результате преобразования полуокружности
получен в результате преобразования полуокружности 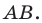
Пример:
Пусть даны некоторая фигура 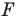 и вектор
и вектор  (рис. 17.3). Каждой точке
(рис. 17.3). Каждой точке 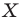 фигуры
фигуры 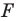 поставим в соответствие точку
поставим в соответствие точку 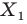 такую, что
такую, что 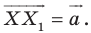 В результате такого преобразования фигуры
В результате такого преобразования фигуры 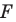 получим фигуру
получим фигуру 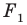 (рис. 17.3). Такое преобразование фигуры
(рис. 17.3). Такое преобразование фигуры 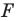 называют параллельным переносом на вектор
называют параллельным переносом на вектор 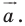
Обобщим приведенные примеры.
Пусть задана некоторая фигура 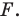 Каждой точке фигуры
Каждой точке фигуры 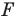 поставим в соответствие (сопоставим) по определенному правилу некоторую точку. Все полученные сопоставленные точки образуют фигуру
поставим в соответствие (сопоставим) по определенному правилу некоторую точку. Все полученные сопоставленные точки образуют фигуру 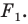 Говорят, что фигура
Говорят, что фигура 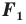 получена в результате преобразования фигуры
получена в результате преобразования фигуры 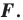 При этом фигуру
При этом фигуру 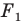 называют образом фигуры
называют образом фигуры 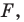 а фигуру
а фигуру 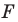 — прообразом фигуры
— прообразом фигуры 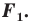
Так, в примере 1 отрезок 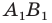 является образом отрезка
является образом отрезка 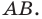 Точка
Точка 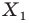 является образом точки
является образом точки 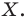 Отрезок
Отрезок 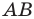 — это прообраз отрезка
— это прообраз отрезка 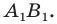
Обратим внимание на то, что в примере 3 фигура 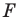 равна своему образу
равна своему образу 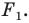 Преобразования, описанные в примерах 1 и 2, таким свойством не обладают.
Преобразования, описанные в примерах 1 и 2, таким свойством не обладают.
Какими же свойствами должно обладать преобразование, чтобы образ и прообраз были равными фигурами? Оказывается, что достаточно лишь одного свойства: преобразование должно сохранять расстояние между точками, то есть если 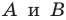 — произвольные точки фигуры
— произвольные точки фигуры 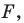 а точки
а точки 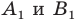 — их образы, то должно выполняться равенство
— их образы, то должно выполняться равенство 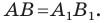
Что такое преобразование фигур
Определение. Преобразование фигуры 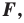 сохраняющее расстояние между точками, называют движением (перемещением) фигуры
сохраняющее расстояние между точками, называют движением (перемещением) фигуры 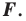
Если каждой точке 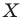 фигуры
фигуры 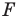 поставлена в соответствие эта же точка
поставлена в соответствие эта же точка 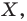 то такое преобразование фигуры
то такое преобразование фигуры 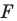 называют тождественным. При тождественном преобразовании образом фигуры
называют тождественным. При тождественном преобразовании образом фигуры 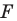 является сама фигура
является сама фигура 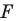 . Очевидно, что тождественное преобразование является движением.
. Очевидно, что тождественное преобразование является движением.
Мы давно используем понятие «равенство фигур», хотя не давали ему строгого определения.
На то, что движение связано с равенством фигур, указывают следующие свойства движения.
Если преобразование является движением, то:
- образом прямой является прямая,
- образом отрезка является отрезок, равный данному;
- образом угла является угол, равный данному,
- образом треугольника является треугольник, равный данному.
Доказательство этих свойств выходит за рамки рассматриваемого курса геометрии.
Свойства движения подсказывают следующее определение.
Определение. Две фигуры называют равными, если существует движение, при котором одна из данных фигур является образом другой.
Запись 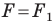 означает, что фигуры
означает, что фигуры 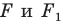 равны.
равны.
Если существует движение, при котором фигура  является образом фигуры
является образом фигуры 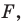 то обязательно существует движение, при котором фигура
то обязательно существует движение, при котором фигура 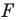 является образом фигуры
является образом фигуры 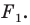 Такие движения называют взаимно обратными.
Такие движения называют взаимно обратными.
Замечание. Ранее равными фигурами мы называли такие фигуры, которые совпадали при наложении. Термин «наложение» интуитивно понятен, и в нашем представлении он связывается с наложением реальных тел. Но геометрические фигуры нельзя наложить в буквальном смысле этого слова. Теперь наложение фигуры 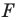 на фигуру
на фигуру 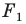 можно рассматривать как движение фигуры
можно рассматривать как движение фигуры 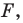 при котором ее образом будет фигура
при котором ее образом будет фигура 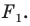
Термин «движение» также ассоциируется с определенным физическим действием: изменением положения тела без деформации.
Именно с этим связано появление этого термина в математике. Однако в геометрии предметом исследования является не процесс, происходящий во времени, а лишь свойства фигуры и ее образа.
То, что изображенные на рисунке 17.3 фигуры 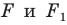 равны, понятно из наглядных соображений. Строгое обоснование этого факта дает следующая теорема.
равны, понятно из наглядных соображений. Строгое обоснование этого факта дает следующая теорема.
Теорема 17.1 (свойство параллельного переноса). Параллельный перенос является движением.
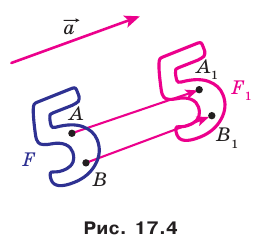
Доказательство: Пусть 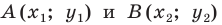 — произвольные точки фигуры
— произвольные точки фигуры 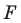 (рис. 17.4), точки
(рис. 17.4), точки 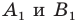 — их соответствующие образы при параллельном переносе на вектор
— их соответствующие образы при параллельном переносе на вектор 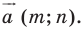 Докажем, что
Докажем, что 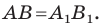
Имеем: 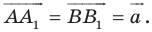 Векторы
Векторы 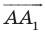 и
и 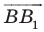 имеют координаты
имеют координаты 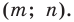 Следовательно, координатами точек
Следовательно, координатами точек  и
и  являются соответственно пары чисел
являются соответственно пары чисел 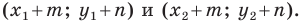
Найдем расстояние между точками 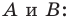
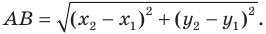
Найдем расстояние между точками 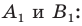
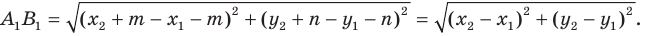
Следовательно, мы показали, что 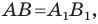 то есть параллельный перенос сохраняет расстояние между точками.
то есть параллельный перенос сохраняет расстояние между точками. 
Следствие. Если фигура  — образ фигуры
— образ фигуры  при параллельном переносе, то
при параллельном переносе, то 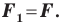
Это свойство используется при создании рисунков на тканях, обоях, покрытиях для пола и т. п. (рис. 17.5). 
Если фигура 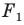 является образом фигуры
является образом фигуры 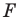 при параллельном переносе на вектор
при параллельном переносе на вектор 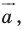 то фигура
то фигура 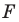 является образом фигуры
является образом фигуры 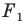 при параллельном переносе на вектор
при параллельном переносе на вектор 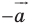 (рис. 17.6).
(рис. 17.6).
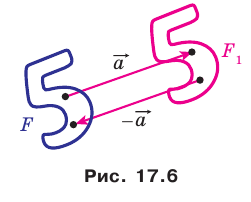
Параллельные переносы на векторы 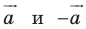 являются взаимно обратными движениями.
являются взаимно обратными движениями.
Пример №1
Каждой точке 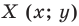 фигуры
фигуры 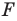 ставится в соответствие точка
ставится в соответствие точка 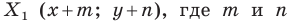 — заданные числа. Докажите, что такое преобразование фигуры
— заданные числа. Докажите, что такое преобразование фигуры 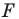 является параллельным переносом на вектор
является параллельным переносом на вектор 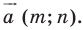
Решение:
Рассмотрим вектор 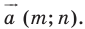 Заметим, что координаты вектора
Заметим, что координаты вектора 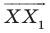 равны
равны 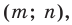 то есть
то есть 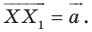 Следовательно, описанное преобразование фигуры
Следовательно, описанное преобразование фигуры  — параллельный перенос на вектор
— параллельный перенос на вектор 
Пример №2
Точка 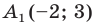 является образом точки
является образом точки 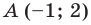 при параллельном переносе на вектор
при параллельном переносе на вектор 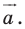 Найдите координаты вектора
Найдите координаты вектора 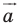 и координаты образа точки
и координаты образа точки 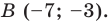
Решение:
Из условия следует, что 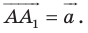 Отсюда
Отсюда 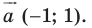
Пусть 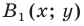 — образ точки
— образ точки 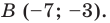 Тогда
Тогда 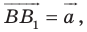 то есть
то есть 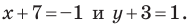 Отсюда
Отсюда 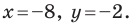
Ответ: 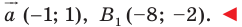
Пример №3
Даны угол 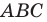 и прямая
и прямая 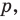 не параллельная ни одной из сторон этого угла (рис. 17.7). Постройте прямую
не параллельная ни одной из сторон этого угла (рис. 17.7). Постройте прямую 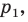 параллельную прямой
параллельную прямой 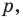 так, чтобы стороны угла отсекали на ней отрезок заданной длины
так, чтобы стороны угла отсекали на ней отрезок заданной длины 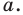
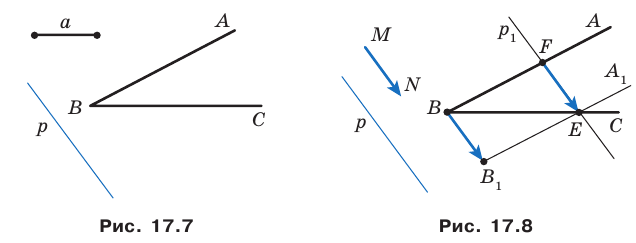
Решение:
Рассмотрим вектор  такой, что
такой, что  и
и  (рис. 17.8). Построим луч
(рис. 17.8). Построим луч 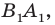 являющийся образом луча
являющийся образом луча 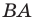 при параллельном переносе на вектор
при параллельном переносе на вектор 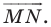 Обозначим точку пересечения лучей
Обозначим точку пересечения лучей 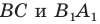 буквой
буквой 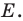 Пусть
Пусть 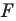 — прообраз точки
— прообраз точки 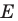 при рассматриваемом параллельном переносе. Тогда
при рассматриваемом параллельном переносе. Тогда 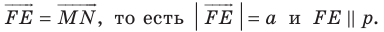
Приведенные рассуждения подсказывают следующий алгоритм построения:
- найти образ луча
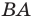 при параллельном переносе на вектор
при параллельном переносе на вектор 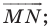
- отметить точку пересечения луча
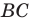 с построенным образом;
с построенным образом; - через найденную точку провести прямую
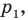 параллельную прямой
параллельную прямой 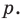 Прямая
Прямая 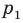 будет искомой.
будет искомой.
Осевая симметрия
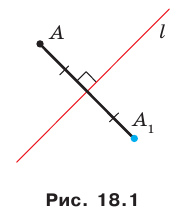
Определение. Точки 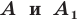 называют симметричными относительно прямой
называют симметричными относительно прямой 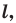 если прямая
если прямая 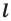 является серединным перпендикуляром отрезка
является серединным перпендикуляром отрезка 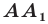 (рис. 18.1). Если точка
(рис. 18.1). Если точка 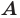 принадлежит прямой
принадлежит прямой 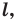 то ее считают симметричной самой себе относительно прямой
то ее считают симметричной самой себе относительно прямой 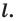
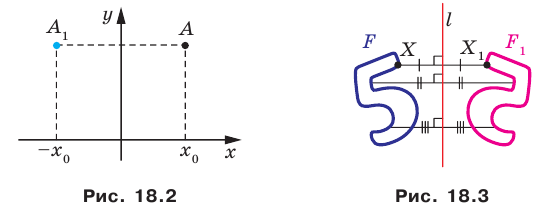
Например, точки 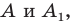 у которых ординаты равны, а абсциссы — противоположные числа, симметричны относительно оси ординат (рис. 18.2).
у которых ординаты равны, а абсциссы — противоположные числа, симметричны относительно оси ординат (рис. 18.2).
Рассмотрим фигуру 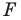 и прямую
и прямую 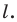 Каждой точке
Каждой точке 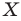 фигуры
фигуры 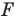 поставим в соответствие симметричную ей относительно прямой
поставим в соответствие симметричную ей относительно прямой 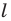 точку
точку 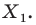
В результате такого преобразования фигуры 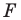 получим фигуру
получим фигуру 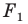 (рис. 18.3). Такое преобразование фигуры
(рис. 18.3). Такое преобразование фигуры 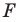 называют осевой симметрией относительно прямой
называют осевой симметрией относительно прямой 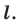 Прямую
Прямую 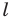 называют осью симметрии. Говорят, что фигуры
называют осью симметрии. Говорят, что фигуры  симметричны относительно прямой
симметричны относительно прямой 
Теорема 18.1 (свойство осевой симметрии). Осевая симметрия является движением.
Доказательство: Выберем систему координат так, чтобы ось симметрии совпала с осью ординат. Пусть  и
и  — произвольные точки фигуры
— произвольные точки фигуры  Тогда точки
Тогда точки 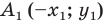 и
и 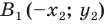 — их соответствующие образы при осевой симметрии относительно оси ординат. Имеем:
— их соответствующие образы при осевой симметрии относительно оси ординат. Имеем:
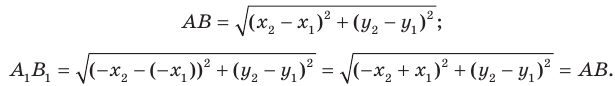
Мы получили, что 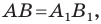 то есть осевая симметрия сохраняет расстояние между точками. Следовательно, осевая симметрия является движением.
то есть осевая симметрия сохраняет расстояние между точками. Следовательно, осевая симметрия является движением. 
Следствие. Если фигуры 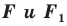 симметричны относительно прямой, то
симметричны относительно прямой, то 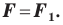
Определение. Фигуру называют симметричной относительно прямой 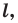 если для каждой точки данной фигуры точка, симметричная ей относительно прямой
если для каждой точки данной фигуры точка, симметричная ей относительно прямой 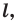 также принадлежит этой фигуре.
также принадлежит этой фигуре.
Прямую  называют осью симметрии фигуры. Также говорят, что фигура имеет ось симметрии.
называют осью симметрии фигуры. Также говорят, что фигура имеет ось симметрии.
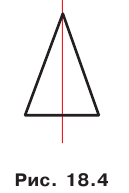
Приведем примеры фигур, имеющих ось симметрии. На рисунке 18.4 изображен равнобедренный треугольник. Прямая, содержащая его высоту, проведенную к основанию, является осью симметрии треугольника.
Любой угол имеет ось симметрии — это пря-Рис. 18.5 мая, содержащая его биссектрису (рис. 18.5). 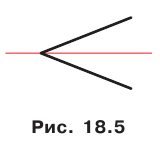
Равносторонний треугольник имеет три оси симметрии (рис. 18.6). Две оси симметрии имеет отрезок: это его серединный перпендикуляр и прямая, содержащая этот отрезок (рис. 18.7).
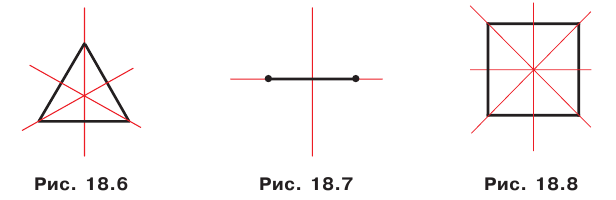
Квадрат имеет четыре оси симметрии (рис. 18.8).
Существуют фигуры, имеющие бесконечно много осей симметрии, например окружность. Любая прямая, проходящая через центр окружности, является ее осью симметрии (рис. 18.9).
Бесконечно много осей симметрии имеет и прямая: сама прямая и любая прямая, ей перпендикулярная, являются ее осями симметрии.
Пример №4
Начертили неравнобедренный треугольник 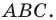 Провели прямую
Провели прямую 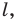 содержащую биссектрису угла
содержащую биссектрису угла 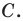 Потом рисунок стерли, оставив только точки
Потом рисунок стерли, оставив только точки 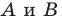 и прямую
и прямую 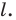 Восстановите треугольник
Восстановите треугольник 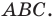
Решение:
Поскольку прямая 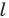 является осью симметрии угла
является осью симметрии угла 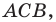 то точка
то точка 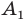 — образ точки
— образ точки 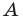 при симметрии относительно прямой
при симметрии относительно прямой 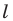 — принадлежит лучу
— принадлежит лучу 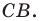 Тогда пересечением прямых
Тогда пересечением прямых 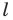 и
и 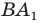 является вершина
является вершина 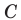 искомого треугольника
искомого треугольника 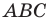 (рис. 18.10).
(рис. 18.10).
Эти соображения подсказывают, как построить искомый треугольник: строим точку 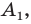 симметричную точке
симметричную точке 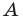 относительно прямой
относительно прямой 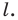 Находим вершину
Находим вершину 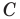 как точку пересечения прямых
как точку пересечения прямых  и
и 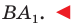
Пример №5
Точка  принадлежит острому углу
принадлежит острому углу 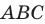 (рис. 18.11). На сторонах
(рис. 18.11). На сторонах 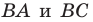 угла найдите такие точки
угла найдите такие точки 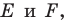 чтобы периметр треугольника
чтобы периметр треугольника 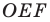 был наименьшим.
был наименьшим.
Решение:
Пусть точки 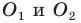 — образы точки
— образы точки 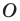 при симметриях относительно прямых
при симметриях относительно прямых 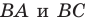 соответственно (рис. 18.12), а прямая
соответственно (рис. 18.12), а прямая 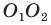 пересекает стороны
пересекает стороны 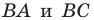 в точках
в точках  соответственно. Докажем, что точки
соответственно. Докажем, что точки  — искомые.
— искомые.
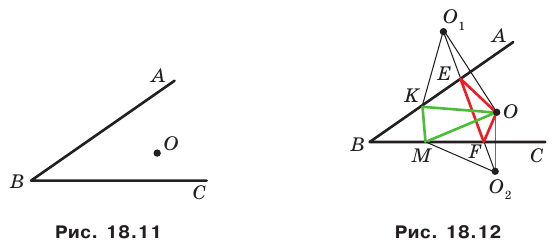
Заметим, что отрезки 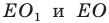 симметричны относительно прямой
симметричны относительно прямой 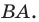 Следовательно,
Следовательно, 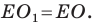 Аналогично
Аналогично 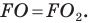 Тогда периметр треугольника
Тогда периметр треугольника 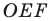 равен длине отрезка
равен длине отрезка 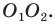
Покажем, что построенный треугольник имеет наименьший периметр из возможных.
Рассмотрим треугольник 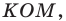 где
где 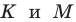 — произвольные точки соответственно лучей
— произвольные точки соответственно лучей 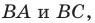 причем точка
причем точка 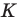 не совпадает с точкой
не совпадает с точкой 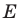 или точка
или точка 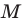 не совпадает с точкой
не совпадает с точкой 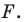
Понятно, что 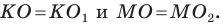
Тогда периметр треугольника 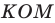 равен сумме
равен сумме 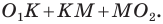 Однако
Однако 
Центральная симметрия. Поворот
Определение. Точки 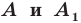 называют симметричными относительно точки
называют симметричными относительно точки 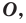 если точка
если точка 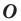 является серединой отрезка
является серединой отрезка 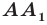 (рис. 19.1). Точку
(рис. 19.1). Точку 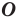 считают симметричной самой себе.
считают симметричной самой себе.
 Например, точки
Например, точки  у которых как абсциссы, так и ординаты — противоположные числа, симметричны относительно начала координат (рис. 19.2).
у которых как абсциссы, так и ординаты — противоположные числа, симметричны относительно начала координат (рис. 19.2).
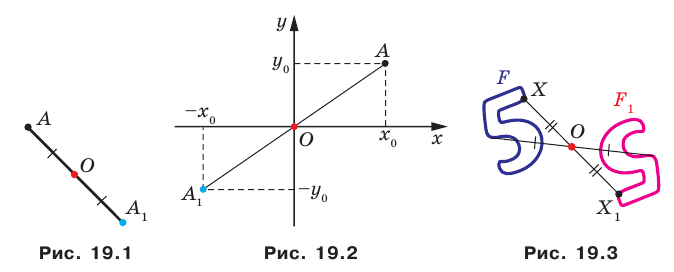
Рассмотрим фигуру 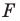 и точку
и точку 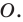 Каждой точке
Каждой точке 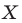 фигуры
фигуры 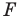 поставим в соответствие симметричную ей относительно точки
поставим в соответствие симметричную ей относительно точки 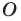 точку
точку 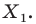 В результате такого преобразования фигуры
В результате такого преобразования фигуры 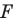 получим фигуру
получим фигуру 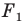 (рис. 19.3). Такое преобразование фигуры
(рис. 19.3). Такое преобразование фигуры 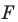 называют центральной симметрией относительно точки
называют центральной симметрией относительно точки 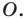 Точку
Точку 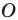 называют центром симметрии. Также говорят, что фигуры
называют центром симметрии. Также говорят, что фигуры 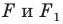 симметричны относительно точки
симметричны относительно точки 
Теорема 19.1 (свойство центральной симметрии). Центральная симметрия является движением.
Доказательство: Выберем систему координат так, чтобы центр симметрии совпал с началом координат. Пусть  и
и  — произвольные точки фигуры
— произвольные точки фигуры  Точки
Точки 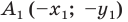 и
и 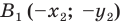 — соответственно их образы при центральной симметрии относительно начала координат. Имеем:
— соответственно их образы при центральной симметрии относительно начала координат. Имеем: 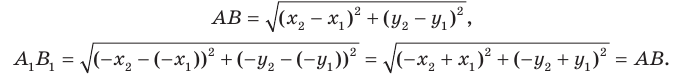
Мы получили, что 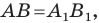 то есть центральная симметрия сохраняет расстояние между точками. Следовательно, центральная симметрия является движением.
то есть центральная симметрия сохраняет расстояние между точками. Следовательно, центральная симметрия является движением. 
Следствие. Если фигуры 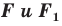 симметричны относительно точки, то
симметричны относительно точки, то 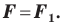
Определение. Фигуру называют симметричной относительно точки 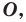 если для каждой точки данной фигуры точка, симметричная ей относительно точки
если для каждой точки данной фигуры точка, симметричная ей относительно точки 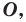 также принадлежит этой фигуре.
также принадлежит этой фигуре.
Точку 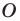 называют центром симметрии фигуры. Также говорят, что фигура имеет центр симметрии.
называют центром симметрии фигуры. Также говорят, что фигура имеет центр симметрии.
Приведем примеры фигур, имеющих центр симметрии.
Центром симметрии отрезка является его середина (рис. 19.4).
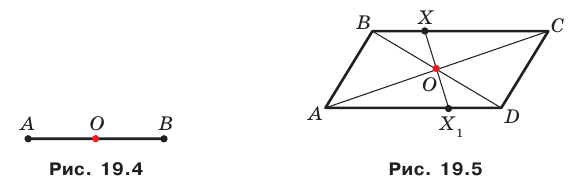
Точка пересечения диагоналей параллелограмма является его центром симметрии (рис. 19.5).
Существуют фигуры, имеющие бесконечно много центров симметрии. Например, каждая точка прямой является ее центром симметрии.
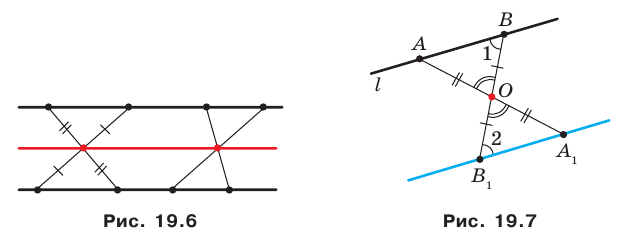
Также бесконечно много центров симметрии имеет фигура, состоящая из двух параллельных прямых. Любая точка прямой, равноудаленной от двух данных, является центром симметрии рассматриваемой фигуры (рис. 19.6).
Пример №6
Докажите, что образом данной прямой 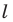 при симметрии относительно точки
при симметрии относительно точки 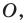 не принадлежащей прямой
не принадлежащей прямой 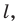 является прямая, параллельная данной.
является прямая, параллельная данной.
Решение:
Поскольку центральная симметрия — это движение, то образом прямой 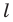 будет прямая. Для построения прямой достаточно найти две любые ее точки.
будет прямая. Для построения прямой достаточно найти две любые ее точки.
Выберем на прямой 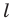 произвольные точки
произвольные точки 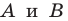 (рис. 19.7). Пусть точки
(рис. 19.7). Пусть точки 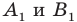 — их образы при центральной симметрии относительно точки
— их образы при центральной симметрии относительно точки 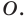 Тогда прямая
Тогда прямая 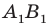 — образ прямой
— образ прямой 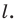
Поскольку 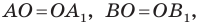 углы
углы 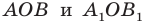 равны как вертикальные, то треугольники
равны как вертикальные, то треугольники 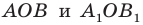 равны по первому признаку равенства треугольников. Отсюда
равны по первому признаку равенства треугольников. Отсюда 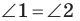 (рис. 19.7). Следовательно, по признаку параллельных прямых
(рис. 19.7). Следовательно, по признаку параллельных прямых 
Пример №7
Точка 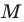 принадлежит углу
принадлежит углу  (рис. 19.8). На сторонах
(рис. 19.8). На сторонах 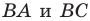 угла постройте такие точки
угла постройте такие точки 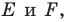 чтобы точка
чтобы точка 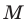 была серединой отрезка
была серединой отрезка 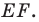
Решение:
Пусть прямая  — образ прямой
— образ прямой 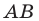 при центральной симметрии относительно точки
при центральной симметрии относительно точки 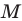 (рис. 19.9). Обозначим буквой
(рис. 19.9). Обозначим буквой 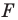 точку пересечения прямых
точку пересечения прямых 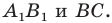
Найдем прообраз точки 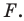 Очевидно, что он лежит на прямой
Очевидно, что он лежит на прямой 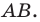 Поэтому достаточно найти точку пересечения прямых
Поэтому достаточно найти точку пересечения прямых 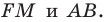
Обозначим эту точку буквой 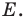 Тогда
Тогда 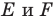 — искомые точки.
— искомые точки.
Изучая окружающий мир, мы часто видим примеры проявления симметрии в природе (рис. 19.10). Объекты, имеющие ось или центр симметрии, легко воспринимаются и радуют взгляд. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота». 
Идея симметрии широко используется в изобразительном искусстве, архитектуре и технике (рис. 19.11).

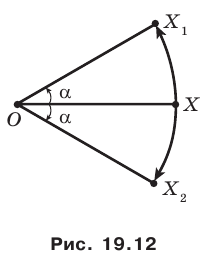
На рисунке 19.12 изображены точки 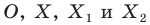 такие, что
такие, что 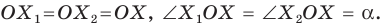
Говорят, что точка 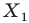 является образом точки
является образом точки 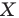 при повороте вокруг центра
при повороте вокруг центра 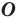 против часовой стрелки на угол
против часовой стрелки на угол 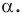
Так же говорят, что точка 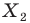 — это образ точки
— это образ точки 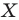 при повороте вокруг центра
при повороте вокруг центра 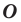 по часовой стрелке на угол
по часовой стрелке на угол 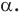
Точку 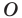 называют центром поворота, угол
называют центром поворота, угол 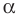 — углом поворота.
— углом поворота.
Рассмотрим фигуру  точку
точку 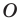 и угол
и угол 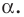 Каждой точке
Каждой точке 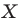 фигуры
фигуры 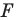 поставим в соответствие точку
поставим в соответствие точку 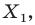 являющуюся образом точки
являющуюся образом точки 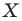 при повороте вокруг центра
при повороте вокруг центра 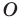 против часовой стрелки на угол
против часовой стрелки на угол 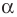 (если точка
(если точка 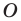 принадлежит фигуре
принадлежит фигуре 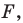 то ей сопоставляется она сама). В результате такого преобразования фигуры
то ей сопоставляется она сама). В результате такого преобразования фигуры 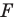 получим фигуру
получим фигуру 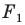 (рис. 19.13). Такое преобразование фигуры
(рис. 19.13). Такое преобразование фигуры 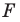 называют поворотом вокруг центра
называют поворотом вокруг центра 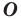 против часовой стрелки на угол
против часовой стрелки на угол 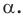 Точку
Точку 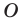 называют центром поворота.
называют центром поворота. 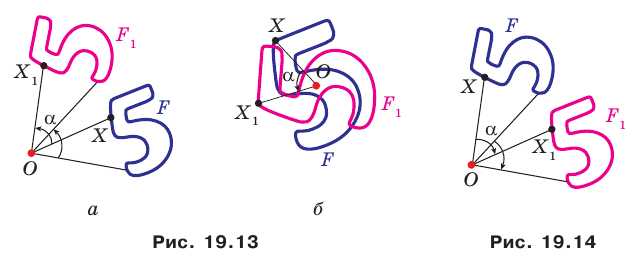
Аналогично определяют преобразование поворота фигуры  по часовой стрелке на угол
по часовой стрелке на угол  (рис. 19.14).
(рис. 19.14).
Заметим, что центральная симметрия является поворотом вокруг центра симметрии на угол 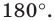
Теорема 19.2 (свойство поворота). Поворот является движением.
Докажите эту теорему самостоятельно.
Следствие. Если фигура 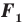 — образ фигуры
— образ фигуры 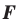 при повороте, то
при повороте, то 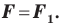
Пример №8
Даны прямая  и точка
и точка 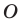 вне ее. Постройте образ прямой
вне ее. Постройте образ прямой 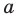 при повороте вокруг точки
при повороте вокруг точки 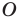 против часовой стрелки на угол
против часовой стрелки на угол 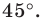
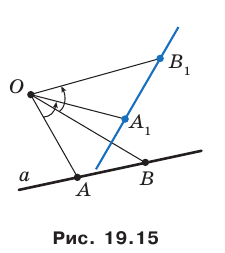
Решение:
Поскольку поворот — это движение, то образом прямой  будет прямая. Для построения прямой достаточно найти две любые ее точки. Выберем на прямой
будет прямая. Для построения прямой достаточно найти две любые ее точки. Выберем на прямой  произвольные точки
произвольные точки  (рис. 19.15). Построим точки
(рис. 19.15). Построим точки 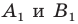 — их образы при повороте вокруг точки
— их образы при повороте вокруг точки 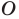 против часовой стрелки на угол
против часовой стрелки на угол 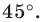 Тогда прямая
Тогда прямая 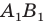 — образ прямой
— образ прямой 
Пример №9
Точка 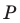 принадлежит углу
принадлежит углу 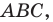 но не принадлежит его сторонам. Постройте равносторонний треугольник, одна вершина которого является точкой
но не принадлежит его сторонам. Постройте равносторонний треугольник, одна вершина которого является точкой 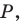 а две другие принадлежат сторонам
а две другие принадлежат сторонам 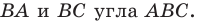
Решение:
Пусть прямая 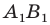 — образ прямой
— образ прямой 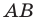 при повороте вокруг центра
при повороте вокруг центра 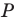 против часовой стрелки на угол
против часовой стрелки на угол 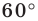 (рис. 19.16). Обозначим буквой
(рис. 19.16). Обозначим буквой  точку пересечения прямых
точку пересечения прямых  и
и 
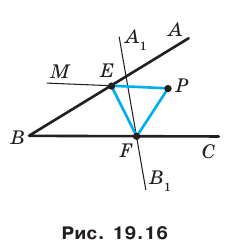
Пусть точка 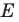 — прообраз точки
— прообраз точки 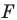 при рассматриваемом повороте. Точка
при рассматриваемом повороте. Точка 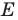 принадлежит стороне
принадлежит стороне 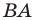 угла
угла 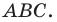
Эти соображения подсказывают, как построить искомый треугольник.
Строим прямую 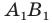 как образ прямой
как образ прямой 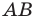 при повороте вокруг центра
при повороте вокруг центра 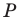 против часовой стрелки на угол
против часовой стрелки на угол 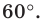 Пусть
Пусть  — точка пересечения прямых
— точка пересечения прямых 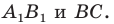
Строим угол 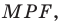 равный
равный 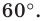 Пусть прямые
Пусть прямые 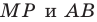 пересекаются в точке
пересекаются в точке 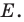 Эта точка и является прообразом точки
Эта точка и является прообразом точки 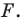
Имеем: 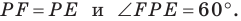 Следовательно, треугольник
Следовательно, треугольник 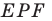 равносторонний.
равносторонний. 
Подобие фигур
На рисунке 20.1 изображены точки 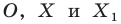 такие, что
такие, что 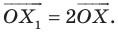 Говорят, что точка
Говорят, что точка 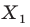 — это образ точки
— это образ точки 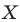 при гомотетии с центром
при гомотетии с центром 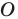 и коэффициентом 2.
и коэффициентом 2. 
На рисунке 20.2 изображены точки 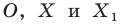 такие, что
такие, что 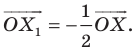 Говорят, что точка
Говорят, что точка 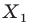 — это образ точки
— это образ точки 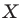 при гомотетии с центром
при гомотетии с центром 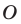 и коэффициентом
и коэффициентом 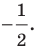
Вообще, если точки 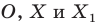 таковы, что
таковы, что 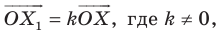 то говорят, что точка
то говорят, что точка 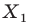 — это образ точки
— это образ точки 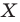 при гомотетии с центром
при гомотетии с центром 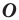 и коэффициентом
и коэффициентом 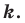
Точку 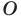 называют центром гомотетии, число
называют центром гомотетии, число 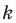 — коэффициентом гомотетии,
— коэффициентом гомотетии, 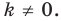
Рассмотрим фигуру 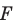 и точку
и точку 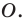 Каждой точке
Каждой точке 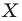 фигуры
фигуры 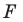 поставим в соответствие точку
поставим в соответствие точку 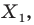 являющуюся образом точки
являющуюся образом точки 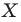 при гомотетии с центром
при гомотетии с центром 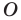 и коэффициентом
и коэффициентом 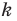 (если точка
(если точка 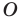 принадлежит фигуре
принадлежит фигуре 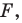 то ей сопоставляется она сама). В результате такого преобразования фигуры
то ей сопоставляется она сама). В результате такого преобразования фигуры 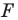 получим фигуру
получим фигуру 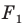 (рис. 20.3). Такое преобразование фигуры
(рис. 20.3). Такое преобразование фигуры 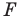 называют гомотетией с центром
называют гомотетией с центром 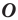 и коэффициентом
и коэффициентом 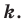 Также говорят, что фигура
Также говорят, что фигура 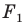 гомотетична фигуре
гомотетична фигуре 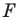 с центром
с центром 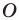 и коэффициентом
и коэффициентом 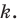
Например, на рисунке 20.4 треугольник  гомотетичен треугольнику
гомотетичен треугольнику  с центром
с центром 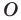 и коэффициентом, равным -3.
и коэффициентом, равным -3.
можно сказать, что треугольник 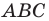 гомотетичен треугольнику
гомотетичен треугольнику 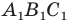 с тем же центром, но коэффициентом гомотетии, равным
с тем же центром, но коэффициентом гомотетии, равным 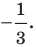
Отметим, что при 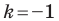 гомотетия с центром
гомотетия с центром 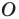 является центральной симметрией с центром
является центральной симметрией с центром 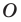 (рис. 20.5). Если
(рис. 20.5). Если 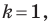 то гомотетия является тождественным преобразованием.
то гомотетия является тождественным преобразованием.
Очевидно, что при 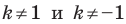 гомотетия не является движением.
гомотетия не является движением.
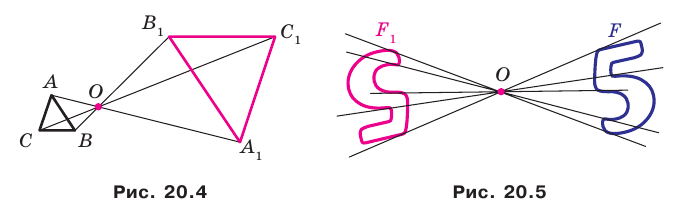
Теорема 20.1. При гомотетии фигуры  с коэффициентом
с коэффициентом  все расстояния между ее точками изменяются в
все расстояния между ее точками изменяются в 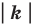 раз, то есть если
раз, то есть если 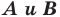 — произвольные точки фигуры
— произвольные точки фигуры 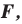 а точки
а точки 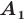 и
и 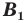 — их соответствующие образы при гомотетии с коэффициентом
— их соответствующие образы при гомотетии с коэффициентом 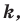 то
то 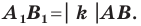
Доказательство: Пусть точка 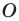 — центр гомотетии. Тогда
— центр гомотетии. Тогда 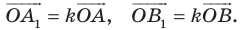 Имеем:
Имеем: 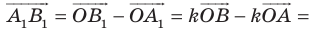
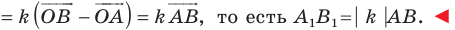
Следствие. Если треугольник 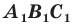 гомотетичен треугольнику
гомотетичен треугольнику 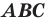 с коэффициентом гомотетии
с коэффициентом гомотетии 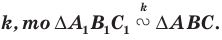
Для доказательства этого утверждения достаточно воспользоваться теоремой 20.1 и третьим признаком подобия треугольников.
Гомотетия обладает целым рядом других свойств.
При гомотетии:
Эти свойства вы можете доказать на занятиях математического кружка.
Перечисленные свойства гомотетии указывают на то, что это преобразование может изменить размеры фигуры, но не меняет ее форму, то есть при гомотетии образ и прообраз являются подобными фигурами. Заметим, что в курсе геометрии 8 класса, говоря о подобии фигур, мы давали определение только подобных треугольников. Сейчас определим понятие подобия для произвольных фигур.
На рисунке 20.6 фигура  гомотетична фигуре
гомотетична фигуре  а фигура
а фигура 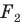 симметрична фигуре
симметрична фигуре  относительно прямой
относительно прямой 
Говорят, что фигура 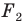 получена из фигуры
получена из фигуры 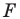 в результате композиции двух преобразований: гомотетии и осевой симметрии.
в результате композиции двух преобразований: гомотетии и осевой симметрии.
Поскольку 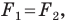 то фигуры
то фигуры 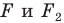 имеют одинаковые формы, но разные размеры, то есть они подобны. Говорят, что фигура
имеют одинаковые формы, но разные размеры, то есть они подобны. Говорят, что фигура 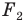 получена из фигуры
получена из фигуры 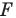 в результате преобразования подобия.
в результате преобразования подобия.
На рисунке 20.7 фигура 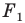 гомотетична фигуре
гомотетична фигуре 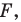 а фигура
а фигура 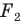 — образ фигуры
— образ фигуры 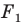 при некотором движении. Здесь также можно утверждать, что фигуры
при некотором движении. Здесь также можно утверждать, что фигуры 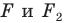 подобны.
подобны.
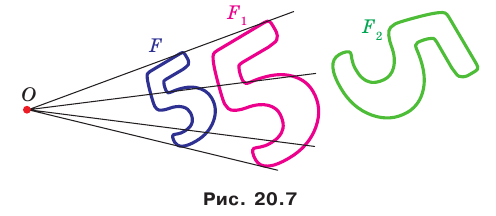
Из сказанного следует, что целесообразно принять такое определение.
Определение. Две фигуры называют подобными, если одну из них можно получить из другой в результате композиции двух преобразований: гомотетии и движения.
Это определение иллюстрирует схема, изображенная на рисунке 20.8. 
Запись 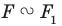 означает, что фигуры
означает, что фигуры 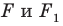 подобны. Также говорят, что фигура
подобны. Также говорят, что фигура 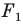 — образ фигуры
— образ фигуры 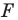 при преобразовании подобия.
при преобразовании подобия.
Из приведенного определения следует, что при преобразовании подобия фигуры  расстояния между ее точками изменяются в одно и то же количество раз.
расстояния между ее точками изменяются в одно и то же количество раз.
Так как тождественное преобразование является движением, то из схемы, изображенной на рисунке 20.8, следует, что гомотетия — частный случай преобразования подобия.
Пусть  — произвольные точки фигуры
— произвольные точки фигуры  а точки
а точки  — их образы при преобразовании подобия. Точки
— их образы при преобразовании подобия. Точки 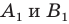 принадлежат фигуре
принадлежат фигуре 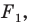 которая подобна фигуре
которая подобна фигуре 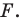 Число
Число 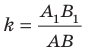 называют коэффициентом подобия. Говорят, что фигура
называют коэффициентом подобия. Говорят, что фигура 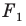 подобна фигуре
подобна фигуре 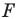 с коэффициентом подобия
с коэффициентом подобия 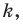 а фигура
а фигура 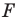 подобна фигуре
подобна фигуре 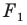 с коэффициентом подобия
с коэффициентом подобия 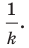
Заметим, что преобразование подобия с коэффициентом 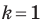 является движением. Отсюда следует, что движение — частный случай преобразования подобия.
является движением. Отсюда следует, что движение — частный случай преобразования подобия.
С преобразованием подобия мы часто встречаемся в повседневной жизни (рис. 20.9). Например, в результате изменения масштаба карты получаем карту, подобную данной. Фотография — это преобразование негатива в подобное изображение на фотобумаге. Перенося в свою тетрадь рисунок, сделанный учителем на доске, вы также выполняете преобразование подобия. 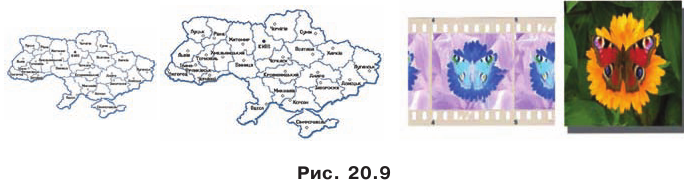 Теорема 20.2. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Теорема 20.2. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Доказательство этой теоремы выходит за рамки рассматриваемого курса геометрии. Мы докажем ее для частного случая, рассмотрев подобные треугольники.
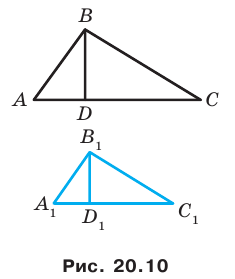
Доказательство: Пусть треугольник  — образ треугольника
— образ треугольника  при преобразовании подобия с коэффициентом
при преобразовании подобия с коэффициентом  (рис. 20.10). Сторона
(рис. 20.10). Сторона 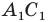 — образ стороны
— образ стороны 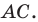 Тогда
Тогда 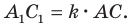 Проведем высоту
Проведем высоту  Пусть точка
Пусть точка 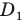 — образ точки
— образ точки 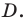
Поскольку при преобразовании подобия сохраняются углы, то отрезок 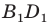 — высота треугольника
— высота треугольника 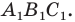
Тогда 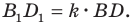 Имеем:
Имеем:
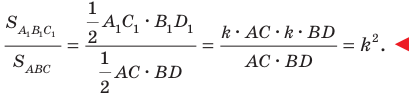
Пример №10
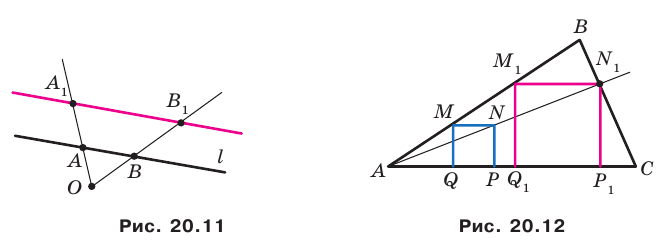
Докажите, что образом прямой 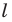 при гомотетии с центром
при гомотетии с центром 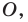 не принадлежащим прямой
не принадлежащим прямой 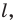 является прямая, параллельная данной.
является прямая, параллельная данной.
Решение:
Из свойств гомотетии следует, что образом прямой 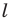 будет прямая. Для построения прямой достаточно найти две любые ее точки. Выберем на прямой
будет прямая. Для построения прямой достаточно найти две любые ее точки. Выберем на прямой 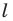 произвольные точки
произвольные точки 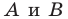 (рис. 20.11). Пусть точки
(рис. 20.11). Пусть точки 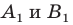 — их образы при гомотетии с центром
— их образы при гомотетии с центром 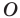 и коэффициентом
и коэффициентом 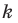 (рисунок 20.11 соответствует случаю, когда
(рисунок 20.11 соответствует случаю, когда 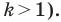 Тогда прямая
Тогда прямая 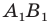 — образ прямой
— образ прямой 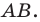
При доказательстве теоремы 20.1 мы показали, что 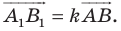 Следовательно,
Следовательно, 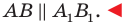
Пример №11
В остроугольный треугольник 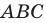 впишите квадрат так, чтобы две его вершины лежали соответственно на сторонах
впишите квадрат так, чтобы две его вершины лежали соответственно на сторонах 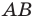 и
и 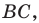 а две другие — на стороне
а две другие — на стороне 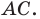
Решение:
Из произвольной точки 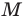 стороны
стороны 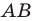 опустим перпендикуляр
опустим перпендикуляр 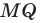 на сторону
на сторону 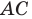 (рис. 20.12). Построим квадрат
(рис. 20.12). Построим квадрат 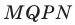 так, чтобы точка
так, чтобы точка 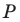 лежала на луче
лежала на луче 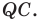 Пусть луч
Пусть луч 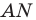 пересекает сторону
пересекает сторону 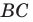 в точке
в точке 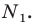
Рассмотрим гомотетию с центром 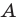 и коэффициентом
и коэффициентом 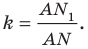 Тогда точка
Тогда точка 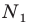 образ точки
образ точки 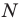 при этой гомотетии. Образом отрезка
при этой гомотетии. Образом отрезка 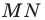 является отрезок
является отрезок 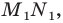 где точка
где точка 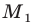 принадлежит лучу
принадлежит лучу 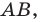 причем
причем 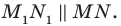 Аналогично отрезок
Аналогично отрезок 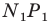 такой, что точка
такой, что точка 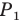 принадлежит лучу
принадлежит лучу 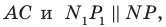 является образом отрезка
является образом отрезка 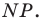 Следовательно, отрезки
Следовательно, отрезки 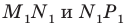 — соседние стороны искомого квадрата. Для завершения построения осталось опустить перпендикуляр
— соседние стороны искомого квадрата. Для завершения построения осталось опустить перпендикуляр 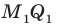 на сторону
на сторону 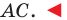
Пример №12
Отрезок 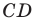 — высота прямоугольного треугольника
— высота прямоугольного треугольника 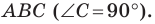 Найдите радиус
Найдите радиус 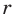 вписанной окружности треугольника
вписанной окружности треугольника  если радиусы окружностей, вписанных в треугольники
если радиусы окружностей, вписанных в треугольники 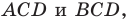 соответственно равны
соответственно равны 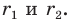
Решение:
Поскольку угол 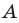 — общий для прямоугольных треугольников
— общий для прямоугольных треугольников 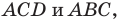 то эти треугольники подобны (рис. 20.13). Пусть коэффициент подобия равен
то эти треугольники подобны (рис. 20.13). Пусть коэффициент подобия равен 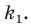 Очевидно, что
Очевидно, что 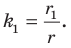 Аналогично
Аналогично 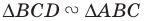 с коэффициентом подобия
с коэффициентом подобия 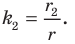
Обозначим площади треугольников 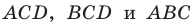 соответственно
соответственно 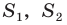 и
и 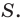 Имеем:
Имеем:
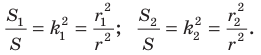
Отсюда 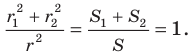 Получаем, что
Получаем, что 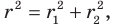
Ответ: 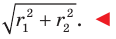
Применение преобразований фигур при решении задач
Преобразование фигур — эффективный метод решения целого ряда геометрических задач. Проиллюстрируем это на примерах.
Пример №13
На сторонах 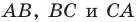 остроугольного треугольника
остроугольного треугольника  постройте такие точки
постройте такие точки 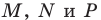 соответственно, чтобы периметр треугольника
соответственно, чтобы периметр треугольника 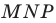 был наименьшим.
был наименьшим.
Решение:
Пусть  — произвольная точка стороны
— произвольная точка стороны  треугольника
треугольника 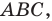 точки
точки 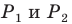 — ее образы при симметрии относительно прямых
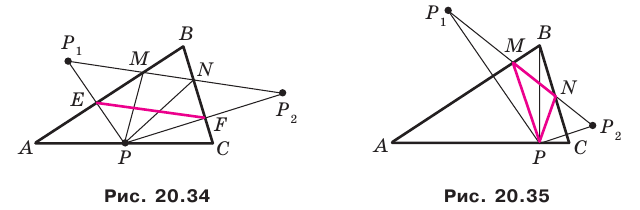
— ее образы при симметрии относительно прямых 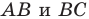 соответственно (рис. 20.34). Прямая
соответственно (рис. 20.34). Прямая 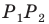 пересекает стороны
пересекает стороны 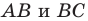 соответственно в точках
соответственно в точках 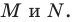 Из решения задачи 2 п. 18 следует, что из периметров всех треугольников, для которых точка
Из решения задачи 2 п. 18 следует, что из периметров всех треугольников, для которых точка 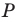 фиксирована, а точки
фиксирована, а точки 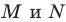 принадлежат сторонам
принадлежат сторонам 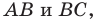 периметр треугольника
периметр треугольника 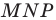 является наименьшим. Этот периметр равен длине отрезка
является наименьшим. Этот периметр равен длине отрезка 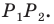
Заметим, что отрезок 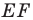 — средняя линия треугольника
— средняя линия треугольника 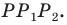
Тогда 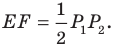
Поскольку 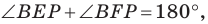 то точки
то точки 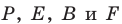 лежат на одной окружности с диаметром
лежат на одной окружности с диаметром 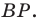 Отсюда
Отсюда 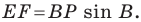 Следовательно, длина отрезка
Следовательно, длина отрезка 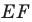 будет наименьшей при наименьшей длине отрезка
будет наименьшей при наименьшей длине отрезка 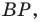 то есть тогда, когда
то есть тогда, когда 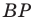 — высота треугольника
— высота треугольника 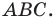
На рисунке 20.35 отрезок 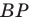 — высота треугольника
— высота треугольника 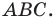 Алгоритм построения точек
Алгоритм построения точек 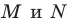 понятен из рисунка.
понятен из рисунка.
Из построения следует, что периметр любого другого треугольника, вершины которого лежат на сторонах треугольника 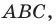 больше периметра треугольника
больше периметра треугольника 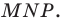 Поэтому искомый треугольник является единственным — это построенный треугольник
Поэтому искомый треугольник является единственным — это построенный треугольник 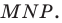
Можно показать (сделайте это самостоятельно), что точки 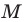 и
и 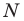 являются основаниями высот, проведенных соответственно из вершин
являются основаниями высот, проведенных соответственно из вершин 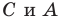 треугольника
треугольника 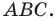
Следовательно, вершины искомого треугольника — это основания высот данного треугольника 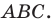 Такой треугольник называют ортоцентрическим.
Такой треугольник называют ортоцентрическим.
Пример №14
Точка  — центр правильного
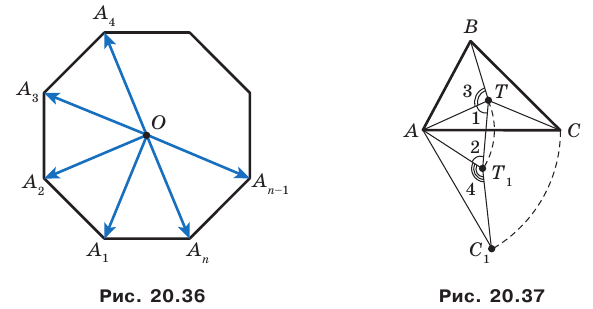
— центр правильного  угольника
угольника 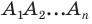 (рис. 20.36). Докажите, что
(рис. 20.36). Докажите, что 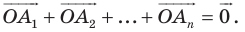
Решение:
Пусть 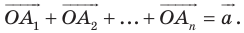 Рассмотрим поворот с центром
Рассмотрим поворот с центром 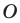 на угол
на угол 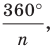 например, против часовой стрелки. При таком преобразовании образом данного
например, против часовой стрелки. При таком преобразовании образом данного 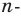 -угольника будет этот же
-угольника будет этот же 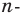 угольник. Следовательно, искомая сумма не изменится. А это возможно лишь тогда, когда
угольник. Следовательно, искомая сумма не изменится. А это возможно лишь тогда, когда 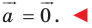
Пример №15
Внутри треугольника  все углы которого меньше
все углы которого меньше  найдите такую точку
найдите такую точку 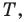 чтобы сумма
чтобы сумма 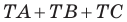 была наименьшей.
была наименьшей.
Решение:
Пусть 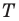 — произвольная точка данного треугольника
— произвольная точка данного треугольника 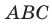 (рис. 20.37). Рассмотрим поворот с центром
(рис. 20.37). Рассмотрим поворот с центром 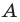 на угол
на угол 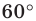 по часовой стрелке. Пусть точки
по часовой стрелке. Пусть точки 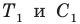 — образы точек
— образы точек 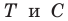 соответственно (рис. 20.37). Поскольку поворот является движением, то
соответственно (рис. 20.37). Поскольку поворот является движением, то 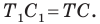 Очевидно, что треугольник
Очевидно, что треугольник 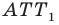 равносторонний. Тогда
равносторонний. Тогда 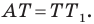
Имеем: 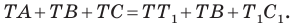
Понятно, что сумма 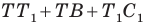 будет наименьшей, если точки
будет наименьшей, если точки  лежат на одной прямой. Поскольку
лежат на одной прямой. Поскольку 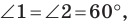 то это условие будет выполнено тогда, когда
то это условие будет выполнено тогда, когда 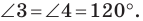
Так как угол  — образ угла
— образ угла 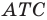 при указанном повороте, то должно выполняться равенство
при указанном повороте, то должно выполняться равенство 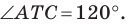
Итак, точки 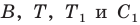 будут принадлежать одной прямой тогда и только тогда, когда
будут принадлежать одной прямой тогда и только тогда, когда 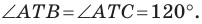 Отсюда
Отсюда 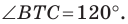
Таким образом, сумма 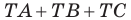 будет наименьшей, если
будет наименьшей, если 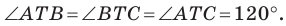
Найти точку 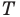 можно, например, построив ГМТ, из которых отрезки
можно, например, построив ГМТ, из которых отрезки 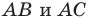 видны под углами
видны под углами 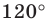 (рис. 20.38).
(рис. 20.38).
Понятно, что если один из углов треугольника 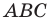 не меньше
не меньше 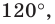 то точка пересечения построенных дуг не будет расположена внутри треугольника. Можно показать, что в треугольнике с углом, не меньшим
то точка пересечения построенных дуг не будет расположена внутри треугольника. Можно показать, что в треугольнике с углом, не меньшим 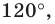 точка
точка 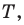 сумма расстояний от которой до вершин треугольника является наименьшей, совпадает с вершиной тупого угла.
сумма расстояний от которой до вершин треугольника является наименьшей, совпадает с вершиной тупого угла. 
Пример №16
Отрезки 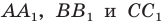 — высоты остроугольного треугольника
— высоты остроугольного треугольника 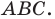 Докажите, что радиус описанной окружности треугольника
Докажите, что радиус описанной окружности треугольника 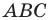 в два раза больше радиуса описанной окружности треугольника
в два раза больше радиуса описанной окружности треугольника 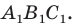
Решение:
Пусть прямые 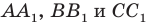 пересекают описанную окружность треугольника
пересекают описанную окружность треугольника 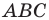 соответственно в точках
соответственно в точках 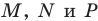 (рис. 20.39). Докажем, что
(рис. 20.39). Докажем, что 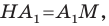 где точка
где точка 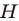 — ортоцентр треугольника
— ортоцентр треугольника 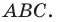
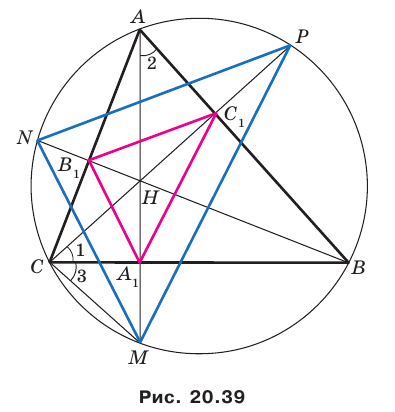
Имеем: 
Углы 2 и 3 равны как вписанные, опирающиеся на дугу  Следовательно,
Следовательно, 
Тогда в треугольнике  отрезок
отрезок 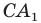 является биссектрисой и высотой, а следовательно, и медианой. Отсюда
является биссектрисой и высотой, а следовательно, и медианой. Отсюда 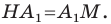
Аналогично можно доказать, что 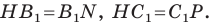
Теперь понятно, что треугольник 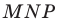 гомотетичен треугольнику
гомотетичен треугольнику 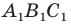 с центром
с центром 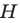 и коэффициентом 2. Тогда радиус описанной окружности треугольника
и коэффициентом 2. Тогда радиус описанной окружности треугольника 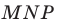 в два раза больше радиуса описанной окружности треугольника
в два раза больше радиуса описанной окружности треугольника 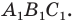 Осталось заметить, что треугольники
Осталось заметить, что треугольники  вписаны в одну и ту же окружность.
вписаны в одну и ту же окружность.
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление
- Возникновение геометрии
- Призма в геометрии
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
Поворот точек на произвольный угол онлайн
| Координаты фигуры, разделенные через пробел |
| Угол поворота в градусах (если положительное то против часовой стрелки) |
| Точка относительно которой проводится поворот |
| Новые координаты полученные при повороте фигуры(точки) на заданный угол |
Поворот – это движение фигуры в пространстве вокруг неподвижной точки, принадлежащей этому же пространству.
Возникают задачи, как определить новые координаты какой либо фигуры при повороте на произвольный угол, относительно произвольной точки.
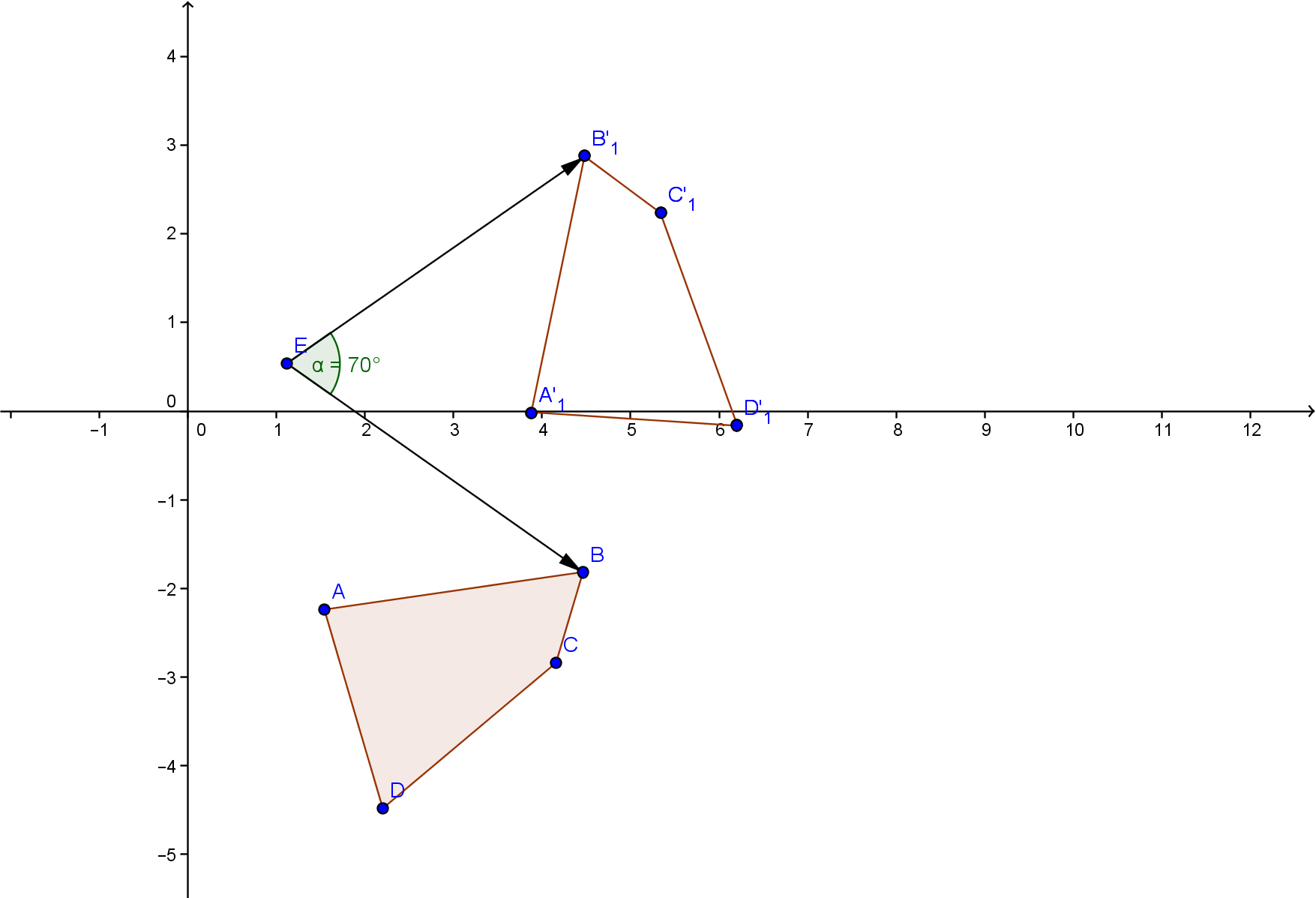
На данном рисунке отобразено поворот фигуры на угол в 70 градусов против часовой стрелки относительно точке Е.
Есть два представления расчета новых координат при решении подобных задач.
Фигура ABCD имеет следующие координаты вершин A=(1.54:-2.24) B=(4.46:-1.82) C=(4.16:-2.84) D=(2.2:-4.48)
точка E=(1.12:0.54) вокруг которой и будет происходить вращение
Алгоритм определения новых координат
Пример будем рассчитывать только для одной точки, так как для остальных точек весь процесс одинаков
1. Приведем начало координат к точке E. То есть точка E будет с координатами (0:0) а точка A (1.54-1.12:-2.24-0.54)
A=(0.42:-2.78)
2. Высчитаем новые координаты точки A1 по следующим формулам
(x1=x*cos(phi)-y*sin(phi))
(y1=x*sin(phi)+y*cos(phi))
где f – угол поворота. Хотелось бы обратить Ваше внимание на то, что не надо высчитывать синус или косинус 70 градусов “в лоб”, как иногда захочется сделать.
Общепринятно, что все расчеты тригонометрических функций осуществляются в радианах.
Поэтому сначала угол 70 градусов приводим к радианам по формуле (phi=70*(cfrac{pi}{180})=1.22173047639603)
А вот теперь считаем по выше указанным формулам, новые координаты.
3. получаем новые координаты точки A=(2.76:-0.56)
4. делаем обратные действия, которые делали в шаге первом, то есть возвращаем начало координат туда, куда и положено
тогда окончательная точка А имеет координаты (2.76+1.12:-0.56+0.54) => (3.88:-0.02)
Преобразовываем таким образом все остальные точки фигуры.
Второе представление в виде умножения матриц.
Координаты точки A представляют в виде вектора
(begin{pmatrix} x\y end{pmatrix})
и умножают на матрицу следующего вида
(begin{pmatrix}cos(phi)&-sin(phi)\sin(phi)&cos(phi)end{pmatrix})
которая называется матрицей поворота
Результат – новые координаты точки.
(begin{pmatrix}x1\y1end{pmatrix}=begin{pmatrix}x\yend{pmatrix}*begin{pmatrix}cos(phi)&-sin(phi)\sin(phi)&cos(phi)end{pmatrix})
Используется в построении и моделировании. Развивает пространственное ориентирование, помогает решать сопутствующие задачи в геометрии, алгебре, физике.
Синтаксис
Для тех, кто пользуется XMPP клиентами: rot <координаты>;<поворот в градусах>;<точка вращения>
Координаты – строка, содержащая координаты в виде x:y (где x – абсцисса координаты, y – ордината координаты), разделенные хотя бы одним пробелом
Точка вращения – точка, относительно которой будет осуществляться поворот, всех заданных координат.
Поворот в градусах – поворот фигуры на заданный угол. Если число положительное – то поворот производится ПРОТИВ часовой стрелке, если отрицательный, то ПО часовой стрелке.
Примеры
Пример: задан треугольник следующими координатами A(1:1) B (5:5) C(0:7)
Необходимо повернуть треугольник на 30 градусов против часовой стрелки относительно точки с координатами 3:3
Тогда запрос будет выглядеть так
rot 1:1 5:5 0:7;30;3:3
и получаем следующее
Новые координаты при повороте на угол 30
Относительно координаты 3:3
A (2.2679491924311 : 0.26794919243112)
B (3.7320508075689 : 5.7320508075689)
C (-1.5980762113533 : 4.9641016151378)
Самое приятное в том, что с помощью Построить график функции c помощью GeoGebra Вы можете сами нарисовать этот треугольник и повернуть его на тот же самый угол. И это будет отображено не только в численной виде, но и в графическом.
А это совсем другой уровень восприятия, и возможность использования этой графики в своих работах, дипломных или аттестационных не может не радовать.
x = отступ + sin(w) * 3,14
y = отступ + cos(w) * 3,14
Это формула построения окружности где W это градусы (0;359), вычисляеш для одной и второй точек отрезка координаты X и У, задавая для одной из них градусы + несколько, это расстояние между двумя точками будет.
Отступы в формулах для Х и У нужео задавать как отступ от левого края до точки вокруг которой вращение + отступ от самой точки до точки отрезка.
Примерно формула для Х и У одной прямой будет выглядеть так:
a , b – отступы от краёв до точки вокруг которой вращение.
с, n – отступы от точки вокруг которой вращение.
отступы расположены как горизонтальный, вертикальный(в условии выше этой строки), Х – горизонтальная координата, У – вертикальная.
повторение в цикле от 0 до 359 (0 = 360)
x1 = a + c + sin(w) * 3,14
y1 = b + n + cos(w) * 3,14
x2 = a + c + sin(w + 20) * 3,14
y2 = b + n + cos(w + 20) * 3,14
w = w + 1
Всё.
