Кикоин А.К. Когда к телу приложены параллельные силы //Квант. — 1985. — № 2. — С. 23-25.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
Содержание
- 1 Если силы параллельны и направлены в одну сторону
- 2 Если направления параллельных сил противоположны
- 3 Пара сил
Хорошо известно, как найти равнодействующую двух сил, приложенных к материальной точке (рис. 1). На векторах, изображающих эти силы, как на сторонах строят параллелограмм; диагональ со стрелкой на конце, проведенная из точки, к которой приложены силы, и есть вектор равнодействующей.
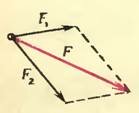
Рис. 1
Когда две силы приложены не к материальной точке, а к телу, но так, как показано на рисунке 2, то равнодействующая определяется таким же образом. Пользуясь тем, что точку приложения силы можно переносить вдоль линии ее действия («Физика 8», § 46), находят точку С, в которой пересекаются линии действия обеих сил.
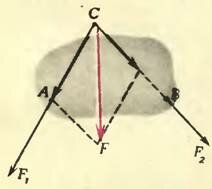
Рис. 2
Полагая, что силы (~vec F_1) и (~vec F_2) приложены именно к этой точке, строят параллелограмм и проводят диагональ. Правда, точка С может оказаться и вне тела, но тогда точку приложения равнодействующей можно выбрать в любом месте на линии ее действия. Действительно, какую бы точку мы не выбрали, равнодействующая сила (~vec F) сообщит телу такое же ускорение или вызовет такой же вращающий момент, как и силы (~vec F_1) и (~vec F_2), вместе взятые.
Если силы параллельны и направлены в одну сторону
Пусть к телу приложены две параллельные сонаправленные силы (рис. 3). Линии действия таких сил нигде не пересекаются, и параллелограмм на них построить нельзя. Тем не менее сложить эти силы и найти их равнодействующую можно.
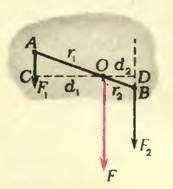
Рис. 3
Нетрудно понять, что равнодействующая направлена параллельно обеим силам и ее модуль равен арифметической сумме модулей складываемых сил. А в какой точке она приложена? Или, другими словами, к какой точке тела надо приложить силу, равную по модулю, но противоположную по направлению равнодействующей, чтобы тело находилось в равновесии?
Чтобы найти точку приложения равнодействующей двух параллельных и одинаково направленных сил, можно воспользоваться правилом моментов («Физика 8», § 48). Проведем прямую, соединяющую точки А и В (см. рис. 3). Где-то на этой прямой должна, очевидно, находиться и точка приложения равнодействующей. Пусть это будет точка О. Допустим, что через эту точку проходит закрепленная ось, перпендикулярная плоскости, содержащей обе складываемые силы (то есть перпендикулярная плоскости рисунка). Если О действительно есть точка приложения равнодействующей, то тело будет находиться в равновесии — равнодействующая уравновешивается силой реакции со стороны оси. С другой стороны, если тело с закрепленной осью находится в равновесии, то алгебраическая сумма моментов сил относительно этой оси должна быть равна нулю. Из рисунка 3 видно, что сила (~vec F_2), будь она единственной, поворачивала бы тело вокруг О по часовой стрелке, то есть ее момент F2d2 положительный, а сила (~vec F_1) если бы она была единственной, поворачивала бы тело против часовой стрелки — ее моменту F1d1 надо приписать отрицательный знак (здесь d1 и d2 — плечи сил (~vec F_1) и (~vec F_2)).
Следовательно,
(~F_2 d_2 – F_1 d_1 = 0), или (~frac{F_1}{F_2} = frac{d_2}{d_1}) .
Из подобия треугольников АОС и BOD находим, что (~frac{d_1}{d_2} = frac{r_1}{r_2}) . Поэтому окончательно получаем
(~frac{F_1}{F_2} = frac{r_2}{r_1}) .
Это значит, что равнодействующая двух параллельных, одинаково направленных сил приложена к точке, делящей отрезок, соединяющий точки приложения складываемых сил, в отношении, обратном отношению модулей сил. Ясно, что эта точка лежит ближе к большей из сил.
Если направления параллельных сил противоположны
Приложенные к телу параллельные силы могут быть направлены и в противоположные стороны (рис. 4). Теперь точка приложения равнодействующей (~vec F) не может находиться где-то между точками приложения сил (~vec F_1) и (~vec F_2). Ведь вокруг любой точки, лежащей между ними, каждая сила поворачивает тело против часовой стрелки, знаки моментов этих сил одинаковы, и их сумма не может быть равна нулю, как это требуется для равновесия.
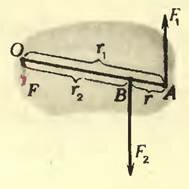
Рис. 4
Легко догадаться, что точка приложения равнодействующей лежит за точкой приложения большей силы, как это и показано на рисунке 4. Модуль же равнодействующей равен модулю разности модулей сил (~vec F_1) и (~vec F_2). В какой же именно точке приложена равнодействующая? На каком расстоянии r2 от точки приложения большей силы? Воспользуемся опять правилом моментов:
(~frac{F_1}{F_2} = frac{r_2}{r_1}), или (~F_2 = F_1 frac{r_1}{r_2}) .
Вычтем из правой и левой частей последнего равенства величину F1:
(~F_2 – F_1 = F_1 frac{r_1}{r_2} – F_1 = F_1 left( frac{r_1}{r_2} – 1 right) = F_1 frac{r_1 – r_2}{r_2}) ,
откуда
(~r_2 = frac{F_1(r_1 – r_2)}{F_2 – F_1} = frac{F_1 r}{F_2 – F_1}) . (*)
Таким образом, точка приложения равнодействующей двух противоположно направленных параллельных сил расположена тем дальше от точки приложения большей из них, чем меньше разность модулей этих сил.
Пара сил
Мы видели, что если к телу приложены параллельные силы, одинаково или противоположно направленные, то всегда можно найти модуль и направление равнодействующей этих сил и определить точку ее приложения. Если к этой точке приложить силу, равную равнодействующей по модулю, но противоположную ей по направлению, то тело будет находиться в равновесии — оно не будет двигаться поступательно и не будет вращаться.
Но, оказывается, есть один случай, когда равнодействующую найти нельзя. Так бывает, если к телу приложены две параллельные, противоположно направленные силы, по модулю равные друг другу. Про такие силы говорят, что они образуют пару сил. Модуль их равнодействующей равен, конечно, нулю, а из формулы (*) видно, что при F2 — F1 =0 расстояние r2 до точки приложения равнодействующей равно бесконечности, то есть что такой точки попросту не существует. И в самом деле, какая же может быть точка приложения равнодействующей, которой нет?
Достаточно, однако, взглянуть на рисунок 5, чтобы понять, что под действием пары сил тело не будет находиться в равновесии — оно будет вращаться. Значит, у пары сил есть некоторый вращающий момент. Но относительно какой оси?
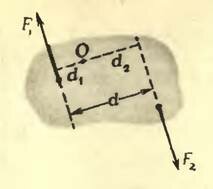
Рис. 5
Нетрудно показать, что суммарный момент сил, составляющих пару, одинаков для любой оси, перпендикулярной плоскости, в которой лежат обе эти силы (перпендикулярной плоскости рисунка). Действительно, возьмем любую точку О и проведем через нее ось вращения. Момент M1 силы (~vec F_1) относительно этой оси равен F1d1, момент M2 силы (~vec F_2) относительно этой же оси равен F2d2. Суммарный момент М обеих сил равен M1 + M2 :
(~M = F_1 d_1 + F_2 d_2) .
Так как F1 = F2 = F, то
(~M = F (d_1 + d_2) = Fd) ,
где d — расстояние между линиями действия сил, составляющих пару, называемое плечом пары сил. Значит, момент пары сил равен произведению модуля одной из сил на плечо пары. Так и говорят — момент пары сил — и не указывают относительно какой оси.
Как же все-таки «ведет» себя тело, к которому приложена пара сил? Чтобы ответить на этот вопрос, вспомним, что центр масс тела (о нем говорится в § 44 «Физики 8») движется так, как будто в нем сосредоточена вся масса тела и к нему приложены все действующие на тело силы (это утверждение называется в физике теоремой о движении центра масс). Но если сумма сил равна нулю, то центр масс не может тронуться с места (если, конечно, он покоился до приложения сил). Когда на тело действует пара сил, сумма сил как раз и равна нулю, и она не может привести в движение центр масс. Тело, однако, вращается. Значит, вращается оно вокруг оси, проходящей через центр масс (ведь все точки на оси вращения находятся в покое). Оси вращения, проходящие через центры масс тел, тем и замечательны, что на них не действуют никакие силы.
Содержание:
- Центр системы параллельных сил
- Нахождение равнодействующей системы параллельных сил
- Координаты центра параллельных сил
- Центр тяжести твердого тела
- Центр весаоднородного тела. Центр веса объема
- Центр веса площади
- Центр веса линии
- Методы нахождения центра веса
- Экспериментальные методы
- Метод симметрии
- Метод разбиения
- Метод дополнения
- Метод интегрирования
- Центр веса некоторых линий, площадей и объемов
- Примеры на определение положения центра веса
- Центр параллельных сил и центр тяжести
- Центр параллельных сил. Координаты центра параллельных сил
- Центр тяжести твердого тела
- Центр тяжести однородного твердого тела
- Центр тяжести плоскости плоской фигуры
- Теоремы Паппа — Гульдина
- Центры масс некоторых фигур
- Центр тяжести конуса и пирамиды
- Центр тяжести дуги окружности
- Центр тяжести кругового сектора
- Центр тяжести сегмента и сектора шара
- Статическая устойчивость положения равновесия твердого тела
- Центр параллельных сил – основные понятия и определения
- Координаты центра параллельных сил
- Центр тяжести тела, объема, площади, линии
- Определение координат центра тяжести тела, объема, площади, линии в интегральной форме
Центр системы параллельных сил — это точка, через которую проходит линия действия равнодействующей системы параллельных сил, при любом повороте всех этих сил и их точек приложения в одну и ту же сторону и на один и тот же угол.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Центр системы параллельных сил
Решая много теоретических и практических инженерных вопросов, приходится определять положение центра тяжести той или иной машины, инженерного сооружения и тому подобное. С понятием веса и центра тяжести тесно связаны понятие равнодействующей и центра системы параллельных сил. Рассмотрим задачу нахождения равнодействующей системы параллельных сил и точки ее приложения.
Нахождение равнодействующей системы параллельных сил
Пусть на тело действует система пяти параллельных сил  приложенных в точках
приложенных в точках  из которых силы
из которых силы  направленные в одну сторону, а
направленные в одну сторону, а  и
и  – в противоположную (рис. 10.1). Найдем равнодействующую данной системы параллельных сил методом последовательного добавления двух параллельных сил, используя правила, приведенные в § 4.1. Модуль равнодействующей сил
– в противоположную (рис. 10.1). Найдем равнодействующую данной системы параллельных сил методом последовательного добавления двух параллельных сил, используя правила, приведенные в § 4.1. Модуль равнодействующей сил  и
и  равна
равна  а точка ее приложения
а точка ее приложения  определится из соотношения
определится из соотношения

Равнодействующая параллельная силам
параллельная силам  и
и  Найдем равнодействующую
Найдем равнодействующую  добавляя силы
добавляя силы  и
и  Модуль равнодействующей
Модуль равнодействующей 
Точку приложения  равнодействующей
равнодействующей  найдем из соотношения
найдем из соотношения 
Аналогично найдем равнодействующую  сил
сил и
и  и точку ее приложения:
и точку ее приложения:
Итак, в результате последовательного добавления заданной системы параллельных сил получено две противоположно направленные параллельные силы  и
и  приложенные в точках
приложенные в точках  и
и  В зависимости от модулей этих сил и размещения их линий действия возможны следующие случаи:
В зависимости от модулей этих сил и размещения их линий действия возможны следующие случаи:
1)  но линии действия этих сил не совпадают. В этом случае заданные силы сводятся к паре сил (§ 4.2).
но линии действия этих сил не совпадают. В этом случае заданные силы сводятся к паре сил (§ 4.2).
2)  и линии действия этих сил совпадают. В этом случае заданная система параллельных сил взаимно уравновешивается согласно аксиомой 1 (§ 1.2).
и линии действия этих сил совпадают. В этом случае заданная система параллельных сил взаимно уравновешивается согласно аксиомой 1 (§ 1.2).
3)  Предположим, что
Предположим, что  Найдем равнодействующую
Найдем равнодействующую  сил
сил  и
и 

То есть равнодействующая равна алгебраической сумме сил системы. При этом за положительный принято направление сил  Точка приложения равнодействующей (точка С) определится из соотношения
Точка приложения равнодействующей (точка С) определится из соотношения и будет размещена за точкой приложения большей силы
и будет размещена за точкой приложения большей силы на луче
на луче 
Аналогично можно найти величину и точку приложения равнодействующей системы n параллельных сил, при этом модуль равнодействующей равна модулю алгебраичннои суммы составляющих сил системы при принятого положительного напрямую.


Равнодействующая будет параллельна силам, а положение точки ее приложения зависит от величин и положений точек приложения составляющих сил системы.
Покажем (на примере рассмотреной системы), положение точки приложения равнодействующей системы параллельных сил С не изменится отьповорота всех сил системы вокруг их точек приложения на один и тот самый угол и в ту же сторону. Для этого вернем силы  вокруг параллельных осей, проведенных через их точки приложения, на один и тот же угол α (рис. 10.1 силы в новом положении показаны штрихами). Получим новую систему параллельных сил
вокруг параллельных осей, проведенных через их точки приложения, на один и тот же угол α (рис. 10.1 силы в новом положении показаны штрихами). Получим новую систему параллельных сил 
Равнодействующая  параллельных сил по модулю равна равнодействующей
параллельных сил по модулю равна равнодействующей 
Поскольку при повороте модули параллельных сил не изменились. Точка приложения равнодействующей С также не изменит своего положения, поскольку ее положение зависит от величины сил и точек их приложения, которые остались неизменными. Итак, точку приложения равнодействующей системы параллельных сил можно найти как точку пересечения линий действия равнодействующих при повороте системы параллельных сил вокруг их точек приложения на один и тот же угол и в одну и ту же сторону. Точку приложения равнодействующей  системы параллельных сил называют центром параллельных сил.
системы параллельных сил называют центром параллельных сил.
Вывод. Основное свойство центра параллельных сил заключается в том, что его положения не зависит от направления сил в пространстве и не меняется от поворота сил системы вокруг точек их приложения на один и тот же угол в одно и то же сторону.
Однако надо заметить, что положение центра системы параллельных сил зависит от положения точек приложения параллельных сил. Поэтому параллельные силы следует считать приложенными в точках твердого тела.
Координаты центра параллельных сил
Пусть имеем систему n параллельных сил  причем принимаем, что силы направлены в одну сторону (рис. 10.2). Найдем координаты центра параллельных сил. Обозначим координаты точек приложения сил в выбранной системе координат через
причем принимаем, что силы направлены в одну сторону (рис. 10.2). Найдем координаты центра параллельных сил. Обозначим координаты точек приложения сил в выбранной системе координат через 

Равнодействующая этой системы сил параллельная заданным силам и равна по модулю сумме модулей составляющих сил

Координаты точки С приложения равнодействующей, то есть координаты центра данной системы параллельных сил, обозначим 
Вернем все силы так, чтобы они стали параллельны оси  Равнодействующая
Равнодействующая  также будет параллельна оси
также будет параллельна оси  Используя теорему Вариньона, определим момент равнодействующей относительно оси
Используя теорему Вариньона, определим момент равнодействующей относительно оси  Согласно этой теореме (§ 5.4), момент равнодействующей относительно оси
Согласно этой теореме (§ 5.4), момент равнодействующей относительно оси  равен алгебраической сумме моментов составляющих сил относительно этой же оси
равен алгебраической сумме моментов составляющих сил относительно этой же оси


В нашем случае 
откуда 
Аналогично возвращая все силы вокруг точек приложения так, чтобы они стали параллельны осям  и
и  соответственно, получим координаты
соответственно, получим координаты  и
и 
Итак, координаты центра системы параллельных сил определяются по зависимостям:

Умножив зависимости (10.3) на единичные орты  и добавив их, получим формулу для радиус-вектора
и добавив их, получим формулу для радиус-вектора центра параллельных сил
центра параллельных сил

где  радиус-вектор точки приложения силы
радиус-вектор точки приложения силы 

Центр тяжести твердого тела
На все тела, которые размещены в пределах поля земного притяжения, действуют силы
притяжения к Земле. Если тело разбить на отдельные элементарные частицы малых объемов, то на каждую такую частицу действуют силы земного притяжения, которые будут направлены к центру Земли. Но поскольку размеры тел малы по сравнению с радиусом Земли, то эти силы можно считать параллельными между собой. Исходя из этих предположений, можно дать определение веса тела и центра веса тела. Вес тела – это равнодействующая системы параллельных сил, с которыми отдельные части тела притягиваются к Земле, а центр веса тела – центр этой системы параллельных сил. Если тело абсолютно твердое, то его центр веса является неизменная относительно тела
точка, положение которой не зависит от ориентации его в пространстве. Действительно, если возвращать твердое тело, то силы веса отдельных частей тела, оставаясь направленными вертикально вниз, будут поворачиваться вокруг точек приложения, сохраняя параллельность между собой. В этом случае, учитывая свойство центра параллельных сил, положение центра веса тела не изменится. Центр веса тела – это геометрическая точка. Иногда он может находиться за пределами тела, как, например, центр веса кольца.

Рассмотрим некоторое тело и разобьем его на n элементарных частиц, силы притяжения которых к Земле обозначим через  (рис.10.3). тогда вес тела
(рис.10.3). тогда вес тела

Координаты центра веса твердого тела определятся как координаты центра параллельных сил.
Используя зависимости (10.3), с учетом (10.5), координаты центра веса тела определим по формулам

где  координаты i-й части тела.
координаты i-й части тела.
Центр весаоднородного тела. Центр веса объема
Для однородного тела, которое занимает объем V, можно определить координаты его центра веса из-за известных координат центров веса отдельных частей тела. Вес однородного тела определяется формулой где γ – вес единицы объема; V – объем тела. Аналогично вес каждой части
где γ – вес единицы объема; V – объем тела. Аналогично вес каждой части  где
где  – объем i-й части тела. Подставим эти значения в (10.6), получим
– объем i-й части тела. Подставим эти значения в (10.6), получим

Как видно из зависимостей (10.7), положение центра веса однородного тела зависит не от физических свойств материала тела, а только от его геометрической формы и размеров. Исходя из этого, можно ввести понятие центра веса объема, площади, линии.
Под центром веса объема понимают центр веса однородного тела, которое занимает данный объем.
Координаты центра веса объема определяются по зависимостям (10.7).
Центр веса площади
Центром веса площади считают центр веса однородной тонкой пластины постоянной толщины, основа которой занимает данную площадь.

Рассмотрим однородную тонкую пластину толщиной h, основа которой занимает
площадь S (рис.10.4). вес однородной тонкой пластины 
где S – площадь основания пластины; ρ -вес единицы объема.
Разобьем тонкую пластину на элементарные части. Вес каждой такой части 
где  – площадь элементарной части. Тогда координаты центра веса площади на основе формул (10.6) с учетом (10.8) и (10.9) определятся по зависимостям:
– площадь элементарной части. Тогда координаты центра веса площади на основе формул (10.6) с учетом (10.8) и (10.9) определятся по зависимостям:

где  – координаты центров веса элементарных площадей
– координаты центров веса элементарных площадей 
Величины, стоящие в числителе зависимостей (10.10), называются статическими моментами площади относительно координатных осей х и у: 
Тогда зависимости (10.10) с учетом (10.11) принимают вид

Центр веса линии
Под центром веса линии понимают центр веса однородного тонкого стержня постоянного поперечного сечения, ось которого совпадает с данной линией.
Рассмотрим однородный тонкий стержень, площадь поперечного сечения которого S. Ось этого стержня совпадает с линией АВ, центр веса которой нужно найти (рис. 10.5).

Вес стержня (линии) 
где L – длина линии АВ;  – удельный вес.
– удельный вес.
Разобьем стержень на элементарные части длиной 
Вес каждой части 
Координаты центра тяжести каждой выделенной части –  тогда координаты центра тяжести С линии АВ, которая совпадает с осью стержня, определяется по зависимостям (10.6) после соответствующих подстановок:
тогда координаты центра тяжести С линии АВ, которая совпадает с осью стержня, определяется по зависимостям (10.6) после соответствующих подстановок:

Методы нахождения центра веса
Существует несколько методов нахождения центра веса.
Экспериментальные методы
а) Способ подвеса. Положение центра веса тела по этому методу определяют следующим образом: подвешивают тело на нити в произвольной точке тела и продолжают направление нити в теле (прорисовывают линию на поверхности тела) подвешивают тело на нити в некоторой другой точке тела и снова отмечают на теле продолжение нити. Точка пересечения продолженных направлений нити и будет центром веса тела.
Этот метод позволяет определить центр веса однородного тела сложной конфигурации, но незначительного веса.
б) Метод взвешивания. Используют его для нахождения центра веса сложных тел (машин, инженерных конструкций) значительный вес. Суть метода взвешивания объясняет рис. 10.6.

Сначала находят вес тела. Для этого тело 1 поочередно устанавливают опорными точками на весы 2 и определяют величины  и
и  Измеряют расстояние L между опорными точками. Тогда координата центра тяжести
Измеряют расстояние L между опорными точками. Тогда координата центра тяжести  тела может быть определена из уравнений равновесия:
тела может быть определена из уравнений равновесия:

Метод симметрии
Лемма 1. Если однородное тело имеет плоскость геометрической симметрии, то центр тяжести тела лежит в этой плоскости.
Докажем это утверждение. Пусть однородное тело имеет плоскость симметрии. Проведем в этой плоскости оси  и
и  (рис. 10.7). вследствие симметрии для частицы
(рис. 10.7). вследствие симметрии для частицы  тела с
тела с
координатами  существует частица
существует частица  такого же объема
такого же объема  с координатами
с координатами 

Поэтому в формулах (10.7)

а значит, и  то есть центр тяжести однородного тела лежит в плоскости симметрии.
то есть центр тяжести однородного тела лежит в плоскости симметрии.
Аналогично можно доказать и следующие две леммы.
Лемма 2. Если однородное тело имеет ось геометрической симметрии, то центр веса находится на этой оси.
Лемма 3. Если однородное тело имеет центр геометрической симметрии, то центр веса тела совпадает с этим центром.
Метод разбиения
Положение центра веса тела можно определить, если разбить его на такие частицы, центры веса которых известны, или их легко можно определить.
Пусть требуется определить положение центра веса некоторой плоской фигуры (рис. 10.8). Разобьем фигуру на три части, для которых координаты центров тяжести  и
и 
соответственно есть
 а площади которых
а площади которых  легко определить, когда известны геометрические размеры. тогда координаты центра веса определим по зависимостям (10.10):
легко определить, когда известны геометрические размеры. тогда координаты центра веса определим по зависимостям (10.10):


Метод дополнения
Этот метод является частным случаем метода разбивки и используется, в частности, для тел, которые имеют вырезы (Рис. 10.9).

Зная площадь  всей фигуры и координаты
всей фигуры и координаты  и
и  ее центра веса, а также величины
ее центра веса, а также величины 
и  вырезанной из фигуры части, можно вычислить координаты центра веса плоской фигуры с вырезом по зависимостями (10.10), принимая в них площадь вырезанной части отрицательной:
вырезанной из фигуры части, можно вычислить координаты центра веса плоской фигуры с вырезом по зависимостями (10.10), принимая в них площадь вырезанной части отрицательной:

Метод интегрирования
Если тело нельзя разбить на несколько частей, положения центров веса которых известны, или их легко найти, то тело делят на элементарные части, число которых стремится к бесконечности, а размеры (объем, площадь и длина) каждой части стремятся к нулю. Тогда суммы в выражениях (10.7), (10.10), (10.15) будут интегралами по объему, площади или длине. Итак, выражения для координат центра веса объема примут вид:

где  – объем тела.
– объем тела.
Координаты центра тяжести плоской фигуры: 
где  площадь плоской фигуры.
площадь плоской фигуры.
Координаты центра веса линии:

где  длина линии.
длина линии.
Центр веса некоторых линий, площадей и объемов
а) Центр веса площади треугольника. Разобьем площадь треугольника АВD (Рис. 10.10) прямыми, параллельными стороне АD, большое количество узких полосок, которые можно
рассматривать как отрезки прямой линии.

Центр тяжести каждой такой линии лежит на ее середине, то есть на медиане ВК треугольника АBD. Значит, и центр веса площади треугольника лежит на этой медиане. Размышляя аналогично, приходим к выводу, что этот центр лежит и на других медианах треугольника: DM и AN.
А это значит, что центр веса площади треугольника совпадает с точкой пересечения его медиан. При этом следует вспомнить, что:

б) Центр тяжести дуги окружности.
Пусть имеем дугу АВ окружности радиуса R с центральным углом  (рис. 10.11).
(рис. 10.11).

Выберем систему координат так, чтобы ось  была осью симметрии дуги АВ. Согласно лемме 2 (§ 10.7, п. 2) центр веса дуги лежать на оси
была осью симметрии дуги АВ. Согласно лемме 2 (§ 10.7, п. 2) центр веса дуги лежать на оси  то есть
то есть  Найдем координату
Найдем координату  методом интегрирования. Для этого выделим на дуге АВ элемент
методом интегрирования. Для этого выделим на дуге АВ элемент положение которого определяется углом φ. Тогда координата x выделенного элемента будет
положение которого определяется углом φ. Тогда координата x выделенного элемента будет

Подставим эти значения в первую формулу зависимости (10.18) и получим:

где угол  измеряется в радианах.
измеряется в радианах.
Для дуги полукруга  получим
получим 
в) Центр веса площади кругового сектора.
Выделим в круговом секторе ОАВ (рис. 10.12) с центральным углом  элемент
элемент  положение которого определяется полярными координатами r и φ.
положение которого определяется полярными координатами r и φ.

Для определения координаты  воспользуемся зависимостью
воспользуемся зависимостью 
где 
Тогда 
Для сектора полукруга  будем иметь
будем иметь 
Приведем данные о положении центров веса еще некоторых однородных линий, фигур и тел (табл. 10.1).
Таблица 10.1
Центры веса однородных линий, фигур, тел



Примеры на определение положения центра веса
Задача 10.1. Найти положение центра веса тела, разрез которого показан на рис. 10.13. Тело состоит из цилиндра радиусом r, высотой h и двух полушарий радиусами  и
и  , Центры которых совпадают с центрами нижней и верхней основ цилиндра. Вычисления провести при следующих данных:
, Центры которых совпадают с центрами нижней и верхней основ цилиндра. Вычисления провести при следующих данных:


Решение. По начало координат выберем точку  – центр веса цилиндра. Поскольку ось
– центр веса цилиндра. Поскольку ось является осью симметрии для тела, то центр веса С будет лежать на этой оси, то есть будем определять только
является осью симметрии для тела, то центр веса С будет лежать на этой оси, то есть будем определять только  Разбиваем тело на три части: два полушария радиусом
Разбиваем тело на три части: два полушария радиусом  и цилиндр высотой h и радиусом r.
и цилиндр высотой h и радиусом r.
Для определения координаты центра веса  используем третью формулу зависимостей (10.7)
используем третью формулу зависимостей (10.7)

где  объем полушария радиусом
объем полушария радиусом 
 -координата его центра веса в выбранной системе
-координата его центра веса в выбранной системе
координат;
 – объем полушария радиусом
– объем полушария радиусом 
 – координата его центра веса;
– координата его центра веса;
 объем цилиндра, а
объем цилиндра, а  – координата его центра веса.
– координата его центра веса.
Подставим полученные значения в формулу и вычислим:

Задача 10.2. Определить положение центра веса фигуры, представляет собой круг
радиуса R с центром в точке О, с которого вырезано три круга с центрами в точках  (Рис. 10.14), если расстояния между центрами этих кругов и их радиусы соответственно равны:
(Рис. 10.14), если расстояния между центрами этих кругов и их радиусы соответственно равны:


Решение. начало координат выберем в центре О большого круга. Для определения координат центра веса  и
и используем метод дополнения (§ 10.7, п. 4). Тогда:
используем метод дополнения (§ 10.7, п. 4). Тогда:

Определим площади  и координаты их центров веса
и координаты их центров веса 

Поскольку центр веса каждого круга совпадает с его центром, то

Площадь большого круга  а площади вырезанных кругов
а площади вырезанных кругов

Полученные величины подставим в формулы (10.22) и определим 

Таким образом, координаты центра веса будут:

Центр параллельных сил и центр тяжести
Центром тяжести тела называют точку, являющуюся центром параллельных сил тяжести, приложенных к отдельным элементарным.
Центром тяжести твердого тела называется геометрическая точка, являющаяся центром параллельных сил тяжести, действующих на все частицы тела. Для абсолютно твердого тела положение центра тяжести относительно тела является неизменным.
Центр параллельных сил. Координаты центра параллельных сил
Центром параллельных сил называется точка на линии действия равнодействующей этих сил, которая не меняет своего положения при повороте всех сил вокруг точек их приложения на один и тот же угол в одном направлении.
С этого определения следует, что взятая точка С2 приложения равнодействующей системы двух параллельных сил, рассмотренной в предыдущем параграфе, является их центром. Предоставим соотношению (5.13) другой вид:
 (6.1)
(6.1)
где  – соответственно радиус-вектора точек
– соответственно радиус-вектора точек  в взятой системе координат (рис. 5.6)
в взятой системе координат (рис. 5.6)
С этого выражения находим :
 (6.2)
(6.2)
Перейдем теперь к системе n параллельных сил  которые приложенные в точках
которые приложенные в точках  и определяются в выбранной системе координат с центром
и определяются в выбранной системе координат с центром  и соответственно радиусами-векторами
и соответственно радиусами-векторами  которые обозначим через
которые обозначим через  Пусть
Пусть 
 – соответственно центры двух, трех и более параллельных сил. Для случая двух параллельных сил выражение для
– соответственно центры двух, трех и более параллельных сил. Для случая двух параллельных сил выражение для  получено в виде (6.2) в случае трех параллельных сил оно имеет аналогичный вид:
получено в виде (6.2) в случае трех параллельных сил оно имеет аналогичный вид:

Учитывая общий закон сложения выражений для радиусов-векторов центров С2, С3, по методу полной индукции переходим от  сил к
сил к силе. Принимая во внимание, что:
силе. Принимая во внимание, что:
 (6.3)
(6.3)
получим:
 (6.4)
(6.4)
Следовательно, точка С, через которую проходит равнодействующая системы  параллельных сил, определяется по формуле:
параллельных сил, определяется по формуле:
 (6.5)
(6.5)
где 
Эти рассуждения для вывода выражения (6.5) принадлежали к системе параллельных сил,
направленных в одну сторону. Однако, если задана система параллельных сил, направленных в разные стороны, то, разделив силы на две группы, каждая из которых включает только силы одного направления, и находим равнодействующую каждой группы, а затем, используя соотношение (5.7), приходим к исходной формулы. Проектируя обе части равенства (6.5) на координатные оси, получим:
 (6.6)
(6.6)
Из выражений (6.5) и (6.6) следует, что положение центра параллельных сил не зависит от направления сил, а зависит только от их модулей и их точек приложения. Это позволяет обобщить свойство системы параллельных сил, сформулированное в предыдущем параграфе для случая двух сил, на систему  сил, а именно: если все силы заданной системы параллельных сил повернуть на один и тот же угол, сохраняя неизменными их точки приложения, то и равнодействующая этих сил повернется на тот же
сил, а именно: если все силы заданной системы параллельных сил повернуть на один и тот же угол, сохраняя неизменными их точки приложения, то и равнодействующая этих сил повернется на тот же
угол, причем положение центра параллельных сил не изменится.
Покажем, что формулы (6.6) для координат центра С параллельных сил (рис. 6.1) можно получить также с помощью теоремы Вариньона о моменте равнодействующей относительно произвольного центра (см. § 5.5). Согласно теореме Вариньона (5.12)
 (6.7)
(6.7)
или
 (6.8)
(6.8)
где


Введем единичный вектор  , параллельный линиям действия сил
, параллельный линиям действия сил  . Тогда каждая из заданной системы сил может быть выражена через вектор
. Тогда каждая из заданной системы сил может быть выражена через вектор  :
:
 (6.9)
(6.9)
где  когда направления векторов
когда направления векторов  и
и  совпадают, и
совпадают, и  когда эти направления противоположны, то есть
когда эти направления противоположны, то есть 
Подставив соотношение (6.9) в выражение (6.8), получим:
 (6.10)
(6.10)
Поскольку вектор  может быть любого направления в пространстве (линии действия сил
может быть любого направления в пространстве (линии действия сил  {можно поворачивать на произвольный одинаковый угол относительно точек их приложения), приходим к выводу, что на этот вектор можно разделить обе части уравнения (6.10), которое после этого примет вид:
{можно поворачивать на произвольный одинаковый угол относительно точек их приложения), приходим к выводу, что на этот вектор можно разделить обе части уравнения (6.10), которое после этого примет вид:
 (6.11)
(6.11)
Отсюда находим векторную формулу (6.5), или эквивалентные ей три скалярных соотношения (6.6). Величины
 называют статическими моментами системы параллельных сил относительно координатных плоскостей соответственно
называют статическими моментами системы параллельных сил относительно координатных плоскостей соответственно 
Если начало координат – точку О – совместить с центром параллельных сил точкой С то эти величины равны нулю.
Если систему параллельных сил связать с образом механической системы материальных точек с массами  которые движутся с одинаковым ускорением, и находятся под действием сил инерции, то вместе с понятием центра параллельных сил, считают также термин центр масс, или центр масс системы. В этом случае радиус-вектор центра масс определяется по формуле, которая аналогична (6.5).
которые движутся с одинаковым ускорением, и находятся под действием сил инерции, то вместе с понятием центра параллельных сил, считают также термин центр масс, или центр масс системы. В этом случае радиус-вектор центра масс определяется по формуле, которая аналогична (6.5).
 (6.12)
(6.12)
Центр тяжести твердого тела
Если твердое тело, размерами которого можно пренебречь по сравнению с размерами Земли, находится в поле сил тяготения, например, вблизи земной поверхности, то с большой степенью точности можно считать, что силы тяжести  отдельных частиц (рис. 6.2) тела составляют систему параллельных сил.
отдельных частиц (рис. 6.2) тела составляют систему параллельных сил.
Эта гипотеза о параллельности сил тяжести оправдана во многих задачах техники.
Например, если представить себе поезд длиной 1870 м, что составляет 1 морскую милю, то
направления сил тяжести первого и последнего вагонов будут отклоняться от параллельности только на 1 дуговую минуту, потому что радиус Земли в среднем равен 6371 км. равнодействующая таких параллельных сил тяжести равна весу всего тела или системы тел, а центр такой параллельной системы сил называют центром массы тела.
Указанная гипотеза эквивалентна гипотезе о том, что поверхность Земли является плоской
и Земля не вращается. Понятно, что в задачах небесной механики, в задачах о движении
искусственных спутников Земли, в задачах о движение кораблей, самолетов, ракет и т.д. силы тяжести рассматривают как центральные силы. В этом случае рабочей гипотезой, но тоже приближенной, является гипотеза о том, что поверхность Земли сферическая и земля равномерно вращается вокруг своей оси.
Пусть  объем элементарного параллелепипеда с центром в точке
объем элементарного параллелепипеда с центром в точке  a
a  – сила тяжести, действующая на этот элемент массы
– сила тяжести, действующая на этот элемент массы  (рис. 6.2). Тогда средней плотностью элемента этого объема называется отношение
(рис. 6.2). Тогда средней плотностью элемента этого объема называется отношение  Стягивая параллелепипед в точку
Стягивая параллелепипед в точку  , получим плотность
, получим плотность  в этой точке тела, как предел средней плотности:
в этой точке тела, как предел средней плотности:
 (6.13)
(6.13)
Предположим, что в центре каждого параллелепипеда приложена сила тяжести  , модуль которой
, модуль которой  (
( – плотность в точке тела, совпадает с центром параллелепипеда). Тогда сила тяжести
– плотность в точке тела, совпадает с центром параллелепипеда). Тогда сила тяжести  образует систему
образует систему  параллельных сил, центр которых определится по формуле (6.5) и имеет вид:
параллельных сил, центр которых определится по формуле (6.5) и имеет вид:
 (6.14)
(6.14)
Переходя в выражении (6.14) к пределу при  и допуская, что размеры всех параллелепипедов стремятся к нулю, получим:
и допуская, что размеры всех параллелепипедов стремятся к нулю, получим:
 (6.15)
(6.15)
Предел сумм в этом выражении это интегралы, которые распространенные на объем V тела, причем предел знаменателя равен весу Р тела.
В результате получим:
 (6.16)
(6.16)
или в проекциях на координатной оси:
 (6.17)
(6.17)

Выражения (6.16) и (6.17) определяют массы неоднородного тела.
Центр тяжести однородного твердого тела
В случае однородного твердого тела его плотность будет постоянной  , поэтому:
, поэтому:
 (6.18)
(6.18)
Подставив значения (6.18) в формулы (6.17), найдем:
 (6.19)
(6.19)
С формул (6.19) видно, что положение центра тяжести однородного тела зависит только от геометрической формы и размеров твердого тела. Поэтому центр тяжести однородного твердого тела можно назвать центром объёма тела. Интегралы, стоящие в числителе формул (6.19), называются статическими моментами объема тела относительно координатных плоскостей, то есть – статический момент относительно плоскости
– статический момент относительно плоскости

 – статический момент относительно плоскости
– статический момент относительно плоскости 
 – статический момент относительно плоскости
– статический момент относительно плоскости  В случае, если параллельные силы непрерывно
В случае, если параллельные силы непрерывно
распределены по некоторой однородной (у = const) поверхности S, то
 , а сила тяжести
, а сила тяжести  элемента поверхности
элемента поверхности  будет
будет  . С помощью формул (6.17) в этом случае получим:
. С помощью формул (6.17) в этом случае получим:
 (6.20)
(6.20)

Формулы (6.20) выражают координаты центра массы однородной поверхности. Очевидно,
они применяются также в частном случае, когда фигура плоская.
Центр тяжести плоскости плоской фигуры
Относительно плоской фигуры интегралы, стоящие в числителе формул (6.20),
называются статическими моментами плоскости плоской фигуры относительно координатных осей  и рис. 6.3):
и рис. 6.3):
 (6.21)
(6.21)
С учетом обозначений (6.21) формулы (6.20) можно переписать в виде:
 (6.22)
(6.22)
Если плоская фигура может быть разбита на конечное число элементарных фигур (например, на рис. 6.4, а фигура состоит из двух прямоугольников и треугольника), то статические моменты выражаются суммой произведений площадей S, элементарных фигур, на которые разбита эта фигура (прямоугольник, треугольник и др.), на расстоянии центра тяжести каждой площади, составляющих эту плоскую фигуру, от соответствующей оси координат:
 (6.23)
(6.23)
Подставляя эти значения статического характера в формулу (6.22), получим:
 (6.24)
(6.24)
где  – соответствующие координаты центра массы и площадей элементарных фигур;
– соответствующие координаты центра массы и площадей элементарных фигур;  – площади элементарных фигур.
– площади элементарных фигур.
Если плоская фигура, центр тяжести которой необходимо определить, имеет вырезы (рис. 6.4, б), то площади вырезанных фигур в формулах (6.24) следует брать со знаком минус, а если она ограничена криволинейным контуром, то применяют формулы (6.20).

Пример. 1. Определить координаты центра массы площади фигуры (рис. 6.5), если 

Решение. Разобьем фигуру на три прямоугольника. Данные о площади элементарных фигур, а также координаты их центров тяжести запишем табл. 6.1.

Координаты центра тяжести всей фигуры найдем по формулам (6.24)

Пример 2. Найти координаты центра массы площади кругового сектора  с центральным углом
с центральным углом  и радиусом
и радиусом  (рис. 6.6).
(рис. 6.6).

Решение. Поскольку круговой сектор имеет ось симметрии  , то центр массы находим на этой же оси. Поэтому следует определить только лишь координату
, то центр массы находим на этой же оси. Поэтому следует определить только лишь координату  . По первой формуле (6.20) найдем:
. По первой формуле (6.20) найдем:

Площадь сектора будет  . Выделив элементарный сектор
. Выделив элементарный сектор  найдем
найдем 


Определим статический момент:

Окончательно получим

его объема и объема всего тела: 
 где S – площадь поперечного сечения стержня,
где S – площадь поперечного сечения стержня,  – длина стержня. Тогда по формулам (6.19) получим:
– длина стержня. Тогда по формулам (6.19) получим:
 (6.25)
(6.25)

Криволинейные интегралы, стоящие в числителе, являются статическими моментами
линии АВ относительно координатных плоскостей. Центр массы однородного криволинейного стержня называют центром тяжести линии.
Теоремы Паппа — Гульдина
С вопросами об определении положения центр масс линий и площадей связаны две элементарные теоремы, которые называются теоремами Паппа — Гульдина.
Теорема I. Площадь поверхности тела, образованного вращением плоской кривой вокруг оси, которая лежит в ее плоскости и ее не пересекает, равна произведению длины этой кривой на длину дуги окружности, описанной ее центром масс.
Пусть АВ (рис. 6.8) – дуга плоской кривой, которая, вращаясь вокруг оси Oz, образует боковую поверхность тела вращения. Выделим на кривой АВ элемент  .
.
Площадь элемента боковой поверхности созданной вращением элемента  может быть
может быть
исчисленная с точностью до величин второго порядка малости, как площадь боковой поверхности усеченного конуса. Итак:
 (6.26)
(6.26)
где  – приближенная координата центра тяжести элемента
– приближенная координата центра тяжести элемента 
Из формулы (6.26) выплывает что
 (6.27)
(6.27)
На основании (6.25) получим:
 (6.28)
(6.28)
Теорема доказана.

Теорема 2. Объем тела, образованного вращением плоской фигуры вокруг оси, которая лежит в ее плоскости и не пересекается с ее контуром, равен произведению площади этой фигуры на длину окружности, описанной ее центром тяжести.
Пусть плоская фигура Q вращается вокруг оси Oz (рис. 6.9). Выделим элемент площади и рассмотрим элемент объема тела вращения, который опишет этот элемент площади.
С точностью до бесконечно малых второго порядка малости, этот элемент объема определяется по формуле:
 (6.29)
(6.29)
где  – приближена координата центра массы элемента dS.
– приближена координата центра массы элемента dS.
На основании формул (6.21) и (6.22) будем иметь:
 (6.30)
(6.30)
Эта формула выражает вторую теорему Паппа – Гульдина. Отметим, что эти теоремы
имеют место, когда вращается тело на любой угол 
Пример 3. Вычислить площадь боковой поверхности и объем V тора. Тором называют тело,
образованное вращением круга радиусом  вокруг оси Oz. Центр окружности находится на расстоянии R от оси вращения,
вокруг оси Oz. Центр окружности находится на расстоянии R от оси вращения, 
Решение. На основании первой теоремы Паппа-Гульдина получим:

На основании второй теоремы


Центры масс некоторых фигур
Центр тяжести треугольника. Воспользуемся способом разбития и разделим треугольник
 (рис. 6.10) на элементарные полоски, проведя линии, параллельные стороне AD.
(рис. 6.10) на элементарные полоски, проведя линии, параллельные стороне AD.
Каждую такую полоску можно считать прямоугольником. Центры масс этих прямоугольников находятся в их серединах, то есть на медиане  треугольника.
треугольника.
Разбивая затем треугольник на элементарные полоски линиями, параллельными стороне АВ, приходим к выводу, что центр тяжести треугольника должен лежать на медиане DL.Итак, центр тяжести треугольника С находится в точке пересечения его медиан. Как известно, эта точка делит каждую из медиан на отрезки в отношении 1: 2, то есть 

 или
или 

Центр тяжести трапеции. Аналогично предыдущему случаю разобьем трапецию
ABDK (рис. 6.11) на элементарные полоски, параллельные основам BD и АК. Центры тяжести этих полосок располагаются на прямой EL, соединяющий середины оснований трапеции. Следовательно, и центр тяжести трапеции лежит на этой прямой.



Для того чтобы найти координату  как расстояние от нижнего основания, разобьем трапецию на два треугольника ABD и ADK. для каждого из них соответственно получим:
как расстояние от нижнего основания, разобьем трапецию на два треугольника ABD и ADK. для каждого из них соответственно получим:
 (6.31)
(6.31)
Воспользовавшись формулой (6.24), получим:

 (6.32)
(6.32)
Центр тяжести конуса и пирамиды
Пусть есть конус, высота которого h. Нужно найти координату центра тяжести точки С конуса (рис. 6.12).
На высоте z выделим элементарный объем, равный произведению площади сечения Р на dz, то есть:
 (6.32)
(6.32)
Дальше, воспользовавшись формулой (6.19), получим:
 (6.34)
(6.34)

Очевидно, что для конуса (рис. 6.12) имеет место соотношение:
 (6.35)
(6.35)
Если учесть, что объем конуса равен  то, подставив его в (6.34) и в выражение для
то, подставив его в (6.34) и в выражение для  из (6.35), получим:
из (6.35), получим:
 (6.36)
(6.36)
Следовательно, центр тяжести конуса лежит на линии  которая соединяет вершину конуса с центром тяжести основания и делит ее в соотношении 1:4, то есть:
которая соединяет вершину конуса с центром тяжести основания и делит ее в соотношении 1:4, то есть:

Очевидно, что такое же соотношение будет и для пирамиды.
Центр тяжести дуги окружности
Рассмотрим дугу АВ окружности радиусом R с центральным углом  . Выберем начало координат в центре круга и направим ось
. Выберем начало координат в центре круга и направим ось  перпендикулярно хорде АВ (рис. 6.13).
перпендикулярно хорде АВ (рис. 6.13).
Вследствие симметрии фигуры относительно оси  центр тяжести ее лежит на оси
центр тяжести ее лежит на оси  , то есть
, то есть  , поэтому остается найти
, поэтому остается найти  Для этого воспользуемся формулой (6.25) для центра тяжести линии, учитывая, что
Для этого воспользуемся формулой (6.25) для центра тяжести линии, учитывая, что 

 (6.37)
(6.37)
где  – половина центрального угла в радианах. В частности для центра массы дуги полукруга
– половина центрального угла в радианах. В частности для центра массы дуги полукруга  получим:
получим:
 (6.38)
(6.38)
Заметим, что последнюю формулу (6.38) для центра тяжести дуги полукруга легко получить с помощью первой теоремы Паппа-Гульдина. Пусть расстояние центра тяжести дуги полукруга от диаметра будет  . Если вращать дугу полукруга вокруг диаметра, на который она опирается, то получим сферу. Тогда на основании формулы (6.28) получим:
. Если вращать дугу полукруга вокруг диаметра, на который она опирается, то получим сферу. Тогда на основании формулы (6.28) получим:
 (6.39)
(6.39)
Откуда,
 (6.40)
(6.40)
Мы снова получили формулу (6.38).
Центр тяжести кругового сектора
Пусть задан круговой сектор с центральным углом
 и радиусом R (рис. 6.14). Выделим в нем элементарный сектор (заштрихованный на рис. 6.14), который можно принять за равнобедренный треугольник, в котором высота и медиана совпадают. Итак, центр тяжести каждого элементарного треугольника лежит на расстоянии
и радиусом R (рис. 6.14). Выделим в нем элементарный сектор (заштрихованный на рис. 6.14), который можно принять за равнобедренный треугольник, в котором высота и медиана совпадают. Итак, центр тяжести каждого элементарного треугольника лежит на расстоянии  от начала координат. Соответственно геометрическим местом центра массы всех элементарных треугольников будет дуга окружности радиусом
от начала координат. Соответственно геометрическим местом центра массы всех элементарных треугольников будет дуга окружности радиусом  .
.

Это означает, что центр массы площади кругового сектора можем искать как центр тяжести материальной линии, по которой непрерывно и равномерно распределен вес сектора. В этом случае можно применить формулу (6.37). В результате получим:
 (6.41)
(6.41)
где  половина центрального угла в радианах. В частности для центра массы дуги полукруга
половина центрального угла в радианах. В частности для центра массы дуги полукруга  получим:
получим:
 (6.42)
(6.42)
Заметим, что для получения формулы (6.42) также эффективно применение второй теоремы Паппа – Гульдина. Вращая полукруг вокруг диаметра, на который он опирается, получим шар. На основании формулы (6.30) получим:
 (6.43)
(6.43)
Откуда:
 (6.44)
(6.44)
то есть мы снова пришли к формуле (6.42)
Центр тяжести сегмента и сектора шара
Приведем без вывода формулы для центра массы поверхности сегмента шара высотой h и радиусом R и соответствующего объема сектора шара (рис. 6.15).
Для поверхности сегмента шара имеем:
 (6.45)
(6.45)
Для сектора шара:
 (6.46)
(6.46)

Статическая устойчивость положения равновесия твердого тела
Положение статического равновесия твердого тела будем называть статически устойчивым, если при небольших отклонениях тела от этого положения момент, возвращающий тело в положение равновесия, будет больше чем возмущающий момент, который отклоняет тело от этого положения. Заметим, что более полное понятие стойкости равновесия с учетом динамики тела мы дадим позже в разделе аналитической механики. Там же введем понятие устойчивости движения системы. Понятие устойчивости статического равновесия тела это лишь необходимое условие устойчивости положения равновесия, когда отсутствует движение тела, то есть без учета его динамики и возмущения начальных условий. Как будет показано ниже, несмотря на узость самого понятия статической устойчивости, оно может быть полезным при решении многих прикладных задач статики, которые сводятся к схеме механизма с одним звеном. Большинство таких механизмов или тел сводятся к схеме физического маятника с верхней или нижней маятниковостью (Рис. 6.16).

Чтобы тело с верхней маятниковостью сохраняло вертикальное положение относительно
опоры тела, нужно создать момент сил, который удерживал бы его в этом положении. Примерами системы с верхней маятниковостью являются, подъемные краны на подвижной основе (на шасси автомобиля или другого подвижного объекта) (рис. 6.17, а), или сами же объекты, движущиеся по поверхности Земли, в воде или в воздухе. если жесткость упругих опор (колес или упоров) обозначить  то при повороте на небольшой угол
то при повороте на небольшой угол  (рис. 6.17, б) в опорах А и В возникнут силы
(рис. 6.17, б) в опорах А и В возникнут силы  которые создадут пару сил с моментом
которые создадут пару сил с моментом  , который противоположно направленный к моменту силы тяжести
, который противоположно направленный к моменту силы тяжести  тела Q относительно точки О (рис. 6.17, б). Очевидно, что тело Q останется в вертикальном положении, если момент пары упругих опор будет больше, чем момент силы тяжести Р, которая пытается перевернуть (возмутить) тело Q. Найдем соотношение между этими силами. При повороте тела на угол
тела Q относительно точки О (рис. 6.17, б). Очевидно, что тело Q останется в вертикальном положении, если момент пары упругих опор будет больше, чем момент силы тяжести Р, которая пытается перевернуть (возмутить) тело Q. Найдем соотношение между этими силами. При повороте тела на угол  , согласно закона Гука, в упругих опорах возникнут силы:
, согласно закона Гука, в упругих опорах возникнут силы:

 (6.47)
(6.47)
где  – коэффициент линейной жесткости опор.
– коэффициент линейной жесткости опор.
Следовательно:
 (6.48)
(6.48)
Момент пары сил упругих опор равен:
 (6.49)
(6.49)
Тем временем момент силы массы, которая поворачивает тело:
 (6.50)
(6.50)
Для устойчивости системы нужно, чтобы момент пары упругих сил опор был больше момент возвращающей силы массы, то есть:
 (6.51)
(6.51)
С учетом соотношений (6.49) и (6.50), неравенство (6.51), сократив на  перепишем в виде:
перепишем в виде:
 (6.52)
(6.52)
или
 (6.53)
(6.53)
Как видно из условия (6.53), устойчивость системы обеспечить тем легче, чем больше
жесткость опор  , и больше расстояние
, и больше расстояние  между опорами. Этот факт используется на практике. Например, краны на автомобильных шасси ставят на дополнительные жесткие металлические опоры, которые выносят за пределы габаритов автомобиля, чтобы увеличить
между опорами. Этот факт используется на практике. Например, краны на автомобильных шасси ставят на дополнительные жесткие металлические опоры, которые выносят за пределы габаритов автомобиля, чтобы увеличить  . При движении автомобиля по кривой к возмущающим силам следует добавить еще возмущающий момент от центробежных сил. Системы с нижней маятниковостью реализуют, например, в подвижных объектах, перемещаются по воде или в воде – корабли, подводные лодки (рис. 6.18) и др. Геометрию этих объектов и расположения масс в них, выбирают так, чтобы центр приложения гидростатических сил Архимеда (точка О) был всегда выше центра тяжести этой конструкции (точка С), то есть реализуют схему физического маятника.
. При движении автомобиля по кривой к возмущающим силам следует добавить еще возмущающий момент от центробежных сил. Системы с нижней маятниковостью реализуют, например, в подвижных объектах, перемещаются по воде или в воде – корабли, подводные лодки (рис. 6.18) и др. Геометрию этих объектов и расположения масс в них, выбирают так, чтобы центр приложения гидростатических сил Архимеда (точка О) был всегда выше центра тяжести этой конструкции (точка С), то есть реализуют схему физического маятника.


Заметим, что определение статической устойчивости касаемо подвижных объектов в устойчивом режиме их движения иногда называют статическим балансировкой этих объектов.
К схеме с верхней маятниковостью (см. Рис. 6.17) сводятся также строительные конструкции, прикрепленные к основанию. Если твердое тело не прикреплено к основанию, то условие его статического равновесия таково, что сила тяжести не должна выходить за пределы основания (рис. 6.19) и создавать момент силы тяжести, который переворачивает тело. В положении а и б на рис. 6.19 конструкция является устойчивой, а в положении в- неустойчивой.
Последнее положение статической устойчивости реализуется в известной игрушке “Ванька-встанька “, в основе конструкции которой нижняя часть выполнена, как правило, в формы полусферы (рис. 6.20), а верхняя может иметь любую форму, например конуса.

Очевидно, что точка О опоры такой конструкции лежит на вертикальном радиусе АО. Если центр тяжести системы (точка  ) лежит ниже точки А, то система устойчива, если выше (точка С2), то неустойчива. Покажем, как рассчитать габариты этой конструкции, чтобы она была устойчивой. Для этого нужно найти формулу для координат центра тяжести конструкции, как центра массы объемов, если конус и полусфера выполнены с одного и того же материала. конусу присвоим индекс 1, а полусфере – 2. Отсчет будем вести от точки В, тогда:
) лежит ниже точки А, то система устойчива, если выше (точка С2), то неустойчива. Покажем, как рассчитать габариты этой конструкции, чтобы она была устойчивой. Для этого нужно найти формулу для координат центра тяжести конструкции, как центра массы объемов, если конус и полусфера выполнены с одного и того же материала. конусу присвоим индекс 1, а полусфере – 2. Отсчет будем вести от точки В, тогда:
 (6.54)
(6.54)
С учетом сведений с пункта 6.4 имеем:
 (для конуса)
(для конуса)
(6.55)
 (для полусферы)
(для полусферы)
Подставив (6.55) в (6.54), учитывая, что  должна быть меньше
должна быть меньше  , получим:
, получим:
 (6.56)
(6.56)
Поделив числитель и знаменатель на  , получим:
, получим:
 (6.57)
(6.57)
или
 (6.58)
(6.58)
Отсюда получим:
 (6.59)
(6.59)
Отметим, что, введенное здесь понятие статической устойчивости системы – это, по сути, схема формирования позиционной отрицательной обратной связи, которой отвечает в характеристическом уравнении положительный свободный член. Это означает, что когда система не имеет статической устойчивости, то не может быть ее устойчивости вообще. Статическая устойчивость системы – необходимое условие любой ее устойчивости.
Центр параллельных сил – основные понятия и определения
Предположим, что к телу в точках A1, A2, A3, …, An приложена система параллельных и одинаково направленных сил  .
.  ,
,  , …,
, …,  (рис. 1.56). Добавим геометрически силы
(рис. 1.56). Добавим геометрически силы  и
и  , то есть определим их равнодействующую
, то есть определим их равнодействующую  . Она будет равняться
. Она будет равняться
 =
=  +
+  .
.

Точка C1 приложения этой равнодействующей  определяется по известному
определяется по известному
правилу сложения двух параллельных сил, которые имеют одинаковое направление. Поскольку силы  и
и  приложены в точках A1 и A2, то, соединив эти точки прямой, можно найти положение точки C1 на этой прямой по известным уравнениям или пропорцией
приложены в точках A1 и A2, то, соединив эти точки прямой, можно найти положение точки C1 на этой прямой по известным уравнениям или пропорцией
P1 · A1C1 = P2 · A2C1.
Далее аналогично добавим силы  и
и  , получая их равнодействующую
, получая их равнодействующую  , которая является фактически равнодействующей трех сил и будет равняться
, которая является фактически равнодействующей трех сил и будет равняться
 =
=  +
+  =
=  +
+  +
+  .
.
Точка C2 приложения этой равнодействующей  также определяется указанным выше правилом на прямой C1A3.
также определяется указанным выше правилом на прямой C1A3.
Таким же образом поступаем с остальными силами, последовательно их добавляя, и,
окончательно получим равнодействующую  системы параллельных сил. Она будет
системы параллельных сил. Она будет
приложена в точке C, направленная в ту же сторону, что и заданные параллельные
силы, величина ее будет равняться

Вернем все заданные силы вокруг их точек приложения в одну сторону на один и тот же угол и снова найдем их равнодействующую. Также начинаем со сложения сил  и
и  . Но, как видно из рис. 1.56, а также из уравнений, ни модуль равнодействующей
. Но, как видно из рис. 1.56, а также из уравнений, ни модуль равнодействующей  , ни положение точки ее приложения C1 на прямой A1A2, не изменяются. Меняется только направление, которое будет параллельным новому направлению сил.
, ни положение точки ее приложения C1 на прямой A1A2, не изменяются. Меняется только направление, которое будет параллельным новому направлению сил.
Если провести до конца добавления параллельных сил, которые уже имеют новое направление, то можно увидеть, что и равнодействующая  в данном случае не меняет ни своего модуля, ни точки приложения C. меняется только направление ее линии действия.
в данном случае не меняет ни своего модуля, ни точки приложения C. меняется только направление ее линии действия.
Таким образом, точка приложения равнодействующей  системы параллельных сил всегда совпадает с точкой C, положение которой по отношению к положению точек A1, A2, A3, …, An всегда будет неизменным. Эта точка называется центром параллельных сил.
системы параллельных сил всегда совпадает с точкой C, положение которой по отношению к положению точек A1, A2, A3, …, An всегда будет неизменным. Эта точка называется центром параллельных сил.
Центр параллельных сил — это точка приложения их равнодействующей, которая не
меняет своего положения при повороте всех сил на одинаковый угол и в одну и ту же сторону.
Координаты центра параллельных сил
Предположим, что к телу в точках A1, A2, A3, …, An приложена система параллельных сил  .
.  ,
,  , …,
, …,  , которая сведена к равнодействующей силе
, которая сведена к равнодействующей силе  , приложена в точке C (рис. 1.57). Выберем пространственную декартову систему координат Oxyz так, чтобы бы одна из осей (например, ось z) была параллельная заданным силам. Найдем моменты всех сил относительно осей координат x, y и z.
, приложена в точке C (рис. 1.57). Выберем пространственную декартову систему координат Oxyz так, чтобы бы одна из осей (например, ось z) была параллельная заданным силам. Найдем моменты всех сил относительно осей координат x, y и z.
Обозначим в принятой системе координаты точек приложения сил
 и точки приложения равнодействующей
и точки приложения равнодействующей 
Вычислим сначала моменты всех сил относительно оси y. поскольку

то по теореме Вариньона

а по-этому


Отсюда координата xC будет равна

Аналогично определим моменты всех сил относительно оси x. Будем иметь

откуда координата yC будет равняться

Далее вернем все силы на один и тот же угол в одну сторону (например, на угол 90º,
перпендикулярно к плоскости yOz). Положение точки C, как известно, при повороте всех сил на одинаковый угол, в одну и то же сторону не меняется. Теперь вычислим моменты всех сил относительно оси y. Будем иметь

откуда координата zC будет равняться

Таким образом, окончательно получим формулы для координат центра параллельных сил

Центр тяжести тела, объема, площади, линии
На произвольное тело, которое расположено вблизи поверхности земли, действует сила,
имеет вертикальный вниз направление и называется силой тяжести (или просто вес). Если считать радиус земли достаточно большим (примерно 6,4 тыс. км), то для тел, размеры которых по сравнению с этим радиусом малы, силы тяжести (притяжения), действующих на частицы тела, можно считать параллельными, они сохраняют свою собственную величину, несмотря на любые повороты тела.

Для определения положения центра тяжести тело условно можно разделить
на много частиц (рис. 1.58). Каждая частица имеет силу тяжести  ,
,  ,
,  , …,
, …,  . Как видим, это система параллельных сил, равнодействующую которой
. Как видим, это система параллельных сил, равнодействующую которой  можно определить используя выражение:
можно определить используя выражение:

При любом повороте тела силы  остаются приложенными в тех же самых точках и остаются параллельными между собой. Меняется только направление этих сил по отношению к телу. А потому равнодействующая
остаются приложенными в тех же самых точках и остаются параллельными между собой. Меняется только направление этих сил по отношению к телу. А потому равнодействующая  будет при произвольном повороте тела приложена в точке, которая является центром параллельных сил. Эта точка называется центр тяжести тела.
будет при произвольном повороте тела приложена в точке, которая является центром параллельных сил. Эта точка называется центр тяжести тела.
Таким образом, центр тяжести тела — это геометрическая точка, неизменно связанная с этим телом, в которой приложена сила тяжести тела и которая не меняет своего положения при произвольном повороте тела.
Определим координаты центра тяжести как центра параллельных сил  ,
,  ,
,  , …,
, …,  на основании выражений, а именно:
на основании выражений, а именно:

где xk, yk и zk — координаты приложения силы притяжения частиц тела  .
.
Если тело однородно, то вес каждой части пропорционален ее объему, а именно
 = ϒ · vk ,
= ϒ · vk ,
где ϒ — удельный вес (вес единицы объема); vk — объем частицы тела.
Вес всего тела определяется
Q = ϒ · V,
где V — объем тела; ϒ — удельный вес тела.
Теперь подставим уравнения. Причем удельный вес ϒ, как общий множитель, сокращается. получим:

Аналогично поступаем и при определении двух других координат. Окончательно получим координаты центра тяжести объема:

Как видим, центр тяжести однородного тела зависит только от его геометрической формы. А потому, точка C, координаты которой определены выражением носит название — центр тяжести объема.

Теперь, рассмотрим пластину (рис. 1.59), толщина которой h относительно мала, то ее координата zC центра ее веса будет равняться zC =  .
.
Для определения двух других координат xC , zC используем выражения выше. Пластину надо представить в виде нескольких частиц, которые имеют собственный вес. Далее считаем, что вес каждой доли пластины будет равняться
 = ϒ · vk = ϒ · h · sk,
= ϒ · vk = ϒ · h · sk,
где ϒ — удельный вес (вес единицы объема); h — толщина пластины; sk — площадь частицы пластины.
Вес всей пластины будет равняться
Q = ϒ · V = ϒ · h · S,
где S — площадь пластины.
Теперь подставим формулы в первые два выражения. Сделаем это сначала для координаты xC, получим

Аналогично вычислим значение и второй координаты yC. Окончательно будем иметь координаты центра тяжести тонкой пластины

Точка C, координаты которой определяются формулами, имеет название центра тяжести площади.
Теперь определим координаты центра тяжести линии. Это может быть, например, проволока малого диаметра и постоянного поперечного сечения (рис. 1.60).
Как и в предыдущих случаях, сначала определим вес каждой доли линии и вес всей линии. Вес доли линии будет равняться
 = ϒ · vk = S · lk,
= ϒ · vk = S · lk,
где ϒ — удельный вес (вес единицы объема); S — площадь поперечного сечения линии; lk — длина доли линии.

Вес всей линии будет равняться
Q = ϒ · V = ϒ · S · L ,
где L — общая длина линии.
Теперь подставим значения и определим сначала координату xC. Она будет равняться

Таким же образом определяем две другие координаты центра тяжести линии.
Итак

Как видно из выражения, координаты центра тяжести линии зависят только от длины каждой доли линии и общей длины.
Определение координат центра тяжести тела, объема, площади, линии в интегральной форме
До сих пор определялись координаты центра тяжести однородных тел, в которых удельный вес ϒ является величиной постоянной (ϒ = const). Теперь определим координаты центра тяжести неоднородного твердого тела.
Представим неоднородное тело произвольной формы (рис. 1.61). Разобьем его на n элементарных элементов и выделим из них один k-й элемент. Обозначим его вес через  , xk, yk и zk — координаты центра тяжести k-того элемента. Подставив в формулы координат центра тяжести тела значение веса элемента
, xk, yk и zk — координаты центра тяжести k-того элемента. Подставив в формулы координат центра тяжести тела значение веса элемента  , получим
, получим


Точка приложения силы  расположена внутри элемента. Для точного определения точек приложения этих сил необходимо, чтобы объем каждого элемента n направлялся к нулю, а число элементов неограниченно росло, то есть n → ∞. Поэтому необходимо, чтобы суммы выражения рассматривались как границы. А именно
расположена внутри элемента. Для точного определения точек приложения этих сил необходимо, чтобы объем каждого элемента n направлялся к нулю, а число элементов неограниченно росло, то есть n → ∞. Поэтому необходимо, чтобы суммы выражения рассматривались как границы. А именно

где Q — вес всего тела.
Как известно, границы сумм, в числителе выражения, не зависят от выбора точек приложения сил  и является интегралами, которые могут быть распространены по всему объему тела, то есть
и является интегралами, которые могут быть распространены по всему объему тела, то есть

Теперь, если подставить выражения, окончательно получим координаты центра тяжести неоднородного тела в интегральной форме

Аналогично можно определить координаты центра тяжести объема тела в интегральной форме. Если считать, что
dq = ϒ · dV,
где dV — элемент объема тела,
Q = ϒ · V ,
где V — объем тела, то, подставляя формулы и сокращая на ϒ, получим

Из формул следует, что положение центра тяжести однородного тела не зависит от физических свойств его материала, а зависит только от геометрической формы и размеров тела.
В интегральной форме можно определить координаты центра тяжести площади. Найдем положение центра тяжести однородной пластины, которая имеет постоянную толщину h (рис. 1.62). Координата zC центра тяжести будет равняться zC =  . Определим другие две координаты. Также выделим в пластине элемент объема dV в форме элементарной призмы с основанием dS, высотой h и ребрами, перпендикулярные плоскости симметрии пластинки. Элементарный объем dV равен
. Определим другие две координаты. Также выделим в пластине элемент объема dV в форме элементарной призмы с основанием dS, высотой h и ребрами, перпендикулярные плоскости симметрии пластинки. Элементарный объем dV равен
dV = h · dS ,
а полный объем пластины равен
V = h · S ,
где S — площадь пластины.

Подставим формулы в первые два уравнения выражения, получим

Формулы являются формулами, определяют координаты центра веса площади.
В формулах в числительных стоят выражения статических моментов площади относительно координатных осей Oy и Ox, а именно:

Таким же образом определим координаты центра тяжести линии в интегральной форме. Для этого возьмем однородное тело, например, в виде проволоки AB с постоянной площадью поперечного сечения S и длиной L (рис. 1.63). Выделим в проводе элемент dl определенного объема. Если элемент имеет форму цилиндра с основанием S и высотой dl, то элементарный объем будет равен
dV = S · dl .

Полный объем тела, который рассматривается будет равен
V = S · L .
Теперь, подставив уравнения, определим координаты центра тяжести данного тела

Интегралы, содержащиеся в числительных выражения, называются криволинейными интегралами. Как видим, положение центра тяжести однородного тела в виде проволоки не зависит от его поперечных размеров. А потому формулы определяют координаты центра тяжести линии.
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
1.9.1.
Сложение
параллельных сил. Центр параллельных
сил.
Пусть
даны две параллельные силы
![]()
и
![]()
,
направленные в одну сторону и приложенные
к точкам
![]()
и
![]()
(рис.34).
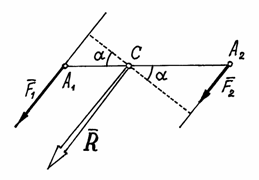
Конечно,
величина их равнодействующей
![]()
.
Вектор её параллелен силам и направлен
в ту же сторону. С помощью теоремы
Вариньона найдём точку приложения
равнодействующей – точку С.
По этой теореме
![]()
Значит
![]()
Отсюда
![]()
То
есть точка приложения равнодействующей
делит расстояние между точками
и
на
части обратно пропорциональные
силам.
Если
параллельные силы направлены в
противоположные стороны (рис.35), то
аналогично можно доказать, что
равнодействующая по величине будет
равна разности сил:
![]()
(если
![]()
),
параллельна им, направлена в сторону
большей силы и расположена за большей
силой – в точке С.
А расстояния от точки С
до
точек приложения сил обратно пропорциональны
силам:
![]()
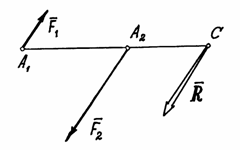
Следует
заметить, что если точка приложения
равнодействующей расположена на
одной прямой с точками
и
,
точками приложения сил, то, при повороте
этих сил в одну сторону на одинаковый
угол, равнодействующая также повернётся
вокруг точки приложения
С
в том же направлении, и останется
параллельной им.
Такая
точка приложения равнодействующей
называется центром
параллельных сил.
Конечно, если хотя
бы одну из сил перенести по своей линии
действия в другую точку, то и точка
приложения равнодействующей, центр
параллельных сил, тоже переместится по
линии действия.
Следовательно,
положение центра параллельных сил
зависит от координат точек приложения
сил.
Центром
нескольких параллельных сил, найденный
последовательным сложением каждых двух
сил, будем называть точку
С,
радиус-вектор которой определяется
формулой
![]()
,
![]()
где
![]()
–
радиусы-векторы
точек приложения сил;
![]()
–
величина равнодействующей параллельных
сил, равная алгебраической сумме этих
сил (знак силы определяется направлением,
которое заранее выбирается и считается
положительным).
Используя
(1), нетрудно найти координаты центра
параллельных сил. Если радиусы-векторы
откладывать из начала координат, то
проекции радиусов-векторов точек на
оси будут равны их координатам. Поэтому,
проектируя векторное равенство (1) на
оси, получим
![]()
где
![]()
–
координаты точек приложения сил.
1.9.2. Параллельные силы, распределенные по отрезку прямой.
а)
общий случай
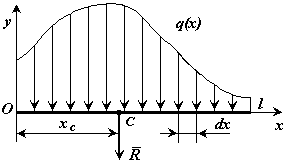
![]()
–
интенсивность распределенной силы
[Н/м],
![]()
–
элементарная сила.
![]()
–
длина
отрезка
Распределенная
по отрезку прямой сила интенсивности
эквивалентна
сосредоточенной силе
![]()
.
Сосредоточенная
сила прикладывается в точке
С
(центре
параллельных сил) с координатой
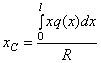
б)
постоянная
интенсивность
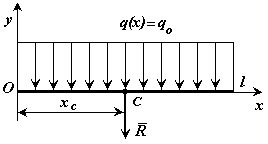
![]()
![]()
![]()
в)
интенсивность,
меняющаяся по линейному закону

![]()
![]()
![]()
.
1.9.3.Центр тяжести тел.
На
все точки тела, находящегося вблизи
поверхности Земли, действуют силы –
силы тяжести этих точек или их вес
![]()
.
Вообще эти силы будут сходящимися –
линии действия их пересекаются в центре
Земли. Но, если пренебречь размерами
тела в сравнении с размерами Земли, то
можно считать их параллельными.
Центр
этих параллельных сил, сил тяжести
точек, называется центром
тяжести
тела.
Значит
находить центр тяжести тел можно как
центр параллельных сил. Например,
координаты его
![]()
где
![]()
–
вес каждой точки тела, а
![]()
–
вес всего тела.

При определении
центра тяжести полезны несколько теорем.
1) Если однородное
тело имеет плоскость симметрии, то центр
тяжести его находится в этой плоскости.
Если
оси х
и у
расположить в этой плоскости симметрии,
то для каждой точки с координатами
![]()
можно
отыскать точку с координатами
![]()
.
И координата
![]()
по
(2), будет равна нулю, т.к. в сумме
![]()
все
члены
имеющие противоположные знаки, попарно
уничтожаются. Значит
центр тяжести расположен
в плоскости симметрии.
2) Если однородное
тело имеет ось симметрии, то центр
тяжести тела находится на этой оси.
Действительно,
в этом случае, если ось z
провести по оси симметрии, для каждой
точки с координатами
можно
отыскать точку с координатами
![]()
и
координаты
![]()
и
![]()
,
вычисленные по формулам (2), окажутся
равными нулю.
Аналогично
доказывается и третья теорема.
3) Если однородное
тело имеет центр симметрии, то центр
тяжести тела находится в этой точке.
И ещё несколько
замечаний.
Первое.
Если тело можно разделить на части, у
которых известны вес и положение центра
тяжести, то незачем рассматривать каждую
точку, а в формулах (2)
–
определять как вес соответствующей
части и
–
как координаты её центра тяжести.
Второе.
Если тело однородное, то вес отдельной
части его
![]()
,
где
![]()
–
удельный вес материала, из которого
сделано тело, а
![]()
–
объём этой части тела. И формулы (1) примут
более удобный вид. Например,
![]()
И
аналогично,
![]()
![]()
где
![]()
–
объём всего тела.
Третье
замечание.
Если тело состоит из однородных пластин
одинаковой, малой толщины, то объём
каждой пластины
![]()
где
![]()
–
площадь пластины, d
– толщина. И координаты центра тяжести
будут определяться только с помощью
площадей:
![]()
где
![]()
–
координаты центра тяжести отдельных
пластин;
![]()
–
общая площадь тела.
Четвёртое
замечание.
Если тело состоит из стержней, прямых
или криволинейных, однородных и
постоянного сечения, то вес их
![]()
где
li
– длина,
![]()
–
вес единицы длины (погонного метра), а
координаты центра тяжести будут
определяться с помощью длин отдельных
участков:
![]()
где
![]()
–
координаты центра тяжести
![]()
-го
участка;
![]()
Отметим, что
согласно определению центр тяжести
– это точка геометрическая; она может
лежать и вне пределов данного тела
(например, для кольца).
Координаты
центров тяжести неоднородных тел.
Координаты
центра тяжести неоднородного
твердого тела
в выбранной системе отсчета определяются
следующим образом:

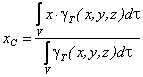

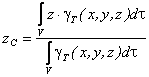
где
![]()
–
вес единицы объема тела (удельный вес)
![]()
–
вес всего тела.
Если
твердое тело представляет собой
неоднородную
поверхность,
то координаты центра тяжести в выбранной
системе отсчета определяются следующим
образом:
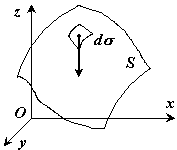
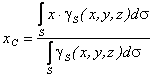


где
![]()
–
вес единицы площади тела,
![]()
–
вес всего тела.
Если
твердое тело представляет собой
неоднородную
линию, то
координаты центра тяжести в выбранной
системе отсчета определяются следующим
образом:

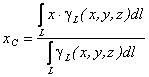
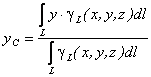

где
![]()
–
вес единицы длины тела
,
![]()
–
вес всего тела.
Координаты
центров тяжести однородных тел.
Для
однородного тела вес
![]()
любой
его части пропорционален объему
![]()
этой
части:
![]()
,
а вес Р
всего тела
пропорционален объему V
этого тела
![]()
,
где
![]()
–
вес единицы объема.
Подставив
эти значения Р
и
в
предыдущие формулы, мы заметим, что в
числителе
как
общий множитель выносится за скобку и
сокращается с
в
знаменателе. В результате получим:
![]()
![]()
![]()
Как
видно, центр тяжести однородного тела
зависит только от его геометрической
формы, а от величины
не
зависит. По этой причине точку
С,
координаты которой определяются
формулами, называют центром тяжести
объема V.
Путем аналогичных
рассуждений легко найти, что если тело
представляет собой однородную плоскую
и тонкую пластину, то для нее
![]()
![]()
где
S
– площадь всей пластины, a
![]()
–
площади ее частей.
Точку,
координаты которой определяются
формулами называют
центром тяжести площади S.
Точно так же
получаются формулы для координат центра
тяжести линии:
![]()
![]()
![]()
где
L
— длина всей
линии, l
— длины ее частей.
Таким образом,
центр тяжести однородного тела
определяется, как центр тяжести
соответствующего объема, площади или
линии.
1.9.4.Способы
определения координат центра тяжести.
Исходя
из полученных выше общих формул,
можно указать конкретные способы
определения
координат центров тяжести тел.

1.
Симметрия.
Если однородное тело имеет плоскость,
ось или центр симметрии, то его центр
тяжести лежит соответственно в плоскости
симметрии, оси симметрии или в центре
симметрии.
2.
Разбиение.
Тело разбивается на конечное число
частей, для каждой из которых положение
центра тяжести и площадь известны.
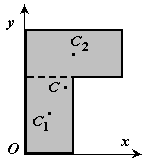
![]()
![]()
![]()
![]()
![]()
.
3.
Дополнение. Частный
случай способа разбиения. Он применяется
к телам, имеющим вырезы, если центры
тяжести тела без выреза и вырезанной
части известны.
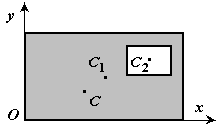
![]()
![]()
![]()
.
Центры тяжести
некоторых однородных тел.
1)
Центр тяжести
дуги окружности.
Рассмотрим дугу АВ
радиуса R
с центральным
углом
![]()
.
В силу симметрии центр тяжести этой
дуги лежит на оси Ox.
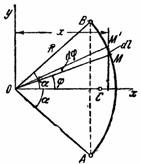
Найдем
координату
![]()
по
формуле
![]()
.
Для этого выделим на дуге АВ
элемент ММ’
длиною
![]()
,
положение которого определяется углом
![]()
.
Координата х
элемента ММ’
будет
![]()
.
Подставляя эти значения х
и
![]()
и
имея в виду, что интеграл должен быть
распространен на всю длину дуги, получим:
![]()
где
L
– длина дуги АВ, равная
![]()
.
Отсюда окончательно находим, что
центр тяжести дуги окружности лежит на
ее оси симметрии на расстоянии от центра
О,
равном
![]()
где
угол
измеряется
в радианах.
2)
Центр тяжести
площади треугольника.
Разобьем площадь треугольника ABD
прямыми, параллельными AD,
на узкие полоски; центры тяжести
этих полосок будут лежать на медиане
BE
треугольника.
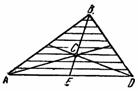
Следовательно, и
центр тяжести всего треугольника
лежит на этой медиане. Аналогичный
результат получается для двух других
медиан. Отсюда заключаем, что центр
тяжести площади треугольника лежит в
точке пересечения его медиан.
При
этом, как известно,
![]()
3)
Центр тяжести
площади кругового сектора.
Рассмотрим круговой сектор ОАВ
радиуса R
с центральным углом
![]()
.
Разобьем мысленно площадь сектора ОАВ
радиусами, проведенными из центра О,
на п
секторов. В пределе, при неограниченном
увеличении числа
![]()
,
эти секторы можно рассматривать как
плоские треугольники, центры тяжести
которых лежат на дуге DE
радиуса
![]()
.
Следовательно, центр тяжести сектора
ОAB
будет совпадать с центром тяжести
дуги DE.
Окончательно получим, что центр тяжести
площади кругового сектора лежит на его
центральной оси симметрии на расстоянии
от начального центра
О,
равном
![]()
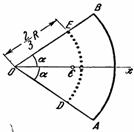
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Система параллельных сил:
Если на тело действуют параллельные силы, не лежащие в одной плоскости (рис. 123), то, выбрав координатные оси так, чтобы ось z была параллельна заданным силам, а плоскость хОу им перпендикулярна, по выражению (49) будем иметь:
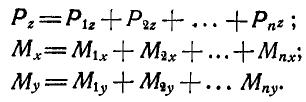
Проекции главного вектора 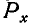
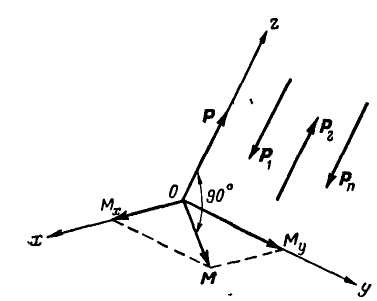
Рис. 123.
Вычисляя по формулам (49а) главный вектор 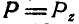 и главный момент
и главный момент 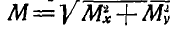 , замечаем, что главный вектор Р при выборе центра приведения в точке О расположен на оси z, а главный момент М в плоскости хОу; поэтому
, замечаем, что главный вектор Р при выборе центра приведения в точке О расположен на оси z, а главный момент М в плоскости хОу; поэтому  . Отсюда следует, что пространственная система параллельных сил никогда не приводится к динаме, а приводится к равнодействующей, если
. Отсюда следует, что пространственная система параллельных сил никогда не приводится к динаме, а приводится к равнодействующей, если 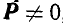 , или к паре, если
, или к паре, если 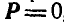 , или взаимно уравновешивается, если
, или взаимно уравновешивается, если 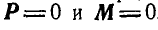 .
.
В последнем случае мы будем иметь три уравнения равновесия:
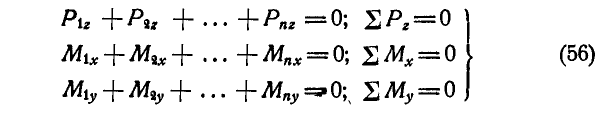
Сложение параллельных сил можно произвести иначе. Пусть на тело (рис. 124) действуют 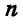 параллельных сил.
параллельных сил.
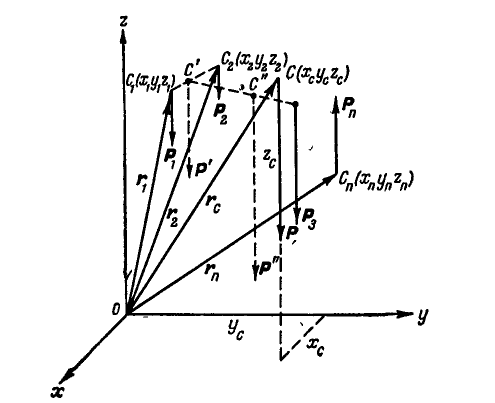
Рис. 124.
Складывая сначала силы 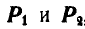 находим их равнодействующую
находим их равнодействующую 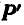 ; далее полученную равнодействующую
; далее полученную равнодействующую 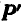 складываем с силой
складываем с силой  и получаем их равнодействующую
и получаем их равнодействующую 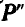 , которую складываем со следующей силой
, которую складываем со следующей силой 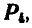 , и т. д. Произведя последовательное сложение всех параллельных сил, получим их общую равнодействующую:
, и т. д. Произведя последовательное сложение всех параллельных сил, получим их общую равнодействующую:
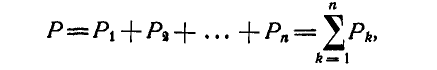
которая имеет определенную линию действия.
Если повернем все силы 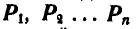 на один и тот же угол, то найдем для них новую равнодействующую, по величине равную первой, но имеющую другую линию действия. Точка пересечения линий действия равнодействующих называется центром параллельных сил.
на один и тот же угол, то найдем для них новую равнодействующую, по величине равную первой, но имеющую другую линию действия. Точка пересечения линий действия равнодействующих называется центром параллельных сил.
Следовательно, центром параллельных сил называется та точка С приложения их равнодействующей, которая не меняет своего положения при повороте всех сил на один и тот же угол.
Если известны координаты точек приложения составляющих сил, то координаты центра параллельных сил найдутся по формулам, аналогичным формуле (54), выражающим равенство моментов равнодействующей и составляющих относительно координатных осей, т. е.:
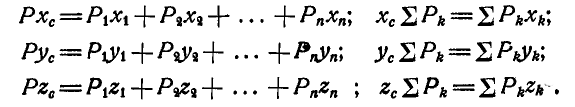
Для получения последнего равенства следует все силы повернуть на 90″ параллельно оси Ох или Оу.
Координаты центра параллельных сил будут:
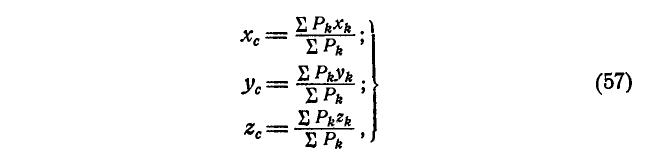
или в векторной форме
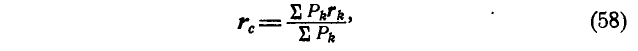
где 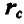 — радиус-вектор, определяющий положение центра параллельных сил;
— радиус-вектор, определяющий положение центра параллельных сил;
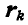 — радиус-вектор
— радиус-вектор 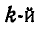 точки.
точки.
Центр тяжести
На каждую 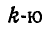 частицу твердого тела, находящегося вблизи земной поверхности, действует сила тяжести
частицу твердого тела, находящегося вблизи земной поверхности, действует сила тяжести 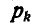 , направленная вертикально вниз. Считая, что силы тяжести всех частиц тела параллельны между собой, найдем координаты центра всех параллельных сил тяжести, который называется центром тяжести тела и определяется по формуле (58):
, направленная вертикально вниз. Считая, что силы тяжести всех частиц тела параллельны между собой, найдем координаты центра всех параллельных сил тяжести, который называется центром тяжести тела и определяется по формуле (58):
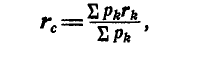
где 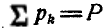 называется весом тела.
называется весом тела.
Если тело однородное, то отношение веса 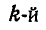 частицы к ее объему
частицы к ее объему 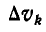 постоянно, т.е.:
постоянно, т.е.:
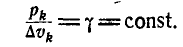
Заменяя в равенстве (58) 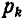 через
через 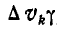 , имеем:
, имеем:
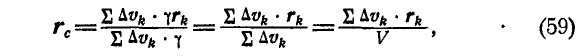
или
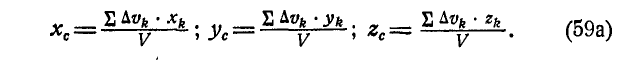
Формулы (59) и (59a) определяют координаты центра тяжести объема.
Выражения 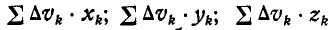 называются статическими моментами объема относительно плоскостей yOz, xOz и хОу.
называются статическими моментами объема относительно плоскостей yOz, xOz и хОу.
Рассуждая аналогично, можно найти также координаты центра тяжести площади:
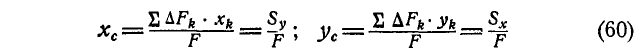
и линии:
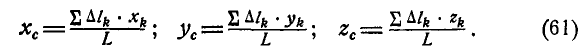
В последних равенствах F—величина всей площади, L — длина всей линии, а V—величина объема. Величины 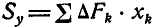 и
и 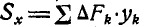 называются статическими моментами плоской фигуры относительно осей у и х.
называются статическими моментами плоской фигуры относительно осей у и х.
Из равенства (60) следует, что если известно положение центра тяжести плоской фигуры, то ее статические моменты относительно осей могут быть найдены также по формулам:
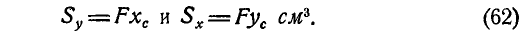
Статический момент плоской фигуры относительно оси х или у может быть величиной положительной, отрицательной и равной нулю, если ось проходит через центр тяжести фигуры. В самом деле из равенств (60) следует, что если 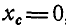 , то и
, то и 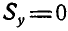 ; при
; при 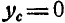 ;
; 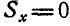 .
.
При нахождении центра тяжести плоской фигуры вместо равенства (60) иногда применяют графический способ, основанный на построении двух веревочных многоугольников. Пусть, например, требуется определить положение центра тяжести фигуры, показанной на рисунке 125. Для этого разбиваем всю фигуру на такие площади, положение центров тяжести которых нам известно (в данном примере на три прямоугольника).
Приложим в центрах тяжести 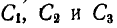 этих площадей вертикальные силы
этих площадей вертикальные силы 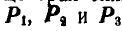 , пропорциональные площадям
, пропорциональные площадям 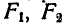 и
и 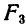 . Построив затем веревочный многоугольник, находим на чертеже положение линии действия равнодействующей сил
. Построив затем веревочный многоугольник, находим на чертеже положение линии действия равнодействующей сил 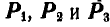 .
.
Так как положение центра параллельных сил, а также центра тяжести не изменяется при повороте всех сил на один и тот же угол, то, повернув все силы 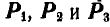 вокруг
вокруг 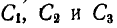 например, на 90°, вновь строим веревочный многоугольник и находим положение линии действия равнодействующей для повернутых сил.
например, на 90°, вновь строим веревочный многоугольник и находим положение линии действия равнодействующей для повернутых сил.
Пересечение линий действия равнодействующих, найденных для двух случаев, и определит положение точки С —центра тяжести всей фигуры.
При построении веревочного многоугольника для сил, повернутых на 90°, можно было бы, не строя многоугольника сил,
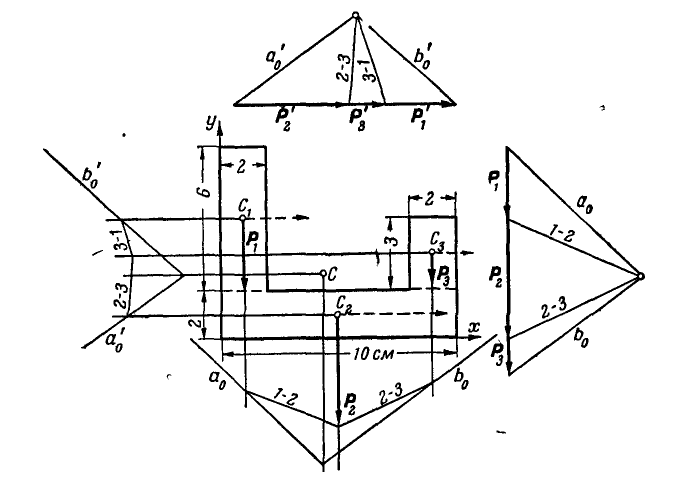
Рис. 125.
построить веревочный многоугольник, стороны которого были бы перпендикулярны соответствующим сторонам имеющегося веревочного многоугольника.
При заданных размерах фигуры (рис. 125) положение точки С можно определить также аналитически. Для этого, разбив фигуру, как и при графическом построении, на три прямоугольника и выбрав координатные оси, перепишем равенства (60) в следующем виде:
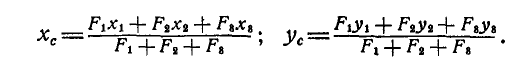
После подстановки численных значений будем иметь:
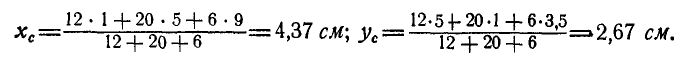
В некоторых случаях при определении положения центра тяжести плоской фигуры или плоской кривой удобно бывает одно из равенств (60) или (61) представить в иной форме, которая была предложена Паппом.
Пусть требуется, например, определить величину 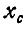 для фигуры, показанной на рисунке 126.
для фигуры, показанной на рисунке 126.
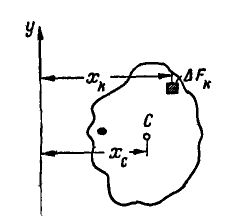
Рис. 126.
Будем вращать контур этой фигуры вокруг оси у, тогда мы получим некоторую замкнутую поверхность. Тело, ограниченное такой поверхностью, называется телом вращения.
Для определения объема тела вращения, разобьем всю площадь F фигуры на элементарные площадки 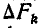 .
.
При вращении фигуры вокруг оси у каждая элементарная площадка 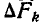 опишет элементарное круговое кольцо, объем которого равен
опишет элементарное круговое кольцо, объем которого равен 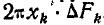 .
.
Следовательно, объем тела вращения определится по формуле:
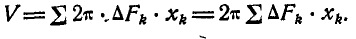
Но так как на основании первого равенства (60) 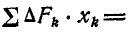
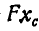 , то окончательно получим:
, то окончательно получим:
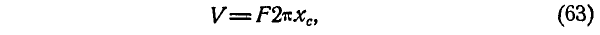
т. е. объем тела, полученного вращением плоской фигуры вокруг оси, расположенной в плоскости этой фигуры, равен произведению площади этой фигуры на длину окружности, описанной ее центром тяжести.
В этом заключается первая теория Паппа.
В качестве примера определим положение центра тяжести площади половины круга радиуса R (рис. 127).
Будем вращать эту площадь вокруг оси у, совпадающей с диаметром, тогда тело вращения будет представлять шар, объем которого равен 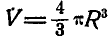 . Площадь плоской фигуры равна половине площади круга, т. е.
. Площадь плоской фигуры равна половине площади круга, т. е. 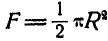 .
.
Подставляя значения V и F в равенство (63), будем иметь:
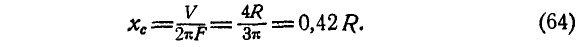
Аналогично можно иногда найти и положение центра тяжести плоской кривой. Пусть центр тяжести С плоской кривой (рис. 128) находится от оси у на расстоянии 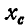 .
.
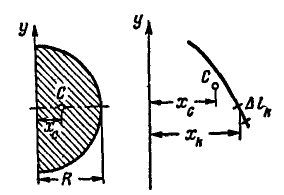
Рис. 127. Рис. 128.
Будем вращать эту кривую вокруг оси у, тогда мы получим некоторую поверхность вращения, величину площади которой обозначим через F. Для определения площади F разобьем кривую на элементарные участки 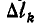 .
.
При вращении кривой вокруг оси у каждый элемент 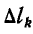 опишет элементарную кольцеобразную поверхность, площадь которой равна:
опишет элементарную кольцеобразную поверхность, площадь которой равна: 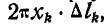 а площадь всей поверхности вращения
а площадь всей поверхности вращения 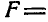
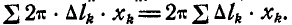
С другой стороны, из первого равенства (61) следует, что 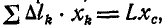 , поэтому
, поэтому 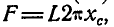 т. е. площадь поверхности, полученной вращением плоской кривой вокруг оси,расположенной в плоскости этой кривой, равна произведению длины этой кривой на длину окружности, описанной ее центром тяжести. В этом заключается вторая теорема Паппа.
т. е. площадь поверхности, полученной вращением плоской кривой вокруг оси,расположенной в плоскости этой кривой, равна произведению длины этой кривой на длину окружности, описанной ее центром тяжести. В этом заключается вторая теорема Паппа.
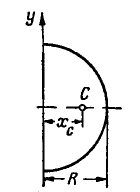
Рис. 129.
Применим эту теорему для определения центра тяжести дуги полуокружности радиуса R (рис. 129). Будем вращать эту дугу вокруг оси у, совпадающей с диаметром, тогда поверхность вращения, представляющая поверхность шара, будет 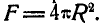 Длина плоской кривой
Длина плоской кривой 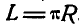 . Подставляя значения F и L в равенство
. Подставляя значения F и L в равенство 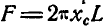 , получим:
, получим:
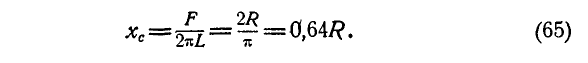
Правила нахождения центра тяжести
При нахождении центров тяжести тел следует помнить следующие правила:
- Если тело имеет плоскость симметрии, то центр тяжести его находится в этой плоскости.
- Если тело имеет две плоскости симметрии, то его центр тяжести находится на линии пересечения этих плоскостей.
- Если тело имеет три плоскости симметрии, то его центр тяжести находится в точке пересечения этих плоскостей.
- Если тело можно разбить на такие части
 , положения центров тяжести которых нам известно, то координаты центра тяжести тела найдутся по формулам (57), (59), (60), (61).
, положения центров тяжести которых нам известно, то координаты центра тяжести тела найдутся по формулам (57), (59), (60), (61).
Чтобы получить вполне точные формулы для определения координат центра тяжести в упомянутых случаях, мы должны перейти к пределу в предположении, что число элементов неограниченно возрастает при стремлении величины каждого элемента к нулю.
При решении многих задач полезно пользоваться справочной таблицей положений центров тяжести.
Задача №1
Определить положение центра тяжести тела, состоящего из однородных стержней (рис. 130). Размеры указаны в сантиметрах.
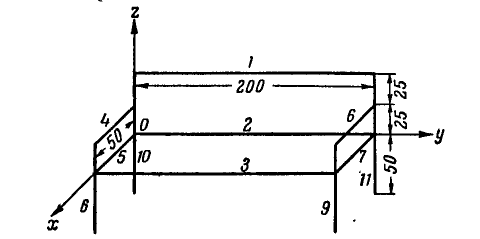
Рис. 130.
Решение. Обозначим стержни, из которых состоит тело, через  , их длины через
, их длины через  , а координаты центра тяжести каждого стержня через
, а координаты центра тяжести каждого стержня через 
Тогда координаты центра тяжести всего тела 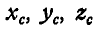 по формуле (61) будут:
по формуле (61) будут: 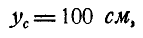 так как тело имеет плоскость симметрии, параллельную плоскости zOx,
так как тело имеет плоскость симметрии, параллельную плоскости zOx,
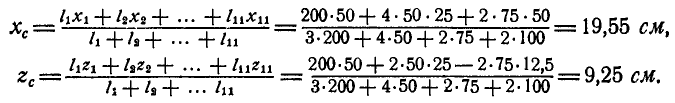
Задача №2
Найти координаты центра тяжести однородной пластинки (рис. 134). Размеры указаны в сантиметрах.
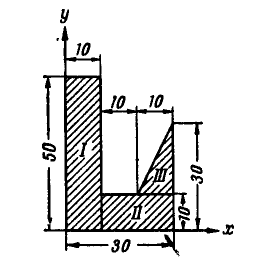
Рис. 134.
Решение. Разобьем площадь пластинки на три площади (два прямоугольника и
один треугольник), положения центров тяжести которых нам известны.
Обозначив эти площади соответственно через 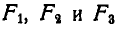 , на основании равенств (60) получим:
, на основании равенств (60) получим:
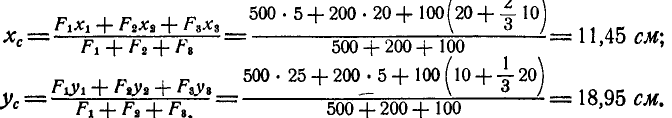
Задача №3
В нижнюю часть прямоугольника вписана окружность (рис. 135). Найти статические моменты заштрихованной площади относительно осей х и у.
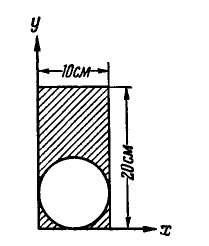
Рис. 134.
Решение. Искомые статические моменты определятся по формулам (62) путем вычитания из статического момента площади прямоугольника статического момента площади круга:
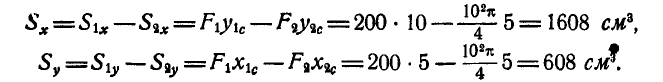
Задача №4
Определить координаты центра тяжести однородного тела, все ребра которого параллельны соответствующим координатным осям (рис. 136). Размеры на чертеже проставлены в сантиметрах.
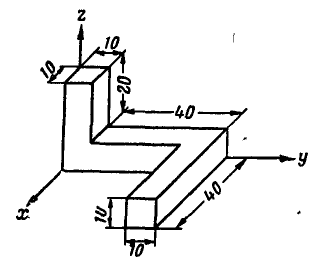
Рис. 136.
Указание: разбиваем все тело каким-либо способом на три прямоугольных параллелепипеда, положения центров тяжести которых нам известны, и по формулам (59а) определяем координаты центра тяжести тела.
Ответ: 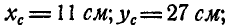
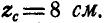
Задача №5
Найти положение центра тяжести дуги окружности, радиус которой R, длина 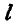 и хорда
и хорда 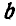 .
.
Решение. Проведем ось 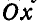 через центр дуги и середину ее хорды; тогда центр тяжести дуги будет находиться на оси
через центр дуги и середину ее хорды; тогда центр тяжести дуги будет находиться на оси 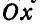 , которая является ее осью симметрии.
, которая является ее осью симметрии.
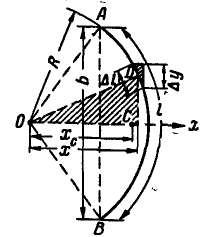
Рис. 137.
Разобьем дугу 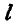 на бесконечное множество элементов
на бесконечное множество элементов 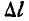 и обозначим абсциссу середины каждого элемента через х. Тогда абсцисса центра тяжести всей дуги может быть найдена по первой формуле (61):
и обозначим абсциссу середины каждого элемента через х. Тогда абсцисса центра тяжести всей дуги может быть найдена по первой формуле (61):
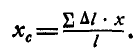
Из подобия заштрихованных ков (рис. 137) находим: 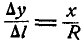 , или
, или 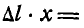
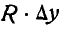 и, следовательно:
и, следовательно: 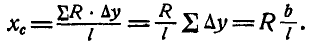
Задача №6
Найти координаты центра тяжести заштрихованной фигуры, контур которой ограничен полуокружностями диаметром 20 см и 10 см (рис. 138).
Рис. 138.
Решение. Будем считать, что заданная фигура состоит из трех частей I, II и III, из которых площади I и III ограничены осью 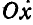 и полуокружностями диаметром 10 см, а площадь II ограничена той же осью и полуокружностью диаметром 20 см. Так как на самом деле площади I не существует, то ее следует брать со знаком минус.
и полуокружностями диаметром 10 см, а площадь II ограничена той же осью и полуокружностью диаметром 20 см. Так как на самом деле площади I не существует, то ее следует брать со знаком минус.
Обозначая площадь I, II и III через 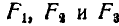 , координаты их центров тяжести через
, координаты их центров тяжести через 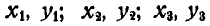 и пользуясь равенством (64), имеем:
и пользуясь равенством (64), имеем:
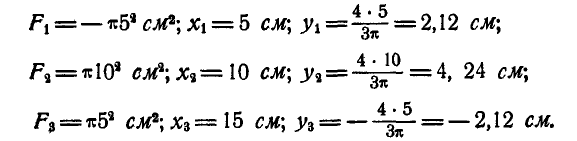
Применяя формулы (60), получим:
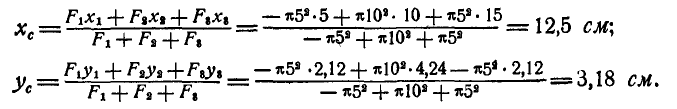
- Заказать решение задач по теоретической механике
Координаты центра параллельных сил
Центром параллельных сил называют точку на линии действия равнодействующей системы параллельных сил, вокруг которой поворачивается эта линия действия, если все силы поворачиваются вокруг точек их приложения, оставаясь параллельными между собой
Центр параллельных сил. Система параллельных сил, приложенных к твердому телу и направленных в одну сторону, не может находиться в равновесии или приводиться к паре сил—такая система приводится к равнодействующей. Пусть параллельные силы 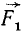 ,
, 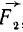 ,
, 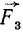 , . . .,
, . . ., 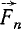 (рис. 70), составляющие данную систему, не лежат в одной плоскости.
(рис. 70), составляющие данную систему, не лежат в одной плоскости.
Для получения равнодействующей применим метод последовательного сложения. Сначала сложим две силы 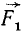 и
и 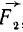 по известному правилу сложения двух параллельных сил. Равнодействующую этих сил обозначим
по известному правилу сложения двух параллельных сил. Равнодействующую этих сил обозначим 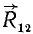 и приложим в точке C12, находящейся на прямой, соединяющей точки приложения А и В слагаемых сил, и определяемой из пропорции
и приложим в точке C12, находящейся на прямой, соединяющей точки приложения А и В слагаемых сил, и определяемой из пропорции
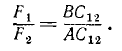 (11)
(11)
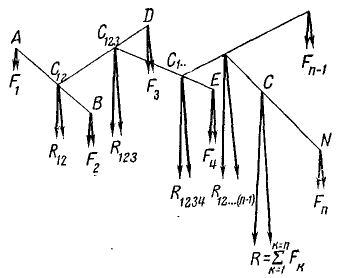
Рис. 70
Затем проведем плоскость через линии действия сил 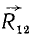 и
и 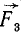 и найдем равнодействующую трех сил R123, которую мы приложим, руководствуясь тем же правилом, в точке
и найдем равнодействующую трех сил R123, которую мы приложим, руководствуясь тем же правилом, в точке 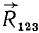 . Поступая далее таким же образом, мы найдем равнодействующую всей системы
. Поступая далее таким же образом, мы найдем равнодействующую всей системы 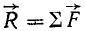 и точку C ее приложения.
и точку C ее приложения.
Предположим, что все параллельные силы повернулись в какую-либо сторону на некоторый угол. Очевидно, что тогда и равнодействующая 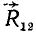 двух первых сил повернется в ту же сторону и на тот же угол, так как равнодействующая параллельных сил параллельна своим составляющим. Точка C12 останется на прежнем месте, так как модули сил F1 и F2 и их точки приложения А и В не изменились, а следовательно, не изменилась и пропорция (11). Не изменится также и модуль равнодействующей, равный, как известно, сумме модулей составляющих сил. Но если величина и точка приложения силы
двух первых сил повернется в ту же сторону и на тот же угол, так как равнодействующая параллельных сил параллельна своим составляющим. Точка C12 останется на прежнем месте, так как модули сил F1 и F2 и их точки приложения А и В не изменились, а следовательно, не изменилась и пропорция (11). Не изменится также и модуль равнодействующей, равный, как известно, сумме модулей составляющих сил. Но если величина и точка приложения силы 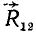 не изменились, а сила повернулась, став параллельной
не изменились, а сила повернулась, став параллельной 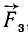 , то, следовательно, не изменится и точка приложения равнодействующей
, то, следовательно, не изменится и точка приложения равнодействующей 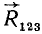 трех сил системы. Рассуждая таким образом и дальше, мы убедимся, что и точка C останется на прежнем месте, а линия действия равнодействующей
трех сил системы. Рассуждая таким образом и дальше, мы убедимся, что и точка C останется на прежнем месте, а линия действия равнодействующей 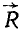 повернется вокруг этой точки, оставаясь параллельной линиям действия сил системы.
повернется вокруг этой точки, оставаясь параллельной линиям действия сил системы.
Точка приложения равнодействующей не является строго фиксированной, так как равнодействующую всегда можно перенести в другую точку ее линии действия, поэтому мы определим центр параллельных сил как точку на прямой действия равнодействующей системы параллельных сил, вокруг которой поворачивается эта прямая, если все параллельные силы поворачиваются вокруг точек их приложения, оставаясь параллельными между собой.
Центром тяжести твердого тела называют центр параллельных сил, представляющих веса материальных частиц твердого тела
Центр тяжести и его координаты
Примером центра параллельных сил может явиться центр подъемных сил корабля или центр давления насыпи на плоскую стенку. Но особенно часто приходится определять центр параллельных сил тяжести, которые, по сути дела, не являются параллельными, но могут с большой точностью быть приняты за параллельные. Под действием силы тяжести каждая материальная частица тела, находящаяся вблизи Земли, притягивается к Земле и вектор силы тяжести направлен «вниз» по отвесу к центру Земли. Таким образом, силы тяжести двух частиц не являются параллельными, так как их линии действия пересекаются в центре Земли. Однако громадные размеры Земли и сравнительно небольшие размеры материальных тел, центры тяжести которых приходится определять, позволяют считать силы тяжести частиц одного тела параллельными. Например, направления сил тяжести двух частиц, находящихся на корме и на носу океанского лайнера длиной 300 м, составляют между собой угол в десять секунд дуги, который невозможно даже отметить на чертеже ввиду его малости. C очень большой точностью можно принимать силы тяжести различных частиц одного и того же тела за параллельные, а общий вес тела считать приложенным в центре этих параллельных сил тяжести, называемом центром тяжести тела.
Как бы ни поворачивали тело и ни изменяли его положение по отношению к Земле, силы тяжести его отдельных частиц останутся вертикальными и параллельными между собой. Относительно тела они будут поворачиваться вокруг своих точек приложения, сохраняя величину и параллельность. При этом линия действия равнодействующей параллельных сил будет проходить через одну и ту же точку— центр тяжести. Отсюда следует, что центр тяжести твердого тела не изменяет своего положения относительно этого тела при изменении положения самого тела. Положение центра тяжести в теле зависит только от формы тела и от распределения в нем материальных частиц.
Координаты центра тяжести определяются равенствами
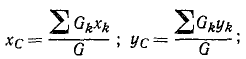
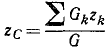
Отыскивать центр тяжести какого-либо тела методом последовательного сложения векторов сил тяжести его частиц не представляется целесообразным из-за громоздкости вычислений. Мы выведем общие формулы, позволяющие сравнительно легко определять координаты центра параллельных сил (или центра тяжести тела).
Разобьем мысленно тело на такие части, центры тяжести которых можно было бы сравнительно легко определить. Заменим каждую такую часть точкой (которую мы будем называть изображающей точкой), совпадающей с центром тяжести этой части и имеющей вес, равный весу этой части тела. Таким образом, изображающая точка характеризуется своим весом и положением в исследуемом теле, а все твердое тело заменено нами системой изображающих точек. Положим, что изображающих точек в теле получилось п. Веса этих точек будем обозначать буквой G с индексом, указывающим принадлежность к той или иной точке: Gl, G2, G3, …. Gn. Построим систему координат, неразрывно связанную с данным телом, направив ось Oz по вертикали вверх (рис. 71, а), и обозначим координаты изображающих точек через х, у и z с индексами, соответствующими точкам. Равнодействующая всех сил тяжести системы изображающих точек равна весу G всего тела, приложенному в его центре тяжести, координаты которого обозначим xc, ус и zc.
Mx=yZ — zY, My = zX—xZ, Mz = xY — yX. (23)
Выразим по первой из этих формул моменты относительно оси х сил тяжести всех частей тела, т. е. сил, приложенных к изображающим точкам. Проекции этих сил на ось у равны нулю, а на ось z — весам соответствующих частей тела с отрицательным знаком:
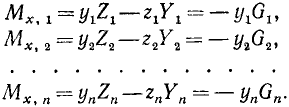
Сложив отдельно левые и правые части этих равенств, получим
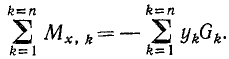
Выразим теперь по той же формуле (23) момент равнодействующей относительно оси Ох:
Mx(G) = -ycG.
В левой части этого равенства записан момент равнодействующей G относительно оси х, а в левой части предыдущего равенства—сумма моментов всех составляющих относительно той же оси. Эти две величины равны ,между собой, следовательно, равны и правые части равенства, т. е.
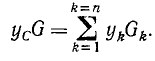
Из этого соотношения находим ординату центра тяжести:
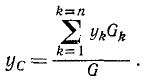
Если воспользоваться вторым из равенств (23)
My = zХ—xZ
и определить сумму моментов сил тяжести, приложенных к изображающим точкам, относительно оси у, приравняв ее моменту равнодействующей относительно той же оси, то аналогично предыдущему получим абсциссу центра тяжести
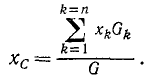
Для определения аппликаты zc центра тяжести тела повернем это тело вместе с осями координат на 90° вокруг оси х в направлении вращения стрелок часов, тогда место оси у займет ось z, а ось у будет направлена по вертикали вниз. В результате этого поворота все силы тяжести повернутся на один и тот же угол 90°, а центр параллельных сил (или в нашем случае—центр тяжести тела) не изменит своего местоположения как относительно тела, так и относительно неразрывно связанных с ним координатных осей (рис. 71,б).
Силы тяжести расположатся теперь параллельно оси у, и их проекции Y на эту ось будут положительны и равны модулям сил тяжести. Найдем моменты сил тяжести относительно оси х при новом положении тела:
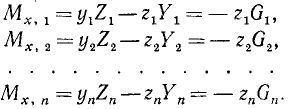
Суммируя отдельно левые и правые части этих равенств, найдем
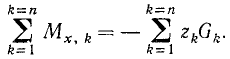
Определив момент равнодействующей относительно той же оси, получим
Мx(G) = -ZcG
и, приравнивая момент равнодействующей сумме моментов составляющих, найдем аппликату центра тяжести:
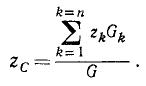
Напишем теперь вместе выведенные нами формулы:
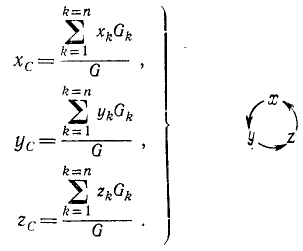
Эти формулы определяют положение центра тяжести.
Суммы произведений сил на координаты точек их приложения, стоящие в числителях этих формул, называют статическими моментами, а в знаменателях всех формул мы имеем вес всего тела.
Координаты х, у и z всякой точки равны проекциям на оси координат радиуса-вектора 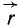 точки относительно начала координат. Следовательно, три аналитических равенства (45) можно заменить одним векторным равенством
точки относительно начала координат. Следовательно, три аналитических равенства (45) можно заменить одним векторным равенством
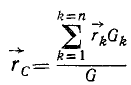
Центр тяжести линий, плоских фигур и тел
Если тело имеет плоскость симметрии (или ось симметрии, или центр симметрии), то центр тяжести тела лежит на этой плоскости (оси или в центре) симметрии
Если тело однородное, то, представляя, вес тела как произведение его объема V на вес γ единицы объема, а вес γ отдельных его частей — как произведение γ на их объем, получим:
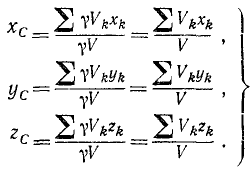 (46)
(46)
В таком смысле можно говорить о центре тяжести объема, понимая под этим центр тяжести однородного тела данной геометрической формы.
В том же смысле говорят о центре тяжести поверхностей и фигур, понимая под этим центр тяжести однородных пластин равной толщины. Его можно определить по аналогичным формулам:
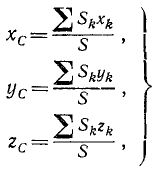 (47)
(47)
где Sk (при k=1, 2, 3, …. n) — площади отдельных частей пластины, S—площадь всей пластины.
В том же смысле говорят и о центре тяжести линий, понимая под линией тонкую однородную нить:
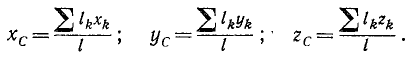 (48)
(48)
Если тело, хотя бы и неоднородное, имеет плоскость симметрии, т. е. каждой частице тела по одну сторону этой плоскости соответствует симметрично расположенная частица такого же веса по другую сторону плоскости, то центр тяжести такого тела лежит на плоскости симметрии. В самом деле, если каждой частице по одну сторону плоскости соответствует такая же по весу и симметрично расположенная частица по другую сторону, то равнодействующая сила тяжести этих двух частиц приложена к точке, лежащей в плоскости симметрии. По той же причине в плоскости симметрии лежат, и точки приложения равнодействующих весов других взятых попарно симметричных частиц. Складывая эти равнодействующие, найдем и их равнодействующую, которая приложена в той же плоскости, а точка приложения этой равнодействующей лежит в центре тяжести тела.
Для случая, если тело имеет ось симметрии или центр симметрии, можно доказать аналогичные теоремы. Из этих теорем можно вывести следующие следствия:
- центр тяжести однородного прямого стержня (или отрезка прямой) лежит в его середине;
- центр тяжести параллелограмма (однородной тонкой пластины, имеющей форму параллелограмма) лежит в точке пересечения его диагоналей, являющейся центром симметрии параллелограмма;
- центры тяжести однородного правильного многоугольника, круга, эллипса, шара лежат в их геометрических центрах.
В виде примеров ограничимся определением центров тяжести дуги окружности и площади треугольника, так как учащиеся будут иметь возможность и даже необходимость определять центры тяжести различных тел на упражнениях по интегральному исчислению. Построим оси координат, как показано на чертеже (рис. 72), и разобьем дугу на n элементарных отрезков Δlk. Центр тяжести дуги лежит на оси симметрии (yc= 0). Абсциссу центра тяжести найдем по (48):
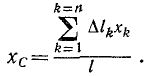
Приняв элементарные отрезки дуги за прямолинейные, разложим один из них на Δxk и Δyk. Если радиус, проведенный на середину этого отрезка, составляет с осью Ox угол ak, то, как видно из чертежа,
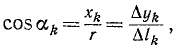
откуда
xkΔlk= r∆yk.
Составим такие выражения для всех отрезков и просуммируем их:
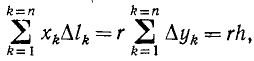
где h—длина хорды. Подставив найденное выражение в (48), определим центр тяжести дуги.
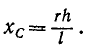
Учитывая, что h = 2r sin α и l = 2ar, этой формуле можно дать следующий вид:
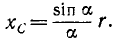
В частности, для полуокружности 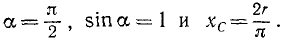
Центр тяжести треугольника лежит на пересечении его медиан на расстоянии от основания, равном одной трети высоты
Разобьем площадь треугольника (рис. 73) прямыми, параллельными основанию, на очень большое число узких полосок, которые можно рассматривать как отрезки прямых линий. Центр тяжести каждого отрезка лежит на его середине, а потому и центр тяжести всей площади треугольника лежит где-то на медиане, соединяющей вершину треугольника с серединой его основания. Разбив площадь треугольника прямыми, параллельными какой-либо другой стороне, и рассуждая аналогично, мы придем к заключению, что центр тяжести треугольника должен лежать и на другой медиане. Следовательно, центр тяжести площади треугольника лежит в точке пересечения его медиан. Как известно из планиметрии, медианы пересекаются на расстоянии одной трети от основания и двух третей от вершины.
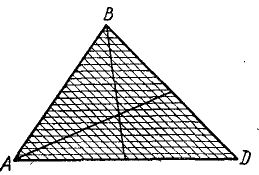
Рис. 73
Для определения координат центра тяжести тел и фигур сложной формы эти тела и фигуры заменяют системой точек и определяют координаты по формулам (45)
Для нахождения координат центра тяжести тела (или фигуры), имеющего сложную форму, нужно мысленно разбить это тело (или эту фигуру) на такие простейшие формы (если, конечно, это возможно), для которых положение центра тяжести и вес могут быть легко определены. В центре тяжести каждой такой части тела считают приложенным вес этой части. Будем называть, как мы это уже сделали выше, центры тяжести частей с приложенными в них весами этих частей изображающими точками. Для нахождения координат центра тяжести тела сложной формы остается лишь найти центр тяжести всех изображающих точек по формулам (45). Однако на практике эти подсчеты содержат большие трудности. Так, например, некоторые тела (пароходы, самолеты, автомобили и т. п.) приходится иногда заменять тысячами изображающих точек. В этих случаях может оказаться удобным подсчет по таблице, приведенной нами при решении следующей задачи.
Задача №7
Определить координаты центра тяжести контура прямоугольного параллелепипеда (рис. 74), ребра которого суть однородные бруски длиной: OA =8 дм; ОВ = 4 дм; OC = 6 дм; веса брусков, выраженные в ньютонах: OA =250; OB, ОС и CD по 75; CG = 200, AF= 125; AG и GE — по 50; BD, BF, DE и EF — по 25.
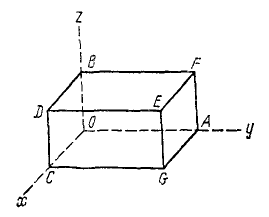
Рис. 74
Решение. Заменим стержни изображающими точками. Каждая из них имеет координаты середины того стержня который она изображает, и его вес.
Заполняем таблицу:
| № п.п. | Название | Gk | xk | yk | zk | Gkxk | Gkyk | Gkzk |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
OB OC CD BD BF OA CG DE AG AF EG EF |
75 75 75 25 25 250 200 25 50 125 50 25 |
0 3 6 3 0 0 6 6 3 0 6 3 |
0 0 0 0 4 4 4 4 8 8 8 8 |
2 0 2 4 4 0 0 4 0 2 2 4 |
0 225 450 75 0 0 1200 150 150 0 300 75 |
0 0 0 0 100 1000 800 100 400 1000 400 200 |
150 0 150 100 100 0 0 100 0 250 100 100 |
 |
1000 | 2625 | 4000 | 1050 |
Суммируя третий столбец и подсчитав суммы трех последних, определяем вес системы и статические моменты, и нам остается лишь поделить статические моменты на вес системы.
Ответ. xc=2,625 дм; yc = 4,000 дм; zc= 1,050 дм.
Если в теле или фигуре имеются полости или отверстия, то для определения центра тяжести пользуются теми же приемами и формулами, считая при этом объемы и площади вырезанных частей отрицательными. Этот метод иногда называют методом отрицательных масс.
Поясним применение этого метода решением задачи.
Задача №8
В диске радиуса r сделан эксцентрический вырез в виде круга, построенного на Радиусе как на диаметре. Найти центр тяжести оставшейся части диска (рис. 75).
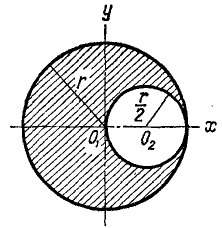
Рис. 75
Решение. Оставшаяся часть диска имеет ось симметрии. Начало координат возьмем в центре диска и ось симметрии примем за ось Ох. Искомый центр тяжести лежит на оси симметрии, следовательно, уc = 0. Найдем абсциссу центра тяжести. Для решения задачи воспользуемся методом отрицательных масс и представим оставшуюся часть диска двумя изображающими точками. Первая — это точка, лежащая в центре диска и имеющая массу, равную массе диска (считаем, что вырез в диске не сделан). Так как диск однородный, то за массу диска можно принять его площадь. Следовательно,
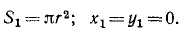
Вторая точка — это точка, лежащая в центре выреза, имеющая массу, равную массе вырезанной части диска, но взятую с обратным знаком. Опять вместо массы вырезанной части возьмем площадь. Имеем
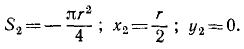
От присоединения этой «отрицательной площади» к площади первого диска и получается фигура, изображенная на рис. 75.
Абсциссу центра тяжести оставшейся части диска находим по формуле
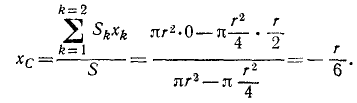
Ответ. 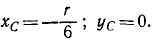
Объем тела, полученного от вращения плоской фигуры вокруг оси, лежащей в ее плоскости, равен произведению площади фигуры на длину дуги, описанной ее центром тяжести
Теоремы Паппы
При определении центров тяжести часто оказываются полезными две следующие теоремы. Пусть даны какая-либо плоская фигура, ее центр тяжести C (рис. 76) и ось zz, не пересекающая фигуры, но лежащая в ее плоскости. Разобьем площадь S фигуры на n элементарных частей ΔSk. Поворачивая фигуру вокруг оси zz, получим тело вращения, которое можно представить как состоящее из элементарных колец, объемом 2πxkΔSk каждое.
Тогда объем тела
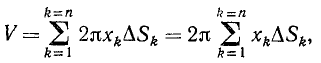
но 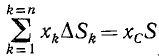 —статический момент площади, а потому
—статический момент площади, а потому
V=2πxCΔS (49)
Если объем тела и площадь образующей фигуры известны, то по (49) легко найти положение центра тяжести фигуры.
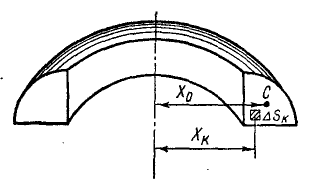
Рис. 76
Задача №9
Найти центр тяжести площади полуокружности.
Решение. Объем шара 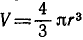 , площадь полукруга
, площадь полукруга 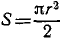 , подставляя в (49), получаем
, подставляя в (49), получаем
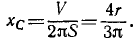
Ответ. хc = 0,4244r.
Легко доказать аналогично и вторую теорему: площадь поверхности, описанной при вращении плоской кривой вокруг оси, лежащей в ее плоскости, но не пересекающей эту кривую, равна произведению длины кривой на длину траектории, описанной ее центром тяжести.
S = 2πxCl. (50)
Задача №10
Найти центр тяжести дуги полуокружности.
Решение. Поверхность шара S = 4πr2, длина полуокружности l= πr. Подставляя в (50), получаем уже известный нам результат
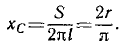
Ответ. хс = 0,6366r.
- Поступательное движение твердого тела
- Вращение твердого тела вокруг неподвижной оси
- Сферическое движение твердого тела
- Плоско-параллельное движение твердого тела
- Пространственная система сходящихся сил
- Момент силы относительно точки и относительно оси
- Теория пар, не лежащих в одной плоскости
- Произвольная пространственная система сил
Параллельными силами называются силы, линии действия которых параллельны. Определим правила сложения и вычитания параллельных сил.
Задача 1. Сложить две параллельные силы, направленные в одну сторону.
Рассмотрим абсолютно твердое тело, на которое действует система двух параллельных сил и
, приложенных к точкам
и
, находящихся на расстоянии
друг от друга. Для определенности будем считать, что силы
и
направлены вертикально вниз.
Определим равнодействующую этих сил и точку ее приложения.
Решение.
Приложим силы и
в соответствующих точках
и
(рис.С.30)

- В соответствие с аксиомой №2, добавим к системе сил
уравновешенную систему сил
, как показано на рисунке.
- Складывая попарно соответствующие силы,
получим силы и
, линии действия которых пересекаются в точке
.
- Поскольку силы
и
являются скользящими векторами (следствие из аксиомы №2), то их можно перенести вдоль линии действия в точку пересечения
.
- Теперь разложим силы
и
, приложенные к точке
на вертикальное и горизонтальное направления. Получим, что
и
.
- Вычтем уравновешенную систему сил
, приложенную к точке
(аксиома №2). Тогда
.
- Силы
и
теперь приложены к точке
, поэтому (в силу аксиомы №3) их можно сложить
.
Сила приложена к точке
. Так как сила
является скользящим вектором (следствие из аксиомы №2), то ее можно перенести вдоль линии действия в точку
, являющейся точкой пересечения прямой
и линией действия силы
.
Примем расстояние от точки до точки
равной
. То есть
, тогда расстояние между точками
и
равно
.
Таким образом, равнодействующая двух параллельных сил
и
равна
, причем ее модуль
. Равнодействующая
приложена в точке
.
- Определим теперь положение точки
.
Из подобия треугольников и
(
) следует справедливость пропорции
или
(С.12)
Из подобия треугольников и
следует справедливость пропорции
или
(С.13)
В равенствах (С.12) и (С.13) правые части равны, следовательно, равны и левые части
или
.
Отсюда следует, что (С.14).
Таким образом, определено положение точки приложения равнодействующей параллельных сил и
.
Частный случай. Если , то
, и
.
Задача 2. Сложить две параллельные силы, направленные в разные стороны.
Рассмотрим абсолютно твердое тело, на которое действует система двух параллельных сил и
, приложенных к точкам
и
, находящихся на расстоянии
друг от друга. Для определенности будем считать, что сила
направлена вертикально вниз, а
направлена вертикально вверх.
Определим равнодействующую этих сил и точку ее приложения.
Решение.
Приложим силы и
в соответствующих точках
и
(рис.С.31)
Проведем построения, аналогичные задаче 1.

- В соответствие с аксиомой №2, добавим к системе сил
уравновешенную систему сил
, как показано на рис.С.31.
- Складывая попарно силы,
получим силы и
, линии действия которых пересекаются в точке
(рис.С.31).
- Поскольку силы
и
являются скользящими векторами (следствие из аксиомы №2), то их можно перенести вдоль линии действия в точку пересечения
.
- Теперь разложим силы
и
, приложенные к точке
на вертикальное и горизонтальное направления. Получим, что
и
.
- Вычтем уравновешенную систему сил
, приложенную к точке
(аксиома №2). Тогда
.
- Силы
и
теперь приложены к точке
, поэтому (в силу аксиомы №3) их можно сложить
.
Сила приложена к точке
. Так как сила
является скользящим вектором (следствие из аксиомы №2), то ее можно перенести вдоль линии действия в точку
, являющейся точкой пересечения прямой
и линией действия силы
.
Примем расстояние от точки до точки
равной
. То есть
, тогда расстояние между точками
и
равно
.
Таким образом, как следует из рисунка, равнодействующая двух параллельных разнонаправленных сил
и
равна
, причем ее модуль
. Равнодействующая
приложена в точке
.
Определим теперь положение точки .
Из
подобия треугольников и
(
) следует справедливость пропорции
или
(С.15)
Из подобия треугольников и
(
) следует справедливость пропорции
или
(С.16)
В равенствах (С.15) и (С.16) правые части равны, следовательно равны и левые части
или
.
Отсюда следует, что (С.17)
Таким образом, определено положение точки приложения равнодействующей параллельных и направленных в разные стороны сил и
.
