Как найти точку приложения силы тяжести

Сила тяжести

Сила тяжести — равнодействующая сил притяжения к Земле, она распределена по всему объему тела. Силы притяжения, приложенные к частицам твердого тела, образуют систему сил, линии действия которых сходятся в центре Земли (рис. 8.1). Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.

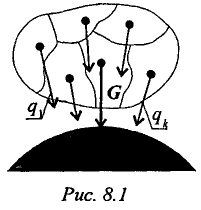
Точка приложения силы тяжести

Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:

Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.

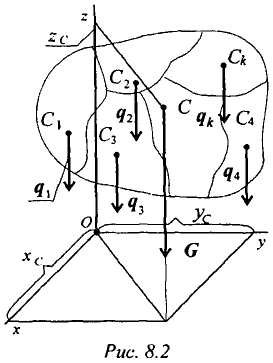
Изображаем тело, составленное из некоторых частей, в пространственной системе координат (рис. 8.2).

Тело состоит из частей, силы тяжести которых qk приложены в центрах тяжести (ЦТ) этих частей.

Пусть равнодействующая (сила тяжести всего тела) приложена в неизвестном пока центре .

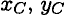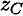и — координаты центра тяжест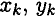и .

и 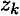— координаты центров тяжести частей тела.

Из теоремы Вариньона следует:

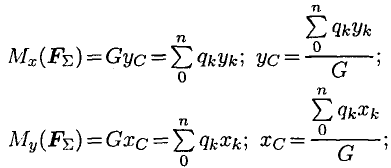
аналогично для оси :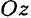

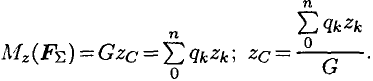
В однородном теле сила тяжести пропорциональна объему :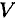

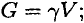
где 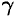— вес единицы объема.

Следовательно, в формулах для однородных тел:

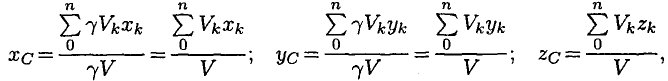
где 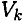— объем элемента тела; 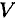— объем всего тела.

Эта теория взята со страницы решения задач по предмету «техническая механика»:

Примеры решения задач технической механике

Возможно эти страницы вам будут полезны:

Центр тяжести (центр масс):

Любое твердое тело можно представить как состоящее из множества материальных точек, на каждую из которых действует сила тяжести.

Центр тяжести – геометрическая точка абсолютно твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на данное тело при любом его положении в пространстве.

На каждую точку тела в поле сил тяжести действует сила, а на все тело – равнодействующая этих сил. Точка приложения равнодействующей называется центром тяжести тела.

Центр масс (центр инерции) – точка, характеризующая распределение масс в теле или системе тел. Представляется она как материальная точка, в которой сосредоточена вся масса системы и на которую действуют все приложенные к системе  внешние силы.

При определенных условиях положение центра тяжести тела совпадает с положением центра его масс.

Положение центра масс тела в однородном поле тяжести совпадает с положением его центра тяжести.

При небольших размерах тел возле поверхности Земли поле сил тяжести можно считать однородным, а силы, действующие на каждую точку тела, – параллельными.

Чтобы сила тяжести не вызывала движения, необходимо соблюдать определенные условия.

 Положение центра масс тела в однородном поле тяжести | совпадает с положением его центра тяжести.

Если тело закреплено в одной точке, например подвешено или лежит на опоре и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали: сила тяжести, действующая на тело, уравновешивается реакцией точки опоры.

Если тело закреплено в одной точке (подвешено или лежит на опоре) и пребывает в покое, то центр тяжести и точка опоры лежат на одной вертикали.

Рассмотрим примеры определения центра тяжести (центра масс) тел правильной несложной геометрической формы.

1. Найдем центр тяжести однородного стержня (рис. 2.48). Разделим стержень на несколько одинаковых небольших объемов (в нашем случае на пять слева и справа от середины стержня). Если добавить две параллельные силы, которые действуют на объемы 1 и 1′, то их равнодействующая будет расположена в точке О – середине стержня.

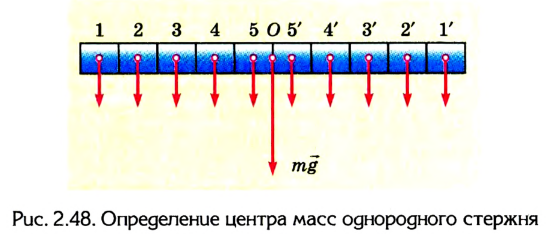
Аналогично и для пар сил 2-2′, 3-3′ и т. д. На основании этого можно сделать вывод: центр тяжести однородного стержня 99 расположен в точке О — середине стержня.

Центр тяжести однородного стержня расположен в середине стержня.

2. Пользуясь рассмотренным выше приемом, можно установить, что центр тяжести однородного круга совпадает с его центром (рис. 2.49).

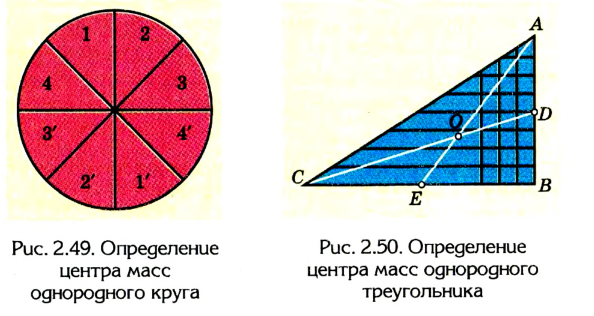
Таким образом, в однородных телах, имеющих центр симметрии (прямоугольник или круглая пластинка, шар, цилиндр и т. д.), центр тяжести совпадает с центром симметрии. Центр тяжести может находиться и вне тела, например у кольца или спичечной коробки, мяча или пустого стакана.

Центр тяжести однородного круга совпадает с его центром.

Центр тяжести однородного треугольника находится в точке пересечения его медиан.

3. Найдем центр тяжести однородного треугольника (рис. 2.50), представим, что вся площадь треугольника поделена на узкие поло-
сы, параллельные любой из сторон треугольника, например АВ. Центр тяжести каждой такой полосы, как однородного стержня, находится в ее середине. Центр тяжести всего треугольника лежит где-то на медиане CD, которая проходит через середины всех отрезков, параллельных стороне АВ.

Если поделить треугольник на отрезки, параллельные стороне СВ, то с учетом предыдущих вычислений можно сделать вывод: центр тяжести треугольника будет лежать на медиане АЕ. На обеих медианах центр тяжести может лежать лишь в том случае, если он совпадает с точкой их пересечения О.

4. Чтобы найти центр тяжести плоской фигуры, надо ее подвесить за какую-нибудь точку 1; тогда фигура развернется так, что ее центр тяжести окажется на вертикали, которая проходит через точку подвеса (рис. 2.51).

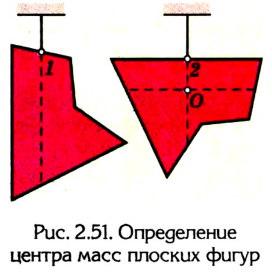
Отметив направление этой вертикали, подвесим фигуру за другую точку 2. И в этом случае фигура развернется так, чтобы центр тяжести находился на вертикали, проходящей через новую точку подвеса. Отметим направление и этой вертикали.

Центр тяжести плоской фигуры расположен в точке О пересечения вертикалей, проведенных через две любые точки подвеса.

Когда нужно определить центр сил тяжести сложных фигур, необходимо исходить из того, что сила тяжести равна сумме сил тяжести частей тела и всегда приложена к центру этих сил.

• Заказать решение задач по физике

Центр тяжести тела и центр масс тела

Когда мы рассматривали опыты с подвешенными телами, находящимися в равновесии, точка приложения сил натяжения была нам известна. А где приложена сила тяжести? В какой точке? Из этих опытов следует только то, что точка приложения силы тяжести при равновесии лежит на линии действия силы натяжения подвеса. Но это позволяет решить задачу о нахождении точки приложения силы тяжести экспериментальным путем. Если подвешивать плоское тело в разных точках (рис. 151), то линии действия сил натяжения пересекутся в одной точке С. Эта точка и будет точкой приложения силы тяжести. Она называется центром тяжести. Подобным образом можно определить положение центра тяжести не только плоского тела, но и любого другого.

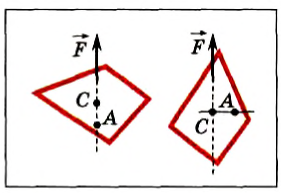
Рис. 151

Очевидно, что положение центра тяжести тел правильной формы можно указать, не выполняя описанный опыт. Так, например, центр тяжести однородного шара находится в его геометрическом центре, поскольку любой диаметр является осью симметрии шара. Центр тяжести круглого диска также находится в его геометрическом центре, как и центр тяжести обруча или кольца, и т. д. Последний пример показывает, что центр тяжести тела может находиться вне тела.

Положение центра тяжести тела можно и вычислить. Предварительно рассмотрим следующий опыт. Пусть тело состоит из двух шаров массами m₁ и m₂, насаженных на стержень (рис. 152, а). Если масса стержня значительно меньше масс шаров, то ею можно пренебречь. На каждый из шаров действуют силы тяжести, приложенные в их центре тяжести. Для того чтобы система находилась в равновесии, призму надо расположить так, чтобы линия действия силы реакции призмы проходила через центр тяжести этой системы — точку С. В этом случае суммарный момент сил относительно точки C равен нулю, т. е. выполняется условие:

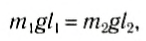
или

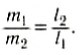
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Соотношение (1) можно получить и иначе. Поскольку момент сил тяжести равен нулю, то он должен быть равен нулю и относительно любой горизонтальной оси, проходящей, например, через точку О. Иначе тело вращалось бы вокруг этой оси. Обозначим расстояние между точками C и О через а. Тогда алгебраическая сумма моментов всех сил, действующих на тело, относительно точки О примет вид:

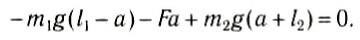
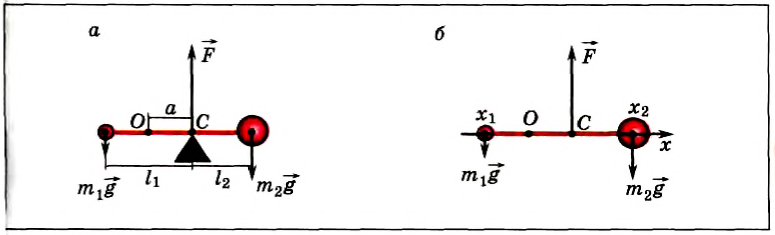
Рис. 152

Поскольку F=(m₁ + m₂)g, то после несложных преобразований получим соотношение (1). Такой подход позволяет находить положение центра тяжести аналитически.

Направим ось Ox вдоль стержня (рис. 152, б). Выберем начало отсчета в произвольной точке О. тогда координаты точек приложения сил соответственно будут х₁, х_с и х₂. Запишем условие моментов относительно точки О:

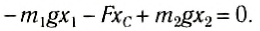
Отсюда

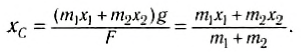
При выводе этой формулы было использовано значение силы F = (m₁ + m₂) g. Таким образом, центр тяжести этой системы тел отстоит от точки О на расстоянии х_с, определенном формулой (2).

Напомним, что выражение (2) является следствием правила моментов при равновесии тела, но в правой части отсутствует ускорение свободного падения. В него входят только координаты центра тяжести тел и их массы, поэтому точка, координата которой определяется формулой (2), называется центром масс тела. Следует отметить, что центр масс и центр тяжести совпадают, если тело находится в однородном гравитационном поле.

Понятие центра масс является более общим, чем понятие центра тяжести. Центр масс является характеристикой тела или системы тел, важной не только для задач, где речь идет о силе тяжести, но и для решения других физических проблем.

Если произвольное тело можно разбить на n элементов, массы которых m₁, m₂…,    m_n, и если известны координаты центров масс этих элементов x₁, x₂…,   x_n относительно выбранной системы координат, то координата центра масс тела вычисляется по формуле:

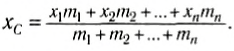
Естественно, что такие же соотношения можно записать и для у_с и z_c. Для примера вычислим положение центра масс столярного угольника. Он состоит из деревянного бруска 1 и деревянной линейки 2, соединенных под прямым углом (рис. 153). Положим, что масса бруска 1 в два раза больше массы линейки (m₁ = 2m₂). Так как линейка и брусок — однородные параллелепипеды, то центры масс находятся в их геометрических центрах. Очевидно, что центр масс угольника находится где-то на линии, соединяющей центры масс бруска (C₁) и линейки (C₂).

Выберем наиболее оптимальным образом систему координат, как показано на рисунке. Тогда координаты центра масс бруска: х₁ = 0, y₁ =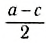, а координаты центра масс линейки: 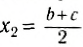, y₂ = 0 .
По формуле (3):    .

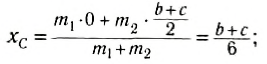
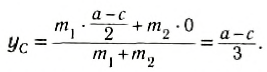
Таким образом, центр масс угольника находится вне тела.

Главные выводы:

1. Центр тяжести — точка, в которой приложена сила тяжести.
2. Центр масс симметричных однородных тел находится в их геометрическом центре.
3. Координаты центра масс тела можно вычислить по формуле (3).

Дано определение силы тяжести. Показано, что сила тяжести является частным случаем силы гравитации. Описаны факторы, определяющие силу тяжести: направление, точка приложения и численное значение. Приведен пример расчета силы тяжести, действующей на штангу со стороны Земли.

Сила тяжести, действующая на тело

Закон всемирного тяготения

Закон о взаимодействии  тел друг с другом (Закон всемирного тяготения) открыл английский ученый Исаак Ньютон около 1666 года. А в 1687 году он был опубликован в его труде «Математические начала натуральной философии».

Закон всемирного тяготения формулируется так: » Все  тела притягиваютс друг к другу с силой, модуль которой прямо пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними».   Сила притяжения между телами называется силой гравитации.

Определение силы тяжести

Сила тяжести (F_тяж) — это сила, характеризующая меру притяжения материальных тел к Земле. Поэтому она считается частным случаем силы гравитации. Можно сказать, что сила тяжести — это сила гравитации вблизи поверхности Земли.

Действие любой силы определяется тремя факторами:

• направлением;
• точкой приложения;
• численным значением.

Разберем эти факторы относительно силы тяжести.

Направление

Сила тяжести направлена вертикально вниз (рис.1).

Точка приложения

Любое тело можно представить состоящим из множества частиц, на каждую из которых действует сила тяжести. Однако условно считают, что сила тяжести приложена в точке, называемой центром масс тела или центром тяжести тела (ЦТ).

Численное значение

Численно значение силы тяжести рассчитывается по формуле:

F_тяж=m*g,

где: m – масса тела, кг

g – ускорение свободного падения тела, которое приближенно равно 9,8 м/c².

Рассмотрим следующий пример.

Определить силу тяжести, действующую на штангу со стороны Земли. Масса штанги равна 100 кг.

Решение

Значение силы тяжести определяем по формуле:

Fтяж=m*g = 100*9,8 = 980 Н.

То есть на штангу массой 100 кг со стороны Земли действует сила, равная 980 Н.

С уважением, А.В. Самсонова

Похожие записи:

---

Биомеханика рывка и толчка в тяжелой атлетике

Приведена рецензия на книгу докт. пед. наук, профессора А.А. Шалманова «Биомеханика движения штанги в рывке и толчке у…

---

Мышечно-сухожильный комплекс

Приведена рецензия на книгу  В.Т.Тураева и В.В. Тюпа «Мышечно-сухожильный комплекс: анатомия, биомеханика, спортивная практика» зав. кафедрой биомеханики НГУ…

---

Сила

Дано определение силы в механике. Описаны факторы, определяющие действие на тело силы: направление, точка приложения и численное значение.

---

Типы телосложения (соматотип) по Башкирову

Описана краткая биография П.Н. Башкирова и его научные труды. Дается классификация типов телосложения человека: долихоморфного (астенического), мезоморфного…

---

Типы телосложения (конституции) по Э. Кречмеру

Описана биография Эрнста Кречмера – немецкого психиатра и психолога, разработавшего типологию тела человека. Дано описание типов телосложения…

---

Типы конституции женщин по И.Б. Галанту

Описана биография известного советского психиатра И.Б.Галанта, предложившего естественную систему конституциональных типов женщин. Дана характеристика предложенных И.Б.Галантом  конституциональных…

В однородном
теле сила тяжести пропорциональна
объему V:

G
= γV;
где γ
– вес единицы объема. Следовательно,
в формулах для однородных тел:

;

;

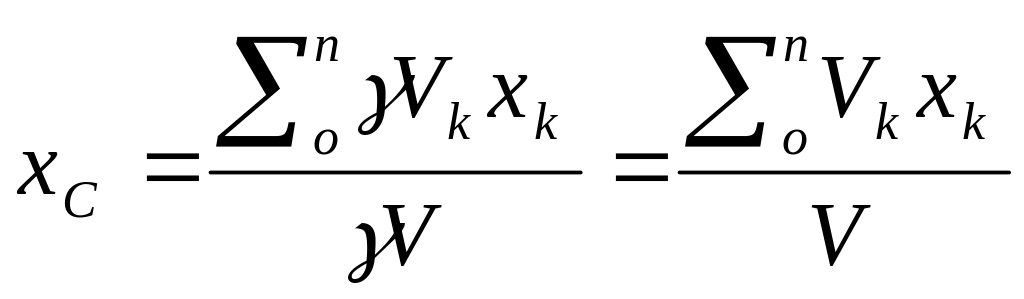
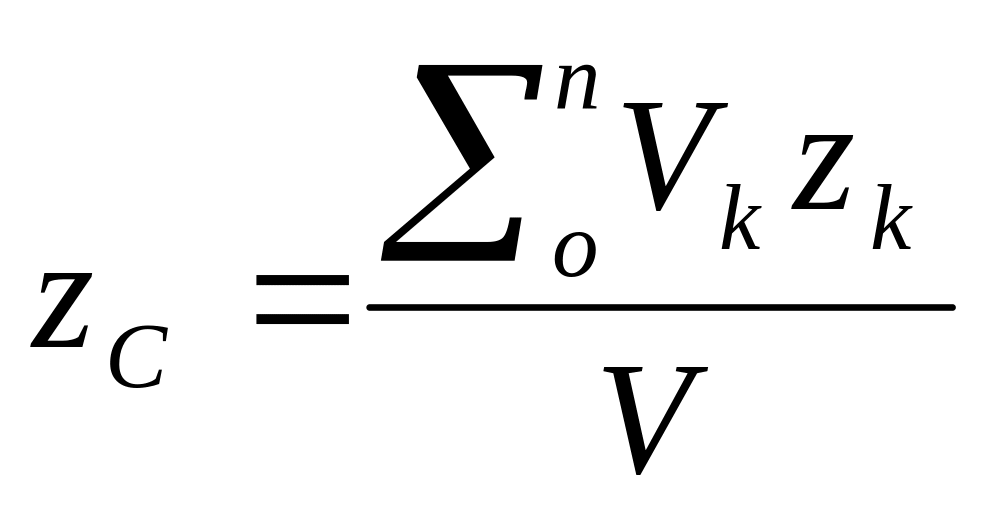
,где
V_k
– объем элемента тела; V
– объем всего тела.

________________________________________________________________________________________________

22 билет Основные
понятия кинематики. Кинематика
рассматривает движение как перемещение
в про­странстве.
Причины, вызывающие движение, не
рассматриваются. Кинематика
устанавливает способы задания движения
и определяет методы
определения кинематических параметров
движения.Основные
кинематические параметрыТраектория-Линию,
которую очерчивает материальная
точка при движении в
пространстве, называют траекторией.Траектория
может быть прямой и кривой, плоской
и простран­ственной
линией.Уравнение траектории при
плоском движении: у = f(x).Пройденный
путь-Путь
измеряется вдоль траектории в
направлении движения. Обозначение
— S, единицы
измерения — метры.Уравнение
движения точки-Уравнение,
определяющее положение движущейся
точки в зави­симости
от времени, называется уравнением
движения.

Положение точки в каждый момент времени можно опреде­лить по расстоянию, пройденно­му вдоль траектории от некото­рой неподвижной точки, рассматриваемой как начало отсчета (рис. 9.1). Такой способ задания дви­жения называется естественным.

Таким
образом, уравнение движения можно
представить в виде S=
f(t).
Положение
точки можно также определить, если
известны ее координаты в зависимости
от времени (рис. 9.2). Тогда в случае
движения
на плоскости должны быть заданы два
уравнения:

	x = f1 (t);
y = f2 (t).

В случае пространственного движе­ния добавляется и третья координата z = f3 (t).Такой способ задания движения на­зывают координатным.

Скорость
движения

Векторная
величина, характеризующая в данный
момент бы­строту и направление
движения по траектории, называется
скоро­стью.

Скорость
— вектор, в любой
момент направленный по каса­тельной
к траектории в сторону направления
движения (рис. 9.3).

Если точка за равные проме­жутки времени проходит равные расстояния, то движение называ­ют равномерным. Средняя скорость на пути AS определяется как где ΔS — пройденный путь за время Δt; Δt — промежуток времени.

Если
точка за равные промежутки времени
проходит неравные пути,
то движение называют неравномерным.
В
этом случае скорость — величина
переменная и зависит от времени
v=f(t).
При
рассмотрении малых промежутков
времени (At
→
0) сред­няя
скорость становится равной истинной
скорости движения в дан­ный
момент. Поэтому скорость в данный
момент определяют как производную
пути по времени:

.За
единицу скорости принимают 1 м/с.
Иногда скорость изме­ряют в км/ч,
1км/ч = 1000/3600 = 0,278 м/с.
Ускорение
точки-Векторная
величина, характеризующая быстроту
изменения скорости
по величине и направлению, называется
ускорением
точки.
Скорость
точки при перемещении из точки М₁
в
точку М₂
ме­няется
по величине и направлению. Среднее
значение ускорения за этот
промежуток времени

При рассмотрении бесконечно ма­лого промежутка времени среднее ускорение превратится в ускорение в данный момент: . Обычно для удобства рассматривают две взаимно перпендикулярно составляющие ускорения: нормальное и касательное

Нормальное
ускорение a_n
характеризует изменение скорости по
направлению и определяется как

,

где r
– радиус кривизны траектории в данный
момент времени. Нормальное ускорение
всегда направлено перпендикулярно
скорости к центру дуги. Касательное
ускорение a_t
характеризует изменение скорости по
величине и всегда направлено по
касательной к траектории; при ускорении
его направление совпадает
с направлением скорости, а при
замедлении оно направлено противоположно
направлению
век-гора скорости.
Формула
для определения касательного ускорения
имеет вид:

Значение
полного
ускорения определяется как

23 билет Кинематика
точки

Равномерное
движениеРавномерное
движение —
это движение с постоянной скоро­стью:

v
= const.
Для
прямолинейного равномерного движения

Полное ускорение движения точки равно нулю: а = 0. При криволинейном равномерном движении (рис. 10.1б).

Полное
ускорение равно нормальному ускорению:
а
=
а_п.
Уравнение
(закон) движения точки при равномерном
движении можно
получить, проделав ряд несложных
операций.
Так
как v
= const,
закон равномерного движения в общем
виде является уравнением прямой: S
= So+vt,
где
Sо
— путь, пройденный до
начала отсчета.

Равнопеременное
движение
Равнопеременное
движение —
это движение с постоянным ка­сательным
ускорением:

at
— const.
Для
прямолинейного равнопеременного
движения

a
= a_t
= const.
Полное
ускорение равно касательному ускорению.
Криволинейное
равнопеременное движение. a_n
≠ 0; a_t
= const
≠ 0.

Учитывая, что ; аt = const и сделав ряд преобразований: получим значение скорости при равнопеременном движении

После
интегрирования будем иметь закон
равнопеременного движения
в общем виде, представляющий уравнение
параболы:

где
v₀
— начальная скорость движения; So
—
путь, пройденный до начала отсчета;
a_t
—
постоянное касательное ускорение.

Неравномерное
движение.
При
неравномерном
движении численные
значения скорости и ускорения
меняются.Уравнение
неравномерного движения в общем виде
представля­ет
собой уравнение третьей S
= f(t³)
и выше степени.

_____________________________________________________________________________________

25 билет Простейшие
движения твердого тела

Поступательное
движение

Поступательным
называют
такое движение твердого тела, при
котором всякая прямая линия на теле
при движении остается парал­лельной
своему начальному положению.
При
поступательном движении все точки
тела движутся одина­ково:
скорости и ускорения в каждый момент
одинаковы. Поэтому для
описания движения тела можно
рассматривать движение одной его
точки, обычно центра масс.
Поступательное
движение может быть прямолинейным и
кри­волинейным.

Вращательное
движение При вращательном движении
все точки тела описывают окруж­ности
вокруг общей неподвижной оси.
Неподвижная ось, вокруг которой
вращаются все точки тела, называется
осью вращения. При этом каждая
точка движется по окружности, радиус
кото­рой равен расстоянию точки до
оси вращения. Точки на оси враще­ния
не перемещаются. Для описания
вращательного движения тела вокруг
непо­движной оси можно использовать
только угловые параметры.φ
— угол поворота тела, [φ] = рад;
ω — угловая скорость, определяет
изменение угла поворота в единицу
времени, [ω] = рад/с.

Для определения положения тела в любой момент времени ис­пользуется уравнение φ =f/(t). Следовательно, для определе­ния угловой скорости можно пользоваться выражением . Иногда для оценки быстро­ты вращения используют угловую частоту вращения n, которая оце­нивается в оборотах в минуту. Угловая скорость и частота вращения физически близкие ве­личины:

Изменение
угловой скорости во времени определяется
угловым ускорением
ε,
[ε]
=
рад/с²;
Частные случаи вращательного движения
Равномерное
вращение (угловая
скорость постоянна):

ω
=
const.
Уравнение
(закон) равномерного вращения в данном
случае име­ет
вид:
φ
= φ₀
+ φt,

где
φ₀
—
угол поворота до начала отсчета.
Кинематические
графики для этого вида движения
изображены на
рис. 11.4.

Равнопеременное
вращение (угловое
ускорение постоянно):ε
= const.,Уравнение
(закон) равнопеременного вращения

,где
ω₀
— начальная угловая скорость.
Угловое
ускорение при
ускоренном движении
— величина поло­жительная;
угловая
скорость будет все время возрастать.
Угловое
ускорение при
замедленном движении
— величина от­рицательная;
угловая
скорость убывает.

Скорости
и ускорения точек вращающегося тела.
Тело
вращается вокруг точки О.
Определим
параметры дви­жения
точки Л, расположенной на расстоянии
г
а
от
оси вращения.Путь
точки
А: S_A
= φr_A.

Линейная
скорость точки
А: v_A
= ωr_A.

Ускорение
точки
А: a_tA
= εr_A
– касательное;
:
a_tA
= εr_A

Центр тяжести. Условия равновесия

«Не существует тела, у которого

бы не было этой важнейшей характеристики.

Кто-то ею доволен, кто-то не очень,

но очень хочет ее изменить»

Альберт Эйнштейн

В данной теме речь пойдет о центре тяжести и условиях равновесия твердого тела.

Вспомним материал прошлых тем. Сила тяжести — это сила, с которой Земля притягивает к себе любое тело.

Рычаг – это любое твердое тело, способное поворачиваться относительно неподвижной опоры или оси. Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.

В прошлых темах было получено правило моментов, согласно которому рычаг будет находиться в равновесии, если сумма моментов сил, вращающих его по ходу часовой стрелки, равна сумме моментов сил вращающих рычаг против хода часовой стрелки.

Что такое равновесие? В физике под равновесием понимают такое состояние тела, при котором воздействие на него одних сил компенсируется воздействием других сил. Иными словами, тело находится в состоянии покоя или движется равномерно и прямолинейно.

Каким образом можно добиться равновесия тела? Для ответа на это вопрос, возьмем какое-нибудь тело прямоугольной формы и, обвязав его петлей, подвесим на нити в произвольном месте. Как видим, тело начинает поворачиваться.

                       

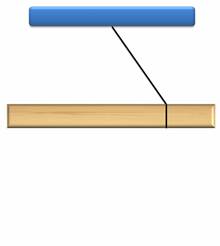
Изменим положение петли — брусок опять приходит в движение.

             

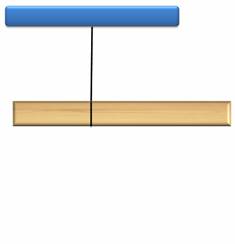
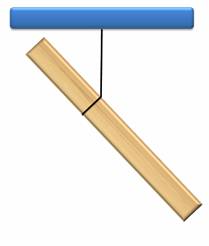
Однако можно найти такое положение петельки, при котором брусок будет находиться в состоянии покоя, т.е. в равновесии. Так вот, в этом случае говорят, что брусок подвешен в центре тяжести.

А что такое центр тяжести? До сих пор говорилось о силе тяжести как одной силе, действующей на тело целиком. Но на самом деле сила тяжести складывается из множества сил, приложенных к каждой части тела.

           

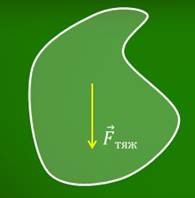
Можно ли заменить множество этих сил тяжести одной? А если можно, то в какой точке ее следует приложить?

Поставим опыт. Подвесим на нити динамометр, а к нему легкий жесткий стержень с двумя различными грузами на концах. Точку подвеса стержня подберем так, чтобы грузы уравновесили друг друга. Стержень с грузами будем рассматривать как одно тело, на которое действуют сила упругости нити и силы тяжести грузов.

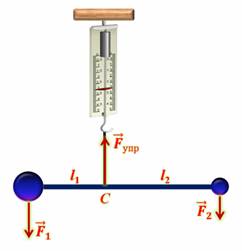
Как показывает опыт, для того, чтобы сила тяжести всего тела заменила силы тяжести грузов, ее нужно приложить в точке, относительно которой грузы уравновешивают друг друга, — т.е. в точке подвеса стержня. Только в этом случае не изменятся ни показания динамометра, ни положение стержня. Точку приложения равнодействующей сил тяжести, действующих на отдельные части тела называют центром тяжести тела.

Как можно найти центр тяжести в различных телах?

Если тело однородно и имеет правильную форму, то все просто. У однородных тел правильной формы центр тяжести совпадает с его геометрическим центром. Так, например, центр тяжести шара лежит в его геометрическом центре, у прямоугольного параллелепипеда — в точке пересечения диагоналей, а у треугольника — на пересечении его медиан.

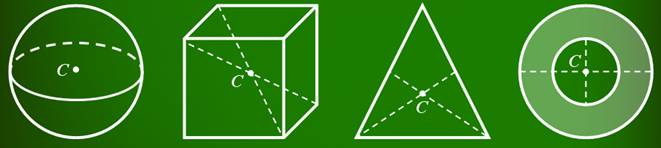
В некоторых случаях центр тяжести может находиться и вне тела. Например, у кольца он лежит на пересечении его диаметров.

А если тело имеет неправильную форму?

Поставим опыт. Возьмем пластину неправильной формы и, по ее периметру, проделаем несколько одинаковых отверстий. Теперь подвесим пластину за одно из них. Если качать пластину, то она, после нескольких колебаний, всегда будет останавливаться в одном и том же равновесном положении. Чтобы запомнить это положение, прикрепим к оси отвес и проведем вдоль него прямую линию. Теперь подвесим пластину за другое отверстие и повторим все действия с отвесом. При этом все три отвеса проходят через одну точку — это точка и будет являться центром тяжести пластины.

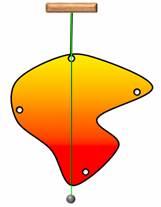
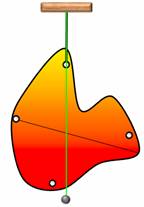
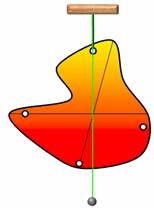
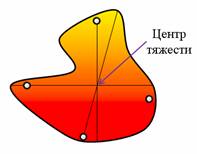
За какую бы точку не подвешивали пластину, ее центр тяжести оказывается в наинизшем положении на отвесе.

Что будет, если подвесить пластину за сам центр тяжести? В этом случае, пластина может висеть в покое или вращаться.

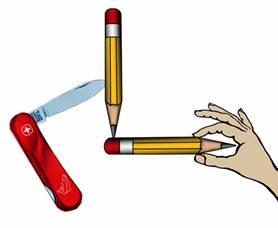
Известно, что карандаш невозможно поставить на острие, так как опорная площадка слишком мала. Однако, зная понятие центра тяжести, это можно сделать без труда. Как? Возьмем перочинный ножик, воткнем его в карандаш и поставим карандаш острием на резинку. В данном случае карандаш не падает и его даже можно слегка раскачивать. А дело все в том, что центр тяжести такой конструкции находится под опорной площадкой.

Для простоты, возьмем однородное тело прямоугольной формы. Как Центр тяжести такого тела будет располагать в его геометрическом центре — в точке пересечения диагоналей. Подвесим его так, чтобы оно заняло положение равновесия.

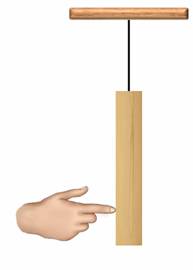
Теперь, если попытаться отклонить тело в сторону, то под действием силы тяжести, оно возвратится в первоначальное положение. Таким образом, равновесие, при котором выведенное из положения равновесия тело вновь к нему возвращается, называют устойчивым равновесием. При таком равновесии, центр тяжести тела располагается ниже оси вращения и находится на вертикальной прямой, проходящей через эту ось.

Если поставить тело на одну из его малых граней, то его центр тяжести будет располагаться на одной вертикальной линии с точкой опоры, но выше нее.

Если попытаться вывести тело из положения равновесия, например, толкнув его пальцем, то оно больше в начальное положение не вернется — этому будет препятствовать сила тяжести, действующая на тело. Таким образом, равновесие, при котором тело, выведенное из положения равновесия, не возвращается в начальное положение, называется неустойчивым равновесием. При неустойчивом равновесии центр тяжести тела расположен выше оси вращения и находится на вертикальной прямой, проходящей через эту ось.

Подвесим тело так, чтобы его центр тяжести совпал с точкой опоры. Толкнем его пальцем. С какой бы силой не толкать это тело, от толчков оно будет менять свое положение, но равновесия не потеряет.

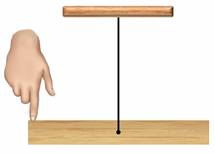
Таким образом, если при отклонении или перемещении тела оно остается в равновесии, то равновесие называется безразличным. При безразличном равновесии ось вращения тела проходит через его центр тяжести, при этом центр тяжести тела остается на одном и том же уровне при любых положениях тела.

Примером устойчивого равновесия является любое тело, подвешенное на нити. Это, например, бабочки, висящие на люстре и сама люстра, лимон, висящий на лимонном дереве, маятник часов. В положении устойчивого равновесия находятся и, так называемые, висящие камни. Вот что про них пишет Александр Степанович Грин в своем произведении «Качающаяся скала»: Надо сказать, что в этих местах не редкость встретить так называемую «качающуюся скалу» — весьма любопытное явление, суть которого в том, что отдельный огромный кусок скалы в незапамятные времена получает устойчивость равновесия. Он обыкновенно стоит на каменной площадке, узким концом вниз, и, если его раскачивать, он, подобно ваньке-встаньке, принимает первоначальное положение. Такие скалы весят иногда тысячи тонн, но послушны движению руки человека средней силы. Такая скала упасть не может, если, конечно, ее не взорвут динамитом.

Примерами безразличного равновесия могут служить колеса автомобиля или мотоцикла — у них ось вращения проходит через их центр тяжести.

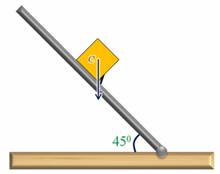
Об устойчивости положения тела можно судить и о величине угла поворота, необходимого для приведения тела в состояние неустойчивого равновесия. Для примера рассмотрим наклонную плоскость с невысокой ступенькой и два кубика. Выясним, при каком значении угла наклона произойдет опрокидывание кубика. Однородный кубик опрокинется при угле в 45 градусов.

Теперь возьмем кубик, склеенный из двух половинок — деревянной и стальной. Если поставить его деревянной частью книзу, то кубик опрокинется при значительно меньшем значении угла. Если же внизу будет стальная его часть, то опрокидывание произойдет лишь при угле больше 60 градусов.

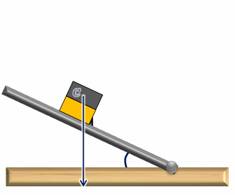
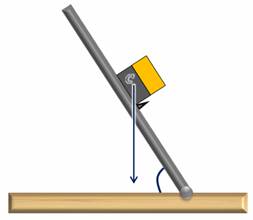
Из этого опыта можно сделать вывод, что чем больше угол, на который нужно повернуть тело, для того, чтобы оно заняло положение неустойчивого равновесия, тем устойчивее его первоначальное положение. Величина угла поворота зависит от площади опоры тела и от положения его центра тяжести.

Упражнения.

Задача 1. Однородный массивный стержень с укрепленными на его концах грузами массой 5,5 кг и 1 кг, находится в равновесии, если подпереть его на расстоянии, равном 1/5 его длины, от более тяжелого груза. Какова масса стержня?

Основные выводы:

– Центр тяжести тела – это точка приложения равнодействующей сил тяжести, действующих на отдельные части тела.

– При любом положении тела его центр тяжести находится в одной и той же точке.

– Положение центра тяжести может измениться только при изменении относительного расположения частей тела (например, при его деформации).

– Равновесие бывает трех видов — устойчивым, неустойчивым и безразличным.

– Устойчивое равновесие — это равновесие, при котором выведенное из положения равновесия тело вновь к нему возвращается. При таком равновесии, центр тяжести тела располагается ниже оси вращения и находится на вертикальной прямой, проходящей через эту ось.

– Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия, не возвращается в начальное положение. При неустойчивом равновесии центр тяжести тела расположен выше оси вращения и находится на вертикальной прямой, проходящей через эту ось.

– При безразличном равновесии ось вращения тела проходит через его центр тяжести, при этом центр тяжести тела остается на одном и том же уровне при любых положениях тела.

Домашняя работа

Стр. 185 — 189 читать