Расстояние между двумя точками 
а) Пусть С (х; 0; 0) — точка на оси Ох, равноудаленная от точек А и В. Следовательно, СА=СВ, или в координатах: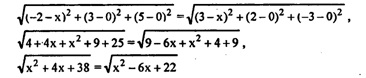
х2+4х+3 8=х2 – 6х+22, 10х= -16, х= – 1,6; С (- 1,6; 0; 0).
Равноудаленной от точек А и В будет точка С (-1,6; 0; 0).
б) Пусть D (0; у, 0) — точка на оси Оу, равноудаленная от А и В. AD=DB.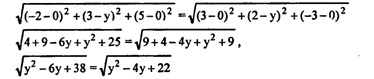
у2 -бу+38=y2 -4у+22 2у=16, у=8; D (0; 8; 0).
в) Пусть Е (0; 0; z) —точка на оси Oz, равноудаленная от А и В.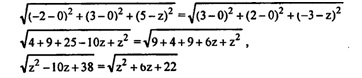
z2-10z+3 8=z2+6z+22, 16z = 16, z= 1 ; E (0; 0; 1 ).
437. Найдите точку, равноудаленную от точек А (— 2; 3; 5) и В(3; 2; —3) и расположенную на оси: а) Ох; б) Оу; в) Oz.
а) Пусть С (х; 0; 0) — точка на оси Ох, равноудаленная от точек А и В. Следовательно, СА=СВ, или в координатах:
Равноудаленной от точек А и В будет точка С (-1,6; 0; 0).
б) Пусть D (0; у, 0) — точка на оси Оу, равноудаленная от А и В. AD=DB.
в) Пусть E (0; 0; z) —точка на оси Oz, равноудаленная от А и B.
Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №437
к главе «Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора.».
Как найти точку равноудаленную от двух точек вектора
Найти геометрическое место точек, равноудаленных от двух данных точек.
Возьмем прямоугольную систему координат, и пусть две данные точки B и C лежат на оси абсцисс и имеют координаты (x1, 0) и (x2, 0) (см. рисунок). Пусть точка A принадлежит искомому геометрическому месту. Обозначим ее координаты через x и y: A(x, y).
На основании формулы для определения расстояния между двумя точками , значит, так как по условию AB = AC, можем написать, что . Это и есть уравнение искомого геометрического места.
Возводя в квадрат обе части искомого равенства, будем иметь
После очевидных упрощений получим 2x(x2 – x1) = (x2 – x1)(x2 + x1); сокращая на , имеем 2x = x1 + x2, или .
Это уравнение прямой, перпендикулярной оси Ox и проходящей через середину отрезка BC.
Итак, искомым геометрическим местом является прямая, перпендикулярная к отрезку BC, соединяющему данные точки, и проходящая через его середину.
Замечание. При решении задачи нам пришлось уничтожить радикалы в уравнении искомого геометрического места
(1)
в результате чего было получено уравнение
(2)
Как найти координаты точки?
О чем эта статья:
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
[spoiler title=”источники:”]
http://www.pm298.ru/reshenie/jtwtxds.php
http://skysmart.ru/articles/mathematic/kak-najti-koordinaty-tochki
[/spoiler]
как можно найти точку равноудаленную от двух точки?
Антон Фандофан
Ученик
(178),
закрыт
12 лет назад
Ольга
Просветленный
(23331)
12 лет назад
Соедините эти две точки, через центр этого отрезка проведите прямую, перпендикулярную отрезку, все точки, принадлежащие этой прямой будут равноудалены от концов отрезка.
Erlk
Гуру
(2676)
12 лет назад
Я тоже отвечу – вопрос легкий.
Берешь циркул, ставишь на точку и на чуть меньше до второй точки. Очень легко проводиш полуокружность, с одной стороны, затем с другой. усе.
На данной плоскости найдите точки, равноудаленные от двух данных точек.
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Кузнецов Л.А. Аналитическая геометрия. Задача 10
Постановка задачи . Найти координаты точки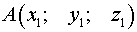 
, равноудаленной от точек 
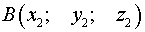и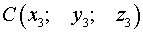 
.
План решения . Расстояние между точкам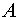и 
и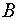 
определяется равенством
.
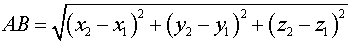
1. Находим расстояние между точкам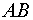и: 
и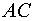 
.
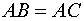
2. Так как по условию задачи эти расстояния равны, то составляем равенство и разрешаем его относительно неизвестных координат.
Задача 10. Найти координаты точки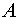 
, равноудаленной от точек 
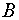и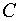 
.
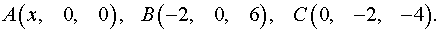
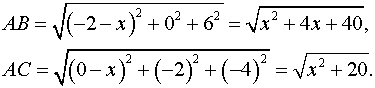
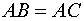
Так как по условию задачи , то
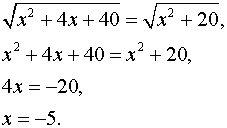
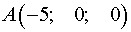
Таким образом .
:: Рекомендуемая литература. Ремендуем покупать учебную литературу в интернет-магазине Озон
Геометрическое место точек. Теорема о геометрическом месте точек, равноудалённых от двух данных точек, в геометрической и аналитической формах
Определение. Геометрическое место точек – фигура, которая состоит из всех точек на плоскости, обладающих определённым свойством.
Теорема. Геометрическое место точек, равноудалённых от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки, то есть прямая, перпендикулярная этому отрезку и проходящая через его середину.
1) 
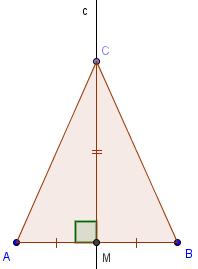
Пусть точка C равноудалена от A и B. Отметим точку M – середину отрезка AB. Треугольники ACM и BCM равны по трём сторонам. Углы AMC и BMC равны и дают в сумме развёрнутый угол. Значит, они оба равны 90°.
Мы доказали, что все точки, равноудалённые от двух данных точек, лежат на серединном перпендикуляре.
2) Пусть точка C лежит на серединном перпендикуляре к AB. Треугольники AMC и BMC равны двум катетам, значит, AC=BC.
Мы доказали, что все точки серединного перпендикуляра к отрезку равноудалены от его концов.
Таким образом, геометрическое место точек, равноудалённых от двух данных точек, и серединный перпендикуляр к отрезку, соединяющему эти точки, совпадают.
The distance formula is used to calculate the distance between any two points in a two-dimensional or three-dimensional plane. In other words, it gives the distance between two different locations on a cartesian plane.
What is the Distance Formula?
It applies the Pythagorean theorem to determine the required distance. Its formula claims that the distance between any two coordinates is equal to the square root of the differences between the x-coordinates and y-coordinates of the points. It is used to evaluate the distance between point to point, point to plane, and plane to plane.
D = √((x2 – x1)2 + (y2 – y1)2)
where,
- D is the distance between the points,
- (x1, y1) and (x2, y2) are the coordinates.
How to find the equidistant points on the Y-axis?
Consider two points A (a, b) and B (p, q) lying at a distance from each other on a two dimensional plane.
We have to find a point on the y-axis which is equidistant from these points. It is known that any point that lies on y-axis is of the form (0, y).
Suppose C is (0, y). According to the problem we can conclude that,
AC = BC
AC2 = BC2
Using distance formula we have,
(0 – a)2 + (y – b)2 = (0 – p)2 + (y – q)2
a2 + y2 + b2 – 2yb = p2 + y2 + q2 – 2yq
2y (q – b) = p2 – q2 – a2 – b2
y = (p2 – q2 – a2 – b2)/2(q – b)
The above value is calculated by substituting the given values of a, b, p and q. This gives us the point required (0, y).
Sample Problems
Problem 1: Find the point on the y-axis which is equidistant from (-3, 4) and (5, 2).
Solution:
Suppose the required point is (0, y).
Using distance formula we get,
(-3 – 0)2 + (4 – y)2 = (5 – 0)2 + (2 – y)2
9 + 16 + y2 – 8y = 25 + 4 + y2 – 4y
-8y + 4y – 4 = 0
4y = -4
y = -1
So, the required point is (0, -1).
Problem 2: Find the point on the y-axis which is equidistant from (6, 3) and (4, 1).
Solution:
Suppose the required point is (0, y).
Using distance formula we get,
(6 – 0)2 + (3 – y)2 = (4 – 0)2 + (1 – y)2
36 + 9 + y2 – 6y = 16 + 1 + y2 – 2y
45 – 6y – 17 + 2y = 0
4y = 28
y = 7
So, the required point is (0, 7).
Problem 3: Find the point on the y-axis which is equidistant from (3, 2) and (8, 4).
Solution:
Suppose the required point is (0, y).
Using distance formula we get,
(3 – 0)2 + (2 – y)2 = (8 – 0)2 + (4 – y)2
9 + 4 + y2 – 4y = 64 + 16 + y2 – 8y
13 – 4y – 80 + 8y = 0
4y = 67
y = 67/4
So, the required point is (0, 67/4).
Problem 4: Find the point on the y-axis which is equidistant from (5, 1) and (7, 2).
Solution:
Suppose the required point is (0, y).
Using distance formula we get,
(5 – 0)2 + (1 – y)2 = (7 – 0)2 + (2 – y)2
25 + 1 + y2 – 2y = 49 + 4 + y2 – 4y
26 – 2y – 53 + 4y = 0
2y = 27
y = 27/2
So, the required point is (0, 27/2).
Problem 5: Find the value of x if (0, 3) is equidistant from (x, 5) and (3, 6).
Solution:
Using the distance formula we get,
(x – 0)2 + (5 – 3)2 = (3 – 0)2 + (6 – 3)2
x2 + 4 = 9 + 9
x2 = 18 – 4
x2 = 14
x = ±3.74
Problem 6: Find the value of x if (0, 2) is equidistant from (x, 1) and (5, 2).
Solution:
Using the distance formula we get,
(x – 0)2 + (1 – 2)2 = (5 – 0)2 + (2 – 2)2
x2 + 1 = 25 + 0
x2 = 25 – 1
x2 = 24
x = ±4.89
Problem 7: Find the value of x if (0, 6) is equidistant from (x, 3) and (7, 4).
Solution:
Using the distance formula we get,
(x – 0)2 + (3 – 6)2 = (7 – 0)2 + (4 – 6)2
x2 + 9 = 49 + 4
x2 = 53 – 9
x2 = 44
x = ±6.63
Last Updated :
24 May, 2022
Like Article
Save Article
