Расстояние между двумя точками 
а) Пусть С (х; 0; 0) — точка на оси Ох, равноудаленная от точек А и В. Следовательно, СА=СВ, или в координатах: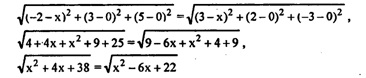
х2+4х+3 8=х2 – 6х+22, 10х= -16, х= – 1,6; С (- 1,6; 0; 0).
Равноудаленной от точек А и В будет точка С (-1,6; 0; 0).
б) Пусть D (0; у, 0) — точка на оси Оу, равноудаленная от А и В. AD=DB.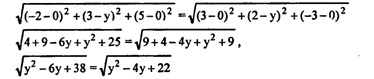
у2 -бу+38=y2 -4у+22 2у=16, у=8; D (0; 8; 0).
в) Пусть Е (0; 0; z) —точка на оси Oz, равноудаленная от А и В.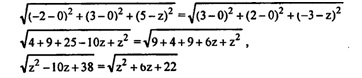
z2-10z+3 8=z2+6z+22, 16z = 16, z= 1 ; E (0; 0; 1 ).
как можно найти точку равноудаленную от двух точки?
Антон Фандофан
Ученик
(178),
закрыт
12 лет назад
Ольга
Просветленный
(23331)
12 лет назад
Соедините эти две точки, через центр этого отрезка проведите прямую, перпендикулярную отрезку, все точки, принадлежащие этой прямой будут равноудалены от концов отрезка.
Erlk
Гуру
(2676)
12 лет назад
Я тоже отвечу – вопрос легкий.
Берешь циркул, ставишь на точку и на чуть меньше до второй точки. Очень легко проводиш полуокружность, с одной стороны, затем с другой. усе.
На данной плоскости найдите точки, равноудаленные от двух данных точек.
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Кузнецов Л.А. Аналитическая геометрия. Задача 10
Постановка задачи . Найти координаты точки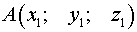 
, равноудаленной от точек 
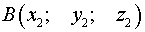и 
.
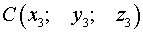План решения . Расстояние между точкам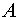и 
и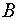 
определяется равенством
.
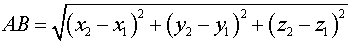
1. Находим расстояние между точкам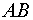и: 
и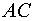 
.
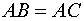
2. Так как по условию задачи эти расстояния равны, то составляем равенство и разрешаем его относительно неизвестных координат.
Задача 10. Найти координаты точки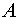 
, равноудаленной от точек 
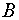и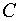 
.
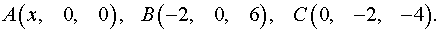
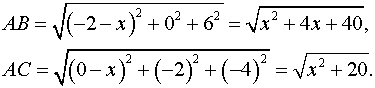
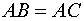
Так как по условию задачи , то
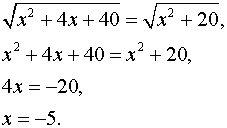
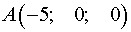
Таким образом .
:: Рекомендуемая литература. Ремендуем покупать учебную литературу в интернет-магазине Озон
Геометрическое место точек. Теорема о геометрическом месте точек, равноудалённых от двух данных точек, в геометрической и аналитической формах
Определение. Геометрическое место точек – фигура, которая состоит из всех точек на плоскости, обладающих определённым свойством.
Теорема. Геометрическое место точек, равноудалённых от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки, то есть прямая, перпендикулярная этому отрезку и проходящая через его середину.
1) 
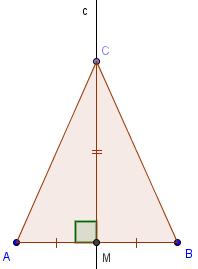
Пусть точка C равноудалена от A и B. Отметим точку M – середину отрезка AB. Треугольники ACM и BCM равны по трём сторонам. Углы AMC и BMC равны и дают в сумме развёрнутый угол. Значит, они оба равны 90°.
Мы доказали, что все точки, равноудалённые от двух данных точек, лежат на серединном перпендикуляре.
2) Пусть точка C лежит на серединном перпендикуляре к AB. Треугольники AMC и BMC равны двум катетам, значит, AC=BC.
Мы доказали, что все точки серединного перпендикуляра к отрезку равноудалены от его концов.
Таким образом, геометрическое место точек, равноудалённых от двух данных точек, и серединный перпендикуляр к отрезку, соединяющему эти точки, совпадают.
Задачи, вроде как, легкие. Но, как бы я не решил (решал с помощью формулы квадрата расстояния между двумя точками) все равно ответ получается не тот что в книге. Есть вероятность что ошибается не книжка, а я сам. Поэтому, хотелось бы увидеть как математики бы это решили. Заранее всем спасибо за помощь.
На прямой найти точку равноудаленную от двух заданных точек и
Решение:
Т.к. они равноудаленные, то можно считать скажем, что точка находится на середине прямой , из этого вывод что .
Т.е. на помощь приходит формула расстояния между двумя точками: .
Решая, получим: .
Сделаем систему:
После решения, у нас получается
На прямой найти точку равноудаленную от двух заданных точек и
Все так же:
Ответ:
Но, дело в том, что в обеих случаях ответ неверный (по книжке). В книжке ответы:
Может быть я думаю как-то не правильно? Может надо сделать по другому? Или же все таки ошибка в книжке? Помогите, пожалуйста )).
