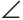Как найти точку равноудаленную от сторон угла

Биссектриса угла

2 июня 2018

• Домашняя работа
• Ответы и решения

Сегодня будет очень лёгкий урок. Мы рассмотрим всего один объект — биссектрису угла — и докажем важнейшее её свойство, которое очень пригодится нам в будущем.

Только не надо расслабляться: иногда ученики, желающие получить высокий балл на том же ОГЭ или ЕГЭ, на первом занятии даже не могут точно сформулировать определение биссектрисы.

И вместо того, чтобы заниматься действительно интересными задачами, мы тратим время на такие простые вещи. Поэтому читайте, смотрите — и берите на вооружение.:)

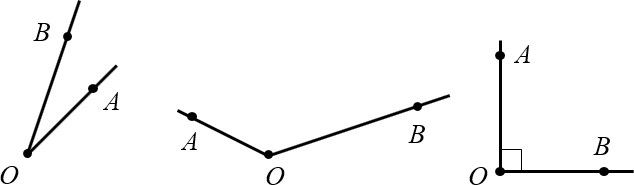
Для начала немного странный вопрос: что такое угол? Правильно: угол — это просто два луча, выходящих из одной точки. Например:

Как видно из картинки, углы могут быть острыми, тупыми, прямыми — это сейчас неважно. Часто для удобства на каждом луче отмечают дополнительную точку и говорят, мол, перед нами угол $AOB$ (записывается как $angle AOB$).

Капитан очевидность как бы намекает, что помимо лучей $OA$ и $OB$ из точки $O$ всегда можно провести ещё кучу лучей. Но среди них будет один особенный — его-то и называют биссектрисой.

Определение. Биссектриса угла — это луч, который выходит из вершины этого угла и делит угол пополам.

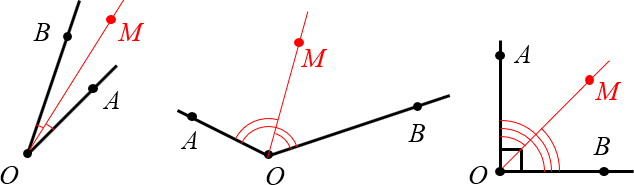
Для приведённых выше углов биссектрисы будут выглядеть так:

Поскольку на реальных чертежах далеко не всегда очевидно, что некий луч (в нашем случае это луч $OM$) разбивает исходный угол на два равных, в геометрии принято помечать равные углы одинаковым количеством дуг (у нас на чертеже это 1 дуга для острого угла, две — для тупого, три — для прямого).

Хорошо, с определением разобрались. Теперь нужно понять, какие свойства есть у биссектрисы.

Основное свойство биссектрисы угла

На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:

Теорема. Биссектриса угла — это геометрическое место точек, равноудалённых от сторон данного угла.

В переводе с математического на русский это означает сразу два факта:

1. Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
2. И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.

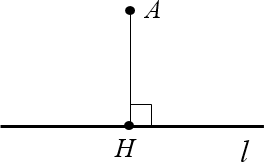
Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:

Определение. Расстояние от точки до прямой — это длина перпендикуляра, проведённого из данной точки к этой прямой.

Например, рассмотрим прямую $l$ и точку $A$, не лежащую на этой прямой. Проведём перпендикуляр $AH$, где $Hin l$. Тогда длина этого перпендикуляра и будет расстоянием от точки $A$ до прямой $l$.

Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:

Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.

Как и обещал, разобьём доказательство на две части:

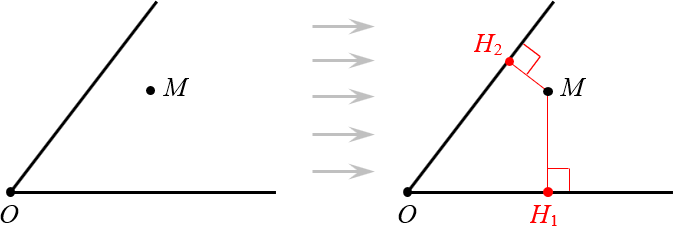
1. Расстояния от точки на биссектрисе до сторон угла одинаковы

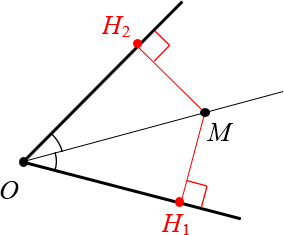
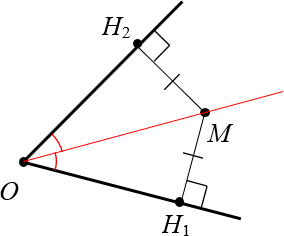
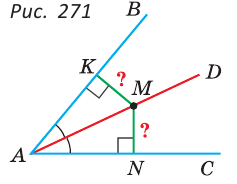
Рассмотрим произвольный угол с вершиной $O$ и биссектрисой $OM$:

Докажем, что эта самая точка $M$ находится на одинаковом расстоянии от сторон угла.

Доказательство. Проведём из точки $M$ перпендикуляры к сторонам угла. Назовём их $M{{H}_{1}}$ и $M{{H}_{2}}$:

Получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. У них общая гипотенуза $OM$ и равные углы:

1. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$ по условию (поскольку $OM$ — биссектриса);
2. $angle M{{H}_{1}}O=angle M{{H}_{2}}O=90{}^circ $ по построению;
3. $angle OM{{H}_{1}}=angle OM{{H}_{2}}=90{}^circ -angle MO{{H}_{1}}$, поскольку сумма острых углов прямоугольного треугольника всегда равна 90 градусов.

Следовательно, треугольники равны по стороне и двум прилежащим углам (см. признаки равенства треугольников). Поэтому, в частности, $M{{H}_{2}}=M{{H}_{1}}$, т.е. расстояния от точки $O$ до сторон угла действительно равны. Что и требовалось доказать.:)

2. Если расстояния равны, то точка лежит на биссектрисе

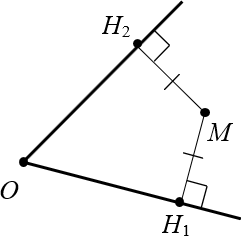
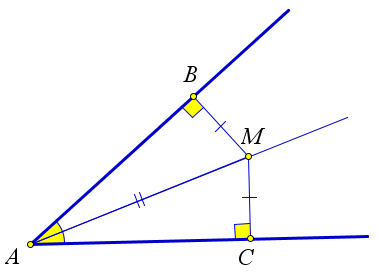
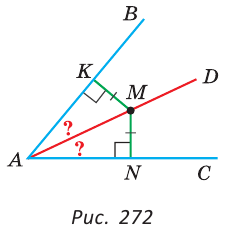
Теперь обратная ситуация. Пусть дан угол $O$ и точка $M$, равноудалённая от сторон этого угла:

Докажем, что луч $OM$ — биссектриса, т.е. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$.

Доказательство. Для начала проведём этот самый луч $OM$, иначе доказывать будет нечего:

Снова получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. Очевидно, что они равны, поскольку:

1. Гипотенуза $OM$ — общая;
2. Катеты $M{{H}_{1}}=M{{H}_{2}}$ по условию (ведь точка $M$ равноудалена от сторон угла);
3. Оставшиеся катеты тоже равны, т.к. по теореме Пифагора $OH_{1}^{2}=OH_{2}^{2}=O{{M}^{2}}-MH_{1}^{2}$.

Следовательно, треугольники $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$ по трём сторонам. В частности, равны их углы: $angle MO{{H}_{1}}=angle MO{{H}_{2}}$. А это как раз и означает, что $OM$ — биссектриса.

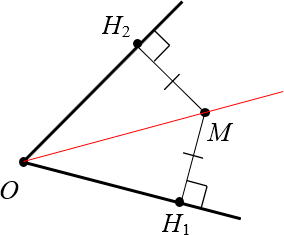
В заключение доказательства отметим красными дугами образовавшиеся равные углы:

Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)

Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.

Смотрите также:

1. Перпендикулярные прямые — определение и свойства
2. Что такое вертикальные углы
3. Следствия из теоремы Виета
4. Работа с формулами в задаче B12
5. Пример решения задачи 15
6. Задача B15: частный случай при работе с квадратичной функцией

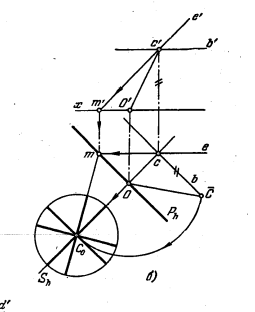
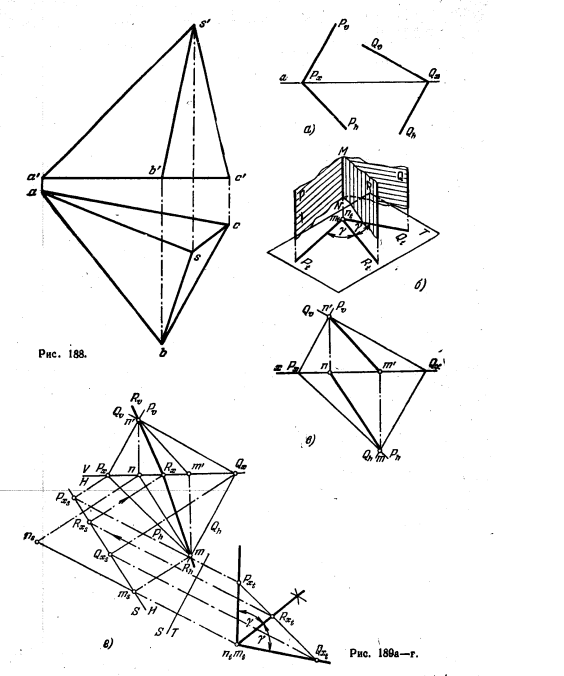
187*. Поворотом вокруг прямой MN ввести точку АВ пл H (рис. 173,а).

Решение. Ось вращения — прямая М N – в данном случае параллельна пл. Н. Поэтому плоскость вращения точки А является горизонтально-проецирующей. Ее след S_h (рис. 173, б) проходит через проекцию а. Точка А при повороте ее вокруг МN описывает в пл. S окружность, горизонт. проекция которой совпадает с S_h; центр этой окружности находится в точке О пересечения оси вращения МN с пл. S. Так как пл. S составляет с пл. V острый угол, то проекция окружности, расположенной в пл. S, получится на пл. V в виде эллипса. Чтобы избежать построения этого эллипса, совместим пл. S и лежащие в ней точки О и А с пл. Н. Это даст возможность изобразить дугу окружности, по которой перемещается точка А, без искажения. По условию

задачи точка А, находясь в пл. S, должна оказаться в пл. Н; следовательно, точка А должна получиться после поворота на следе S_h, и совпасть со своей горизонт. проекци-

ей. Поэтому, проведя дугу радиусом O₀A₀, получим точки а₁ и а₂ горизонт. проекции трчки А, приведенной в пл. Н. По точкам а₁ и а₂ строим на оси х проекции a’₁ и a’₂.

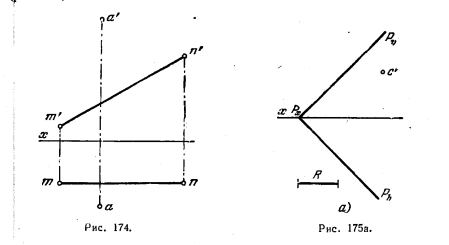
188. Поворотом вокруг прямой MN ввести точку АВ пл V (рис. 174).

189*. Построить проекции окружности, расположенной в пл. Р (рис. 175, а). Известна величина радиуса этой окружности (R) и положение фронт. проекции (с’) ее центра. 

Решение. Прежде всего находим проекцию с центра окружности (при помоги горизонтали CN). Точки с’ и с будут центрами эллипсов — проекций окружности, расположенной в плоскости общего положения Р.

На рис. 175,6 показано построение осей эллипса — горизонт. проекции окружности. Большая ось расположена на горизонт. проекции горизонтали CN и равна 2R. Положение малой оси также известно: она перпендикулярна к 1—2. Для определения величины этой оси (а также малой оси фронт. проекции) применено совмещение пл. Р с пл. Н, что дает возможность изобразить окружность без искажения. Ее диаметр 1₀2₀ соответствует отрезку 1—2, т. е. большой оси эллипса — горизонт. проекции окружности, а диаметр 3₀4₀ — малой оси этого эллипса. Проведя через точку 3₀ фронталь плоскости Р в ее совмёщенном положении (|| Р_ϑ0), а затем горизонт. проекцию этой фронтали, находим точку 3 и тем самым получилось с—3. Откладывая с—4 = с—3, получаем малую ось эллипса 3—4.

Построение осей эллипса—фронт. проекции окружности—показано на рис. 175,в. Здесь также известно положение большой оси — она лежит на фронт. проекции фронтали, проходящей через с’,— и величина этой оси (7’S’=2R). Малая ось перпендикулярна к 7’8′. Величина же малой оси определяется при помощи диаметра 5₀6₀ окружности в ее совмещенном с пл. Н положении: большой оси эллипса 7’8′ соответствует диаметр 7₀8₀ окружности, а малой оси 5’6′ — диаметр 5₀6₀, перпендикулярный к 7₀8₀. Проведя через 6₀ фронталь плоскости Р до пересечения с Р_h, находим затем

фронт. проекцию этой фронта ли и на ней точку 6’— конец малой оси эллипса. Откладывая с’5’= с’6′, получаем малую ось 5’6′. ‘

На рис. 175, г показано построение проекций некоторых точек окружности. Взяты точки 9₀ и 10₀ на прямой А₀В₀. Построив горизонт. и фронт. проекции этой прямой, находим сначала проекции 9 и 10, а затем 9′ и 10′.

Найдя ряд точек, проводим через ник и через концы осей эллипсы — проекции окружности.

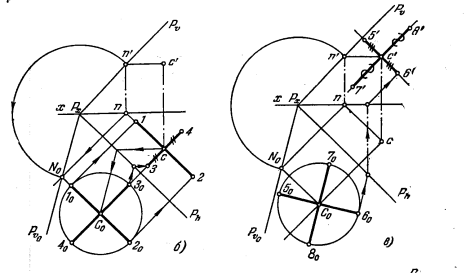
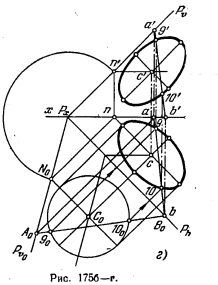
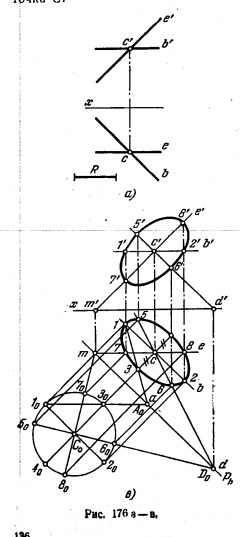
190*. Построить проекции окружности, расположенной в плоскости, заданной ее горизонталью ВС и фронталью СЕ (рис. 176, а). Известны величина радиуса этой окружности и положение центра — точка С.

Решение. Находим горизонт. след фронталн (рис. 176, б) и проводим через точку m след P_h параллельно cb. Определяем величину радиуса СО как величину гипотенузы прямоугольного треугольника с катетами сО и сС и находим совмещенное с пл. H положение центра окружности С₀. На рис. 176, в точка 3 построена с помощью прямой 1₀3₀, продолженной до пересечения с P_h в точке А₀(а), а точки 5 и 6 — с помощью прямой 5₀6₀, проходящей через центр С₀ и пересекающей при своем продолжении след P_h в точке D₀(d).

Дальнейшие построения аналогичны выполненным на рис. 175, б и в. Они ясны из чертежа.

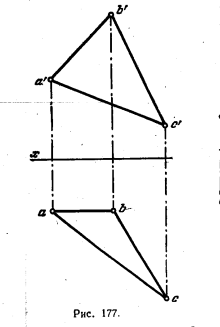
191. Построить проекции окружности, описанной вокруг треугольника ABC (рис. 177).

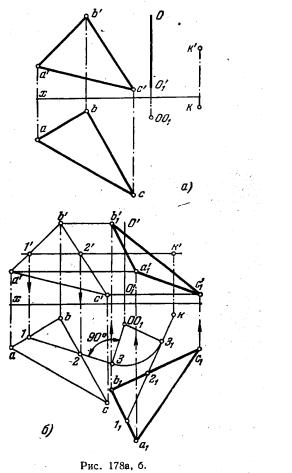
192*. Плоскость, заданную треугольником AВС, повернуть вокруг оси OO₁ так, чтобы точка К оказалась в этой плоскости (рис. 178, а).

Решение. Если точка К войдет в плоскость, то она окажется на одной из горизонталей этой плоскости, а именно на той, которая расположена на одном уровне с точкой К (рис.178,6). Поэтому проводим через k’ фронт. проекцию горизонтали, находим точки 1′ и 2′, а по ним точки 1 и 2 и проводим горизонт. проекцию 1—2 горизонтали.

Теперь надо повернуть горизонталь так, чтобы она прошла через точку К. Для этого опускаем из точки 0(0₁) перпендикуляр на 1—2 и радиусом О—3 проводим дугу

окружности, по отношению к которой горизонт. проекция горизонтали является касательной в любом положении при повороте плоскости вокруг данной оси ООг. Поэтому, проведя из к касательную к этой окружности, мы определяем положение горизонт. проекции горизонтали, на которой должна находиться точка К после требуемого поворота. Наносим на нее точки 1₁ и 2₁ (3₁ 1₁ = 1—3 и 1₁2₁=1—2), а затем строим точки a₁,b₁ и c₁ на основании известного вывода, устанавливающего неизменяемость горизонтальной проекции фигуры по форме и по размерам при повороте вокруг оси, перпендикулярной к пл. Н.

По проекции a₁b₁c₁ строим проекцию а’₁b’₁с’₁. В положении A₁B₁C₁ треугольник проходит через точку K.

Если из К провести вторую касательную к окружности, то получится второе решение. Предоставляем читателю найти это положение треугольника ABC.

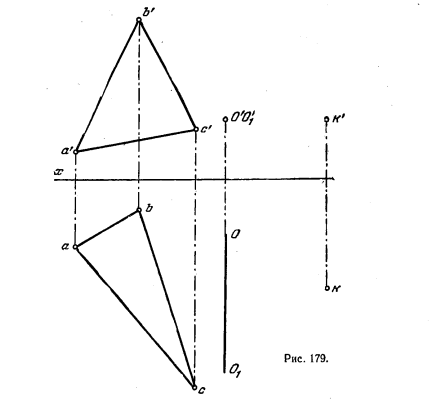
193. Плоскость, заданную треугольником ABC, повернуть вокруг оси OO₁ так, чтобы точка К оказалась в этой плоскости (рис. 179),

194*. Найти предельное положение осей, при котором еще возможно получить решение в задаче 192.

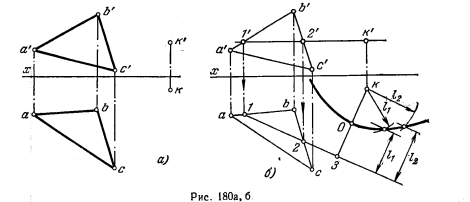
Решение. Положим, что плоскость, как и в задаче 192, задана треугольником (рис. 180, а), ось, вокруг которой надо повернуть плоскость, должна быть перпендикулярна к пл. H и точка К должна оказаться в плоскости треугольника.

Из рассмотрения рис. 180,6 следует, что горизонт. проекция оси ОО₁ должна буть расположена так, чтобы проекция k не оказалась внутри окружности с радиусом O—3, так как из точки А надо провести касательную к этой окружности. Следовательно, расстояние точки О от k должно быть не меньше расстояния этой же точки до прямой 1—2.

равны между собой, принадлежат параболе с фокусом в точке k и директрисой в виде прямой 1—2. Следовательно, предельное положение осей получается, если их горизонт. проекции образуют параболу, а самые оси представляют собою образующие параболического цилиндра. На рис. 180, б показано построение параболы с фокусом в точке А и с директрисой 1—2. Если взять отрезок, например l₁, провести прямую параллельно 1—2 на расстоянии l₁ и дугу радиуса l₁ из точки k, то получатся две точки параболы. Вершина параболы — в точке О.

Очевидно, оси, горизонт. проекции которых оказались бы внутри параболы, непригодны для соблюдения условия задачи 192. Если же взять оси вне параболического цилиндра, то за один оборот плоскости точка дважды окажется в ней.

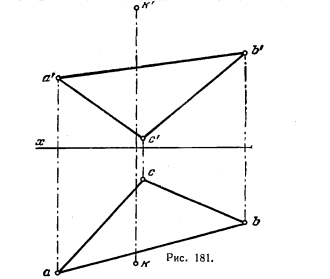
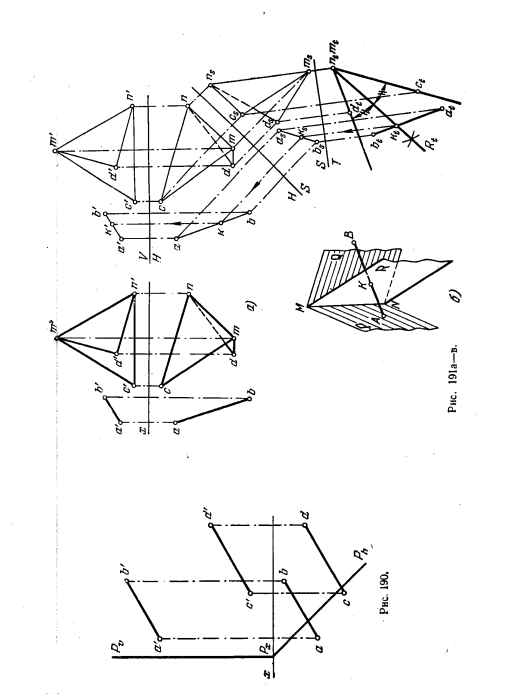
195. Найти предельное положение осей, перпендикулярных к пл. V, при повороте вокруг которых точка К окажется в плоскости, заданной треугольником ABC (рис. 181). 

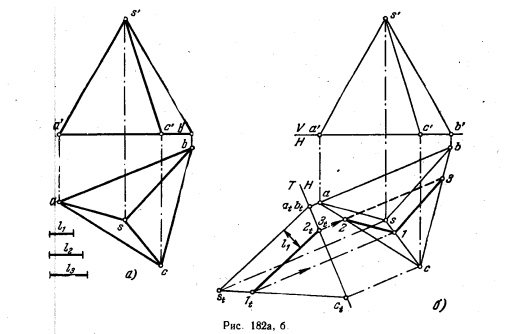
196*. Найти точку К, находящуюся внутри пирамиды и отстоящую от грани SAB на расстояние l₁, от грани SAC — на l₂, от грани ABC (основание пирамиды) — на l₃ (рис. 182, а).

Решение. Искомая точка нолучится как точка пересечения трех плоскостей, из; которых каждая является геометрическим местом точек, отстоящих на определенное расстояние от граней пирамиды.

Введя дополнительную пл. T, перпендикулярную к грани SAB (рис. 182, б), поручаем проекцию пирамиды, на которой грань SAB изображается прямой s_ta_t. Плоскость, параллельная грани SAB и удаленная от нее на расстояние l₁ изображается прямой l_t2_t ; эта плоскость пересекает пирамиду по треугольнику 1—2—3 (па рис. 182, б показана только горизонт. проекция).

Плоскость, удаленная от грани SAC на расстояние l₂, изображается на дополнительной пл. Q, перпендикулярной к этой грани (рис. 182, в), в виде прямой 4_q5_q и пересекает пирамиду по треугольнику 4—5—6 (дана лишь горизонт. проекция этого треугольника).

Искомая точка К должна принадлежать линии пересечения плоскостей, заданных треугольниками 1—2—3 и 4—5—6. Эта прямая проходит через точки М и N, получаемые при пересечении сторон 2—3 и 6—5, 1—3 и 4—5 треугольников 1—2—3 и 4—5—6 (рис. 182, г).

Находим фронт. проекцию k’ (рис. 182, д) на m’n’ из условия, что точка К отстоит от грани ABC на расстояние l₃.

Геометрическим местом таких точек является пл. Р, параллельная грани ABC. По k’ находим k на mn.

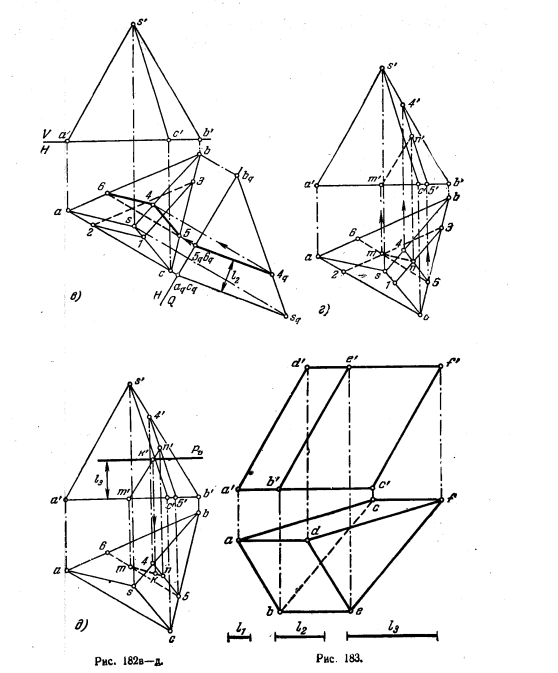
197. Найти точку К, находящуюся внутри призмы на расстояниях: l₁ — от грани BCEF, l₂ — от грани ABDE, l₃ — от основания AВС (рис. 183).

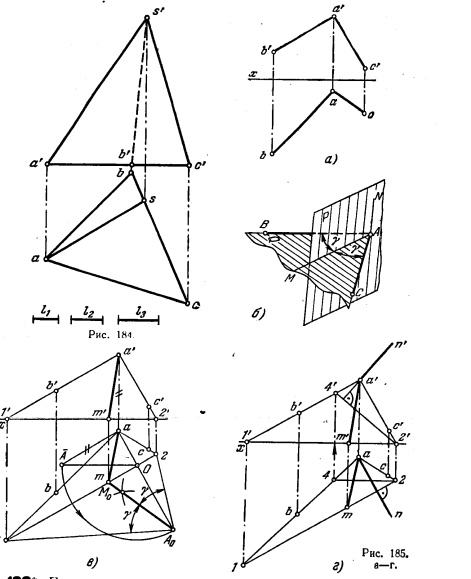
198. Найти точку К, находящуюся внутри пирамиды SABC на расстояниях: l₁ — от грани SAC, l₂ — от грани SBC, l₃ — от грани SAB (рис. 184).

199*. Построить геометрическое место точек, равноудаленных от сторон угла ВАС (рис. 185, а).

Решение. Искомым геометрическим местом является плоскость, проходящая через биссектрису данного угла перпендикулярно к его плоскости (рис. 185, б). Следовательно, искомая плоскость будет определяться этой биссектрисой и пересекающим ее перпендикуляром к плоскости угла ВАС.

Для проведения биссектрисы угла ВАС приходится построить его натуральный вид, так как непосредственное проведение биссектрисы в заданных проекциях угла возможно лишь в особых случаях, например при одинаковом наклоне сторон угла к плоскости проекций. На рис. 185, в показано совмещение плоскости угла ВАС с пл. H, для чего построен горизонт. след (1—2) этой плоскости.Теперь может быть проведейа биссектриса угла 1А₀2 — прямая А₀М₀ — и построены ее проекции am и a’m’.

Остается провести перпендикуляр к плоскости угла ВАС через какую-либо точку его биссектрисы и этим определить искомую плоскость. На рис. 185, г перпендикуляр проведен через вершину угла—точку А, для чего использован горизонт. след 1—2 и проведена фронталь 2—4; проекция перпендикуляра an ⊥ 1—2 и проекция а’n’ ⊥ 2’4′.

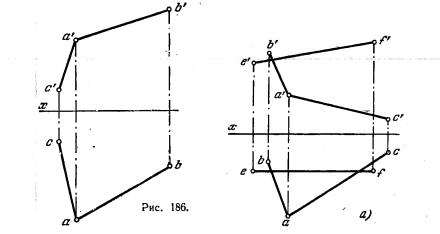
200. Построить геометрическое место точек, равноудаленных от сторон угла ВАС (рис. 186). Искомую плоскость задать следами.

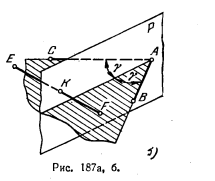
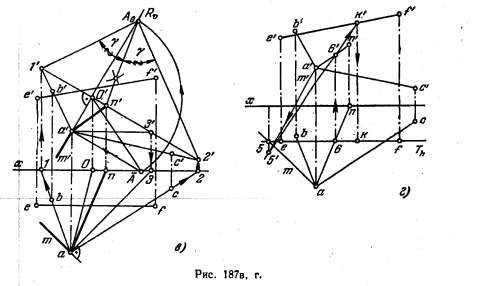
201*. На прямой EF (EF || пл. V) найти точку, равноудаленную от сторон угла ВАС (рис. 187, а).

Решение. Геометрическим местом точек, равноудаленных от сторон угла ВАС, является плоскость Р, проходящая через биссектрису этого угла и перпендикулярная к его плоскости (рис.187,б). Очевидно, Искомая точка (К) на прямой EF получится при пересечении этойй с пл. P.

Построение пл. Р на рис. 187, в аналогично построению на рис. 185, а, с той лишь разницей, что на рис. 187, в угол. ВАС совмещен с пл. V вращением вокруг фронт. следа 1’2′ плоскости этого угла. Для построения проекций перпендикуляра AM рспользован след 1’2′ и горизонталь А—3: a’m’ ⊥ 1’2′ и am ⊥ a3

Точка К на прямой EF найдена обычным способом построения точки пересечения прямой с плоскостью (рис. 187, г);

1) через EF проведена вспомогательная пл. Т (так как прямая EF||пл. V, то окзалось возможным провести через нее фронтальную плоскость T),

2) построена прямая пересечения пл. P (заданной прямыми AM и AN) с пл. Т (это фронталь плоскости P — прямая с проекциями 5’6′, 5—6),

3) найдена точка пересечения этой фронтали с прямой EF — точка К.

202. На стороне АВ основания пирамиды SABC (рис. 188) найти трчку К, равноудаленную от ребер SA и SC.

203. На ребре SC пирамиды SABC (см. рис. 188) найти точку M, равноудаленную от ребра SA и стороны АВ основания.

204*. Найти геометрическое место точек, равноудаленных, от пл. Р и пл. Q (рис. 189, а).

Решение. Искомым геометрическим местом является (рис. 189, б) пл. R, делящая пополам двугранный угол, образованный данными плоскостями. Пл. R проходит через ребро двугранного угла, т. е. через прямую MN. Если ребро MN расположить перпендикулярно к какой-либо пл. проекций Т, то каждая из плоскостей P и Q, а также и пл. R изобразятся на этой плоскости проекций в виде прямых, как это показано на рис. 189, б, причем R_t делит угол между P_t и Q_t пополам.

Построив (рис. 189, в) прямую MN пересечения плоскостей P и Q, вводим (рис. 18В, г) дополнительные плоскости S (S ⊥ H и S||MN) и Т(T ⊥ S и Т ⊥ МN). Угол между построенными прямыми m_tP_xt и m_tQ_xt равен углу между плоскостями P и Q, а биссектриса этого угла m_tR_xt представляет собою след искомой пл. R на дополнительной пл. Т. Относя точку R_x к прямой Р_x Q_x, т. е, к оси V/H, находим проекцию R_xs на P_xsQ_xs и R_x на Р_xO_x, т. е. на оси V/H. В точке R_x следы искомой плоскости пересекают ось V/Н, а так как пл. R проходит через прямую МN, то след R_ϑ проходит через точку n’, а след R_h — через m.

205. Найти геометрическое место точек, равноудаленных от пл. Р и плоскости, заданной прямыми АВ и CD (рис.

206*. Найти на прямой АВ точку, равноудаленную от плоскостей, заданных треугольниками MNC и MND (рис. 191, а).

Решение. Искомой точкой является точка пересечения прямой АВ с плоскостью (R), делящей угол между данными плоскостями пополам (рис. 191, б).

Ход построения аналогичен примененному в задаче 204. Путем введения дополнительных пл. проекций S и Т получаем положение, при котором ребро MN проецируется на пл. Т в точку (рис. 191, а).

В этом положении изображаем плоскость, делящую пополам угол между гранями MNC и MND, в виде прямой R_t. В пересечении прямой a_tb_t c R_t получим проекцию искомой точки К на пл. Т; по ней находим k_s, на a_sb_s, а затем k на ab и k’ на а’b’.

207. На ребре SB пирамиды SABC найти точку К, равноудаленную от грани SAС и основания ABC (см. рис. 188).

208. На стороне АВ основания ABC пирамиды SABC найти точку М, равноудаленную от граней SAC и SBC (см. рис. 188).

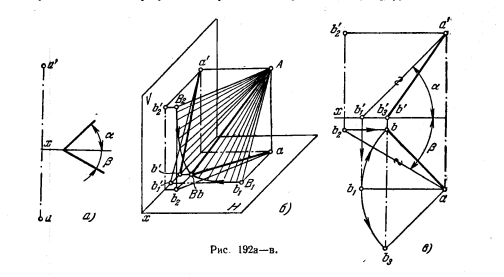
209*. Через точку А провести прямую общего положения, расположенную под углом α к пл. Н и под углом β к пл. V (рис. 192, а).

Решение. Известно (см. задачу 22), что для прямой общего положения α + β < 90°.

На рис. 192, бив показано построение искомой прямой с применением способа вращения. На этих рисунках изображены две прямые: одна (AB₁) расположена

параллельно пл. V и другая (AВ₂) — параллельно пл. Н. На обеих прямых отложены равные отрезки АВ₁ и AB₂: a’b’₁ = ab₂.

Если теперь повернуть отрезок AВ₁ вокруг оси, перпендикулярной к пл. Н, a отрезок АВ₂— вокруг оси, перпендикулярной к пл. V, причем обе оси вращения проходят через точку А, то в некоторый момент оба этих отрезка совпадут (на рис. 192, б это показано в виде отрезка АВ), и, следовательно, искомая прямая окажется построенной.

Всего можно провести через точку А четыре прямые. На чертеже (рис. 192, в) проводим дугу окружности радиуса ab₁ до пересечения в точке b с прямой, проходящей через точку b₂ параллельно оси х. По точке b находим b’.

На рис. 192, в показано еще одно (из четырех возможных) положение прямой, обозначенное АВ₃.

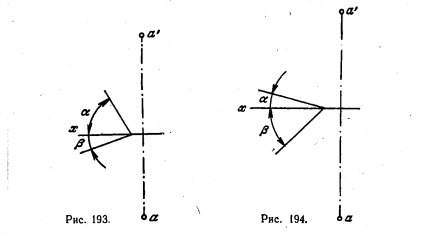
240. Через точку А провести вправо от нее прямую общего положения АВ, расположенную под углом α к пл. Р и под углом β к пл. V (рис. 193), при условии, что точка В расположена в пл. H и ближе к пл. V, чем точка А.

211. Через точку А провести вправо от нее отрезки АВ, AC, AD и АЕ, расположенные под углом α к пл. H и под углом β к пл.- V (вис. 194).

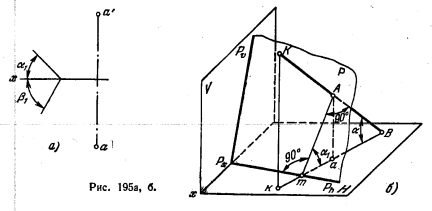
212*. Провести через точку А плоскость, составляющую с пл. H угол α₁ и с пл. V угол β₁ (рис. 195, а).

Решение. Для построения искомой плоскости в данном случае использована зависимость между углами, составляемыми некоторой прямой с пл. Н (у гол α) и с пл. V (угол β), и углами, составляемыми плоскостью, перпендикулярной к этой прямой, с теми же плоскостями проекций Н (угол α₁) и V (угол β₁). Известно, что α₁ + α = 90°

(рис. 195, б) и β₁ + β = 90°. Отсюда следует, что 180° > α₁ + β
> 90°. Это позволяет проверить правильность задания углов α₁ и β₁ (рис. 195, о)β.

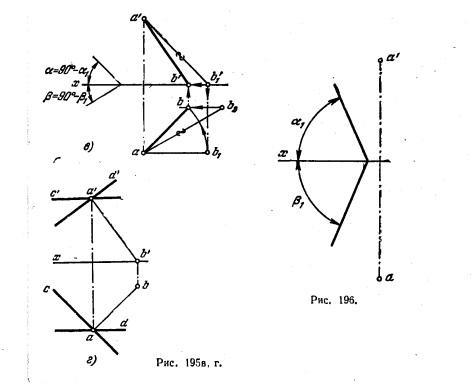
Итак, определив утлы α = 90° — α₁ и β = 90° — β₁ проводим через точку А прямую под углами α и β соответственно к пл. H и пл. V (рис. 195, в), как это имело место в задаче 209. Теперь через точку А проводим плоскость, перпендикулярную к построенной прямой АВ. Эта плоскость на рис. 195, г выражена горизонталью ифронталыо: a’d’ ⊥ a’b’, ас ⊥ аb.

213. Провести через точку А две плоскости (выразив их следами) под углами α₁ к пл. Н и β₁ к пл. V (рис. 196), построив вспомогательные прямые под углами α = 90° — α₁ к пл. H и β = 90° — β₁ пл. V — одну вправо, вглубь, вниз, от точки А, другую — вправо, вглубь, вверх.

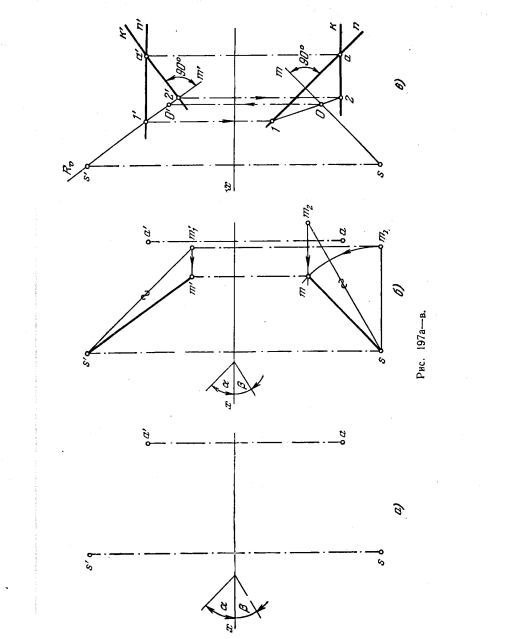
214* . Построить правильную треугольную пирамиду с вершийой в точке S. Высота пирамиды наклонена к пл. Н под углом α и к пл. V под углом β. Точка А — одна из вершин основания (рис 197, а).

Решение. Проводим (рис. 197, б) через точку S прямую SM под заданными углами α и β к пл. H и пл. V (см. задачу 209). Плоскость основания пирамиды должна пройти через точку А перпендикулярно к SM; задаем эту плоскость горизонталью AN й фронталью АК (рис. 197, в). Находим точку О пересечения прямой SM с плоскостью основания. Для этого заключаем SM в фронтально-проецирующую

пл. R, изображенную только фронт. следом R_ϑ. Для построения вершин В я С пирамиды поворачиваем плоскость основания вокруг горизонтали А—3 до совмещения ее с пл. T (рис. 197, г).

В плоскости основания через точку О проводим произвольную прямую 3—4. Строим совмещенное с пл. T положение точки 4 |4₁| и соединяем 4₁ с точкой 3. На прямой 3—4₁ находим точку O₁, из которой радиусом О₁ проводим окружность. Разделив ее на три части, находим вершины b₁ и с₁. Зная b₁ и c₁ находим (рис. 197, д) горизонт. проекци: с— на продолжении прямой а—5 (найдя сначала точку 5 по 5,), b — на прямой а—6 (найдя сначала точку 6 по 6₁). Затем строим прямые а’5′ и а’6′ и на них точки с’и b’; а’b’с’ и abc — проекции основания пирамиды. На рис. 197, е проекции—вершин s’ и s соединены с одноименными с ними проекциями вершин основания.

215. Построить правильную четырехугольную пирамиду с вершиной в точке S. Высота пирамиды наклонена к пл.H под углом α и к пл. V под углом β. Точка А — одна из вершин основания (рис. 198).

216*. Построить куб с основанием на плоскости, расположенной под углом α₁ к пл. Н и углом β₁ к пл. V. Отрезок а’b’— фронт. проекция стороны основания куба (рис. 199, а).

Решение. Строим произвольную прямую MS (рис. 199, б), расположенную под углом α = 90° — α₁ к пл. H и β = 90° — β₁, к пл. V.

Эта прямая дает нам направление боковых ребер куба. Теперь проводим через точку А пл. Р (рис. 199, в), перпеидакулярную к этой прямой, и находим в пл. Р точку В. Совмещаем пл. Р и лежащий в ней отрезок АВ с пл. H (рис. 199, г) и достраиваем квадрат A₀B₀C₀D₀. Затем поднимаем точки D₀ и С₀ в пространство: точку D₀ с помощью прямой 1₀2₀ и точку С₀ с помощью совмещенной фронтали 3₀С₀.

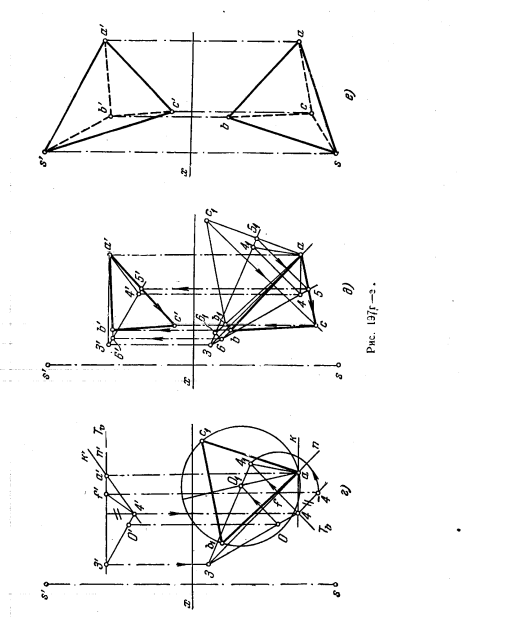
Так как ребра куба перпендикулярны к основанию, то через точку А проводим (рис. 199, д) прямую, перпендикулярную к пл. Р (а’4′ ⊥ Р_ϑ и a ⊥ 4 ⊥ P_h). На этой прямой откладываем отрезок АЕ, равный стороне основания, хотя бы А₀В₀. Это сделано при помощи построения прямоугольного треугольника. Получив таким образом проекции а’е’ и ае, строим (рис. 199, е) проекции куба.

217. Пстроить прямую треугольную призму с основанием в виде равнобедренного треугольника ABC на плоскости, расположенной под

углом α₁ к пл.H и углом β₁ к пл. V. Вершина С треугольника ABC лежит на пл. Н. Высота призмы равна стороне AВ основания — треугольника ABC (рис. 200).

Свойство точек биссектрисы угла:

По определению биссектриса угла делит угол пополам.

У биссектрисы есть еще одно важное свойство.

Теорема (о биссектрисе угла).

Любая точка биссектрисы угла равноудалена от сторон угла. Если точка внутри угла равноудалена от сторон угла, то она лежит на биссектрисе этого угла.

В данной теореме два утверждения: прямое и ему обратное. Докажем каждое из этих утверждений отдельно.

1) Дано: AD — биссектриса

Доказать: MK=MN.

Доказательство:

Прямоугольные треугольники АКМ и ANM равны по гипотенузе и острому углу (гипотенуза AM — общая, KAM =NAM, так как AD — биссектриса). Катеты МК и MN равны как соответствующие в двух равных треугольниках.

2) Дано: BAC, МКAB, MNAC, МК = MN, MAD (рис. 272).

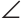
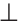
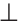
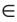
Доказать: луч AD — биссектриса BAC.

Доказательство:

Прямоугольные треугольники АКМ и ANM равны по катету и гипотенузе (гипотенуза AM — общая, МК = MN по условию). Углы КAM и NAM равны как соответствующие в двух равных треугольниках, откуда луч AD — биссектриса BAC. Теорема доказана.

Из доказанной теоремы следует, что биссектриса является геометрическим местом точек плоскости, находящихся внутри угла и равноудаленных от сторон угла.

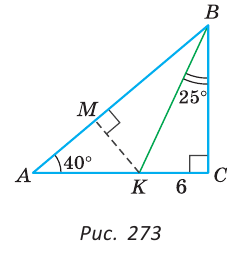
Пример:

В прямоугольном треугольнике ABC C = 90°, A = 40° (рис. 273). На катете АС взята точка К так, что КС=6 см и KBC = 25°. Найти расстояние от точки К до прямой АВ.

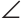
Решение:

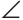
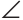
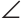
Искомое расстояние равно длине перпендикуляра КМ к прямой АВ. Так как ABC = 90° –A = 90° – 40° = 50°, то ABK = 50° – 25° = 25°. Следовательно, ВК — биссектриса угла ABC. Поскольку любая точка биссектрисы угла равноудалена от сторон угла, то КМ = КС = 6 см.

Ответ: 6 см.

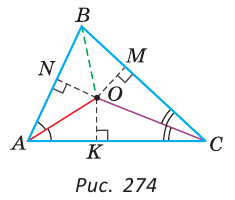
Пример: (2-я замечательная точка треугольника).

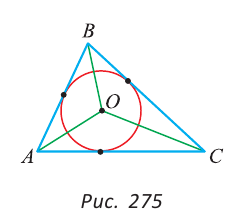
Доказать, что биссектрисы треугольника пересекаются в одной точке.

Доказательство:

Проведем в АВС биссектрисы углов А и С. Пусть О — точка их пересечения (рис. 274).

Так как точка О лежит на биссектрисе АО угла А, то она равноудалена от сторон угла А, то есть равны перпендикуляры ON и ОК к сторонам угла А. Так как точка О лежит на биссектрисе СО угла С, она равноудалена от сторон угла С, то есть равны перпендикуляры ОК и ОМ к сторонам угла С. Тогда ОК = ОМ = ON. Так как перпендикуляры ON и ОМ равны, то точка О равноудалена от сторон угла В. Точка, равноудаленная от сторон угла, лежит на биссектрисе этого угла. Поэтому биссектриса угла В пройдет через точку О, и, следовательно, все три биссектрисы пересекутся в одной точке.

Замечание. Точка пересечения биссектрис треугольника является центром вписанной в него окружности (рис. 275), которая касается всех трех сторон треугольника (имеет с каждой из сторон только одну общую точку).

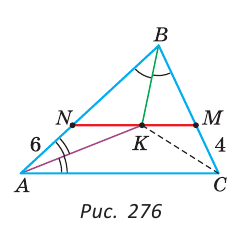
Пример:

В треугольнике ABC биссектрисы углов А и В пересекаются в точке К. Через точку К проведен отрезок NM, параллельный стороне АС с концами на сторонах АВ и ВС соответственно; AN = 6 см, МС = 4 см. Найти отрезок NM.

Решение:

Так как биссектрисы треугольника пересекаются в одной точке, то СК — биссектриса угла С (рис. 276).

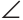
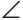
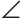
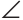
Треугольник ANK — равнобедренный. Действительно, NAK =CAK, поскольку АК — биссектриса, CAK =AKN как накрест лежащие при параллельных прямых NM и АС и секущей АК, откуда NAK =AKN и треугольник ANК —  равнобедренный по признаку равнобедренного треугольника. Тогда NK=AN=6 см. Аналогично доказываем, что треугольник KMC — равнобедренный и КМ=МС=4 см.

Искомый отрезок NM = NK + КМ = 6 + 4=10 (см).

Ответ: 10 см.

Замечание. Решив задачу 3, мы доказали, что если NM || АС и отрезок NM проходит через точку пересечения биссектрис, то периметр NBM равен АВ+ВС.