Как найти точку штейнера

Точка Штейнера
Названо в честь	Якоб Штейнер
Медиафайлы на Викискладе

Точка Штейнера — одна из замечательных точек треугольника^[1] и она обозначается как точка X(99) в энциклопедии центров треугольника Кларка Кимберлинга (Clark Kimberling).

История[править | править код]

Якоб Штейнер (Jakob Steiner) (1796—1863), швейцарский математик, описал эту точку в 1826 году. Этой точке было дано имя Штейнера Жозефом Нойбергом (Joseph Neuberg) в 1886 году^[1][2].

Определение[править | править код]

Точка Штейнера определяется следующим образом. (Мы используем не тот способ, каким эту точку определял сам Штейнер.^[1])

Пусть дан любой треугольник . Пусть  — его центр описанной окружности и  — точка пересечения симедиан. Окружность, построенная на как на диаметре, представляет собой окружность Брокара треугольника . Прямая, проходящая через перпендикулярно к прямой , пересекает окружность Брокара в другой точке . Прямая, проходящая через перпендикулярно к прямой , пересекает окружность Брокара в другой точке . Прямая, проходящая через перпендикулярно к прямой , пересекает окружность Брокара в другой точке (треугольник есть треугольник Брокара для треугольника ). Пусть есть прямая, проходящая через параллельно прямой , есть прямая, проходящая через параллельно прямой , и есть прямая, проходящая через параллельно прямой . Тогда все три прямых , и пересекаются в одной точке. Точка их пересечения и есть точка Штейнера треугольника .

Трилинейные координаты[править | править код]

Трилинейные координаты точки Штейнера равны

.

Свойства[править | править код]

.

Этот треугольный центр обозначается как X(1115) в энциклопедии центров треугольника.

Точка Тарри[править | править код]

Точка Тарри треугольника тесно связана с точкой Штейнера треугольника. Пусть — любой данный треугольник. Точка на описанной окружности треугольника , диаметрально противоположная к точке Штейнера треугольника, называется точкой Тарри треугольника . Точка Тарри представляет собой центр треугольника и он обозначен как центр X(98) в энциклопедии центров треугольника. Трилинейные координаты точки Тарри равны

,

где является углом Брокара треугольника .

Примечания[править | править код]

См. также[править | править код]

• Центр Штейнера — центр тяжести кривизны Гаусса поверхности выпуклого тела.

Алгоритмы о выборе дороги и сетях. Сети Штейнера. Лекция Владимира Протасова в Яндексе

Сегодня мы поговорим об одной из первых задач теории больших сетей, которая может быть решена полностью на самом простом базовом уровне, но которая от этого не становится менее интересной. Это задача о кратчайшей системе дорог или задача Штейнера.

Впервые она появилась, когда еще никаких практических надобностей для больших сетей не было: в тридцатые годы XX века. На самом деле Штейнер начал ее изучать еще раньше, в XIX веке. Это была чисто геометрическая задача, практические приложения которой стали известны только несколько десятилетий спустя.

Разговор пойдет о той области математики, которая впоследствии выросла в теорию больших сетей и разбилась на несколько областей. Это прикладная отрасль, которая задействует очень много методов из других математических дисциплин: дискретной математики, теории графов, функционального анализа, теории чисел и т.д. Бурное развитие теории больших сетей пришлось на конец девяностых и начало двухтысячных годов. Связано это конечно, с прикладными задачами: развитием интернета, мобильной связи, транспортных задач для больших городов. Кроме того теория сетей используется в биологии (нейронные сети), при построении больших электронных плат и т.п.

Сама задача формулируется очень просто. Есть несколько точек на плоскости, которые нужно связать системой дорог наименьшей суммарной длины таким образом, чтобы по этим дорогам можно было из каждой точки добраться в любую другую. Число точек конечно.

Начать рассказ стоит с истории о том, как на Малом мехмате двум группам учеников – восьмиклассникам и одиннадцатиклассникам дали решать одну и ту же задачу. Четыре деревни расположены в вершинах квадрата со стороной четыре километра. Существует ли система дорог, которая связывала бы все эти деревни между собой и имела бы суммарную длину не превосходящую 11 километров.

Если соединять деревни последовательно, то ничего короче, чем три стороны квадрата мы не придумаем. При таком соединении у нас будет ровно 12 километров. Можно соединять по диагонали, но это будет только хуже, т.к. диагональ длиннее стороны.

Если поставить дополнительную вершину, тогда из нее можно будет проехать в любые четыре деревни. Если мы возьмем дороги, связывающие диаметрально противоположные вершины, то по неравенству треугольника, сумма их длин будет больше, чем длина диагонали. У и двух других сумма длин тоже больше, чем длина диагонали. Соответственно, сумма всех дорог у нас будет ≥2∙4√2=8√2≈11.31. Примерно так рассуждали одиннадцатиклассники, которые пытались доказать невозможность существования такой системы дорог.

В это же самое время в соседней аудитории восьмиклассники при помощи обычной линейки с делениями строили эту самую систему дорог. И в итоге им это удалось. Система представляет собой нечто похожее на букву Н, все углы в которой равны 120°. Ее длина составляет ≈10.98 километра. Это и есть сеть Штейнера, соединяющая четыре точки. Таких сетей может быть много, может быть несколько кратчайших, но такую задачу о кратчайшей системе дорог можно решить полностью методами элементарной геометрии.

Чтобы окончательно покончить с этой задачей, найдем ошибку в первом решении, где мы вроде как доказали, что ничего короче 8√2 быть не может. Просто в этом решении не была учтена возможность многократно использовать один и тот же участок.

Три точки

Сеть Штейнера для треугольника была известна еще за 200 лет до самого Якоба Штейнера, в XVII веке. Это так называемая точка Ферма-Торичелли-Штейнера.

Начнем мы с того, что докажем одно вспомогательное утверждение, называемое иногда теоремой Помпею. Если мы возьмем на плоскости равносторонний треугольник и любую другую точку плоскости, тогда сумма расстояний до двух вершин A и B всегда больше или равно расстоянию до третьей вершины C: MA + MB ≥ MC. Более того, MA + MB = MC только в том случае, когда точка M лежит на дуге описанной окружности, не содержащей точку С. Т.е. угол AMB должен быть равен 120°. В противном случае MA + MB > MC.

Конечно, если речь идет о равностороннем треугольнике, нам часто в таких задачах помогает поворот на 60° относительно какой-нибудь вершины. Это мы и сделаем: повернем заштрихованный треугольник AMB относительно вершины A по часовой стрелке. Точка B у нас перейдет в точку C, а Точка M – в точку M’. В итоге у нас получается, что AM = AM’ = MM’, а M’C = MB.Теперь мы можем применить обычное неравенство треугольника на треугольнике MM’C. В нем сумма двух сторон M’M и M’C больше, чем MC. Соответственно, MA + MB ≥ MC. А когда же достигается равенство? Равенство достигается, когда точка M’ точно попадает на прямую MC, т.е. когда угол AMC равен 120°.

Теперь перейдем непосредственно к задаче Штейнера для трех точек. Формулируется она следующим образом. Задан треугольник. Нужно найти точку на плоскости, сумма расстояний от которой до вершин этого треугольника наименьшее. TA + TB + TC → min.

Что же это за точка? Мы знаем несколько замечательных точек треугольника: центры вписанной и описанной окружностей, точка пересечения медиан, точка пересечения высот. К сожалению, ни одна из них на роль точки с наименьшей суммой расстояний не подходит. Эта точка совершенно особая, и называется по-разному: точкой Торичелли, точкой Ферма, точкой Штейнера. Представляет она собой точку, из которой все три вершины треугольника видны под одинаковыми углами – 120°. Разберемся, почему это именно так. Впервые решение задачи о точке с наименьшей суммой расстояний до всех вершин треугольника документально впервые появилось в книге итальянского физика и математика Винченцо Вивиани в середине XVII века. Однако известно, что решение этой задачи было получено еще раньше другом Вивиани, Эванджелиста Торичелли – оба они были учениками Галилея. Приведенное в книге решение не было геометрическим, оно было основано на физических принципах. Эту задачу до Торичелли знал, а возможно, и решил Пьер Ферма: они состояли в переписке, и про эту задачу Торичелли узнал именно от Ферма, но было ли у нег свое решение – неизвестно.

Первое геометрическое решение этой задачи появилось лишь спустя 200 лет, и автором его стал Якоб Штейнер. Он был одним из первых синтетических геометров, решавшим геометрические задачи исключительно геометрическими методами. Основывалось решение Штейнера на рассмотренной нами выше теореме Помпею.

Существует ли вообще такая точка, из которой все углы треугольника видны под углом 120°? Существует она не всегда, а только в том случае, если все углы треугольника строго меньше 120°.

Если все углы треугольника > 120°, то существует единственная точка Торичелли. Построим равносторонний треугольник во внешнюю сторону относительно стороны BC. Построим окружность, которая проходила бы через точки B, A’ и C. Если тока Торичелли в данном случае существует, то она должна лежать на этой окружности, на дуге между точками B и C. Во вписанном четырехугольнике сумма противоположных углов составляет 180°. Треугольник BA’C равносторонний, соответственно, все углы в нем равны 60°. А значит, если мы поставим точку на дуге между точками B и C, а затем достроим четырехугольник, угол напротив вершины A’ будет равен 120°.

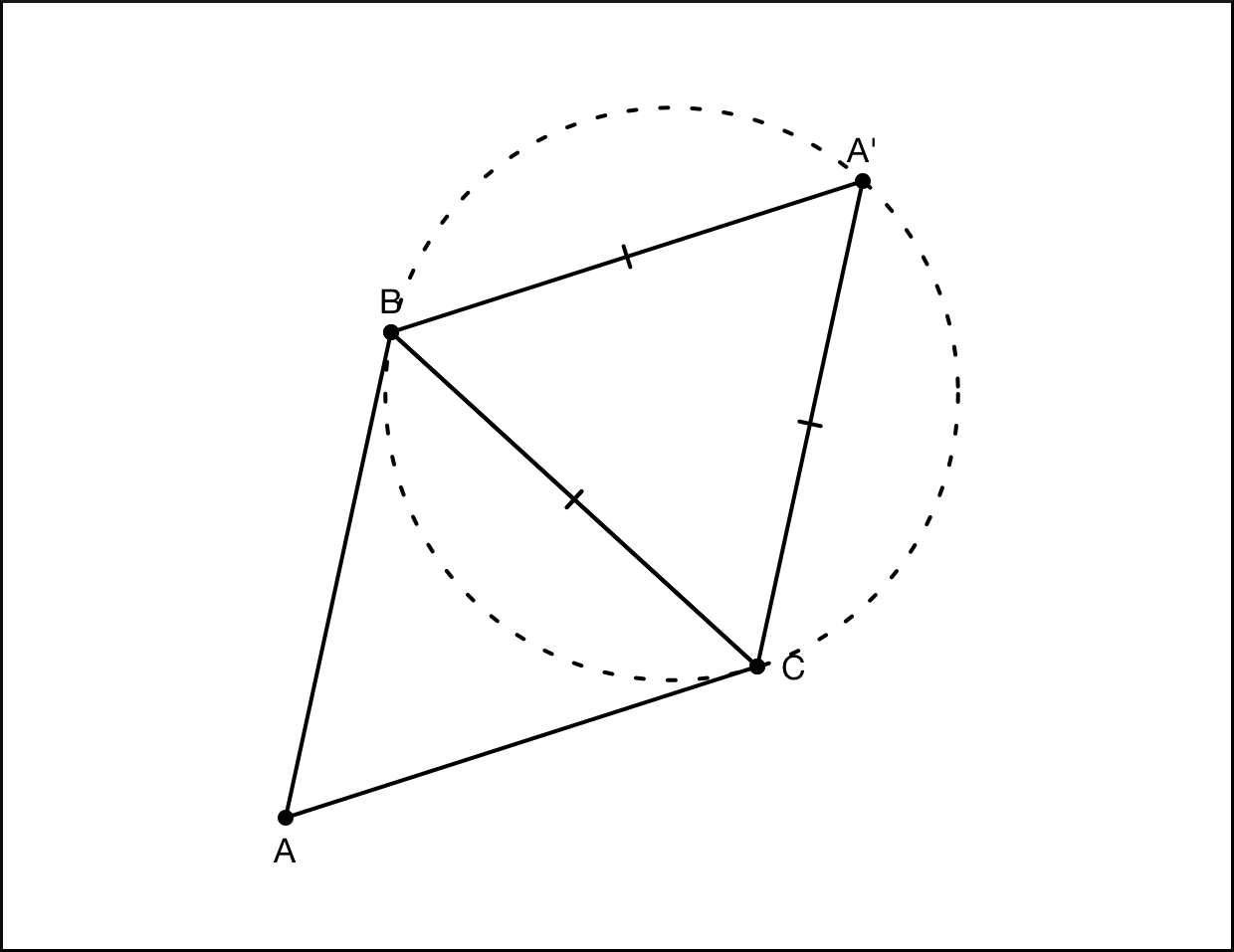
Но где именно расположить точку, чтобы все вершины были видны под углом 120°. Нужно построить еще один равносторонний треугольник, на этот раз – относительно стороны AC. И точно так же впишем его в окружность. Точка пересечения двух окружностей и будет точкой Торичелли. Мы уже определили, что угол BTC равен 120°, угол ATC получен тем же способом и также равен 120°. В сумме все три угла должны дать 360°, а значит, угол BTA также равен 120°. Таким образом, мы доказали не только существование точки Торичелли, но и то, что она может быть только одна, так как построенные нами дуги могут иметь не более одной точки пересечения. Теоретически окружности могли бы пересечься вне треугольника ABC, но случиться это могло бы только в том случае, если хотя бы один из его углов был больше 120°.

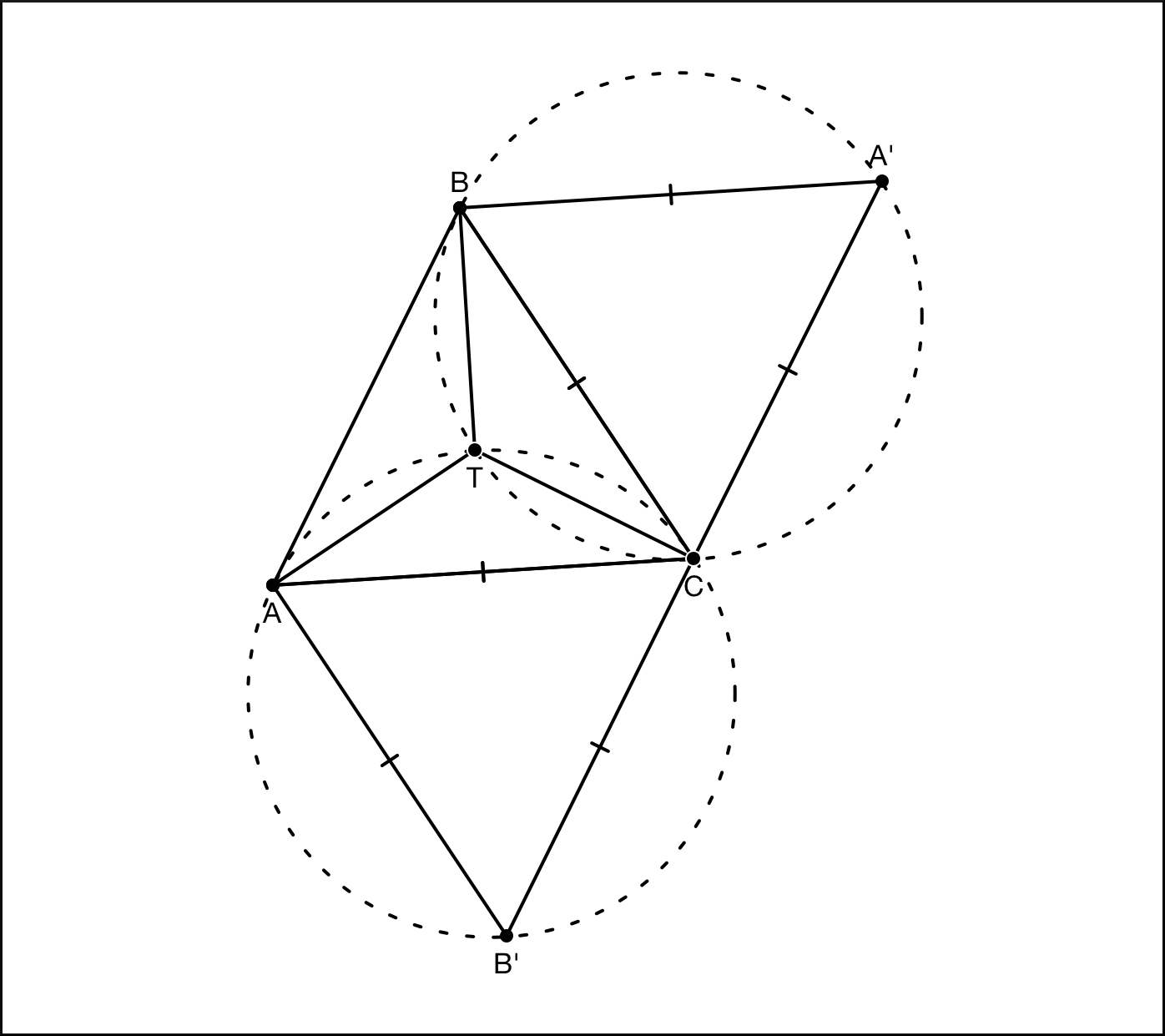
Итак, мы научились находить местоположение точки Торичелли, но так и не объяснили, почему с ее помощью можно решить задачу Штейнера о минимальной сумме расстояний до вершин треугольника. Снова возьмем треугольник ABC, где все углы будут меньше 120° и построим внешний равносторонний треугольник относительно стороны AC. Назовем его AB’C. Далее возьмем произвольную точку M на плоскости и соединим ее со всеми тремя вершинами треугольника ABC. В силу теоремы Помпею MA + MC ≥ MB’. Значит, MA + MB + MC ≥ MB’ + MB, а MB + MB’ ≥ BB’. Так как MB + MB’ не может быть меньше BB’, точка M будет иметь наименьшую сумму расстояний до вершин треугольника ABC только в том случае, когда MB + MB’ = BB’. При каких же условиях такое равенство будет верно? По теореме Помпею для этого нужно, во-первых, чтобы MA + MC было равно MB’, т.е. угол AMC должен быть равен 120°, а во-вторых, сумма отрезков BM и MB’ должна быть равна BB’, т.е. точка M должна лежать на отрезке BB’. Соответственно, углы AMB и BMC также будут равны 120°. Из всего этого следует, что MB + MB’ = BB’ только в том случае, когда точка M совпадает с точкой Торичелли. В этом и заключается решение задачи Штейнера для трех точек.

Каково же решение этой задачи для того случая, когда один из углов треугольника больше или равен 120°? Не будем подробно рассматривать доказательство для этого варианта, скажем лишь, что минимальная сумма расстояний достигается в вершине наибольшего угла треугольника. Доказать это самостоятельно несложно, нужно лишь учесть все то, что мы уже проделали выше.

Оказывается, что точка Ферма-Торичелли-Штейнера – это все, что нужно для построения систем дорог наименьшей длины. Основная задача формулируется следующим образом. На плоскости задано конечное множество (k ≥ 2) точек. Нужно соединить их кратчайшей системой дорог. Сам Штейнер решил эту задачу для k = 3 и привел некоторые примеры для k = 4. Для k ≥ 2 Штейнер даже не ставил задачи. Впервые эта задача была поставлена через 70 лет после смерти Якоба Штейнера двумя чешскими математиками Кесслером и Ярником. В 1934 году задача была опубликована в чешском математическом журнале, но первые несколько лет ей никто не интересовался. Однако в 1941 году два уже известных на тот момент американских математика Гурвиц и Курант поместили ее со ссылкой на Кесслера и Ярника в своей книге, после чего задача стала очень известной.

Досмотрев лекцию до конца, вы узнаете, как решается задача Штейнера в общем виде на плоскости и в пространстве.

Сети Штейнера

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Задача Штейнера заключается в поиске наименьшего дерева Штейнера — кратчайшей сети, объединяющей заданный конечный набор точек плоскости. Свое название получила в честь Якоба Штейнера (1796—1863).

История данной задачи восходит ко временам Пьера Ферма (1601—1665), который, после изложения своего метода исследования минимумов и максимумов, написал.

Тот же, кто этот метод не оценил, пусть он решит [следующую задачу]: для заданных трех точек найти такую четвертую, что если из нее провести три отрезка в данные точки, то сумма этих трех отрезков даст наименьшую величину.

Эта задача была частично решена Э. Торричелли (1608—1647) и Б. Кавальери (1598—1647), учениками Б. Кастелли (1577—1644), затем найденная ими конструкция была модифицирована Т.

Симпсоном (1710—1761) и окончательно уточнена Ф. Хейненом и Ж. Бертраном (1822-1900). В результате, был получено геометрическое построение точки S, ныне называемой точкой Ферма (иногда точкой Торричелли), которая для трёх заданных точек A, B и C даёт минимально возможную сумму длин отрезков AS, BS, CS.

В 1934 году В. Ярник и O. Кесслер сформулировали обобщение задачи Ферма, заменив три точки на произвольное конечное число. А именно, их задача состоит в описании связных плоских графов наименьшей длины, проходящих через данное конечное множество точек плоскости.

Актуальность и значимость исследования:

Изученный и представленный материал может быть использован на уроках геометрии в школе, а также будет полезен для учеников.

Такие задачи могут встречаться на олимпиадах в школах, они развивают логическое мышление и кругозор школьников, что является актуальным.

Глава 1. Алгоритм Штейнера (Поиск кратчайших сетей)

В общей форме задача Штейнера была в первый раз сформулирована в статье Милоша Кёсслера и Войцеха Ярника, опубликованной в 1934 году, однако сама эта проблема не приобрела широкой известности вплоть до 1941 года, когда Рихард Курант и Герберт Е. Роббинс включили её в свою книгу «Что такое математика?». Курант и Роббинс связали эту задачу с исследованиями Якоба Штейнера, немецкого математика XIX столетия, работавшего в Берлинском университете. Работа Штейнера была посвящена поиску одной точки, сумма расстояний от которой до всех точек заданного множества была бы минимальной. Однако ещё в 1640 году впервые была поставлена задача, являющаяся частным случаем обеих описанных задач — той, над которой работал Штейнер, и той, которая носит его имя: найти точку P, сумма расстояний от которой до каждой из трёх заданных точек минимальна. Эванджелиста Торричелли и Бонавентура Кавальери независимо друг от друга решили эту задачу. Торричелли и Кавальери обосновали, чту суммарное расстояние минимально, когда все сопряжённые углы в точке P больше или равны 120°.

Необходимо провести отрезки прямых, соединяющие исходные точки (назовем их A, B и C), с точкой в вершине наибольшего угла (скажем, B). Если угол B больше или равен 120°, то искомая точка P совпадает с точкой B. Другими словами, кратчайшая сеть в данном случае представляет собой просто два отрезка прямых между точками A и B и точками B и C. Если угол в точке B меньше 120°, то точка P должна находиться где-то внутри треугольника. Чтобы найти её, следует построить равносторонний треугольник с основанием на самой большой стороне треугольника ABC, а именно на отрезке AC. Третья вершина равностороннего треугольника (обозначим её X) находится на противоположной стороне от точки B относительно AC. Вокруг построенного равностороннего треугольника описываем окружность и проводим прямую, соединяющую точки B и X. Точка P будет на пересечении этой прямой и окружности. Соединив точки A, B и C с точкой P, мы получаем три угла, в точности равные 120° каждый, и искомую кратчайшую сеть. Более того, длина отрезка BX оказывается равной длине кратчайшей сети. В дальнейшем в нашей статье мы будем называть точку X замещающей точкой, поскольку замена точек A и C одной точкой X не изменяет длину сети.

Задача с тремя точками и задача Штейнера для многих точек обладают много общих свойств. Их решения, имеющие вид дерева, типичны тем, что при удалении любого отрезка из кратчайшей сети мы должны будем исключить одну из заданных точек. Другими словами, мы не можем пройти по сети из какой-либо заданной точки и вернуться в неё, без того чтобы не пройти те или иные отрезки повторно. По этой причине графические решения задачи с тремя точками и задачи со многими точками называются деревьями Штейнера. Отрезки прямых называются рёбрами, а точки, роль которых аналогична точке P и которые нужно добавить для построения дерева, называются точками Штейнера.

Задача Штейнера для трёх точек даёт также некоторую информацию о геометрии кратчайших деревьев Штейнера. Во-первых, каждый угол равен 120° или больше, а это означает, что каждая точка соединяется с остальным деревом не более чем тремя рёбрами. Во-вторых, в каждой точке Штейнера сходятся ровно три ребра, образуя друг с другом углы, в точности равные 120°. В-третьих, число рёбер дерева всегда на единицу меньше суммарного числа заданных исходных точек и точек Штейнера. И наконец, последнее свойство: поскольку в каждой точке Штейнера сходятся ровно три ребра и по крайней мере одно ребро должно касаться каждой из заданного множества точек, максимальное число точек Штейнера для любой задачи на две меньше, чем число заданных исходных точек.

При одном и том же количестве и расположении исходных точек можно построить много различных деревьев Штейнера, удовлетворяющих перечисленным выше условиям. Некоторые из этих деревьев, называемые локально минимальными решениями, нельзя сократить за счёт мелкомасштабных изменений, таких как небольшое перемещение ребра или расщепление точки Штейнера. Всё же не всякое локально минимальное дерево Штейнера даёт кратчайшее из возможных решений задачи. Для того чтобы преобразовать сеть в кратчайшее дерево, называемое глобально минимальным деревом Штейнера, могут потребоваться крупномасштабные перемещения точек Штейнера.

Глава 2. Планирование сети дорог

Рассмотренная прежде постановка задачи о прокладке коммуникаций может не включать требования о том, что коммуникации могут разветвляться лишь на территории связываемых объектов. Зачастую реальность не накладывает этих ограничений, например, при строительстве дорог, которые могут менять направление, иметь повороты, развилки и перекрестки любого вида. Данная задача известна как ”задача Штейнера на графах”.

Вообще говоря, известно два типа такого рода задач.

Евклидова задача Штейнера состоит в соединении множества точек на плоскости так, чтобы сумма длин отрезков была минимальна.

Линейная задача Штейнера вместо евклидова расстояния между точками оперирует линейным расстоянием: d(X, Y) = |x1-x2| + |y1 – y2|. При этих условиях если через каждую точку из множества Р провести вертикальные и горизонтальные линии, то решение задачи Штейнера можно получить, рассматривая в качестве возможных точек Штейнера точки пересечения полученной сетки линий.

Линейные задачи Штейнера имеют применение при монтаже печатных схем электронных устройств и в логистике практически не используются, в отличие от евклидовых задач.

Сразу же зададимся вопросом: а может ли расположение развилок вне связываемых объектов уменьшить длину кратчайшей системы дорог? Для случая, когда четыре города расположены в углах квадрата, допустим со стороной равной 1 км, кратчайшая система дорог с разветвлением только в городах имеет длину 3, тогда как интуитивное расположение перекрестка в центре квадрата дает результирующую длину примерно 2,8.

Итак, улучшение результата возможно. Однако можно ли утверждать что 2 корня из 2 – это уже минимум? Вряд ли, по крайней мере никаких оснований для этого нет. Но зато уже видно, что в такой постановке проблема поиска кратчайшей системы дорог, связывающей все имеющиеся объекты, существенно усложняется.

Данный алгоритм в общем случае не существует. Евклидова задача Штейнера является нерешенной с вычислительной точки зрения, поскольку существующие точные алгоритмы находят решение за разумное время только при очень небольшом количестве вершин (порядка 10).

Анализ сложности: Возрастание сложности связано с потерей дискретности, поскольку расположение перекрестков уже не совпадает с самими объектами, и строго говоря, на площади в 1 кв. м. существует бесконечное количество возможных мест расположения развилок. Очевидно, что в общем случае теория графов уже не может давать достоверного результата при решении этой задачи. В настоящее время неизвестно точных и эффективных алгоритмов, решающих эту задачу в том случае, если города заданы произвольной сетью.

Постановка Задачи Штейнера

На плоскости задано N точек. Требуется соединить эти точки ломаными линиями таким образом, чтобы каждая точка была соединена с каждой и чтобы суммарная длина всех проведенных линий была минимальной

Довольно быстро было установлено, что задача достаточно сложная. В 1977 г. Р.Грехем и Д.Джонсон доказали NP – полноту этой задачи, поэтому метода нахождения точного минимума не существует даже на данный момент.

Это обстоятельство послужило стимулом для разработки многочисленных эвристических алгоритмов. Наибольший практический интерес представляет алгоритм последовательного введения дополнительных вершин в дерево Прима-Краскала.

Использование предложенного алгоритма позволяет строить деревья Штейнера, длина которых в среднем не превышает длину оптимального дерева Штейнера более чем на 0.5 процента. Временные характеристики модификаций алгоритма позволяют успешно использовать его на данном этапе построения маршрута.

Глава 3. Задача Штейнера и методы её решения

Задача Штейнера состоит в поиске минимального дерева Штейнера —кратчайшей сети, соединяющей заданный конечный набор точек плоскости.

Свое название получила в честь Якоба Штейнера (1796—1863). Для трех точек на плоскости она формулируется следующим образом: в заданном треугольнике нужно найти точку на плоскости, сумма расстояний от которой до вершин этого треугольника наименьшая.

В задаче Штейнера допускается при необходимости введение новых вершин дерева, отличных от заданных. Эти вершины называют точками Штейнера.

Хорошо известны достаточные условия: в решение могут входить промежуточные точки, и все соединения должны быть отрезками, соединяющими точки (исходные и промежуточные). В каждой промежуточной точке должны сходиться три отрезка, а в исходных точках – более трех. Угол между отрезками, сходящимися в данной точке, не должен быть меньше 120°. Основное внимание следует уделять поиску абсолютно минимальной сети среди всех имеющихся сетей, использующих фиксированное конечное множество N точек плоскости. Существует несколько подходов к указанной проблеме Штейнера.

Один из них предполагает поиск абсолютно минимальной сети в классе сетей, все вершины которых принадлежат N. В этом случае минимальная сеть является деревом (не имеет циклов), которое называется минимальным деревом. Э. Гилберт и Г. Поллак показали, что дерево Штейнера не более чем на 13,4% короче минимального остовного дерева.

Однако, как было доказано группой ученых, эта проблема является NP трудной. Это означает, что нахождение ее решения за полиномиальное время затруднительно. По мнению М. Херринга, текущим наиболее оптимальным и интересным алгоритмом, решающим задачу Штейнера, является алгоритм GeoSteiner до 2 000 точек, реализованный Д. Вармом, П. Винтером и М. Захариасеном.

Наиболее простой задачей является задача нахождения точки Штейнера для трех точек (трехточечная задача Штейнера). Существуют следующие варианты решения данной задачи.

1. Если каждый из углов между отрезками, соединяющий точку Штейнера с каждой из заданныхточек (вершин треугольника), составляет 120°, тогда точка Штейнера либо лежит внутри данного треугольника, либо совпадает с одной из этих вершин.

2. Угол, образованный отрезками, соединяющими эту точку с другими заданными, равен или больше 120°. Если же один из углов треугольника с вершинами в этих точках больше или равен 120°, то сеть состоит из 2 ребер (сторон этого угла). Если все углы меньше 120°, т.е. точка Штейнера состоит из 3 ребер, соединяющих дополнительную точку Штейнера с тремя вершинами.

Указанный алгоритм решения трехточечной задачи Штейнера рассмотрен на примере строительства нового дорожного участка автомобильной дороги «Автомобильная дорога Р-16 Тюхиничи — Высокое — граница Республики Польша (Песчатка), км20,000 —км 41,000»

Глава 4. Задачи

Задача 1

Для трех коллинеарных терминалов решением задачи будет отрезок, соединяющий два крайних терминала.

Как изменится решение, если терминалы слегка «подвигать», чтобы они стали неколлинеарными? — Интуитивно ожидаемый ответ: решение должно слегка измениться, т.е. из отрезка превратиться в ломаную, соединяющую крайние терминалы с «внутренним». Пусть этим внутренним терминалом является P2

Увеличим величину его отклонения от прямой P3 т.е.уменьшим величину угла P1P2P3. Можно ли ожидать, что минимальное дерево Штейнера останется совпадающим с ломаной P1P2P3 — Оказывается, что это заключение справедливо только до определенного значения угла P1P2P3, а именно до тех пор, пока он остается

Что происходит с решением при переходе этого значения? — Оказывается минимум длины обеспечивается теперь принципиально иной конфигурацией: не ломаной P1P2P3, а трехзвенной конструкцией, в которой терминалы связываются посредством некоторой вспомогательной, «узловой», точки S, расположенной внутри терминального треугольника.

Эта точка называется точкой Ферма-Торричелли треугольника P1P2P3 и она формально определяется именно как точка треугольника, обеспечивающая минимальное значение величин.

|P1P| + |P2P| + |P3P|

Где P — произвольная точка треугольника.

Выяснение свойств точки Ферма-Торричелли и способы ее нахождения излагаются в следующих пунктах. А пока, забегая вперед, ответим на ожидаемый вопрос: если добавление одной дополнительной точки оптимизирует решение построения кратчайшей сети, соединяющей три терминала, то, возможно, добавление двух (или более) дополнительных даст еще бóльшую выгоду? — Ответ оказывается отрицательным.

Задача 2

Для решения задачи строительства автомобильной дороги «Автомобильная дорога Р-16 Тюхиничи — Высокое — граница Республики Польша (Песчатка), км20,000 —км41,000» использовалась трехточечная задача Штейнера. Часть автомобильной дороги Р-16 «Граница Республики Польша (Песчатка) – Волковичи» уже реконструирована. Поэтому необходимо было соединить сетью дорог только три точки: д. Волковичи, г. Высокое, автомобильная дорога Р-16 Тюхиничи. Строение местного рельефа определяется расположением ее в пределах Восточно-Европейской равнины. Рельеф территории представляет собой слабо приподнятую, слегка волнистую, наклоненную на север и запад равнину. Такие свойства территории позволяют рассматривать ее как однородную.

В настоящий момент населенные пункты соединены между собой дорогой, суммарная длина которой составляет 8,8 км, по данным карт Яндекс. Карты. Предлагается рассмотреть возможность соединения указанных населенных пунктов другой, более короткой дорогой.

Так как все углы треугольника АВС, вершины которого находятся в данных населенных пунктах, меньше 120, то точка Штейнера лежит внутри треугольника ABC. Для ее нахождения воспользуемся следующим алгоритмом.

Шаг 1. На одной из сторон треугольника ABC построим равносторонний треугольник. Например, возьмем сторону BC и строим равносторонний треугольник BCD, причем точка A не принадлежит этому треугольнику.

Шаг 2. Опишем вокруг треугольника BCD окружность.

Шаг 3. Найдем точку Штейнера (Т) как точку пересечения описанной окружности с отрезком AD.

Для соединения автомобильной дорогой д. Волковичи, г. Высокое и автомобильная дорога Р-16 Тюхиничи взяли следующие точки: д. Волковичи(точка K), д. Оберовщина (точка M), поворот на д. Мыкшицы со стороны г.

Высокое (В), г. Высокое (точка А) и автомобильная дорога Р-16 Тюхиничи (С).

При нахождении точки Штейнера треугольника АВС были выполнены следующие построения:

Шаг 1. На стороне ВС треугольника ABC построили равносторонний треугольник, причем точка A не принадлежит этому треугольнику. Для этого провели дуги радиуса ВС из каждой точки В и С. Точку пересечения дуг обозначили точкой D. Получился треугольник BCD.

Шаг 2. Для нахождения центра окружности, проходящейчерез точки B, С и D построили серединные перпендикуляры сторон треугольника ВСD. Точкапересечения данных серединных перпендикуляров О – центр искомой окружности.

Шаг 3. Вокруг треугольника BCD описали окружность с центром в точке О и радиусом ОD (Рис. 1)

Шаг 4. Для нахождения точки Штейнера нашли точку пересечения

описанной окружности с отрезком AD. Искомая точка Т является точкой Штейнера (Рис. 2).

Шаг 5. Соединив точки В, Т и С получим минимальный путь между населенными пунктами д. Оберовщина, г. Высокое и автомобильная дорога Р-16 Тюхиничи.

Так как часть дороги ТС проходит на местности по пойме реки Пульва и является заболоченной местностью, то строительство такой дороги является нецелесообразным. Изменим направление оптимальногопути без изменения его протяженности.

Шаг 6. Проведем через точки В и С прямую – ось симметрии.

Шаг 7. Относительно оси симметрии ВС построим точку Т` симметричную точке Т. Длина ломанной ВТ`С равна длине ломанной ВТС (Рис. 3).

На местности отрезок ВТ` является частью существующей дороги, соединяющей д. Оберовщина и д. Мыкшицы.

В треугольнике KMB градусная мера угла KMB оказалась равна больше 120, поэтому точка Штейнера при совпадет с точкой M, и кратчайший путь будет представлять собой ломанную KMB. Изменим направление пути, не изменяя длину пути. Для этого построим точку Т“ симметричную точке Mотносительно прямой BK.

Соединив последовательно точки K, Т“, B, Т` и С получим необходимый минимальный путь между точками: д. Волковичи, г. Высокое, автомобильная дорога Р-16 Тюхиничи (Рис. 4)

Заключение

Данная работа помогла понять мне, что такое сети Штейнера. Дала понимание, как можно решать задачи с использованием сетей, дерева, а также с алгоритмом Штейнера. Научная работа помогла разобраться в задачах и различных методах решения их. Работа очень познавательна, интересна и полезна ученикам средней школы.

Данную работу можно использовать для проведения кружков и дополнительных занятий. Такие задания развивают логическое мышление, могут встречаться в олимпиадах.

Источники

https://ru.wikipedia.org/

http://vmath.ru/

https://dic.academic.ru/

https://testmf.grsu.by/

https://habr.com

http://lmatrix.ru

Просмотров работы: 269

Представим себе такую ситуацию: некая телефонная компании Steiner Telephone Company подсчитала, что можно сэкономить несколько миллионов долларов, если удастся найти кратчайшую из возможных сетей телефонных линий, соединяющих 100 населённых пунктов. Чтобы решить эту задачу, компания заключила контракт с компьютерной компанией Cavalieri Computer Company, располагающей самыми быстродействующими в мире компьютерами и самыми квалифицированными программистами. Через неделю Cavalieri продемонстрировала в действии программу для решения поставленной задачи. Программа действительно нашла кратчайшую сеть для 15 абонентов всего за один час. Steiner заплатила 1000 долл. за программу и пообещала платить по одному центу за каждую секунду машинного времени, которое потребуется компьютеру для полного решения задачи. К тому времени, когда компьютер завершил вычисления для всех 100 абонентов, телефонная компания задолжала компьютерной многие триллионы долларов, а сами абоненты переместились на много километров со своих мест — либо по своему желанию, либо по причине континентального дрейфа!

Может быть, Cavalieri продала Steiner неправильную программу? Попробуем разобраться. Здесь мы столкнулись с одним из примеров так называемой задачи Штейнера, в которой требуется найти кратчайшую сеть прямолинейных отрезков, связывающих между собой заданное множество точек.

Задачу Штейнера невозможно решить, просто рисуя линии между заданными точками. Для решения необходимо добавить новые точки, называемые точками Штейнера и служащие в качестве узлов искомой кратчайшей сети. Чтобы определить количество и расположение точек Штейнера, математики и программисты разработали специальные алгоритмы. Однако даже лучшие из этих алгоритмов, выполняющиеся на самых быстродействующих компьютерах, не в состоянии дать решение для большого множества заданных точек за реально приемлемое время. Более того, задача Штейнера принадлежит к классу задач, для которых, по мнению многих современных исследователей, эффективные алгоритмы, по-видимому, так никогда и не будут найдены. Поэтому компьютерная компания Cavalieri должна быть реабилитирована.

В то же время фирма Cavalieri могла бы разработать практически полезную программу, которая находила бы сеть, несколько более длинную по сравнению с кратчайшей. Приближённые методы решения довольно часто применяются в различных приложениях задачи поиска кратчайших сетей. Среди них — конструирование интегральных электронных схем, построение эволюционного дерева для группы биологических видов и минимизация расхода материалов на создание сетей телефонных линий, трубопроводов и шоссейных дорог.

 

 

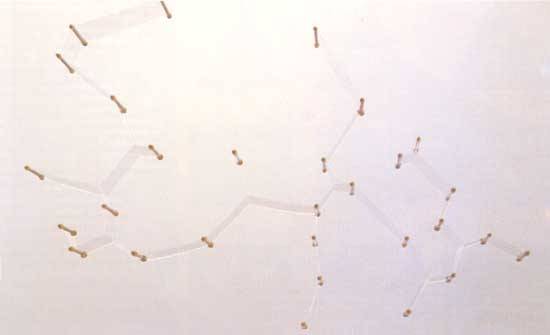
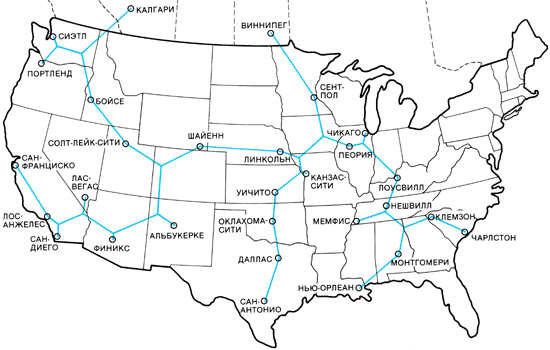
Компьютер из мыльной плёнки (вверху) соревнуется с электронным компьютером (внизу), отыскивая кратчайшую сеть, связывающую между собой 29 городов. Компьютер из мыльной плёнки, в котором расположение штырьков моделирует географию городов, минимизирует длину плёночных соединений в локальной области. Он даёт короткую сеть, но необязательно кратчайшую. Электронный компьютер реализует алгоритм Э. Кокейна и Д. Хьюджилла из Университета Виктории. Алгоритм гарантирует кратчайшую сеть. Задача с 29 точками на сегодня близка к пределу вычислительных возможностей.

В общей форме задача Штейнера была впервые сформулирована в статье Милоша Кёсслера и Войцеха Ярника, опубликованной в 1934 году, однако сама эта проблема не приобрела широкой известности вплоть до 1941 года, когда Рихард Курант и Герберт Е. Роббинс включили её в свою книгу «Что такое математика?». Курант и Роббинс связали эту задачу с исследованиями Якоба Штейнера, немецкого математика XIX столетия, работавшего в Берлинском университете. Работа Штейнера была посвящена поиску одной точки, сумма расстояний от которой до всех точек заданного множества была бы минимальной. Однако ещё в 1640 году впервые была поставлена задача, являющаяся частным случаем обеих описанных задач — той, над которой работал Штейнер, и той, которая носит его имя: найти точку P, сумма расстояний от которой до каждой из трёх заданных точек минимальна. Эванджелиста Торричелли и Бонавентура Кавальери независимо друг от друга решили эту задачу. Торричелли и Кавальери доказали, чту суммарное расстояние минимально, когда все сопряжённые углы в точке P больше или равны 120°.

Зная, что углы с вершинами в точке P должны быть не меньше 120°, Торричелли и Кавальери придумали процедуру геометрического построения для нахождения точки P (см. рис.).

 

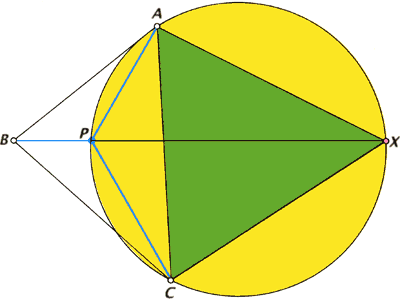
Кратчайшая сеть для трёх точек A, B и C. На самой длинной стороне треугольника ABC строится равносторонний треугольник ACX (зелёный цвет), и вокруг него описывается окружность (жёлтый цвет). На пересечении её с отрезком BX находится точка P, называемая точкой Штейнера. Отрезки AP, BP и CP образуют три сопряжённых угла по 120° и кратчайшую сеть, причём их суммарная длина равна BX.

Нужно провести отрезки прямых, соединяющие исходные точки (назовем их A, B и C), с точкой в вершине наибольшего угла (скажем, B). Если угол B больше или равен 120°, то искомая точка P совпадает с точкой B. Другими словами, кратчайшая сеть в данном случае представляет собой просто два отрезка прямых между точками A и B и точками B и C. Если угол в точке B меньше 120°, то точка P должна находиться где-то внутри треугольника. Чтобы найти её, следует построить равносторонний треугольник с основанием на самой большой стороне треугольника ABC, а именно на отрезке AC. Третья вершина равностороннего треугольника (обозначим её X) находится на противоположной стороне от точки B относительно AC. Вокруг построенного равностороннего треугольника описываем окружность и проводим прямую, соединяющую точки B и X. Точка P будет на пересечении этой прямой и окружности. Соединив точки A, B и C с точкой P, мы получаем три угла, в точности равные 120° каждый, и искомую кратчайшую сеть. Более того, длина отрезка BX оказывается равной длине кратчайшей сети. В дальнейшем в нашей статье мы будем называть точку X замещающей точкой, поскольку замена точек A и C одной точкой X не изменяет длину сети.

Задача с тремя точками и задача Штейнера для многих точек имеют много общих свойств. Их решения, имеющие вид дерева, характерны тем, что при удалении любого отрезка из кратчайшей сети мы должны будем исключить одну из заданных точек. Другими словами, мы не можем пройти по сети из какой-либо заданной точки и вернуться в неё, без того чтобы не пройти те или иные отрезки повторно. По этой причине графические решения задачи с тремя точками и задачи со многими точками называются деревьями Штейнера. Отрезки прямых называются рёбрами, а точки, роль которых аналогична точке P и которые нужно добавить для построения дерева, называются точками Штейнера.

Задача Штейнера для трёх точек даёт также некоторую информацию о геометрии кратчайших деревьев Штейнера. Во-первых, каждый угол равен 120° или больше, а это означает, что каждая точка соединяется с остальным деревом не более чем тремя рёбрами. Во-вторых, в каждой точке Штейнера сходятся ровно три ребра, образуя друг с другом углы, в точности равные 120°. В-третьих, число рёбер дерева всегда на единицу меньше суммарного числа заданных исходных точек и точек Штейнера. И наконец, последнее свойство: поскольку в каждой точке Штейнера сходятся ровно три ребра и по крайней мере одно ребро должно касаться каждой из заданного множества точек, максимальное число точек Штейнера для любой задачи на две меньше, чем число заданных исходных точек.

Задача поиска сети для точек, расположенных в вершинах равностороннего треугольника, прямоугольника и «лестницы» имеет различные решения. В случаях a, d и g точки соединяются без дополнительных промежуточных точек и такое решение называется минимальным остовным деревом. Деревья Штейнера, полученные путём добавления узловых точек, показаны для случаев b, c, e, f, h и i. Только c, f и i являются кратчайшими деревьями Штейнера, или кратчайшими сетями. Числа под каждым решением указывают примерную суммарную длину отрезков сети.

При одном и том же количестве и расположении исходных точек можно построить много различных деревьев Штейнера, удовлетворяющих перечисленным выше условиям. Некоторые из этих деревьев, называемые локально минимальными решениями, невозможно сократить за счёт мелкомасштабных изменений, таких как небольшое перемещение ребра или расщепление точки Штейнера. Однако не всякое локально минимальное дерево Штейнера даёт кратчайшее из возможных решений задачи. Для того чтобы преобразовать сеть в кратчайшее дерево, называемое глобально минимальным деревом Штейнера, могут потребоваться крупномасштабные перемещения точек Штейнера.

Рассмотрим для примера множество исходных точек, образующих четыре угла прямоугольника, размерами три метра на четыре. Решения содержат две точки Штейнера, которые можно расположить двумя различными способами. При каждом расположении мы получаем дерево Штейнера, причём в каждой точке Штейнера сходятся по три ребра под углом 120°. Если точки Штейнера расположить на линии, параллельной поперечной стороне прямоугольника, то получается локально минимальное дерево Штейнера длиной 9,9 м. Если расположить точки Штейнера на линии, параллельной продольной стороне прямоугольника, то получится глобально минимальное дерево длиной 9,2 м.

Действуя методом полного перебора, можно найти кратчайшую сеть путём построения всех возможных локально минимальных деревьев Штейнера, вычислением их длины и выбором кратчайшего. Но поскольку расположение точек Штейнера неоднозначно, возникает сомнение в том, что вычислить все локально минимальные деревья Штейнера можно за конечное время. З. Мелзак из Университета Британской Колумбии сумел преодолеть это затруднение и составил первый алгоритм для решения задачи Штейнера.

В алгоритме Мелзака рассматриваются многие возможные соединения между заданными точками и многие возможные расположения точек Штейнера. Алгоритм можно условно разбить на две части. В первой его части множество исходных точек просто подразделяется на всевозможные подмножества. Во второй части для каждого такого подмножества создается ряд возможных деревьев Штейнера с использованием построения, аналогичного тому, которое мы применили к задаче с тремя точками.

Так же как и для трёх точек, вместо двух исходных точек можно подставить одну заменяющую их точку, не изменяя результата (длины сети) решения. Однако в общем случае алгоритм должен угадать, какую пару следует заменить, и поэтому он перебирает все возможные пары. Более того, заменяющая точка может размещаться по любую сторону от прямой, соединяющей две заменяемые точки, поскольку равносторонний треугольник, используемый при построении, может быть ориентирован в одном из двух направлений. После того как одна из точек в подмножестве заменена одной из двух возможных заменяющих точек, на каждом последующем шаге алгоритма замещаются либо две другие исходные точки, либо одна исходная и одна замещающая, либо две замещающие другой замещающей точкой; и так до тех пор, пока всё подмножество не будет сведено к трём точкам.

Как только для этих трёх точек найдена точка Штейнера, алгоритм начинает работать в обратном направлении, пытаясь определить точку Штейнера, соответствующую каждой замещающей точке (см. рис.).

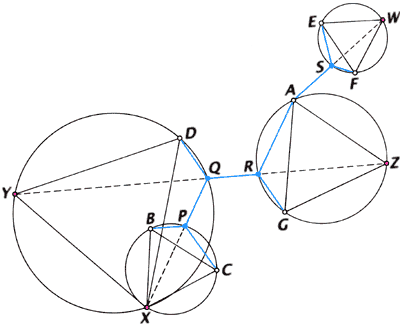
Алгоритм Мелзака разбивает задачу поиска кратчайшей сети на подзадачи. Точка A подходит для разбиения задачи на подзадачи из 3 и 5 точек. Чтобы построить возможные деревья Штейнера для 5 точек, пару точек (например, B и C) можно заменить одной (здесь X), построив равносторонний треугольник с основанием BC. Теперь задача сведена к 4 точкам: X, D, G и A. Пару точек опять можно заменить — сначала D и X на Y, а потом G и A на Z. Вокруг каждого из полученных равносторонних треугольников (XDY, AGZ и BCX) описываем окружности. Точки Q и R, в которых прямая YZ пересекает две окружности, — это точки Штейнера, а пересечение прямой XQ с третьей окружностью определяет точку Штейнера P. Поскольку невозможно заранее предугадать наилучшее разбиение на подзадачи и группировки на пары, необходимо рассмотреть все варианты, чтобы найти кратчайшее дерево.

Попытка может окончиться неудачей, поскольку на расположение точек Штейнера накладываются противоречащие друг другу ограничения. Однако успешная попытка приводит к возникновению дерева Штейнера, соединяющего каждую исходную точку подмножества с деревом одним ребром. Рассмотрев, таким образом, все замещающие последовательности, алгоритм выбирает кратчайшее из этих деревьев Штейнера для подмножества. Комбинируя между собой всевозможными способами кратчайшие деревья Штейнера для подмножеств так, чтобы охватить исходное множество точек, можно построить всевозможные локально минимальные деревья Штейнера и определить геометрию кратчайшей сети.

Алгоритм Мелзака может потребовать колоссального времени даже для небольших задач, поскольку в нём рассматривается очень много вариантов. Например, задача для 10 точек может быть распределена на 512 подмножеств исходных точек. И хотя двухточечные подмножества не требуют большого объёма работы, каждое из 45 подмножеств с восемью точками имеет два миллиона замещающих последовательностей. Кроме того, существуют ещё более 18 000 способов объединить эти подмножества в деревья.

 Разумеется, исследователи нашли более эффективные пути организации вычислений и сумели повысить быстродействие алгоритма. Вместо того чтобы рассматривать геометрию задачи, они фокусируют внимание на возможных конфигурациях соединений в сети, т.е. на её топологии. Топология указывает, какие точки соединены друг с другом, а не действительные расположения точек Штейнера. Приняв определённую топологию, можно найти соответствующую замещающую цепочку относительно быстро. При такой организации процесса скорость вычисления кратчайших деревьев Штейнера для подмножеств немного возрастает. Например, для подмножества из 8 точек алгоритм должен рассмотреть лишь около 10 000 различных топологий вместо двух миллионов различных последовательностей замещения.

Так как количество возможных топологий быстро возрастает с размером подмножества, задачи Штейнера могут стать менее трудоёмкими лишь в том случае, если требуется рассматривать только очень небольшие подмножества исходного множества точек. Эксперименты, проведённые с алгоритмом Мелзака, показали, что кратчайшая сеть для числа случайных точек больше 6 обычно может быть разбита на кратчайшие сети для меньших наборов точек. Однако, рассмотрев специальные конфигурации точек, называемые лестницами, Ф. Чанг из фирмы Bell Communications Research совместно с одним из авторов настоящей статьи (Грэмом) показал, что существуют бесконечно большие множества точек, для которых кратчайшее дерево Штейнера невозможно расчленить. Лестница — это конфигурация, в которой исходные точки расположены равномерно вдоль двух параллельных линий. Для этой весьма частной задачи Штейнера было найдено общее решение. Оно показало, что число точек Штейнера в кратчайшем дереве Штейнера для лестницы с нечётным количеством «ступенек» максимально: оно равно числу исходных точек минус 2. Такое дерево Штейнера невозможно расчленить, потому что для каждой точки Штейнера нужно одновременно учитывать все исходные точки. Следовательно, не всегда можно сократить размер подмножеств, рассматриваемых алгоритмом Мелзака.

Некоторым исследователям удалось улучшить эффективность алгоритмов по сравнению с алгоритмом Мелзака за счёт применения более тонких способов, позволяющих уменьшить объём вычислений (см. рис.).

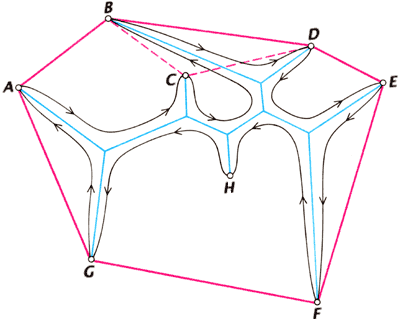
Методы усечения повышают эффективность алгоритмов поиска кратчайших сетей. Один из приёмов усечения, или исключения, возможных сетей (изобретённый Кокейном) заключается в том, чтобы рассмотреть порядок, в котором резиновое кольцо (красный цвет), натянутое вокруг заданного множества точек, касается их. Резинка касается всех точек, за исключением C и H, но C можно включить в последовательность, поскольку угол, образуемый точкой C с двумя соседними точками, находящимися в контакте с резинкой, не меньше 120°. Тогда порядок точек будет ABCDEFG. Непрерывный путь (чёрный цвет), проходящий вдоль возможной сети (синий цвет), касается точек в порядке ACBDEFHG. Поскольку B и C здесь переставлены местами по отношению к последовательности, образованной резинкой, эту сеть можно исключить из рассмотрения.

В их алгоритмах производится усечение вычислительной процедуры, т.е. прекращаются те ветви вычисления, которые заведомо должны привести к сравнительно длинным сетям. Новые методы усечения действительно значительно сокращают объём вычислений. Программы, основанные на алгоритме Мелзака, как, скажем, программа Э. Кокейна из Университета Виктории, написанная в 1969 году, могли решить любую задачу для 9 точек и некоторые задачи для 12 точек приблизительно за полчаса. Программа же, недавно написанная Кокейном и его коллегой из Университета Виктории Д. Хьюджиллом, использует мощный метод усечения, изобретённый Р. Винтером из Копенгагенского университета. Эта программа смогла решить все задачи для 17 точек и большинство случайно сгенерированных задач для 30 точек всего за несколько минут. Метод усечения Винтера оказался настолько удачным, что благодаря устранению большинства возможных топологий, основной объём вычислительной работы связан с комбинированием решений, полученных для отдельных подмножеств.

 Однако для всех этих программ время решения задачи может сильно зависеть от геометрии и от количества точек. Более того, время вычислений даже для самых изощрённых алгоритмов растёт по экспоненциальному закону с ростом числа точек, и задачи Штейнера для 100 точек остаются практически неразрешимыми. Будет ли когда-нибудь найден эффективный алгоритм, позволяющий решать большие задачи Штейнера?

Прогресс, достигнутый в теории вычислительной математики, убедил большинство исследователей, что существующие алгоритмы решения задачи Штейнера практически невозможно улучшить. В этой теории каждой задаче сопоставляется определённый размер. Для каждого конкретного случая задачи Штейнера таким естественным размером является число заданных исходных точек. Затем рассматривается количество элементарных компьютерных операций — таких как сложение, вычитание и умножение, — которое может потребоваться алгоритму для решения какого-то частного случая задачи определённого размера. Поскольку различные частные случаи одного и того же размера могут потребовать различного количества операций, следует рассматривать максимальное количество операций как функцию размера задачи. Если число операций растет с размером задачи (n) пропорционально некоторой степени размера, например, как в выражениях n², 5n или 6n + n¹⁰, то процедура решения называется алгоритмом с полиномиальным временем, или просто полиномиальным алгоритмом. Такие алгоритмы считаются эффективными, по крайней мере в теоретическом смысле. Если же количество операций возрастает экспоненциально с размером задачи, как, например, в случаях 2ⁿ, 5ⁿ или 3n²·4ⁿ, процедура решения называется алгоритмом с экспоненциальным временем или просто экспоненциальным алгоритмом.

Хотя для очень маленьких задач и полиномиальные, и экспоненциальные алгоритмы достаточно практичны, для больших задач время решения у экспоненциальных алгоритмов настолько велико, что практически они оказываются безнадёжными (см. H. Lewis, C. Papadimitriou. The Efficiency of Algorithms, Scientific American, January, 1978). Для достаточно больших задач полиномиальный алгоритм, выполняющийся даже на самой медленной машине, даёт решение всё-таки значительно быстрее, чем экспоненциальный алгоритм, выполняющийся на суперкомпьютере.

Хотя для задачи Штейнера были найдены экспоненциальные алгоритмы (например, алгоритм Мелзака), ни одного полиномиального алгоритма найти для неё не удалось. И шансы на то, что эффективный алгоритм будет когда-нибудь найден, очень малы. В 1971 году С. Кук из Университета в Торонто доказал, что если будет найден полиномиальный алгоритм для любой задачи, принадлежащей классу труднорешаемых задач, называемых NP-полными, то этим же алгоритмом можно будет воспользоваться для эффективного решения широкого класса труднорешаемых задач, включая класс NP-полных. Позже один из авторов настоящей статьи (Грэм), работая совместно с М. Гэри и Д. жонсоном из AT&T Bell Laboratories, доказал, что задача Штейнера относится к классу NP-полных. Поскольку до сегодняшнего дня все NP-полные задачи оказались не по силам тысячам исследователей, то маловероятно, чтобы какая-нибудь NP-полная задача, в том числе и задачи Штейнера, была решена алгоритмом с полиномиальным временем. Однако доказательство того, что NP-полные задачи невозможно решить эффективным способом, остаётся одной из основных теоретических проблем вычислительной математики.

Хотя представляется очень маловероятным, чтобы появился эффективный алгоритм с полиномиальным временем, вычисляющий кратчайшие сети, существуют практичные алгоритмы, отыскивающие несколько более длинные сети. Одним из примеров является в этом смысле алгоритм, решающий задачу минимального остовного дерева, который отыскивает кратчайшую систему прямолинейных отрезков, связывающих данное множество точек без добавления новых. Чтобы решить эту задачу, нужно соединить две точки, ближе всего расположенные друг к другу, и на каждом последующем шаге соединять ближайшую пару точек, которую можно соединить, не образуя замкнутого пути. В конце концов, можно удалить одно ребро из замкнутого пути, и заданные исходные точки останутся всё же связанными остающимися рёбрами.

Е. Гилберт и X. Поллак высказали предположение о том, что отношение длины кратчайшего дерева Штейнера к длине минимального остовного дерева равно, самое меньшее, √3/2, т.е. дерево Штейнера не более чем на 13,4% короче минимального остовного дерева. Это отношение √3/2 возникает в простом примере, когда три исходные точки являются вершинами равностороннего треугольника. Хотя это предположение остаётся недоказанным, Чанг и один из авторов данной статьи (Грэм) показали, что дерево Штейнера короче минимального остовного дерева не более чем на 17,6%.

Минимальные остовные деревья можно часто укоротить на 3 или 4% путём тщательного выбора дополнительных точек Штейнера и небольшой переделки дерева. Одному из авторов (Берну) удалось показать, что этот неточный алгоритм до какой-то степени оправдан в теоретическом смысле, поскольку в среднем длина модифицированного дерева будет немного меньше средней длины минимального остовного дерева.

 Задачи отыскания минимального остовного дерева и кратчайшей сети решались в применении к планированию топологии телефонных сетей, трубопроводов и шоссейных дорог. Решения, приближённые или точные, помогают спланировать геометрию сети и подсчитать необходимые количества материалов. В более сложных формулировках задачи Штейнера можно учитывать такие факторы, как необходимость избежания определённых географических свойств местности, а также отыскивать кратчайшие соединения между узлами уже существующих сетей.

Возможно, наиболее важным практическим применением задачи Штейнера является конструирование интегральных электронных схем. Более короткая сеть проводящих линий на интегральной схеме требует меньшего времени зарядки-разрядки по сравнению с более длинной сетью и повышает, таким образом, быстродействие схемы. Однако задача отыскания кратчайшей сети на интегральной схеме имеет другую геометрию, так как проводники на ней обычно проходят лишь в двух направлениях — горизонтальном и вертикальном.

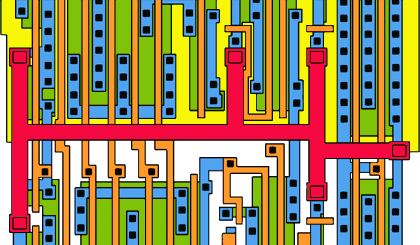
Разновидности задачи о кратчайшей сети применялись при конструировании электронных интегральных схем, с тем чтобы повысить их быстродействие. Кратчайшая сеть из вертикальных и горизонтальных проводников, связывающих множество выводов, выделена красным цветом. Здесь показаны также проводники и выводы в более глубоких слоях схемы.

Такая задача, получившая название прямоугольной задачи Штейнера, была впервые изучена в 1965 году Морисом Хэнаном из Исследовательского центра им. Томаса Уотсона корпорации IBM в Йорктаун-Хейтсе (шт. Нью-Йорк). Как и в классической задаче Штейнера, решение для прямоугольной её версии также содержит точки Штейнера и исходные точки, но рёбра встречаются в них под углом либо 90°, либо 180°. Хотя точки Штейнера могут, казалось бы, лежать повсеместно в прямоугольной задаче, так же как и в классической задаче Штейнера, Хэнан показал, что в кратчайшей прямоугольной сети на расположение точек Штейнера можно наложить определённые ограничения. Через каждую исходную точку проводятся горизонтальная и вертикальная прямые, и каждое пересечение двух линий даёт возможное положение точки Штейнера. Чтобы найти кратчайшую сеть, алгоритм может рассмотреть все подмножества возможных точек Штейнера. Однако по мере того, как число исходных точек возрастает, время решения для каждого алгоритма, осуществляющего полный перебор вариантов, растёт экспоненциально. Более тонкие, но всё же экспоненциальные алгоритмы способны решать прямоугольные задачи Штейнера размером порядка 40 точек.

Прямоугольная версия задачи поиска минимального остовного дерева может быть эффективно решена алгоритмом, выбирающим на каждом шаге кратчайшее соединение, если это соединение не образует замкнутого пути. Ф. Хванг из фирмы Bell Laboratories показал, что прямоугольное дерево Штейнера не бывает короче прямоугольного остовного дерева более чем на одну треть.

Наиболее удивительное применение задача Штейнера нашла в биологии, в одной из областей, изучающей происхождение видов. Д. Сэнкофф из Монреальского университета и ряд других исследователей сформулировали одну из версий задачи Штейнера для того, чтобы вычислять наиболее вероятные филогенетические деревья. Учёные сначала изолируют какой-то определённый белок, общий для организмов, которые они намереваются классифицировать. Затем для каждого организма они определяют последовательность аминокислот, составляющих этот белок, и устанавливают точку в позиции, определяемой числом различий между белком соответствующего организма и белком других организмов. Организмы с похожими последовательностями аминокислот определяются, таким образом, как близкие, а организмы с непохожими последовательностями — как далёкие. В кратчайшей сети для этого абстрактного множества исходных точек точки Штейнера соответствуют наиболее вероятным предкам, а рёбра представляют связь между данным организмом и предком, обладающую наименьшим числом мутаций. Однако, поскольку филогенетическая задача Штейнера не легче других задач подобного рода, эта задача — за исключением случаев с небольшим числом организмов — послужила скорее в качестве мысленного эксперимента, нежели практического инструмента исследований.

Хотя за последние годы наши познания в области алгоритмов значительно расширились, задача поиска кратчайшей сети остаётся всё такой же неприступной. Несмотря на то что формулировка этой задачи очень проста, её решения трудно поддаются анализу. Крошечное изменение геометрии задачи, кажущееся несущественным, может коренным образом изменить кратчайшую сеть, являющуюся её решением. Такая чувствительность к исходным данным делает даже периферийные вопросы, касающиеся кратчайших сетей, весьма не простыми. Задача поиска кратчайшей сети будет ещё долгие годы привлекать наше воображение.

LMatrix: Дополнительно можно почитать здесь: http://rain.ifmo.ru/cat/data/theory/unsorted/steiner-problem-2010/article.pdf

И здесь: http://www.ict.edu.ru/ft/002174/sb4_page96_105.pdf

И вот еще здесь: http://www.mathnet.ru/links/548ae346a9e9c8556678bda07a5dfbf2/dm674.pdf

Литература

1.	E. N. Gilbert and H. О. Pollak. Steiner Minimal Trees. In: SIAM Journal on Applied Mathematics, 1968, v. 16, No 1, pp. 1–29.
2.	Z. A. Melzak. Companion to Concrete Mathematics. John Wiley & Sons, Inc., 1973.
3.	Pawel Winter. An Algorithm for the Steiner Problem in the Euclidean Plane. In: Networks, 1985, v. 15, No 3, pp. 323–345.
4.	Pawel Winter. Steiner Problem in Networks: A Survey. In: Networks, 1987, v. 17, No 2, pp. 129–167.
5.	М. Гэри, Д. Джонсон. Вычислительные машины и труднорешаемые задачи. — Перев. с англ. М.: Мир, 1982.

М АРШАЛЛ У. БЕРН, РОНАЛЬД Л. ГРЭМ

⊗

Раздел – в процессе разработки. Строительные работы: 18.05.2015 – ??.??.????.

---

Дерево Штейнера

Три терминала

Геометрия

Аналитика

Четыре терминала

Фундаментальные свойства дерева Штейнера

Четыре терминала: геометрия

Четыре терминала: аналитика

Физические модели

О равновесии системы стержней

Источники