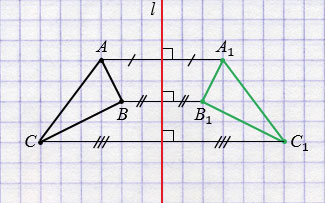Как найти точку, симметричную относительно прямой
Пусть даны некоторая прямая, заданная линейным уравнением, и точка, заданная своими координатами (x0, y0) и не лежащая на этой прямой. Требуется найти точку, которая была бы симметрична данной точке относительно данной прямой, то есть совпадала бы с ней, если плоскость мысленно согнуть пополам вдоль этой прямой.
Инструкция
Ясно, что обе точки — заданная и искомая — должны лежать на одной прямой, причем эта прямая должна быть перпендикулярна данной. Таким образом, первая часть задачи заключается в том, чтобы найти уравнение прямой, которая была бы перпендикулярна некоторой данной прямой и при этом проходила бы через данную точку.
Прямая может быть задана двумя способами. Каноническое уравнение прямой выглядит так: Ax + By + C = 0, где A, B, и C — константы. Также прямую можно определить при помощи линейной функции: y = kx + b, где k — угловой коэффициент, b — смещение.
Эти два способа взаимозаменяемы, и от любого можно перейти к другому. Если Ax + By + C = 0, то y = – (Ax + C)/B. Иными словами, в линейной функции y = kx + b угловой коэффициент k = -A/B, а смещение b = -C/B. Для поставленной задачи удобнее рассуждать, исходя из канонического уравнения прямой.
Если две прямые перпендикулярны друг другу, и уравнение первой прямой Ax + By + C = 0, то уравнение второй прямой должно выглядеть Bx – Ay + D = 0, где D — константа. Чтобы найти конкретное значение D, нужно дополнительно знать, через какую точку проходит перпендикулярная прямая. В данном случае это точка (x0, y0).
Следовательно, D должно удовлетворять равенству: Bx0 – Ay0 + D = 0, то есть D = Ay0 – Bx0.
После того как перпендикулярная прямая найдена, нужно вычислить координаты точки ее пересечения с данной. Для этого требуется решить систему линейных уравнений:
Ax + By + C = 0,
Bx – Ay + Ay0 – Bx0 = 0.
Ее решение даст числа (x1, y1), служащие координатами точки пересечения прямых.
Искомая точка должна лежать на найденной прямой, причем ее расстояние до точки пересечения должно быть равно расстоянию от точки пересечения до точки (x0, y0). Координаты точки, симметричной точке (x0, y0), можно, таким образом, найти, решив систему уравнений:
Bx – Ay + Ay0 – Bx0 = 0,
√((x1 – x0)^2 + (y1 – y0)^2 = √((x – x1)^2 + (y – y1)^2).
Но можно поступить проще. Если точки (x0, y0) и (x, y) находятся на равных расстояниях от точки (x1, y1), и все три точки лежат на одной прямой, то:
x – x1 = x1 – x0,
y – y1 = y1 – y0.
Следовательно, x = 2×1 – x0, y = 2y1 – y0. Подставив эти значения во второе уравнение первой системы и упростив выражения, легко убедиться, что правая его часть становится идентична левой. Дополнительно учитывать первое уравнение уже нет смысла, поскольку известно, что точки (x0, y0) и (x1, y1) ему удовлетворяют, а точка (x, y) заведомо лежит на той же прямой.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Координаты на плоскости
- Осевая и центральная симметрии
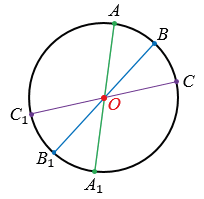
Осевая симметрия
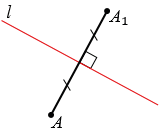
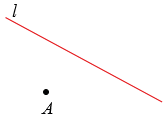
Рассмотрим построение точки, симметричной данной точке А относительно данной прямой 
Пусть дана точка А и прямая 
Точку симметричную точке А относительно прямой 



Пусть прямые 


Получаем точки А и А1, которые симметричны относительно прямой 
Также можно построить фигуры, симметричные относительно прямой.
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой 
Пусть дан треугольник АВС и прямая 
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно прямой 

Обратите внимание, любые две фигуры, симметричные относительно прямой, равны.
Если фигура имеет ось симметрии (прямая 
Центральная симметрия
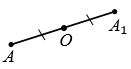
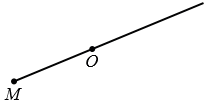
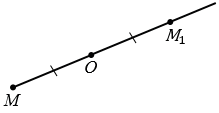
Точки М и М1 называют симметричными относительно точки О, если точка О является серединой отрезка ММ1 (смотри рисунок ниже).
Рассмотрим построение точки, симметричной данной точке М относительно данной точки О.
Пусть даны точки М и О. Точку, симметричную точке М относительно точки О, можно построит так. Проведем луч МО.
На луче МО отложим отрезок ОN , равный отрезку ОМ.
Точки М и М1, которые симметричны относительно точки О.
Также можно построить фигуры, симметричные относительно точки.
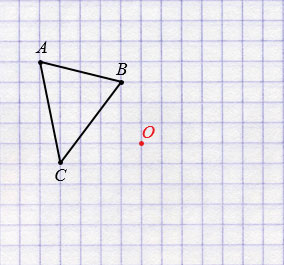
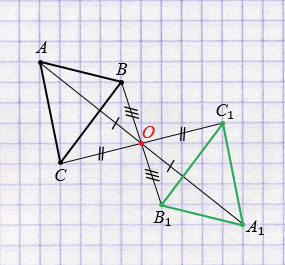
Построим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
Пусть дан треугольник АВС и точки О.
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно точки О (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.
Обратите внимание, любые две фигуры, симметричные относительно точки, равны.
Рассмотрим окружность с центром в точке О. Все точки окружности можно разбить на пары точек, симметричных относительно точки О.
В таком случае говорят, что окружность имеет центр симметрии – точку О.
Также центр симметрии имеют такие фигуры, как отрезок, прямоугольник, эллипс.
Советуем посмотреть:
Перпендикулярные прямые
Параллельные прямые
Координатная плоскость
Координаты на плоскости
Правило встречается в следующих упражнениях:
6 класс
Номер 1244,
Мерзляк, Полонский, Якир, Учебник
Номер 1249,
Мерзляк, Полонский, Якир, Учебник
Номер 1250,
Мерзляк, Полонский, Якир, Учебник
Номер 1253,
Мерзляк, Полонский, Якир, Учебник
Номер 1259,
Мерзляк, Полонский, Якир, Учебник
Номер 1262,
Мерзляк, Полонский, Якир, Учебник
Номер 1264,
Мерзляк, Полонский, Якир, Учебник
Номер 1265,
Мерзляк, Полонский, Якир, Учебник
Номер 1267,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Точка
пересечения прямой и плоскости
Постановка
задачи.
Найти точку пересечения прямой
и
плоскости
.
План
решения.
1.
Находим параметрические уравнения
прямой. Для этого полагаем
.
откуда
получаем

2.
Подставляя эти выражения для
в
уравнение плоскости и решая его
относительно t,
находим значение параметра
,
при котором происходит пересечение
прямой и плоскости.
3.
Найденное значение
подставляем
в параметрические уравнения прямой и
получаем искомые координаты точки
пересечения:

Замечание.
Если в результате решения уравнения
относительно параметра
получим
противоречие, то прямая и плоскость
параллельны (это эквивалентно условию
).
Задача
13.
Найти точку пересечения прямой и
плоскости.

Запишем
параметрические уравнения прямой.

Подставляем
в уравнение плоскости:
Откуда
координаты точки пересечения прямой и
плоскости будут
Задача 14
Симметрия
относительно прямой или плоскости
Симметрия относительно прямой
Постановка
задачи.
Найти координаты точки
,
симметричной точке
относительно
прямой
.
План
решения.
1.
Находим уравнение плоскости, которая
перпендикулярна данной прямой и проходит
через точку
.
Так плоскость перпендикулярна заданной
прямой, то в качестве ее вектора нормали
можно взять направляющий вектор прямой,
т.е.
Поэтому
уравнение плоскости будет
2.
Находим точку
пересечения
прямой
и
плоскости
(см.
задачу 13).
3.
Точка
является
серединой отрезка
,
где точка
является
точкой симметричной точке
,
поэтому
Задача
14.
Найти точку
,
симметричную точке
относительно
прямой.
.
Уравнение
плоскости, которая проходит через точку
перпендикулярно
заданной прямой будет:
Найдем
точку пересечения прямой и плоскости.

Откуда
–
точка пересечения прямой и плоскости.
является
серединой отрезка
,
поэтому



Т.е.
.
Симметрия относительно плоскости
Постановка
задачи.
Найти координаты точки
,
симметричной точке
относительно
плоскости
.
План
решения.
1.
Находим уравнение прямой, которая
перпендикулярна данной плоскости и
проходит через точку
.
Так прямая перпендикулярна заданной
плоскости, то в качестве ее направляющего
вектора можно взять вектор нормали
плоскости, т.е.
.
Поэтому
уравнение прямой будет
.
2.
Находим точку
пересечения
прямой
и
плоскости
(см.
задачу 13).
3.
Точка
является
серединой отрезка
,
где точка
является
точкой симметричной точке
,
поэтому
Задача
14.
Найти точку
,
симметричную точке
относительно
плоскости.
Уравнение
прямой, которая проходит через точку
перпендикулярно
заданной плоскости будет:

Найдем
точку пересечения прямой и плоскости.

Откуда
–
точка пересечения прямой и плоскости.
является
серединой отрезка
,
поэтому



Т.е.
.
Литература
-
Ван дер Варден
Б.Л. Алгебра. – СПб. : Лань, 2004. – 624 с. -
Кузнецов Л.А.
Сборник заданий по высшей математике
(типовые расчеты). — СПб: «Лань»,
2008.- 240 c. -
Привалов И.И.
Аналитическая геометрия. – СПб. ; М. ;
Краснодар: Лань, 2007. – 304 с. -
Цубербиллер О.Н.
Задачи и упражнения по аналитической
геометрии. – СПб.: Лань, 2003. – 336 с. -
Фаддеев Д.К.,
Соминский И.С. Задачи по высшей алгебре.
– СПб.; М. ; Краснодар : Лань, 2007. – 288 с. -
Курош А.Г. Курс
высшей алгебры. – СПб. ; М. ; Краснодар :
Лань, физматкнига, 2007. – 432 с. -
Окунев Л.Я. Высшая
алгебра.- СПб.: Лань, 2009. – 336 с.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2.5.5. Как вычислить расстояние от точки до прямой?
Как найти точку, симметричную относительно прямой?
Впереди прямая река и задача состоит в том, чтобы дойти до неё кратчайшим путём. Препятствий нет, и самым оптимальным маршрутом будет движение
по перпендикуляру. То есть, расстояние от точки до прямой – это длина перпендикулярного отрезка.
Расстояние от точки до прямой
, заданной в ортонормированном базисе
, выражается формулой
Расстояние в геометрии традиционно обозначают греческой буквой «ро», в частности: – расстояние от точки «эм» до прямой «дэ».
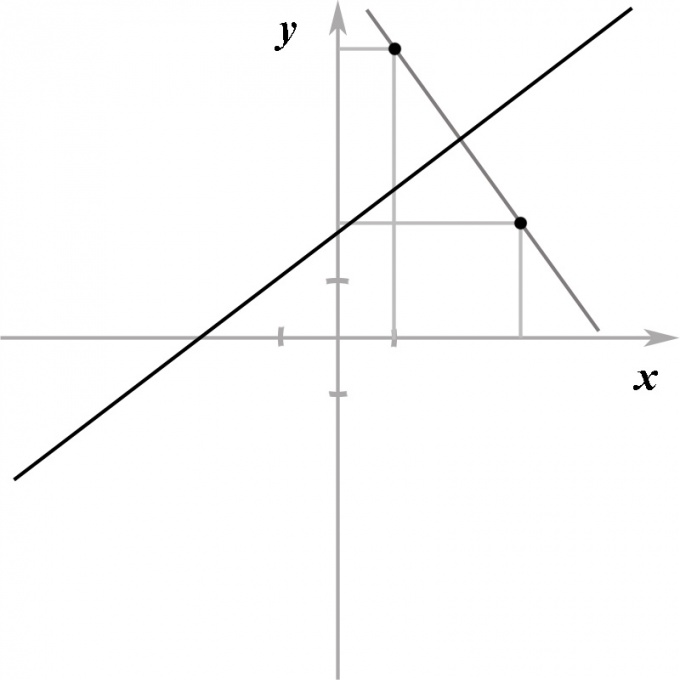
Задача 81
Найти расстояние от точки до прямой
Решение: всё что нужно, это аккуратно подставить числа в формулу и провести вычисления:
Ответ:
Найденное расстояние – это в точности длина красного отрезка:
1 см (2 клетки), то расстояние можно измерить обыкновенной линейкой.
Рассмотрим ещё одно задание по этому же чертежу:
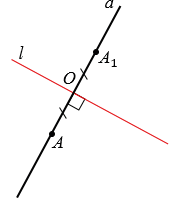
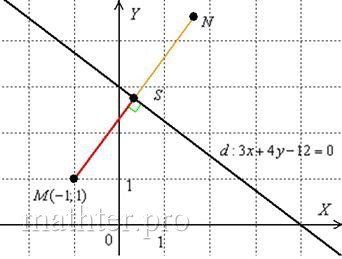
Как найти точку, симметричную относительно прямой?
Задача состоит в том, чтобы найти координаты точки , которая симметрична
точке относительно прямой
.
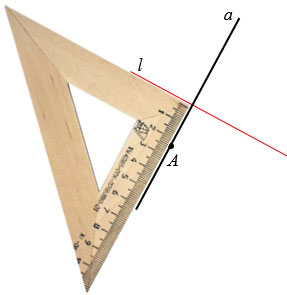
Предлагаю выполнить действия самостоятельно:
1) Находим прямую , которая
перпендикулярна прямой .
2) Находим точку пересечения прямых: .
3) Точка является серединой отрезка
. Нам известны координаты середины и одного из концов. По формулам
координат середины отрезка находим
…слишком «страшные» дроби? Обычное дело! И лёгкое, если у вас есть калькулятор-«дробовик». Проверьте, что расстояние тоже равно 2,2 единицам.


| Оглавление |
Автор: Aлeксaндр Eмeлин