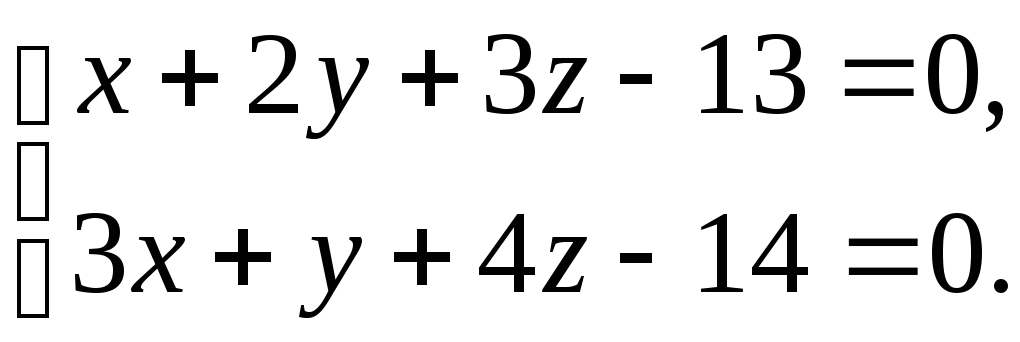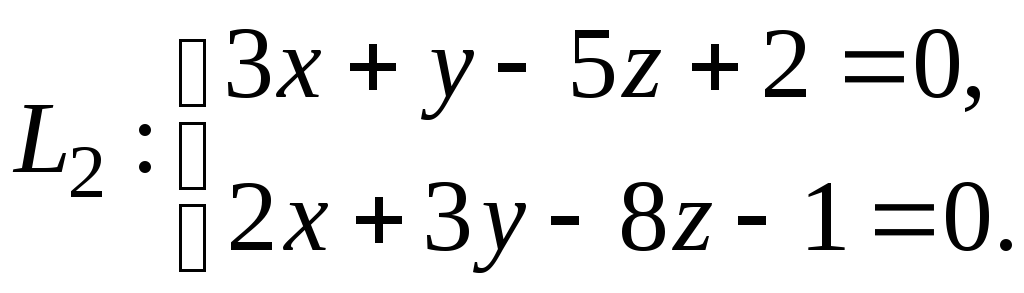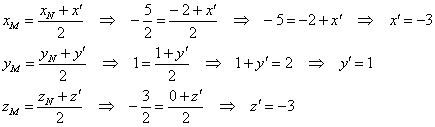Прямую в пространстве
всегда можно определить как линию
пересечения двух непараллельных
плоскостей. Если уравнение одной
плоскости
,
уравнение второй плоскости,
тогда уравнение прямой задаётся виде
здесь
неколлинеарен
.
Эти уравнения называютсяобщими
уравнениями
прямой в пространстве.
Канонические
уравнения прямой
Любой ненулевой
вектор, лежащий на данной прямой или
параллельный ей, называется направляющим
вектором этой прямой.
Если известна
точка
прямой и её направляющий вектор
,
то канонические уравнения прямой имеют
вид:
.
(9)
Параметрические
уравнения прямой
Пусть заданы
канонические уравнения прямой
.
Отсюда, получаем
параметрические уравнения прямой:

Эти уравнения
удобны при нахождении точки пересечения
прямой и плоскости.
Уравнение прямой,
проходящей через две точки
Уравнение прямой,
проходящей через две точки
и
имеет
вид:
.
Угол между прямыми
Угол между прямыми
и
равен углу между
их направляющими векторами. Следовательно,
его можно вычислить по формуле (4):

Условие параллельности
прямых:
.
Условие
перпендикулярности плоскостей:
.
Расстояние точки
от прямой
П
дана точкаи прямая
.
Из канонических
уравнений прямой известны
точка
,
принадлежащая прямой,и
её направляющий
вектор
.
Тогда расстояние точкиот прямой равно высоте параллелограмма,
построенного на векторахи
.
Следовательно,
.
Условие пересечения
прямых
Две непараллельные
прямые
,
пересекаются тогда
и только тогда, когда

Взаимное
расположение прямой и плоскости.
Пусть заданы прямая
и плоскость
.
Уголмежду ними можно найти по формуле
.
Задача 73.
Написать канонические уравнения прямой
(11)
Решение.
Для того чтобы записать канонические
уравнения прямой (9), необходимо знать
любую точку, принадлежащую прямой, и
направляющий вектор прямой.
Найдём вектор
,
параллельный данной прямой. Так как он
должен быть перпендикулярен к нормальным
векторам данных плоскостей, т. е.
,
,
то
.
Из общих уравнений
прямой имеем, что
,
.
Тогда

Так как точка
любая точка прямой, то её координаты
должны удовлетворять уравнениям прямой
и одну из них можно задать, например,,
две другие координаты найдём из системы
(11):

Отсюда,
.
Таким образом,
канонические уравнения искомой прямой
имеют вид:
или
.
Задача 74.
Вычислить расстояние между параллельными
прямыми:
и
.
Решение.
Из канонических уравнений первой прямой
известны координаты точки
,
принадлежащей прямой, и координаты
направляющего вектора.
Из канонических уравнений второй прямой
также известны координаты точкии координаты направляющего вектора
.
Расстояние между
параллельными прямыми равно расстоянию
точки
от второй прямой. Это расстояние
вычисляется по формуле
.
Найдём координаты
вектора
.
Вычислим векторное
произведение
:

Тогда
Задача 75.
Найти точку
симметричную точке
относительно прямой
.
Решение.
Запишем уравнение плоскости перпендикулярной
к данной прямой и проходящей через точку
.
В качестве её вектора нормалиможно взять направляющий вектор прямой.
Тогда.
Следовательно,
.
Найдём точку
точку
пересечения данной прямой и плоскости
П. Для этого запишем параметрические
уравнения прямой, используя уравнения
(10), получим
Далее, решим
систему, в которую входит уравнение
плоскости и параметрические уравнения
прямой:
Следовательно,
.
Пусть
точка
симметричная точкеотносительно данной прямой. Тогда точка
середина
отрезка.
Для нахождения координат точкииспользуем формулы координат середины
отрезка:
,
,
.
Получим
,
,
.
Итак,
.
Задача 76.
Написать уравнение плоскости, проходящей
через прямую
и
а) через точку
;
б) перпендикулярно
плоскости
.
Решение.
Запишем общие уравнения данной прямой.
Для этого рассмотрим два равенства:
Это означает, что
искомая плоскость принадлежит пучку
плоскостей с образующими
и её уравнение может быть записано в
виде (8):
(12)
а) Найдём
и
из условия, что плоскость проходит через
точку,
следовательно, её координаты должны
удовлетворять уравнению плоскости.
Подставим координаты точкив уравнение пучка плоскостей:
.
Найденное значение
подставим в уравнение (12). получим
уравнение искомой плоскости:
б) Найдём
и
из условия, что искомая плоскость
перпендикулярна плоскости.
Вектор нормали данной плоскости,
вектор нормали искомой плоскости(см. уравнение пучка плоскостей (12).
Два вектора
перпендикулярны тогда и только тогда,
когда их скалярное произведение равно
нулю. Следовательно,
.
Отсюда,
Подставим найденное
значение
в уравнение пучка плоскостей (12). Получим
уравнение искомой плоскости:
Задачи для
самостоятельного решения
Задача 77.
Привести к каноническому виду уравнения
прямых:
1)

Задача 78.
Написать параметрические уравнения
прямой
,
если:
1)
,
;
2),
.
Задача 79.
Написать уравнение плоскости, проходящей
через точку
перпендикулярно прямой
Задача 80.
Написать уравнения прямой, проходящей
точку
перпендикулярно плоскости
.
Задача 81.
Найти угол между прямыми:
1)
и
;
2)
и
Задача 82.
Доказать параллельность прямых:
и

Задача 83.
Доказать перпендикулярность прямых:
и
Задача 84.
Вычислить расстояние точки
от прямой:
1)
;
2).
Задача 85.
Вычислить расстояние между параллельными
прямыми:
и
.
Задача 86.
В уравнениях прямой
определить параметр
так, чтобы эта прямая пересекалась с
прямой и найти точку их пересечения.
Задача 87.
Показать, что прямая
параллельна плоскости
,
а прямаялежит в этой плоскости.
Задача 88.
Найти точку
симметричную точке
относительно плоскости
,
если:
1)
,
;
2)
,
;.
Задача 89.
Написать уравнение перпендикуляра,
опущенного из точки
на прямую
.
Задача 90.
Найти точку
симметричную точке
относительно прямой
.
ОТВЕТЫ
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
5.5.8. Как найти точку, симметричную относительно прямой?
Это полный аналог соответствующей «плоской» задачи.:
в) Решение: Найдём точку ,
симметричную точке относительно прямой
. Точка
известна, середина
отрезка известна:
, и по формулам координат середины отрезка:
Ответ:
Проверку легко выполнить с помощью тех же самых формул. Причём, устно.
И после этой бойни вам не составит труда разобраться в следующей задаче:
Задача
158
Треугольник задан координатами своих вершин . Найти высоту
и её длину.
Полное решение и ответ в конце книги.
Не забывайте выполнять схематические чертежи!
Это здОрово помогает понять алгоритм решения.


| Оглавление |
Автор: Aлeксaндр Eмeлин
Как найти точку, симметричную относительно прямой
Пусть даны некоторая прямая, заданная линейным уравнением, и точка, заданная своими координатами (x0, y0) и не лежащая на этой прямой. Требуется найти точку, которая была бы симметрична данной точке относительно данной прямой, то есть совпадала бы с ней, если плоскость мысленно согнуть пополам вдоль этой прямой.
Инструкция
Ясно, что обе точки — заданная и искомая — должны лежать на одной прямой, причем эта прямая должна быть перпендикулярна данной. Таким образом, первая часть задачи заключается в том, чтобы найти уравнение прямой, которая была бы перпендикулярна некоторой данной прямой и при этом проходила бы через данную точку.
Прямая может быть задана двумя способами. Каноническое уравнение прямой выглядит так: Ax + By + C = 0, где A, B, и C — константы. Также прямую можно определить при помощи линейной функции: y = kx + b, где k — угловой коэффициент, b — смещение.
Эти два способа взаимозаменяемы, и от любого можно перейти к другому. Если Ax + By + C = 0, то y = – (Ax + C)/B. Иными словами, в линейной функции y = kx + b угловой коэффициент k = -A/B, а смещение b = -C/B. Для поставленной задачи удобнее рассуждать, исходя из канонического уравнения прямой.
Если две прямые перпендикулярны друг другу, и уравнение первой прямой Ax + By + C = 0, то уравнение второй прямой должно выглядеть Bx – Ay + D = 0, где D — константа. Чтобы найти конкретное значение D, нужно дополнительно знать, через какую точку проходит перпендикулярная прямая. В данном случае это точка (x0, y0).
Следовательно, D должно удовлетворять равенству: Bx0 – Ay0 + D = 0, то есть D = Ay0 – Bx0.
После того как перпендикулярная прямая найдена, нужно вычислить координаты точки ее пересечения с данной. Для этого требуется решить систему линейных уравнений:
Ax + By + C = 0,
Bx – Ay + Ay0 – Bx0 = 0.
Ее решение даст числа (x1, y1), служащие координатами точки пересечения прямых.
Искомая точка должна лежать на найденной прямой, причем ее расстояние до точки пересечения должно быть равно расстоянию от точки пересечения до точки (x0, y0). Координаты точки, симметричной точке (x0, y0), можно, таким образом, найти, решив систему уравнений:
Bx – Ay + Ay0 – Bx0 = 0,
√((x1 – x0)^2 + (y1 – y0)^2 = √((x – x1)^2 + (y – y1)^2).
Но можно поступить проще. Если точки (x0, y0) и (x, y) находятся на равных расстояниях от точки (x1, y1), и все три точки лежат на одной прямой, то:
x – x1 = x1 – x0,
y – y1 = y1 – y0.
Следовательно, x = 2×1 – x0, y = 2y1 – y0. Подставив эти значения во второе уравнение первой системы и упростив выражения, легко убедиться, что правая его часть становится идентична левой. Дополнительно учитывать первое уравнение уже нет смысла, поскольку известно, что точки (x0, y0) и (x1, y1) ему удовлетворяют, а точка (x, y) заведомо лежит на той же прямой.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
плоскости
прямая
пересечения прямой и плоскости:
канонические уравнения прямой, проходящей через
точку М0(2; -4; -1) и
середину отрезка прямой
уравнение прямой, проходящей через точку М0(2; -3; -5) перпендикулярно
к плоскости
уравнение плоскости, проходящей через точку М0(1; -1; -1) перпендикулярно
к прямой
уравнение плоскости, проходящей через точку М0(1; -2; 1) перпендикулярно
к прямой
прямая
С прямая
A и D прямая
в плоскости
А и В плоскость
прямой
l и C прямая
плоскости
точки Р(2; -1; 3) на прямую
симметричную точке Р(4; 1; 6) относительно прямой
симметричную точке Р(2; -5; 7) относительно прямой,
проходящей через точки М1(5; 4; 6) и М2(-2; -17; -8).
точки Р(5; 2; -1) на плоскость
симметричную точке Р(1; 3; -4) относительно
плоскости
найти такую точку Р, сумма расстояний которой до
точек А(-1; 2; 5) и В(11; -16; 10) была бы наименьшей.
найти такую точку Р, разность расстояний которой
до точек M1(3; 2; -5), М2(8; -4; -13) была
бы наибольшей.
расстояний которой до точек А(3; -4; 7) и В(-5; -14; 17)
была бы наименьшей.
расстояний которой до точек М1(5; 2; -7) и М2(7; -25; 10) была
бы наибольшей.
движется прямолинейно и равномерно из
начального положения М0(15; -24; -16)
со скоростью v=12 в направлении
вектора s={-2; 2; 1}. Убедившись, что траектория точки
М пересекает плоскость
пересечения;
на движение точки М от М0 до Р;
движется прямолинейно и равномерно из
начального положения М0(28; -30; -27)
со скоростью v=12,5 по
перпендикуляру, опущенного из точки М0 на плоскость
уравнения движения точки М и определить:
ее траектории с этой плоскостью;
на движение точки М от М0 до Р;
движется прямолинейно и равномерно из
начального положения М0(11; -21; 20) в направлении вектора s={-1; 2; -2} со
скоростью v=12. Определить, за какое время она
пройдет отрезок своей траектории, заключенный
между параллельными плоскостями
расстояние d точки Р(1; -1; -2) от прямой
расстояние d от точки Р(2; 3; -1) до следующих прямых:
прямые
вычислить расстояние d между ними.
уравнение плоскости, проходящей через точку М1(1; 2; -3) параллельно
прямым
Доказать,
что уравнение плоскости, проходящей через точку
М0(x0; y0; z0) параллельно прямым ,
, может быть
представлено в следующем виде:
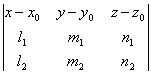
Доказать,
чо уравнение плоскости, проходящей через точки М1(x1; y1; z1) и М2(x2; y2; z2)
паралелльно прямой , может
быть представлено в следующем виде:
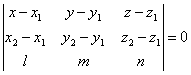
уравнение плоскости, проходящей через прямую
-2; 1).
Доказать,
что уравнение плоскости, проходящей через прямую
,
,
и точку М1(x1;
y1; z1), может быть
представлено в следующем виде:
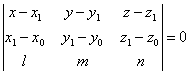
прямые
плоскости, и составить уравнение этой плоскости.
Доказать,
что если две прямые ,
пересекаются, то уравнение
плоскости, в которой они лежат, может быть
представлено в следующем виде:
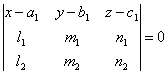
уравнение плоскости, проходящей через две
параллельные прямые
Доказать,
что уравнение плоскости, проходящей через две
параллельные прямые ,
,
и
,
,
, может быть
представлено в следующем виде:
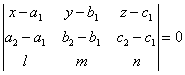
точки С(3; -4; -2) на плоскость, проходящую через
параллельные прямые
симметричную точке Р(3; -4; -6) относительно
плоскости, проходящей через М1(-6;
1; -5), М2(7; -2; -1) и М3(10; -7; 1).
симметричную точке Р(-3; 2; 5) относительно
плоскости, проходящей через прямые
уравнение плоскости, проходящей через прямую
Доказать,
что уравнение плоскости, проходящей через прямую
параллельно прямой
,
,
, может быть представлено в следующем
виде:
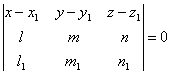
уравнение плоскости, проходящей через прямую
Доказать,
что уравнение плоскости, проходящей через прямую
,
,
перпендикулярно к
плоскости , может быть представлено в следующем
виде:
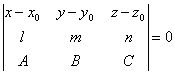
канонические уравнения прямой, которая проходит
через точку М0(3; -2; -4) параллельно плоскости
пересекает прямую
1082
проходит параллельно плоскостям
пересекает прямые
кратчайшее расстояние между двумя прямыми в
каждом из следующих случаев:
Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
I. Две точки A(xA;yA) и B(xB;yB) симметричны относительно точки O(xO;yO), если точка O является серединой отрезка AB.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
Примеры.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Решение:
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
Ответ: (13;15).
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Решение:
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
Ответ: (-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Пример
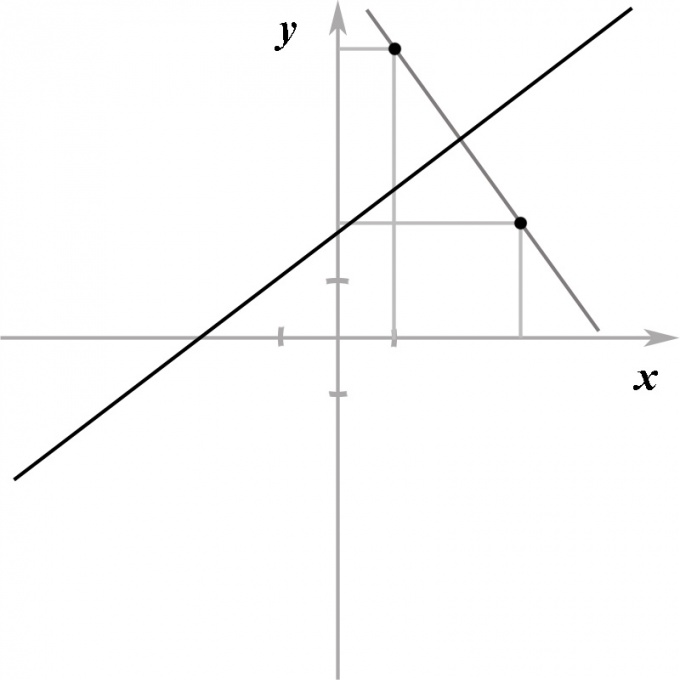
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Решение:
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
5=-0,5·(-4)+b, откуда b=3.
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Найдём координаты точки пересечения прямых:
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Ответ: (3,2;1,4).
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
| для точки A(x;y) | |
| симметрия относительно: | |
| оси Ox | A1(x;-y) |
| оси Oy | A2(-x;y) |
|
биссектрисы I и II координатных четвертей (прямой y=x) |
A3(y;x) |
|
биссектрисы I b II координатных четвертей (прямой y= -x) |
A4(-y;-x) |