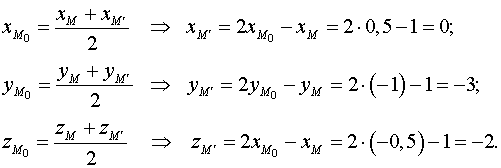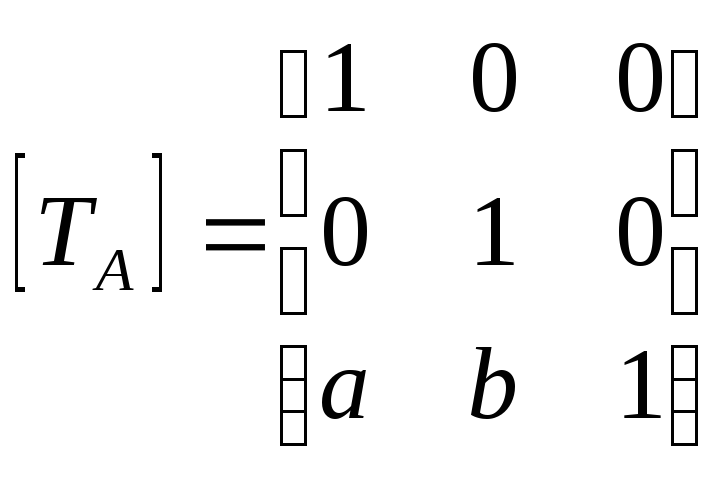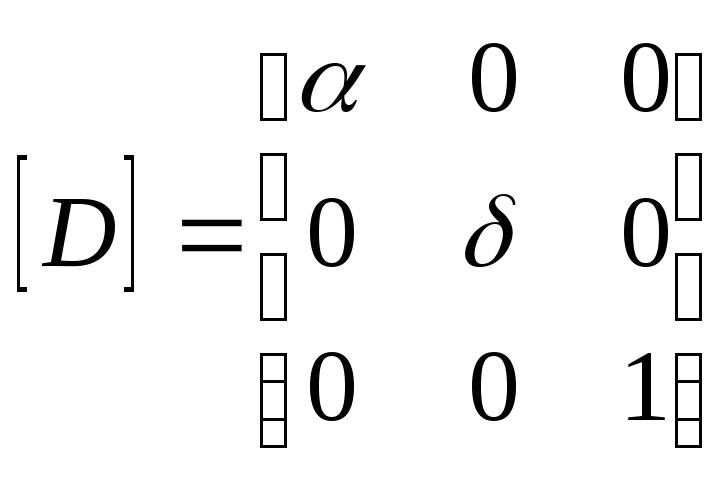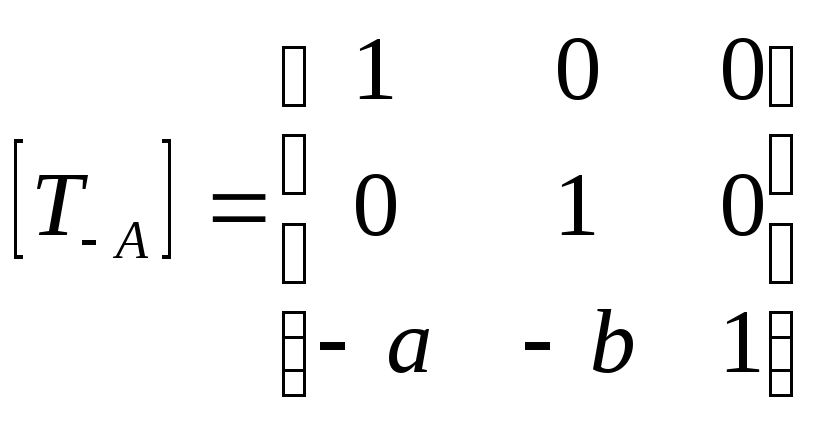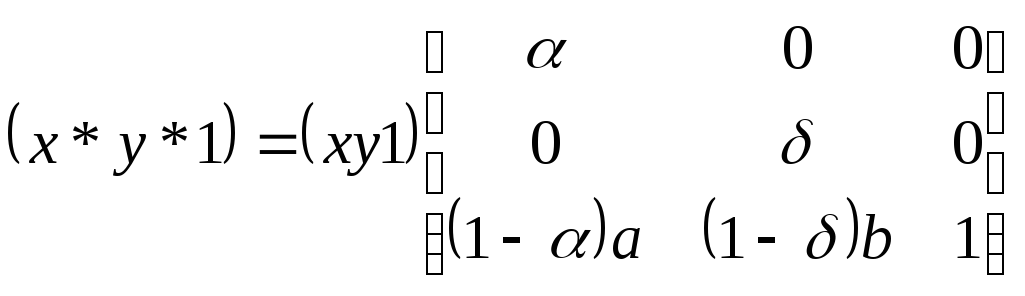Как найти точку симметричную точке относительно плоскости - Сайт, где вы сможете решить свои вопросы

Симметрия относительно плоскости

Постановка
задачи.
Найти координаты точки
,
симметричной точкеотносительно
плоскости.

План
решения.

1.
Находим уравнение прямой, которая
перпендикулярна данной плоскости и
проходит через точку
.
Так прямая перпендикулярна заданной
плоскости, то в качестве ее направляющего
вектора можно взять вектор нормали
плоскости, т.е.

Поэтому
уравнение прямой будет

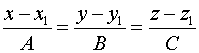
2.
Находим точку
пересечения
прямойи
плоскости(см.
задачу 13).

3.
Точка
является
серединой отрезка,
где точкаявляется
точкой симметричной точке,
поэтому

Задача
14.
Найти точку
,
симметричную точкеотносительно
плоскости.

Уравнение
прямой, которая проходит через точку
перпендикулярно
заданной плоскости будет:

Найдем
точку пересечения прямой и плоскости.

Откуда
–
точка пересечения прямой и плоскости.является
серединой отрезка,
поэтому

Т.е.
.

Однородные координаты плоскости.
Аффинные преобразования на плоскости.

Пусть М
– произвольная точка плоскости с
координатами х
и у,
вычисленными относительно заданной
прямолинейной координатной системы.
Однородными координатами этой точки
называется любая тройка одновременно
неравных нулю чисел х₁,
х₂,
х₃,
связанных с заданными числами х и у
следующими соотношениями:

При решении задач
компьютерной графики однородные
координаты обычно вводятся так:
произвольной точке М
(х,
у)
плоскости ставится в соответствие точка
Мэ
(х,
у,
1) в пространстве (рис. 8).

Рис. 8

Заметим, что
произвольная точка на прямой, соединяющей
начало координат, точку 0(0, 0, 0), с точкой
Мэ
(х,
у,
1), может быть задана тройкой чисел вида
(hx,
hy,
h).

Будем считать, что
h 
0.

Вектор с координатами
hx,
hy, является направляющим вектором
прямой, соединяющей точки 0 (0, 0, 0) и Мэ
(х,
у,
1). Эта прямая пересекает плоскость z
= 1 в точке (х, у, 1), которая однозначно
определяет точку (х, у) координатной
плоскости ху.

Тем самым между
произвольной точкой с координатами (х,
у) и множеством троек чисел вида

(hx,
hy,
h),
h

0,

устанавливается
(взаимно однозначное) соответствие,
позволяющее считать числа hx,
hy,
h
новыми координатами этой точки.

Замечание

Широко используемые
в проективной геометрии однородные
координаты позволяют эффективно
описывать так называемые несобственные
элементы (по существу те, которыми
проективная плоскость отличается от
привычной нам евклидовой плоскости).
Более подробно о новых возможностях,
предоставляемых введенными однородными
координатами, говорится в четвертом
разделе этой главы.

В проективной
геометрии для однородных координат,
принято следующее обозначение:

х : у : 1 , или, более
обще, x₁
: х₂
: х₃

(напомним, что
здесь непременно требуется, чтобы числа
х₁,
х₂,
х₃
одновременно, в нуль не обращались).

Применение
однородных координат оказывается
удобным уже при решении простейших
задач.

Рассмотрим,
например, вопросы, связанные с изменением
масштаба. Если устройство отображения
работает только с целыми числами (или
если необходимо работать только с целыми
числами), то для произвольного значения
h
(например, h
= 1) точку с однородными координатами

(0.5 0.1 2.5)

представить нельзя.
Однако при разумном выборе h
можно добиться того, чтобы координаты
этой точки были целыми числами. В
частности, при h = 10 для рассматриваемого
примера имеем

(5, 1, 25).

Рассмотрим другой
случай. Чтобы результаты преобразования
не приводили к арифметическому
переполнению, для точки с координатами
(80000 40000 1000) можно взять, например, h=0,001.
В результате получим (80 40 1).

Приведенные примеры
показывают полезность использования
однородных координат при проведении
расчетов. Однако основной целью введения
однородных координат в компьютерной
графике является их несомненное удобство
в применении к геометрическим
преобразованиям.

При помощи троек
однородных координат и матриц третьего
порядка можно описать любое аффинное
преобразование плоскости.

В самом деле, считая
h
= 1, сравним две записи: помеченную
символом * и нижеследующую, матричную:

Нетрудно заметить,
что после перемножения выражений,
стоящих в правой части последнего
соотношения, мы получим обе формулы (*)
и верное числовое равенство 1=1.

Тем самым сравниваемые
записи можно считать равносильными.

Замечание

Иногда в литературе
используется другая запись – запись
по столбцам:

Такая запись
эквивалентна приведенной выше записи
по строкам (и получается из нее
транспонированием).

Элементы произвольной
матрицы аффинного преобразования не
несут в себе явно выраженного
геометрического смысла. Поэтому чтобы
реализовать то или иное отображение,
то есть найти элементы соответствующей
матрицы по заданному геометрическому
описанию, необходимы специальные приемы.
Обычно построение этой матрицы в
соответствии со сложностью рассматриваемой
задачи и с описанными выше частными
случаями разбивают на несколько этапов.

На каждом этапе
ищется матрица, соответствующая тому
или иному из выделенных выше случаев
А, Б, В или Г, обладающих хорошо выраженными
геометрическими свойствами.

Выпишем соответствующие
матрицы третьего порядка.

А. Матрица вращения,
(rotation)

Б. Матрица растяжения
(сжатия) (dilatation)
•

В. Матрица отражения
(reflection)

Г. Матрица переноса
(translation)

Рассмотрим примеры
аффинных преобразований плоскости.

Пример 1.

Построить матрицу
поворота вокруг точки А (а, b)
на угол 
(рис. 9).

Рис. 9.

1-й шаг.
Перенос на вектор – А (-а, -b)
для совмещения центра поворота с началом
координат;

матрица
соответствующего преобразования.

2-й шаг.
Поворот на угол 

матрица
соответствующего преобразования.

3-й шаг.
Перенос на вектор А(а,b)
для возвращения центра поворота в
прежнее положение;

матрица
соответствующего преобразования.

Перемножим матрицы
в том же порядке, как они выписаны:

В
результате получим, что искомое
преобразование (в матричной записи)
будет выглядеть следующим образом:

Элементы полученной
матрицы (особенно в последней строке)
не так легко запомнить. В то же время
каждая из трех перемножаемых матриц по
геометрическому описанию соответствующего
отображения легко строится.

Пример 3

Построить матрицу
растяжения с коэффициентами растяжения

вдоль оси абсцисс и 
вдоль оси ординат и с центром в точке
А(а, b).

1-й шаг.
Перенос на вектор -А(-а, -b) для совмещения
центра растяжения с началом координат;

матрица
соответствующего преобразования.

2-й шаг.
Растяжение вдоль координатных осей с
коэффициентами 
и 
соответственно; матрица преобразования
имеет вид

3-й шаг.
Перенос на вектор А(а, b) для возвращения
центра растяжения в прежнее положение;
матрица соответствующего преобразования
–

Перемножив .матрицы
в том же порядке

получим окончательно

Замечание

Рассуждая подобным
образом, то есть разбивая предложенное
преобразование на этапы, поддерживаемые
матрицами [R],[D],[M],[T],
можно построить
матрицу любого аффинного преобразования
по его геометрическому описанию.

Рис. 8

Будем считать, что
h 
0.

Тем самым между
произвольной точкой с координатами (х,
у) и множеством троек чисел вида

(hx,
hy,
h),
h

0,

Замечание

В проективной
геометрии для однородных координат,
принято следующее обозначение:

х : у : 1 , или, более
обще, x₁
: х₂
: х₃

(напомним, что
здесь непременно требуется, чтобы числа
х₁,
х₂,
х₃
одновременно, в нуль не обращались).

Применение
однородных координат оказывается
удобным уже при решении простейших
задач.

(0.5 0.1 2.5)

(5, 1, 25).

В самом деле, считая
h
= 1, сравним две записи: помеченную
символом * и нижеследующую, матричную:

Тем самым сравниваемые
записи можно считать равносильными.

Замечание

Иногда в литературе
используется другая запись – запись
по столбцам:

Такая запись
эквивалентна приведенной выше записи
по строкам (и получается из нее
транспонированием).

Выпишем соответствующие
матрицы третьего порядка.

А. Матрица вращения,
(rotation)

Б. Матрица растяжения
(сжатия) (dilatation)
•

В. Матрица отражения
(reflection)

Г. Матрица переноса
(translation)

Рассмотрим примеры
аффинных преобразований плоскости.

Пример 1.

Построить матрицу
поворота вокруг точки А (а, b)
на угол 
(рис. 9).

Рис. 9.

1-й шаг.
Перенос на вектор – А (-а, -b)
для совмещения центра поворота с началом
координат;

матрица
соответствующего преобразования.

2-й шаг.
Поворот на угол 

матрица
соответствующего преобразования.

3-й шаг.
Перенос на вектор А(а,b)
для возвращения центра поворота в
прежнее положение;

матрица
соответствующего преобразования.

Перемножим матрицы
в том же порядке, как они выписаны:

В
результате получим, что искомое
преобразование (в матричной записи)
будет выглядеть следующим образом:

Пример 3

1-й шаг.
Перенос на вектор -А(-а, -b) для совмещения
центра растяжения с началом координат;

матрица
соответствующего преобразования.

Перемножив .матрицы
в том же порядке

получим окончательно

Замечание

Сдвиг
реализуется сложением, а масштабирование
и поворот – умножением.

Преобразование
масштабирования
(дилатация) относительно начала координат
имеет вид:

или
в матричной форме:

где
Dx,
Dy
– коэффициенты
масштабирования по осям, а

–
матрица масштабирования.

При
D
> 1-происходит расширение, при 0<=D<1-
сжатие

Преобразование
поворота
относительно начала координат имеет
вид:

или
в матричной форме:

где
φ – угол поворота, а

–
матрица поворота.

Замечание:
Столбцы
и строки матрицы поворота представляют
собой взаимно ортогональные единичные
векторы. В самом деле квадраты длин
векторов-строк равны единице:

cosφ·cosφ+sinφ·sinφ
= 1 и (-sinφ)
·(-sinφ)+cosφ·cosφ
= 1,

а
скалярное произведение векторов-строк
есть

cosφ·(-sinφ)
+ sinφ·cosφ=
0.

Так
как скалярное произведение векторов A
·B
= |A|
·|B|
·cosψ, где |A|
– длина вектора A,
|B|
– длина вектора B,
а ψ – наименьший положительный угол
между ними, то из равенства 0 скалярного
произведения двух векторов-строк длины
1 следует, что угол между ними равен 90^°.

Источник

как найти точку, симметричную Р относительнно данной плоскости????подскажите пожайлуйста ))))))))))

Ученик

(34),
закрыт

12 лет назад

Дополнен 13 лет назад

плоскость: x+2y+3z -36=0. P(6, 10, 8) , найти точку, симметричную Р относительнно данной плоскости )))

Марина Васильевна

Гений

(65102)

13 лет назад

Сначала напишем уравнения прямой, проходящей через Р, перпендикулярно данной плоскости: X=6+t; Y=10-2t; Z=8+3t. Теперь найдём точку пересечения этого перпендикуляра и плоскости. Подставляем в плоскость параметрические уравнения прямой: (6+t)+2(10+2t)+3(8+3t)-36=0; выразим t=-1 и подставим опять в параметрические уравнения прямой: X=5,Y=8,Z=5, значит точка пересечения перпендикуляра и плоскости Р0(5,8,5). Теперь заметим, что Р0-середина отрезка РР1,где Р1-искомая точка, симметричная точке Р относительно данной плоскости. Пусть Р1(X,Y.Z), тогда 5=(6+X)/2; 8=(10+Y)/2; 5=(8+Z)/2; X=4; Y=6;Z=2 . Ответ Р1(4,6,2).

Источник

Геометрия, 11 класс

Урок №5. Метод преобразований решения задач

Перечень вопросов, рассматриваемых в теме:

симметрия относительно произвольной плоскости;
понятие «метод движений» в пространстве.

Глоссарий по теме

Метод геометрических преобразований

Сущность метода геометрических преобразований при решении геометрических задач заключается в привлечении того или иного геометрического преобразования, опираясь на свойства которого, задача может быть решена.

Метод параллельного переноса

Сущность этого метода состоит в том, что наряду с данными и искомыми фигурами рассматриваются некоторые другие фигуры, которые получаются из данных или искомых фигур или их частей путём переноса на некоторый вектор.

Метод симметрии

Применение симметрии к решению задач на построение называют методом симметрии. Метод симметрии состоит в том, что наряду с данными и искомыми фигурами рассматриваются также фигуры, симметричные некоторым из них относительно некоторой точки/оси/плоскости.

Метод поворота

Идея метода поворота состоит в том, чтобы повернуть какую-либо данную или искомую фигуру около целесообразно избранного центра/оси на соответствующий угол так, чтобы облегчить проведение анализа задачи или даже непосредственно прийти к решению.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255, сс. 121-126.

Дополнительная литература:

Шарыгин И.Ф., Геометрия. 10–11 кл.: учеб. для общеобразоват. учреждений /– М.: Дрофа, 2009. – 235,: ил., ISBN 978–5–358–05346–5, сс. 178-196. Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. учреждений– М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

1. Метод геометрических преобразований

1.1. Метод параллельного переноса.

Этим путём иногда удаётся облегчить проведение анализа. Метод параллельного переноса применяют главным образом для объединения разрозненных частей фигур, когда часто построение фигуры становится затруднительным только от того, что части этой фигуры слишком удалены друг от друга, и потому трудно ввести в чертёж данные. В этих случаях какую-нибудь часть искомой фигуры переносят параллельно самой себе на такое расстояние, чтобы вновь полученная фигура могла быть построена или непосредственно, или легче, чем искомая фигура. Направление такого переноса зависит от условий задачи и должно быть выбрано так, чтобы во вновь полученную фигуру вошло, по возможности, большое количество данных.

1.2. Метод симметрии.

Применение осевой симметрии к решению задач на построение называют методом симметрии. Метод симметрии состоит в том, что наряду с данными и искомыми фигурами рассматриваются также фигуры, симметричные некоторым из них относительно некоторой оси. При удачном выборе оси и преобразуемой фигуры решение задачи может значительно облегчиться, а в некоторых случаях симметрия непосредственно даёт искомые точки.

Метод симметрии заключается в следующем. Предполагают задачу решённой и одну из данных точек (прямую или окружность) отражают в какой-нибудь известной оси; иногда эта ось проходит через известную точку. Тогда полученную симметричную точку (прямую или окружность) подчиняют тем же условиям, которым должна была удовлетворять заменённая точка (прямая или окружность). После этого получится новая задача, которую решают способами, уже нам известными. Обыкновенно, с решением этой новой задачи предложенная задача уже будет решена сама собой, и только в редких случаях придётся ещё переходить к первоначальным условиям задачи. Таким образом, метод симметрии приводит решение предложенной задачи к решению новой задачи.

1.3. Метод поворота.

Поворотом также пользуются как методом решения геометрических задач на построение. Идея метода вращения состоит в том, чтобы повернуть какую-либо данную или искомую фигуру около целесообразно избранного центра/оси на соответствующий угол так, чтобы облегчить проведение анализа задачи или даже непосредственно прийти к решению.

2. Решение задач методом преобразований

2.1. Симметрия относительно произвольной плоскости

Постановка задачи. Найти координаты точки , симметричной точке , относительно плоскости Ax + By + Cz + D = 0.

План решения.

1. Находим уравнение прямой, которая перпендикулярна данной плоскости и проходит через точку . Так как прямая перпендикулярна заданной плоскости, то в качестве ее направляющего вектора можно взять вектор нормали плоскости, т.е. .

Поэтому уравнение прямой будет:

2. Находим точку пересечения прямой и плоскости Ax + By + Cz + D = 0.

Для этого обозначим и выразим x, y, z:

Подставим x, y, z в уравнение плоскости:

найдем значение t.

Затем найдем x, y, z. Найденные координаты будут являться координатами точки .

3. Точка является серединой отрезка , где точка является точкой симметричной точке , поэтому

, , .

Задача 1. Найти точку M’, симметричную точке M относительно плоскости.

M(1, 1, 1), x + 4y + 3z + 5 = 0.

Решение:

Уравнение прямой, которая проходит через точку M перпендикулярно заданной плоскости будет:

Найдем точку пересечения прямой и плоскости.

(1 + t) + 4(1 + 4t) + 3(1 + 3t) + 5 = 0,

t = -0,5.

Откуда – точка пересечения прямой и плоскости. является серединой отрезка MM’, поэтому

2.2. Задача 2

Даны плоскость α: x + 2y – z – 2 = 0 и две точки А(1, -2, -3) и В (-1, -1, -2). Найдите на этой плоскости точку С такую, чтобы ломаная АСВ имела наименьшую длину.

Решение:

Данная плоскость пересекает оси координат в точках

M (2, 0, 0) (ось OX)

N (0, 1, 0) (ось OY)

K (0, 0, 2) (ось OZ)

Две заданные точки лежат по одну сторону от данной плоскости.

Если бы две точки лежали по разные стороны от плоскости α, то очевидно, искомой точкой С была бы точка пересечения отрезка, концами которого являются данные точки, с плоскостью α, а ломаная выродилась бы в отрезок.

Сведем нашу задачу к описанной ситуации.

Для этого найдем точку, симметричную любой из заданных относительно данной плоскости α.

Например, точке А.

Используя решение задачи 1, получим следующую последовательность действий.

Уравнение прямой, которая проходит через точку А перпендикулярно заданной плоскости будет:

Найдем точку пересечения полученной прямой и плоскости α.

(1 + t) + 2(2t – 2) – (-t– 2) – 2 = 0

t = 0,5

Откуда точка пересечения прямой, перпендикулярной плоскости α и проходящей через точку А, с плоскость α . Точка пересечения прямой и плоскости. является серединой отрезка АА’, поэтому

A'(2; 0; -4)

Теперь найдем точку пересечения отрезка A’B с плоскостью α.

Прямая A’B имеет направляющий вектор .

Уравнение прямой A’B:

Найдем точку пересечения полученной прямой и плоскости α.

3t-1+2(t-2)-(-2t-2)-2=0

7t-5=0

Таким образом, координаты искомой точки .

Ответ: .

Примеры и разбор решения заданий тренировочного модуля

1. Напишите уравнение образа плоскости 2x + 5y – z – 5 = 0 при симметрии относительно плоскости Oxz.

Решение:

Найдем координаты двух точек плоскости 2x + 5y – z – 5 = 0, лежащих в плоскости Oxz. Для этого найдем точки плоскости, принадлежащие осям координат.

OX: z = y = 0, x = 2,5 A(2,5; 0; 0)

OZ: x = y = 0, z = -5 B(0; 0; -5).

Эти точки принадлежат и образу плоскости 2x + 3y – z – 5 = 0 при симметрии относительно плоскости Oxz.

Теперь найдем точку данной плоскости, принадлежащую оси ординат.

OY: z = x = 0, y = 2,5 С(0; 1; 0).

Точка, симметричная точке С относительно плоскости Oxz, имеет координаты С'(0; -1; 0).

Теперь напишем уравнение плоскости через три полученные точки.

Оно имеет вид:

– 5x + 12.5y + 2.5z + 12.5 = 0

2x – 5y – z – 5 = 0

Ответ: 2x – 5y – z – 5 = 0

Источник

Тема: Найти точку M’ симметричную точке M, относительно плоскости. (Прочитано 87968 раз)

0 Пользователей и 1 Гость просматривают эту тему.

Проверьте моё решение,пожалуйста, а то уж больно “неприглядные” ответы получились.
Задание: найти точку M’ симметричную точке M (1,3,1), относительно плоскости 4х+6y-4z-25=0.
Решение:
вектор нормали плоскости (4;6;-4)
Уравнение прямой, которая проходит через точку M перпендикулярно заданной плоскости будет:
(х-1)/4=(y-3)/6=(z-1)/(-4)
Найдем точку пересечения прямой и плоскости:
х=4t+1
y=6t+3
z=-4t+1

4(4t+1)+6(6t+3)-4(-4t+1)-25=0
16t+4+36t+18+16t-4-25=0
68t=7
t=7/68
точка пересечения прямой и плоскости M₀ (96/68 ; 246/68;40/68)
сократили, получили M₀ (24/17; 123/34; 10/17)

M₀ -это середина отрезка MM’ , поэтому:
х_M’= 2х_M0-х_M=2*24/17-1=31/17
y_M’=2*123/34-3=144/34
z_M’=2*10/17-1=3/17
вот как-то так смущают меня эти ответы очень

Вроде все похоже на правду.

В качестве проверки можно сделать следующее: расстояние от заданной точки М до плоскости должно равняться расстоянию от найденной точки М’ до этой же плоскости.

Проверила, не смотря на невзрачные цифры, сошлось:
1) расстояние от M до плоскости
A=4 B=6 C=-4 M(1;3;1)

d=|Ax1+By1+Cz1+D/sqrt(A²+B²+C²)|= |(4*1+6*3-4*1-25)/sqrt(16+36+16)|=|-7/sqrt68|=7/sqrt68

2) расстояние от M’ до плоскости
M’ (31/17;144/34;3/17)

d=|(4*31/17+6*144/34-4*3/17-25)/sqrt68|=|((224+864-850)/34)/sqrt68|=7/sqrt68

Это хорошо, даже очень.

Напишите пожалуйста что вы сделали что у вас в “точка пересечения прямой плоскости М 0 получилось (96/68;246/68;40/68)
сократили получили М (24/17;123/4;10/17) я не пойму что на что вы умножали или делили. У меня то же самое уравнение что и у вас только у вас М (1,3,1),а у меня М (1,6,1).Помогите пожалуйста решить

Источник

§ 4.Симметрия относительно плоскости

4.1.Определение симметрии относительно плоскости

Рис. 19

Определение. Точка m′ пространства, не лежащая на плоскости α, называется симметричной точке М относительно плоскости α, если отрезок ММ′ перпендикулярен этой плоскости и делится ею пополам. Любая точка плоскости α считается симметричной самой себе относительно этой плоскости (рис. 19).

Из определения следует, что если точка M′ симметрична точке M относительно плоскости α, то точка М симметрична точке М′ относительно той же плоскости α.

Зададим теперь следующее отображение пространства на себя. Каждой точке М пространства поставим в соответствие точку М′, симметричную ей относительно плоскости α. Аналогично центральной симметрии, можно доказать, что это отображение является преобразованием пространства. При этом каждая точка плоскости α отображается на себя.

Определение. Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α, называется симметрией пространства относительно плоскости α. Плоскость α называется плоскостью симметрии.

Симметрия относительно плоскости α обозначается Sα. Если при этой симметрии точка М (фигура F) отображается на точку М′ (фигуру F′), то записывают Sα(М) = М′ (Sα(F) = F′). Это преобразование ещё называют «отражением в плоскости», или «зеркальной симметрией», или «зеркальным отражением от плоскости», проводя аналогию с «отражением в зеркале».

Из определения симметричных точек относительно плоскости α следует

Sα(M) = M′ ⇔ Sα(M′) = M.

Поэтому говорят, что точки М и М′ симметричны относительно плоскости α. С другой стороны, ранее было показано, что точка M′ отображается на свой прообраз — точку M — преобразованием, обратным данному. Значит,

Sα(M) = M′ ⇒ (M′) = M.

Получили

Таким образом, симметрия относительно плоскости есть преобразование пространства, совпадающее со своим обратным преобразованием.

Тогда для любой точки М пространства имеем

(Sα ∘ Sα)(M) = Sα(Sα (M)) = Sα(M′) = (M′) = M.

Рис. 20

Но для тождественного преобразования E справедливо Е(М) = М. Так как точка М — любая, то преобразования Sα ∘ Sα и Е равны: Sα ∘ Sα = Е, т. е. композиция двух симметрий относительно одной и той же плоскости есть тождественное преобразование.

Если при симметрии относительно плоскости α фигура F отображается на себя (Sα(F) = F), то плоскость α называется плоскостью симметрии этой фигуры. При этом говорят, что фигура F симметрична относительно плоскости α (или плоскость α является плоскостью симметрии фигуры F).

Например, плоскость, проходящая через середины параллельных рёбер AD, ВС, B1C1 и A1D1 куба АВСDA1B1C1D1 (рис. 20), является плоскостью симметрии этого куба. Докажите это и найдите другие плоскости симметрии данного куба.

Симметрия относительно плоскости может быть задана парой соответственных (симметричных) точек А и A′ (почему?).

4.2.Симметрия относительно плоскости в координатной форме

Выведем формулы, которые позволяли бы по координатам произвольной точки М пространства находить координаты её образа — точки M′ = Sα(M).

Рис. 21

Выберем прямоугольную систему координат Oхyz так, чтобы её координатная плоскость Оху совпадала с плоскостью симметрии α. Рассмотрим в этой системе координат произвольную точку M(x; y; z) и её образ М′(x′; y′; z′) при симметрии относительно плоскости Oxy (рис. 21).

По определению симметрии относительно плоскости имеем MM′ ⟂ (Оху), | M0M | = | M0M′ |, где M0 — точка пересечения прямой ММ′ с плоскостью Оху. Это означает, что точки М и M′ расположены в разных полупространствах относительно плоскости Oxy, одинаково удалены от неё, а прямая MM′ параллельна координатной оси Oz. Поэтому координаты этих точек связаны соотношениями

x′ = x, y′ = y, z′ = –z,

которые называются формулами npeoбразованuя симметрии относительно плоскости Oxy.

4.3.Симметрия относительно плоскости — движение пространства

Используя формулы симметрии в координатах, докажем, что симметрия относительно плоскости — движение пространства.

Пусть A(x1; y1; z1), C(x2; y2; z2) — данные точки, тогда A′(x1; y1; –z1), C′(x2; y2; –z2) — их образы при симметрии S(Oxy).

Находим:

| АC | = ;

| A′C′ | = =

= = | AC |,

т. е. рассматриваемая симметрия является движением, что и требовалось доказать. ▼

4.4. Свойства симметрии относительно плоскости

Рассмотрим вопрос о неподвижных точках, неподвижных прямых и неподвижных плоскостях зеркальной симметрии.

Неподвижной точкой симметрии относительно плоскости α является каждая точка плоскости α; других неподвижных точек при данной симметрии нет.

Неподвижные прямые симметрии Sα относительно плоскости α можно разделить на два вида:

—каждая прямая плоскости α; любая точка такой прямой является неподвижной точкой симметрии Sα, а симметрия Sα индуцирует на каждой из этих прямых тождественное преобразование Е;

—каждая прямая пространства, перпендикулярная плоскости α; на любой такой прямой индуцируется центральная симметрия относительно точки пересечения этой прямой с плоскостью α.

Рис. 22

Неподвижные плоскости симметрии Sα можно разделить также на два вида:

—сама плоскость α; каждая её точка является неподвижной точкой симметрии Sα, а симметрия Sα индуцирует на этой плоскости тождественное преобразование E;

—каждая плоскость, перпендикулярная плоскости α; на любой такой плоскости индуцируется известная вам из планиметрии осевая симметрия относительнo прямой пересечения этой плоскости с плоскостью α.

Для исследования вопроса о том, меняет ли симметрия относительно плоскости ориентацию тетраэдра, выберем такую тройку единичных попарно взаимно перпендикулярных векторов , и , чтобы точки O, А и В лежали в плоскости α. Тогда при симметрии Sα тетраэдр ОАВС отобразится на такой тетраэдр ОАВC′, что ′ = – (рис. 22). Это означает, что ориентации тетраэдров ОАВС и ОАВC′ = Sα(OABC) различны, т. е. симметрия относительно плоскости меняет ориентацию тетраэдра, следовательно, является движением второго рода.

Интересно заметить, что если три плоскости α, β и γ попарно взаимно перпендикулярны, то композиция симметрий относительно этих трёх плоскостей является центральной симметрией относительно их общей точки (точки пересечения плоскостей α, β и γ), т. е. Sγ ∘ Sβ ∘ Sα = ZО, где О — общая точка этих трёх плоскостей. Попробуйте самостоятельно доказать это координатным методом.

Источник

Симметрия относительно плоскости

как найти точку, симметричную Р относительнно данной плоскости????подскажите пожайлуйста ))))))))))

Вам также может понравиться

Загруженные песни на айфоне как их найти

Как найти бобровую плотину

Как найти коэффициент использования торговой площади

Добавить комментарий Отменить ответ