Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
I. Две точки A(xA;yA) и B(xB;yB) симметричны относительно точки O(xO;yO), если точка O является серединой отрезка AB.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
Примеры.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Решение:
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
Ответ: (13;15).
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Решение:
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
Ответ: (-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Пример
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Решение:
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
5=-0,5·(-4)+b, откуда b=3.
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Найдём координаты точки пересечения прямых:
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Ответ: (3,2;1,4).
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
| для точки A(x;y) | |
| симметрия относительно: | |
| оси Ox | A1(x;-y) |
| оси Oy | A2(-x;y) |
|
биссектрисы I и II координатных четвертей (прямой y=x) |
A3(y;x) |
|
биссектрисы I b II координатных четвертей (прямой y= -x) |
A4(-y;-x) |
Точка
пересечения прямой и плоскости
Постановка
задачи.
Найти точку пересечения прямой
и
плоскости
.
План
решения.
1.
Находим параметрические уравнения
прямой. Для этого полагаем
.
откуда
получаем

2.
Подставляя эти выражения для
в
уравнение плоскости и решая его
относительно t,
находим значение параметра
,
при котором происходит пересечение
прямой и плоскости.
3.
Найденное значение
подставляем
в параметрические уравнения прямой и
получаем искомые координаты точки
пересечения:

Замечание.
Если в результате решения уравнения
относительно параметра
получим
противоречие, то прямая и плоскость
параллельны (это эквивалентно условию
).
Задача
13.
Найти точку пересечения прямой и
плоскости.

Запишем
параметрические уравнения прямой.

Подставляем
в уравнение плоскости:
Откуда
координаты точки пересечения прямой и
плоскости будут
Задача 14
Симметрия
относительно прямой или плоскости
Симметрия относительно прямой
Постановка
задачи.
Найти координаты точки
,
симметричной точке
относительно
прямой
.
План
решения.
1.
Находим уравнение плоскости, которая
перпендикулярна данной прямой и проходит
через точку
.
Так плоскость перпендикулярна заданной
прямой, то в качестве ее вектора нормали
можно взять направляющий вектор прямой,
т.е.
Поэтому
уравнение плоскости будет
2.
Находим точку
пересечения
прямой
и
плоскости
(см.
задачу 13).
3.
Точка
является
серединой отрезка
,
где точка
является
точкой симметричной точке
,
поэтому
Задача
14.
Найти точку
,
симметричную точке
относительно
прямой.
.
Уравнение
плоскости, которая проходит через точку
перпендикулярно
заданной прямой будет:
Найдем
точку пересечения прямой и плоскости.

Откуда
–
точка пересечения прямой и плоскости.
является
серединой отрезка
,
поэтому



Т.е.
.
Симметрия относительно плоскости
Постановка
задачи.
Найти координаты точки
,
симметричной точке
относительно
плоскости
.
План
решения.
1.
Находим уравнение прямой, которая
перпендикулярна данной плоскости и
проходит через точку
.
Так прямая перпендикулярна заданной
плоскости, то в качестве ее направляющего
вектора можно взять вектор нормали
плоскости, т.е.
.
Поэтому
уравнение прямой будет
.
2.
Находим точку
пересечения
прямой
и
плоскости
(см.
задачу 13).
3.
Точка
является
серединой отрезка
,
где точка
является
точкой симметричной точке
,
поэтому
Задача
14.
Найти точку
,
симметричную точке
относительно
плоскости.
Уравнение
прямой, которая проходит через точку
перпендикулярно
заданной плоскости будет:

Найдем
точку пересечения прямой и плоскости.

Откуда
–
точка пересечения прямой и плоскости.
является
серединой отрезка
,
поэтому



Т.е.
.
Литература
-
Ван дер Варден
Б.Л. Алгебра. – СПб. : Лань, 2004. – 624 с. -
Кузнецов Л.А.
Сборник заданий по высшей математике
(типовые расчеты). — СПб: «Лань»,
2008.- 240 c. -
Привалов И.И.
Аналитическая геометрия. – СПб. ; М. ;
Краснодар: Лань, 2007. – 304 с. -
Цубербиллер О.Н.
Задачи и упражнения по аналитической
геометрии. – СПб.: Лань, 2003. – 336 с. -
Фаддеев Д.К.,
Соминский И.С. Задачи по высшей алгебре.
– СПб.; М. ; Краснодар : Лань, 2007. – 288 с. -
Курош А.Г. Курс
высшей алгебры. – СПб. ; М. ; Краснодар :
Лань, физматкнига, 2007. – 432 с. -
Окунев Л.Я. Высшая
алгебра.- СПб.: Лань, 2009. – 336 с.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти центр симметрии
Одним из видов симметрии является центральная. Центр симметрии – некоторая точка O, относительно которой вращают плоскость, поворачивая ее на 180°. Каждая точка A переходит в такую точку A’, что O – середина отрезка AA’.

Инструкция
Если даны две точки, центром симметрии между ними, по определению, будет середина отрезка, соединяющего их. Сложнее обстоит дело с геометрической фигурой: здесь уже надо рассмотреть все точки, составляющие ее. Любая произвольная точка должна переходить в центрально симметричную ей, иначе принцип симметрии будет нарушен.
Если даны две фигуры, про которые сказано, что они являются симметричными относительно неизвестного центра, попробуйте мысленно вращать каждую из фигур. В итоге вы должны представить переход на 180° (пол-окружности). Найдите любые две симметричные точки, проведите между ними отрезок. В его центре будет располагаться центр симметрии и этих двух точек, и всей фигуры.
Пусть надо построить окружность, симметричную данной относительно точки O. Центр окружности пусть обозначен точкой C. Проведите прямую от точки C через точку O. Ножками циркуля отмерьте расстояние OC, отложите такое же расстояние на прямой от точки O в другую сторону. Зафиксируйте результат, это будет центр новой окружности. Измерьте циркулем радиус исходной окружности и достройте симметричную.
Чтобы построить многоугольник, симметричный данному относительно центра O, найдите образ каждой из его вершин. Исходная точка называется «прообразом», конечная – «образом». Последовательно соедините точки между собой. Мысленно повращайте фигуры, оцените, правильным ли получился результат.
Если дана пространственная фигура, и необходимо найти центр симметрии между какими-либо двумя точками, вспомните свойства этого объемного тела. Возможно, центр симметрии лежит на пересечении диагоналей, биссектрис, медиан, перпендикуляров. Докажите, что указанная вами точка является именной центром симметрии, используя свойства фигуры, другие данные в задаче условия и определение симметричности.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
плоскости
прямая
пересечения прямой и плоскости:
канонические уравнения прямой, проходящей через
точку М0(2; -4; -1) и
середину отрезка прямой
уравнение прямой, проходящей через точку М0(2; -3; -5) перпендикулярно
к плоскости
уравнение плоскости, проходящей через точку М0(1; -1; -1) перпендикулярно
к прямой
уравнение плоскости, проходящей через точку М0(1; -2; 1) перпендикулярно
к прямой
прямая
С прямая
A и D прямая
в плоскости
А и В плоскость
прямой
l и C прямая
плоскости
точки Р(2; -1; 3) на прямую
симметричную точке Р(4; 1; 6) относительно прямой
симметричную точке Р(2; -5; 7) относительно прямой,
проходящей через точки М1(5; 4; 6) и М2(-2; -17; -8).
точки Р(5; 2; -1) на плоскость
симметричную точке Р(1; 3; -4) относительно
плоскости
найти такую точку Р, сумма расстояний которой до
точек А(-1; 2; 5) и В(11; -16; 10) была бы наименьшей.
найти такую точку Р, разность расстояний которой
до точек M1(3; 2; -5), М2(8; -4; -13) была
бы наибольшей.
расстояний которой до точек А(3; -4; 7) и В(-5; -14; 17)
была бы наименьшей.
расстояний которой до точек М1(5; 2; -7) и М2(7; -25; 10) была
бы наибольшей.
движется прямолинейно и равномерно из
начального положения М0(15; -24; -16)
со скоростью v=12 в направлении
вектора s={-2; 2; 1}. Убедившись, что траектория точки
М пересекает плоскость
пересечения;
на движение точки М от М0 до Р;
движется прямолинейно и равномерно из
начального положения М0(28; -30; -27)
со скоростью v=12,5 по
перпендикуляру, опущенного из точки М0 на плоскость
уравнения движения точки М и определить:
ее траектории с этой плоскостью;
на движение точки М от М0 до Р;
движется прямолинейно и равномерно из
начального положения М0(11; -21; 20) в направлении вектора s={-1; 2; -2} со
скоростью v=12. Определить, за какое время она
пройдет отрезок своей траектории, заключенный
между параллельными плоскостями
расстояние d точки Р(1; -1; -2) от прямой
расстояние d от точки Р(2; 3; -1) до следующих прямых:
прямые
вычислить расстояние d между ними.
уравнение плоскости, проходящей через точку М1(1; 2; -3) параллельно
прямым
Доказать,
что уравнение плоскости, проходящей через точку
М0(x0; y0; z0) параллельно прямым ,
, может быть
представлено в следующем виде:
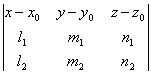
Доказать,
чо уравнение плоскости, проходящей через точки М1(x1; y1; z1) и М2(x2; y2; z2)
паралелльно прямой , может
быть представлено в следующем виде:
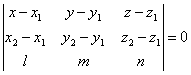
уравнение плоскости, проходящей через прямую
-2; 1).
Доказать,
что уравнение плоскости, проходящей через прямую
,
,
и точку М1(x1;
y1; z1), может быть
представлено в следующем виде:
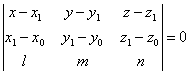
прямые
плоскости, и составить уравнение этой плоскости.
Доказать,
что если две прямые ,
пересекаются, то уравнение
плоскости, в которой они лежат, может быть
представлено в следующем виде:
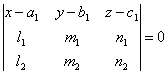
уравнение плоскости, проходящей через две
параллельные прямые
Доказать,
что уравнение плоскости, проходящей через две
параллельные прямые ,
,
и
,
,
, может быть
представлено в следующем виде:
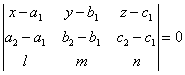
точки С(3; -4; -2) на плоскость, проходящую через
параллельные прямые
симметричную точке Р(3; -4; -6) относительно
плоскости, проходящей через М1(-6;
1; -5), М2(7; -2; -1) и М3(10; -7; 1).
симметричную точке Р(-3; 2; 5) относительно
плоскости, проходящей через прямые
уравнение плоскости, проходящей через прямую
Доказать,
что уравнение плоскости, проходящей через прямую
параллельно прямой
,
,
, может быть представлено в следующем
виде:
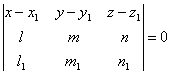
уравнение плоскости, проходящей через прямую
Доказать,
что уравнение плоскости, проходящей через прямую
,
,
перпендикулярно к
плоскости , может быть представлено в следующем
виде:
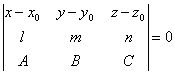
канонические уравнения прямой, которая проходит
через точку М0(3; -2; -4) параллельно плоскости
пересекает прямую
1082
проходит параллельно плоскостям
пересекает прямые
кратчайшее расстояние между двумя прямыми в
каждом из следующих случаев:
Центральная симметрия с центром в точке C (a,b) описывается уравнениями $frac{x+x’}2=a, x’=-x+2a$ или, что то же самое, $frac{y+y’}2=b, y’=-y+2b$.
Например, если центр симметрии находится в точке C(1,2), то симметричной точке А(2, 3) будет точка А'(0,1), так как $x’=-2+2 times 1=0, y’=-3+2 times 2=1$.
Декартовы уравнения, описывающие осевую симметрию, более сложны, так как осью симметрии может быть любая прямая на плоскости, и чтобы описать ее, потребуется прибегнуть к тригонометрическим функциям. Существуют, однако, три простых случая.
Осевая симметрия относительно оси ОХ
x’=x
y’=-y
Таким образом, чтобы найти точку, симметричную заданной, достаточно оставить неизменной первую координату и поменять знак у второй. Например, точкой, симметричной точке A(3,-2), будет точка А’(3,2).
Симметрия относительно оси OY
x’=-x
y’=y
В этом случае для нахождения симметричной точки нужно поменять знак первой координаты и оставить неизменной вторую. Например, точкой, симметричной точке А (-3, 9) относительно оси ОУ, является точка А’(3,9).
Симметрия относительно биссектрисы y=x
x’=y
y’=x
Таким образом, достаточно только поменять значения координат местами. То есть точкой, симметричной точк с А(5,1), будет точка А’(1,5).
Симметрии в пространстве
В пространстве также существуют центральная и осевая симметрии (относительно точки или прямой), определяемые примерно так же, как и на плоскости, но с тремя координатами вместо двух. Безусловно, существует еще и третья возможность — симметрия относительно плоскости, так называемая зеркальная симметрия. Строится она следующим образом. Предположим, что Р — плоскость симметрии (симметрия в таком случае обычно обозначается символом ). Чтобы найти преобразование точки А, проводится перпендикуляр к плоскости, проходящий через данную точку. Точкой, симметричной заданной, будет точка А’ находящаяся на этом перпендикуляре и удаленная от плоскости Р на такое же расстояние, что и точка А.
Инвариантные элементы зеркальной симметрии:
- все точки на плоскости Р;
- прямые, перпендикулярные Р (но не точки этих прямых);
- плоскости, перпендикулярные Р (тоже плоскости в целом, но не элементы, их составляющие).
Зеркальная симметрия не только является инволютивным преобразованием, но и имеет следующие свойства:
- сохраняет расстояния между точками;
- переводит прямые в прямые;
- переводит плоскости в плоскости.
Материалы по теме:
- Симметрия
- Временная симметрия
- Находим онлайн уравнение прямой на плоскости и в пространстве!
- Циклоиды.
Загрузка…








