Как найти точку симметрии на графике

Симметрии графиков функций

Прямая х=а является осью симметрии графика функции у=f(x) тогда и только тогда, когда для любого $xin D(f)$ выполняется равенство f(x)=f(2a-x).

Прямая х=а является осью симметрии графика функции f в том и только в том случае, когда для любого х из ее области определения выполняется равенство f(a+х)=f(a-х).

Точка (а, b) является центром симметрии графика функции у=f(x) тогда и только тогда, когда для любого $xin D(f)$ выполняется равенство f(x)+f(2а-х)=b.

Точка (а, b) является центром симметрии графика функции f в том и только в том случае, когда для любого х из ее области определения выполняется равенство f(a+х)+f(a-х)=b.

Пример 1: Сколько вертикальных осей симметрии может иметь график периодической функции?

Ответ: Если график функции f с периодом Т имеет ось симметрии х=а, то скорее всего — из геометрических соображений — осью симметрии будет и прямая х=а+Т. Но так как прямая х=с является осью симметрии графика функции у=f(x) тогда и только тогда, когда для любого $xin D(f)$ выполняется равенство f(x)=f(2с-х), то для прямой х=а+Т надо проверить выполнение равенства f(а+Т)=f(2а-а-Т), или f(a+Т)=f(aТ), a это равенство верно.

Так как периодов у периодической функции бесконечно много, то и осей симметрии бесконечно много, если, конечно, есть хотя бы одна.

Пример 2: График функции у=f(x) имеет вертикальную ось и центр симметрии. Что можно сказать о графике функции у=2f(x)-1?

Ответ: Так как график функции у=f(x) имеет вертикальную ось симметрии, например х=а, то для всякого х имеет место равенство f(a+х)=f(а-х), а тогда очевидно 2f(a+х)-1=2f(а-x)-1, так что функция у=2f(x)-1 имеет ту же ось симметрии. Если же график функции у=f(x) имеет центр симметрии, например, Q=(а, b), то для всякого х имеет место равенство f(а+х)+f(а-х)=2b, и в этом случае (2f(а+х)-1)+(2f(а-х)-1)=2b<-2, так что функция у=2f(x)-1 имеет центр симметрии в точке (а, 2b-2).

Комментарий. При рассуждении можно употреблять термины «растяжение-сжатие» и «сдвиг». Можно также пользоваться утверждением «Прямая х=а является осью симметрии графика функции у=f(x) тогда и только тогда, когда для любого $xin D(f)$ выполняется равенство f(x)=f(2а-x)».

Материалы по теме:

• Пример нахождения площади криволинейной трапеции через определённый интеграл.
• Функции четные и нечетные
• Находим асимптоты до графика функции.
• Периодические функции

Загрузка…

Была ли эта статья полезной?

Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.

Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.

Что называют квадратичной функцией

Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.

Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».

Квадратичная функция	Коэффициенты
y = 2x2 − 7x + 9	a = 2 b = −7 с = 9
y = 3x2 − 1	a = 3 b = 0 с = −1
y = −3x2 + 2x	a = −3 b = 2 с = 0

Как построить график квадратичной функции

Парабола выглядит следующим образом.

Также парабола может быть перевернутой.

Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.

Чтобы было проще понять этот алгоритм, сразу разберем его на примере.

Построим график квадратичной функции «y = x² −7x + 10».

1. Направление ветвей параболы

   Запомните!
   

   Если «a > 0», то ветви направлены вверх.
   

   Если «a < 0», то ветви направлены вниз.
   

   В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
   

2. Координаты вершины параболы

   Запомните!
   

   Чтобы найти «x₀»
   (координата вершины по оси «Ox»)
   нужно использовать формулу:

   Найдем «x₀» для нашей функции «y = x² −7x + 10».

   Теперь нам нужно найти «y₀»
   (координату вершины по оси «Oy»).
   Для этого нужно подставить найденное значение «x₀» в исходную функцию.
   Вспомнить, как найти значение функции можно в уроке
   «Как решать задачи на функцию» в подразделе
   «Как получить значение функции».

   y₀(3,5) =
   (3,5)² − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =

   −12,25 + 10 = −2,25

   Выпишем полученные координаты вершины параболы.

   (·) A (3,5; −2,25) — вершина параболы.

   Отметим вершину параболы на системе координат.
   Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
   относительно оси «Oy».

   

3. Нули функции

   Для начала давайте разберемся, что называют нулями функции.

   Запомните!
   

   Нули функции — это точки пересечения графика функции с осью «Ox»
   (осью абсцисс).

   Наглядно нули функции на графике выглядят так:

   

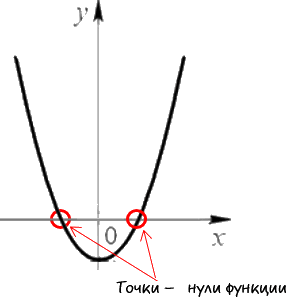
   Свое название нули функции получили из-за того, что у этих точек координата
   по оси «Oy» равна нулю.

   Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.

   Запомните!
   

   Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
   «y = 0».

   Подставим в заданную функцию «y = x² −7x + 10»
   вместо «y = 0» и решим полученное
   квадратное уравнение
   относительно
   «x» .

   0 = x² −7x + 10
   x² −7x + 10 = 0

   x_1;2 =

   7 ± √49 − 4 · 1 · 10

   2 · 1

   x_1;2 =

   x_1;2 =

   x1 =	x2 =
   x1 =	x2 =
   x1 = 5	x2 = 2

   Мы получили два корня в уравнении, значит, у нас две точки пересечения
   с осью «Ox».
   Назовем эти точки и выпишем их координаты.

   • (·) B (5; 0)
   • (·) C (2; 0)

   Отметим полученные точки («нули функции») на системе координат.

   

4. Дополнительные точки для построения графика

   Возьмем четыре произвольные числовые значения для «x».
   Целесообразно брать целые числовые значения на оси «Ox»,
   которые наиболее близки к оси
   симметрии. Числа запишем в таблицу в порядке возрастания.

   x	1	3	4	6
   y

   Для каждого выбранного значения «x»
   рассчитаем «y».

   • y(1) = 1² − 7 · 1 + 10 = 1 − 7 + 10 =
     4
   • y(3) = 3² − 7 · 3 + 10 = 9 − 21 + 10 =
     −2

   • y(4) = 4² − 7 · 4 + 10 = 16 − 28 + 10 =
     −2
   • y(6) = 6² − 7 · 6 + 10 = 36 − 42 + 10 =
     4

   Запишем полученные результаты в таблицу.

   x	1	3	4	6
   y	4	−2	−2	4

   Отметим полученные точки графика на системе координат (зеленые точки).

   

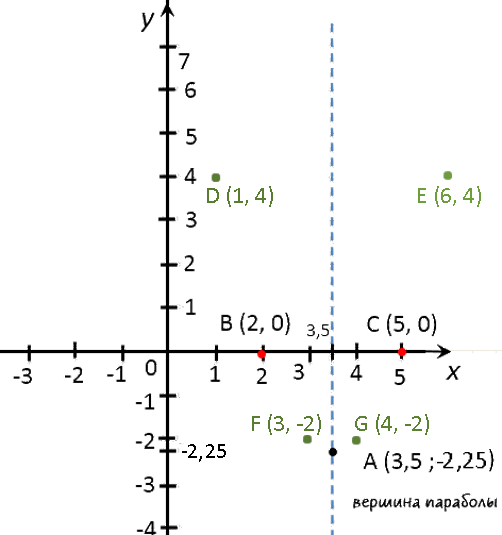
   Теперь мы готовы построить график.
   На забудьте после построения подписать график функции.

   

Краткий пример построения параболы

Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.

Пусть требуется построить график функции
«y = −3x² − 6x − 4».

1. Направление ветвей параболы

«a = −3» — ветви параболы направлены вниз.


2. Координаты вершины параболы

   x₀ =
   x₀ = =

   = −1

   y₀(−1) = (−3) · (−1)² − 6 · (−1) − 4 =
   −3 · 1 + 6 − 4 = −1

   (·) A (−1; −1)

   — вершина параболы.

   

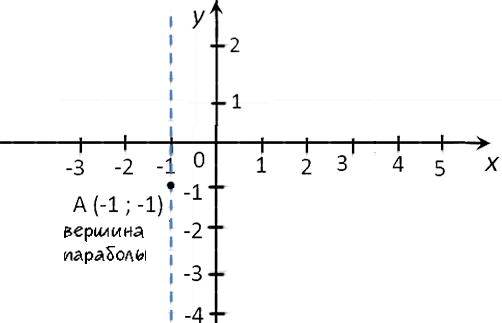
3. Нули функции

   Точки пересечения с осью «Ox» (y = 0).

   0 = −3x² − 6x − 4

   −3x² − 6x − 4 = 0 |·(−1)

   3x² + 6x + 4 = 0

   x_1;2 =

   −6 ± √62 − 4 · 3 · 4

   2 · 1

   x_1;2 =

   x_1;2 =

   
   Ответ: нет действительных корней.

   Так как корней нет, значит, график функции не пересекает ось
   «Ox».

4. Вспомогательные точки для: «x = −3»;
   «x = −2»;
   «x = 0»;
   «x = 1». Подставим в исходную функцию
   «y = −3x² − 6x − 4».
   • y(−3) = −3 · (−3)² − 6 · (−3) − 4
     = −3 · 9 + 18 − 4 = −27 + 14 = −13
   • y(−2) = −3 · (−2)² − 6 · (−2) − 4
     = −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4

   • y(0) = −3 · 0² − 6 · 0 − 4
     = −4
   • y(1) = −3 · 1² − 6 · 1 − 4
     = −3 −6 − 4 = −13

   x	−3	−2	0	1
   y	−13	−4	−4	−13

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.

---

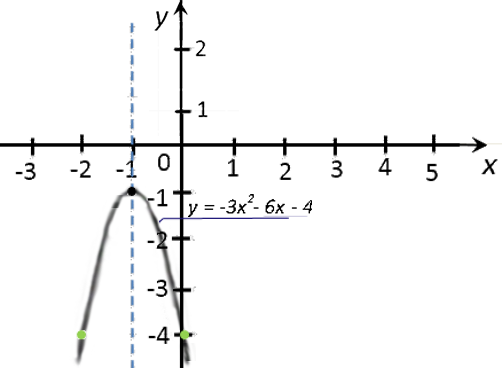
Ваши комментарии

Оставить комментарий:

---

Функция вида  , где  называется квадратичной функцией. 

График квадратичной функции – парабола. 

Рассмотрим случаи:

I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА 

, то есть , ,

Для построения заполняем таблицу, подставляя значения x в формулу:

Отмечаем  точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:

Нетрудно заметить, что если мы возьмем случай , , , то есть , то мы получим параболу, симметричную относительно оси (ох). Убедиться  в этом несложно, заполнив аналогичную таблицу:

II СЛУЧАЙ,  «a» ОТЛИЧНО ОТ ЕДИНИЦЫ

Что же будет, если мы будем брать , , ? Как изменится поведение параболы? При парабола   изменит форму, она “похудеет” по сравнению с параболой (не верите – заполните соответствующую таблицу – и убедитесь сами):

На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях  ордината    каждой точки умножилась на 4.  Это произойдет со всеми ключевыми точками исходной  таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.

А при парабола  «станет шире»  параболы :

Давайте подитожим:

III СЛУЧАЙ, ПОЯВЛЯЕТСЯ  «С»

 Теперь давайте введем в игру (то есть рассматриваем случай, когда ), будем рассматривать параболы вида . Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы вдоль оси вверх или вниз в зависимости от знака :

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»

Когда же парабола “оторвется” от оси и будет, наконец, “гулять” по всей координатной плоскости? Когда перестанет быть равным .

Здесь для построения параболы нам понадобится формула для вычисления вершины: ,   .

Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу , что уже нам по силам. Если  имеем дело со случаем , то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с , например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.

Например, вершина параболы :

,  . Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы ,  ведь в нашем случае.

При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:

1) парабола обязательно пройдет через точку .  Действительно, подставив в формулу x=0, получим, что . То есть ордината точки пересечения параболы  с осью (оу), это .   В нашем примере (выше), парабола пересекает ось ординат в точке , так как .

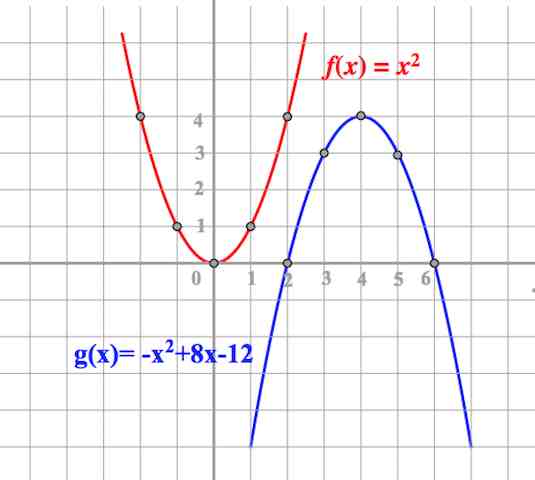
2) осью симметрии параболы является прямая , поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.

3) Приравнивая к , мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение . В зависимости от дискриминанта, будем получать одну (,  ), две (, ) или нИсколько () точек пересечения с осью (ох). В предыдущем примере у нас  корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения  с осью (ох) у нас будут (так как ), хотя, в общем, это видно и без дискриминанта.

Итак, давайте выработаем

Алгоритм для построения параболы, если она задана  в виде

1) определяем направление ветвей ( а>0 – вверх, a<0 – вниз)

2) находим координаты вершины параболы по формуле ,   .

3) находим точку пересечения параболы с осью (оу) по свободному члену , строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение велико… пропускаем этот пункт…)

4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу . Если , то парабола становится у’же по сравнению с , если , то парабола расширяется по сравнению с 

5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение

Пример 1

Пример  2

Замечание 1. Если же парабола изначально нам задана в виде , где – некоторые числа (например, ), то построить ее будет еще легче, потому что нам уже заданы координаты вершины . Почему?

Возьмем квадратный трехчлен и выделим в нем полный квадрат:  Посмотрите, вот мы и получили, что , . Мы с вами ранее называли   вершину параболы , то есть теперь , .

Например,  . Отмечаем на плоскости вершину параболы , понимаем, что ветви направлены вниз, парабола расширена (относительно ). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).

Замечание 2. Если парабола задана в виде, подобном этому (то есть представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае  – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.