Преподаватель который помогает студентам и школьникам в учёбе.
Сопряжения в инженерной графике на чертежах с примерами
Содержание:
В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.
- Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный в точку касания К, перпендикулярен к касательной прямой.
- Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).
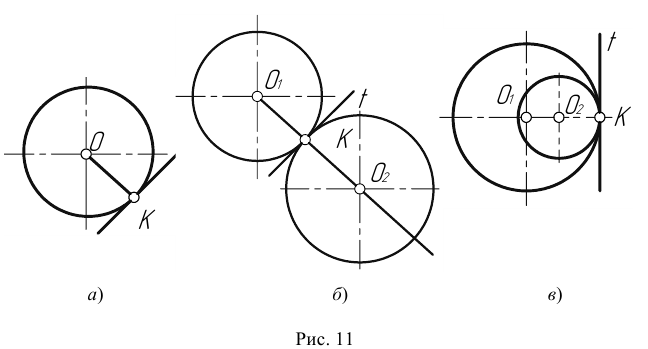
Точка касания К и центры окружностей 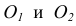
- Центром сопряжения О называется точка, равноудаленная от сопрягаемых линий (рис. 12).
- Точкой сопряжения А (В) называется точка касания двух сопрягаемых линий (рис. 12).
- Дуга сопряжения АВ – это дуга окружности, с помощью которой выполняется сопряжение (рис. 12).
- Радиус сопряжения R – это радиус дуги сопряжения (рис. 12).
Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.
Сопряжение двух пересекающихся прямых линий
Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.
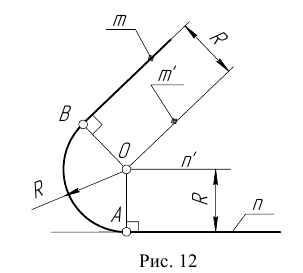
Выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от прямой n на расстояние радиуса R сопряжения. Таким множеством является прямая
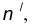 параллельная данной прямой n и отстоящая от неё на расстояние R.
параллельная данной прямой n и отстоящая от неё на расстояние R. - Построим множество точек центров сопряжения, удаленных от прямой m на расстояние радиуса сопряжения. Таким множеством является прямая
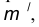 параллельная m и отстоящая от последней на расстояние R.
параллельная m и отстоящая от последней на расстояние R. - В пересечении построенных прямых
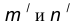 найдем центр сопряжения О.
найдем центр сопряжения О. - Определим точку А сопряжения на прямой n. Для этого опустим из центра О перпендикуляр на прямую n . Для определения точки сопряжения В на прямой m необходимо опустить соответственно перпендикуляр из центра О на прямую m.
Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.
Сопряжения прямой с окружностью
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.
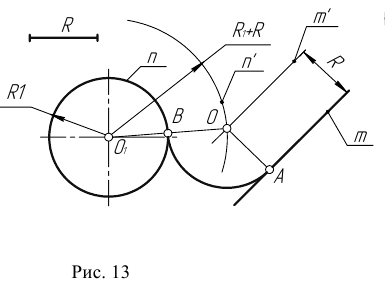
Пример 1. Пусть задана окружность радиусом R с центром в точке 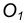 и прямая m. Требуется построить сопряжение окружности с прямой дугой окружности заданного радиуса R (рис. 13).
и прямая m. Требуется построить сопряжение окружности с прямой дугой окружности заданного радиуса R (рис. 13).
Для решения задачи выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает прямая
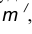 параллельная m и отстоящая от неё на расстояние R.
параллельная m и отстоящая от неё на расстояние R. - Множество точек центров сопряжения, удаленных от окружности n на рас- стояние R, есть окружность
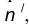 проведенная радиусом
проведенная радиусом 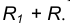
- Центр сопряжения О находим как точку пересечения линий
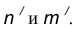
- Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо про- вести линию центров
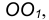 т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В. - Проведем дугу сопряжения АВ.
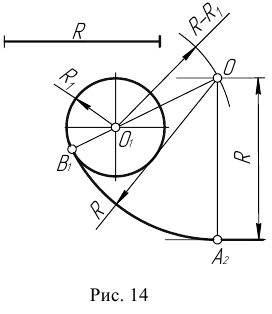
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 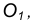 , радиусом
, радиусом 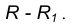
- Заказать чертежи
Сопряжение двух окружностей
Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 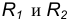 дугой заданного радиуса R (рис. 15а).
дугой заданного радиуса R (рис. 15а).
- Для нахождения центра сопряжения О проведем окружность
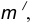 удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности 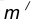 равен
равен 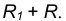
- Радиусом
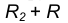 проведем окружность
проведем окружность 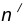 , удаленную от данной окружности n на расстояние R.
, удаленную от данной окружности n на расстояние R. - Найдем центр сопряжения О как точку пересечения окружностей
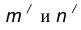 .
. - Найдем точку сопряжения А как пересечение линии центров
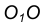 с дугой m.
с дугой m. - Аналогично найдем точку В как пересечение линии центров
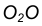 с дугой n .
с дугой n . - Проведем дугу сопряжения АВ.
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами 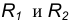 дугой радиусом R (рис. 15б).
дугой радиусом R (рис. 15б).
- Для нахождения центра сопряжения О проведем окружность
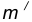 на расстоянии
на расстоянии 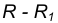 от данной окружности m.
от данной окружности m. - Проведем окружность
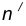 на расстоянии
на расстоянии 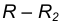 от данной окружности n.
от данной окружности n. - Центр сопряжения О найдем как точку пересечения окружностей
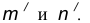
- Точку сопряжения А найдем как точку пересечения линии центров
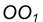 с заданной окружностью m.
с заданной окружностью m. - Точку сопряжения В найдем как точку пересечения линии центров
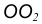 c заданной окружностью n.
c заданной окружностью n. - Проведем дугу сопряжения AВ с центром в точке O.
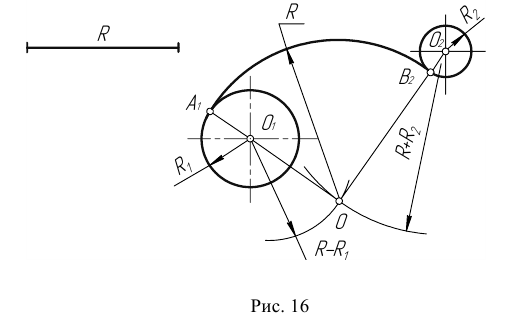
Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.
Построение касательных
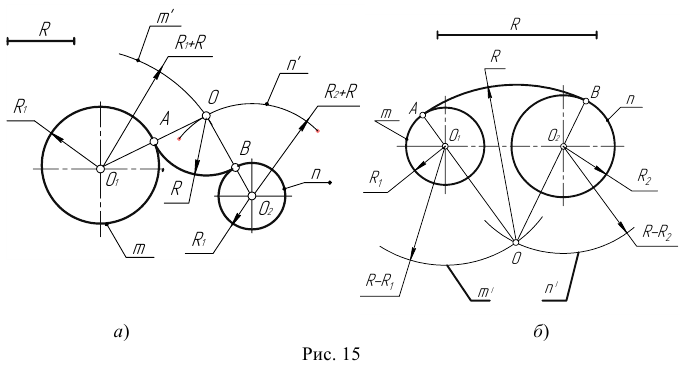
Пример 1. Дана окружность с центром в точке 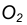 и точка
и точка 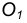 вне её. Через данную точку
вне её. Через данную точку 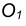 провести касательную к данной окружности (рис. 17).
провести касательную к данной окружности (рис. 17).
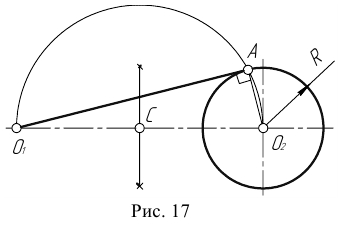
Для решения задачи выполним следующие построения.
- Соединим точку
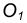 с центром окружности
с центром окружности 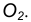
- Находим середину С отрезка
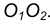
- Из точки С, как из центра, проведем вспомогательную окружность радиусом
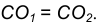
- В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку
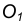 с точкой А.
с точкой А.
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 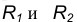 (рис. 18).
(рис. 18).
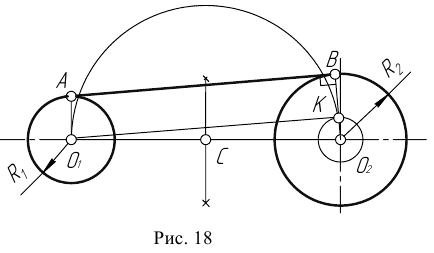
- Находим середину С отрезка
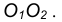
- Из точки С, как из центра, радиусом
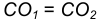 проведем вспомогательную окружность.
проведем вспомогательную окружность. - Из центра большей окружности
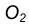 проведем вторую вспомогательную окружность радиусом
проведем вторую вспомогательную окружность радиусом 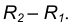
- Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус
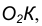 идущий в точку касания В. 5. Для построения второй точки касания А проведем
идущий в точку касания В. 5. Для построения второй точки касания А проведем 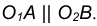
- Соединим точки А и В отрезком прямой линии.
- Нанесение размеров на чертежах
- Резьба на чертеже
- Соединения разъемные и неразъемные в инженерной графике
- Виды конструкторских документов
- Виды в инженерной графике
- Разрезы в инженерной графике
- Сечения в инженерной графике
- Выносные элементы в инженерной графике
Сопряжения
В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.
Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.
Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.
Ниже будут рассмотрены основные типы сопряжений.
Сопряжение углов (Сопряжение пересекающихся прямых)
Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.
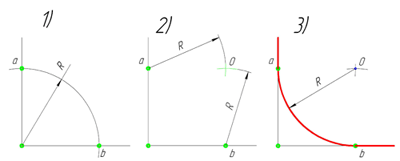
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.
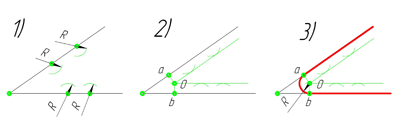
Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.
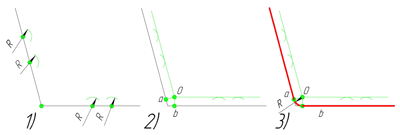
Сопряжение параллельных прямых линий
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.
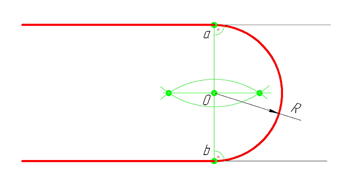
Сопряжение окружностей(дуг) с прямой линией
Внешнее сопряжение дуги и прямой линии
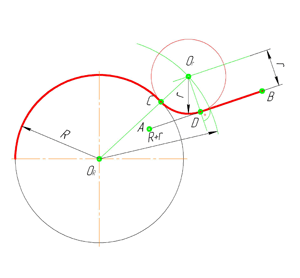
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.
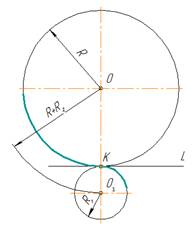
Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.
Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.
Внутреннее сопряжение прямой линии с дугой
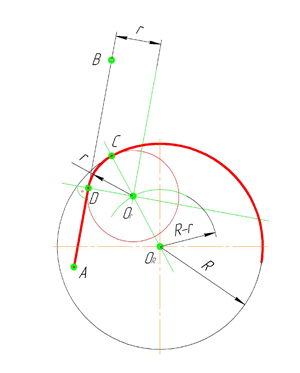
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r. Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.
Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.
Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.
Сопряжение окружностей (дуг)
Внешнее сопряжение дуг окружностей
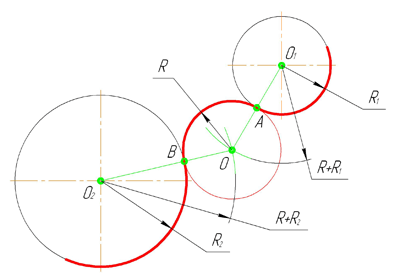
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
Внутреннее сопряжение дуг окружностей
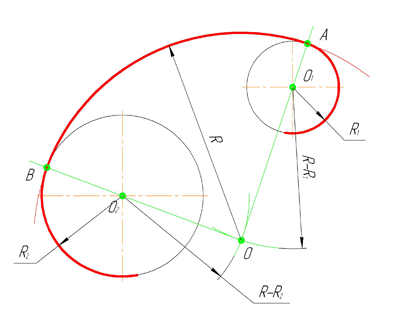
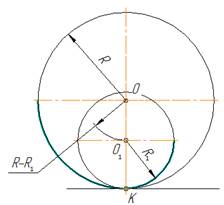
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.
Смешанное сопряжение дуг окружностей
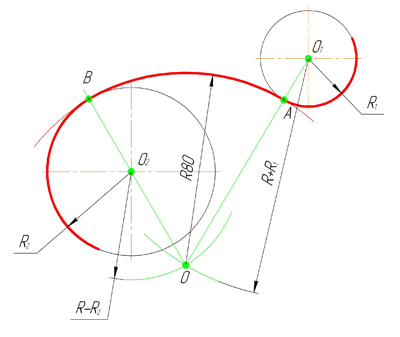
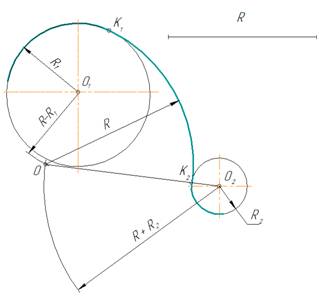
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.
При изучении дисциплины «Начертательная геометрия и
инженерная графика» студенты должны усвоить правила и последовательность
выполнения геометрических построений и сопряжений. В этом отношении лучшим
способом приобретения навыков построения являются задания по вычерчиванию
контуров сложных деталей.
Прежде чем приступить к выполнению контрольного задания,
нужно изучить технику выполнения геометрических построений и сопряжений по
методическому пособию.
Сопряжения линий
Сопряжением называется
плавный переход от одной линии к другой. Для построения любого сопряжения дугой
заданного радиуса нужно найти:
- Центр
сопряжения – центр, из которого проводят дугу; - Точки
сопряжения (касания) – точки, в которых одна линия переходит в другую.
Центр сопряжения
находится от точек сопряжения на одинаковых расстояниях, равных радиусу
сопряжения R. Переход от прямой к
окружности будет плавным в том случае, если прямая касается к окружности. Точка
сопряжения К лежит на перпендикуляре, опущенном из центра О окружности к прямой
(рис.
1)
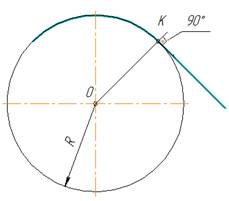
рис. 1
Переход от одной
окружности к другой будет плавным, если окружности касаются.
Различают два случая
касания дуг окружностей: внешнее (рис.
2) и внутреннее (рис.3).
При внешнем касании
центры окружностей лежат по разные стороны от их общей касательной L (рис. 2). Расстояние между их центрами ОО1 равно
сумме радиусов окружностей R+R1 и точка касания лежит на прямой ОО1,
соединяющей их центры.
При внутреннем касании
центры окружностей лежат по одну сторону от их общей касательной L. Расстояние
между их центрами ОО1 равно разности их радиусов R-R1 и точка касания К окружностей
лежит на продолжении прямой ОО1 (рис.
3).
|
|
|
|
рис. 2 |
рис. 3 |
Касание дуг окружностей:
рис. 2 – сопряжение двух окружностей (внешнее касание)
рис. 3 – сопряжение двух окружностей (внутреннее касание)
Сопряжение двух пересекающихся прямых
Даны
пересекающиеся под прямым, острым и
тупым углами прямые линии.
Требуется построить сопряжения этих прямых дугой заданного
радиуса R.
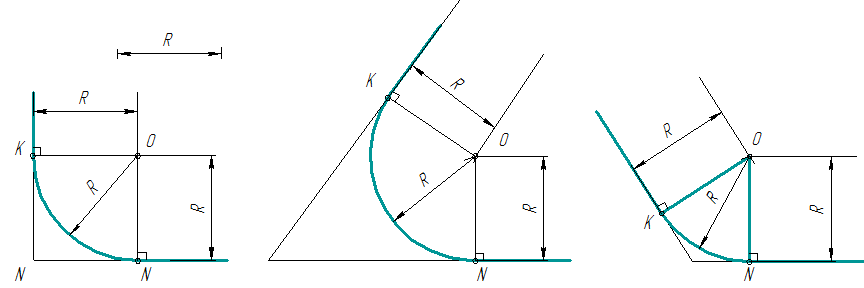
рис. 4
- Для
нахождения центра сопряжения проводят вспомогательные прямые, параллельные
данным на расстоянии равном радиусу R. Точка пересечения этих прямых т.О и
будет центом дуги сопряжения (рис.
4). - Перпендикуляры,
опущенные из центра дуги сопряжения т.О на данные прямые, определяют точки
касания К и N. - Из
точки О, как центра, описывают дугу заданного радиуса R.
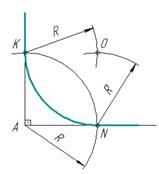
рис. 5
Примечание.Для
прямых углов центр сопряжения удобнее находить с помощью циркуля (рис. 5).
Сопряжение дуги окружности и прямой
линии дугой заданного радиуса.
Внешнее касание
Дана окружность радиуса
R и прямая АВ. Требуется соединить их дугой
радиусом R1.
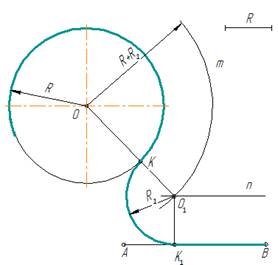
рис. 6
- Для
нахождения центра сопряжения из центра О заданной окружности проводят дугу m радиуса R + R1 и
на расстоянии R1 – прямую n // AB. Точка О1 пересечения прямой n и дуги m будет центром
сопряжения. - Для
получения точек сопряжения: К и К1 проводят линию центров ОО1 и
восстанавливают к прямой АВ перпендикуляр ОК1. - Из
центра сопряжения О1 между точками К и К1 проводят дугу сопряжения радиусом R1
Внутреннее касание
В случае внутреннего
касания выполняют те же построения, но дугу m
вспомогательной окружности проводят радиусом R – R1.
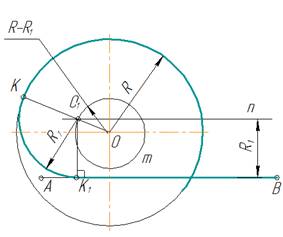
рис. 7
Сопряжение двух окружностей дугой
заданного радиуса
Заданы две окружности
радиусом R1 и R2. Требуется построить сопряжение дугой
заданного радиуса R.
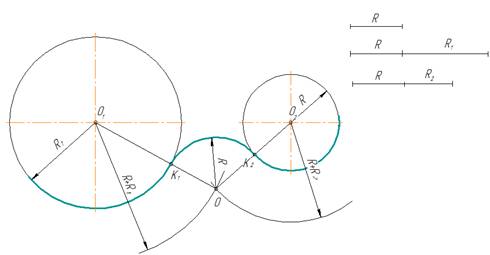
рис. 8
Внешнее касание
- Для
определения центра сопряжения О проводят вспомогательные дуги: из центра О1окружности радиусом R + R1 и из центра О2 окружности радиуса R
+ R2. Точка О пересечения этих дуг является центом сопряжения. - Соединяя
центры О и О1, а так же О и О2 , определяют точки
сопряжения (касания) К1 и К2. - Из
центра О радиусом R проводят дугу сопряжения между точками К1
и К2
Внутреннее касание
При внутреннем касании
выполняют те же построения, но дуги проводят радиусами
R -R1 и R – R2.
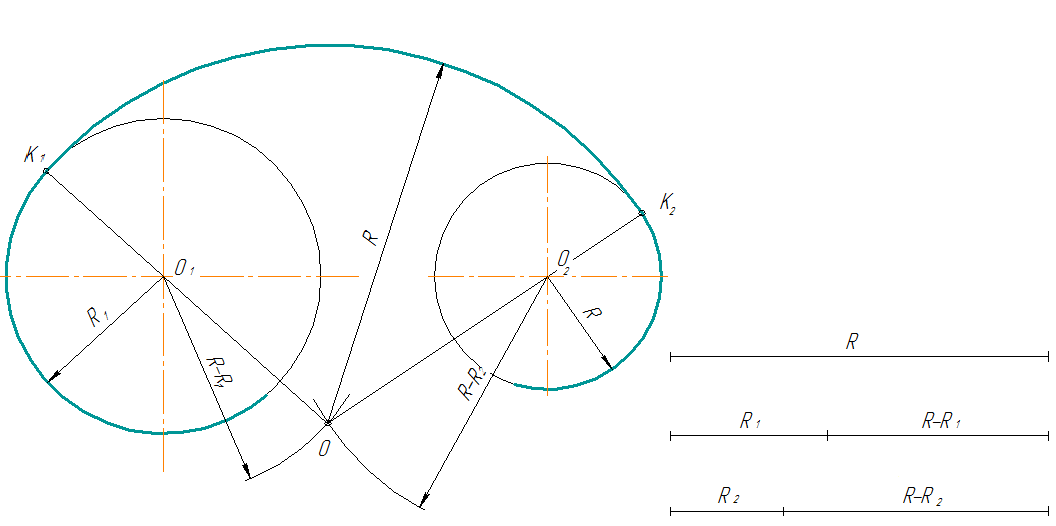
рис. 9
Смешанное касание
рис. 10
Центр сопряжения О
находится в пересечении двух дуг, описанных из центра О1 радиусом R
– R1 и из центра О2 радиусом R + R2
Примечание. При
смешанном сопряжении центр О1 одной из сопрягаемых дуг лежит внутри
сопрягающей дуги радиуса R , а центр О2 другой дуги – вне ее.
Частные случаи
Нахождение
центра дуги заданного радиуса.
Задана дуга радиусом R,
соединяющая две параллельные прямые mи n и проходящая через точку А ∈ m (рис. 11). Требуется найти центр О заданной дуги.
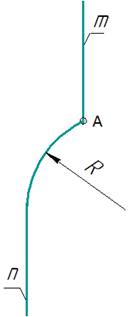
рис. 11
В основу построения положено нахождение
точки О, равноудаленной от заданных прямых (рис.
11).
- Из
точки А ∈ m, как из центра, проводят дугу
вспомогательной окружности с заданным радиусом R. - Проводят
вспомогательную прямую l,
параллельную прямой n, на
расстоянии, равном заданному радиусу R. - Точка О – точка пересечения этих
вспомогательных линий является центром заданной дуги. (рис. 12)
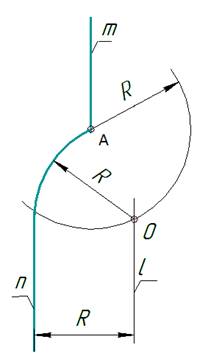
рис. 12
Литература
- Боголюбов
С.К. Инженерная графика: Учебник для средних специальных учебных заведений. –
3-е изд., испр. И доп. – М.: Машиностроение, 2006. – с.392: ил. - Куприков
М.Ю. Инженерная графика: учебник для ССУЗов – М.: Дрофа, 2010 – 495 с.: ил. - Федоренко
В.А., Шошин А.И. Справочник по машиностроительному черчению Л.: Машиностроение.
1976. 336 с.
Лист
№ 4
Цель
задания:
ознакомление с правилами построения
плавного перехода от одной линии к
другой.
Выполнить
на листе формата А4 задание «Сопряжение»,
взяв данные по своему варианту из таблицы
6 (стр. 38-41).
Сопряжением
линий
называется плавный переход по кривой
от одной линии к другой. Точкой
сопряжения линий называется
общая точка двух сопрягаемых линий, это
точка в которой одна линия переходит в
другую линию.
Построение
сопряжений основано на геометрических
понятиях о прямых, касательных к
окружностям и на свойствах касающихся
между собой окружностей.
Для
правильного выполнения чертежей
необходимо уметь выполнять построения
сопряжений, которые основаны на двух
положениях:
1.
Для сопряжения прямой линии и дуги
необходимо, чтобы центр окружности,
которой принадлежит дуга, лежал на
перпендикуляре к прямой, восстановленном
из точки сопряжения (рисунок 38). При
сопряжении прямой линии и кривой прямая
должна являться одновременно касательной
к кривой.
2.
Для сопряжения двух дуг необходимо,
чтобы центры окружностей, которым
принадлежат дуги, лежали на прямой,
проходящей через точку сопряжения и
перпендикулярной к общей касательной
этих дуг (рисунок 38). Точку сопряжения
находят на прямой, соединяющей центры
окружностей. Точка сопряжения (В) является
границей двух линий, здесь кончается
одна линия и начинается другая.
Следовательно, точки сопряжения являются
вместе с тем и точками касания прямой
и дуги или двух дуг.

Рисунок
38 – Построение сопряжений
Рассмотрим
построение
сопряжений сторон угла
(острого, тупого, прямого) дугой заданного
радиуса R (рисунок 39).
На
рисунке 39а выполнено построение
сопряжения сторон острого угла дугой,
на рисунке 39б – тупого угла, на рисунке
39в – прямого.
Сопряжение
выполняется следующим образом: параллельно
сторонам угла на расстоянии, равном
радиусу дуги R, проводят две вспомогательные
прямые линии. Точка пересечения этих
линий будет центром дуги радиуса R, т.е.
центром сопряжения. Из центра О описывают
дугу, плавно переходящую в прямые –
стороны угла. Дугу заканчивают в точках
М и N – это точки сопряжения, они являются
основаниями перпендикуляров, опущенных
из центра О на стороны угла.

Рисунок
39 – Построение сопряжений
Рассмотрим
построение
сопряжения дуги с дугой.
Сопряжение
двух дуг окружностей может быть
внутренним, внешним и смешанным.
При
внутреннем сопряжении центры О и О1
сопрягаемых дуг находятся внутри
сопрягающей дуги радиуса R (рисунок
40а).
При
внешнем сопряжении центры О и О1
сопрягаемых дуг радиусов R1
и R2
находятся вне сопрягающей дуги радиуса
R (рисунок 40б).
При
смешанном сопряжении центр О1
одной из сопрягаемых дуг лежит внутри
сопрягающей дуги радиуса R, а центр О
другой сопрягаемой дуги вне её (рисунок
40в).
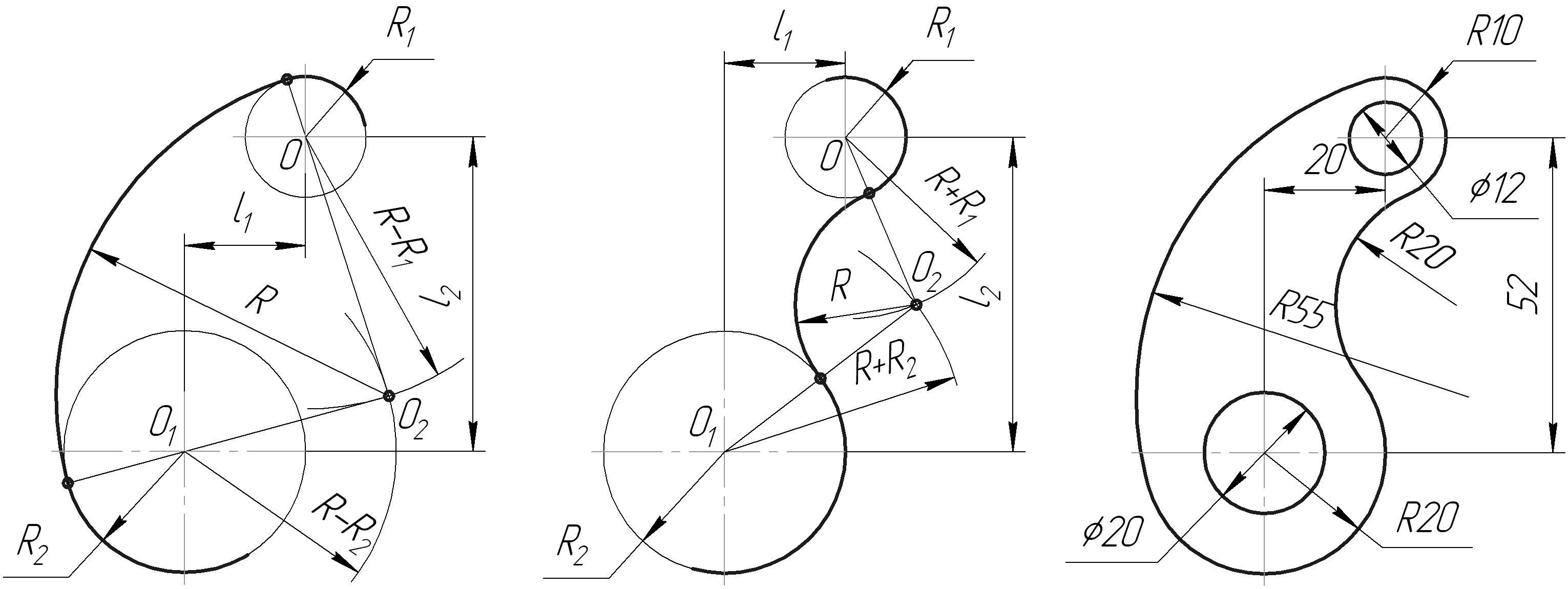
а)
б)
в)
Рисунок 40 –
Построение сопряжений
Построение
внутреннего сопряжения.
Задано:
а)
радиусы сопрягаемых окружностей R1
и R2;
б)
расстояние l1
и l2
между
центрами этих дуг;
в)
радиус R сопрягающей дуги.
Требуется:
а)
определить положение центра О2
сопрягающей дуги;
б)
найти точки сопряжения S
и S1;
в)
провести дугу сопряжения.
Построение
сопряжения показано на рисунке 40а. По
заданным расстояниям между центрами
l1
и l2
на чертеже намечают центры О и О1,
из которых описывают сопрягаемые дуги
радиусов R1
и R2.
Из центра О1
проводят вспомогательную дугу окружности
радиусом, равным разности радиусов
сопрягающей дуги R и сопрягаемой R2,
а из центра О – радиусом, равным разности
радиусов сопрягающей дуги R и сопрягаемой
R1.
Вспомогательные дуги пересекутся в
точке О2
, которая и будет искомым центром
сопрягающей дуги.
Для
нахождения точек сопряжения точку О2
соединяют с точками О и О1
прямыми линиями. Точки пересечения
продолжения прямых О2О
и О2О1
с сопрягаемыми дугами являются искомыми
точками сопряжения (точки S
и S1).
Радиусом
R из центра О2
проводят сопрягающую дугу между точками
сопряжения S
и S1.
Построение
внешнего сопряжения.
Задано:
а)
радиусы R1
и R2
сопрягаемых дуг окружностей;
б)
расстояние l1
и l2
между
центрами этих дуг;
в)
радиус R сопрягающей дуги.
Требуется:
а)
определить положение центра О2
сопрягающей дуги;
б)
найти точки сопряжения S
и S1;
в)
провести дугу сопряжения.
Построение
внешнего сопряжения показано на рисунке
40б. По заданным расстояниям между
центрами l1
и l2
на чертеже намечают центры О и О1,
из которых описывают сопрягаемые дуги
радиусов R1
и R2.
Из центра О проводят вспомогательную
дугу окружности радиусом, равным сумме
радиусов сопрягаемой дуги R1
и сопрягающей R, а из центра О1
– радиусом, равным сумме радиусов
сопрягаемой R2
и сопрягающей R. Вспомогательные дуги
пересекутся в точке О2,
которая и будет искомым центром
сопрягающей дуги.
Для
нахождения точек сопряжения центры дуг
соединяют прямыми линиями ОО2
и О1О2.
Эти две прямые пересекают сопрягаемые
дуги в точках сопряжения S
и S1.
Из
центра О2
радиусом R проводят сопрягающую дугу,
ограничивая её точками сопряжения S
и S1.
Построение
смешанного сопряжения.
Задано:
а)
радиусы R1
и R2
сопрягаемых дуг окружностей;
б)
расстояние l1
и l2
между
центрами этих дуг;
в)
радиус R сопрягающей дуги.
Требуется:
а)
определить положение центра О2
сопрягающей дуги;
б)
найти точки сопряжения S
и S1;
в)
провести дугу сопряжения.
Пример
смешанного сопряжения приведен на
рисунке 41 а,б.
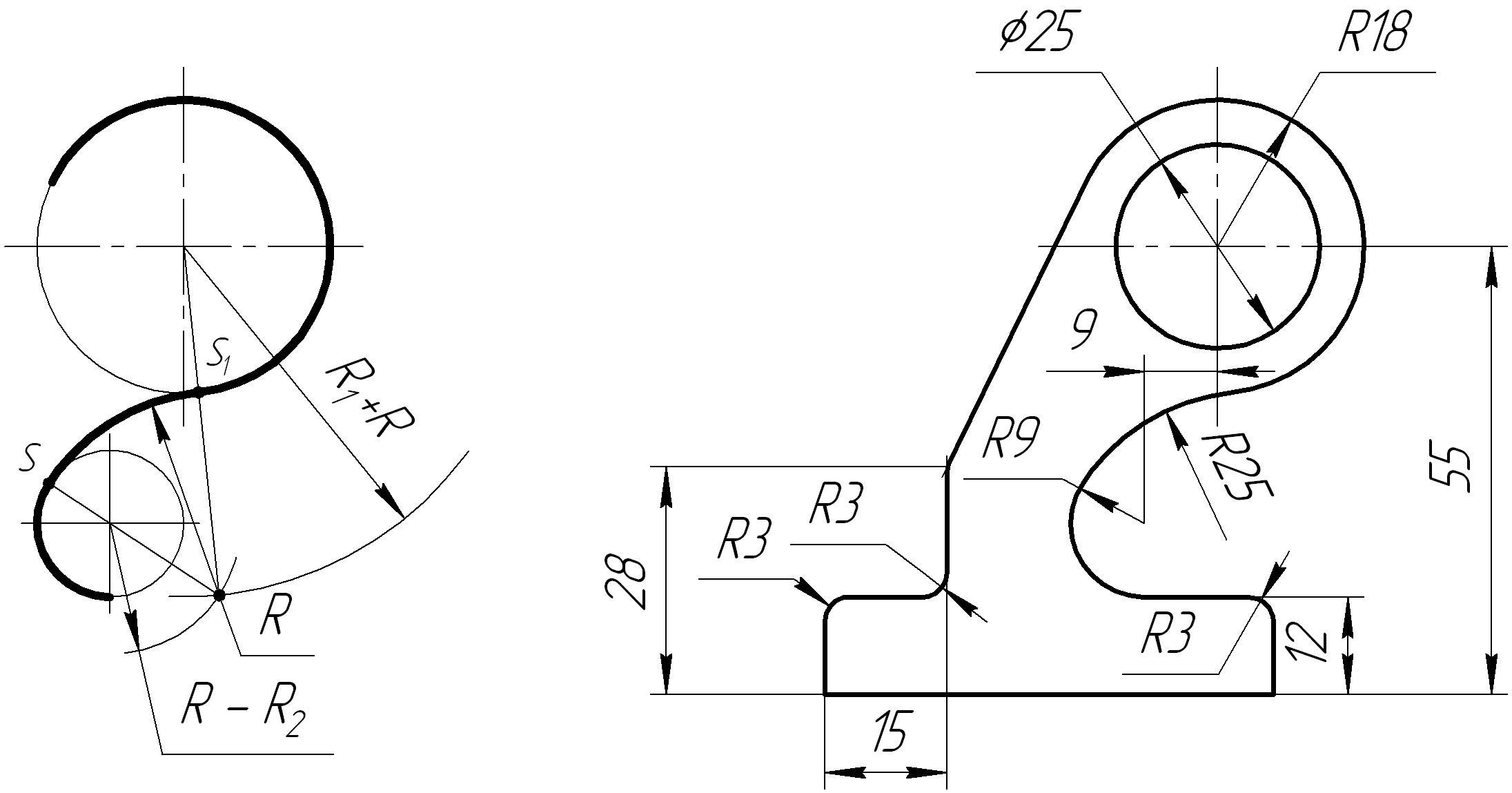
а)
б)
Рисунок 41 –
Построение сопряжений
По
заданным расстояниям между центрами
l1
и l2
на чертеже намечают центры О и О1,
из которых описывают сопрягаемые дуги
радиусов R1
и R2.
Из центра О проводят вспомогательную
дугу окружности радиусом, равным сумме
радиусов сопрягаемой дуги R1
и сопрягающей R, а из центра О1
– радиусом, равным разности радиусов
R и R2.
Вспомогательные дуги пересекутся в
точке О2,
которая и будет искомым центром
сопрягающей дуги.
Соединив
точки О и О2
прямой получают точку сопряжения S1,
соединив точки О1
и О2
находят точку сопряжения S.
Из центра О2
проводят дугу сопряжения от S
до S1.
Таблица
6 – Варианты графической работы на
построение сопряжений
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение
таблицы 6
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение
таблицы 6
|
|
|
|
|
|
|
|
|
Продолжение
таблицы 6
|
|
|
|
|
|
|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
11.1 Сопряжения. Контур многих деталей машин и приборов состоит из прямых линий и дуг окружностей с плавными переходами от одной линии к другой. Итак, плавный переход одной линии в другую называется сопряжением. Эта дуга называется дугой сопрягающей окружности (рис.27). Радиус этой окружности – это радиус сопряжения. Центр этой окружности – это центр сопряжения. Точка, где одна линия переходит в другую – это точка сопряжения.
Сопряжение прямой линии и окружности и сопряжение окружности с другой окружностью бывает внешнее, внутреннее, смешанное (рис.28).
Внешнее сопряжение (рис.28,а). Сопрягаются две окружности. Их центры лежат внутри сопрягающей окружности. Такое сопряжение называется внешним.
Внутреннее сопряжение (рис.28,б). Сопрягаются две окружности. Их центры лежат вне сопрягающей окружности. Такое сопряжение называется внутренним.
Смешанное сопряжение (рис.28,в). Сопрягаются две окружности. Центр одной окружности лежит вне сопрягающей окружности, центр другой окружности лежит внутри сопрягающей окружности. Такое сопряжение называется смешанным.
Построить сопряжение – это значит найти центр сопряжения и точки сопряжения.
1. Сопряжение прямых дугой окружности применяется при скруглении углов (если задан радиус сопряжения R). На рис.29,а показана последовательность построения сопряжения сторон угла дугой радиуса R. Сначала проводят две прямые, параллельные сторонам угла, на расстоянии радиуса R сопряжения. Точка О пересечения вспомогательных прямых – центр дуги сопряжения. Перпендикуляры, опущенные из центра О на данные прямые, определяют точки сопряжения А и В. Радиусом R проводят дугу сопряжения между точками А и В. На рис.29,б показано практическое применение сопряжение.
Внешнее сопряжение дуги окружности и прямой. Сопряжение дуги окружности радиуса R с прямой а дуги радиуса R1 показано на рис.30.
Для построения такого сопряжения вычерчивают дугу окружности радиуса R + R1 с центром в т.О1 . Затем проводим прямую в, параллельную прямой а, на расстоянии равном радиусу сопрягающей дуги R1. Получаем точку О – центр сопряжения. Проводим прямую ОО1, получаем точку сопряжения 1. Опускаем из т.О перпендикуляр на прямую а. Получаем точку сопряжения 2. Проводим сопрягающую дугу радиуса R1 от точки 1 до точки 2.
2. Внешнее сопряжение двух дуг (рис.31). При внешнем сопряжении дуги радиуса R1 и дуги радиуса R2 дугой окружности сопряжения радиуса R центр сопряжения О определяется в точке пересечения вспомогательных дуг радиусов
R1+ R и R2+ R, которые проведены из центров О1 и О2. Пересечение лучей ОО1 и ОО2 с заданными окружностями даёт точки сопряжения А и В. Радиусом R проводят дугу сопряжения между точками А и В.
3. При внутреннем сопряжении (рис.32) центр сопряжения О определяется в точке пересечения вспомогательных дуг радиусов R – R1 и R – R2, которые проводятся соответственно из центров О1 и О2. Точки сопряжения А и В лежат на пересечении продолжений прямых ОО1 и ОО2 с окружностями. Радиусом R проводят дугу сопряжения между точками А и В.
Графическая работа
На листе формата А4 выполнить построение детали «Коромысло» на рис.31,б.
Дано: R1= 30, R2 = 15, О1О2 = 60, два отверстия Ø30 с центром О1 и Ø10 с центром О2 .
Масштаб 1:1.
Материал: Ст 3
Дополнительная информация:
Черчение Урок №1 Основы черчения Линии чертежа”
Черчение Урок №1 (продолжение) Как наносят размеры по стандарту
Черчение Урок №2 Графическая работа Чертеж плоской детали
Черчение Урок №3 Шрифты чертежные ГОСТ 2.304-81
Черчение Урок №4 Чертежи в системе прямоугольных проекций
Черчение Урок №5 Прямоугольное проецирование
Черчение Урок №6 Расположение видов на чертеже
Черчение Урок №7 Геометрические построения
Черчение Урок №8 Геометрические построения (продолжение)
Черчение Урок №9 Окружность Построение многоугольников
Черчение Урок №10 Касательная к окружности
Черчение Урок №11 Графические построения Сопряжения
Черчение Урок №12 Графические построения Овалы
Черчение Урок №13 Графические построения Завиток
Черчение Урок №14 Графические построения Лекальные кривые

 1
1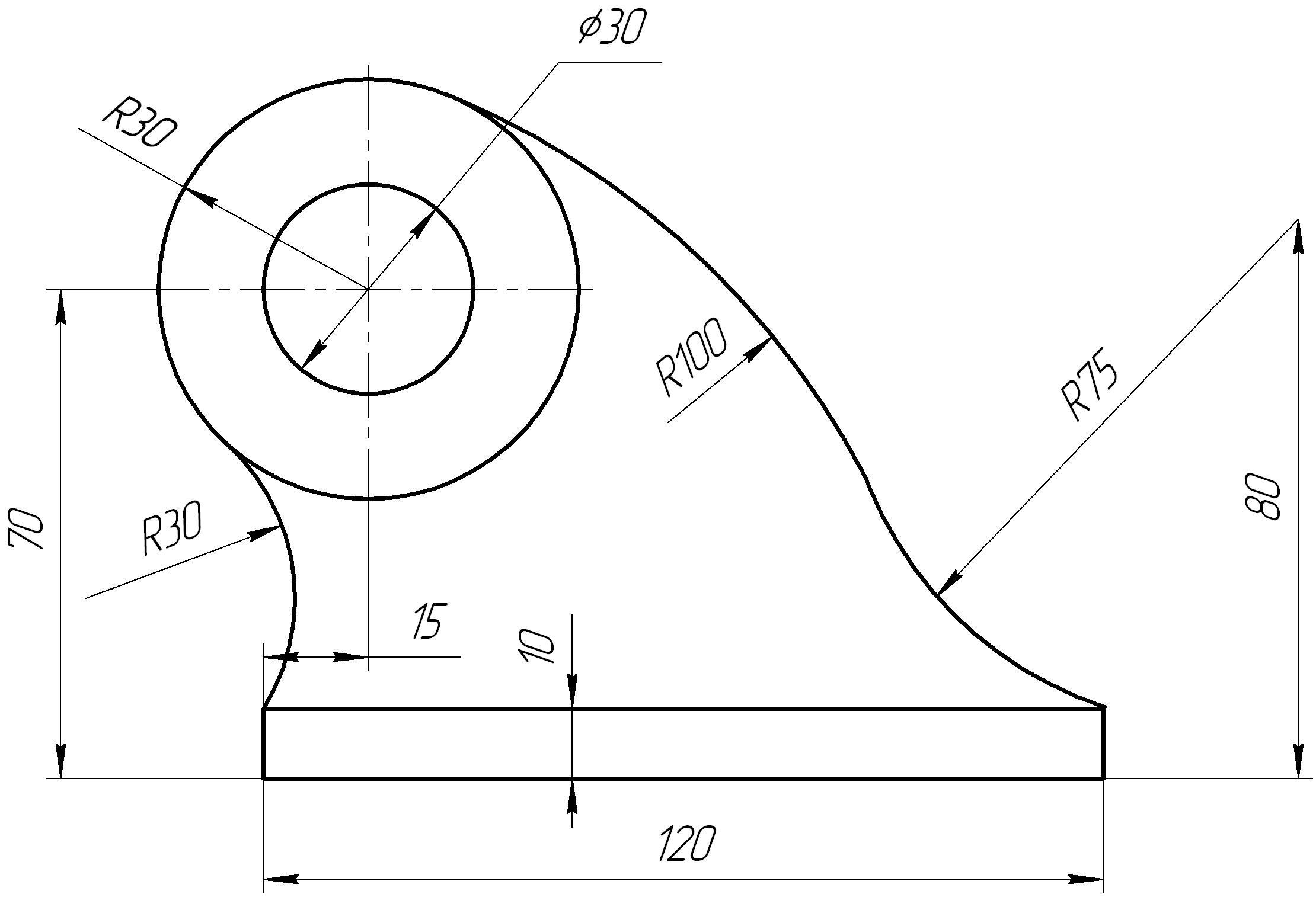 2
2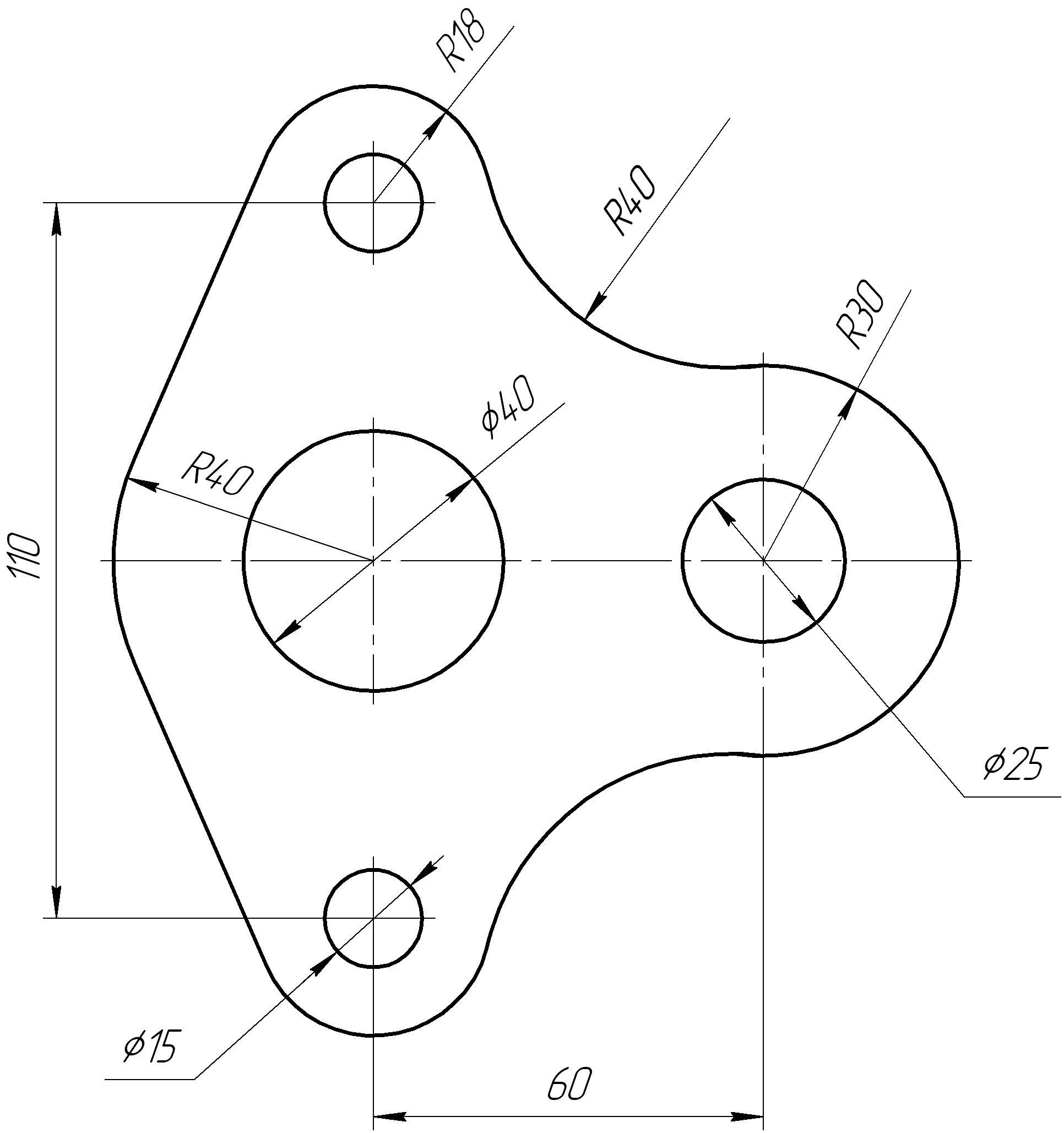 3
3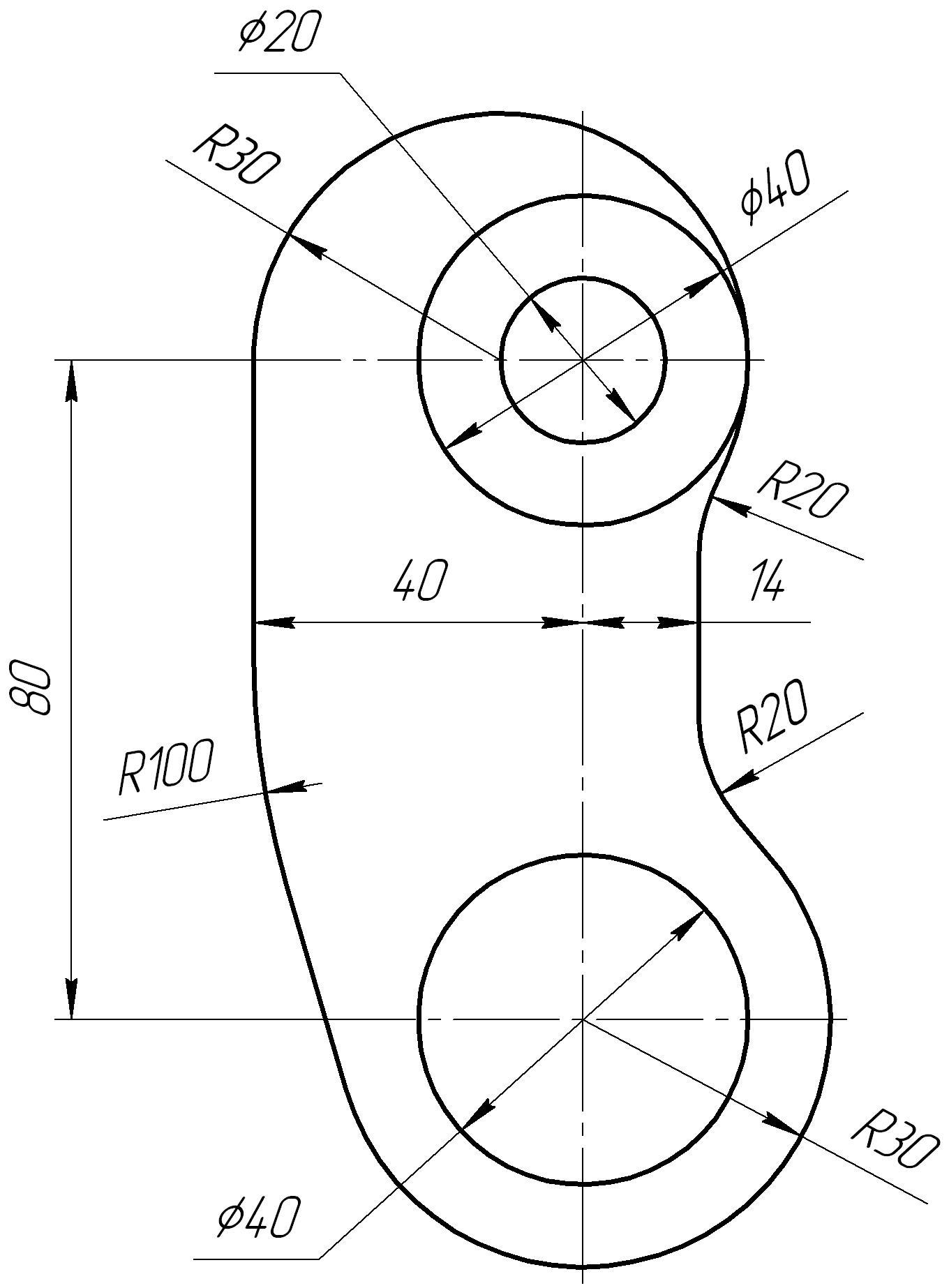 4
4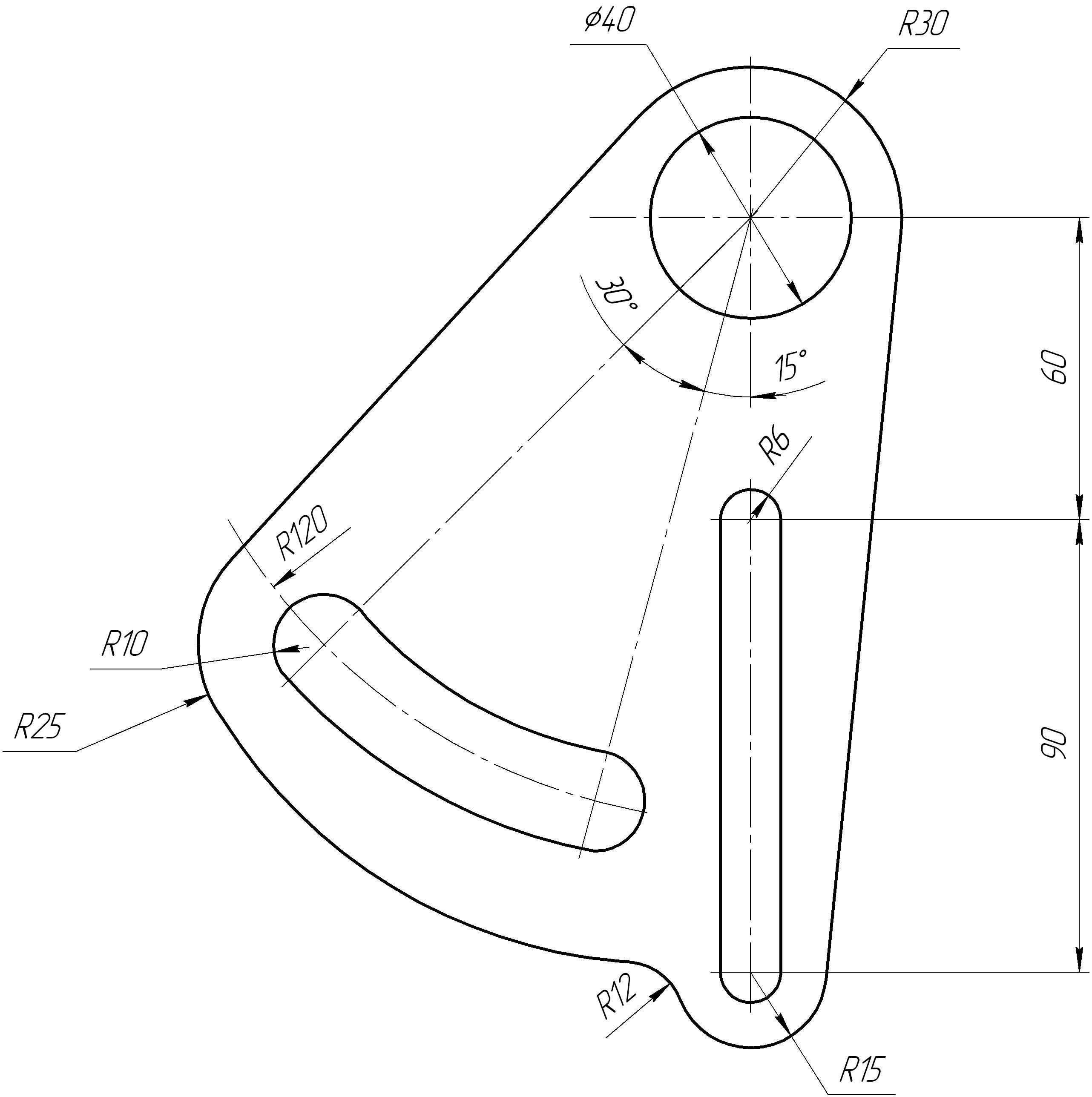 5
5 6
6 7
7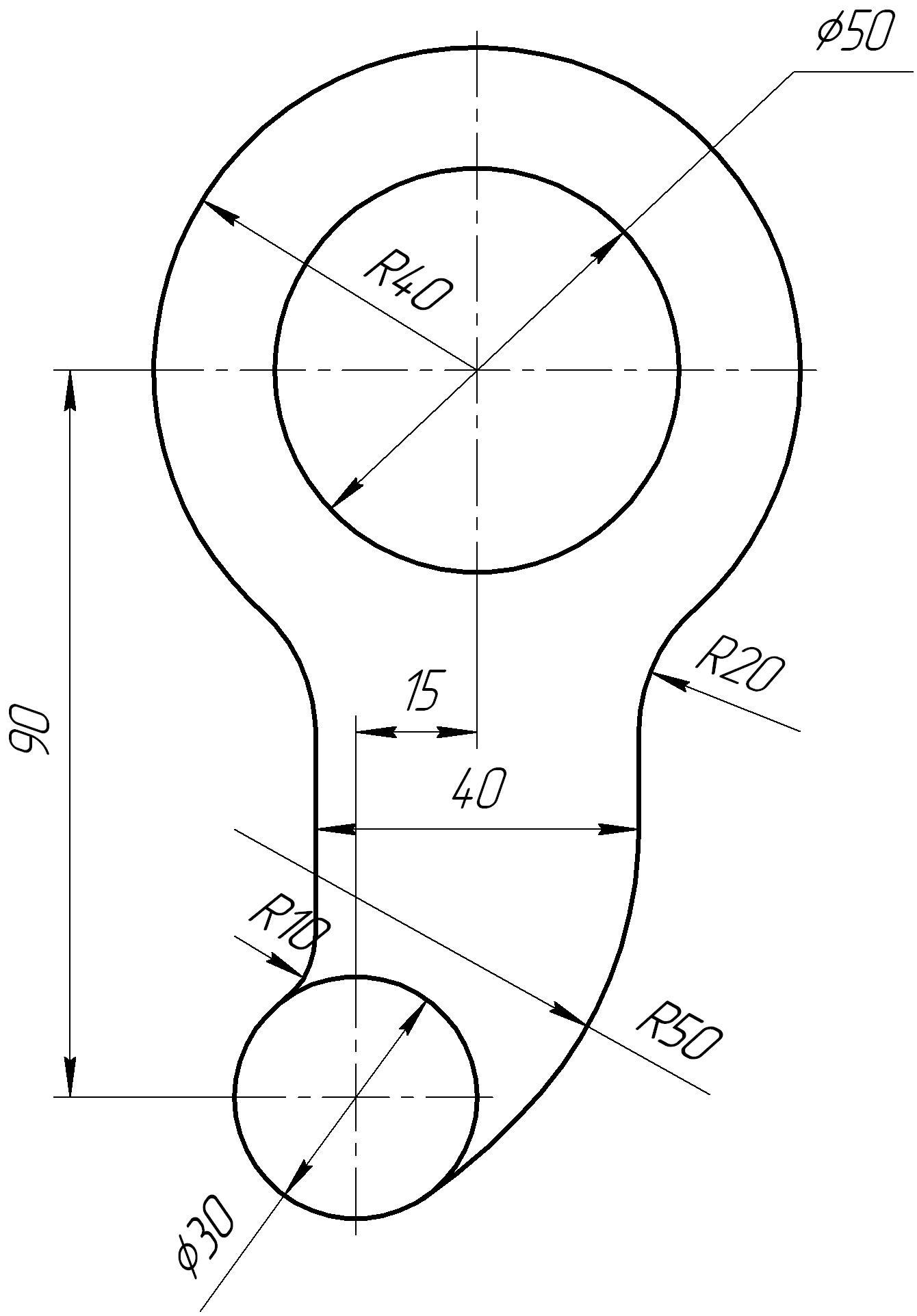 8
8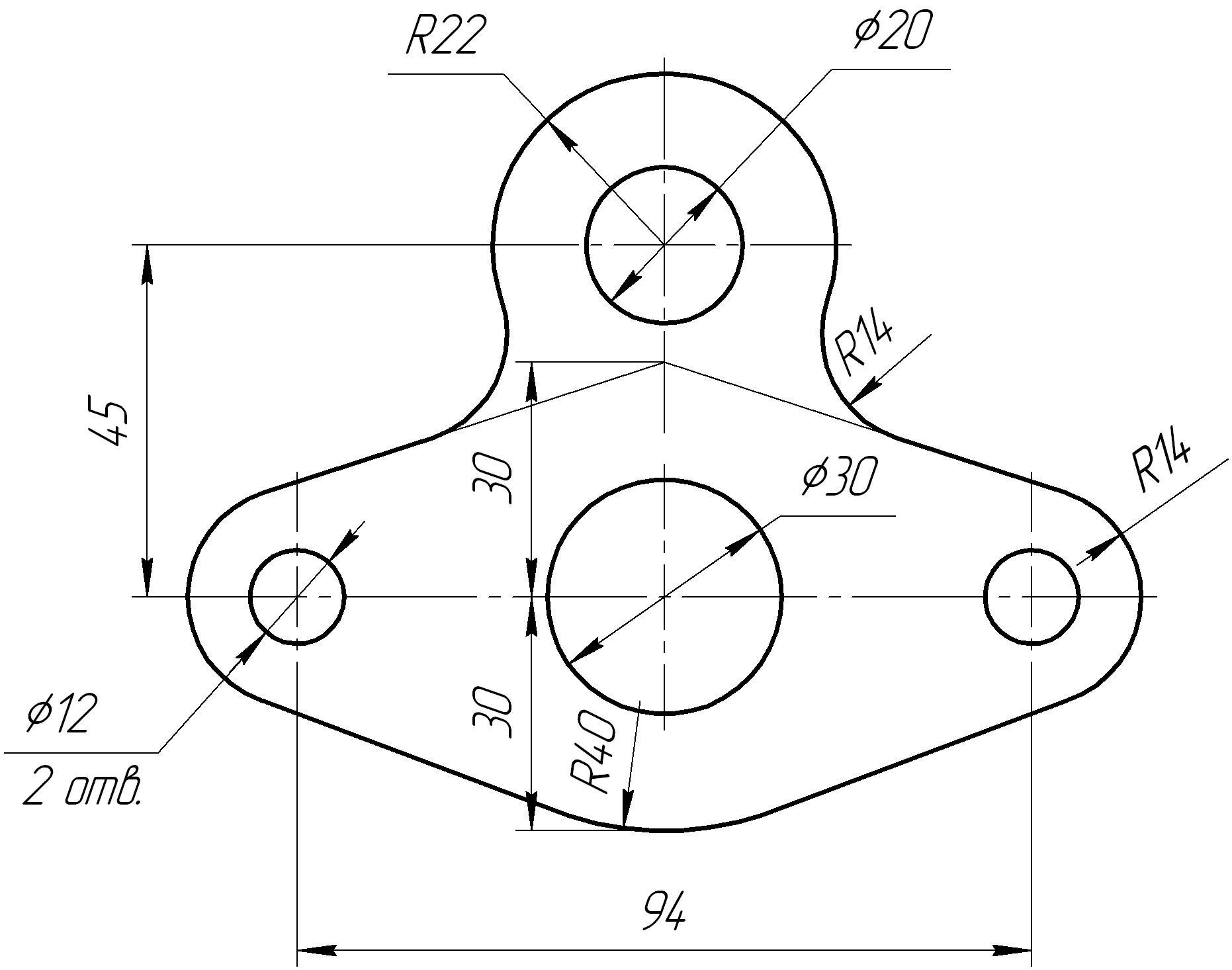 9
9 10
10 11
11 12
12 13
13 14
14 15
15 16
16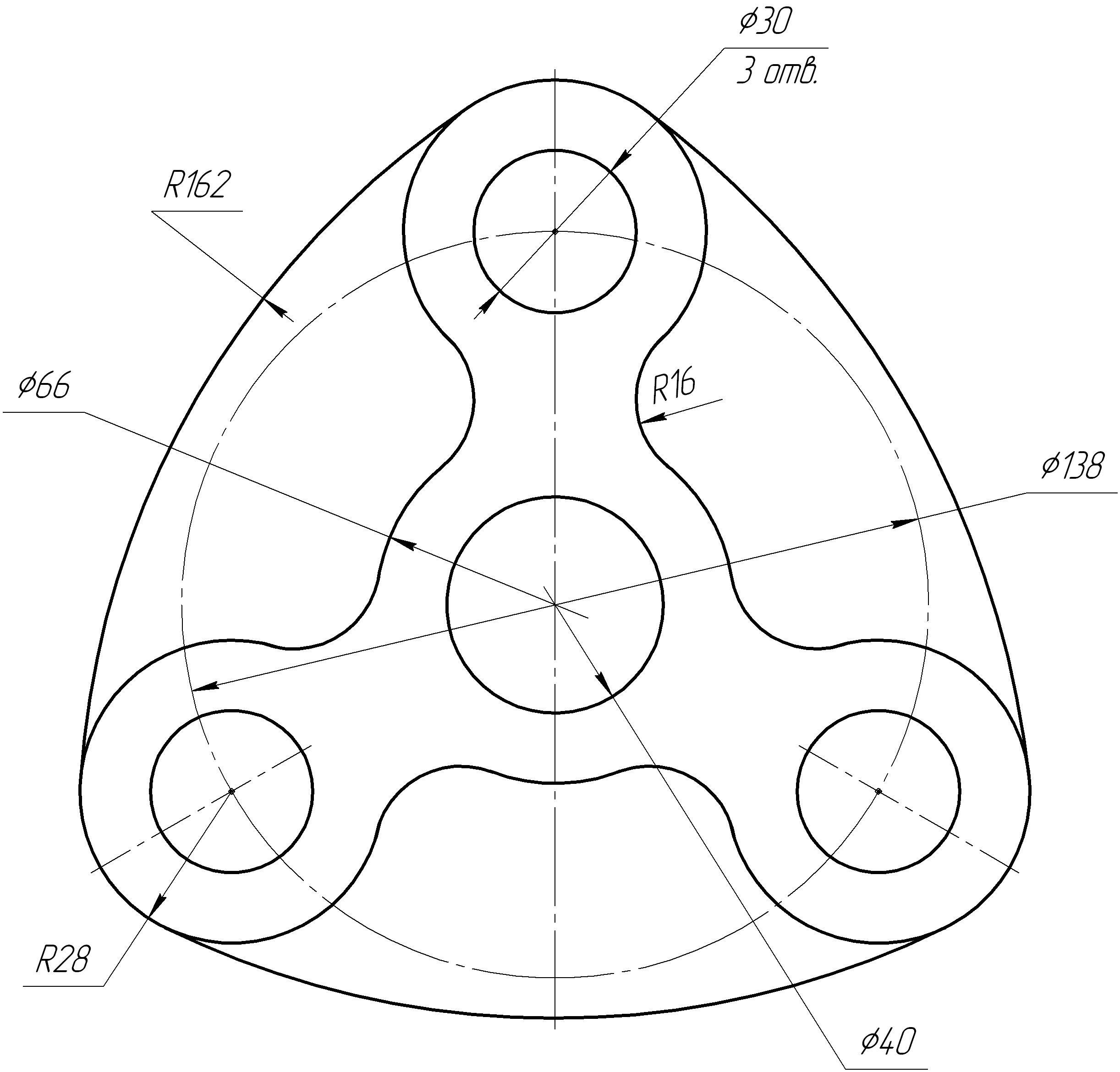 17
17 18
18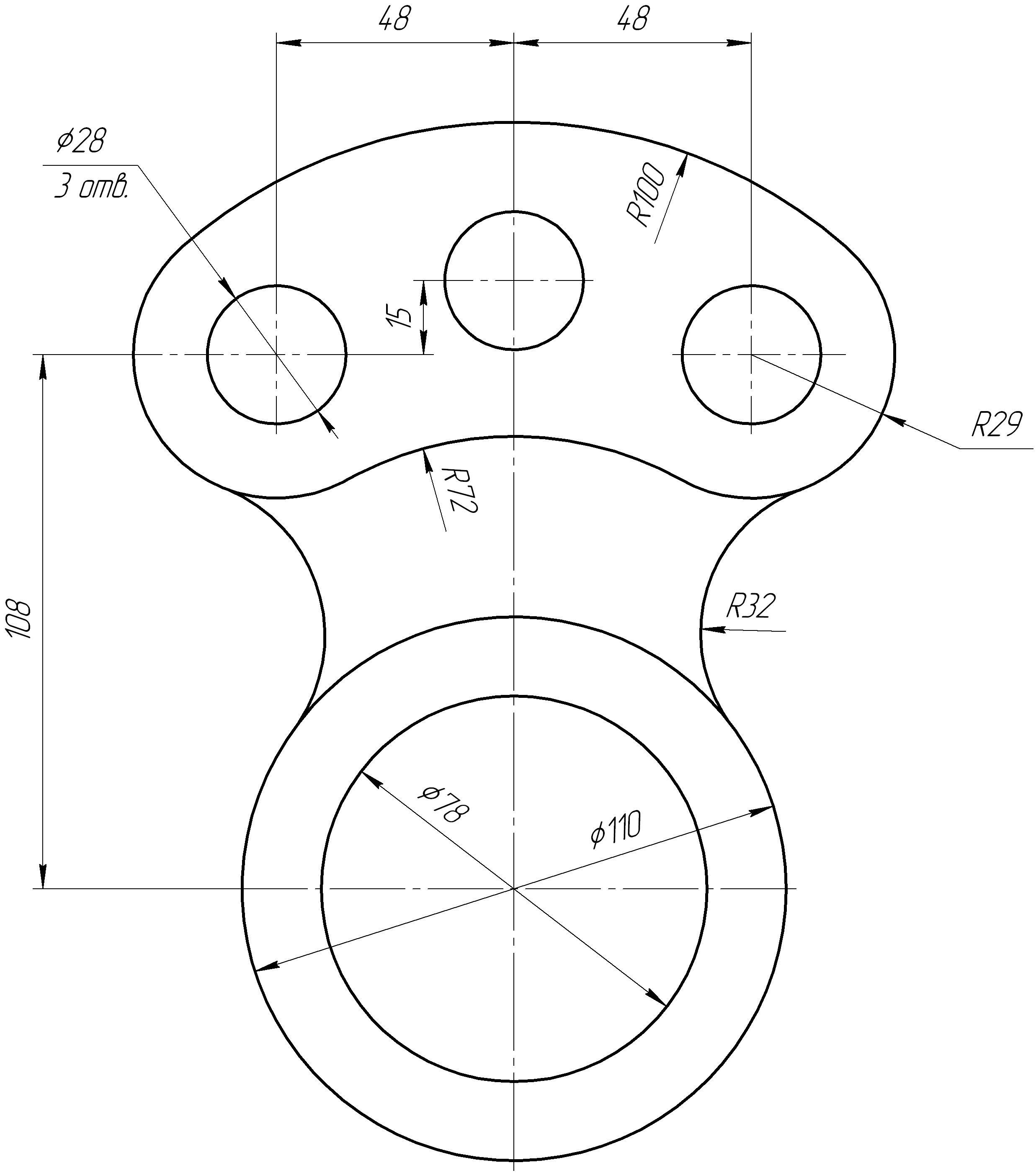 19
19 20
20 21
21 22
22 23
23 24
24 25
25 26
26 28
28 29
29