Проекции точек на поверхностях геометрических тел
Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.
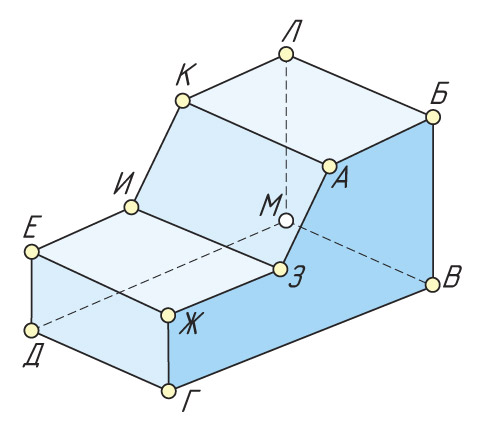
![]() Укажите количество вершин, ребер и граней изображенного предмета.
Укажите количество вершин, ребер и граней изображенного предмета.
|
Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки. |
 |
|
Рассмотрим проекции точки на геометрических телах. Проецирование точек на поверхности цилиндра Последовательность проецирования точек 1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью. 2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи. |
 |
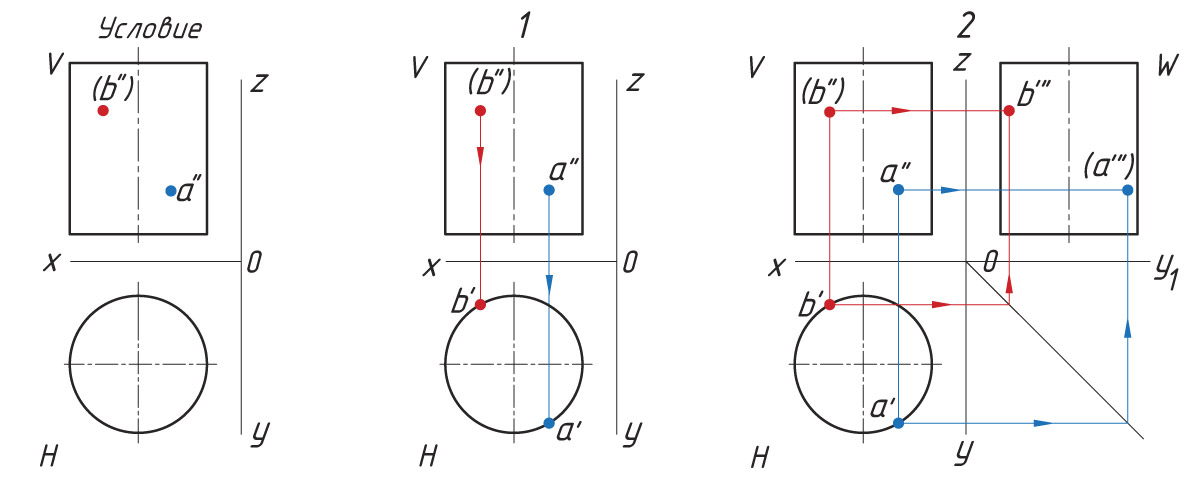
Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).
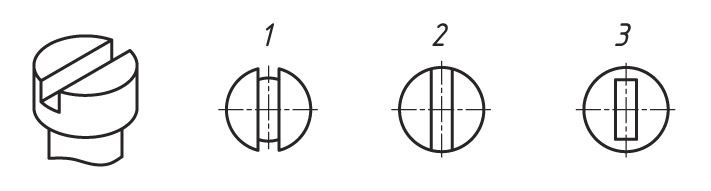
![]() Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.
Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта.
|
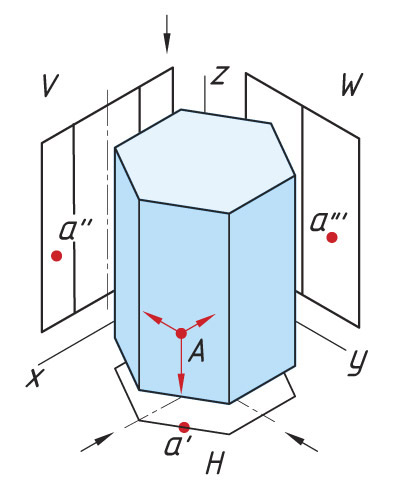
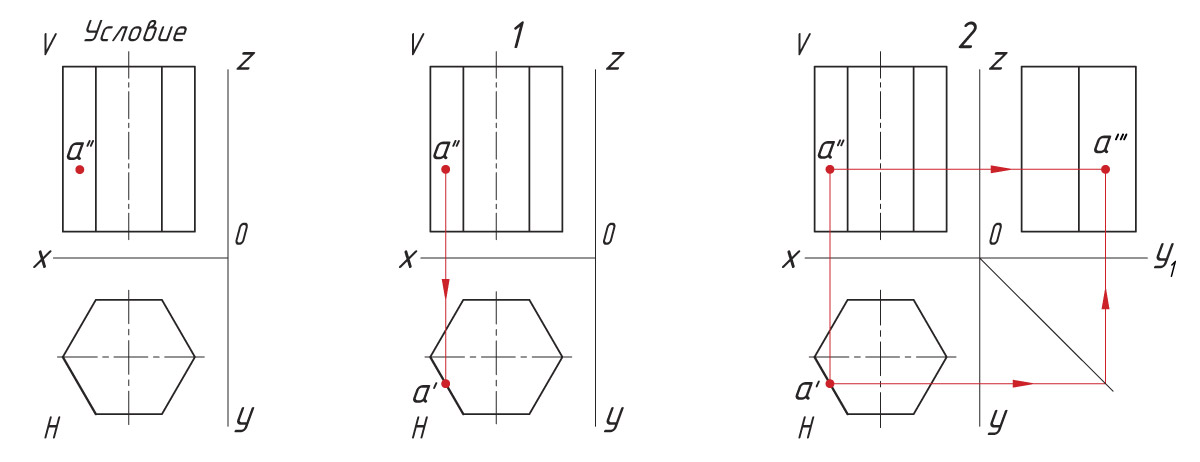
Проецирование точек на поверхности призмы Последовательность проецирования точек 1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы). 2. Проекцию точки а′″ находят на пересечении линий проекционной связи. |
 |
![]()
Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.
Проецирование точек на поверхности пирамиды
Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.

![]() Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.
Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.
Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.
Построение проекции точки, лежащей на грани
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.
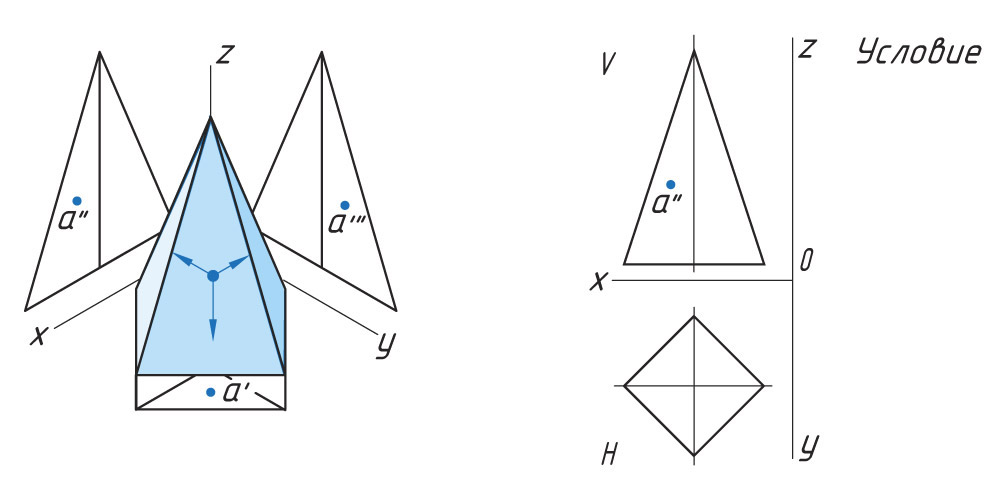
Проекции точек можно определить несколькими способами. Рассмотрим каждый из них.
|
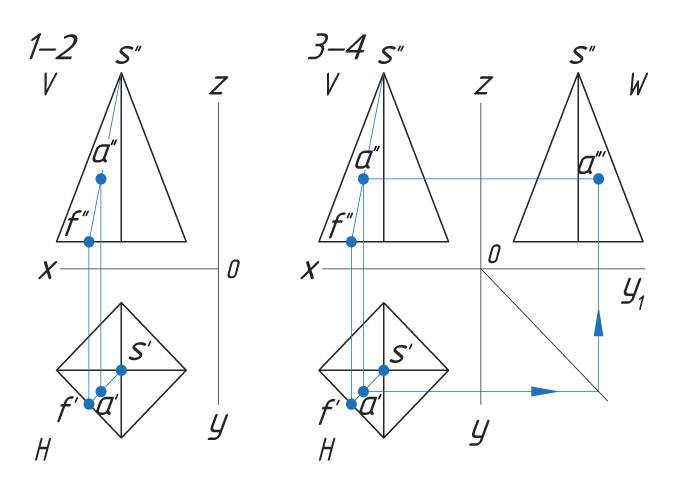
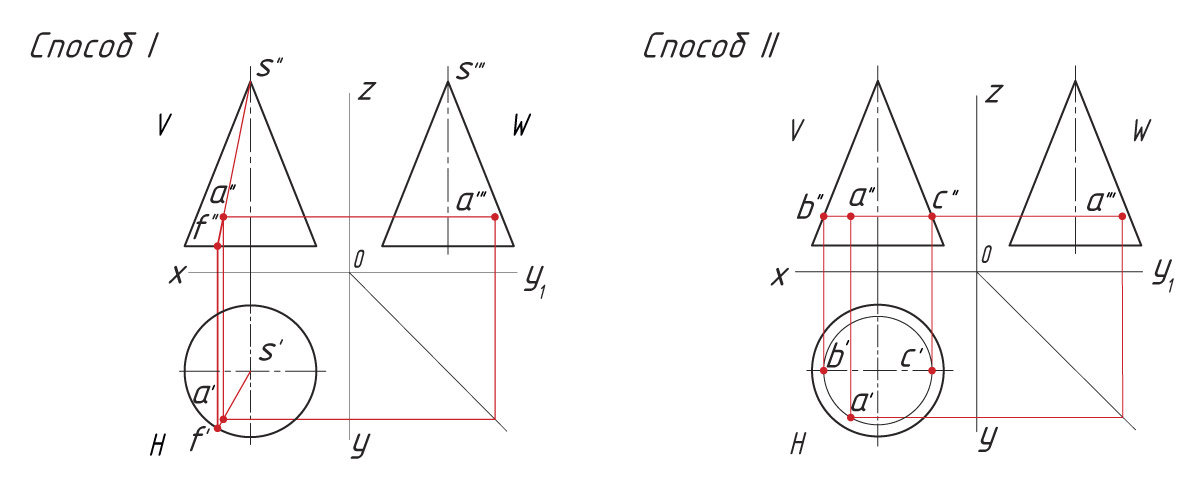
Способ I. 1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″. |
 |
|
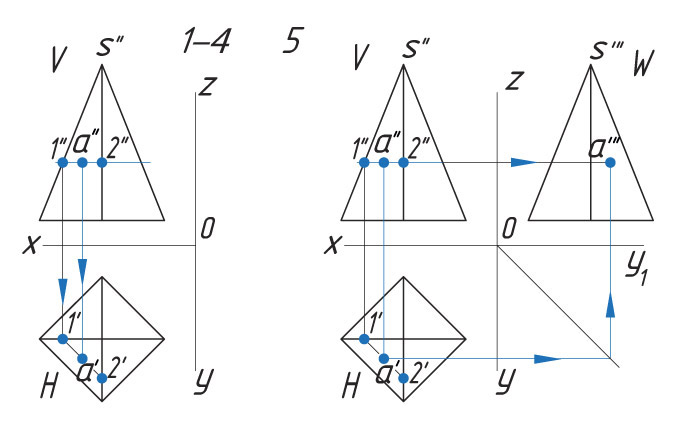
Способ II. 1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″. |
 |
![]() На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?
На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?
|
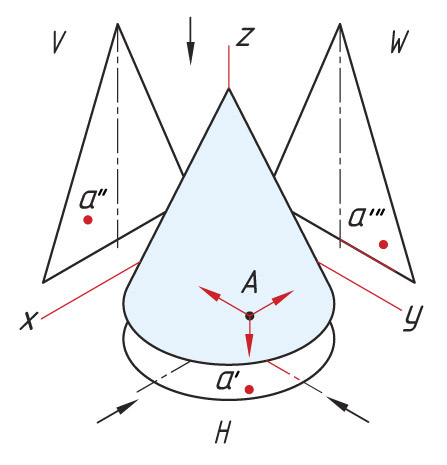
Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами. Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А. |
 |
Изучение
способов построения проекций любых
объектов начинают с изучения
правилпостроения проекций точек. Возьмем
в пространстве две взаимно перпендикулярные
плоскости. Одна из них располагается
горизонтально – ее называют горизонтальной
плоскостью проекций и обозначают буквой
ᴨ1.
Другая плоскость перпендикулярна
горизонтальной и называется фронтальной
плоскостью проекций. Эта плоскость
обозначается буквой ᴨ2
(рис. 1.9). Линияпересечения плоскостей
проекций называется осью проекций. Ось
проекций x разделяет каждую из плоскостей
на две полуплоскости. Четыре двугранных
угла I, II, III, IV, образованныхпри пересечении
плоскостей, называются четвертями или
квадрантами пространства.
Спроецируем
точку А, расположенную в I четверти, на
плоскости проекций 1 и 2.
Горизонтальной
проекцией точки называют прямоугольную
проекцию точки на горизонтальной
плоскости проекций. Горизонтальную
проекцию находим как точку пересечения
перпендикуляра, проведенного из точки
А, с плоскостью ᴨ1
. Обозначим ее символом А’. Проведем
източки А’ в плоскости ᴨ1
перпендикуляр на ось Оx и отметим
вспомогательную точку Ах.
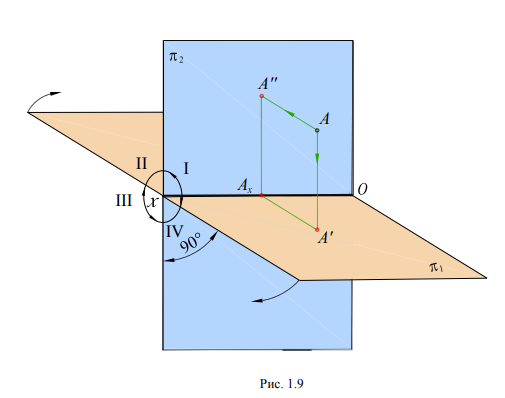
Фронтальной
проекцией точки называют прямоугольную
проекцию точки на фронтальной плоскости
проекций. Фронтальную проекцию находим
как точку пересечения перпендикуляра,
проведенного из точки А, с плоскостью
ᴨ2.
Обозначим ее А”. Опустив перпендикуляр
източки А” в плоскости ᴨ2
на ось Оx, получим вспомогательную точку
Ах.
Рассмотрим
обратную задачу – построение точки А
в пространстве по двум заданным
еепроекциям – горизонтальной А’ и
фронтальной А”. Точку А находим в
пересечении перпендикуляров, проведенных
из проекции А’ к плоскости ᴨ1
и из проекции А” к плоскости ᴨ2.
Эти перпендикуляры пересекутся в
единственной искомой точке А пространства.
Таким
образом, две прямоугольные проекции
точки вполне определяют ее положение
впространстве относительно данной
системы взаимно перпендикулярных
плоскостей проекций –т. е. чертеж
становится обратимым.
Для
получения плоского чертежа точки
необходимо совместить плоскость ᴨ1
с плоскостьюᴨ2
поворотом вокруг оси Оx на угол 90 вниз
по стрелке, как это показано на рис. 1.9.
При этомотрезки АхА” и АхА’ образуют
один отрезок А”А’, перпендикулярный к
оси Оx. Этот отрезок А”А’называется
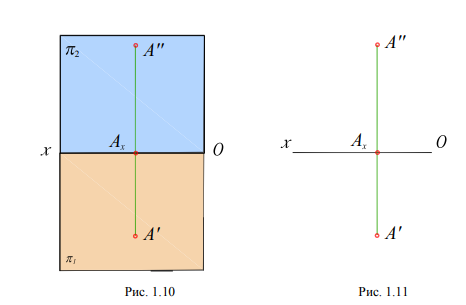
линией проекционной связи (рис. 1.10). В
результате совмещения плоскостей
проекций получается чертеж, известный
под названием эпюр Монжа (Epure – чертеж
(франц.)). Онбыл назван в честь основоположника
начертательной геометрии французского
ученого ГаспараМонжа. Без обозначения
плоскостей ᴨ1
и ᴨ2
этот чертеж будет выглядеть так, как
это показанона рис. 1.11.
Иногда
двух проекций геометрического элемента
бывает недостаточно, чтобы определитьего
форму и истинные размеры. Тогда выполняют
построение изображения на третьей
плоскости.
Введем
в систему ᴨ1,
ᴨ2
третью плоскость проекций, перпендикулярную
плоскостям ᴨ1
и ᴨ2.
Ее называют профильной плоскостью
проекций и обозначают ᴨ3
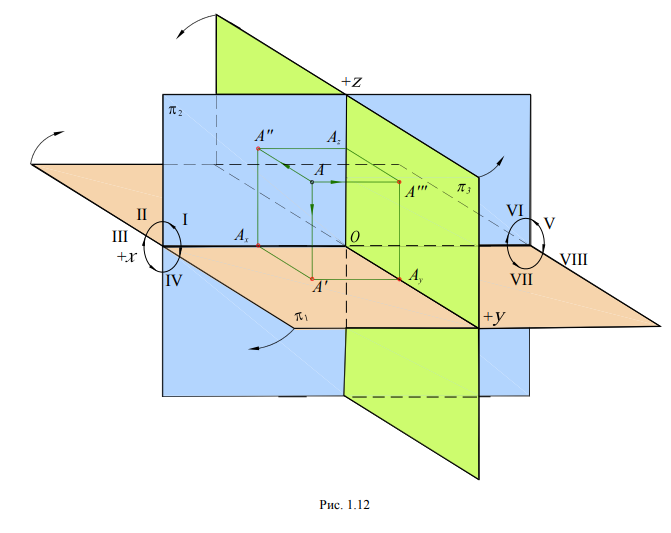
(рис. 1.12).
Три
взаимно перпендикулярные плоскости
проекций называются координатными
плоскостями. Они пересекаются по трем
взаимно перпендикулярным прямым Оx, Oy,
Oz, которыеназываются осями координат
и обозначаются x, y, z. Общая точка О –
начало координат.
Плоскости
ᴨ1,
ᴨ2,
ᴨ3,
пересекаясь между собой, делят пространство
на восемь частей, называемых октантами,
как это показано на рис. 1.12. В зависимости
от положения точки относительно
плоскостей проекций ее координаты могут
иметь положительные и отрицательные
значения. Например, в первом октанте
все координаты имеют положительные, а
в седьмом – отрицательные значения.
Соседние файлы в папке НГ 1курс. Лекции
- #
- #
- #
- #
- #
- #
- #
Лекция № 2. Точка
1. Проекции точки на две плоскости проекций
Рассмотрим проекции точек на две плоскости, для чего возьмем две перпендикулярные плоскости (рис. 4), которые будем называть горизонтальной фронтальной и плоскостями. Линию пересечения данных плоскостей называют осью проекций. На рассмотренные плоскости спроецируем одну точку А с помощью плоской проекции. Для этого необходимо опустить из данной точки перпендикуляры Аа и A на рассмотренные плоскости.
Проекцию на горизонтальную плоскость называют горизонтальной проекцией точки А, а проекцию а́ на фронтальную плоскость называют фронтальной проекцией.

Точки, которые подлежат проецированию, в начертательной геометрии принято обозначать с помощью больших латинских букв А, В, С. Для обозначения горизонтальных проекций точек применяют малые буквы а, b, с… Фронтальные проекции обозначают малыми буквами со штрихом вверху а́, b́, с́…
Применяется также и обозначение точек римскими цифрами I, II,… а для их проекций — арабскими цифрами 1, 2… и 1́, 2́…
При повороте горизонтальной плоскости на 90° можно получить чертеж, в котором обе плоскости находятся в одной плоскости (рис. 5). Данная картина называется эпюром точки.

Через перпендикулярные прямые Аа и Аа́ проведем плоскость (рис. 4). Полученная плоскость является перпендикулярной фронтальной и горизонтальной плоскостям, потому что содержит перпендикуляры к этим плоскостям. Следовательно, данная плоскость перпендикулярна линии пересечения плоскостей. Полученная прямая пересекает горизонтальную плоскость по прямой аах, а фронтальную плоскость — по прямой а́ах. Прямые аах и а́ах являются перпендикулярными оси пересечения плоскостей. То есть Аааха́ является прямоугольником.
При совмещении горизонтальной и фронтальной плоскостей проекции а и а́ будут лежать на одном перпендикуляре к оси пересечения плоскостей, так как при вращении горизонтальной плоскости перпендикулярность отрезков аах и а́ах не нарушится.
Получаем, что на эпюре проекции а и а́ некоторой точки А всегда лежат на одном перпендикуляре к оси пересечения плоскостей.
Две проекции а и а́ некоторой точки А могут однозначно определить ее положение в пространстве (рис. 4). Это подтверждается тем, что при построении перпендикуляра из проекции а к горизонтальной плоскости он пройдет через точку А. Точно так же перпендикуляр из проекции а́ к фронтальной плоскости пройдет через точку А, т. е. точка А находится одновременно на двух определенных прямых. Точка А является их точкой пересечения, т. е. является определенной.
Рассмотрим прямоугольник Aaaха́ (рис. 5), для которого справедливы следующие утверждения:
1) Расстояние точки А от фронтальной плоскости равно расстоянию ее горизонтальной проекции а от оси пересечения плоскостей, т. е.
Аа́ = аах;
2) расстояние точки А от горизонтальной плоскости проекций равно расстоянию ее фронтальной проекции а́ от оси пересечения плоскостей, т. е.
Аа = а́ах.
Иначе говоря, даже без самой точки на эпюре, используя только две ее проекции, можно узнать, на каком расстоянии от каждой из плоскостей проекций находится данная точка.
Пересечение двух плоскостей проекций разделяет пространство на четыре части, которые называют четвертями (рис. 6).
Ось пересечения плоскостей делит горизонтальную плоскость на две четверти — переднюю и заднюю, а фронтальную плоскость — на верхнюю и нижнюю четверти. Верхнюю часть фронтальной плоскости и переднюю часть горизонтальной плоскости рассматривают как границы первой четверти.

При получении эпюра вращается горизонтальная плоскость и совмещается с фронтальной плоскостью (рис. 7). В этом случае передняя часть горизонтальной плоскости совпадет с нижней частью фронтальной плоскости, а задняя часть горизонтальной плоскости — с верхней частью фронтальной плоскости.

На рисунках 8-11 показаны точки А, В, С, D, располагающиеся в различных четвертях пространства. Точка А расположена в первой четверти, точка В — во второй, точка С — в третьей и точка D — в четвертой.

При расположении точек в первой или четвертой четвертях их горизонтальные проекции находятся на передней части горизонтальной плоскости, а на эпюре они лягут ниже оси пересечения плоскостей. Когда точка расположена во второй или третьей четверти, ее горизонтальная проекция будет лежать на задней части горизонтальной плоскости, а на эпюре будет находиться выше оси пересечения плоскостей.

Фронтальные проекции точек, которые расположены в первой или второй четвертях, будут лежать на верхней части фронтальной плоскости, а на эпюре будут находиться выше оси пересечения плоскостей. Когда точка расположена в третьей или четвертой четверти, ее фронтальная проекция — ниже оси пересечения плоскостей.
Чаще всего при реальных построениях фигуру располагают в первой четверти пространства.
В некоторых частных случаях точка (Е) может лежать на горизонтальной плоскости (рис. 12). В этом случае ее горизонтальная проекция е и сама точка будут совпадать. Фронтальная проекция такой точки будет находиться на оси пересечения плоскостей.
В случае, когда точка К лежит на фронтальной плоскости (рис. 13), ее горизонтальная проекция k лежит на оси пересечения плоскостей, а фронтальная ḱ показывает фактическое местонахождение этой точки.

Для подобных точек признаком того, что она лежит на одной из плоскостей проекций, служит то, что одна ее проекция находится на оси пересечения плоскостей.
Если точка лежит на оси пересечения плоскостей проекций, она и обе ее проекции совпадают.
Когда точка не лежит на плоскостях проекций, она называется точкой общего положения. В дальнейшем, если нет особых отметок, рассматриваемая точка является точкой общего положения.
2. Отсутствие оси проекций
Для пояснения получения на модели проекций точки на перпендикулярные плоскости проекций (рис. 4) необходимо взять кусок плотной бумаги в форме удлиненного прямоугольника. Его нужно согнуть между проекциями. Линия сгиба будет изображать ось пересечения плоскостей. Если после этого согнутый кусок бумаги вновь расправить, получим эпюр, похожий на тот, что изображен на рисунке.
Совмещая две плоскости проекций с плоскостью чертежа, можно не показывать линию сгиба, т. е. не проводить на эпюре ось пересечения плоскостей.
При построениях на эпюре всегда следует располагать проекции а и а́ точки А на одной вертикальной прямой (рис. 14), которая перпендикулярна оси пересечения плоскостей. Поэтому, даже если положение оси пересечения плоскостей остается неопределенным, но ее направление определено, ось пересечения плоскостей может находиться на эпюре только перпендикулярно прямой аа́.

Если на эпюре точки нет оси проекций, как на первом рисунке 14 а, можно представить положение этой точки в пространстве. Для этого проведем в любом месте перпендикулярно прямой аа́ ось проекции, как на втором рисунке (рис. 14) и согнем чертеж по этой оси. Если восстановить перпендикуляры в точках а и а́ до их пересечения, можно получить точку А. При изменении положения оси проекций получаются различные положения точки относительно плоскостей проекций, но неопределенность положения оси проекций не влияет на взаимное расположение нескольких точек или фигур в пространстве.
3. Проекции точки на три плоскости проекций
Рассмотрим профильную плоскость проекций. Проекции на две перпендикулярные плоскости обычно определяют положение фигуры и дают возможность узнать ее настоящие размеры и форму. Но бывают случаи, когда двух проекций оказывается недостаточно. Тогда применяют построение третьей проекции.
Третью плоскость проекции проводят так, чтобы она была перпендикулярна одновременно обеим плоскостям проекций (рис. 15). Третью плоскость принято называть профильной.
В таких построениях общую прямую горизонтальной и фронтальной плоскостей называют осью х, общую прямую горизонтальной и профильной плоскостей — осью у, а общую прямую фронтальной и профильной плоскостей — осью z. Точка О, которая принадлежит всем трем плоскостям, называется точкой начала координат.

На рисунке 15а показана точка А
Конец ознакомительного фрагмента.
Проецирование точки на две и три плоскости проекций:
Если из точки А, находящуюся в пространстве, относительно двух плоскостей проекций 
Они характеризуются координатами, которые численно равны расстоянию от точки А до соответствующих плоскостей проекций. Координаты обозначаются теми же буквами, что и оси вдоль которых измеряется расстояние, с присвоением индекса самой буквы.
Так, для точки А: 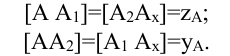
Плоскость прямоугольника 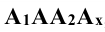 , перпендикулярна к: оси x, а линии пересечений плоскостей
, перпендикулярна к: оси x, а линии пересечений плоскостей 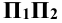 и плоскости
и плоскости 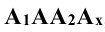 являются прямыми
являются прямыми 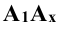 и
и 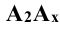 , перпендикулярными к оси х.
, перпендикулярными к оси х.
Изображение точки и её проекций на рис.3.1 является пространственным чертежом, что не всегда удобно для практики.
Рис. 2.4 Чтобы получить плоский чертёж, поворачивают плоскость  , вокруг оси х и совмещают её с плоскостью
, вокруг оси х и совмещают её с плоскостью 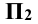 (рис. 3.1), получая таким образом. комплексный чертеж (эпюр Монжа)
(рис. 3.1), получая таким образом. комплексный чертеж (эпюр Монжа)
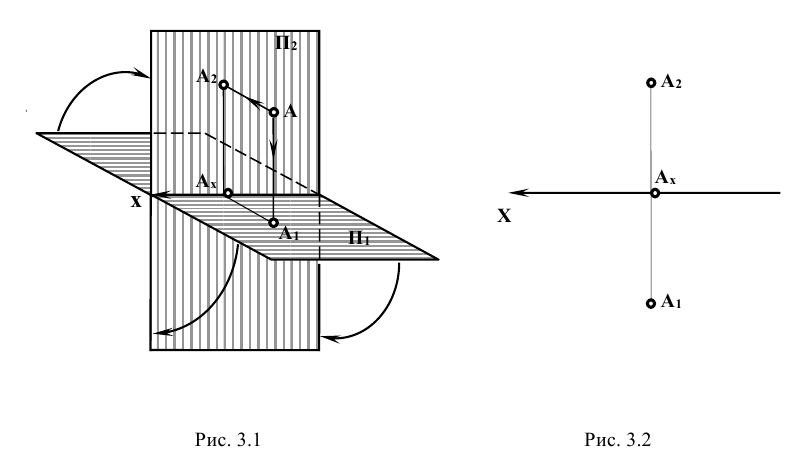
Проекции 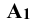 и
и 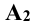 оказываются на одной линии, которая называется линией проекционной связи. Она перпендикулярна к оси х (рис. 3.2). При проецировании точки А на три плоскости проекций от плоскости
оказываются на одной линии, которая называется линией проекционной связи. Она перпендикулярна к оси х (рис. 3.2). При проецировании точки А на три плоскости проекций от плоскости 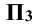 она отстоит на расстоянии
она отстоит на расстоянии  (рис. 3.3). При этом, аналогично вышесказанному:
(рис. 3.3). При этом, аналогично вышесказанному: 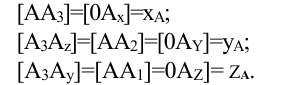
Для получения плоского чертежа в этом случае уже две плоскости  и
и 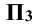 совмещаются с плоскостью
совмещаются с плоскостью 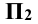 путём поворота их соответственно вокруг осей х и z. При этом ось у как бы раздваивается (как бы разрезается вдоль), и положение плоскостей будет таким, как показано на рис. 3.3. Профильная проекция
путём поворота их соответственно вокруг осей х и z. При этом ось у как бы раздваивается (как бы разрезается вдоль), и положение плоскостей будет таким, как показано на рис. 3.3. Профильная проекция 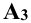 точки А находится на пересечении линий связи
точки А находится на пересечении линий связи 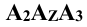 и
и 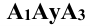 (расстояние
(расстояние 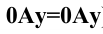 ).
).
Перенос точки Ау в точку (Aу) – понятен из чертежа, а сам отрезок есть не что иное, как координата YA.
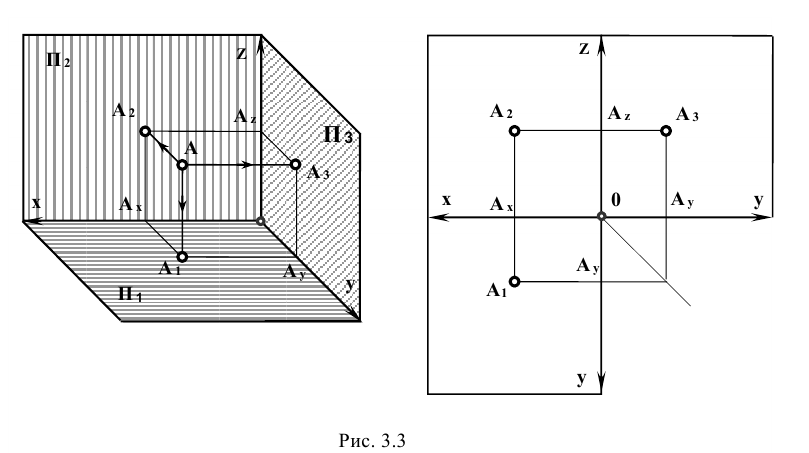
На плоском трёхмерном чертеже положительное направление оси х совпадает с отрицательным направлением оси у, а отрицательное направление оси y – с положительным направлением оси z. 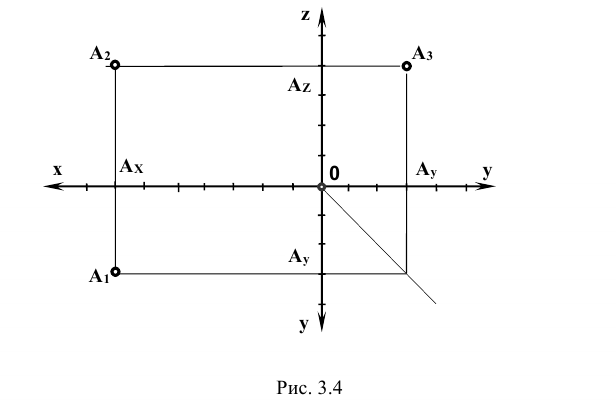
Это не означает, что модули этих величин обязательно равны между собой, т.е. 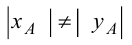 (в частном случае это равенство Ах Ау может быть). Те же рассуждения будут справедливы и в отношении направлений осей z и y (рис. 3.4).
(в частном случае это равенство Ах Ау может быть). Те же рассуждения будут справедливы и в отношении направлений осей z и y (рис. 3.4).
Таким образом, горизонтальная и фронтальная проекции точки А на плоском чертеже лежат на одной линии проекционной связи, перпендикулярной к оси x, а фронтальная и профильная проекции точки А на линии проекционной связи, перпендикулярной к оси z.
- Заказать чертежи
Определение по плоскому чертежу принадлежности точки тому или другому октанту пространства
Точка, например А, принадлежит:
Определение по плоскому чертежу принадлежности точки плоскостям проекций
Точка А принадлежит:
Любая точка лежит на оси проекций, если её смежные две проекции совпадают.
Так, точка А лежит на оси х, если 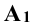 совпадает с
совпадает с 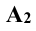 ; на оси у, если
; на оси у, если 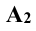 совпадает с
совпадает с 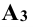 , и оси z, если
, и оси z, если 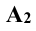 совпадает с
совпадает с 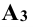 .
.
Правила знаков координат проекции точки
При построении проекции точки координата x всегда откладывается от начала координат (точка 0).
Положительное значение координаты у будут иметь точки, находящихся перед фронтальной плоскостью проекций 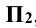 , отрицательное – расположенная за ней. Координату у можно откладывать непосредственно от оси х, от точки пересечения осей 0 (вниз – положительное значение, вверх – отрицательное).
, отрицательное – расположенная за ней. Координату у можно откладывать непосредственно от оси х, от точки пересечения осей 0 (вниз – положительное значение, вверх – отрицательное).
Положительное значение координаты z будут иметь точки, расположенные выше горизонтальной плоскости проекций 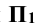 , а отрицательное – точки находящиеся ниже
, а отрицательное – точки находящиеся ниже 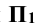 . Координату z на чертеже также можно откладывать от оси x, от точки пересечения осей 0 (вверх – положительное значение, вниз – отрицательное). Если рассматривать все восемь октантов пространства, то знаки для всех трёх координат точки (х, у, z) приведены в табл. 3.1
. Координату z на чертеже также можно откладывать от оси x, от точки пересечения осей 0 (вверх – положительное значение, вниз – отрицательное). Если рассматривать все восемь октантов пространства, то знаки для всех трёх координат точки (х, у, z) приведены в табл. 3.1
Таблица 3.1 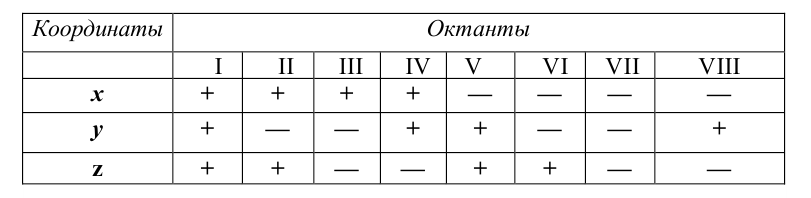
- Прямая в пространстве и ее изображение на чертеже
- Многогранники
- Поверхности вращения
- Пересечение прямой линии с поверхностью
- Собственные тени поверхностей вращения
- Построение падающих теней
- Проекции с числовыми отметкам
- Гранные поверхности
Построение ортогональных проекций точек
Положение точки в пространстве может быть задано двумя её ортогональными проекциями, например, горизонтальной и фронтальной, фронтальной и профильной. Сочетание любых двух ортогональных проекций позволяет узнать значение всех координат точки, построить третью проекцию, определить октант, в котором она находится. Рассмотрим несколько типичных задач из курса начертательной геометрии.
По заданному комплексному чертежу точек A и B необходимо:
- Записать их координаты.
- Достроить проекции т. A и B на плоскость П3.
- Определить положение точек в пространстве (октант или плоскость проекций).
- Построить наглядное изображение точек в системе плоскостей П1, П2, П3.

Определение координат точек по их проекциям
Определим сначала координаты т. A, которые можно записать в виде A (x, y, z). Горизонтальная проекция т. A – точка A’, имеющая координаты x, y. Проведем из т. A’ перпендикуляры к осям x, y и найдем соответственно Aх, Aу. Координата х для т. A равна длине отрезка AхO со знаком плюс, так как Aх лежит в области положительных значений оси х. С учетом масштаба чертежа находим х = 10. Координата у равна длине отрезка AуO со знаком минус, так как т. Aу лежит в области отрицательных значений оси у. С учетом масштаба чертежа у = –30. Фронтальная проекция т. A – т. A” имеет координаты х и z. Опустим перпендикуляр из A” на ось z и найдем Az. Координата z точки A равна длине отрезка AzO со знаком минус, так как Az лежит в области отрицательных значений оси z. С учетом масштаба чертежа z = –10. Таким образом, координаты т. A (10, –30, –10).
Координаты т. B можно записать в виде B (x, y, z). Рассмотрим горизонтальную проекцию точки B – т. В’. Так как она лежит на оси х, то Bx = B’ и координата Bу = 0. Абсцисса x точки B равна длине отрезка BхO со знаком плюс. С учетом масштаба чертежа x = 30. Фронтальная проекция точки B – т. B˝ имеет координаты х, z. Проведем перпендикуляр из B” к оси z, таким образом найдем Bz. Аппликата z точки B равна длине отрезка BzO со знаком минус, так как Bz лежит в области отрицательных значений оси z. С учетом масштаба чертежа определим значение z = –20. Таким образом, координаты B (30, 0, -20). Все необходимые построения представлены на рисунке ниже.

Построение проекций точек
Точки A и B в плоскости П3 имеют следующие координаты: A”’ (y, z); B”’ (y, z). При этом A” и A”’ лежат одном перпендикуляре к оси z, так как координата z у них общая. Точно также на общем перпендикуляре к оси z лежат B” и B”’. Чтобы найти профильную проекцию т. A, отложим по оси у значение соответствующей координаты, найденное ранее. На рисунке это сделано с помощью дуги окружности радиуса AуO. После этого проведем перпендикуляр из Aу до пересечения с перпендикуляром, восстановленным из точки A” к оси z. Точка пересечения этих двух перпендикуляров определяет положение A”’.
Точка B”’ лежит на оси z, так как ордината y этой точки равна нулю. Для нахождения профильной проекции т. B в данной задаче необходимо лишь провести перпендикуляр из B” к оси z. Точка пересечении этого перпендикуляра с осью z есть B”’.

Определение положения точек в пространстве
Наглядно представляя себе пространственный макет, составленный из плоскостей проекций П1, П2 и П3, расположение октантов, а также порядок трансформации макета в эпюр, можно непосредственно определить, что т. A расположена в III октанте, а т. B лежит в плоскости П2.
Другим вариантом решения данной задачи является метод исключений. Например, координаты точки A (10, -30, -10). Положительная абсцисса x позволяет судить о том, что точка расположена в первых четырех октантах. Отрицательная ордината y говорит о том, что точка находится во втором или третьем октантах. Наконец, отрицательная аппликата z указывает на то, что т. A расположена в третьем октанте. Приведенные рассуждения наглядно иллюстрирует следующая таблица.
| Октанты | Знаки координат | ||
| x | y | z | |
| 1 | + | + | + |
| 2 | + | – | + |
| 3 | + | – | – |
| 4 | + | + | – |
| 5 | – | + | + |
| 6 | – | – | + |
| 7 | – | – | – |
| 8 | – | + | – |
Координаты точки B (30, 0, -20). Поскольку ордината т. B равна нулю, эта точка расположена в плоскости проекций П2. Положительная абсцисса и отрицательная аппликата т. B указывают на то, что она расположена на границе третьего и четвертого октантов.
Построение наглядного изображения точек в системе плоскостей П1, П2, П3

Используя фронтальную изометрическую проекцию, мы построили пространственный макет III октанта. Он представляет собой прямоугольный трехгранник, у которого гранями являются плоскости П1, П2, П3, а угол (-y0x) равен 45 º. В этой системе отрезки по осям x, y, z будут откладываться в натуральную величину без искажений.
Построение наглядного изображения т. A (10, -30, -10) начнем с её горизонтальной проекции A’. Отложив по оси абсцисс и ординат соответствующие координаты, найдем точки Aх и Aу. Пересечение перпендикуляров, восстановленных из Aх и Aу соответственно к осям x и y определяет положение т. A’. Отложив от A’ параллельно оси z в сторону её отрицательных значений отрезок AA’, длина которого равна 10, находим положение точки A.
Наглядное изображение т. B (30, 0, -20) строится аналогично – в плоскости П2 по осям x и z нужно отложить соответствующие координаты. Пересечение перпендикуляров, восстановленных из Bх и Bz, определит положение точки B.
