Сечение поверхности конуса плоскостью общего положения
При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности.
Ниже мы рассмотрим задачу, в которой требуется построить проекции и натуральную величину сечения конуса ω плоскостью α . Начальные данные представлены на рисунке ниже.
Содержание
- Определение высшей и низшей точки сечения. Границы видимости
- Построение промежуточных точек и проекций эллипса
- Построение натуральной величины сечения методом совмещения
Определение высшей и низшей точки сечения. Границы видимости
Построение линии пересечения следует начинать с нахождения её характерных точек. Они определяют границы сечения и его видимость по отношению к наблюдателю.
Через ось конической поверхности проведем вспомогательную плоскость γ, параллельную П2. Она пересекает конус ω по двум образующим, а плоскость α по фронтали fγ. Точки 1 и 2 пересечения fγ с образующими являются граничными точками. Они делят сечение на видимую и невидимую части.
Определим высшую и низшую точки линии пересечения. Для этого через ось конуса перпендикулярно h0α введем дополнительную секущую плоскость β. Она пересекает коническую поверхность по образующим SL и SK, а плоскость α по прямой MN. Искомые точки 3 = SL ∩ MN и 4 = SK ∩ MN определяют большую ось эллипса. Его центр находится в точке O, которая делит отрезок 3–4 пополам.
Определение промежуточных точек и построение проекций эллипса
Чтобы построить проекции сечения наиболее точно, найдем ряд дополнительных точек. В случае с эллипсом целесообразно определить величину его малого диаметра. Для этого через центр O проводим вспомогательную горизонтальную плоскость δ. Она пересекает коническую поверхность по окружности диаметром AB, а плоскость α – по горизонтали hδ. Строим горизонтальные проекции окружности и прямой hδ. Их пересечение определяет точки 5′ и 6′ малого диаметра эллипса.
Для построения промежуточных точек 7 и 8 вводим вспомогательную горизонтальную плоскость ε. Проекции 7′ и 8′ определяются аналогично 5′ и 6′, как это показано на рисунке.
Соединив найденные точки плавной кривой, мы получили контур эллиптического сечения. На рисунке он обозначен красным цветом. Фронтальная проекция контура меняет свою видимость в точках 1 и 2, как это было отмечено выше.
Построение натуральной величины сечения методом совмещения
Чтобы найти натуральную величину сечения, повернем плоскость α до совмещения её с горизонтальной плоскостью. В качестве оси вращения будем использовать след h0α. Его положение в процессе преобразований останется неизменным.
Построение начинается с определения направления фронтального следа f1α. На прямой f0α возьмем произвольную точку E и определим её проекцию E’. Из E’ опустим перпендикуляр к h0α. Пересечение данного перпендикуляра с окружностью радиусом XαE” определяет положение точки E’1. Через Xα и E’1 проводим f1α.
Строим проекцию горизонтали h’1δ ∥ h0α, как это показано на рисунке. Точки O’1 и 5′1, 6′1 лежат на пересечении h’1δ с прямыми, проведенными перпендикулярно h0α из O’ и 5′, 6′. Аналогично на горизонтали h’1ε находим 7′1 и 8′1.
Строим проекции фронталей f’1γ ∥ f1α, f’3 ∥ f1α и f’4 ∥ f1α. Точки 1′1, 2′1, 3′1 и 4′1 лежат на пересечении этих фронталей с перпендикулярами, восстановленными к h0α из 1′, 2′, 3′ и 4′ соответственно.
Сечение прямого кругового конуса
В сечении конической поверхности плоскостью получаются кривые второго порядка – окружность, эллипс, парабола и гипербола. В частом случае при определенном расположении секущей плоскости и когда она проходит через вершину конуса (S∈γ), окружность и эллипс вырождаются в точку или в сечении попадает одна или две образующих конуса.
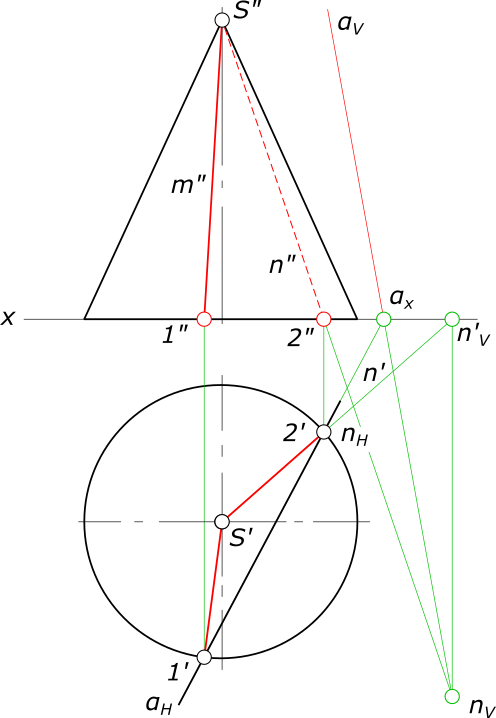
Сечение прямого кругового конуса
Сечение прямого кругового конуса дает – окружность, когда секущая плоскость перпендикулярна к его оси и пересекает все образующие поверхности.
Сечение прямого кругового конуса дает – эллипс, когда секущая плоскость не перпендикулярна к его оси и пересекает все образующие поверхности.
Построим эллиптическое сечение прямого кругового конуса ω плоскостью α, занимающей общее положение.
Решение задачи на сечение прямого кругового конуса плоскостью значительно упрощается, если секущая плоскость занимает проецирующее положение.
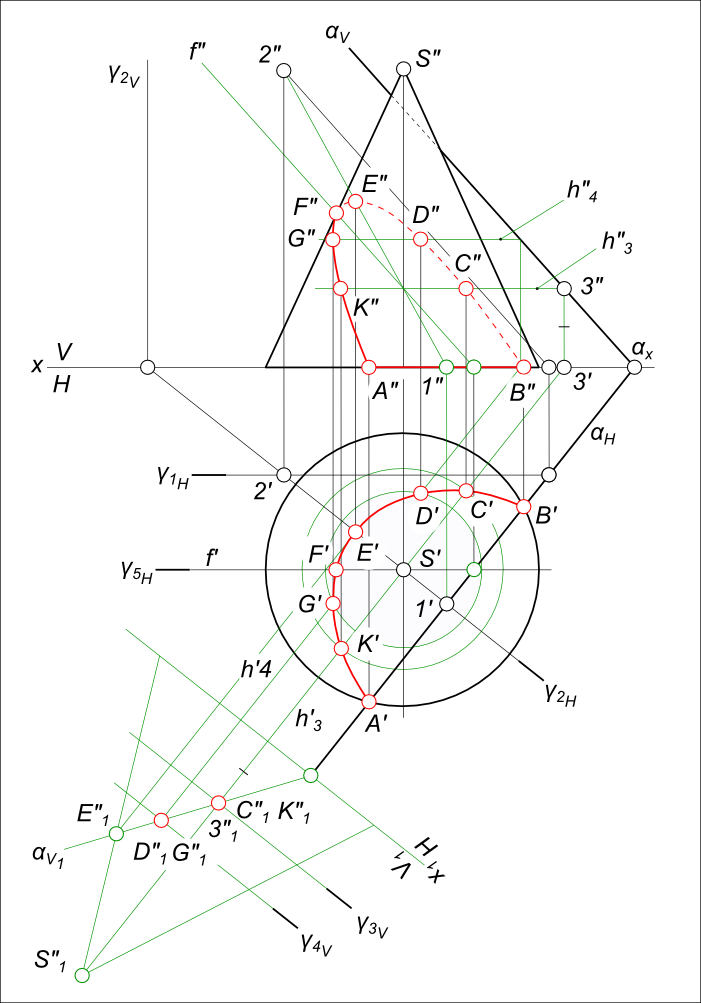
Сечение прямого кругового конуса
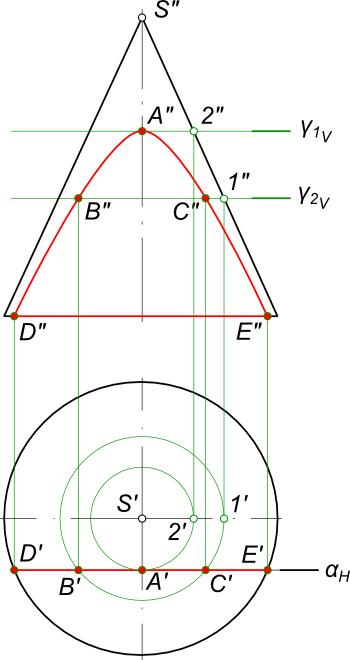
Способом перемены плоскостей проекций переведем плоскость α из общего положения в частное – фронтально-проецирующее. На фронтальной плоскости проекций V1 построим след плоскости α и проекцию поверхности конуса ω. Сечение прямого кругового конуса плоскостью дает эллипс, так как секущая плоскость пересекает все образующие конуса. Эллипс проецируется на плоскости проекций в виде кривой второго порядка.
На следе плоскости αV берем произвольную точку 3″ замеряем ее удаление от плоскости проекций H и откладываем его по линии связи уже на плоскости V1, получая точку 3″1. Через нее и пройдет след αV1. Линия сечения конуса ω – точки A”1, E”1 совпадает здесь со следом плоскости. Далее построим вспомогательную секущию плоскость γ3, проведя на фронтальной плоскости проекций V1 ее след γ3V1. Вспомогательная плоскость пересекаясь с конической поверхностью ω даст окружность, а пересекаясь с плоскостью α даст горизонтальную прямую h3. В свою очередь прямая пересекаясь с окружностью дает искомые точки C`и K` пересечения плоскости α c конической поверхностью ω. Фронтальные проекции искомых точек C” и K” построим как точки принадлежащие секущей плоскости α.
Для нахождения точки E(E`, E”) линии сечения, проводим через вершину конуса горизонтально-проецирующую плоскость γ2H, которая пересечет плоскость α по прямой 1-2(1`-2`, 1″-2″). Пересечение 1″-2″ с линией связи дает точку E” – наивысшую точку линии сечения.
Для нахождения точки указывающей границы видимости фронтальной проекции линии сечения, проводим через вершину конуса горизонтально-проецирующую плоскость γ5H и находим горизонтальную проекцию F`искомой точки. Также, плоскость γ5H пересечет плоскость α по фронтали f(f`, f”). Пересечение f” с линией связи дает точку F”. Соединяем полученные на горизонтальной проекции точки плавной кривой, отметив на ней крайнюю левую точку G – одну из характерных точек линии пересечения.
Затем, строим проекции G на фронтальных плоскостях проекций V1 и V.
Все построенные точки линии сечения на фронтальной плоскости проекций V соединяем плавной линией.
Сечение прямого кругового конуса дает – параболу, когда секущая плоскость параллельна одной образующей конуса.
При построении проекций кривых – конических сечений необходимо помнить о теореме: ортогональная проекция плоского сечения конуса вращения на плоскость, перпендикулярную к его оси, есть кривая второго порядка и имеет одним из своих фокусов ортогональную проекцию на эту плоскость вершины конуса.
Рассмотрим построение проекций сечения, когда секущая плоскость α параллельна одной образующей конуса (SD).
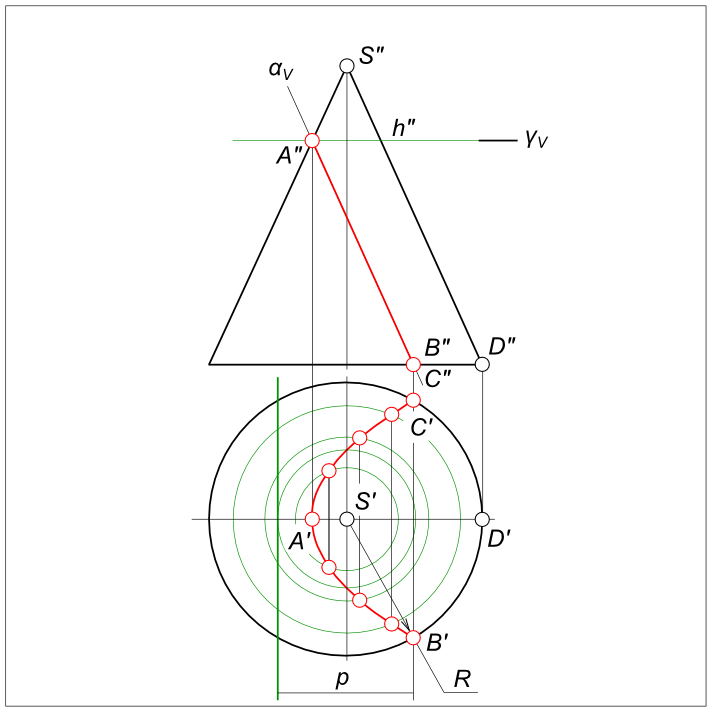
Сечение прямого кругового конуса
В сечении получится парабола с вершиной в точке A(A`, A”). Согласно теореме вершина конуса S проецируется в фокус S`. По известному [S`A`]=RS` определяем положение директрисы параболы. В последующем точки кривой строятся по уравнению p=R.
Построение проекций сечения, когда секущая плоскость α параллельна одной образующей конуса, может быть выполнено:
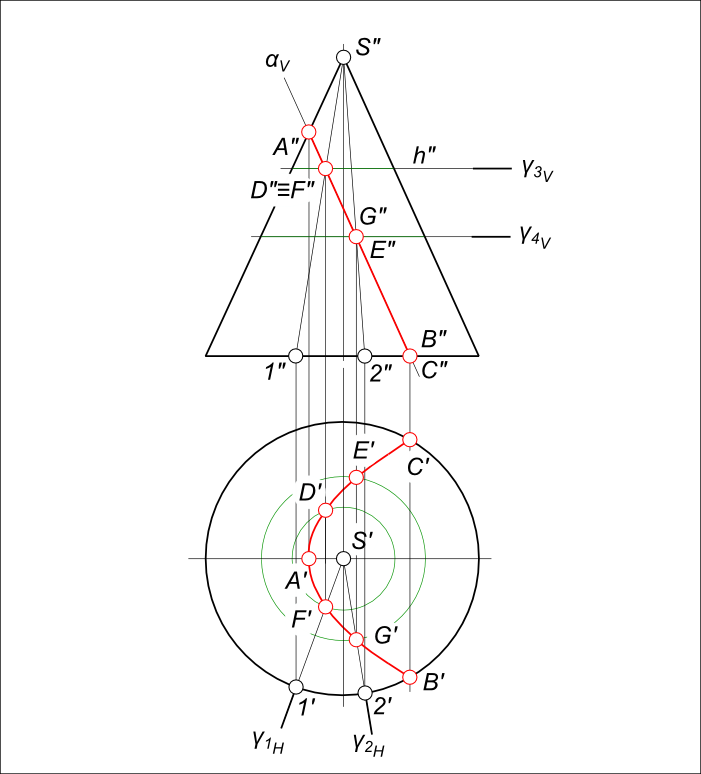
Сечение прямого кругового конуса
– с помощью вспомогательных горизонтально-проецирующих плоскостей проходящих через вершину конуса γ1H и γ2H.
Сначала определятся фронтальные проекции точек F”, G” – на пересечении образующих S”1″, S”2″ и следа секущей плоскости αV. На пересечении линий связи с γ1H и γ2H определяться F`, G`.
Аналогично могут быть определены и другие точки линии сечения, например D”, E” и D`, E`.
– с помощью вспомогательных фронтально-проецирующих плоскостей ⊥ оси конуса γ3V и γ4V.
Проекциями сечения вспомогательных плоскостей и конуса на плоскость H, будут окружности. Линиями пересечения вспомогательных плоскостей с секущей плоскостью α будут фронтально- проецирующие прямые.
Сечение прямого кругового конуса дает – гиперболу, когда секущая плоскость параллельна двум образующим конуса.
Сечение прямого кругового конуса
+
Нахождение проекций точек на поверхности конуса
Для нахождения недостающих проекций точек на поверхности конуса могут применяться следующие линии, принадлежащие поверхности конуса: окружность — параллель конуса (рис. 2.7, а), прямая — образующая конуса (рис. 2.7, б). Рассмотрим оба способа.
Пример 2.1. На поверхности конуса заданы проекции А2 и В, (см. рис. 2.7). Найдите недостающие проекции точек Ли В на поверхности конуса.
Рис. 2.7. Нахождение проекций точек на поверхности конуса
Способ 1. На рис. 2.7, а точка А задана проекцией А. Для нахождения недостающих проекций точки А воспользуемся вышеизложенным алгоритмом.
- 1. Через заданную проекцию точки Аг проводим линию, принадлежащую поверхности конуса — параллель.
- 2. Строим проекции параллели на других изображениях конуса. Па виде сверху она представляет собой окружность радиусом Rvна виде слева — отрезок.
- 3. На проекциях линии находим соответствующие проекции точек.
- 4. На пересечении окружности радиусом Л., с вертикальной линией связи, опущенной из А2, отмечаем проекцию Л,.
- 5. На виде сверху измеряем координату от проекции А, до горизонтальной оси и откладываем ее на проведенной линии связи на виде слева — получаем проекцию Л3.
- 6. Отмечаем проекцию А.л как невидимую. Проекция А., задана как видимая, следовательно, точка лежит в той части конической поверхности, которая обращена к наблюдателю (на виде сверху это часть, расположенная ниже горизонтальной оси). Таким образом, на виде слева ее проекция не видна.
Способ 2. Па рис. 2.7, 6 точка В задана проекцией В,. Построение недостающих проекций аналогично построению проекций точки А, за исключением того, что вместо окружности используется образующая конуса, пересекающая его основание в точке 1.
Коническая поверхность вращения
Коническая поверхность вращения — это линейчатая поверхность, образованная вращением прямолинейной образующей, которая пересекает криво-линейную направляющую (окружность) и проходит через неподвижную точку оси вращения, называемую вершиной.
Конусом называют геометрическое тело, ограниченное конической поверхностью и плоскостью основания, пересекающего все его образующие.
Конус называют прямым, если ось вращения перпендикулярна его основанию. Конус называют круговым, так как направляющей является окружность Конус с двумя параллельными основаниями, т.е. конус со срезанной вершиной, называют усеченным.
Построение проекций прямого кругового конуса
На рис. 4.71 показан пример построения проекций прямою кругового конуса с горизонтально-проецирующей осью вращения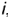 
, заданной высотой 
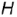и основанием радиусом 
.
Для построения проекций конуса требуется выполнить графо-аналитические действия в следующем порядке:
1-е действие. По заданному условию построить горизонтальную проекцию очерка прямого кругового конуса, которая представляет собой окружность заданного радиуса с вершиной 
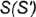, совпадающей с осью вращения 
.
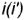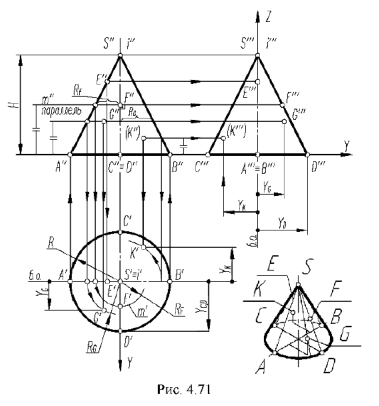
2-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса:
- Круг радиуса является невидимой проекцией основания конуса.
- Круг радиуса с вершиной конуса 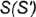является видимой проекцией боковой поверхности конуса.
- Обозначить на горизонтальной проекции характерные образующие конуса
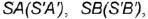
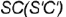и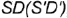 
которые будут определять очерки фронтальной и профильной проекций конуса.
3-е действие. Построить фронтальную проекцию (очерк) конуса, которая представляет собой треугольник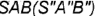 
заданной высоты 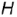, ограниченный:
4-е действие. Построить профильную проекцию (очерк) конуса:
- ‘Задать на окружности горизонтальной проекции конуса положение базовой линии (б.о.), совпадающей с горизонтальной линией оси этой окружности.
- Выбрать положение базовой оси
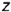(б.о.), которая будет совпадать с вертикальной осью 
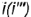вращения на профильной проекции конуса. - Профильная проекция конуса представляет собой треугольник
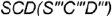ограниченный:
слева и справа очерковыми образующим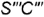и 
и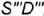 
построенными по координате 
:
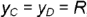вершиной 
, лежащей на базовой оси 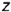; горизонтальным отрезком проекцией основания;
профильными проекциями характерных образующих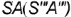 
и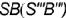 
, которые совпадают с осью вращения конуса .
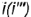. Запомните характерные признаки очерков прямого круговою конуса на чертеже — окружность основания и два треугольника.
. Характерные признаки очерков прямого кругового усеченного конуса окружность основания и две равнобокие трапеции.
Построение проекции точек, лежащих на поверхности конуса
Принадлежность точки поверхности конуса определяется ее принадлежностью образующей поверхности и принадлежностью круговым параллелям (окружностям), по которой точка вращается вокруг оси конуса. Следовательно, проекции точки можно строить либо по принадлежности образующей, либо по принадлежности круговой параллели.
На рис. 4.71 показан пример построения горизонтальных и профильных проекций точек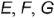 
и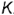 
, заданных фронтальными проекциям 
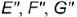и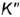 
но их принадлежности круговым параллелям.
Посфоение горизонтальных проекций заданных точек:
горизонтальные проекции точек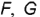 
и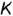 
построены на вспомогательных круговых параллелях, проведенных через заданные фронтальные проекции точек.
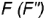
Рассмотрим графический алгоритм для построения горизонтальных проекции точек, лежащих на боковой поверхности конуса (на примере заданной точки , по их при надежности круговым параллелям:
Графический алгоритм I:
1-е действие. Провести фронтальную проекцию вспомогательной круговой параллели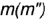 
через заданную фронтальную проекцию точки 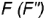: проекция параллели — это прямая, перпендикулярная оси конуса и параллельная его основанию.
2-е действие. Провести окружность горизонтальной проекции параллели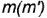 
полученным радиусом 
.
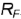3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки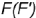 
на горизонтальной проекции параллели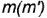
Повторить действия графического алгоритма 1 и построить аналогично горизонтальные проекци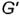и 
и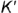 
точек 
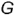и .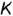
Построение профильных проекций заданных точек. Точки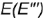 
и 
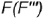построены по принадлежности характерным образующим:
точка 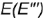лежит на видимой характерной образующей 
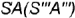, совпадающей с осью конуса;
На рис. 4.72 показан пример построения горизонтальной и профильной проекции точки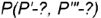 
по ее принадлежности образующей 
.
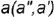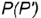
- Построение горизонтальной проекции точки по принадлежности образующей выполняется по графическому алгоритму II:
1-е действие. Провести через вершину конуса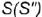 
и заданную невидимую фронтальную проекцию точки 
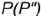вспомогательную образующую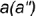 
2-е действие. Построить горизонтальную проекцию образующей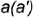 
проходящей через вершину конуса 
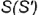и вспомогательную точку 
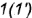, лежащую на основании конуса.
3-е действие. Построить по вертикальной линии связи горизонтальную проекцию точки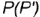 
по ее принадлежности образующей .
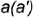- Построение профильной проекции невидимой точки
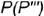выполняется по принадлежности образующей 
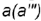, построенной но координате 
.
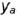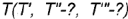
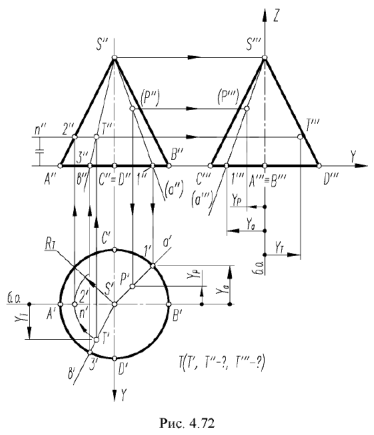
На рис. 4.72 показано построение фронтальной и профильной проекции точки по ее заданной горизонтальной проекции. Построение выполнено по приведенным алгоритмам I и II, но в обратном порядке:
1-е действие. Провести на горизонтальной проекции конуса радиусом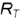 
окружность вспомогательной параллели 
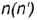или вспомогательную образующую 
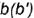, на которых лежит горизонтальная проекция точки 
.
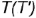2-е действие. Построить фронтальные проекции вспомогательной параллели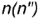 
или вспомогательной образующей 
:
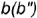параллель 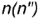провести через вспомогательную точку 
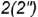на образующей 
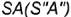параллельно основанию конуса;
образующую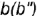 
провести через вспомогательную точку 
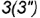на основании конуса и вершину конуса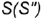 
3-е действие. Построить по вертикальной линии связи фронтальную проекцию точки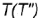 
по ее принадлежности либо параллели 
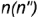, либо образующей .
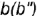Конические сечения
Рассмотрим пять возможных случаев расположения секущей плоскости относительно оси конуса и его образующих, определяющих форму линии ее пересечения с поверхностью конуса (математические доказательства не приводятся):
1-й случаи. Гели секущая плоскость проходит через вершину конуса, то эта плоскость пересекает коническую поверхность по двум образующим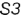 
(фронтально-проецирующая плоскость 
, рис. 4.73).
2-й случай. Если секущая плоскость расположена перпендикулярно оси конуса, то эта плоскость пересекает коническую поверхность но окружности (горизонтальная плоскость рис. 4.73).
3-й случай. Если секущая плоскость расположена параллельно одной образующей конуса, то эта плоскость пересекает коническую поверхность по параболе (фронтально-проецирующая плоскость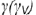 
параллельна одной образующей 
, рис.4.74).
4-и случай. Если секущая плоскость расположена параллельно двум образующим конуса, то эта плоскость пересекает коническую поверхность по гиперболе (фронтальная плоскость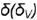 
параллельна двум образующим — и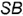 
, рис.4.75).
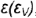
5-й случай. Если плоскость пересекает все образующие конуса под углом, отличным от прямого (или иначе, не параллельна ни одной образующей конуса), то эта плоскость пересекает коническую поверхность по эллипсу (фронтально-проецирующая плоскость ), рис 4.76).
Рассмотрим построение на проекциях конуса линии пересечения для всех пяти случаев сечений.
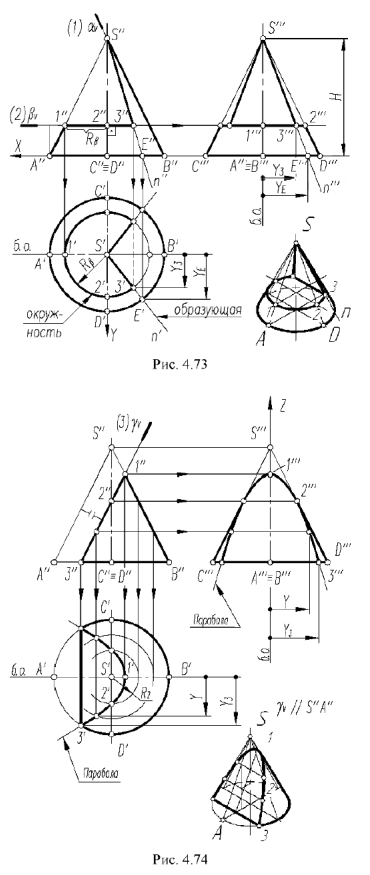
1-й и 2-й случаи. На рис. 4.73 показано построение проекций прямого кругового конуса с вырезом, образованным сечениями конической поверхности фронтально-проецирующей плоскостью , проходящей через вершину конуса (1-й случай), и горизонтальной плоскостью , расположенной перпендикулярно оси конуса (2-й случай).
Плоскость 
пересекает поверхность конуса по образующим 
, горизонтальные и профильные проекции которых строятся с помощью вспомогательной точки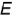 
лежащей на основании конуса.
Плоскость пересекает поверхность конуса по окружности радиуса ограниченной линией 3-3 пересечения плоскостей выреза.
Построение горизонтальной и профильной проекций конуса с вырезом и оформление очерков этих проекций видно из чертежа.
3-й случай. На рис. 4.74 показано построение проекций конуса со срезом фронтально-проецирующей плоскостью 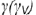, расположенной параллельно одной образующей конуса .
Плоскость пересекает поверхность конуса по параболе, горизонтальная и профильная проекции которой строятся по отмеченным характерным точкам 1, 2 и 3 и промежуточной точке (не обозначена)
Построение проекций этих точек выполнено по их принадлежности:
- проекции промежуточной точки построены по ее принадлежности соответствующей параллели (профильные проекции — по координате
).
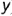Оформление очерков проекций видно из чертежа.
4-й случай. На рис. 4.75 показано построение проекций конуса со срезом фронтальной плоскостью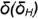 
, расположенной параллельно двум образующим конуса 
и 
.
Плоскость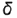 
пересекает поверхность конуса по гиперболе, фронтальная проекция которой строится по отмеченным точкам 1. 2 и 3 по их принадлежности параллелям (обратный алгоритм I), а профильная проекция гиперболы проецируется в вертикальную линию и совпадает с вырожденной проекцией плоскости среза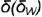 
Оформление очерков проекций видно из чертежа.
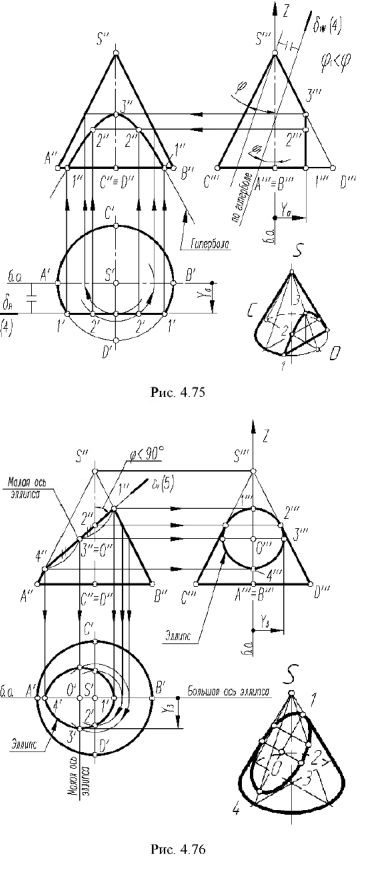
На рис 4 75 на профильной проекции конуса показано положение секущей плоскости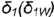 
под углом 
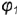к оси конуса. При 
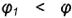плоскость пересекает поверхность конуса также по гиперболе.
5-й ыучай. На рис. 4.76 показано построение проекции конуса со срезом фронтально-проецирующей плоскостью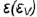 
пересекающей все образующие конуса под углом 
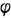к оси, отличным от прямого.
Плоскость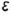 
пересекает поверхность конуса по эллипсу, горизонтальная и профильная проекции которого построены по проекциям отмеченных характерных точек 1, 2, 4 и про-межуточных точек 3, взятых на середине отрезка 1-4, который является совпадающей проекцией эллипса и его большой оси. Почки 3 определяют проекции малой оси эллипса и построены на горизонтальной проекции конуса по радиусу параллели, а на профильной проекции но координате 
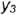(алгоритм I).
Оформление очерков проекций видно из чертежа.
. Количество взятых промежуточных точек должно быть минимальным, но достаточным, чтобы построить на проекциях конуса формы кривых второго порядка (параболы, гиперболы и эллипса), которые выполняют на чертеже по построенным характерным и промежуточным точкам с помощью лекала.
Построении проекции прямого конуса со срезами плоскостями частного положения
На рис. 4.77 показан пример построения проекций прямого круговою конуса со срезами фронтально-проецирующей плоскостью и профильной плоскостью .
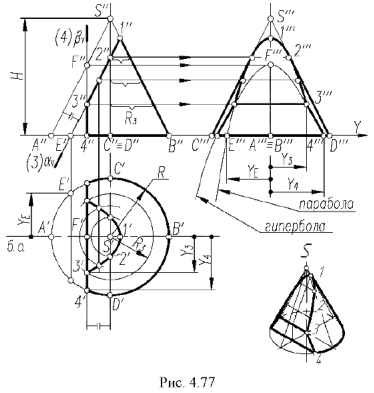
Для построения проекций конуса со срезами следует выполнить графический алгоритм, определяющий порядок действий при решении всех подобных задач.
1-е действие. Построить на чертеже тонкими линиями по заданному радиусу основания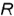 
и высоте 
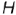фронтальную, горизонтальную и профильную проекции конуса без срезов, а затем выполнить на его фронтальной проекции заданные срезы фронтально-проецирующей плоскостью и профильной плоскостью ;
2-е действие. Обозначить на фронтальной проекции характерные точки пересечения плоскостей срезов с образующими и основанием конуса и выпол-иить графический анализ сечений:
1. Фронтально-проецирующая плоскость параллельна одной образующей конуса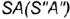 
и пересекает его поверхность по участку параболы 
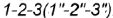, которая проецируется в отрезок и ограничена вырожденной в точку фронтально-проецирующей линией пересечения 
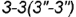плоскостей срезов и .
- Профильная плоскость параллельна двум образующим конуса
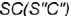и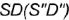 
и пересекает его поверхность по участку гиперболы 
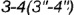, которая проецируется в отрезок и ограничена вырожденными в точки фронтально-проецирующими линиями пересечения плоскостей срезов и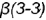 
и плоскости с основанием конуса (4-4).
3-е действие. Достроить горизонтальную проекцию конуса со срезами, построив проекции плоскостей срезов по горизонтальным проекциям обозначенных точек и определить видимость плоскостей срезов:
1. Плоскость среза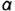 
определяет видимая горизонтальная проекция участка параболы 
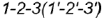построенной по горизонтальным проекциям обозначенных точек:
- Плоскость среза
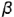определяет вертикальный видимый отрезок 
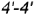вырожденной в линию проекции профильной плоскости, точки 
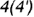которой лежат на очерковой окружности основания конуса.
. Поскольку горизонтальная проекция имеет вертикальную симметрию, точки обозначены на одной ее половине (нижней).
4-е действие. Выполнить графический анализ построенной горизонтальной проекции конуса для определения ее очерка и внутреннего контура:
- Горизонтальный очерк определяют участок окружности и отрезок .
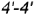- Внутренний контур определяет видимый участок параболы
.
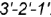5-е действие. Достроить профильную проекцию конуса со срезами, пост-роив проекции плоскостей срезов по профильным проекциям обозначенных точек, и определить видимость плоскостей срезов:
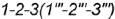
1. Плоскость среза а определяет видимый участок параболы , построенный по профильным проекциям обозначенных точек:
- Плоскость среза 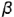определяют видимые участки гиперболы
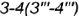, ограниченные видимым отрезком 
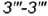(построен) и видимым отрезком 
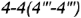. точки которого построены но координате 
.
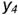6-е действие. Выполнить графический анализ построенной профильной проекции конуса для определения ее очерка и внутреннего контура.
- Профильный очерк определяют:
- Внутренний контур определяют:
7-е действие. Оформить чертеж конуса, выполнив толстыми сплошными линиями очерки и видимый внутренний контур каждой его проекции (оставить сплошными тонкими линиями полные очерки проекций и линии построения).
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Сечение поверхности конуса плоскостью общего положения
При пересечении прямого кругового конуса с плоскостью могут образовываться следующие кривые второго порядка: окружность, эллипс, гипербола и парабола. Вид этих кривых зависит от угла наклона секущей плоскости к оси конической поверхности.
Ниже мы рассмотрим задачу, в которой требуется построить проекции и натуральную величину сечения конуса ω плоскостью α . Начальные данные представлены на рисунке ниже.
Определение высшей и низшей точки сечения. Границы видимости
Построение линии пересечения следует начинать с нахождения её характерных точек. Они определяют границы сечения и его видимость по отношению к наблюдателю.
Через ось конической поверхности проведем вспомогательную плоскость γ, параллельную П2. Она пересекает конус ω по двум образующим, а плоскость α по фронтали fγ. Точки 1 и 2 пересечения fγ с образующими являются граничными точками. Они делят сечение на видимую и невидимую части.
Определим высшую и низшую точки линии пересечения. Для этого через ось конуса перпендикулярно h0α введем дополнительную секущую плоскость β. Она пересекает коническую поверхность по образующим SL и SK, а плоскость α по прямой MN. Искомые точки 3 = SL ∩ MN и 4 = SK ∩ MN определяют большую ось эллипса. Его центр находится в точке O, которая делит отрезок 3–4 пополам.
Определение промежуточных точек и построение проекций эллипса
Чтобы построить проекции сечения наиболее точно, найдем ряд дополнительных точек. В случае с эллипсом целесообразно определить величину его малого диаметра. Для этого через центр O проводим вспомогательную горизонтальную плоскость δ. Она пересекает коническую поверхность по окружности диаметром AB, а плоскость α – по горизонтали hδ. Строим горизонтальные проекции окружности и прямой hδ. Их пересечение определяет точки 5′ и 6′ малого диаметра эллипса.
Для построения промежуточных точек 7 и 8 вводим вспомогательную горизонтальную плоскость ε. Проекции 7′ и 8′ определяются аналогично 5′ и 6′, как это показано на рисунке.
Соединив найденные точки плавной кривой, мы получили контур эллиптического сечения. На рисунке он обозначен красным цветом. Фронтальная проекция контура меняет свою видимость в точках 1 и 2, как это было отмечено выше.
Построение натуральной величины сечения методом совмещения
Чтобы найти натуральную величину сечения, повернем плоскость α до совмещения её с горизонтальной плоскостью. В качестве оси вращения будем использовать след h0α. Его положение в процессе преобразований останется неизменным.
Построение начинается с определения направления фронтального следа f1α. На прямой f0α возьмем произвольную точку E и определим её проекцию E’. Из E’ опустим перпендикуляр к h0α. Пересечение данного перпендикуляра с окружностью радиусом XαE» определяет положение точки E’1. Через Xα и E’1 проводим f1α.
Строим проекцию горизонтали h’1δ ∥ h0α, как это показано на рисунке. Точки O’1 и 5′1, 6′1 лежат на пересечении h’1δ с прямыми, проведенными перпендикулярно h0α из O’ и 5′, 6′. Аналогично на горизонтали h’1ε находим 7′1 и 8′1.
Строим проекции фронталей f’1γ ∥ f1α, f’3 ∥ f1α и f’4 ∥ f1α. Точки 1′1, 2′1, 3′1 и 4′1 лежат на пересечении этих фронталей с перпендикулярами, восстановленными к h0α из 1′, 2′, 3′ и 4′ соответственно.
§ 18. Конус
18.1.Определение конуса и его элементов
Определение. Тело, которое образуется при вращении прямоугольного треугольника вокруг прямой, содержащей его катет, называется прямым круговым конусом (рис. 165, 166).
Отрезок оси вращения, заключённый внутри конуса, называется осью конуса.
Круг, образованный при вращении второго катета, называется основанием конуса. Длина этого катета называется радиусом основания конуса или, короче, радиусом конуса. Вершина острого угла вращающегося треугольника, лежащая на оси вращения, называется вершиной конуса. На рисунках 165, б и 166 вершиной конуса является точка Р.
Высотой конуса называется отрезок, проведённый из вершины конуса перпендикулярно его основанию. Длину этого перпендикуляра также называют высотой конуса. Высота конуса имеет своим основанием центр круга — основания конуса — и совпадает с осью конуса.
Отрезки, соединяющие вершину конуса с точками окружности его основания, называются образующими конуса. Все образующие конуса равны между собой (почему?).
Как и в случае с цилиндром, можно рассматривать конус в более широком, чем у нас, понимании, когда в основании конуса может быть, например, эллипс (эллиптический конус), парабола (параболический конус). Мы будем изучать только определённый выше прямой круговой конус (конус вращения), поэтому слова «прямой круговой» мы будем опускать.
Рис. 165
Рис. 166
Рис. 167
Поверхность, полученная при вращении гипотенузы, называется боковой поверхностью конуса, а её площадь — площадью боковой поверхности конуса и обозначается Sбок. Боковая поверхность конуса является объединением всех его образующих.
Объединение боковой поверхности конуса и его основания называется полной поверхностью конуса, а её площадь называется площадью полной поверхности конуса или, короче, площадью поверхности конуса и обозначается Sкон. Из этого определения следует, что
Sкон = Sбок + Sосн.
Если вокруг данной прямой — оси — вращать пересекающую её прямую, то при этом вращении образуется поверхность, которую называют круговой конической поверхностью или конической поверхностью вращения. Уравнение 
+ 
– 
= 0 задаёт коническую поверхность вращения с осью вращения Oz (рис. 167). Из этого уравнения следует, что коническая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» — в конце этой книги.)
18.2. Сечения конуса
Определение. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением конуса.
Рис. 168
Рис. 169
Рис. 170
Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники. На рисунке 168 осевым сечением конуса является треугольник ABP (АР = ВР). Угол АPВ называют углом при вершине осевого сечения конуса.
Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.
Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP).
Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).
Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением.
Рис. 171
Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками.
О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.
ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60°; б) в 90°. Найти площадь сечения.
Решение. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.
Хорда АВ окружности основания стягивает дугу в 60°, значит, △ AOB — правильный и АВ = R.
Рис. 172
Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S△ ABP = 
АВ•РC. Имеем: ОР = R (по условию); в △ AOB: ОС = 
; в △ ОСР: CP = 
= 
.
Тогда S△ ABP = 
АВ•РС = 
.
Ответ: а) 
.
18.3. Касательная плоскость к конусу
Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.
Рис. 173
Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.
Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.
18.4. Изображение конуса
Рис. 174
Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).
Для достижения наглядности изображения невидимые линии изображают штрихами.
Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.
18.5. Развёртка и площадь поверхности конуса
Пусть l — длина образующей, R — радиус основания конуса с вершиной Р.
Рис. 175
Рис. 176
Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a), то получим развёртку поверхности конуса (рис. 176, б), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):
α = 
.
За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.
Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле
Sбок = 
α•l2,(1)
где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = 
, получаем:
Sбок = πRl.(2)
Таким образом, доказана следующая теорема.
Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼
Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.
Sкон = πRl + πR2.(3)
Следствие. Пусть конус образован вращением прямоугольного треугольника ABC вокруг катета АС (рис. 177). Тогда Sбок = π•BC•АВ. Если D — середина отрезка АВ, то AB = 2AD, поэтому
Sбок = 2 π ВС•AD.(4)
Рис. 177
Проведём DE ⟂ АB (E ∈ l = AС). Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А) имеем
= 
⇒ BC•AD = DE•АС.(5)
Тогда соотношение (4) принимает вид
Sбок = (2π•DE)•AC,(6)
т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.
Это следствие будет использовано в п. 19.7.
18.6. Свойства параллельных сечений конуса
Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Рис. 178
Доказательство. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α, параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).
Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β, α || β, то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O1 = α ∩ РО. Обозначим этот круг F1.
Рассмотрим гомотетию 
с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия 
отображает основание F конуса на его параллельное сечение — круг F1, при этом центр О основания отображается на центр О1 круга F1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии 
точка X отображается на точку X1 = РX ∩ α. Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:
= 
= k,(*)
где k — коэффициент гомотетии 
, т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.
А поскольку гомотетия является подобием, то круг F1, являющийся параллельным сечением конуса, подобен его основанию.
Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO1 : РО, где РO1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
Sсечен : Sоснов = k2 = 
: PO2.
Теорема доказана. ▼
18.7.Вписанные в конус и описанные около конуса пирамиды
Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.
Для построения изображения правильной пирамиды, вписанной в конус:
—строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;
—соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;
—выделяют видимые и невидимые (штрихами) линии изображаемых фигур.
На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:
—прямоугольный треугольник (см. рис. 179);
—правильный треугольник (см. рис. 180);
—квадрат (см. рис. 181);
—правильный шестиугольник (см. рис. 182).
Рис. 179
Рис. 180
Рис. 181
Рис. 182
Определение. Пирамида называется описанной около конуса, если у них вершина общая, а основание пирамиды описано около основания конуса. В этом случае конус называют вписанным в пирамиду (рис. 183).
Рис. 183
Рис. 184
ЗАДАЧА (3.080). В равносторонний конус вписана правильная пирамида. Найти отношение площадей боковых поверхностей пирамиды и конуса, если пирамида: а) треугольная; б) четырёхугольная; в) шестиугольная.
Решение. Рассмотрим случай а). Пусть R — радиус основания равностороннего конуса, РАВС — правильная пирамида, вписанная в этот конус (рис. 184); △ DPE — осевое сечение конуса, CF — медиана △ АBС. Тогда в △ АВС (правильный): АВ = R
, OF = 
R; в △ DPE (правильный): ОР = 
= R
; в △ ОРF (∠ FOP = 90°):
PF = 
= 
.
Так как CF — медиана △ АВС, то PF — высота равнобедренного треугольника АВР. Поэтому
S△ ABP = 
AB•PF = 
R
• 
= 
.
Обозначим: S1 — площадь боковой поверхности пирамиды, S2 — площадь боковой поверхности конуса. Тогда
S1 = 3S△ ABP = 
,
S
2 = πR•PA = πR•2R = 2πR2.
Следовательно,
S1 : S2 = 
: 2πR2 = 
.
Ответ: а) 
.
Во многих пособиях по геометрии за площадь боковой поверхности конуса принимают предел последовательности боковых поверхностей правильных вписанных в конус (или описанных около конуса) п-угольных пирамид при n → +∞. Действительно, Sбок. пов. пирам = 
•a•Poсн. пирам, где Рoсн. пирам — периметр основания пирамиды, а — апофема боковой грани. Для правильных описанных около конуса пирамид апофема a — постоянная величина, равная образующей l конуса, а предел последовательности периметров правильных многоугольников, описанных около окружности радиуса R основания конуса, равен 2πR — длине этой окружности. Таким образом, мы вновь получаем: Sбок = πRl.
18.8. Усечённый конус
Рис. 185
Пусть дан конус с вершиной Р. Проведём плоскость α, параллельную плоскости основания конуса и пересекающую этот конус (рис. 185). Эта плоскость пересекает данный конус по кругу и разбивает его на два тела: одно из них является конусом, а другое (расположенное между плоскостью основания данного конуса и секущей плоскостью) называют усечённым конусом. Таким образом, усечённый конус представляет собой часть полного конуса, заключённую между его основанием и параллельной ему плоскостью. Основание данного конуса и круг, полученный в сечении этого конуса плоскостью α, называются соответственно нижним и верхним основаниями усечённого конуса. Высотой усечённого конуса называется перпендикуляр, проведённый из какой-либо точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённого конуса. (Часто за высоту усечённого конуса принимают отрезок, соединяющий центры его оснований.)
Рис. 186
Рис. 187
Часть боковой поверхности данного конуса, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса, а отрезки образующих конуса, заключённые между основаниями усечённого конуса, называются образующими усечённого конуса. Так как все образующие данного конуса равны и равны все образующие отсечённого конуса, то равны все образующие усечённого конуса.
Построение изображения усечённого конуса следует начинать с изображения того конуса, из которого получился усечённый конус (рис. 186).
На рисунке 187 показана развёртка усечённого конуса.
Из теоремы 28 следует, что основания усечённого конуса — подобные круги.
Определения усечённой пирамиды, вписанной в усечённый конус и описанной около него, аналогичны определениям пирамиды, вписанной в конус и описанной около него.
Заметим, что построение изображений усечённой пирамиды, вписанной в усечённый конус и описанной около него, следует начинать с изображений того конуса или той пирамиды, из которых получены соответственно усечённые конус и пирамида.
Полной поверхностью усечённого конуса называется объединение боковой поверхности этого конуса и двух его оснований. Иногда полную поверхность усечённого конуса называют его поверхностью, а её площадь — площадью поверхности усечённого конуса. Эта площадь равна сумме площадей боковой поверхности и оснований усечённого конуса.
Усечённый конус может быть образован также вращением прямоугольной трапеции вокруг боковой стороны трапеции, перпендикулярной её основанию.
Рис. 188
На рисунке 188 изображён усечённый конус, образованный вращением прямоугольной трапеции ABCD вокруг стороны CD. При этом боковая поверхность усечённого конуса образована вращением боковой стороны АВ, а основания его — вращением оснований AD и ВС трапеции.
18.9. Поверхность усечённого конуса
Выразим площадь Sбок боковой поверхности усечённого конуса через длину l его образующей и радиусы R и r оснований (R > r).
Рис. 189
Пусть точка Р — вершина конуса, из которого получен усечённый конус; точки О, O1 — центры оснований усечённого конуса; AA1 = l — одна из образующих усечённого конуса (рис. 189).
Используя формулу (2) п. 18.5, получаем
Sбок = πR•PA – πr•РA1 =
= πR(РA1 + А1A) – πr•PA1 =
= πR•A1A + π(R – r)•PA1.
Учитывая, что A1A = l, имеем
Sбок = πRl + π(R – r)PA1.(7)
Выразим PA1 через l, R и r. Так как O1A1 || OA и OO1 — высота усечённого конуса, то прямоугольные треугольники POA и PO1A1 подобны. Поэтому АО : А1O1 = PA : PA1 или
R : r = (PA1 + A1A) : PA1, откуда
R•PA1 = r(PA1 + l) ⇒ (R – r)PA1 = rl ⇒ PA1 = 
.
Подставив это значение РА1 в (7), получаем
Sбок = π(R + r)l.(8)
Таким образом, доказана следующая теорема.
Теорема 29. Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую. ▼
Площадь полной поверхности усечённого конуса находится по формуле:
Sполн = π•(R + r)•l + π•R2 + π•r2.
Следствие. Пусть усечённый конус образован вращением прямоугольной трапеции ABCD вокруг её высоты AD (рис. 190). Тогда Sбок = π (АВ + DC)•ВС. Если KЕ — средняя линия трапеции, то АВ + DC = 2KE, поэтому
Sбок = 2π•KE•BC.(9)
Рис. 190
Проведём EF ⟂ ВС. Из подобия прямоугольных треугольников ВСН и EFK имеем
BC : EF = BH : KE ⇒ ⇒ KE•BC = EF•BH.(10)
Тогда равенство (9) принимает вид
Sбок = (2π•EF)•ВH,(11)
т. е. боковая поверхность усечённого конуса равна произведению его высоты на длину окружности, радиус которой равен серединному перпендикуляру, проведённому из точки оси конуса к его образующей.
18.10. Объёмы конуса и усечённого конуса
Найдём объём конуса, высота которого равна h и радиус основания — R. Для этого расположим этот конус и правильную четырёхугольную пирамиду, высота которой равна h и сторона основания — R, так, чтобы их основания находились на одной и той же плоскости α, а вершины — также в одной и той же плоскости β, параллельной плоскости α и удалённой от неё на расстояние h (рис. 191).
Рис. 191
Каждая плоскость, параллельная данным плоскостям и пересекающая конус, пересекает также пирамиду; причём площади сечений, образованных при пересечении обоих тел, относятся к площадям оснований этих тел, как квадраты их расстояний от вершин. А так как секущие плоскости для пирамиды и для конуса равноудалены от их вершин, то 
= 
. Тогда 
= 
= 
= π, значит, для объёмов этих тел выполняется:
Vкон : Vпир = π : 1 или Vкон : 
R2•h = π : 1, откуда
Vкон = 
πR2 •h.
Рис. 192
Самостоятельно рассмотрите усечённые конус и пирамиду, расположенные в соответствии с условиями принципа Кавальери. Тогда вы получите формулу вычисления объёма усечённого конуса:
Vус. кон = 
π•h•(R2 + r•R + r2).
Эту же формулу вы можете вывести, если используете идею подобия так же, как это сделано в случае с выводом формулы площади боковой поверхности усечённого конуса.
Используя принцип Кавальери, докажите, что объём каждого из тел, на которые конус разбивается его сечением плоскостью, проходящей через вершину (рис. 192), может быть вычислен по формуле V = 
•h•Scегм, где h — длина высоты конуса, а Sceгм — площадь соответствующего сегмента основания конуса.
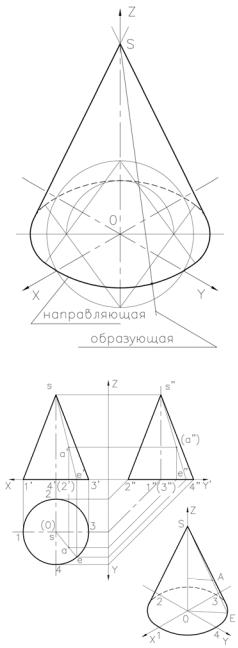
Лекция 16. ПРОЕКЦИИ КОНУСА
Конус – тело вращения.
Прямой круговой конус относится к одному из видов тел вращения.
Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки некото-
рой кривой направляющей линии. Неподвижная точка S называется вершиной. Основанием конуса служит поверхность образованная замкнутой направляющей.
Конус, основанием которого является окружность, а вершина S находится на оси
перпендикулярной основанию, проходящей через его середину, называется прямым кру-
говым конусом. Рис. 1.
Построение ортогональных проекций конуса, приведено на рис. 2.
Горизонтальная проекция конуса представляет собой окружность, равную основанию конуса, а вершина конуса S совпадает с ее центром. На фронтальную и профильную проекции конус проецируется в виде треугольни-
ка, ширина основания которого равна диаметру основания. А высота равна высоте конуса. Наклонные стороны треугольника – проекции крайних (очерковых) образующих конуса.
|
Построение конуса в прямоуголь- |
||
|
ной изометрии приведено на рис. 2. |
||
|
Рис. 1 |
Построение начинаем с расположе- |
|
|
ния аксонометрических осей OX, OY, OZ, |
||
|
проведя их под углом 1200 друг к другу. Ось |
||
|
конуса направим по оси OZ, и отложим на |
||
|
ней высоту конуса, получив точку S. Прини- |
||
|
мая точку O за центр основания конуса, |
||
|
строим овал, представляющий основание |
||
|
конуса. Затем проводим две наклонные ка- |
||
|
сательные из т. S к овалу, которые будут |
||
|
крайними (очерковыми) образующими кону- |
||
|
са. Невидимую часть нижнего основания ко- |
||
|
нуса выполним штриховой линией. |
Построение точек на поверхности конуса в ортогональных и аксонометриче-
ской проекциях показано на рис. 2, 3.
Если на фронтальной проекции конуса Рис. 2 заданы точки А и В, то недостающие проек-
ции этих точек можно построить двумя способами.
Первый способ: с помощью проекций вспомогательной образующей проходящей через заданную точку.
Дано: фронтальная проекция точки А – точка (а’), расположенная в пределах видимой части конуса.
Через вершину конуса и заданную точку (a’) проводим прямую линию до основания конуса и получаем точку (e’) – основание образующей s’e’.
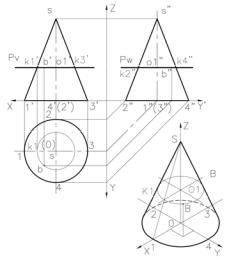
Далее строим горизонтальную проекцию этой образующей на плоскости
H. Найдем горизонтальную проекцию т. e в пределах видимой части окружности основания конуса, проведя проецирующую прямую e’e, и соединим полученную т. е с горизонтальной проекцией вер-
шины конуса s.
Так как искомая т. А принадлежит обра-
зующей s’e’ то она должна лежать на ее горизонтальной проекции. Поэтому с помощью линии связи мы переносим ее на линию se и по-
лучаем горизонтальную проекцию т. a. Профильная проекция a” т. А определя-
ется пересечением той же образующей s”e” на профильной проекции с линиями связи, переносящими т. а с горизонтальной и фронталь-
ной проекций.
Профильная проекция a” т. А в данном
случае невидимая, т. к. находится за проекцией крайней образующей s”4” и обозначается в круглых скобках.
Рис. 3 Второй способ: с помощью построения проекций сечения конической поверхности горизонтальной плоскостью Pv па-
раллельной основанию конуса и проходящей через заданную точку В. Рис. 3. Дано: фронтальная проекция точки В – т. b’, расположенная в пределах
видимой части конуса.
Через т. b’ проводим прямую, Pv параллельную основанию конуса, кото-
рая является фронтальной проекцией секущей плоскости P. Эта линия пересе-
кает ось конуса в т. 01’ и крайние образующие в т. k1’ и k3’. Отрезок прямой k1’k3’ является фронтальной проекцией сечения конуса через т. b’.
Горизонтальной проекцией этого сечения будет окружность, радиус которой определяется на фронтальной проекции как расстояние 01’k1’ от оси ко-
нуса до крайней образующей.
Так как точка b’ лежит в плоскости сечения, то с помощью линии связи переносим ее на горизонтальную проекцию сечения в пределах видимой части конуса.
Профильная проекция т. b” определяется как пересечение профильной
проекции сечения k2”k4” с линией связи, переносящей положение т. b с гори-
зонтальной проекции.
Построение точек на поверхности конуса в аксонометрии.
Строим конус в прямоугольной изометрии. Построение окружности основания конуса в аксонометрии повторяет построение основания цилиндра. (См. раздел 8.2.1.). Отложив на вертикальной оси высоту конуса, проводим две образующие – касательные к овалу основания.
Первый способ. Рис. 2.
Строим образующую SE: на оси X или Y откладываем координаты Х или
Y соответствующие т. Е на горизонтальной проекции и проведем через них линии параллельные оси Y или X соответственно. Пересечение их дает положение точки Е на основании конуса.
Соединим т. Е с вершиной конуса S и с центром основания т. 0. Рассмотрим полученный треугольник S0E: сторона 0S – ось симметрии конуса совпадающая с осью Z. Сторона SE – образующая конуса, на которой находится т. А. Сторона 0E – основание треугольника составляющая с осью Z угол 900.
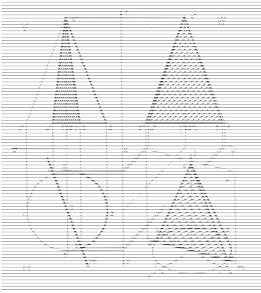
Рис. 4
Высоту т. А берем на фронтальной проекции по перпендикуляру от ос-
нования конуса до т. a’ и откладываем ее в аксонометрии на оси Z, то есть на стороне 0S.
Через полученную засечку проводим прямую в плоскости треугольника
параллельно основанию треугольника до пересечения с образующей SE. Таким образом, переносим высоту положения т. А на поверхность кону-
са.
Второй способ. Рис. 3.
Строим сечение конуса плоскостью параллельной основанию и проходящей через т. В. Такое сечение конуса есть окружность с радиусом равным
отрезку ОК расположенной на высоте равной высоте т. В. В аксонометрии эта окружность строиться в виде эллипса (или заменяющего его овала).
Затем, на осях X и Y в основании конуса откладываем соответствующие
координаты X и Y т. В взятые с горизонтальной проекции и из точки их пересечения восстанавливаем перпендикуляр до пересечения с эллипсом сечения,
что определит положение т. В.
Сечения конуса.
Взависимости от направления в пространстве секущей плоскости, проходящей через конус, в сечении прямого кругового конуса могут получаться
различные плоские фигуры:
А – прямые (образующие) Б – гипербола
В– окружность
Г – парабола
Д – эллипс Конические сечения – эллипс, парабола и гипербола являются лекаль-
ными кривыми, которые строятся по точкам принадлежащим кривой сечения.
А. Сечение конуса вертикальной плоскостью проходящей через его вершину представляет собой прямые. Рис. 4.
На горизонтальной проекции конуса через точку S проводим линию Ph под произвольным углом к осям X и Y, которая является горизонтальной проекцией секу-
щей вертикальной плоскости. Эта линия
пересекает окружность основания конуса в двух точках a и b, а отрезок aob является горизонтальной проекцией сечения конуса.
Мысленно отбросим левую часть конуса от линии Ph и справа от нее получим горизонтальную проекцию усеченного ко-
нуса.
Отрезки SA и SB – горизонтальные
проекции образующих конуса, по которым и проходит секущая плоскость Ph.
Строим образующие SA и SB на
фронтальной проекции, перенеся на нее точки A и B и соединив полученные точки a’ и b’ с вершиной s’. Треугольник a’s’b’ и будет фронтальной проекцией сечения
конуса, а линия s’3’ – крайней образующей конуса.
Рис. 5
Аналогично строим профильную проекцию сечения конуса, перенеся
точки a и b с горизонтальной проекции на профильную и соединив полученные точки a” и b” с вершиной конуса s”. Треугольник a”s”b” является профильной проекцией сечения конуса, а линия s”2” есть крайняя образующая конуса.
Построение аксонометрии. Рис. 4.
Строим конус в аксонометрии, как описано выше.
Далее с горизонтальной проекции конуса берем координаты по оси X или Y для точек A и B и переносим их на аксонометрические оси X или Y. Через полученные точки проводим вспомогательные линии параллельные осям Y
или X соответственно. Их пересечение с линией основания конуса позволяет получить точки A и B на аксонометрии. Соединив их между собой, и каждую из
них с вершиной конуса S, получим треугольник ABS являющийся сечением конуса вертикальной плоскостью P.
Б. Сечение конуса вертикальной плоскостью, не проходящей через его вершину, представляет собой гиперболу. Рис. 5.
Строим три проекции конуса – горизонтальную, фронтальную и про-
фильную.
Если вертикальная секущая плоскость P не проходит через вершину конуса, то она уже не совпадает с образующими его боковой поверхности, а наоборот – пересекает
их.
На горизонтальной проекции конуса проводим секущую плоскость Ph на произвольном расстоянии от вершины S и парал-
лельную оси Y. В общем случае положение
секущей плоскости относительно осей X и Y может быть любое.
Линия Ph пересекает окружность основания конуса в двух точках a и b. Отрезок ab этой прямой есть горизонтальная проек-
ция сечения конуса. Часть окружности слева от линии Ph делим на произвольное коли-
чество равных частей, в донном случае на 12 и, затем каждую полученную точ-
ку на окружности соединяем с вершиной конуса s. Эти образующие пересека-
ются секущей плоскостью Ph и мы получаем ряд точек, которые принадлежат образующим и проекции сечения конуса ab одновременно.
Строим полученные образующие на фронтальной проекции конуса
.Переносим с горизонтальной проекции все точки на основании конуса (a, 1, …,
5, b) и на фронтальной проекции получаем точки (a’, 1’, …, 5’, a’) и соединяем из с вершиной конуса s’. Проводим на фронтальной проекции через точку b’ секущую плоскость Pv перпендикулярно основанию конуса. Линия Pv пересекает
все образующие, и точки их пересечения принадлежат проекции сечения конуса.
Повторим построение всех образующих на профильной проекции конуса, перенеся на нее точки (a, 1, …, 5, b) с горизонтальной проекции. Полученные точки (a”, 1”, …, 5”, b”) соединим с вершиной s”.
На полученные образующие перенесем с фронтальной проекции точки пересечения соответствующих образующих с секущей плоскостью Pv. Полученные точки соединим кривой линией, которая представляет собой лекальную
кривую – гиперболу.
Построение аксонометрии. Рис. 5.
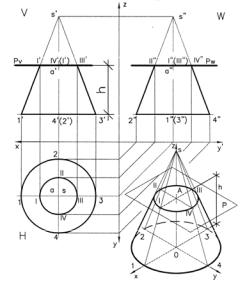
Рис. 6
Строим конус в аксонометрии, как описано выше.
Далее с горизонтальной проекции конуса берем координаты по оси X или Y для всех точек a, 1, …, 5, b и переносим их на аксонометрические оси X или Y находим их положение на основании конуса в аксонометрии. Соединяем
их последовательно с вершиной конуса S и получаем ряд образующих на поверхности конуса соответствующих образующим на ортогональных проекциях.
На каждой образующей найдем точку ее пересечения с секущей плоскостью P аналогично тому, как это было описано выше (см. построение точек на поверхности конуса, первый способ).
Соединив полученные на образующих точки лекальной кривой, а также точки A и B получим аксонометрическую проекцию усеченного конуса.
В Сечение конуса горизонтальной плоскостью. Рис. 6.
Сечение прямого кругового конуса горизонтальной плоскостью параллельной основанию – есть окружность.
Если рассечь конус на произвольной высоте h от основания конуса через точку a’
лежащую на его оси o’s’ плоскостью параллельной его основанию, то на фронтальной проекции мы увидим горизонтальную линию Pv являющуюся фронтальной проекцией секущей плоскости, которая образует сечение
конуса I’, II’, III’, IV’. На профильной проекции
W вид секущей плоскости и сечение конуса аналогичен и соответствует линии Pw.
На горизонтальной проекции сечение
конуса представляет собой круг в натураль-
ную величину, радиус окружности которого проецируется с фронтальной проекции как расстояние от оси конуса в точке a’ до точки I’, лежащей на крайней образующей 1’s’.
Построение аксонометрии. Рис. 6.
Строим конус в аксонометрии, как опи-
сано выше.
Затем на оси Z откладываем высоту h точки А от основания конуса. Через точку А проводим линии параллельные осям X и Y и строим окружность в
аксонометрии радиусом R=a’I’ взятым с фронтальной проекции.
Г Сечение конуса наклонной плоскостью, параллельной образующей. Рис. 7.
Строим три проекции конуса – горизонтальную, фронтальную и профильную. (см. выше).
На фронтальной проекции конуса проводим секущую плоскость Pv параллельно очерковой образующей s’6’на произвольном расстоянии от ее нача-
ла на основании конуса через т. a’(b’). Отрезок a’c’ есть фронтальная проекция сечения конуса.
На горизонтальной проекции строим проекцию основания секущей плоскости Р через точки a, b. Отрезок ab – есть проекция основания сечения конуса.
Далее окружность основания конуса делим на произвольное количество частей и полученные точки соединяем с вершиной конуса s. Получаем ряд образующих конуса, которые последовательно переносим на фронтальную и профильную проекции. (см. пункт Б).
На фронтальной проекции след секущей плоскости Pv пересекает обра-
зующие и в пересечении дает ряд точек, которые принадлежат как секущей плоскости, так и образующим конуса одновременно.
Переносим линиями связи эти точки на проекции образующих на гори-
зонтальную и профильную проекции.
Полученные точки соединим кривой линией, которая представляет собой
лекальную кривую – параболу.
Построение аксонометрии. Рис. 7.
Строим аксонометрическую проекцию конуса, как описано выше.
Далее с горизонтальной проекции конуса берем координаты по оси X или Y для
всех точек (a, b, 1, …, 6) и переносим их на аксонометрические оси X или Y соответственно, определив, таким образом их поло-
жение на основании конуса в аксонометрии. Соединяем их последовательно с вершиной
конуса S и получаем ряд образующих на поверхности конуса, соответствующих образующим на ортогональных проекциях.
На каждой образующей найдем точку ее пересечения с секущей плоскостью P
аналогично тому, как это было описано выше (см. построение точек на поверхности конуса).
|
Соединив полученные на образующих |
||
|
Рис. 7 |
||
|
точки лекальной кривой, а также точки A и B |
||
|
получим сечение конуса в виде параболы. |
||
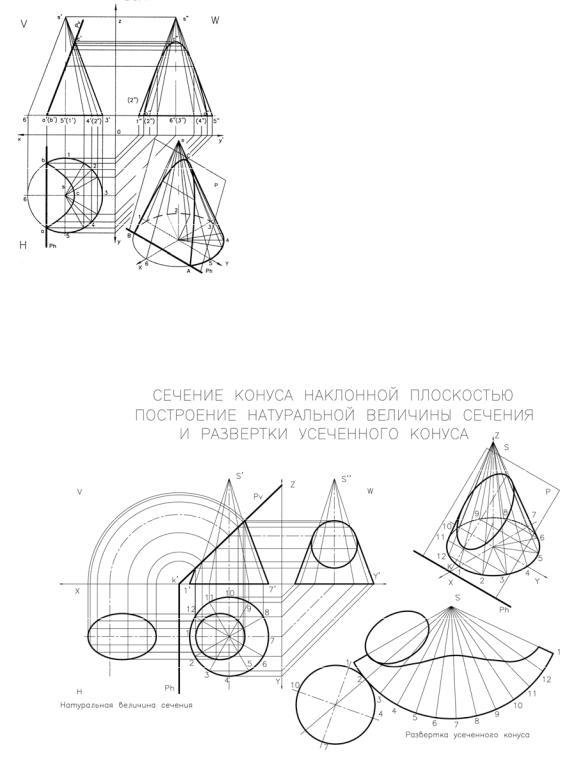
Д. Сечение конуса наклонной плоскостью, расположенной под произвольным углом к основанию конуса представляет собой эллипс. Рис. 8.
Рис. 8
Строим три проекции конуса – горизонтальную, фронтальную и про-
фильную. (см. выше).
На фронтальной проекции конуса проводим линию секущей плоскости Pv под произвольным углом к основанию конуса.
На горизонтальной проекции, окружность основания конуса делим на произвольное количество равных частей ( в данном случае на 12) и получен-
ные точки соединяем с вершиной конуса S. Получаем ряд образующих, которые с помощью линий связи, последовательно переносим на фронтальную и профильную проекции.
На фронтальной проекции секущая плоскость Pv пересекает все образующие, и полученные точки их пересечения принадлежат одновременно и се-
кущей плоскости и боковой поверхности конуса, являясь фронтальной проекцией искомого сечения.
Переносим эти точки на горизонтальную проекцию конуса.
Затем строим и профильную проекцию сечения конуса (см. выше), соединяя полученные точки лекальной кривой, которая представляет собой эл-
липс.
Построение натуральной величины сечения.
Лекальные кривые (эллипсы) на горизонтальной и профильной проекции представляют собой искаженные изображения сечения конуса.
Истинная (натуральная) величина сечения получается путем совмеще-
ния секущей плоскости P с горизонтальной плоскостью проекций H. Все точки сечения конуса на фронтальной проекции переносим на ось X при помощи циркуля, поворачивая их вокруг точки k’. Далее, на горизонтальной проекции, линиями связи, параллельными оси Y продолжаем их до пересечения их с ли-
ниями связи, взятыми с горизонтальной проекции соответствующих точек. Пе-
ресечение горизонтальных и вертикальных линий связи соответствующих точек позволяет получить точки, принадлежащие натуральной величине сечения. Соединив их лекальной кривой, мы получим эллипс натуральной величины сечения конуса.
Построение аксонометрии усеченного конуса. Рис. 8.
Построение аксонометрии усеченного конуса выполняется путем нахождения точек принадлежащих сечению конуса любым из описанных выше способов (см. выше).
Построение развертки поверхности усеченного конуса. Рис. 8.
Предварительно построим развертку боковой поверхности не усеченного
конуса. Задаемся положением т. S на листе и проводим из нее дугу радиусом равным натуральной величине длины образующей конуса (например, s’1’или s’7’). Задаемся положением т. 1 на этой дуге. Последовательно откладываем от нее столько одинаковых отрезков (хорд) на сколько частей разделена окружность основания конуса. Полученные на дуге точки 1, 2, …, 12, 1 соединяем с т. S. Сектор 1S1 представляет собой развертку боковой поверхности не усе-
ченного конуса. Пристроив к ней в нижней части (например, к т. 2) натуральную величину основания конуса в виде круга взятого с горизонтальной проекции мы
получим полную развертку не усеченного конуса.
Для построения развертки боковой поверхности усеченного конуса необходимо определить натуральную величину всех усеченных образующих. На
фронтальной проекции все точки сечения перенесем на очерковую образующую s’7’ линиями параллельными основанию конуса. Затем каждый отрезок образующей от т. 7’ до соответствующей точки сечения переносим на соответствующую образующую на развертке. Соединив эти точки на развертке, получим кривую линию, соответствующую линии сечения боковой поверхности ко-
нуса.
Затем к линии сечения на развертке (например, к образующей S1) при-
страиваем эллипс натуральной величины сечения полученный на горизонтальной проецирующей плоскости Н.
Развертки поверхности геометрических тел представляют собой чертежи
– выкройки из бумаги и служат для выполнения макета фигуры.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
