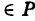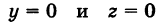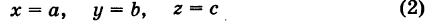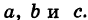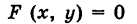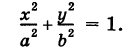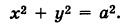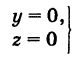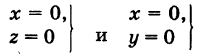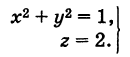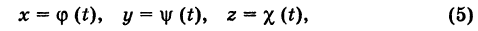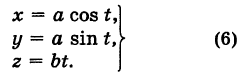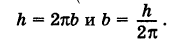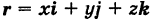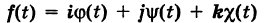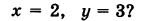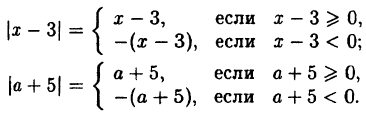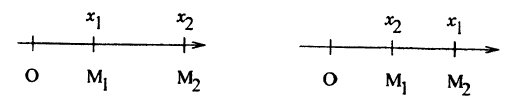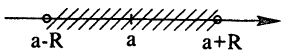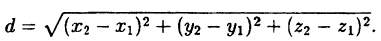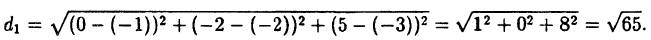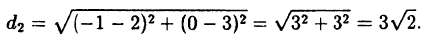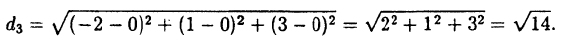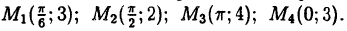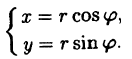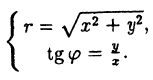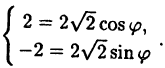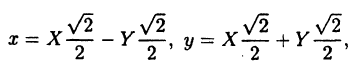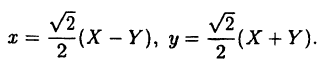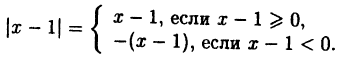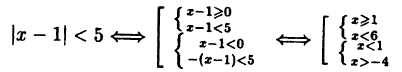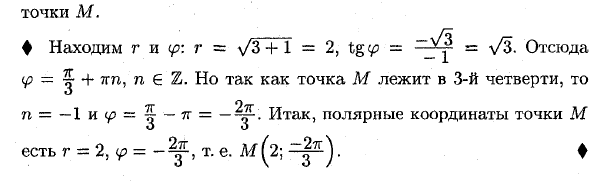Как найти точку в системе координат oxyz - Сайт, где вы сможете решить свои вопросы

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Как найти координаты точки

Поддержать сайт

Каждой точке координатной плоскости соответствуют две координаты.

Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):

находить координаты точки;
найти положение точки.

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.

Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».

Обозначают координаты точки, как указано выше (·) A (2; 3).

Пример (·) A (2; 3) и (·) B (3; 2).

Запомните!

На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.

Особые случаи расположения точек

Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2).
Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0).
Начало координат — точка O имеет координаты, равные нулю O (0,0).
Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
Координаты любой точки, лежащей на оси ординат имеют вид (0, y).

Как найти положение точки по её координатам

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:

Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox».
Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy».
Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.

Второй способ

Чтобы найти точку D (−4 , 2) надо:

Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−».
Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

1. На оси х сдвигаемся на 1 единицу в положительном направлении
2. Через текущую точку (точку, в которой находимся в данный момент) (1; 0; 0) проведем прямую, параллельную оси у – обозначим ее у`
3. На оси у` сдвигаемся на 2 единицы в отрицательном направлении
4. Через текущую точку (1; -2; 0) проведем прямую, параллельную оси z – обозначим ее z`
5. На оси z` сдвигаемся на 4 единицы в отрицательном направлении. Получим искомую точку А(1; -2; -4)

При построении мы сдвинулись по оси х на 1 единицу – значит расстояние до плоскости yOz равно 1. Аналогично, сдвиг по оси y||y` на 2 единицы – расстояние до плоскости xOz равно 2, сдвиг по оси z||z` на 4 единицы – расстояние до плоскости xOy равно 4

Источник

Содержание:

Уравнения поверхности и линии в пространстве

Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если

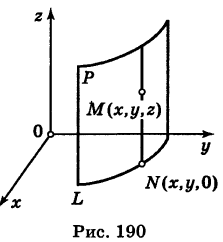
— уравнение поверхности Р (рис. 189), то при М(х, у, z)

Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.

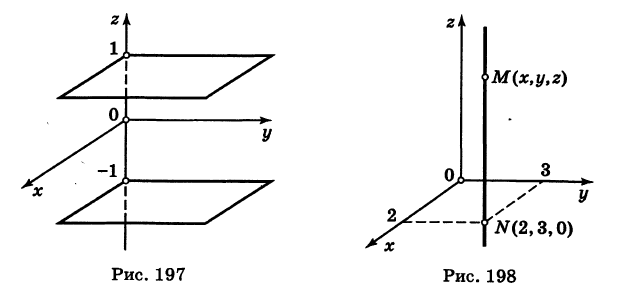
Пример (уравнения координатных плоскостей):

Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,

х = 0

— уравнение координатной плоскости Oyz. Аналогично,

— соответственно уравнения координатных плоскостей Oxz и Оху.

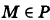
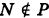
Формула обозначает, что точка М принадлежит Р. Формула обозначает, что точка N не принадлежит Р.

В более общем случае

— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные

Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.

Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 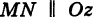(образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).

Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).

Пусть

— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,

является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.

Пример (уравнение эллиптического цилиндра):

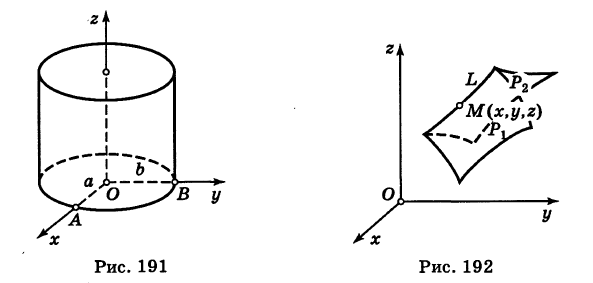
Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение

В частности, при а = b получаем уравнение кругового цилиндра

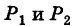
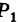
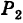
Линию L в пространстве можно задать как пересечение двух данных поверхностей (рис. 192). Точка , лежащая на линии L, принадлежит как поверхности так и поверхности , и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.

Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:

являющихся уравнениями поверхностей, определяющих данную линию.

Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки , координаты которых удовлетворяют обоим уравнениям системы (4).

Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.

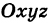
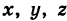
Определение: Уравнениями линии в пространстве называется такая пара уравнений между переменными , которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Пример (уравнения координатных осей):

Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому

— уравнения оси Ох. Аналогично,

— уравнения осей Оу и Oz соответственно.

Пример:

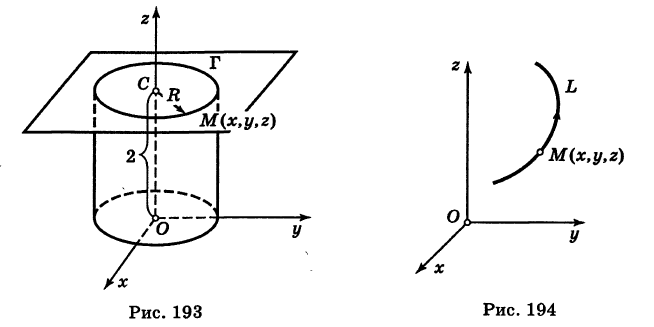
Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).

Решение:

Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть

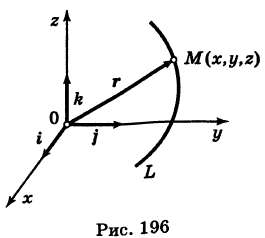
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем

где 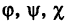— некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)} не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве.

Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.

Заказать решение задач по высшей математике

Пример:

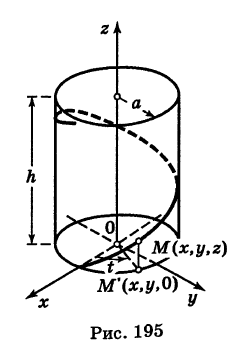
Написать уравнения винтовой линии радиуса а и шага 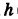(рис. 195).

Решение:

Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.

Приняв за параметр 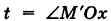и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь

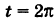
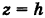
Для определения коэффициента пропорциональности b положим ; тогда . Следовательно,

Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем

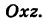
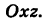
Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости . Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость — косинусоида.

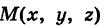
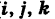
Текущую точку кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)

( — орты). Тогда из (5) получаем векторное уравнение линии

где

— так называемая вектор-функция скалярного аргумента t.

В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).

Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).

Пример:

Какой геометрический образ соответствует уравнению

Решение:

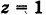
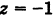
Из уравнения (8) получаем или . Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).

Пример:

Какой геометрический образ соответствует паре уравнений

Решение:

Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).

Общее уравнение плоскости
Угол между плоскостями
Понятие о производной вектор-функции
Криволинейные интегралы
Прямоугольная система координат на плоскости и ее применение
Линии второго порядка
Полярные координаты
Непрерывность функции

Источник

Абсолютная величина действительного числа
Положение точки на прямой
- Положение точки на плоскости
- Положение точки в пространстве
- Параллельный перенос осей координат
- Полярные координаты
- Поворот осей координат
Системы координат — примеры с решением
Система координат на плоскости

Абсолютная величина действительного числа. Положение точки на прямой, на плоскости, в пространстве. Расстояние между двумя точками. Преобразование координат. Полярные координаты.

Абсолютная величина действительного числа

Определение:

Абсолютной величиной или модулем действительного числа х называется само это число, если х ≥ 0 и число -х, если х < 0:
(2.1)

Например: |2| = 2, т. к. 2 > 0, |- 3| = -(-3) = 3, т. к. — 3 < 0,
∣x² + 4| = x² + 4, т. к. x² + 4 > О при всех х ∈ R, |0| = 0.

Модуль дейcтвительного числа х равен расстоянию на числовой оси от точки х до начала координат.

Расстояние между двумя точками на оси с координатами x₁ и х₂ выражается формулой:
(2.2) d = ∣x₂ — x₁∣

Докажем эту формулу для случая, когда х₂ ≥ x₁ ≥ 0 (рис. 15)

В этом случае
OM₁ = x₁ , OM₂ = x₂ и d — M₁M₂ = OM₂ — OM₁ — x₂ — x₁ — ∣ x₂ — x₁ ∣.
Если x₁>x₂ ≥ 0 (рис. 15), то d = M₁M₂ = OM₂ — OM₁ — x₁ — х₂ — (x₂ — x₁) = ∣х₂ — x₁∣ , т. к. х₂ — x₁ < 0.

Рис. 15. Расстояние между точками на оси

Для остальных случаев расположения M₁ и M₂ формула доказывается аналогично.

Пример:

Для данных а и R > 0 отметить на числовой оси множество M = {x|| x — а |< R}.

Решение:

В соответствии с формулой 2.2 множество M есть множество точек числовой оси, расстояние от которых до данной точки меньше R, т.е. интервал с центром в а и длиной 2R:
M = {x||x — α |< R} = {x|x ∈ (а — R; а + R)} =
= {x∣α — R < х < а + R}.

Ответ: см. рис. 16.

Рис. 16. {x||x — а| < R}

Приведем свойства модуля действительного числа, которые вытекают из определения модуля и свойств арифметических операций.

1) ∣x∣ ≥ 0,
2) ∣x∙y∣ = ∣x∣∙∣y∣,
3) =
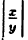
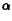
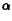
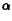
4) ∣x∣ = ∣x∣ если ∃x,
5) |x| = |- x|,
6) |x| ≤ a ⇔ -a ≤ x ≤ а для ∀a > 0,
7) ∣x + y∣ ≤ |x| + |y|,
8) ∣x — y∣ ≤ |x| — |y|.

Заметим, что из свойств модуля и того факта, что арифметический корень квадратный неотрицателен, следует, что корень квадратный из полного квадрата некоторого выражения а равен модулю этого выражения:
(2.3) √a² = |a|.

Так, например, √5² =5; √(-3)² = 3(а не — 3);
√(x + 5)² =| x + 5|.

Аналогичное замечание справедливо при любом сокращении и показателя корня и степени подкоренного выражения на четное число:
(2.4) 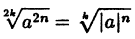∀k, n ∈ N

Положение точки на прямой

Определение:

Координатой точки M на числовой оси называется действительное число х, которое соответствует этой точке (см. п. 1.11 лекции 2).

Положение точки на плоскости

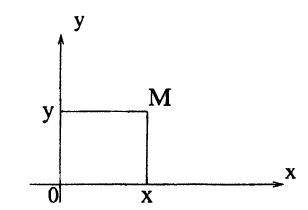
В декартовой системе координат положение точки на плоскости определяется уже двумя числами. Зададим на плоскости две взаимно перпендикулярные числовые оси Ox и Оу, имеющие общее начало О (совпадающее с точкой пересечения). Плоскость в которой, расположены оси, назовем координатной плоскостью Оху. Произвольная точка M плоскости имеет две координаты, одна из которых — ее проекция х на ось Ох, а другая ее проекция у на ось Oy (рис. 17).

Рис. 17. Координатная плоскость Oxy

Определение:

Координата х называется абсциссой точки M, а координата у — ординатой точки M. Упорядоченная пара чисел (х; у) называется прямоугольными или декартовыми координатами точки M на плоскости Оху. Каждой точке M координатной плоскости соответствует единственная упорядоченная пара чисел (х; у) и, наоборот, каждая такая пара чисел определяет единственную точку M плоскости, расположенную на пересечении перпендикуляров к осям в точках х и у соответственно. Ось Ox называется осью абсцисс, ось Oy — осью ординат, точка О — началом координат.

Заметим, что обычно горизонтальную ось называют осью абсцисс и устанавливают положительное направление направо, а вертикальную ось называют осью ординат и устанавливают положительное направление вверх, как на рис. 17. Оси Ox и Oy делят координатную плоскость на четыре четверти (на четыре квадранта): в I-й х > 0, у > 0, во II-й х < 0, у > 0, в III-й х < 0, у < 0, в IV-й х > 0, у < 0. Запись M (1; 2) будет означать, что точка M имеет абсциссу 1 и ординату 2.

Положение точки в пространстве

В декартовой системе координат положение точки в пространстве определяется тремя числами. Зададим в пространстве три взаимно перпендикулярные числовые оси Ox, Оу, Oz, имеющее общее начало О (совпадающее с точкой их пересечения). Оси назовем координатными осями: Ox — ось абцисс, Oy — ось ординат, Oz — ось аппликат. Координатное пространство обозначим Oxyz.

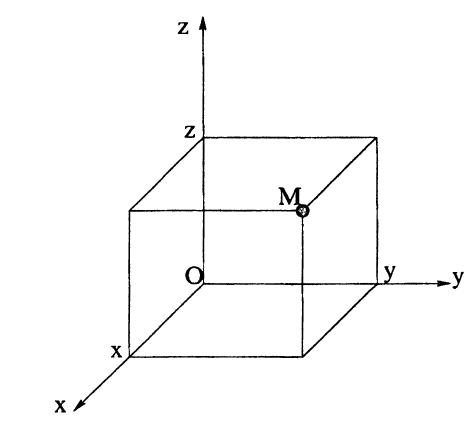
Произвольная точка M пространства Oxyz имеет три координаты — ее проекция х на ось Ox (пересечение плоскости, проходящей через точку M перпендикулярно оси Ох, с этой осью), ее проекция у на ось Oy и ее проекция z на ось Oz (рис. 18). Упорядоченная тройка чисел (x,y,z) называется прямоугольными или декартовыми координатами точки M в пространстве.

Очевидно, между точками в пространстве Oxyz и упорядоченными тройками чисел существует взаимно-однозначное соответствие. Координаты х, у, z называются аналогично осям — абсцисса, ордината и аппликата соответственно. Кроме координатных осей можно рассмотреть также три взаимно перпендикулярные координатные плоскости Оху, Oyz, Ozx, проходящие через оси приведенные в обозначении. Мы будем стараться располагать координатные оси как показано на рис. 18. Координатные плоскости делят пространство на 8 октантов: в I-м х > 0, у > 0, z > 0, во II-м х < 0, у > 0, z > 0, в III-м х < 0, у < 0, z > 0, в IV-M х > 0, у < 0, z > 0, в V-м х > 0, у > 0, z < 0, в VI-м х < 0, у > 0, z < 0, в VII-м х < 0, у < 0, z < 0, в VIII-м х > 0, у < 0, z < 0. Запись М(-1; -2; -3) будет означать, что точка M имеет абсциссу -1, ординату -2, аппликату -3 и расположена, следовательно, в VII октанте.

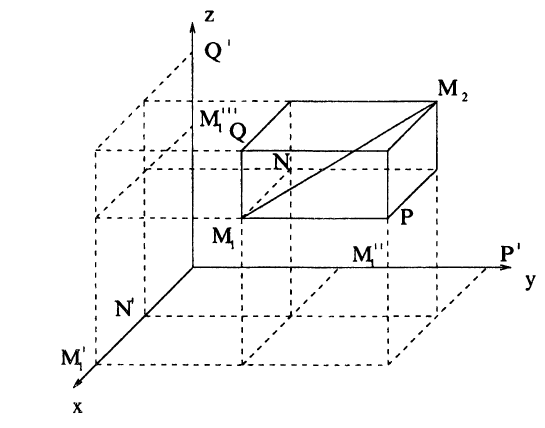
2.5. Расстояние между двумя точками. Найдем расстояние d между точками M₁(x₁,y₁, z₁) и M₂(x₂;y₂; z₂) в пространстве. Построив прямоугольный параллелепипед, диагональю которого является отрезок M₁M₂ и с гранями, параллельными координатным плоскостям (рис. 19), на основании известной теоремы курса стереометрии средней школы получим:
M₁M₂² = M₁N² + M₁P² + M₁Q².

Рис. 18. Координатное пространство Oxyz

Спроектировав концы ребер M₁N, M₁P, M₁Q на оси Ox, Оу, Oz, получим на этих осях отрезки M’₁N’, M»₁P’, M»’₁ Q1 и в соответствии с формулой ( 2.2): M₁N = M’₁N’ = ∣x₂ — x₁∣; M₁P = M₁»P’ = ∣y₂ — y₁∣; M₁Q = M₁»Q’ = ∣z₂ — z₁∣.

Подставив эти выражения в предыдущую формулу, получим:
M₁M₂² = ∣x₂ — x₁∣² + ∣y₂ — y₁∣² + ∣z₂ — z₁∣²,
или:
(2.5)

Данная формула остается, безусловно, справедливой, если отрезок M₁M₂ параллелен каким-либо координатным плоскостям (рассмотрите эти случаи самостоятельно). Если точки M₁ (x₁; y₁) и М₂ (х₂; у₂) лежат в плоскости Оху, то формула для расстояния между этими точками принимает вид:

Рис. 19. Расстояние между двумя точками в пространстве

(2.6)

Пример:

Найти расстояние d₁ между точками M₁ (-1; -2; -3;) и M₂ (0; -2; 5), расстояние d₂ между точками М₃ (2;3) и М₄ (—1;0) и расстояние d₃ между началом координат 0 и точкой M₅ (-2; 1; 3).

Решение:

По формуле ( 2.5):

По формуле ( 2.6):

По формуле ( 2.5):

Параллельный перенос осей координат

В некоторых случаях приходится одновременно рассматривать две системы координат на плоскости и решать следующую задачу: зная координаты точки в одной системе координат, найти ее координаты в другой системе. Эти формулы называются формулами преобразования координат.

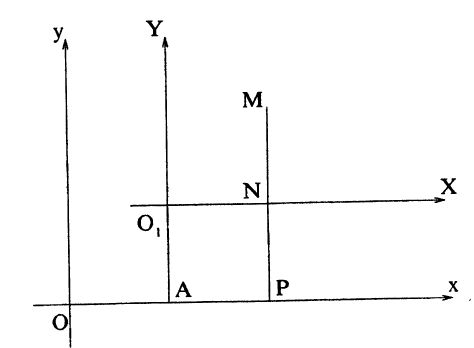
Мы будем предполагать, что обе системы — декартовы (прямоугольные), причем одноименные оси этих систем параллельны и одинаково направлены, и на каждой из осей выбрана одна и та же масштабная единица. На рис. 20 изображены две такие системы Oxy и O₁XY. Система O₁XY может быть получена параллельным переносом осей Ox и Оу.

Рис. 20. Параллельный перенос осей координат

Условимся называть координаты точек в системе Oxy старыми, а в системе O₁XY — новыми. Пусть x₀, y₀ — координаты нового начала O₁ в старой системе. Предположим, что произвольно выбранная точка M на плоскости имеет старые координаты х и у и новые координаты X и Y. Выведем формулы, выражающие старые координаты точки M через новые. Проектируя новое начало O₁ и точку M на ось Ох, а также точку M на ось O₁X, получим соответственно точки A, P и N. Очевидно, O₁N = АР. Но O₁N = |X|, AP = |х — x₀∣, тaκ что
|X| =∣x-x₀∣ ,
т.е. новая абсцисса X и разность x-x₀ равны по модулю. Нетрудно заметить, что и знаки этих величин одинаковы. В самом деле, если N лежит правее O₁ , то P расположена правее А, и обе величины X и (x-x₀) положительны. Если же N находится левее O₁, то P — левее А и, следовательно, X и (x-x₀) отрицательны. В обоих случаях X = x-x₀,

откуда х = X + x₀. Аналогично получается формула для старой ординаты у. Таким образом, мы получили следующие формулы преобразования координат (параллельного переноса осей):
(2.7) х = X + x₀ > У = Y + y₀

Пример:

Дана точка M(2; —1) в системе Оху. Найти ее новые координаты X и Y при параллельном переносе осей, если новое начало в старой системе имеет координаты -1 и 3.

Решение:

По формулам ( 2.7) получим 2 = X — 1, -1 = Y + 3, откуда X = 3, Y = -4

Полярные координаты

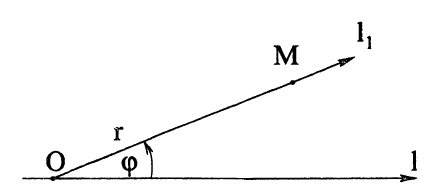
Наряду с декартовыми координатами на плоскости употребляются полярные координаты, в которых положение точки M на плоскости задается (рис. 21) полярным углом и полярным радиусом r, называемыми полярными координатами точки M : M(∙,r). Пусть на плоскости задана числовая ось l. Назовем ее полярной осью, а ее начало — точку О — полюсом. Проведем через точку M и полюс ось l₁, начало которой совпадает с О (см. рис. 21), а положительное направление от О к М. Полярный угол — это угол между полярной осью 1 и осью l₁, отсчитываемый со знаком «+» против часовой стрелки и со знаком «-» по часовой стрелке. Полярный радиус r — это расстояние от О до точки M по оси l₁ (r ≥ 0). Если значение полярного угла ограничить промежутком 0 ≤ < 2π, то между точками плоскости и упорядоченными парами полярных координат (; r) будет существовать взаимно-одназначное соответствие.

Рис. 21. Полярные координаты

Пример:

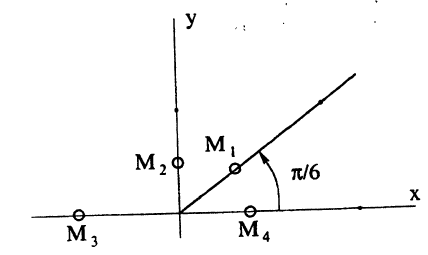
Построить в полярной системе координат точки

Решение:

Точки M₁, M₂, M₃, M₄, отмечены на рис. 22

Рис. 22. Решение примера 2.4

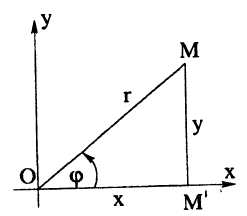
Выведем формулы, связывающие декартовы и полярные координаты точки на плоскости, для чего расположим полярную ось l, совпадающую с осью Ox, а полюс О — с началом координат О (рис. 23)

Рис. 23. Связь декартовых и полярных координат

Из Δ OMM’ находим: cos = , sin =, r² = r² + у², откуда:
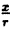
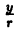
(2.8)
(2.9)

Легко понять,что формулы ( 2.8), ( 2.9) будут справедливы при любом расположении точки M на плоскости. Формулы ( 2.8) дают зависимость декартовых координат (x∙,y) от полярных (r,), а формулы ( 2.9) — наоборот. В последней формуле ( 2.9) из двух значений угла , соответствующих найденной величине tg, выбирается то (0 ≤ < 2π), при котором удовлетворяются условия ( 2.8).

Пример:

Найти полярные координаты точки M с декартовыми координатами х = 2, у =-2.

Решение:

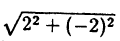
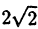
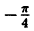
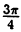
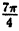
По формулам ( 2.9) находим : r = = , tg = — 1 Найдем угол : tg = — 1 ⇒ = arctg(-1) + nπ, n ∈ Z ⇔ = + nπ, n ∈ Z Условию 0 ≤ < 2π, удовлетворяют два значения: ₁ = , и ₂ = , однако равенства ( 2.8):

удовлетворяются только при = . Ответ: M(; ).

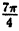
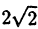
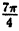
Поворот осей координат

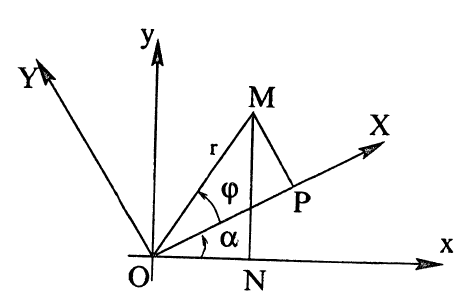
Пусть на плоскости заданы две системы координат, имеющие общее начало О: система Oxy (старая) и система OXY (новая), которая получена поворотом старой системы на угол а. Это значит,что угол (Ox;OX) = а (рис. 24) и, следовательно, угол (Oy, OY) = а. Найдем формулы, выражающие старые координаты х и у произвольной точки M плоскости через ее новые координаты X и Y.

Рис. 24. Поворот осей координат

Введем полярные координаты: старые — с полярной осью, совпадающей с осью Ох, и новые — с полярной осью ОХ. Пусть точка M в новой

полярной системе имеет полярный угол и полярный радиус r. В старой полярной системе полярный угол точки M равен α + , а полярный радиус такой же, как и в новой системе. Поэтому по формулам ( 2.8) имеем:
х = r cos (α + ), у = r sin (α + ).

Используя тригонометрические тождества для косинуса и синуса суммы двух углов, получим:
х = r (cos α cos — sin α sin ) = (r cos ) cos α — (r sin ) sin α;
у = r (sin α cos + cos α sin ) = (r cos ) sin α + (r sin )cos α.

Ho r cos = X и r sin = Y, поэтому
(2.10) x = X cos α -Y sin α, у = X sin α + Y cos α.

Формулы ( 2.10) называются формулами поворота осей. Выразив отсюда X и Y, получим
(2.11) X = x cos α + y sin α, Y =-x sin α + у cos α.

Пример:

Выразить старые координаты точки х и у через ее новые координаты X и Y при повороте осей на угол α = π∕4.

Решение:

Так как cos(π∕4) = √2∕2, то по формулам ( 2.10) получим:

или

Системы координат — примеры с решением

В этом практическом занятии на основании материала лекций 1 и 2 решите примеры с модулями, а также — на преобразование координат.

Пример:

Запишите с помощью знака модуля неравенство -3 < х < 3.

Решение:

Неравенство -3 < х < 3 на основании свойства 6 модуля действительного числа (лекция 2) равносильно неравенству |х| < 3.

Ответ: -3 < х < 3 ⇔|x| < 3.

Пример:

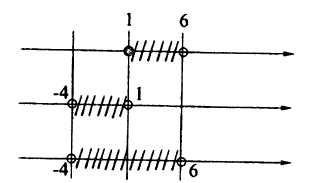
Решите неравенство |х — 1| < 5.

Решение:

Неравенство можно решить с помощью свойства 6 модуля действительного числа (2), однако здесь целесообразно использовать определение модуля:

Исходное неравенство равносильно совокупности двух систем:

Решение последней совокупности представлено на рис. 25. Следует
помнить, что решение системы неравенств получается как пересечение множеств решений каждого, а решение совокупности систем (неравенств) получается как объединение множеств решений каждой.