
f0a
x
h0a
|
a’ |
b’ |
D’ |
|
E’ |
||
|
F’ |
||
|
x |
x |
|
|
E” |
||
|
b” |
F” |
|
|
D” |
||
|
a” |
||
|
â |
ã |
|
|
Рис. 4.7 |
c”  d”
d”
c’
d’
Прежде всего уточним, что же такое в общем случае точка встречи (или точка пересечения) прямой и плоскости. Совершенно очевидно, что это точка, которая принадлежит одновременно как прямой, так и плоскости.
Поставим конкретную задачу: определить точку встречи прямой l с горизонтальнопроецирующей плоскостью (рис. 4.8,а). Обозначим эту искомую точку как точку A. Из условия принадлежности точки прямой мы знаем, что точка принадлежит прямой, если ее проекции лежат на соответствующих проекциях прямой. Поэтому фронтальная проекция будет где-то на l′′, а горизонтальная – где-то на l′ (рис. 4.8,б). Поскольку плоскость горизонтально-проецирующая и обладает свойством собирательности, горизонтальная проекция искомой точки A будет лежать на горизонтальном следе плоскости α(рис. 4.8,в).
Таким образом, A′ должна находиться и на l′ и на h0α , следовательно, ей уготовано единственное место, где l′ и h0α пересекутся (рис. 4.8,г). Проведя линию проекционной связи, мы
легко получим фронтальную проекцию искомой точки (рис. 4.8,д).
На рис. 4.9 приведены примеры решения подобных задач при различных способах задания проецирующей плоскости. Искомая точка пересечения прямой с плоскостью обозначена как точка A. Обратите внимание на рис. 4.9,г. Здесь искомая точка A вышла за границы CDE. Ничего удивительного в этом нет. Не следует забывать, что плоскость бесконечна. Сам треугольник CDE лишь задает эту плоскость, а не ограничивает ее.
48

f0a
l”
x
|
l’ |
|||
|
h0a |
|||
|
à |
f0a |
||
|
f0a |
|||
|
A”2A”3 |
A”4 |
||
|
A”1 |
|||
|
x |
x |
||
|
A’1 A’2 A’3 A’4 h0a |
A’ |
||
|
â |
ã |
Рис. 4.8
l”
A”1 A”2 A”3 A”4
l’
A’1 A’2 A’3 A’4
á
f0a
l” l”
|
A” |
|
|
x |
l’ |
|
l’ |
|
|
h0a |
A’ |
|
h0a |
|
|
ä |
|
a” |
l” |
D” |
||||
|
A” |
||||||
|
Ñ” |
||||||
|
A” |
||||||
|
b” |
l” |
|||||
|
x |
x |
E” |
||||
|
l’ |
Ñ’ |
|||||
|
A’ |
a’ |
b’ |
E’ |
A’ |
l’ |
|
|
D’ |
||||||
|
a(a,b) |
p1 |
a( CDE) |
p1 |
|||
|
à |
á |
|||||
|
Рис. 4.9 |
49

|
l” |
E” |
D” |
|||
|
A” |
a” |
b” |
A” |
||
|
C” |
|||||
|
l” |
|||||
|
x |
x |
||||
|
l’ |
E’ |
||||
|
Ñ’ |
|||||
|
A’ |
a’ |
b’ |
A’ |
||
|
l’ |
D’ |
||||
|
a(a,b) p2 |
a( |
CDE) p2 |
|||
|
â |
ã |
Рис. 4.9 (окончание)
4.1.4. Линия пересечения двух плоскостей, одна из которых проецирующая
Прежде всего определим, что же такое в общем случае линия пересечения двух плоскостей. Во-первых, это прямая, а во-вторых, эта прямая принадлежит каждой из пересекающихся плоскостей. При этом полезно вспомнить, что прямая линия в пространстве задается двумя несовпадающими точками.
Сейчас мы рассмотрим, пожалуй, самую простую задачу на тему «плоскость». Требуется построить линию пересечения двух плоскостей, одна из которых горизонтально-проецирующая (плоскость α ), а другая фронтально-проецирующая (плоскость β). Исходные данные этой задачи изображены на рис. 4.10,а.
Пусть линия пересечения этих плоскостей обозначена как прямая l. Прямая l будет принадлежать как плоскости α , так и плоскости β.
Мы хорошо помним о свойстве собирательности проецирующих плоскостей. Следовательно, горизонтальная проекция прямой l, как принадлежащей горизонтально-проецирующей плоскости α , будет совпадать с горизонтальным следом этой плоскости, т.е. l′≡ h0α . Фронтальная проекция прямой l совпадает с фронтальным следом плоскости β, т.е. l′′ ≡ f0β . Таким образом, для решения этой задачи никаких геометрических построений не понадобилось, достаточно лишь обозначить проекции искомой прямой (рис. 4.10,б).
Теперь перейдем к случаю, когда одна плоскость – горизонтально-проецирующая, а другая является плоскостью общего положения (рис.4.11а). Определим проекции линии их пересечения – прямой l. Прямая l принадлежит горизонтально-проецирующей плоскости α , поэтому ее горизонтальная проекция совпадает с горизонтальным следом этой плоскости (рис. 4.11,б).
С другой стороны, прямая l принадлежит плоскости общего положения β. Поскольку горизонтальная проекция прямой l уже известна, отметим на ней горизонтальные проекции точек 1 и 2, принадлежащих плоскости β (рис. 4.11,в). Построим фронтальные проекции этих точек (рис. 4.11,г), что даст нам возможность, соединив их, определить фронтальную проекцию искомой прямой l. Задача решена.
50

|
f0b |
f0a |
l” |
f0b |
f0a |
|
|
h0a |
h0a |
l’ |
|
|
h0b |
h0b |
||
|
à |
á |
||
|
Рис. 4.10 |
|
h0b |
h0a |
h0b |
h0a l’ |
|
|
à |
á |
|||
|
f0b |
f0a |
f0b |
f0a |
|
|
2″ |
l” |
|||
|
x |
x |
1″ |
||
|
2′ |
2′ |
|||
|
1′ |
1′ |
|||
|
h0b |
h0a l’ |
h0b |
h0a l’ |
|
|
â |
ã |
|||
|
Рис. 4.11 |
51
Пересечение прямой с плоскостью
Задача на пересечение прямой с плоскостью – это одна из основных задач, с ее применением сталкиваются при рассмотрении сечения тел плоскостями и пересечения поверхностей.
Нахождение точки встречи прямой с плоскостью, заданной пересекающимися прямыми
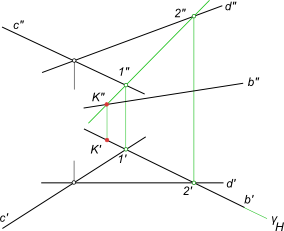
Пересечение прямой с плоскостью
Плоскость и пересекающая ее прямая занимают общее положение.
(γ ∩ α) = l – прямая, пересекающаяся с прямой b.
На пересечение прямой с плоскостью составляем алгоритм нахождения их точки встречи :
1) проводим через b` горизонтальный след γH – горизонтально-проецирующей
плоскости γ;
2) определяем фронтальную проекцию линии пересечения l, вспомогательной секущей плоскости γ
с данной плоскостью α, используя для этого точки 1` и 2` (принадлежащие данной прямой), в которых горизонтальный след γH пересекает прямые c` и d`;
3) определяем точку K”=l”∩b”. Зная K”, находим K` на пересечении b` с линией проекционной связи.
Нахождение точки встречи прямой с плоскостью, заданной параллельными прямыми
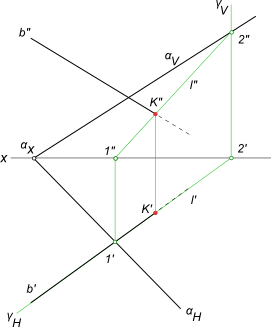
Пересечение прямой с плоскостью
Задача по нахождению точки встречи прямой с плоскостью заданной следами.
Пересечение прямой с плоскостью
Алгоритм решения не меняется, если плоскость будет задана параллельными прямыми или прямыми, по
которым она пересекает плоскости проекций (следы плоскости).
При решении задач на пересечение прямой с плоскостью в качестве вспомогательных плоскостей применяют проецирующие плоскости. Но в случае, например, профильной прямой они бесполезны и тогда надо применить плоскость общего положения.
Найти точку встречи профильной прямой AB с плоскостью α заданной следами
Пересечение прямой с плоскостью
Алгоритм выполнения геометрических построений:
1) Заключаем отрезок AB во вспомогательную секущую плоскость общего положения β;
2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости β
с данной плоскостью α;
3) Определяем проекцию K” точки K на пересечении 1″-2″ с прямой A”B”. Проекция K` точки K может быть найдена: – на пересечении A`B` с 1`-2`; – или как принадлежащая плоскостям α и β.
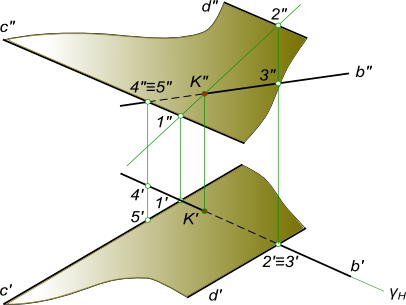
Найти точку встречи прямой d с плоскостью α(b, c), определить видимость
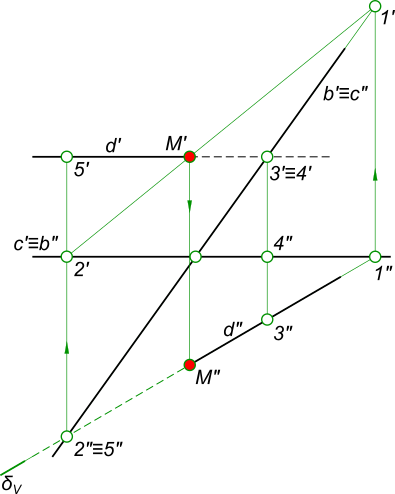
Пересечение прямой с плоскостью
Алгоритм выполнения геометрических построений:
1) Заключаем прямую d во вспомогательную секущую фронтально проецирующую плоскость δ;
2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости δ
с данной плоскостью α;
3) Определяем проекцию K` точки K на пересечении 1`-2` с прямой d`. Проекцию K” точки K находим в пересечении d” с линией проекционной связи.
Данный способ решения задачи – найти точку встречи профильной прямой с плоскостью заданной следами применен в статье:
Сечение пирамиды плоскостью
Определение видимости пересечения прямой с плоскостью на плоскостях проекций выполняем, используя Конкурирующие точки 2, 3 и 4, 5.
+
Построение точки пересечения прямой и плоскости
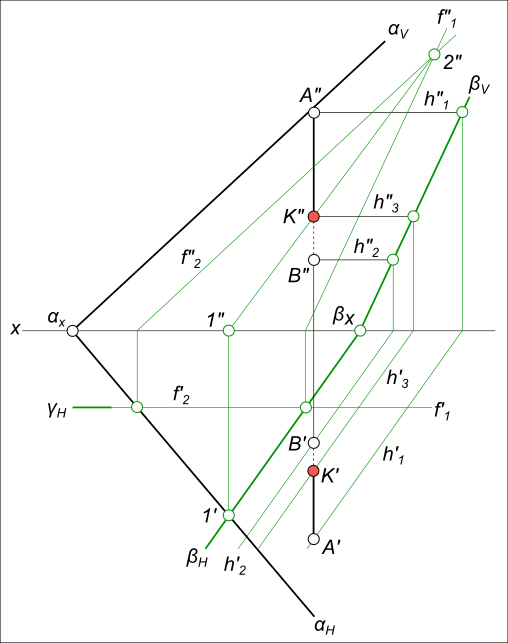
Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h0α, f0α.
Алгоритм
- Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h0γ, f0γ.
- Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B’ = h0α ∩ h0γ, A” = f0α ∩ f0γ. Точки A’ и B” лежат на оси x, их положение определяется по линиям связи.
- Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K’ = a’ ∩ A’B’. Фронтальная проекция K” лежит на прямой a”.

Алгоритм решения останется тем же, если пл. α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими возможными способами.
Видимость прямой a относительно плоскости α. Метод конкурирующих точек

- Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A” и С” совпадают, но при этом т. A и С удалены от плоскости проекций П2 на разное расстояние.
- Найдем горизонтальные проекции A’ и C’. Как видно на рисунке, точка C’ удалена от плоскости П2 на большее расстояние, чем т. A’, принадлежащая пл. α. Следовательно, участок прямой а”, расположенный левее точки K”, будет видимым. Участок a” правее K” является невидимым. Отмечаем его штриховой линией.
- Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D’ и E’ совпадают, но при этом т. D и E удалены от плоскости П1 на разное расстояние.
- Определим положение фронтальных проекций D” и E”. Как видно на рисунке, точка D”, находящаяся в пл. α, удалена от плоскости П1 на большее расстояние, чем т. E”, принадлежащая прямой a. Следовательно, участок а’, расположенный правее точки K’, будет невидимым. Отмечаем его штриховой линией. Участок a’ левее K’ является видимым.
Дополнительные материалы:
- Построение линии пересечения двух плоскостей
- Способы задания плоскости на чертеже
Пересечение прямой линии с плоскостью. Определение видимости прямой
 6 февраля, 2014
6 февраля, 2014  Анна Веселова
Анна Веселова
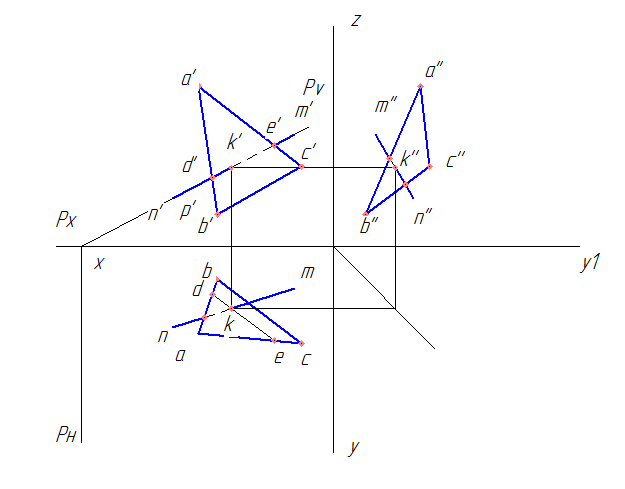

Здравствуйте друзья! Сегодня разбираем тему из начертательной геометрии – пересечение прямой линии с плоскостью и определение видимости прямой.
Задание берем из сборника Боголюбова, 1989 год, стр. 63, вар. 1. Нам требуется по заданным координатам построить комплексный чертеж треугольника ABC и прямой MN. Найти точку встречи (пересечения) прямой с непрозрачной плоскостью ABC.Определить видимые участки прямой.

Пересечение прямой линии с плоскостью
1. По координатам точек A, B и C строим комплексный чертеж треугольника и прямой NM. Начинаем чертить с горизонтальной проекции. Координаты точек проекции находим при помощи вспомогательных прямых.

2. Получаем вот такой комплексный чертеж.

3. Для определения координат точки пересечения прямой и плоскости выполним следующее.
a) Через прямую NM проводим вспомогательную плоскость Р, т.е. на фронтальной проекции проводим след плоскости Pv, на горизонтальную плоскость опускаем перпендикуляр Рн – горизонтальный след плоскости Р.
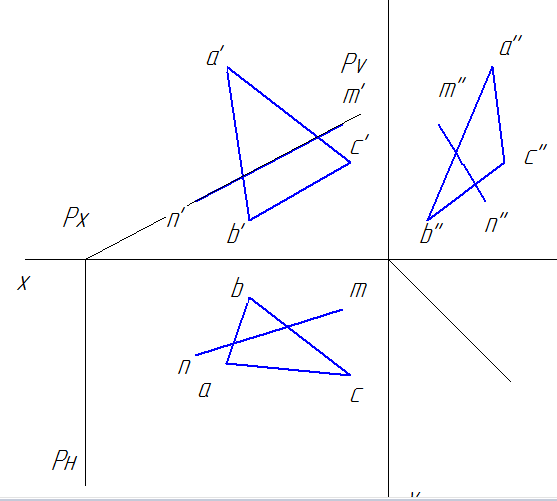
b) Находим фронтальную проекцию линии пересечения следа плоскости Р с треугольником АВС. Это отрезок d’e’. Горизонтальную проекцию находим по линиям связи до пересечения со сторонами ab (т. d) и ac (т. e) треугольника. Точки d и e соединяем.
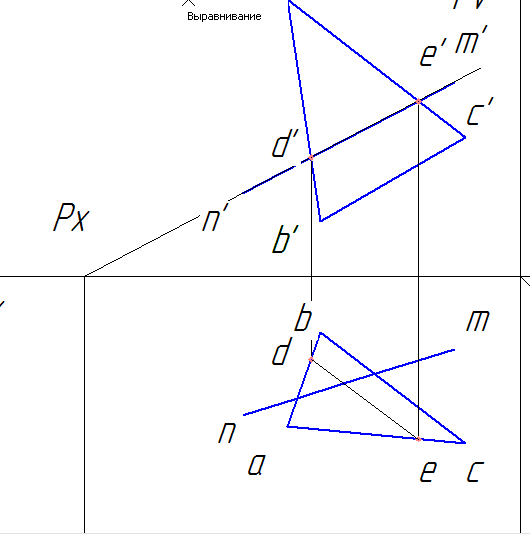
c) Вместе пересечения de и nm будет находиться горизонтальная проекция искомой точки пересечения прямой линии с плоскостью k.
d) Проводим линию связи из k до пересечения с d’e’, получаем фронтальную проекцию точки k’.
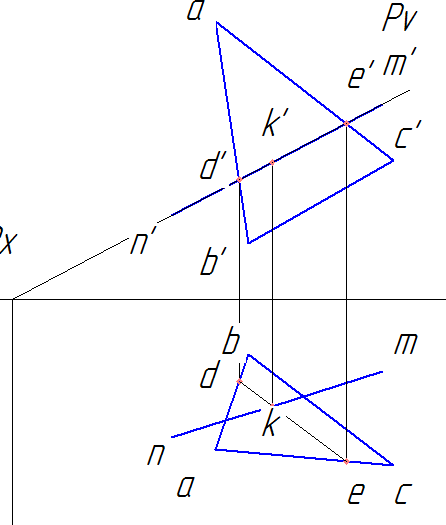
e) по линиям связи находим профильную проекцию точки k’’.
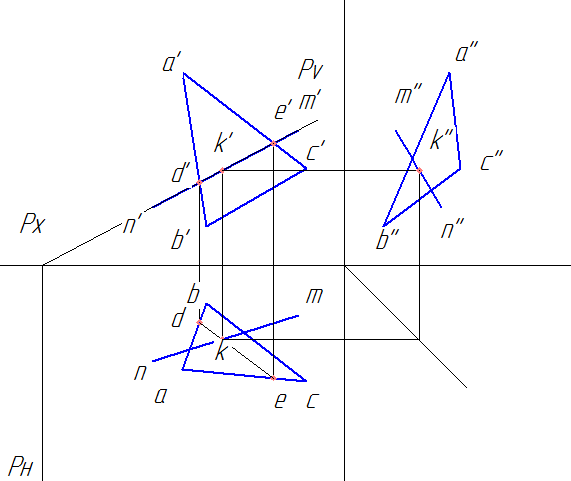
Координаты точки пересечения прямой и плоскости К найдены. Эта точка также называется точкой встречи прямой и плоскости.
Определение видимости прямой
Для определения видимости прямой воспользуемся методом конкурирующих точек.
Конкурирующие точки – это точки, расположенные на одной проекционной прямой и имеющие одинаковые одноименные координаты.
Применительно к нашему чертежу конкурирующими будут точки:
— точки: d’ принадлежащая a’b’ и e’ принадлежащая n’m’ (фронтально конкурирующие),
— точки: g принадлежащая bc и h принадлежащая nm (горизонтально конкурирующие),
— точки: l’’ принадлежащая b’’c’’ и p’’ принадлежащая n’’m’’ (профильно конкурирующие).
Из двух конкурирующих точек видимой будет та, высота которой будет больше. Граница видимости ограничена точкой К.
Для пары точек d’ и e’ видимость определяем так: опускаем перпендикуляр до пересечения с ab и nm на горизонтальной проекции, находим точки d и f. Видим, что координата по y для точки f больше, чем у d → точка f видима → видима прямая nm на участке f’k’, а на участке k’m’ невидима.
Аналогично рассуждаем и для пары точек g и h: на фронтальной проекции координата по z у точки h’ больше, чем у g’ → точка h’ видима, g’ – нет → прямая nm на отрезке hk видима, а на участке kn невидима.
И для пары точек l’’p’’: на фронтальной проекции координата по x больше у точки p’, а значит она закрывает собой точку l’’ на профильной проекции → р’’ видима, l’’ нет → отрезок прямой n’’k’’ видим, k’’m’’ невидим.
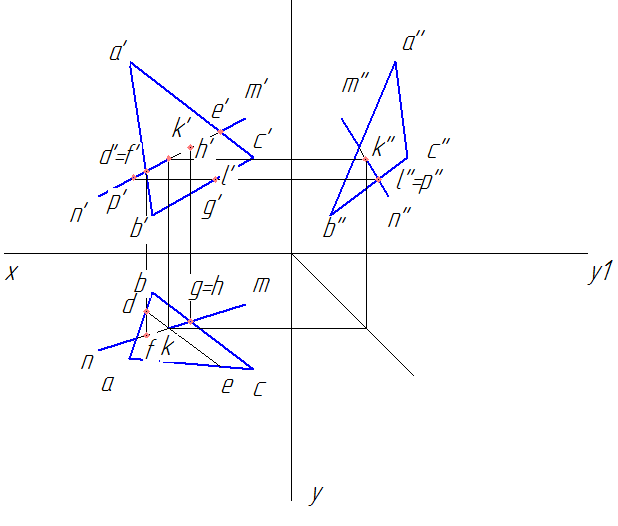
Заменяем в нужных местах линию nm на невидимую. На этом определение видимости прямой NM на комплексном чертеже треугольника АВС завершено.
Окончательно чертеж выглядит следующим образом.

Еще полезные материалы по начертательной геометрии
Как построить линию пересечения поверхностей двух взаимно перпендикулярных цилиндров?
Все о построении усеченных цилиндра и призмы, а также разверток этих геометрических тел.
Подробно весь процесс построения и определения видимости прямой описан в видеоуроке.
Скачать чертеж бесплатно можно здесь
Теперь у вас не вызовет затруднений нахождение точки пересечения прямой линии с плоскостью и определение видимости прямой на проекциях чертежа.


The following two tabs change content below.
- Bio
- Latest Posts
Рада приветствовать Вас в своем блоге! Я создала его с целью помочь всем желающим освоить программу Компас 3d. Мы пройдем весь путь от азов черчения до создания серьезных сборок. Присоединяйтесь!
Понравился материал? Подпишись на обновления!
Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.
Пересечение прямой линии с поверхностью:
Для построения точки пересечения прямой с поверхностью через прямую следует провести вспомогательную плоскость и найти линию пересечения этой плоскости с поверхностью. Точка пересечения (или точка встречи заданной прямой и построенной линии или фигуры сечения) на поверхности и будет искомой точкой пересечения прямой с поверхностью. Сложность решения задачи зависит от трудоемкости нахождения линии пересечения, которая определяется следами поверхности и расположением прямой относительно как поверхности, так и плоскости проекций. Чтобы получить рациональное решение, следует пользоваться наиболее простым способом определения линии пересечения. Этого можно достичь двумя путями:
- выбором положения вспомогательной секущей плоскости;
- переводом секущей прямой в частное положение.
Вспомогательная секущая плоскость -проецирующая
Задание: определить точки пересечения прямой m с поверхностью пирамиды SABC (рис. 12.1).
Решение: для решения задачи прямую m заключают во фронтально проецирующую плоскость Σ (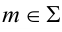
Задание: определить точки пересечения прямой m с поверхностью прямого кругового цилиндра (рис. 12.2).
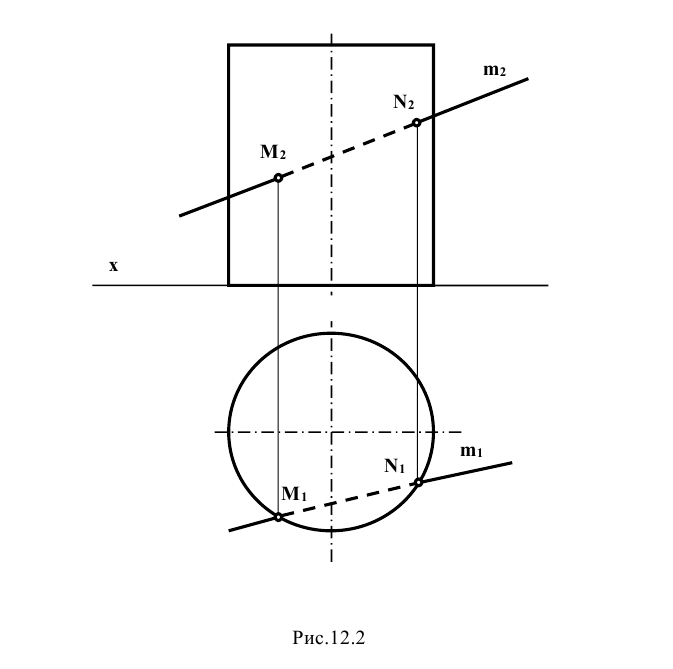
Решение: при решении задачи выделим проекции точек пересечения М и N прямой m с поверхностью цилиндра на горизонтальной проекции – точки 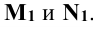 . Так как образующие прямого кругового цилиндра являются горизонтально проецирующими прямыми, фронтальные проекции точек пересечения прямой m с поверхностью цилиндра
. Так как образующие прямого кругового цилиндра являются горизонтально проецирующими прямыми, фронтальные проекции точек пересечения прямой m с поверхностью цилиндра 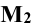 и
и 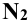 находят с помощью линий проекционной связи, как это показано на рисунке.
находят с помощью линий проекционной связи, как это показано на рисунке.
Вспомогательная секущая плоскость общего положения
Вспомогательную секущую плоскость, проводимую через прямую, при пересечении ею какой-либо поверхности, следует выбирать так, чтобы в результате получилось простейшее сечение. Например, при пересечении конической поверхности прямой линией такой плоскостью является плоскость, проходящая через вершину и пересекающая эту поверхность по прямым линиям (образующим).
При пересечении цилиндрической поверхности прямой линией вспомогательную плоскость целесообразно проводить через заданную прямую параллельно образующим цилиндра.
Задание: определить точки пересечения прямой m с поверхностью прямого кругового конуса (рис. 12.3).
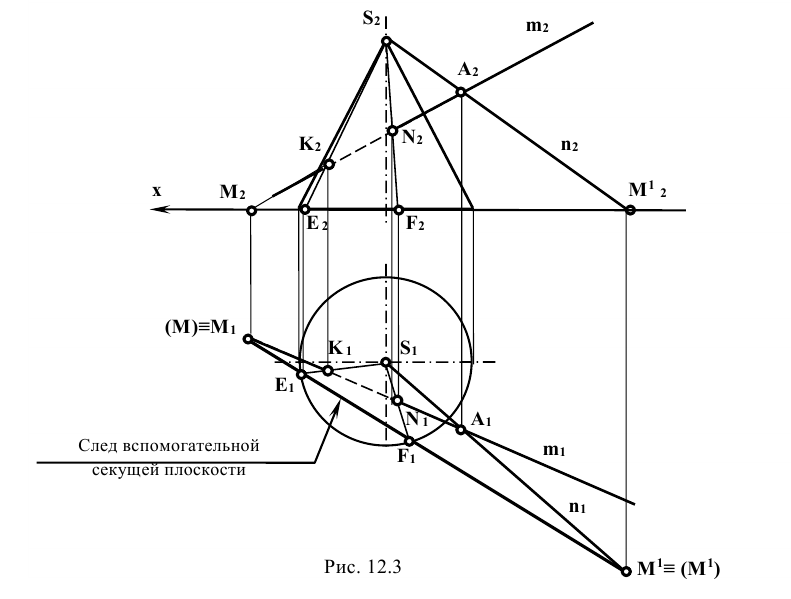
Решение: прямую m заключают в плоскость Р, проходящую через вершину конической поверхности S. Плоскость Р задана пересекающимися прямыми m и n, проходящими через точку А, которая выбирается произвольно на заданной прямой m.
Для определения горизонтального следа плоскости Р находят горизонтальные следы прямых m и n. Следы отмечают точками, например, 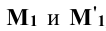 , в которых горизонтальный след
, в которых горизонтальный след 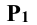 плоскости Р пересекает основание конической поверхности. Проекции
плоскости Р пересекает основание конической поверхности. Проекции 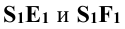 – образующие поверхности конуса, по которым она пересекается плоскостью Р.
– образующие поверхности конуса, по которым она пересекается плоскостью Р.
Точки 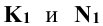 – горизонтальные проекции искомых точек пересечения. Зная положение
– горизонтальные проекции искомых точек пересечения. Зная положение 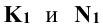 определяют фронтальные проекции
определяют фронтальные проекции 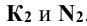 .
.
Перевод прямой общего положения, пересекающей заданную поверхность в частное положение
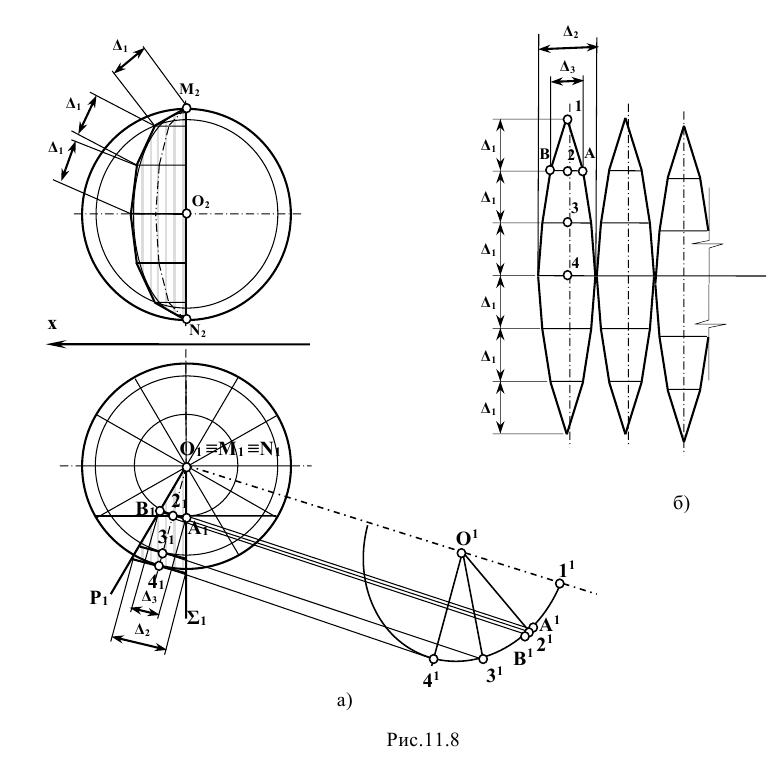
При пересечении поверхности сферы плоскостью в сечении получается окружность, которая проецируется на плоскости проекции в виде эллипсов или прямой и эллипса (если секущая плоскость – проецирующая). В случае, когда секущая плоскость параллельна плоскости проекции, окружность проецируется на эту плоскость проекции без искажения. Поэтому для упрощения решения задачи следует произвольно расположенную прямую перевести в положение, параллельное какой-либо плоскости проекции. Тогда прямую можно заключить в плоскость, параллельную плоскости проекции.
- Заказать чертежи
Задание: определить точки встречи прямой m, заданной отрезком АВ, с поверхностью сферы (рис. 12.4).
Решение: при решении этой задачи переводят прямую m общего положения в положение, параллельное плоскости проекции. Для этого вводят новую систему плоскостей 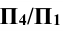 в которой
в которой 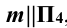 , и переходят от системы
, и переходят от системы 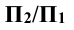 к системе
к системе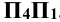 . Новую ось проекций
. Новую ось проекций 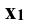 проводят параллельно горизонтальной проекции прямой
проводят параллельно горизонтальной проекции прямой 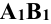 .
.
Далее от концов горизонтальной проекции прямой, точек 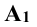 и
и 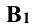 проводят линии проекционной связи, перпендикулярные к новой оси проекций, и на них на плоскости
проводят линии проекционной связи, перпендикулярные к новой оси проекций, и на них на плоскости 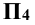 откладывают координаты
откладывают координаты 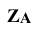 и
и 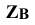 т.е. расстояния от оси проекций х до фронтальных проекций точек
т.е. расстояния от оси проекций х до фронтальных проекций точек 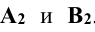 . Новая проекция
. Новая проекция 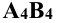 будет натуральной длиной отрезка прямой АВ.
будет натуральной длиной отрезка прямой АВ. 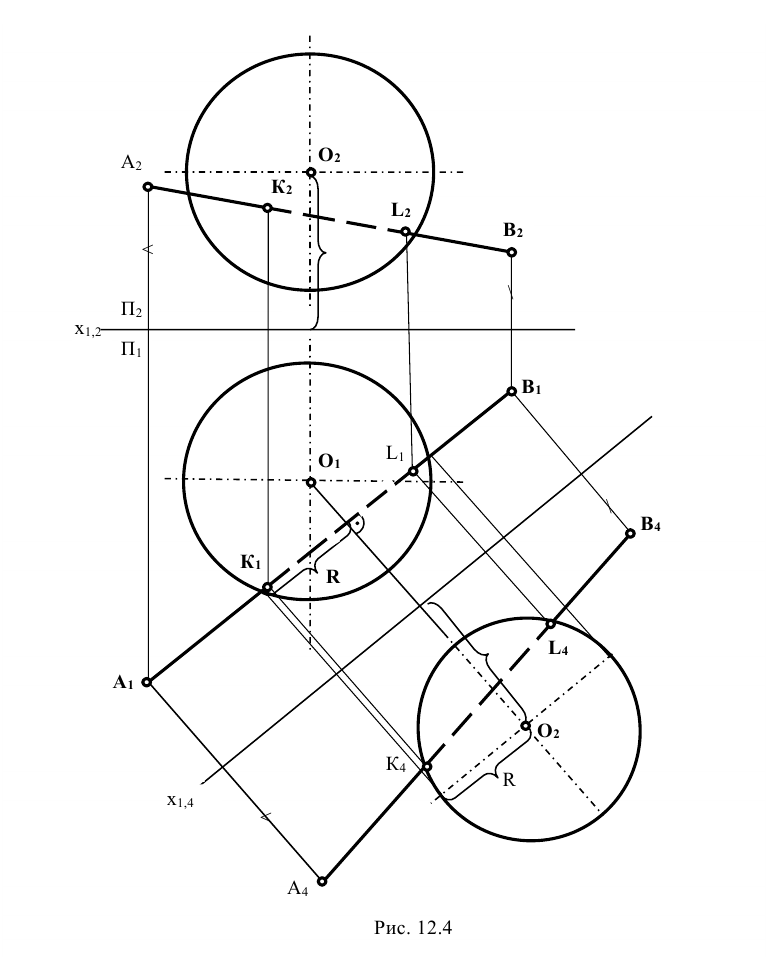
Аналогично находят и центр сферы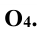
В новой системе горизонтально проецирующая плоскость Р 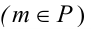 пересечет поверхность сферы по окружности радиусом R, которая спроецируется на плоскость
пересечет поверхность сферы по окружности радиусом R, которая спроецируется на плоскость 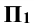 в отрезок (1-2), а на плоскость
в отрезок (1-2), а на плоскость 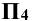 в окружность тем же радиусом R. Точки
в окружность тем же радиусом R. Точки 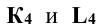 – вспомогательные проекции точек пересечения, по которым определяют проекции точек
– вспомогательные проекции точек пересечения, по которым определяют проекции точек 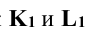 а затем
а затем 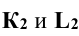 .
.
Плоскость, касательная к поверхности
Плоскость, касательная к поверхности в заданной на поверхности точке, есть множество всех прямых — касательных, проведенных к поверхности через заданную точку.
Для задания плоскости, касательной к поверхности в заданной точке, достаточно провести через эту точку две произвольные линии, принадлежащие поверхности (желательно простые по форме) и к каждой их них построить касательные в точке пересечения этих линий. Построенные прямые (касательные) определяют касательную плоскость.
Задание: построить плоскость Р, касательную к поверхности сферы и проходящую через точку К (рис. 12.5).
Решение: плоскость, касательная к сфере, перпендикулярна к радиусу, проведенному в точку касания. Поэтому, проведя радиус ОК, строят плоскость, задавая ее горизонталью КВ и фронталью КС. 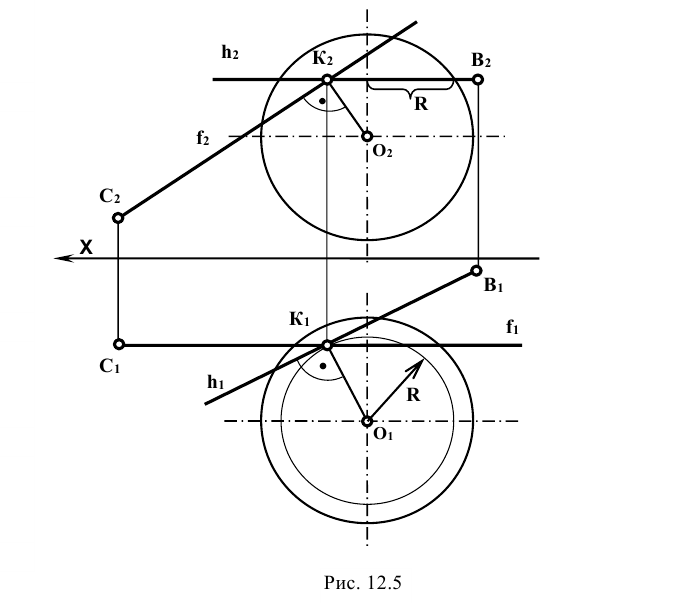
При этом горизонтальная проекция 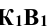 перпендикулярна к
перпендикулярна к 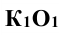 , а фронтальная проекция
, а фронтальная проекция 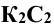 перпендикулярна к
перпендикулярна к 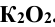 .
.
- Построение линии пересечения поверхностей
- Проецирование прямой
- Взаимное положение плоскостей, прямой линии и плоскости
- Взаимное расположение точки, прямых и плоскостей
- Проецирование точки
- Прямая в пространстве и ее изображение на чертеже
- Многогранники
- Поверхности вращения
