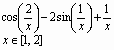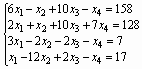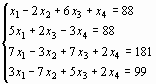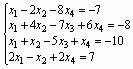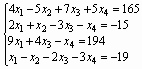Как найти точное значение в маткаде

1. Задайте
   начальное приближение x:=0.6

2. Введите
   функцию root(f(x),x)=

Функция вернет
значение 0.6161

2 Способ:

1. аналогично
   первому способу задайте начальное
   приближение и вызовите функцию root,
   но вместо параметра f(x)
   задайте само уравнение cos(x)
   x0.2

3 Способ:

1. решим
   систему уравнения, задав область где
   искать корень непосредственно при
   вызове функции root:
   root(cos(x)
   x0.2,x,0,1).

Нахождение
корней полинома

Для нахождения
корней выражения, имеющего вид

v_nxⁿ
+ … +
v₂x²
+ v₁x
+ v₀,

лучше
использовать функцию polyroots,
нежели root.
В отличие от функции root,
функция polyroots
не требует
начального приближения и возвращает
сразу все корни, как вещественные, так
и комплексные.

Polyroots(v)

Возвращает
корни полинома степени
n. Коэффициенты
полинома находятся в векторе v
длины n +
1. Возвращает вектор длины n,
состоящий из корней полинома.

Аргументы:

v
– вектор,
содержащий коэффициенты полинома.

Задание
2. Найти корни
полинома 0.75x³-8x+5

Решение:

1. Введите полином

2. Представьте
   полином в виде вектора, для этого

• установите
  курсор в полиноме над x

• выберите
  команду Символика 
  Полиномиальные коэффициенты, после
  этого появится вектор

• выберите
  команду Правка 
  Вырезать

• напечатайте
  v:=
  и вызовите команду Правка 
  Вставить (рис. 2)

Установите
курсор ниже введенного вектора и вызовите
функцию (команда Вставка 
Функция…) polyroots,
в качестве аргумента задайте вектор v.
Как видно у данного полинома три корня.

Рис. 2. Нахождение
корней полинома

1. Найдем корни
   полинома графически. Для этого:

• представьте
  полином в виде функции от f(x)

• установите
  x
  как диапазон значений от -4 до 4 с шагом
  0.1

• постройте
  график функций f(x)
  (рис. 3)

1. С
   помощью команды ФорматированиеГрафикТрейс…определите
   точки пересечения графика с горизонтальной
   осью f(x)=0.
   Сравните полученные значения с уже
   найденными значениями корней полинома.

Рис. 3. Графический
способ нахождения корней полинома

Решение систем
уравнений

MathCAD дает возможность
решать также и системы уравнений.
Максимальное число уравнений и переменных
равно 50. Результатом решения системы
будет численное значение искомого
корня.

Для решения системы
уравнений необходимо выполнить следующее:

1. Задать начальное
   приближение для всех неизвестных,
   входящих в систему уравнений. Mathcad
   решает систему с помощью итерационных
   методов.

2. Напечатать
   ключевое слово Given.
   Оно указывает Mathcad, что далее следует
   система уравнений.

3. Введите
   уравнения и неравенства в любом порядке.
   Используйте [Ctrl]=
   для печати символа =. Между левыми и
   правыми частями неравенств может стоять
   любой из символов <, >,
   и.

4. Введите
   любое выражение, которое включает
   функцию Find,
   например: а:=
   Find(х, у).

Функция
Find(z1,
z2,
. . .)
возвращает
точное решение системы уравнений. Число
аргументов должно быть равно числу
неизвестных.

Ключевое
слово Given,
уравнения и неравенства, которые следуют
за ним, и какое-либо выражение, содержащее
функцию Find,
называют блоком
решения уравнений.

Следующие выражения
недопустимы внутри блока решения:

• ограничения
  со знаком
  .

• дискретный аргумент
  или выражения, содержащие дискретный
  аргумент в любой форме.

• неравенства
  вида a
  < b
  < c.

Блоки
решения уравнений не могут быть вложены
друг в друга, каждый блок может иметь
только одно ключевое слово Given
и имя функции
Find.

Функция, которая
завершает блок решения уравнений, может
быть использована аналогично любой
другой функции. Можно произвести с ней
следующие три действия:

• Можно вывести
  найденное решение, напечатав выражение
  вида:

Find(var1,
var2,…)
=.

• Определить
  переменную с помощью функции Find:

a
:= Find(x)
– скаляр,

var
:= Find(var1,
var2,…)
– вектор.

Это удобно сделать,
если требуется использовать решение
системы уравнений в другом месте рабочего
документа.

• Определить
  другую функцию с помощью Find

f(a,
b, c, …)
:= Find(x,
y, z, …).

Эта
конструкция удобна для многократного
решения системы уравнений для различных
значений некоторых параметров a, b, c,…,
непосредственно входящих в систему
уравнений.

Сообщение
об ошибке
(Решение
не найдено) при решении уравнений
появляется, когда:

• поставленная
  задача может не иметь решения,

• для уравнения,
  которое не имеет вещественных решений,
  в качестве начального приближения
  взято вещественное число и наоборот,

• в процессе поиска
  решения последовательность приближений
  попала в точку локального минимума
  невязки; для поиска искомого решения
  нужно задать различные начальные
  приближения;

• возможно,
  поставленная задача не может быть
  решена с заданной точностью, попробуйте
  увеличить значение TOL.

Приближенные
решения

Функция
Minner очень
похожа на функцию
Find (использует
тот же алгоритм). Если в результате
поиска не может быть получено дальнейшее
уточнение текущего приближения к
решению, Minner
возвращает это приближение. Функция
Find в этом
случае возвращает сообщение об ошибке.
Правила использования функции Minner
такие же, как и функции
Find.

Minerr(z1,
z2,
. . .)

Возвращает
приближенное решение системы уравнений.
Число аргументов должно быть равно
числу неизвестных.

Если
Minner используется
в блоке решения уравнений, необходимо
всегда включать дополнительную проверку
достоверности результатов.

Задание
3. Решение
системы уравнений с помощью функции
Find.
Система уравнений:

Решение:

1. Задайте
   начальные приближения: x1:=0,
   x2:=0,
   x3:=0

2. Начните
   блок решения уравнений с ключевого
   слова Given

3. Введите
   три уравнения, используя [Ctrl]+=
   для печати
   символа =

4. Вызовите
   функцию find
   с аргументами x1,
   x2,
   x3
   для получения точного решения системы
   уравнения (рис. 4).

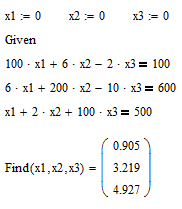
Рис. 4. Решение
системы уравнений

Символьное
решение уравнений

В
Mathcad можно быстро и точно найти численное
значение корня с помощью функции root.
Но имеются некоторые задачи, для которых
возможности Mathcad позволяют находить
решения в символьном (аналитическом)
виде.

Решение уравнений
в символьном виде позволяет найти точные
или приближенные корни уравнения:

1. Если решаемое
   уравнение имеет параметр, то решение
   в символьном виде может выразить искомый
   корень непосредственно через параметр.
   Поэтому вместо того, чтобы решать
   уравнение для каждого нового значения
   параметра, можно просто заменять его
   значение в найденном символьном решении.

2. Если нужно найти
   все комплексные корни полинома со
   степенью меньше или равной 4, символьное
   решение даст их точные значения в одном
   векторе или в аналитическом или цифровом
   виде.

Команда
Символы 
Переменные  Вычислить
позволяет решить уравнение относительно
некоторой переменной и выразить его
корни через остальные параметры
уравнения. Чтобы решить уравнение
символьно необходимо:

1. Напечатать
   выражение (для ввода знака равенства
   используйте комбинацию клавиш [Ctrl]=).

2. Выделить переменную,
   относительно которой нужно решить
   уравнение, щелкнув на ней мышью.

3. Выбрать
   пункт меню
   Символы 
   Переменные  Вычислить.

Нет необходимости
приравнивать выражение нулю. Если
Mathcad не находит знака равенства, он
предполагает, что требуется приравнять
выражение нулю.

Чтобы решить
систему уравнений в символьном виде,
необходимо выполнить следующее:

1. Напечатать
   ключевое слово Given.

2. Напечатать
   уравнения в любом порядке ниже слова
   Given.
   Удостоверьтесь, что для ввода знака =
   используется [Ctrl]=.

3. Напечатать
   функцию Find,
   соответствующую системе уравнений.

4. Нажать
   [Ctrl]. (клавиша
   CTRL, сопровождаемая точкой). Mathcad отобразит
   символьный знак равенства  .

5. Щелкнуть
   мышью на функции Find.

Задание
4. Решение
системы уравнений в символьном виде

Решение:

1. Начните
   блок решения уравнений с ключевого
   слова Given

2. Введите
   два уравнения, используя [Ctrl]+=
   для печати
   символа =

3. Вызовите
   функцию find
   с аргументами x
   и y
   для получения символьного решения
   системы уравнений. Вместо равенства
   вставьте знак символьной оценки
   ([Ctrl]+.)(рис.
   5).

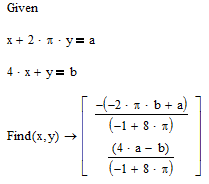
Рис. 5. Символьное
решение системы уравнений

Решение матричных
уравнений

Рассмотрим
систему n
линейных алгебраических уравнений
относительно n
неизвестных х₁,
х₂,
…, х_n:

В соответствии с
правилом умножения матриц рассмотренная
система линейных уравнений может быть
записана в матричном виде

Ах
= b,

где:

.

 Матрица
А,
столбцами которой являются коэффициенты
при соответствующих неизвестных, а
строками – коэффициенты при неизвестных
в соответствующем уравнении, называется
матрицей
системы;
матрица-столбец b,
элементами которой являются правые
части уравнений системы, называется
матрицей
правой части
или просто правой
частью системы.
Матрица-столбец х,
элементы которой – искомые неизвестные,
называется решением
системы.

Если
матрица А
– неособенная, то есть det
A
0
то система уравнений или эквивалентное
ей матричное уравнение , имеет единственное
решение.

В
самом деле, при условии det
A
0
существует обратная матрица А^-1.
Умножая обе части уравнения на матрицу
А^-1
получим:

Эта формула дает
решение уравнения и оно единственно.

Системы
линейных уравнений удобно решать с
помощью функции lsolve.

lsolve(А,
b)

Возвращается
вектор решения x
такой, что
Ах =
b. Аргументы
функции:

• А
  – квадратная, не сингулярная матрица.

• b
  – вектор, имеющий столько же рядов,
  сколько рядов в матрице А.

Задание
5. Решить
систему уравнений матричным методом

Решение:

1. Представьте
   систему уравнений в виде матриц A
   и b.
   Для создания матриц подключите панель
   Матрицы,
   нажав на кнопку Панель
   векторов и матрицна панели
   Математика.

2. Создайте
   матрицу A,
   столбцами которой являются коэффициенты
   при соответствующих неизвестных. Для
   этого:

• введите
  A:=

• нажмите
  кнопку Матрица
  или Вектор
  на панели Матрицы

• в
  появившемся окне Вставка
  матрицы в
  строку ввода Строки
  (Rows)
  введите количество строк в матрице, а
  в строку ввода Колонки
  (Columns)
  – количество столбцов, в данном случае
  33

• заполните элементы
  матрицы (рис. 6)

1. Аналогично
   создайте вектор b.

2. Вычислите
   определитель матрицы, для этого на
   панели Матрицы
   нажмите
   кнопку Эпитоп
   и введите имя матрицы A,
   введите знак =, чтобы получить результат.
   Так как определитель отличен от 0, то
   система уравнений будет иметь единственное
   решение.

3. Вычислите
   решение системы
   (1 способ):

• введите
  x:=

• введите
  A
  и нажмите кнопку Инверсия на панели
  Матрицы

• умножите
  на вектор b

• далее
  определите матрицу значений x,
  для этого введите x=

1. Вычислите
   решение системы
   (2 способ):

• присвойте
  x
  функцию lsolve
  с аргументами A
  и b

• определите
  матрицу значений x,
  для этого введите x=

1. Осуществите
   проверку решения с помощью выражения
   Ax
   – b,
   которое должно вернуть нули.

Рис. 6. Решение
системы уравнений матричным методом

Задачи для
самостоятельного выполнения

 1.
Построить график функции f(x)
(таблица 1)
и приблизительно определить один из
корней уравнения. Решить уравнение
f(x)=
0
с точностью
e = 10 ^{– 4} с
помощью встроенной функции Mathcad root;

Таблица 1. Варианты
задачи 1

№ варианта	f(x)	№ варианта	f(x)
1		9
2		10	arccos –x, х [ 2, 3]
3		11
4		12
5		13
6		14
7		15	х5 – х – 0,2, х [ 1, 2]
8

2.
Для полинома g(x)
(таблица 2) выполнить следующие действия:

1. с
   помощью команды Символы
   
   Коэффициенты полинома
   создать
   вектор V,
   содержащий коэффициенты полинома;

2. решить
   уравнение g(x)
   = 0 с помощью функции polyroots;

3. решить
   уравнение символьно, используя команду
   Символы 
   ПеременныеВычислить.

Таблица 2. Варианты
задачи 2

№ варианта	g(x)	№ варианта	g(x)
1	x4 – 2x3 + x2 – 12x + 20	9	x4 + x3 – 17x2 – 45x – 100
2	x4 + 6x3 + x2 – 4x – 60	10	x4 – 5x3 + x2 – 15x + 50
3	x4 – 14x2 – 40x – 75	11	x4 – 4x3 – 2x2 – 20x + 25
4	x4 – x3 + x2 – 11x + 10	12	x4 + 5x3 + 7x2 + 7x – 20
5	x4 – x3 – 29x2 – 71x -140	13	x4 – 7x3 + 7x2 – 5x + 100
6	x4 + 7x3 + 9x2 + 13x – 30	14	x4 + 10x3 +36x2 +70x+ 75
7	x4 + 3x3 – 23x2 – 55x – 150	15	x4 + 9x3 + 31x2 + 59x+ 60
8	x4 – 6x3 + 4x2 + 10x + 75

3.
Решить
систему линейных уравнений (таблица
3):

1. используя
   функцию Find;

2. матричным
   способом и используя функцию lsolve.

Таблица 3. Варианты
задачи 3

№ варианта	Система линейных уравнений	№ варианта	Система линейных уравнений
1		9
2		10
3		11
4		12
5		13
6		14
7		15
8

4.
Преобразовать нелинейные уравнения
системы из таблицы 4 к виду f ₁(x) = y
и f ₂ (y)= x.
Построить их графики и определить
начальное приближение решения. 
Решить систему нелинейных уравнений с
помощью функции Minerr.

 Таблица
4. Варианты задачи 4

№ варианта	Система нелинейных уравнений	№ варианта	Система нелинейных уравнений
1		9
2		10
3		11
4		12
5		13
6		14
7		15
8

5.
Символьно решить системы уравнений:

1. 

2. 

Контрольные
вопросы

1. Назовите способы
   нахождения начального приближения.

2. Какие функции для
   решения одного уравнения в MathCAD вы
   знаете? В чем их отличие?

3. Какие
   аргументы функции root
   не обязательны?

4. В каких случаях
   MathCAD не может найти корень уравнения?

5. Какая системная
   переменная отвечает за точность
   вычислений?

6. Как
   изменить точность, с которой функция
   root
   ищет корень?

7. Как системная
   переменная TOL влияет на решение уравнения
   с помощью функции root?

8. Назовите функции
   для решения систем уравнений в MathCAD и
   особенности их применения.

9. Опишите структуру
   блока решения уравнений.

10. Какой знак равенства
    используется в блоке решения? Какой
    комбинацией клавиш вставляется в
    документ?

11. Какие выражения
    не допустимы внутри блока решения
    уравнения?

12. Опишите
    способы использования функции Find.

13. В каких случаях
    MathCAD не может найти решение системы
    уравнений?

14. Дайте
    сравнительную характеристику функциям
    Find и
    Minerr.

15. Какие уравнения
    называются матричными?

16. Как решать матричные
    уравнения? Назовите способы решения
    матричных уравнений.

17. Как символьно
    решить уравнение или систему уравнений
    в MathCAD? Какой знак равенства используется?
    Какой комбинацией клавиш вставляется
    в документ?

18. Назовите особенности
    использования символьного решения
    уравнений.

Расчеты с использованием системы MathCAD

Методическое пособие для студентов специальности 27.02.04

Автоматические
системы управления

Пособие представляет собой руководство к выполнению практических
работ по МДК «Теоретические основы технического обслуживания и ремонта
электронного оборудования электронной части станков с ЧПУ», а также может быть
использовано при изучении дисциплин «Математика», «Прикладная математика»,
«Электротехника», «Электроника».

Каждая практическая работа содержит краткое описание методов
вычислений, примеры, снабженные необходимыми комментариями, порядок выполнения практической
работы и варианты индивидуальных заданий для группы студентов из 15 человек,
контрольные вопросы.

Содержание

Содержание

Предисловие

Практическая работа 1.
Основы работы с MathCAD

Математические выражения

Текстовые фрагменты

Графические области

Порядок выполнения
лабораторной работы № 1

Контрольные вопросы

Практическая работа 2.
Решение уравнений средствами MathCad

Численное решение нелинейного
уравнения

Нахождение корней полинома

Решение систем уравнений

Символьное решение уравнений

Порядок выполнения
лабораторной работы 2

Контрольные вопросы

Практическая работа №3.
Символьные вычисления

Выделение выражений для символьных
вычислений

Символьные операции

Стиль представления результатов
вычислений

Операторы вычисления пределов
функций

Задание операторов пользователя

Порядок выполнения
лабораторной работы 3

Контрольные вопросы

Приложение

Системные переменные

Встроенные операторы

Встроенные функции

Литература

Предисловие

Одной из основных областей применения ПК являются математические и
научно-технические расчеты. Сложные вычислительные задачи, возникающие при
моделировании технических устройств и процессов, можно разбить на ряд
элементарных: вычисление интегралов, решение уравнений, решение
дифференциальных уравнений и т. д. Для таких задач уже разработаны методы
решения, созданы математические системы, доступные для изучения студентам
младших курсов втузом.

Цель пособия – научить пользоваться простейшими методами вычислений
с использованием современных информационных технологий. Наиболее подходящей для
этой цели является одна из самых мощных и эффективных математических систем – MathCAD,
которая занимает особое место среди множества таких систем (Matlab,
Maple, Mathematica
и др.).

MathCAD — это мощная и в то же время простая
универсальная среда для решения задач в различных отраслях науки и техники,
финансов и экономики, физики и астрономии, математики и статистики… MathCAD
остается единственной системой, в которой описание решения математических задач
задается с помощью привычных математических формул и знаков. MathCAD
позволяет выполнять как численные, так и аналитические (символьные) вычисления,
имеет чрезвычайно удобный математико-ориентированный интерфейс и прекрасные
средства научной графики.

Система MathCAD существует в нескольких основных
вариантах:

•        
MathCAD Standard – идеальная система для повседневных
технических вычислений. Предназначена для массовой аудитории и широкого
использования в учебном процессе;

•        
MathCAD Professional – промышленный стандарт
прикладного использования математики в технических приложениях. Ориентирована
на математиков и научных paGoiпиков, проводящих сложные и трудоемкие
расчеты.

•        
MathCAD Professional Academic – пакет программ для профессионального использования
математического аппарата с электронными учебниками и ресурсами.

Данное пособие ориентировано на использование
пакета MathCAD Professional.

Практическая
работа 1. Основы работы с MathCAD

MathCAD
работает с документами. С точки зрения пользователя, документ – это
чистый лист бумаги, на котором можно размещать блоки трех основных типов:
математические выражения, текстовые фрагменты и графические области.

Расположение
нетекстовых блоков в документе имеет принципи­альное значение — слева направо
и сверху вниз.

Математические выражения

К
основным элементам математических выражений MathCAD
относятся типы данных, операторы, функции и управляющие структуры.

Операторы

Операторы
– элементы MathCAD, с помощью которых можно создавать
математические выражения. К ним, например, относятся символы арифметических
операций, знаки вычисления сумм, произведений, производной и интеграла и т.д.

Оператор
определяет:

1.  действие,
которое должно выполняться при наличии тех или иных значений операндов;

2.            
сколько, где и какие операнды должны быть введены в оператор.

Операнд
– число или выражение, на которое действует оператор.

Например,
в выражении 5! + 3 число 3 и выражение 5! – операнды оператора + (плюс), а
число 5 операнд оператора факториал (!). После указания операндов операторы
становятся исполняемыми по документу блоками. В Приложении 2 данного пособия
приведен список наиболее часто используемых операторов.

Типы
данных

К
типам данных относятся числовые константы, обычные и системные
переменные, массивы (векторы и матрицы) и данные файлового типа.

Константами
называют поименованные объекты, хранящие некоторые значения,
которые не могут быть изменены. Переменные являются поименованными
объектами, имеющими некоторое значение, которое может изменяться по ходу
выполнения программы. Тип переменной определяется ее значением; переменные
могут быть числовыми, строковыми, символьными и т. д. Имена констант,
переменных и иных объектов

Рисунок
1. Математические выражения

называют
идентификаторами. Идентификаторы и MathCAD
представляют собой набор латинских или греческих букв и цифр.

В MathCAD содержимся небольшая группа особых
объектов, которые нельзя отнести ни к
классу констант, ни к классу переменных, значения которых определены сразу после запуска программы. Их правильнее считать
системными переменными, имеющими предопределенные системой начальные значения (см. Принижение 1) Изменение значений системных переменных производят во вкладке Встроенные переменные диалогового окна Math Options команды Математика _
Опции.

Обычные переменные отличаются от системных тем, что они должны быть предварительно определены пользователем,
т. е. им необходимо хотя бы однажды присвоить значение. В
качестве оператора присваивания
используется знак :=,
тогда как знак = отведен для вывода значения константы или
переменной.

Если переменной присваивается начальное значение с помощью
оператора :=, вызывается нажатием клавиши: (двоеточие) на
клавиатуре, такое присваивание называется локальным. До этого
присваивания переменная не определена и ее нельзя использовать. Однако с
помощью знака а (клавиша ~ на клавиатуре) можно обеспечить глобальное присваивание
(см. Пример 1 Рисунка 1). MathCAD
прочитывает весь документ дважды слева направо и сверху вниз. При первом
проходе выполняются все действия, предписанные локальным оператором
присваивания (=), а при втором – производятся действия, предписанные локальным
оператором присваивания (:=), и отображаются все необходимые результаты
вычислений (=).

Существуют также жирный знак равенства = (комбинация клавиш Ctrl +
=), который используется, например, как оператор приближенного равенства при
решении систем уравнений, и символьный знак равенства —> (комбинация
клавиш Ctrl + .).

Дискретные аргументы – особый класс
переменных, который в пакете MathCAD
зачастую заменяет управляющие структуры, называемые циклами (однако
полноценной такая замена не является). Эти переменные имеют ряд фиксированных
значений, либо целочисленных (1 способ), либо в виде чисел с определенным
шагом, меняющихся от начального значения до конечного (2 способ).

1.   Name:
= Nbegin .. Nend,
где Name – имя
переменной, Nbegin – ее
начальное значение, Nend – конечное
значение, ..- символ, указывающий на изменение переменной в заданных пределах
(вводится клавишей ;). Если Nbegin < Nend,
то шаг переменной будет равен+1, иначе-1.

2.   Name :=
Nbegin, (Nbegin
+ Step).. Nend.
Здесь Step – заданный шаг изменения переменной (он
должен быть положительным, если Nbegin
< Nend, или
отрицательным в обратном случае).

Дискретные аргументы значительно расширяют возможности MathCAD,
позволяя выполнять многократные вычисления или циклы с повторяющимися
вычислениями, формировать векторы и матрицы (Пример 3 Рисунка 1).

Массив – имеющая уникальное имя
совокупность конечного числа числовых или символьных элементов, упорядоченных
некоторым образом и имеющих определенные адреса. В пакете MathCAD
используются массивы двух наиболее распространенных типов:

•        
одномерные (векторы);

•        
двумерные (матрицы).

Порядковый номер элемента, который
является его адресом, называется индексом. Индексы могут иметь только
целочисленные значения. Они могут начинаться с нуля или единицы, в соответствии
со значением системной переменной ORIGIN (см.
Приложение 1).

Векторы
и матрицы можно задавать различными способами:

•       
с помощью команды Вставка _
Матрица, или комбинации клавиш Ctrl +
М, или щелчком на кнопке  панели Матрица, заполнив
массив пустых полей для не слишком больших массивов;

•       
с использованием дискретного аргумента, когда имеется некоторая
явная зависимость для вычисления элементов через их индексы (Пример 3 Рисунка
1).

Функции

Функция –
выражение, согласно которому проводятся некоторые вычисления с аргументами и
определяется его числовое значение.

Следует особо отметить разницу между аргументами
и параметрами функции. Переменные, указанные в скобках после имени
функции, являются ее аргументами и заменяются при вычислении функции
значениями из скобок. Переменные в правой части определения функции, не
указанные скобках в левой части, являются параметрами и должны задаваться
до определения функции (см. Пример 2 Рисунка 1).

Главным признаком функции является возврат значения, т.е.
функция в ответ на обращение к ней по имени с указанием ее аргументов должна
возвратить свое значение.

Функции в пакете MathCAD могут
быть встроенные (см. Приложение 3),т. е. заблаговременно введенные
разработчиками, и определенные пользователем.

Способы
вставки встроенной функции:

1.             
Выбрать пункт меню Вставка => Функция.

2.     
Нажать комбинацию клавиш Ctrl +
Е.

3.     
Щелкнуть на кнопке .

Текстовые фрагменты

Текстовые фрагменты представляют собой
куски текста, которые пользователь хотел бы видеть в своем документе.
Существуют два вида текстовых фрагментов:

•    текстовая
область предназначена для небольших кусков текста – подписей, комментариев
и т. п. Вставляется с помощью команды Вставка => Текстовая регион или
комбинации клавиш Shift + ” (двойная кавычка);

• текстовый абзац применяется в том случае, если
необходимо работать с абзацами или страницами. Вставляется
с помощью ком­бинации клавиш Shift + Enter.

Рисунок
2. Пример построения на одном рисунке двух 3D
– графиков разного типа

Графические области

Графические области делятся на три основных типа – двумерные графики,
трехмерные графики и импортированные графические образы. Двумерные и трехмерные графики строятся самим MathCAD на
основании обработанных данных.

Для создания декартового графика:

1.            
Установить визир в пустом месте рабочего
документа.

2.          
Выбрать команду Вставка_График _ X–Y график,
или нажать комбинацию
клавиш Shift + @, или щелкнуть кнопку  панели

Графики. Появится
шаблон декартового графика.

Рисунок
3. Построение 3D
Точечных графиков

3.     Введите
в средней метке под осью X первую
независимую переменную, через запятую и так до 10, например x1,
x2, …

4.     Введите
в середину метке с лева от вертикальной оси Y
первую независимую переменную, через запятую ит.д., например y1(x1),
y2(x2), …,
или соответствующие выражения.

5.     Щелкните
за приделами области графика, что бы начать его построение.

Трехмерные
или 3D-графики,
отображают функции переменных вида Z(X,
Y). При построении трех мерных графиков в
ранних версиях MathCAD поверхность нужно было определить
математически (Рисунок 2. способ 2). Теперь применяют функцию MathCAD CreateMesh.

CreateMesh
F (или G, или
f1, f2, f3,),
x0, x1, y1, xgrid, ygrid, fmap)

Создаёт
сетку на поверхности, определенной функции F x0,
x1, y0,
y1 – диапазон изменения переменных, xgrid,
ygrid – размеры сетки переменных,
fmap – функция
отображения. Все параметры, за исключением F,
– факультативные. Функция CreateMesh по
умолчанию создает сетку на поверхности с диапазоном изменения переменных от -5
до 5 и с сеткой 20×20 точек.

Пример
использования функции CreateMesh для
построения 3D-графиков приведен на Рисунке 2, способ 1. На Рисунке 2 построена
одна и та же поверхность разными способами, с разным форматированием, причем
изображены поверхности и под ними те же поверхности в виде контурного графика.
Такое построение способно придать рисунку большую наглядность.

Нередко
поверхности и пространственные кривые представляют в виде точек, кружочков или
иных фигур. Такой график создается операцией Вставка => График => 3D
Точечный, причем поверхность задается параметрически – с помощью трех
матриц (X, Y, Z) (см.
Рисунок 3, способ 2), а не одной как в примере на Рисунке 2. Для определения
исходных данных
для такого вида графиков используется функция CreateSpace (см. Рисунок 3, способ
1).

Рисунок
4. Построение двух пересекающихся поверхностей и одновременно контурного
графика одной из них

CreateSpace (F , t0, t1, tgrid,  fтар

Возвращает вложенный массив трех векторов, представляющих х-, у-, и z-координаты
пространственной кривой, определенной функцией F. t 0 и t 1 –
диапазон изменения переменной, tgrid – размер
сетки переменной, тар – функция отображения. Все
параметры, за исключением F_, –
факультативные.

Построение
пересекающихся фигур

Особый интерес представляет собой возможность
построения на одном графике ряда разных фигур или поверхностей с автоматическим
учетом их взаимного пересечения. Для этого надо раздельно задать матрицы
соответствующих поверхностей и после вывода шаблона 3D-графика перечислить
эти матрицы под ним с использованием в качестве разделителя запятой (Рисунок
4).

Создание
анимационного клипа

MathCAD имеет
встроенную переменную FRAME, чье единственное назначение- управление анимациями:

•             
Создайте объект, чей
вид зависит от FRAME.

•             
Убедитесь, что
установлен режим автоматического расчета (Математика => Автоматическое
Вычисление).

•             
Выберите Вид
=> Анимация для вызова одноименного диалогового окна.

•             
Заключите в
выделяющий пунктирный прямоугольник часть рабочего документа, которую нужно
анимировать.

•             
Установите нижние и
верхние границы FRAME (поля От: и До:).

•             
В поле Скорость
введите значение скорости воспроизведения (кадров/сек).

•             
Выберите Анимация.
Сейчас анимация только создается..

•             
Сохраните анимацию
как AVI файл (Сохранить как).

•             
Воспроизведите
сохраненную анимацию Вид =>Воспроизведение.

Порядок выполнения
лабораторной работы № 1

Упражнение
1. Вычислить:

                   |-10|=              10! =

Это и все остальные
задания снабдить комментариями, используя команду Вставка => Текстовая область.

Упражнение 2. Определить
переменные: а:=3.4, b:=6.22, с:= 0.149 (причем переменную с глобально) и выражения:

•             
Вычислить выражения.

•             
С помощью команды Формат => Результат
=> Формат чисел => Число знаков изменить точность
отображения результатов вычисления глобально.

Упражнение 3. Вывести на экран
значение системной константы и установить максимальный формат ее
отображения локально.

Упражнение 4. Выполнить следующие
операции с комплексными числами:

Упражнение 5. Выполнить следующие
операции:

i	di	Si	Ri
0	0.5	3.3	2
1	1	5.9	3.9
2	1.5	7	4.5
3	2	6.3	3.7
4	2.5	4.2	1.2

Упражнение 6. Определить векторы d, S и R через дискретный аргумент i. Отобразить
графически таблично заданные функции S_i(d_i) и R_i(d_i), используя команду Вставка => График => X – Y
Зависимость. Чтобы
оформить график, необходимо выполнить следующие команды:

•             
Щелкнуть левой
клавишей мыши на графике, чтобы выделить его. Затем щелкнуть правой клавишей
мыши, при этом появится контекстное меню в котором необходимо выбрать команду Формат
(появится диалоговое окно “Formatting Currently Selected X–Y Plot“).

•             
Нанести линии сетки
на график (Оси X–Y => Вспом. линии) и отобразить легенду (След => Скрыть
легенду)

•             
Отформатировать
график так, чтобы в каждой узловой точке графика функции S₁{d₁) стоял знак вида □ (След => Символ => bох), а график функции R₁(di) отобразить в виде гистограммы (След => Тип => bar).

Упражнение 7. Построить декартовы (X–Y Зависимость) и полярные (Полярные Координаты)
графики следующих функций:

Для этого необходимо определить  как дискретный аргумент на интервале от 0 до 2π
с шагом π/30.

Определить по графику X–Y
Зависимость координаты
любой из точек пересечения графиков  и ,  для этого
необходимо:

•             
Выделить график и
выбрать из контекстного меню Масштаб (появится диалоговое окно “X–Y Zoom“) для увеличения части графика в области точки
пересечения.

•             
На чертеже выделить
пунктирным прямоугольником окрестность точки пересечения графиков Y(а) и Р(а), которую нужно увеличить.

•             
Нажать кнопку Масштаб+,
чтобы перерисовать график.

•             
Чтобы сделать это
изображение постоянным, выбрать ОК.

•             
Выбрать из
контекстного меню Трассировка (появится диалоговое окно “X–Y Trace“).

•        
Внутри чертежа нажать кнопку мыши и переместить
указатель мыши на точку, чьи координаты нужно увидеть.

•        
Выбрать Copy
X (или Copy Y),
на свободном поле документа набрать Хреr := (или Yper :=)
и выбрать пункт меню Правка =>Вставка.

Вычислить
значения функций X(a) и Y(a) при
a:=π/2.

Упражнение
8. Используя команду Вставка => Матрица
создать матрицу Q размером
6×6, заполнить ее произвольно и отобразить графически с помощью команды ВставкаГрафик =>Поверхности.

Упражнение
9. Построить
график поверхности (Поверхности) и карту линий уровня (Контурный)
для функции двух переменных,
двумя способами:

1.      
С помощью функции CreateMesh (сетка
размером 40 х 40, диапазон изменения t от
-5 до 5, а – от 0 до 2^.π).

2.      
Задав поверхность математически, для этого:

·           
Определить функцию

·           
Задать на осях переменных t и a по
41 точке

 

для
переменной t₁ со
значениями, изменяющимися от -5 до 5 с шагом 0.25  t₁:=
-5 + 0.25 • i а для переменной a _j = от 0 до 2^.π с
шагом π/20   a _j := π/20 •
j

•    Определить матрицу Mi  j :=
X(t_i, a_j ) и
отобразить ее графически.

С
помощью команды Формат контекстного меню вызвать диало­говое окно “Формат
3-D графика” и изменить:

•        
характеристики просмотра (Общее =>Вид
=>Вращение, Наклон),

•        
цвета и линии поверхности (Внешний Вид
=>Свойства линии, Свойства заливки),

•        
параметры осей (Оси),

•        
вид заголовка графика (Название).

Упражнение
10. Отобразить графически 
пересечение поверхностей

 и

Матрицы
для построения поверхностей задать с помощью функции CreateMesh,значения
факуль­тативных параметров не указывать. Выполнить однотонную заливку для поверхностей, выбрав из контекстного меню
команду Формат. Также из контекстного меню выбрать эффекты Туман, Освещение, Перспектива.

Упражнение 11. Используя переменную FRAME и команду Вид => Анимация, создать анимационные клипы с
помощью данных приведенных в Таблице 1.

Таблица 1

Варианта
упражнения 11

Контрольные
вопросы

1.                      
С помощью какого оператора можно вычислить выражение?

2.                      
Как вставить текстовую область в документ Mathcad?

3.                      
Чем отличается глобальное и локальное определение переменных? С помощью
каких операторов определяются?

4.                      
Как изменить формат чисел для всего документа?

5.                      
Как изменить формат чисел для отдельного выражения?

6.                      
Какие системные (предопределенные) переменные Вам известны? Как узнать
назначение? Как изменить их значение?

7.                      
Какие виды функций в Mathcad Вам известны?

8.                      
Как вставить встроенную функцию в документ Mathcad?

9.                      
С помощью каких операторов можно вычислить интегралы, произ­водные,
суммы и произведения?

10.                  
Как определить дискретные переменные с произвольным шагом? Какой шаг по
умолчанию?

11.                  
Как определить индексированную переменную?

12.                  
Какие виды массивов в Mathcad Вам известны?

13.                  
Какая системная переменная определяет нижнюю границу индекса­ции
элементов массива?

14.                  
Опишите способы создания массивов в Mathcad.

15.                  
Как просмотреть содержимое массива, определенного через дис­кретный
аргумент?

16.                  
Как построить графики: поверхности; полярный; декартовый?

17.                  
Как построить несколько графиков в одной системе координат?

18.                  
Как изменить масштаб графика?

19.                  
Как определить координату точки на графике?

20.                  
Как построить гистограмму?

21.                  
Какие функции используются для построения трехмерных графи­ков?

22.                  
Как создать анимацию в Mathcad?

23.                  
Какое расширение имеют сохраненные файлы анимаций?

Практическая
работа 2. Решение уравнений средствами MathCad

Как
известно, многие уравнения и системы уравнений не имеют аналитических решений.
В первую очередь это относится к большинству, трансцендентных уравнений.
Доказано также, что нельзя построить формулу, по которой можно было бы решить
произвольное алгебраическое уравнение степени выше четвертой¹. Однако
такие уравнения могут решаться численными методами с заданной точностью (не
более значения заданного системной переменной TOL).

Численное решение
нелинейного уравнения

Для простейших
уравнений вида f(х) = 0 решение в Mathcad находится с помощью функции root (Рисунок 5).

Возвращает значение x1, принадлежащее отрезку [а, b], при котором
выражение или функция f(х) обращается в 0. Оба аргумента этой функции должны быть скалярами.
Функция возвращает скаляр.

Аргументы:

f(х1,
х2, …) – функция,
определенная где-либо в рабочем документе, или выражение. Выражение должно
возвращать скалярные значения.

x1 – – имя переменной,
которая используемся в выражении. Этой переменной перед использованием функции root необходимо присвоить
чи­словое значение. Mathcad использует его как начальное приближение
при поиске корня.

а,
b — необязательны, если
используются, то должны быть вещественными числами, причем а
< b

Приближенные
значения корней (начальные
приближения) могут быть:

1.       
Известны из физического смысла задачи.

2.           
Известны из решения аналогичной задачи при других исходных данных.

3.       
Найдены графическим способом.

Рисунок 5.
Решение уравнений средствами Mathcad

Наиболее
распространен графический
способ определения начальных приближений. Принимая во
внимание, что действительные корни уравнения f( x)= 0 – это точки пересечения графика функции
f(x) с осью абсцисс, достаточно построить график
функции f(x) и отметить точки пе­ресечения f(x) с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню.
Построение графиков часто удается сильно упростить, заменив уравнение f(x) = 0 равносильным ему уравнением:

где функции f₁(x) и f₂(х) – более простые,
чем функция f(x). Тогда построив графики функций у = f₁(x) иу= f₂(х) искомые корни
получим как абсциссы точек пересечения этих графиков.

Пример. Графически
отделить корни уравнения:

Уравнение (1)
удобно переписать в виде равенства:

Отсюда ясно, что корни уравнения (1) могут быть найдены как
абсциссы точек пересечения логарифмической кривой у = lg х и гиперболы у = . Построив эти кривые, приближенно найдем единственный
корень £«2,5 уравнения (1) или
определим его содержащий отрезок [2,3].

Отсутствие сходимости функции root

Если после многих итераций Mathсad не находит подходящего
приближения, то там появится сообщение Can`t converge to a colution. (отсутствует
сходимость). Эта ошибка может быть вызвана следующими причинами:

·       Уравнение не имеет корней.

·       Корни уравнения расположены далеко от начального приближения.

·       Выражение имеет локальные max и min между начальным
приближением и корнями.

·       Выражение имеет разрывы между начальными приближениями и
корнями.

·      
Выражение имеет комплексный корень,
но начальное приближение было вещественным.

Чтобы установить причину ошибки,
исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x) = 0 и,
если они есть, то определить приблизительно их значения. Чем точнее выбрано
начальное приближение корня, тем быстрее будет root сходиться.

Рекомендации
по использованию функции root

• Для изменения точности, с которой функция root ищет корень, нужно изменить значение системной переменной TOL.
Если значение TOL
увеличивается, функция root будет
сходиться быстрее, но ответ будет менее точен. Если значение TOL
уменьшается, то функция root будет
сходиться медленнее, но ответ будет более то­чен. Чтобы изменить значение TOL
в определенной точке рабоче го документа,

Рисунок 6.
Определение корней полинома.

используйте определение
вида TOL:=0.0l Чтобы изменить значение TOL для
всего рабочего документа, выберите команду Математика => Параметры…
=> Переменные => Допуск сходимости (TOL).

• Если
два корня расположены близко друг от друга, следуем умень­шить TOL,
чтобы различить их.

• Если
функция f(x)
имеет малый наклон около искомого корня, функция root(f(x),
х) может сходиться к значению г, отстоящему от корня
достаточно далеко. В таких случаях для нахождения более точного значения корня
необходимо уменьшить значение TOL. Другой вариант
заключается в замене уравнения f(x)
= 0 на g(x)
= 0

•             
Для выражения f(x) с известным корнем а нахождение дополнительных корней f(x) эквивалентно поиску корней уравнения h(x)=f(x)/(x – а). Подобный прием полезен для нахождения корней, расположенных
близко друг к другу. Проще искать корень выражения А(х), чем пробовать искать другой корень уравнения fix) =
О, выбирая различные
начальные приближения.

Нахождение корней полинома

Для нахождения корней выражения, имеющего вид:

лучше использовать
функцию polyroots, нежели
root. В
отличие от функции root, функция
polyroots не
требует начального приближения и возвращает сразу все корни, как вещественные,
так и комплексные.

Polyroots(v)

Возвращает корни
полинома степени п. Коэффициенты полинома находятся в векторе v
длины п + 1. Возвращает вектор длины n,
состоящий из корней полинома.

Аргументы:

v–
вектор, содержащий коэффициенты полинома.

Вектор
v удобно создавать использую команду Символы => Коэффициенты
полинома. Рисунок 6 иллюстрирует определение корней полинома средствами Mathcad.

Решение систем уравнений

MathCAD
дает возможность решать также и системы уравнений. Максимальное число уравнений
и переменных равно 50.  Результатом решения системы будет численное значение
искомого корня.

Для
решения системы уравнений необходимо выполнить следующее:

•             
Задать начальное приближение для всех неизвестных, входящих в
систему уравнений. Mathcad решает систему с помощью итерационных
методов.

•             
Напечатать ключевое слово Given.
Оно указывает Mathcad, что
далее следует система уравнений.

•             
Введите уравнения и неравенства в любом порядке. Используйте [Ctrl]=
для печати символа =. Между левыми и правыми частями неравенств может стоять
любой из символов <, >, ≥ и ≤.

Рисунок 7. Решение систем уравнений в MathCAD

•                            
Введите любое выражение,
которое включает функцию Find, например:

Find(z1,z2, . . .)

Возвращает точное решение системы уравнений.
Число аргументов должно быть равно числу
неизвестных.

Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо
выражение, содержащее функцию Find, называют блоком
решения уравнений.

Следующие выражения недопустимы внутри блока
решения:

•             
Ограничения со
знаком .

•             
Дискретный аргумент
или выражения, содержащие дискретный аргумент в любой форме.

•             
Неравенства вида а<Ь<с.

Блоки решения
уравнений не могут быть вложены друг в друга, каждый блок может иметь только
одно ключевое слово Given и имя; функции Find.

Функция,
которая завершает блок решения уравнений, может быть использована аналогично
любой другой функции. Можно произвести с ней следующие три действия:

•             
Можно вывести найденное решение, напечатав выражение вида:

•             
Определить переменную с помощью функции Find:

скаляр,

–вектор

Это
удобно сделать, если требуется использовать решение системы уравнений в другом
месте рабочего документа.

•             
Определить другую функцию с помощью Find

Эта
конструкция удобна для многократного решения системы уравнений для различных
значений некоторых параметров a,b,c…,
непосредственно входящих в систему уравнений.

Сообщение об ошибке

(Решение не найдено)
при решении уравнений появляется, когда:

•             
Поставленная задача может не иметь решения.

•             
Для уравнения, которое не имеет вещественных решений, в качест­ве
начального приближения взято вещественное число и наоборот.

•             
В процессе поиска решения последовательность приближений по­пала в
точку локального минимума невязки. Для поиска искомого решения нужно задать
различные начальные приближения.

Возможно,
поставленная задача не может быть решена с заданной точностью. Попробуйте
увеличить значение TOL.

Пример
1 Рисунка 7 иллюстрирует решение системы уравнений в MathCAD.

Решение матричных уравнений

Рассмотрим
систему п линейных алгебраических уравнений отно­сительно п неизвестных

Рисунок 8. Решение
матричных уравнений

(2)

В
соответствии с правилом умножения матриц рассмотренная систе­ма линейных
уравнений может быть записана в матричном виде:

(3)

где:

Матрица
A, столбцами которой являются
коэффициенты при соответствующих неизвестных, а строками – коэффициенты при
неизвестных в соответствующем уравнении, называется матрицей системы; матрица-столбец
b, элементами
которой являются правые части уравнений систе­мы, называется матрицей правой
части или просто правой частью системы. Матрица-столбец
x,
элементы которой – искомые неизвестные, называется решением системы.

Если матрица А
– неособенная, то есть det A 0 то
система (2), или эквивалентное ей матричное уравнение (3), имеет единственное
решение.

В самом деле, при
условии det A 0 существует обратная матрица Умножая
обе части уравнения (3) на матрицу  получим:

	(5)

Формула
(5) дает решение уравнения (3) и оно единственно.

Системы
линейных уравнений удобно решать с помощью функции Isolve.

Isolve(A/b)

Возвращается
вектор решения х такой, что Ах = b.

Аргументы:

А
– квадратная, не сингулярная матрица.

b
– вектор, имеющий столько же рядов, сколько рядов в матрице А.

На
Рисунке 8 показано решение системы трех линейных уравнений относительно трех
неизвестных.

Приближенные решения

Функция
Minerr -очень
похожа на функцию Find (использует
тот же алгоритм). Если в результате поиска не может быть получено дальнейшее
уточнение текущего приближения к решению, Minerr возвращает
это приближение. Функция Find в
этом случае возвращает сообщение об ошибке. Правила использования функции Minerr такие
же, как и функции Find.

Minerr
(z1,
z2,…)

Возвращает
приближенное решение системы уравнений. Число аргумен­тов должно быть равно
числу неизвестных.

Если Minerr используется
в блоке решения уравнений, необходимо всегда включать дополнительную проверку
достоверности результатов.

Символьное решение
уравнений

В Mathcad
можно быстро и точно найти численное значение корня с помощью функции root.
Но имеются некоторые задачи, для которых возможности Mathcat
позволяют находить решения в символьном (ана­литическом) виде.

Решение
уравнений в символьном виде позволяет найти точные или приближенные корни
уравнения:

•             
Если решаемое уравнение имеет.параметр, то решение в символь­ном
виде может выразить искомый корень непосредственно через параметр. Поэтому
вместо того, чтобы решать уравнение для каждого нового значения параметра,
можно просто заменять его значение в найденном символьном решении.

•             
Если нужно найти все комплексные корни полинома со степенью меньше
или равной 4, символьное решение даст их точные значения в одном векторе или в
аналитическом или цифровом виде.

Команда
Символы Переменные => Вычислить позволяет решить уравнение
относительно некоторой переменной и выразить его корни через остальные
параметры уравнения.

Чтобы
решить уравнение символьно необходимо:

•             
Напечатать выражение (для ввода знака равенства используйте
комбинацию клавиш [Ctrl]=).

•             
Выделить переменную, относительно которой
нужно решить уравнение, щелкнув на ней мышью.

•             
Выбрать пункт меню Символы => Переменные => Вычислить.

Нет
необходимости приравнивать выражение нулю. Если
MathCAD не находит знака равенства, он
предполагает, что требуется приравнять выражение нулю.

Чтобы
решить систему уравнений в символьном виде, необходимо выполнить следующее:

•             
Напечатать ключевое слово Given.

•             
Напечатать уравнения в любом порядке ниже слова Given.
Удостоверьтесь, что для ввода знака = используется [Ctrl]-.

•             
Напечатать функцию Find,
соответствующую системе уравнений.

•             
Нажать [Ctrl],
(клавиша CTRL, сопровождаемая точкой). Mathcad
отобразит символьный знак равенства

•             
Щелкнуть мышью на функции Find.

Пример
2 Рисунка 7 иллюстрирует символьное решение системы уравнений в MathCAD.

Порядок
выполнения лабораторной работы 2

Упражнение
1. Построить график функции f(x)
(Таблица 1) и приблизительно определить один из корней уравнения.
Решить уравнение f(x)
= 0 с точностью

s = 10^-4с
помощью встроенной функции Mathcad root;

Таблица
1

Варианты
упражнения 1

№ варианта		№ варианта
1		9
2		10
3		11
4		12
5		13
6		14
7		15
8

Упражнение
2. Для полинома g(x)
(Таблица 2) выполнить следующие действия:

1.    с
помощью команды Символы => Коэффициенты полинома создать вектор
содержащий коэффициенты полинома;

2.    решить
уравнение g(x)
= 0 с помощью функции polyroots;

3.    
решить уравнение символьно, используя команду Символы Переменные
=> Вычислить.

Таблица
2

Варианты
упражнения 2

№ варианта		№ варианта
1		9
2		10
3		11
4		12
5		13
6		14
7		15
8

Упражнение 3. Решить систему линейных
уравнений (Таблица 3):

1)    Используя
функцию Find;

2)    Матричным
способом и используя функцию Isolve.

Таблица
3

Варианты
упражнения 3

№ варианта	Система линейных уравнений	№ варианта	Система линейных уравнений
1		9
2		10
3		11
4		12
5		13
6		14
7		15
8

Упражнение
4. Преобразовать нелинейные уравнения
системы из Табли­цы 4 к виду f1
(x) = у и f1(y)=
х. Построить их графики и определить начальное приближение решения.
Решить cистему нелинейных уравнений с помощью функции Minerr.

Таблица
4.

Варианты
упражнения 4.

№ варианта	Система нелинейных уравнений	№ варианта	Система нелинейных уравнений
1		9
2		10
3		11
4		12
5		13
6		14
7		15
8

Упражнение
5. Символьно решить системы уравнений:

Контрольные вопросы

1.                  
Назовите способы нахождения начального приближения.

2.                  
Какие функции для решения одного уравнения в MathCAD
вы знаете? В чем их отличие?

3.                  
Какие аргументы функции root не
обязательны?

4.                  
В каких случаях MathCAD не
может найти корень уравнения?

5.                  
Какая системная переменная отвечает за точность вычислений?

6.                  
Как изменить точность, с которой функция root ищет
корень?

7.                  
Как системная переменная TOL
влияет на решение уравнения с помощью функции root?

8.                  
Назовите функции для решения систем уравнений в MathCAD
и особенности их применения.

9.                  
Опишите структуру блока решения уравнений.

10.              
Какой знак равенства используется в блоке решения? Какой
комбинацией клавиш вставляется в документ?

11.              
Какие выражения не допустимы внутри блока решения уравнения?

12.              
Опишите способы использования функции Find.

13.              
В каких случаях MathCAD не
может найти решение системы уравнений!

14.              
Дайте сравнительную характеристику функциям Find и
Minerr.

15.              
Какие уравнения называются матричными?

16.              
Как решать матричные уравнения? Назовите способы решения матричных
уравнений.

17.              
Как символьно решить уравнение или систему уравнений в MathCAD?
Какой знак равенства используется? Какой комбинацией клавиш вставляется в
документ?

18.              
Назовите особенности использования символьного решения уравнений.

Практическая
работа №3. Символьные вычисления

Системы
компьютерной алгебры снабжаются специальным процессором для выполнения
аналитических (символьных) вычислений. Его основой является ядро, хранящее всю
совокупность формул и формульных преобразований, с помощью которых производятся
аналитические вычисления. Чем больше этих формул в ядре, тем надежней работа
символьного процессора и тем вероятнее, что поставленная задача будет решена,
если такое решение существует в принципе (что бывает далеко не всегда).

Ядро
символьного процессора системы MathCAD —
несколько упрощенный вариант ядра известной системы символьной математики Maple
V фирмы Waterloo Maple Software, у которой фирма MathSoft
(разработчик MathCAD) приобрела лицензию на его применение,
благодаря чему MathCAD стала (начиная с версии 3. 0) системой
символьной математики. Символьные вычислениям выполняются столь же просто (для
пользователя),как вычисление квадрата х.

Символьные
операции можно выполнять двумя способами:

•             
Непосредственно в командном режиме (используя операции меню Символы);

•             
С помощью операторов символьного преобразования (используя палитру
инструментов Символы).

Рассмотрим
первый способ.

Выделение выражений для
символьных вычислений

Чтобы
символьные операции выполнялись, процессору необходимо указать, над каким выражением
эти операции должны производиться, т. е. надо выделить выражение. Для ряда
операций следует не только указать выражение, к которому они относятся, но и
наметить переменную, относительно которой выполняется та или иная символьная
операция. Само – выражение в таком случае не выделяется.

Таким
образом, для выполнения операций с символьным процессором нужно выделить объект
(целое выражение или его часть) синими сплошными линиями.

Символьные
операции разбиты на пять характерных разделов. Первыми идут наиболее часто
используемые операции. Они могут выполняться с выражениями, содержащими
комплексные числа или имеющими решения в комплексном виде.

Символьные операции

Операции
с выделенными выражениями

Если в
документе есть выделенное выражение, то с ним можно выполнять различные
операции, представленные ниже:

Расчеты
— преобразовать выражение с выбором вида преобразований из подменю;

Символические
[Shift] F9
— выполнить символьное преобразование выделенного выражения;

С
плавающей запятой…- вычислить выделенное выражение
в вещественных числах;

Комплексные
– выполнить вычисления в комплексном виде;

Упростить
— упростить выделенное выражение с выполнением таких знаменателю, использование
основных тригонометриче­ских тождеств и т д.;

Расширить
— раскрыть выражение [например, для (X + Y)
(X – Y) получаем
X²– Y²];

Фактор
— разложить число или выражение на множители [например, X²–
Y²
даст (X+Y)
(Х- Y )];

Подобные
— собрать слагаемые, подобные выделенному выражению, которое может быть
отдельной переменной или функцией со своим аргументом (результатом будет
выражение, полиномиальное относительно выбранного выражения);

Коэффициенты
Полинома — по заданной переменной найти коэффициенты полинома,
аппроксимирующего выражение, в котором эта переменная использована.

Операции
с выделенными переменными

Для
ряда операций надо знать, относительно какой переменной они выполняются. В этом
случае необходимо выделить переменную, установив на ней маркер ввода. После
этого становятся доступными следующие операции подменю Переменные:

Вычислить
— найти значения выделенной переменной, при которых содержащее ее выражение
становится равным нулю;

Замена
— заменить указанную переменную содержимым буфера обмена;

Дифференциалы
— дифференцировать выражение, содержащее выделенную переменную, по этой
переменной (остальные переменные рассматриваются как константы);

Интеграция
— интегрировать все выражение, содержащее переменную, по этой переменной;

Разложить
на составляющие… — найти несколько членов разложения
выражения в ряд Тейлора относительно выделенной пе­ременной;

Преобразование
в Частичные Доли — разложить на элементарные дроби
выражение, которое рассматривается как рациональная дробь относительно
выделенной переменной.

Операции
с выделенными матрицами

Операции
с выделенными матрицами представлены позицией подменю Матрицы, которая
имеет свое подменю со следующими операциями:

Транспонирование
— получить транспонированную матрицу;

Инвертирование
— создать образую матрицу;

Определитель
— вычислить детерминант (определитель) матрицы.

Результаты
символьных операций с матрицами часто оказываются чрезмерно громоздкими и
поэтому плохо обозримы.

Операции
преобразования

В
позиции Преобразование содержится раздел операций преобразования,
создающий подменю со следующими возможностями:

Фурье
— выполнить прямое преобразование Фурье относительно выделенной переменной;

Фурье 
Обратное — выполнить обратное преобразование Фурье относительно выделенной
переменной;

Лапласа
— выполнить прямое преобразование Лапласа относительно выделенной переменной
(результат—функция переменной s);

Лапласа 
Обратное — выполнить обратное преобразование Лапласа относительно
выделенной переменной (результат— функция переменной t);

Рисунок
9. Стиль вычислений

Рисунок
10. Символьные вычисления

Z —
выполнить прямое Z-преобразование выражения относительно выделенной переменной
(результат — функция переменной z);

Обратное
Z — выполнить обратное Z-преобразование
‘относительно выделенной переменной (результат — функция переменной п).

Стиль представления результатов
вычислений

На
наглядность вычислений влияет стиль представления их резуль­татов. Следующая
команда позволяет задать тот или иной стиль:

Стиль
Вычислений… —  задать вывод результата символьной
операции под основным выражением, рядом с ним или вместо него (Рисунок 9).

Примеры
символьных операций в командном режиме

Большинства
символьных операций легко выполняются, так что ниже мы остановимся лишь на
некоторых примерах. Символьная операция

Рисунок
11. Разложение функции в ряд Тейлора

Расчеты
обеспечивает работу с математическими выражениями, содержащими встроенные в
систему функции и представленными в различном виде: полиномиальном,
дробно-рациональном, в виде сумм и произведений, производных и интегралов и т.
д. (Рисунок 10). Операция стремится произвести все возможные численные
вычисления и представить выражение в наиболее простом виде. Она возможна над
матрицами с символьными элементами. Производные и определенные интегралы,
символьные значения которых вычисляются, должны быть представлены в своей
естественной форме.

Особо
следует отметить возможность выполнения численных вычислений с повышенной
точностью — 20 знаков после запятой. Для перехода в такой режим вычислений
нужно числовые константы в вычисляемых объектах задавать с обязательным
указанием десятичной точки, например 10.0 или 3.0, а не 10 или 3. Этот признак
является указанием на проведение вычислений такого типа.

На
Рисунке 10 показаны типовые примеры действия операции Расчеты.

Здесь
слева показаны исходные выражения, подвергаемые символьным преобразованиям, а
справа результат этих преобразований.

Операция
Расчеты одна из самых мощных. Как видно из Рисунка 6, она позволяет в
символьном виде вычислять суммы (и произведения) рядов, производные и
неопределенные интегралы, выполнять символьные и численные операции с
матрицами»

Эта
операция содержит подменю. Команда Символические тут наиболее важная.
Назначение других команд очевидно: они нужны, если результат требуется получить
в форме комплексного или действительного числа. К примеру, если вы хотите
вместо числа п получить 3.141…, используйте команду С
плавающей запятой…. В режиме символьных вы­числений результат может
превосходить машинную бесконечность системы см. пример на вычисление
ехр(1000.0) на Рисунке 10. При этом число точных значащих цифр результата
практически не ограничено (или, точнее говоря, зависит от емкости ОЗУ).

Операция
Разложить на составляющие… возвращает разложение в ряд Тейлора
выражения относительно выделенной переменной с заданным по запросу числом членов
ряда п (число определяется по степеням ряда). По умолчанию задано. В разложении указывается остаточная
погрешность разложения. На Рисунке 11 представлено применение этой

операции для разложения
функции  Минимальная погрешность получается при
малых х (см. графическое представление функции и ее ряда).

Операторы вычисления
пределов функций

Для
вычисления пределов функций в систему введен символьный оператор limit.
Помимо ввода с наборной панели Матанализ, его в трех формах можно ввести
нажатием следующих комбинаций клавиш:

[Ctrl]
L — ввод шаблона оператора вычисления
предела функции при х, стремящемся к заданному значению,

[Ctrl]
А — ввод шаблона вычисления предела функции слева от за­данной
точки,

[Ctrl]
В — ввод шаблона вычисления предела функции справа от заданной
точки.

На
Рисунке 12 показаны примеры вычисления пределов. При вы­числении пределов нужно
заполнить шаблоны, входящие в главный шаблон для вычисления пределов, а затем
ввести функцию, имя переменной, по которой ищется предел, и значение
переменной  аргумента функции.

Рисунок
12. Вычисление пределов

Для
получения результата установите после блока вычисления предела стрелку с
острием, направленным вправо. Предел (если он существует) будет вычислен и
появится в шаблоне у острия стрелки. Если функция не имеет предела, вместо
результата появится надпись Undefine.

Задание операторов
пользователя

Еще
одна экзотическая возможность, присущая новым версиям системы MathCAD,
— задание новых операторов пользователя. Такой оператор задается практически
так же, как функция пользователя, но вместо имени выбирается какой-либо
подходящий знак. Например, можно задать оператор деления в виде:

-задание
нового оператора

-применение
функции деления

-применение
нового оператора

При
кажущейся простоте такого задания здесь есть проблемы. Встроенные в систему
операторы нельзя переопределить. Поэтому набор доступных знаков для обозначения
новых операторов ограничен. Нельзя задать новый оператор деления знаком / (он
уже использован), но можно взять знак ÷, поскольку этот символ системой не
используется.

Вторая
проблема связана с вводом символа нового оператора. Скорее всего, его напрямую
ввести нельзя. Придется воспользоваться типовыми приемами ввода новых символов
в документы windows. Один из этих приемов
использование приложения, выдающего таблицу символов, с возможностью его
экспорта из этой таблицы в документ другого приложения (в нашем случае  в
документ MathCAD).

Можно
также воспользоваться подходящим знаком из набора MATH SYMBOI^
имеющегося в составе Шпаргалок, доступ к которым дает Ресурс Центр (? =>
Ресурс Центр = Справочный стол и краткое руководство => Дополнительные
математические символы). На Рисунке 8 показан такой вариант задания нового
оператора пользователя. Для перетаскивания знака можно скопировать его в буфер
обмена с по­мощью операции Копировать, а затем ввести в документ,
используя операцию Вставка.

После
того как оператор задан, его можно использовать, как функцию и как оператор.
Примеры показаны на Рисунке 13. Для применения нового оператора надо вывести
его шаблон с помощью панели математических знаков (она также показана Рисунке
13). В нашем случае следует нажать кнопку  этой
панели она выводит особый шаблон вида ■ ■ ■. Введите операнды, например 6 и 3 в
крайние прямоугольники, а символ оператора в средний. Поставив после этой
конструкции знак равенства, увидите результат число 2.

Можно
задать и другие операторы, например, для работы с одним операндом. Так, вы
можете задать оператор для пересчета значения тем­пературы по шкале Цельсия, с
тем чтобы определить соответствующее ему значение по шкале Фаренгейта,
следующим образом

         

Затем,
используя кнопку наборной панели символов отношения, можно
выполнять операцию пересчета в виде.

Рисунок
13. Задание оператора пользователя с выбором имени из набора знаков

Есть
области математики и физики, где задание новых операторов необходимо, поскольку
является частью специфического языка их описания.

Порядок
выполнения лабораторной работы 3

Упражнение
1. Используя операцию Символы => Расчеты => С плавающей
запятой…, представьте:

1)    число
π в 7 позициях;

2)    число
12,345667 в 3 позициях.

Упражнение
2. Выведите следующие числа в комплексной форме, используя операцию
Расчеты => Комплексные меню Символы:

1)    ;

2)    ;

3)   

4)    для
выражения 3) последовательно выполните операции Расчеты => Комплексные и
Упростить меню Символы.

Упражнение
3. Для полинома g(x)
(см. Таблица 1) выполнить следующие действия:

1)    разложить
на множители, используя операцию Символы Фактор;

2)    подставьте
выражение в  используя
операцию Символы => Переменные => Замена (предварительно
скопировав подставляемое выражение в буфер обмена, выделив его и нажав
комбинацию клавиш Ctrl + С);

3)    используя
операцию Символы => Расширить, разложите по степеням выражение,
полученное в 2);

4)    используя
операцию Символы => Подобные, сверните выражение, полученное в 3), по
переменной z.

Таблица
1

Варианты
упражнения 3

№ Варианта		№ Варианта
1		9
2		10
3		11
4		12
5		13
6		14
7		15
8

Упражнение
4. Разложить выражения на элементарные дроби используя операцию СимволыПеременныеПреобразование
в частичные доли:

Упражнение
5. Разложите выражения в ряд с заданной точностью, используя
операцию Символы => Переменные => Разложить на составляющие:

1)                 
, порядок разложения;

2)                 
, порядок разложения.

Упражнение
6. Найти первообразную аналитически заданной функции (Таблица 4), используя операцию Символы
Переменные => Интеграция.

Упражнение
7. Определить символьное значение первой и второй произ­водных (Таблица 4), используя
команду Символы Переменные =>
Дифференциалы.

Таблица
4

Варианты
упражнений 6 и 7

№ Варианта		№ Варианта		№ Варианта
1		6		11
2		7		12
3		8		13
4		9		14
5		10		15

Упражнение
8.

1)    Транспонируйте
матрицу M

с помощью операции Символы
=> Матрицы Транспонирование.

2)    Инвертируйте
матрицу

с помощью операции Символы
=> Матрицы => Инвертирование.

3)    Вычислите
определитель матриц M

с помощью операции Символы
=> Матрицы => Определитель.

Упражнение
8. Вычислите пределы:

1)		2)
3)		4)
5)		6)
7)		8)

Упражнения
9. Задайте операторы пользователя:

1)    Для
пересчета единиц электрической энергии (кВт.ч  в Дж, эВ в Дж) если известно,
что

2)    Для
пересчета единиц магнитной индукции (Вб/смв
Т,Гс в Т) если известно, что

3)    Для
пересчета единиц мощности (эрг/с в Вт, кгс*м/с в Вт) если известно, что

Контрольные
вопросы

1.                 
Назовите способы выполнения символьных операций в MathCAD.

2.                 
Что необходимо сделать с выражением перед применением символьных
преобразований в командном режиме?

3.                 
Перечислите символьные операции с выделенными выражениями.

4.                 
Перечислите символьные операции с выделенными переменными.

5.                 
Перечислите символьные операции с выделенными матрицами.

6.                 
Перечислите символьные операции преобразования.

7.                 
Какие параметры определяет стиль представления результатов
вычислений и где он задается?

8.                 
В каких случаях результат символьных преобразований помещается в
буфер обмена?

9.                 
Каким образом можно вычислить предел в MathCAD?

10.             
Для чего необходимо задание операторов пользователя?

11.             
Как задать оператор пользователя?

Приложение

Системные
переменные

Ниже приведены
системные переменные и константы Mathcad с их значениями
по умолчанию.

Встроенные
операторы

В таблице,
приведенной ниже, используются следующие обозначения:X и Y–переменные
или выражения любого типа; x и y–вещественные
числа; z и w–вещественные
или комплексные числа; m и n –целые
числа; A и B–массивы
(векторы или матрицы); i-дискретный аргумент; t-любая
переменная; f–любая
функция.

Встроенные
функции

Тригонометрические
функции

	– синус
	– косеканс
	– косинус
	– секанс
	– тангенс
	– котангенс

Гиперболические
функции

	– гиперболический синус
	– гиперболический тангенс
	– гиперболический косеканс
	– гиперболический косинус
	– гиперболический секанс
	– гиперболический котангенс

Обратные тригонометрические функции

	– обратный тригонометрический синус
	– обратный тригонометрический косинус
	– обратный тригонометрический тангенс

Показатель
и логарифмические функции

	– экспоненциальная функция (или e)
	– натуральный логарифм (по основанию e)
	– десятичный логарифм (по основанию 10)

Функции
работы с частью числа (округление и пр.)

	-выделение действительной части z
	–выделение мнимой части z
	-выделение аргумента (фазы)
	-наибольшее целое, меньшее или равное x
	-наименьшее целое, большее или равное x
	-остаток от деления x/y
	-положительный угол с осью x для точки с координатами (x,y)

Литература

1.        
Mathcad 6.0 Plus.
Финансовые, инженерные и научные расчеты в среде Windows
95./ Перевод с англ. – М.: Информационно – издательский  дом «Филинъ»,
1996-712 с.

2.        
Дьяконов В.П. Справочник по MathCAD 
PLUS 6.0 PRO.- M.: “CK Пресс”, 1995.-336 c.:
ил.

3.        
Дьяконов В.П., Абраменкова И.В. MathCAD
8 PRO в математике, физике и Internet.-
М.:”Нолидж”,2000.-512 c.:ил.

4.        
Кудрявцев Е.М. Mathkad 2000 Pro.-M.:ДМК
Пресс, 2001.-576 с.:ил.

5.        
Очков В.Ф. MathCAD 7 Pro
для студентов и инженеров. – М.: Компьютер Пресс, 1998. – 384 с.:ил.

6.        
Плис А.И., Сливина Н.А. MathCAD
2000. Лабораторный прктикум по высшей математике.

7.        
Ханова А.А., Макарова И.Г.Лабораторный
практикум по математическому моделированию и методом в расчетах на ЭВМ.-
Астрахань: Изд-во АГТУ, 1998-93

8.        
Ханов А.А. Численное решение уравнений и
систем. – Астрахань: Изд-во АГТУ, 2001. – 44 с.

9.        
Ханов А.А. Символьные вычисления в среде MathCAD.
– Астрахань: Изд-во АГТУ, 2001. – 34 с.