Вычисление погрешности функций. Определение допустимой погрешности аргументов по допустимой погрешности функций
Страницы работы
Фрагмент текста работы
б) 0,096835; ![]() . б)
. б)
0,66385; ![]() .
.
3) а)12,688 ; б)
4,636. 3) а) 6,743; б) 0,543 .
18.4.
ВЫЧИСЛЕНИЕ ПОГРЕШНОСТИ ФУНКЦИЙ
18.4.1. Функции одной переменной. Абсолютная погрешность дифференцируемой
функции ![]() , вызываемая достаточно малой погрешностью
, вызываемая достаточно малой погрешностью
аргумента ![]() , оценивается величиной
, оценивается величиной
![]() ,
,
(18.12)
Если значения функции ![]() положительны, то для относительной погрешности
положительны, то для относительной погрешности
имеет место оценка
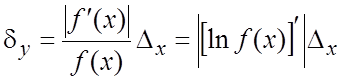 . (18.13)
. (18.13)
Например, для
тригонометрических функций абсолютные погрешности синуса и косинуса не
превосходят абсолютных погрешностей аргумента:
![]() ,
, ![]() . (18.14)
. (18.14)
18.4.2. Функции нескольких
переменных. Пусть
задана некоторая функция ![]() , от п аргументов
, от п аргументов
![]() и пусть значения каждого из аргументов
и пусть значения каждого из аргументов ![]() , определены с некоторыми погрешностями
, определены с некоторыми погрешностями ![]() , i = 1, 2,…, п.
, i = 1, 2,…, п.
Требуется найти погрешность данной функции.
Для
решения этой задачи будем предполагать, что функция ![]() является
является
дифференцируемой в некоторой области D. Абсолютная погрешность ![]() функции
функции
y при заданных абсолютных погрешностях
![]() аргументов
аргументов ![]() равна
равна
![]() . (18.15)
. (18.15)
Предполагая, что величины ![]() , i = 1, 2,…, п достаточно
, i = 1, 2,…, п достаточно
малы, можно записать приближенные равенства ![]()
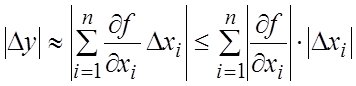 (18.16)
(18.16)
Следовательно, предельная абсолютная
погрешность ![]() функции y равна
функции y равна
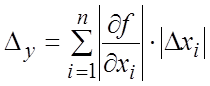 ,
,
(18.17)
где ![]() предельная
предельная
абсолютная погрешность аргумента ![]() .
.
Оценка для относительной
погрешности функции получается путем деления обеих частей неравенства (18.15)
на ![]()
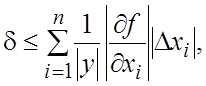 (18.18)
(18.18)
Из формулы (18.18) получаем выражение
для предельной относительной погрешности функции у
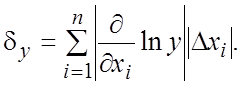 (18.19)
(18.19)
Рассмотрим
отдельные примеры на вычисление погрешностей различных функциональных
соотношений. Будем предполагать, что в каждом примере заданы те или иные
погрешности аргументов.
1. Пусть ![]() .
.
По формуле (18.17) предельная абсолютная погрешность суммы п слагаемых
равна
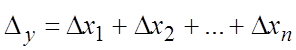 . (18.20)
. (18.20)
2. Пусть ![]() . По
. По
формуле (18.17) предельная абсолютная погрешность разности двух чисел равна
![]() .
.
3. Пусть ![]() , причем xi (i=1, 2, …, п) положительны. В соответствии с формулой (18.19)
, причем xi (i=1, 2, …, п) положительны. В соответствии с формулой (18.19)
проведем преобразования с целью получения выражения для предельной
относительной погрешности произведения п сомножителей
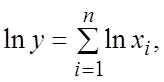
![]() .
.
4. Пусть 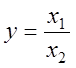 . По
. По
формуле (18.19) предельная относительная погрешность частного равна
![]() .
.
5. Пусть ![]() . Тогда
. Тогда ![]() .
.
![]() .
.
6. Пусть ![]() .
.
Следовательно, 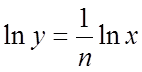 .
.
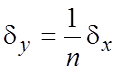 .
.
18.5. Определение допустимой погрешности аргументов по допустимой
погрешности функций
Задача определения какими должны быть
погрешности исходных приближений, чтобы полученный результат имел заданную
степень точности, имеет однозначное решение только для функции одной переменной
![]() : если эта функция дифференцируема и
: если эта функция дифференцируема и ![]() , то
, то
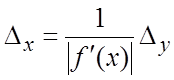 .
.
(18.21)
Для функций
нескольких переменных ![]() эта задача решается
эта задача решается
неоднозначно. Для ее решения необходимо наложить какие-либо условия на
погрешность исходных данных. Если использовать принцип равных влияний, считая что в формуле (18.17) все
слагаемые 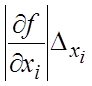 равны между собой, получим
равны между собой, получим
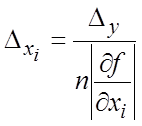
![]() .
.
(18.22)
Пример
8. Даны числа ![]() ;
; ![]() . Тогда
. Тогда
![]() . Причем последняя цифра сомнительная.
. Причем последняя цифра сомнительная.
Пример
9. Найти сумму ![]() , где
, где ![]() ;
; ![]() ;
; ![]() . Причем
. Причем
все цифры верные.
![]()
Имеем ![]() . Предельная абсолютная погрешность суммы
. Предельная абсолютная погрешность суммы ![]() . Стало быть, 7.84 < y< 7.87. В результате верными будут
. Стало быть, 7.84 < y< 7.87. В результате верными будут
цифры 7.8. Последняя цифра 4 сомнительная. #
Похожие материалы
- Вычисление приближенных значений
- Вычисление тройного интеграла в декартовых координатах
- Действительные функции одного переменного
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
14
Лекция 2 продолжение «Теория
погрешностей»
В) Погрешность
вычитания
Абсолютная
погрешность
![]()
Относительная
погрешность
![]()
Обсудим операцию
вычитания при близких значениях
операндов, имеющих большие абсолютные
погрешности. Относительная погрешность
из-за деления на очень малый знаменатель
может оказаться недопустимо большой.
Рекомендуется по возможности избегать
вычитания близких чисел.
При обработке
нескольких операндов погрешности
аддитивных операций можно вычислять
по указанным выше правилам. Но при
большом количестве операндов получаемые
таким способом предельные оценки
чрезмерно завышаются. Обычно в этих
случаях используют вероятностные
оценки.
С
Можно не учитывать
) Погрешность умножения
А бсолютная
бсолютная
погрешность
![]()
Относительная
погрешность
![]()
![]() Видно,
Видно,
что здесь опасны деления больших по
модулю чисел на значительно меньшие
из-за роста абсолютной погрешности.
D)
Погрешность деления чисел:
Абсолютная
погрешность
![]()
Относительная
погрешность
![]()
E)
Погрешность функции
Абсолютная
погрешность
![]()
Относительная
погрешность
![]()
Здесь особо опасны
быстро меняющиеся функции.
Баланс внутренних
погрешностей.
Рассмотрим простейшую задачу вычисления
суммы членов бесконечного сходящегося
ряда
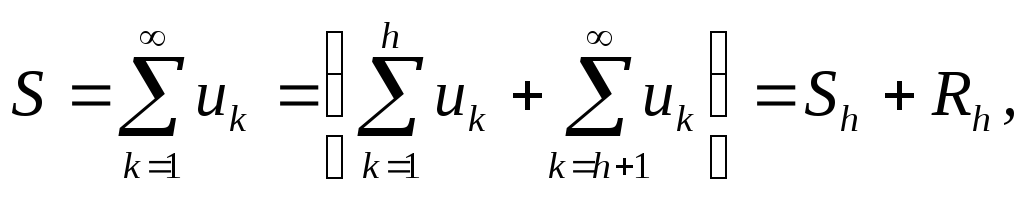
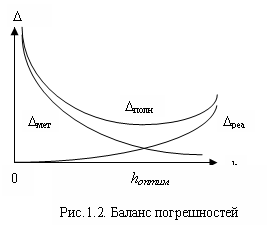
где Sh
– это частичная сумма ряда, Rh
– остаток.
Сходимость ряда означает, что Rh
0 при h
∞, поэтому при достаточно большом h
принимают S
Sh
с
абсолютной методической погрешностью
метS=
Rh.
Чем больше членов
в сумме Sh,
тем меньше эта составляющая полной
погрешности. Другая составляющая – это
суммарная погрешность реализации реаS
вычисления удерживаемых членов ряда и
их сложения.
Ясно, что она растёт
по мере удлинения части Sh.
Качественная картина баланса
погрешностей этого процесса приведена
на рис.1.2.
Верные знаки.
Определение
Говорят, что n
первых чисел приближенного числа
являются верными , если абсолютная
погрешность этого числа не превышает
5 единиц разряда, который следует
за этим знаком.
Например,
с точностью до 10-9
число =3.141592654.
Есть простое правило приближенного
вычисления:
![]()
![]() 22/7=
22/7=
3.142857143
(также с точностью 10-9).
Абсолютная погрешность здесь 0.001264489.
Следовательно,
верными являются только три знака:
3.14;
знак
2 на четвертой позиции уже неверен, так
как погрешность 0.0013 больше допустимого
для этого знака барьера 0.0005.
Не
рекомендуется сохранять неверные знаки
при использовании данных, особенно при
выдаче результатов.
-
Заказанная точность
-
Потенциально
достижимая точность -
Реально достижимая
точность.
Заказанную точность
определяют инициаторы постановки
задачи как желательную или необходимую
для достижения конечных целей. Эти цели
обычно предполагают принятие некоторых
решений человеком или ЭВМ. Точный
ответ ведёт к принятию лучшего решения,
приближенный (неточный)
— не к лучшему. Эти решения инициируют
последствия, различие которых и является
конечным мерилом точности. Это особенно
важно при постановке неустойчивых задач
с порогами принятия решений.
Потенциально
достижимая точность зависит от свойств
используемой математико-логической
модели и от точности её числовых
параметров.
Реально достигаемая
точность оказывается меньшей из-за
искажающих факторов компьютерной
реализации. Она может маскироваться
значностью ответов, выдаваемых ЭВМ. Не
исключено, что даже самый старший разряд
не будет верным. Лишние показанные знаки
создают иллюзию хорошей точности даже
там, где она очень плохая; количество
же показанных знаков может быть заданно
пользователем почти произвольно.
Если заказанная
точность недосягаема, остаётся хотя бы
приблизить реально достигаемую точность
к потенциально достижимой.
2.5 Точность определения аргумента для функции , заданной таблицей.
В вычислительной
практике часто возникает необходимость
определить аргумент по значению функции
, заданной таблицей.
Понятно , что при
этом погрешность в определении функции
вызывает погрешность в определении
аргумента .
Пусть имеем таблицу
с одним входом для функции y=f(x).
Если функция f(x)
дифференцируема , то для достаточно
малых значений х
имеем :![]()
Отсюда
![]()
или
![]()
2.6. Пространства объектов. Типы вычисляемых объектов.
Простейшие
вычисляемые
математические
объекты –
это скаляры.
Вычисляются также комплексные числа,
функции одного или нескольких аргументов,
структурированные объекты – упорядоченные
наборы скаляров (векторы и матрицы) и
функций (вектор-функции) и еще более
сложные объекты. Для вычисления объектов
разных типов используются свои методы.
Важно иметь
достаточно общие математические средства
для описания и анализа объектов и
численных методов. Такие средства
являются предметом функционального
анализа –
сравнительно новой математической
науки. Она трактует математические
объекты как элементы некоторых
общностей
— пространств.
Одним элементам могут ставиться
в
соответствие другие; при этом должны
быть определены процедуры
установления соответствия, которые
называют операторами.
Понятие пространства
тесно связано с вопросами точности.
Пространство –
это совокупность однотипных объектов,
в которой
-
объекты отличимы
друг от друга; -
установлена
структура, т.е. формальные соотношения
между элементами:
-
выполнение
простейших операций над элементами
(линейность), -
измерение
расстояния между элементами (метричность), -
измерение величины
элемента (нормированность).
Принадлежность
элемента Z или нескольких элементов
Z1,
Z2,
Z3
пространству Q обозначают Z![]() Q
Q
или Z1,
Z2,
Z3![]() Q
Q
.
Линейность
означает,
что определены
операции сложения элементов
и их
умножения на числовые множители так,
что
-
для любой пары
элементов Z1,
Z2
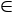 Q
Q
и любой пары чисел а1,
а2
результат есть элемент того же
пространства, т.е.
а1
Z1
+ а2 Z2
= Z3
, Z3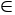 Q;
Q; -
выполняются
сочетательный, переместительный и
распределительный законы умножения
объектов на числа и сложения.
Эти условия в
инженерно-технических задачах обычно
соблюдаются.
В линейном
пространстве задаётся нулевой
элемент
,
такой, что
Z
+
= Z
и 0
Z
=
для любого
элемента Z![]() Q
Q
.
Метричность
означает, что
между любыми элементами Z1,
Z2
![]() Q
Q
может
быть определено расстояние (Z1,Z2),
которое
выражается числом
и удовлетворяет
следующим требованиям:
-
( Z1,
Z2)

0; равенство возможно только при
совпадении Z1
и Z2
; -
( Z1,
Z2)
= (
Z2,
Z1)
(аксиома симметрии); -
( Z1,
Z2)
(
Z1,
Z3)
+ (
Z2,
Z3)
, Z3 Q
Q
(аксиома треугольника).
Способ определения
(Z1,Z2)
называют метрикой
пространства.
В пространствах
из однотипных объектов метрику
можно вводить
по-разному.
При этом и пространства
считаются разными.
По аналогии с
привычными геометрическими понятиями,
элементы
пространств
часто называют
точками этих
пространств.
Множество точек,
удаленных от точки Z0
не более, чем на расстояние (Z,
Z0)
![]()
, называют
-окрестностью
Z0
или -шаром
с центром
Z0
.
Нормированность
означает, что
каждому элементу Z![]() Q
Q
ставится в соответствие действительное
число – норма
(обозначается![]() ),
),
такое, что:
Норма
обобщает понятие величины
для элементов разных типов.
В линейном
метрическом пространстве норму обычно
определяют как расстояние между Z
и нулевым элементом пространства:
![]() =
=
(Z,
)
.
Наоборот,
нормированное пространство можно
считать метрическим
с
метрикой,
равной норме разности: (
Z1,
Z2)
=![]() .
.
Тип объектов
пространства определяет, какие операции
и преобразования могут к ним применяться.
Соседние файлы в папке Vychmat_lektsii
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основная задача теории погрешности заключается в следующем: с какой точностью можно найти значение функции Y=f(X1*, x2*,…, xn*), если аргументы XI* Известны с некоторой точностью. И обратная задача: с какой точностью надо задать значения аргументов функции, чтобы погрешность функции не превосходила заданной величины? Решение таких задач опираются на теорему Лагранжа, согласно которой предельная абсолютная погрешность функции равна произведению абсолютной величины ее производной на предельную абсолютную погрешность аргумента D(F*)=|F ’|D(X*). Если задана дифференцируемая функция Y= f(X1, x2,…, xn) и ее приближенное значение Y*= f(X1*, x2*,…, xn*), где Xi – Точные значения аргументов функции, а Xi* – приближенные к ним, и пусть D(Xi*) (I=1,2,…,n) абсолютные погрешности аргументов функции.
Определение. Предельной абсолютной погрешностью функции А(Y*) называют наилучшую при имеющейся информации оценку погрешности величины Y*= f(X1*+D(X1*), x2+D(X2*) , …, xn+D(Xn*) ),
Т. е. А(Y*)=Sup| F(X1, X2,…, Xn)- F(X1*, X2*,…, Xn*)|.
Линейная оценка погрешности функции записывается в виде:
 .
.
Разделив обе части неравенства на y*, будем иметь оценку для Предельной относительной погрешности функции D (Y*):
 =D(Y*).
=D(Y*).
| < Предыдущая | Следующая > |
|---|
Вычислить приближенное значение функции
Исследуем график функции y=f(x), для этого задайте функцию f(x).
Примеры
С применением степени
(квадрат и куб) и дроби
С применением синуса и косинуса
Гиберболические синус и косинус
Гиберболические тангенс и котангенс
Гиберболические арксинус и арккосинус
Гиберболические арктангенс и арккотангенс
Что исследует?
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:

- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
- Минимум и максимум функции: Да
Правила ввода выражений и функций
3.14159.. e Число e — основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности
Применение дифференциала в приближенных вычислениях
Напомним, что дифференциалом функции ![]() называется выражение
называется выражение ![]() . Дифференциал функции можно применять для приближенного вычисления функции в окрестности точки
. Дифференциал функции можно применять для приближенного вычисления функции в окрестности точки ![]() зная значение функции и ее производной в самой точке
зная значение функции и ее производной в самой точке ![]() .
.
Приближенная формула имеет вид:
![]()
Если представить геометрически, то мы вычисляем значение функции ,как если бы она была касательной в точке ![]() .
.
Имеется два момента, которые нужно учесть.
Первое . Мы не знаем, насколько функция может измениться при переходе от точки ![]() к точке
к точке ![]() . Это зависит от того насколько меняется ее производная.
. Это зависит от того насколько меняется ее производная.
И второе , мы не можем оценить точность нашего вычисления. Поэтому задачу о вычислении приближенного значения функции ставят так: найти значение функции в точке alt=»изменение точки х0″ width=»87″ height=»25″ />используя дифференциал. Иногда просят оценить погрешность или относительную погрешность, зная точное значение в точке alt=»изменение точки х0″ width=»87″ height=»25″ />.
Приведем несколько примеров.
Пример 1
Пусть мы хотим найти приближенное значение функции
в точке
, используя дифференциал, зная значение функции и ее производной в точке
:
и оценить абсолютную и относительную погрешность. По приближенной формуле имеем:
.
Поскольку
, то абсолютная погрешность
, и относительная погрешность
.
Посмотрим, как влияет расстояние между точками
и
на погрешность и относительную погрешность. Пусть мы хотим найти приближенное значение функции
в точке
. Тогда, применяя приближенную формулу, найдем:
. С другой стороны
, так что абсолютная погрешность
, и относительная погрешность
.
Мы видим, что при удалении точки достаточно далеко от исходной , погрешность может сильно возрасти.
Сделаем следующий вывод: для достаточно близких точек погрешность может быть вполне удовлетворительной. Но самое главное, мы не можем вычислить значение в близкой точке с нужной нам точностью. Это можно сделать, используя формулу Тейлора и взяв в ней достаточное число членов.
Рассмотрм еще несколько примеров.
Пример 2
Найти приближенное значение
, используя дифференциал. Находим:
Подставим в приближенную формулу:
.
Найдем абсолютную и относительную погрешности наших вычислений. Точное значение
.
Абсолютная погрешность
, относительная погрешность
.
Относительная погрешность маленькая. Это связано с тем, что мы взяли значение в точке близкой к исходной точке
.
Пример 3
Найти приближенное значение
, используя дифференциал. Исходной точкой, в которой мы знаем значение функции и ее производной, берем точку
.
По приближенной формуле находим:
.
По калькулятору найдем точное значение функции
.
Оценим абсолютную погрешность:
.
Относительная погрешность
.
Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Решение.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.
Применение производной к приближенным вычислениям

Выберем на кривой (y=f(x)) начальную точку (A(x_0,y_0)). Если мы начнем перемещаться к точке (B(x,y)), то приращению аргумента (triangle x=AC) соответствует приращение функции (triangle y=BC). Если считать, что кривая приблизительно совпадает со своей касательной при малых приращениях (triangle x), то (BCapprox MC) и (triangle yapprox dy).
п.2. Алгоритм приближенных вычислений с помощью дифференциала
На входе: функция (y=f(x)), точка x*, в которой нужно посчитать значение функции
Шаг 1. Определяем ближайшую к x* начальную точку (x_0), для которой значение (y_0=f(x_0)) известно или легко находится.
Шаг 2. Находим выражение для первой производной (f'(x)).
Шаг 3. Находим значение производной в начальной точке (f'(x_0))
Шаг 4. Находим линейное приближение значения функции $$ y^*approx f(x_0)+f'(x_0)(x^*-x_0) $$ На выходе: значение y*
Например:
1) Найдем значение корня (sqrt)
Функция (y=sqrt, x^*=65)
Начальная точка (x_0=64). Начальное значение функции (y_0=sqrt=8)
Производная: (f'(x)=frac>)
Производная в начальной точке: (f'(x_0)=frac>=frac)
Подставляем: (y^*=sqrtapprox 8+frac(65-64)=8+frac=8,0625)
Оценим относительную ошибку для полученного результата.
Значение, полученное на калькуляторе: (sqrtapprox 8,062258). Откуда: $$ partial=fraccdot 100textapprox 0,003text $$ Таким образом, в данном случае линейное приближение имеет высокую точность, т.к. для (x_0=64) и (x^*=65) кривая (y=sqrt) очень близка к прямой, т.е. своей касательной.
2) Найдем значение корня (sqrt)
Пусть начальная точка (x_0=4). Начальное значение функции (y_0=sqrt=2)
Производная в начальной точке: (f'(x_0)=frac>=frac14)
(y^*=sqrtapprox 2+frac14 (5-4)=2,25)
Значение, полученное на калькуляторе: (sqrtapprox 2,23607) $$ partial=fraccdot 100textapprox 0,06text $$ Точность стала хуже. Однако, её можно повысить, если взять (x_0=4,84).
3) Найдем (sqrt) при (x_0=4,84).
(y_0=sqrt =2,2)
Производная в начальной точке: (f'(x_0 )=frac=frac)
(y^*=sqrtapprox 2,2+frac(5-4,84)=2,2+frac=2,2+frac=2,23636…)
Значение (sqrtapprox 2,23607) $$ partial=fraccdot 100textapprox 0,01text $$ Точность повысилась.
Вывод: точку (x_0) следует выбирать, исходя из поведения функции (y=f(x)) в окрестности (x^*). Чем ближе (x_0) к (x^*) и чем ближе кривая к касательной, тем точнее будет линейное приближение с помощью дифференциала.
п.3. Приближение с точностью до квадрата приращения
Например:
1) Найдем квадратичное слагаемое для (x^*=65, x_0=64, y=sqrt)
Вторая производная: (f»(x)=left(frac>right)’=frac12cdotleft(-frac12right)cdotfrac>=-frac>) $$ frac(x^*-x_0)^2=-frac=-fracapprox -0,0002 $$ Значит, квадратичное слагаемое дает поправку в 4-м знаке.
Используя полученное выше линейное приближение, получаем: $$ y^*=sqrtapprox 8,0625-0,0002=8,0623approx 8,062 $$ Квадратичное слагаемое указывает, что округлить результат нужно до 3-го знака после запятой.
2) Найдем квадратичное слагаемое для (x^*=5, x_0=4, y=sqrt) $$ frac(x^*-x_0)^2=-frac=-fracapprox -0,02 $$ Получаем: $$ y^*=sqrtapprox 2,25-0,02=2,23approx 2,2 $$ Квадратичное слагаемое указывает, что округлить результат нужно до 1-го знака после запятой.
3) Найдем квадратичное слагаемое для (x^*=5, x_0=4,84, y=sqrt) $$ frac(x^*-x_0)^2=-frac=-fracapprox -0,0003 $$ Получаем: $$ y^*=sqrtapprox 2,2367-0,0003=2,2364approx 2,236 $$ Квадратичное слагаемое указывает, что округлить результат нужно до 3-го знака после запятой.
п.4. Полезные формулы приближений для функций вблизи нуля
Рассмотрим свойства приближений некоторых функций при (x_0=0) и (triangle x=xrightarrow 0).
В разложении ограничимся слагаемым (y(0)) и линейным приближением. Только если линейное приближение равно 0, будем учитывать слагаемое квадратичного приближения.
1) (y=sinx)
(y’=cosx, y»=-sinx)
(y(0)=0, y'(0)=1, y»(0)=0)
(sinxapprox 0+1cdot x-frac02cdot x^2approx x)
4) (y=e^x)
(y’=y»=e^x)
(y(0)=y'(0)=y»(0)=1)
(e^xapprox 1+1cdot x+frac12cdot x^2approx 1+x)
Пренебрегаем (frac) как очень малым слагаемым.

