Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим:  . То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):
. То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):
 (5.1)
(5.1)
Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0  0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.
0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» – смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
Итоги:
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:
 и указывает на качество измерения. Ее можно выразить в процентах.
и указывает на качество измерения. Ее можно выразить в процентах.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
- выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
- подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
- вычесть из большего значения меньшее (4 см – 3 см = 1 см) и результат разделить на число делений.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
- Для линейки 1:
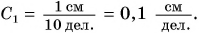
- Для линейки 2:
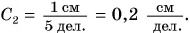
- Для линейки 3:
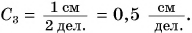
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2:


А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше  Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы
Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы  ), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления
), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления  ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.
). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
- Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
- Цена деления шкалы равна значению наименьшего деления шкалы.
- Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
- Заказать решение задач по физике
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:
1) Цена деления нижней шкалы:

Цена деления средней шкалы:

Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10°  определенный по средней шкале с точностью до 5°
определенный по средней шкале с точностью до 5°  определенный по верхней шкале с точностью до 1°
определенный по верхней шкале с точностью до 1° 
- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
Помогите определить цену деления термометра… с погрешностью плииииииииииииз
Оракул
(53330),
закрыт
14 лет назад
БезОного
Профи
(502)
14 лет назад
Цена деления – это расстояние между двумя ближайшими делениями на нём (в термометре обычно градус) , а погрешность – это половина цены деления (т. е. полградуса)
Дмитрий Алябьев
Мастер
(1542)
14 лет назад
ТЕМПЕРАТУРНЫЕ ШКАЛЫ
Современными термометрами можно измерить, практически, любую температуру.
Интересен тот факт, что в разных странах температурные шкалы термометров могут отличаться. Известны следующие температурные шкалы, применяемые при конструировании и изготовлении термометров:
Температура может измеряться термометрами в градусах по шкалам Фаренгейта (F), Цельсия (С) или Кельвина (К) . Минимальная возможная температура, 0° по шкале Кельвина, называется «абсолютным нулем» . Вышепредложенные температурные шкалы, которые можно встретить у различных термометров, связаны между собой соотношениями:
Шкала Кельвина (K, Kelvin)- температурная шкала термометра, в которой
начало отсчета сдвинуто по сравнению со шкалой Цельсия на 273.15 единиц в область отрицательных температур.
Минимальная возможная температура, определяемая термометром, 0° по шкале Кельвина, называется «абсолютным нулем» .
К = С + 273,16
Шкала Фаренгейта (°F, Fahrenheit) – температурная шкала термометра, в
которой опорными точками являются температура смеси снега и нашатыря (0 град. F) и нормальная температура человеческого тела (100 град. F), а
величина градуса в шкале термометра определяется как сотая часть интервала между опорными точками. Применяется в США при градуировке шкал термометров и в некоторых других странах.
0 град. C = 32 град. F
100 град. C = 212 град. F
F=1.8C+32 (F = 9/5 С + 32)
Шкала Цельсия (°C, Celsius, centigrade) – температурная шкала термометра, в
которой опорными точками являются температура плавления льда (0 град. C) и температура кипения воды при нормальном атмосферном давлении (100 град. C), а величина градуса в шкале термометра определяется как сотая часть интервала между опорными точками.
0° – температура затвердения воды
100° – температура закипания воды
C=5/9(F-32)
C=(K–273)
Шкала Реомюра – температурная шкала, в которой опорными точками являются точка таяния льда (0 град. R) и точка кипения воды при нормальном атмосферном давлении (80 град. R), а величина градуса в шкале термометра определяется как восьмидесятая часть интервала между опорными точками. В настоящее время почти не используется в термометрах для определения температуры.
Шкалы Фаренгейта и Цельсия совпадают в точке –40°, т. е. –40° F = –40° C,
что можно проверить по приведенным выше формулам. Во всех прочих случаях значения температур, определяемых термометрами, в градусах по шкалам Фаренгейта и Цельсия будут различаться. В научных исследованиях и при градуировке шкал термометров обычно используются шкалы Цельсия и Кельвина.
В нашей стране распространены термометры, отградуированные по шкале
Цельсия. Электронные термометры могут переключаться в различные режимы измерений.
PriMus
Мыслитель
(8925)
14 лет назад
цена деления определяется, как отношение между значениями двух ближайших подписанных штрихов шкалы на количество штрихов между ними.
а погрешность не превосходит половины цены деления по определению
Сергей Карпенко
Знаток
(412)
6 лет назад
не совсем точные ответы у вас – хотя и вопрос был задан не совсем точно- вопрос какую погрешность нужно определить? их несколько! Есть например погрешность измерения данного прибора- должна быть указана в документации на него – и она далеко не факт что равна половине цены деления – она может быть отлична от половины цены деления – а половина цены деления это если не изменяет память – погрешность отсчета- есть погрешность абсолютная – она равна разности истинного значения и измеренного – в общем погрешностей может быть много – за более точным ответом вам к учебнику метрологии=)
динар митюков
Знаток
(399)
6 лет назад
Уличный термометр. От 0 до 10 градусов (две соседние цифры на шкале) -всего 10 делений 10 градусов делим на 10 делений и получаем цену деления-1 градус.
Ма медицинском градуснике между соседними отметками 36 и 37 тоже 10 делений, следовательно цена деления та же.
*~Diana~*
Ученик
(195)
6 лет назад
Берем два числа. Например 40 и 30 градусов. Эти числа минусуем получаем 10.смотрим сколько делений. Например 10.Делим 10 на 10 и получаем 1 градус и деление.
Пользуясь рисунком 11,б, определите погрешность измерения термометра.

рис. 11, б

reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. §5. Задание. Номер №2
Решение
![]() Получай решения и ответы с помощью нашего бота
Получай решения и ответы с помощью нашего бота
Погрешность измерений равна половине цены деления шкалы измерительного прибора. Цена деления термометра − 1°С. Погрешность измерения термометра равна
1
2
°С = 0,5 °С.
Обновлено: 19.05.2023
Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.
- Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
- Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.
Математическая погрешность: формула для каждого типа
Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?
Формулы погрешностей вычисляются следующим образом.
Абсолютная погрешность измерений: формула
Формула дает разницу между измеренным и реальным значением.
Относительная погрешность: формула
Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.
Приведенная погрешность: формула
Классификация оценочной погрешности
Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.
Что такое случайная погрешность
Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.
Что такое систематическая погрешность
Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.
В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.
Погрешность выборки
Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.
Погрешность структуры
Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.
Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.
Погрешность аудитории
Погрешность отбора
Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.
Как минимизировать погрешность выборки
- Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам. - Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию. - Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.
Погрешность измерения
Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.
К погрешностям измерения приводят следующие виды ошибок.
Ошибка цели
Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.
Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.
Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.
Предвзятость интервьюера
Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.
Ошибка обработки
Ошибка ввода
Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.
Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.
Как минимизировать погрешность измерения
- Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью. - Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка. - Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования. - Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.
Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.
Подпишитесь на рассылку ROMI center:
Погрешность измерения – это отклонение измеренного значения величины от её истинного (действительного) значения.
Виды погрешности измерений
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Теоретическая погрешность
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Систематическая и случайная погрешности
Систематической погрешностью называют погрешность, которая остаётся постоянной или изменяется закономерно во времени при повторных измерениях одной и той же величины.
Систематическую погрешность можно легко определить, если известно эталонное (табличное) значение измеряемой величины. Для других случаев разработаны эффективные статистические методы выявления систематических погрешностей. Причиной систематической погрешности может быть неправильная настройка приборов или неправильная оценка параметров (завышенная или заниженная) в расчётных формулах.
Случайной погрешностью называют погрешность, которая не имеет постоянного значения при повторных измерениях одной и той же величины.
Случайные погрешности неизбежны и всегда присутствуют при измерениях.
Определение абсолютной погрешности
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины:
При пяти взвешиваниях гири с маркировкой 100 г были получены различные значения массы. Если принять маркировку за истинное значение, то получаем следующие значения абсолютной погрешности:
Вычисление погрешностей измерения является заключительным этапом расчетов. Оно позволяет выявить степень отклонения полученного значения от истинного. Существует несколько видов таких отклонений, но иногда достаточно определить только абсолютную погрешность измерения.

- Как определить абсолютную погрешность измерения
- Как определить погрешность прибора
- Как найти абсолютную и относительную погрешность
Чтобы определить абсолютную погрешность измерения, нужно найти величину отклонения от действительного значения. Она выражается в тех же единицах, что и оцениваемая, и равняется арифметической разности между истинным и расчетным значениями:∆ = x1 – x0.
Абсолютную погрешность часто используют в записи некоторых постоянных величин, имеющих бесконечно малое или бесконечно большое значение. Это касается многих физических и химических констант, например, постоянная Больцмана равна 1,380 6488×10^(−23) ± 0,000 0013×10^(−23) Дж/К, где значение абсолютной погрешности отделяется от истинного с помощью знака ±.
В рамках математической статистики измерения производятся в результате серии экспериментов, итогом которой является некоторая выборка значений. Анализ этой выборки опирается на методы теории вероятностей и предполагает построение вероятностной модели. В этом случае за абсолютную погрешность измерения принимается среднеквадратичное отклонение.
Для расчета среднеквадратичного отклонения необходимо определить среднее или арифметическое, где xi – элементы выборки, n – ее объем;xвзв = ∑pi•xi/∑pi – среднее взвешенное.
Как видите, во втором случае учитываются веса элементов pi, которые показывают, с какой вероятностью измеряемая величина примет то или иное значение элемента выборки.
Классическая формула среднеквадратичного отклонения выглядит следующим образом:σ = √(∑(xi – xср)²/(n – 1)).
Существует понятие относительной погрешности, которая находится в прямой зависимости от абсолютной. Она равна отношению абсолютной погрешности к расчетному или действительному значению величины, выбор которого зависит от требований конкретной задачи.
Погрешность указывается на измерительном инструменте. Например 0.1 мм Тогда измерив деталь и получив 10 мм вы просто прибавляете эту погрешность и получете измерение такого вида – 10+/- 0.1 тоесть от 9.9 до 10.1 мм
Абсолютная погрешность показывает разность между действительным и измеренным значением (ошибку измерений) .
1) если есть эталонное значение измеряемой величины или эталонное средство измерений, то находится просто разность между результатом измерений и эталоном.
2) если эталона нет. Производятся многократные измерения одной и той же величины, находится среднее значение результатов измерений, среднее квадратическое отклонение среднего арифметического (формулы можно найти в интернете) . Погрешность находится как произведение среднего квадратического отклонения среднего арифметического на относительную ширину доверительного интервала.
У каждого человека абсолюная погрешность своя, например: у кого-то она равна +- 0,25 сек., а у кого-то +-0,5 сек.
Свидетельство и скидка на обучение каждому участнику
Зарегистрироваться 15–17 марта 2022 г.
Как определять погрешности измерений
Измерение – нахождение значения физической величины опытным путем с помощью средств измерений.
Прямое измерение – определение значения физической величины непосредственно средствами измерения.
Косвенное измерение – определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.
А, В, С, … – физические величины.
Апр. – приближенное значение физической величины.
А – абсолютная погрешность измерения физической величины.
– относительная погрешность измерения физической величины.
иА – абсолютная инструментальная погрешность, определяемая конструкцией прибора.
оА – абсолютная погрешность отсчета, она равна в большинстве случаев
половине цены деления; при измерении времени – цене деления секундомера или часов.
Абсолютную погрешность измерения обычно округляют до одной значащей цифры:
Численное значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности:
Результат измерения записывается так:
Определение погрешности методом среднего арифметического
При многократных измерениях величины погрешность можно оценить следующим образом:
1. Определить среднее значение величины А :
(при трех измерениях).
2.Определить отклонение каждого значения от среднего:
3.Определить среднее значение отклонения, его и принимают за абсолютную погрешность:
4.Определить относительную погрешность и выразить ее в процентах:
Многократные измерения предпочтительнее, так как при их проведении возможна компенсация случайных факторов, влияющих на результат. Обычно многократные измерения проводят, слегка изменяя условия опыта, но предполагая, что значение величины А не изменяются
Определение погрешности косвенных измерений
При косвенных измерениях значение физической величины находится путем расчетов по формуле.
Относительную погрешность определяют так, как показано в таблице:
Формула относительной погрешности
Абсолютную погрешность определяют по формуле:
( выражается десятичной дробью)
Пример : пусть измеряется сопротивление проводника. .
Результаты прямых измерений :
Графическое представление результатов эксперимента
Правила построения графиков
выберите соответствующую бумагу;
выберите масштаб по осям координат;
напишите обозначения измеряемых физических величин;
нанесите на график данные;
нанесите на график доверительные интервалы;
проведите кривую через нанесенные точки;
составьте заголовок графика.
Для построения графиков выпускают специальную бумагу-миллиметровку.
При выборе масштабов по осям координат следует руководствоваться следующими правилами:
– значение независимой переменной откладывают вдоль оси абсцисс, функции – вдоль оси ординат;
– цена наименьшего деления масштабной сетки должна быть сравнимой с величиной погрешности измерения;
– точка пересечения оси абсцисс и оси ординат не обязательно должна иметь координаты (0,0).
При построении графиков следует иметь в виду, что по результатам опытов мы получаем не точку, а прямоугольник со сторонами и .
0 А
При выполнении простых лабораторных работ достаточно обвести экспериментальную точку кружком или пометить крестиком, не указывая доверительных интервалов.
Этот кружок или крестик будут обозначать, что данная точка получена с каким-то приближением и истинное значение измеряемой величины лежит где-то в ее окрестности.
Правила приближенных вычислений
1. Основное правило округления.
Если первая отброшенная цифра равна 5 или больше, то последнюю из сохраняемых цифр увеличивают на единицу; если первая отброшенная цифра меньше 5, то последнюю из сохраняемых цифр оставляют без изменения, например:
2. При сложении и вычитании приближенных чисел в полученном результате сохраняют столько десятичных знаков, сколько их в числе с наименьшим количеством десятичных знаков, например:
3. При умножении и делении приближенных чисел в полученном результате нужно сохранить столько значащих цифр, сколько их имеет приближенное число с наименьшим количеством значащих цифр, например:
4. При возведении в квадрат приближенного числа нужно в результате сохранять столько значащих цифр, сколько их имеет возводимое в степень число, например:
5. При извлечении квадратного корня в результате нужно сохранять столько значащих цифр, сколько их имеет подкоренное число, например:
6. При вычислении промежуточных результатов в них следует сохранять на одну цифру больше, чем требуют правила 2-5. Причем при подсчете значащих цифр запасные цифры не учитываются. В окончательном результате запасная цифра отбрасывается по основному правилу округления.
7. При нахождении углов или тригонометрических функций значение соответствующего угла записывают с точностью до градуса, если значение тригонометрической функции имеет две значащие цифры; если угол задан с точностью до градусов, то в значении тригонометрической функции сохраняют две значащие цифры, например:
- подготовка к ЕГЭ/ОГЭ и ВПР
- по всем предметам 1-11 классов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания

Курс повышения квалификации
Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
- Курс добавлен 31.01.2022
- Сейчас обучается 35 человек из 22 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 613 312 материалов в базе
Материал подходит для УМК
- ЗП до 91 000 руб.
- Гибкий график
- Удаленная работа
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
Свидетельство и скидка на обучение каждому участнику
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
- 08.06.2021 275
- DOCX 171.5 кбайт
- 2 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Суховеенко Надежда Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
40%
- Подготовка к ЕГЭ/ОГЭ и ВПР
- Для учеников 1-11 классов
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Онлайн-тренинг: нейрогимнастика для успешной учёбы и комфортной жизни
Время чтения: 2 минуты
Отчисленные за рубежом студенты смогут бесплатно учиться в России
Время чтения: 1 минута
Рособрнадзор предложил дать возможность детям из ДНР и ЛНР поступать в вузы без сдачи ЕГЭ
Время чтения: 1 минута
Новые курсы: преподавание блогинга и архитектуры, подготовка аспирантов и другие
Время чтения: 16 минут
В Госдуме предложили ввести сертификаты на отдых детей от 8 до 17 лет
Время чтения: 1 минута
Минтруд предложил упростить направление маткапитала на образование
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Читайте также:
- Как выбрать наиболее подходящий кредит кратко
- Объясните почему клетка простейших является самостоятельным организмом кратко
- Презентация про кролика для детского сада где живет чем питается
- Проект патриотическое воспитание в детском саду средняя группа
- Какие последствия вызвал грех адама и евы ответ кратко
Здравствуйте, уважаемые читатели!
В последнее время часто возникает потребность измерять температуру тела. До недавних пор вопроса, с помощью чего это сделать, не возникало. В каждом доме был ртутный градусник, в показаниях которого никто не сомневался.
Однако, всегда есть риск, что ртутный термометр может разбиться, а токсичная ртуть вытечь, создав опасную ситуацию.
Решили купить себе электронный градусник, который измеряет температуру при помощи встроенного датчика. Об окончании измерения он оповещает звуковым сигналом, а результат показывает на цифровом дисплее. Подсветка позволяет использовать его в темноте.
У этого градусника есть память, хранящая историю последних измерений, он водонепроницаем, гигиеничен – снабжен сменным наконечником. Он абсолютно безопасен: сделан из пластика, не содержит ртуть, в отличие от своего стеклянного предшественника.
Несмотря на все достоинства, в электронном градуснике я отметила для себя несколько недостатков:
- он требует бережного отношения, как и любой другой электронный прибор, и может пострадать от удара, вибрации, прямых солнечных лучей и расположенных поблизости электроприборов;
- работает от батареек, которые периодически приходится менять;
- согласно инструкции, для измерения температуры достаточно 1 минуты, но на практике выходит около 5-7 минут;
- такой термометр рассчитан на максимально плотный контакт измерительного датчика с поверхностью тела. Если он не обеспечен, то точность измерения страдает.
Вот как раз точность измерения электронного градусника у меня больше всего вызвало сомнение, и я решила сравнить этот градусник с ртутным.
Для этого я налила в стакан теплую воду, поставила в него ртутный и электронный термометры так, чтобы измерительный элемент электронного термометра и ртутная колба ртутного термометра оказались на одном уровне.
Когда показания на ртутном термометре перестали изменяться, сравнила показания термометров. К счастью, разница оказалась в 0,1 градуса. Такой погрешностью можно пренебречь.
Таким образом, нам повезло, что купили достаточно точный электронный термометр. У моих знакомых, проверявших такой же, отклонение составило 0, 5 градуса, им пришлось менять градусник.
Как выяснилось, они купили электронный термометр не в аптеке, а в супермаркете бытовой техники и электроники, и допустили при этом ошибку, о которой не все знают.
Оказывается, лучше покупать электронный градусник в аптеке или специализированном магазине медицинской техники, так как поступающие сюда приборы проходят соответствующую сертификацию и гарантируют наиболее точное измерение.
Кстати, сейчас для измерения температуры появились инфракрасные термометры, а также термополоски. Однако, они еще не получили такого широкого распространения, поэтому судить об их достоинствах или недостатках мне пока сложно говорить. Но если у вас есть опыт их использования, поделитесь своим мнением под публикацией.
Ценю ваши ЛАЙКи и комментарии. Всем доброго здоровья!
