Чаще всего оценки делятся на два вида: точечная оценка и интервальная оценка.
Определение 1
Точечная оценка — оценка, которая определяется одним числом.
В математической статистике, при оценке различных совокупностей чаще сего используется интервальная оценка.
Определение 2
Интервальная оценка — оценка, которая определяется двумя числами, которые являются концами интервала.
Для понятия интервальной оценки используются параметры точности и надежности оценки.
Определение 3
Точность оценки — положительное число $delta >0$, характеризующие величину расхождения между оценками выборки и генеральной совокупности, а именно:
[left|Q-Q^*right|1.]
Определение 4
Надежность или доверительная вероятность оценки $Q по Q^*$ – вероятность $gamma $, удовлетворяющее равенству:
[Pleft(Q^*-delta
Чаще всего надежность имеет значения $0,95, 0,99 и 0,999$, то есть значения, близкие к единице.
Доверительный интервал
Определение 5
Доверительный интервал — интервал $(Q^*-delta ,Q^*+delta )$, который покрывает неизвестную величину $Q$ c надежностью $gamma $, то есть $Q^*-delta
Понятие доверительного интервала существует для оценки многих параметров выборки: математического ожидания, среднего квадратического отклонения, дисперсии
В данной статье мы не будем вдаваться в подробности вывода формул для нахождения доверительных интервалов.
- Доверительный интервал для оценки математического ожидания при заданном среднем квадратическом отклонении $sigma $.
[left(overline{x}-frac{sigma t}{sqrt{n}};overline{x}+frac{sigma t}{sqrt{n}}right)]
где $t$ находится из равенства $2Фleft(tright)=gamma $.
- Доверительный интервал для оценки математического ожидания при неизвестном среднем квадратическом отклонении $sigma $.
[left(overline{x}-frac{St}{sqrt{n}},overline{x}+frac{St}{sqrt{n}}right)]
- Доверительный интервал для оценки среднего квадратического отклонения.
[left(Sleft(1-qright),Sleft(1+qright)right), при q1.]
- Доверительный интервал для оценки дисперсии.
[left(S^2left(1-qright),S^2left(1+qright)right), при q1.]
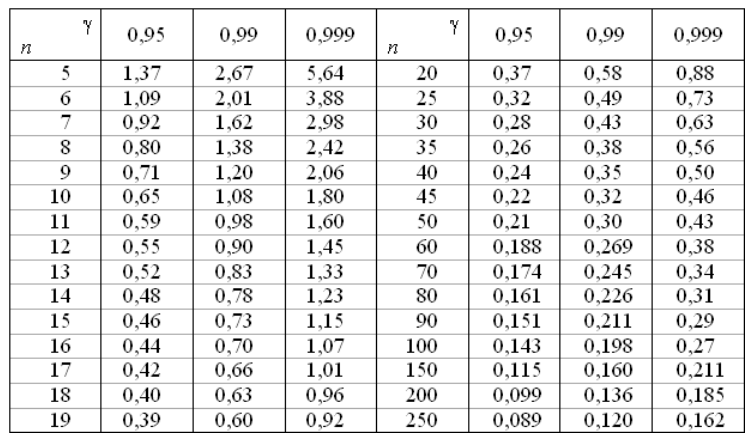
В последних двух пунктах $q$ имеет табличное значение (таблица 1).
Рисунок 1. Значения величины $q$.
Пример задачи на нахождения доверительных интервалов
Пример 1
Пусть величина $X$ имеет нормальное распределение с дисперсией $sigma =2$ и исправленным среднем квадратическим отклонением $S=1,8$. Пусть объем выборки $n=25$, а надежность равна $gamma =0,99$.
Найти:1) доверительный интервал для оценки математического ожидания.
2) доверительный интервал для оценки среднего квадратического отклонения.
3) доверительный интервал для оценки дисперсии.
Решение:
1) Для нахождения доверительного интервала для оценки математического ожидания необходимо найти интервал вида
[left(overline{x}-frac{sigma t}{sqrt{n}};overline{x}+frac{sigma t}{sqrt{n}}right)]
Параметр $t$ найдем из формулы
[2Фleft(tright)=gamma ]
Откуда
[Фleft(tright)=frac{gamma }{2}=frac{0,99}{2}=0,495]
Из таблицы значений функции Лапласа получим, что $t=2,6$.
Имеем интервал:
[left(overline{x}-frac{4,6}{sqrt{25}};overline{x}+frac{4,6}{sqrt{25}}right)=left(overline{x}-0,92;overline{x}+0,92right)]
2) Для начала найдем значение величины $q$. Так как $n=25$ и $gamma =0,99$, то из таблицы 1, получим, что $q=0,49$.
Видим, что $q
[left(Sleft(1-qright),Sleft(1+qright)right)] [left(1,8cdot 0,51;1,8cdot 1,49right)=(0,918;2,682)]
3) Так как, как было показано в пункте 2, $q
[left(S^2left(1-qright),S^2left(1+qright)right)]
end{enumerate}
Получим:
[left(1,6524;4,8276right)]
Точечной называют оценку, которая
определяется одним числом. Все оценки,
рассмотренные выше,- точечные. При
выборке малого объема точечная оценка
может значительно отличаться от
оцениваемого параметра, т. е. приводить
к грубым ошибкам. По этой причине при
небольшом объеме выборки следует
пользоваться интервальными оценками.
Интервальной называют
оценку, которая определяется двумя
числами – концами интервала. Интервальные
оценки позволяют установить точность
и надежность оценок (смысл этих понятий
выясняется ниже).
Пусть найденная по данным
выборки статистическая характеристика
Θ* служит оценкой неизвестного параметра
Θ. Будем считать Θ постоянным числом (Θ
может быть и случайной величиной). Ясно,
что Θ* тем точнее определяет параметр
Θ, чем меньше абсолютная величина
разности |Θ – Θ*|. Другими словами, если
δ>0
и |Θ – Θ*|<δ,
то чем меньше δ,
тем оценка точнее. Таким образом,
положительное число δ
характеризует точность
оценки.
Однако статистические
методы не позволяют категорически
утверждать, что оценка Θ * удовлетворяет
неравенству |Θ – Θ*|<δ;
можно лишь говорить о вероятности γ, с
которой это неравенство осуществляется.
Надежностью (доверительной
вероятностью)
оценки Θ по Θ* называют
вероятность γ,
с которой осуществляется
неравенство |Θ – Θ*|<δ.
Обычно надежность оценки задается
наперед, причем в качестве γ берут число,
близкое к единице. Наиболее часто задают
надежность, равную 0,95; 0,99 и 0,999.
Пусть вероятность того, что
|Θ – Θ*|<δ,
равна γ:
Р[|Θ –
Θ*|<δ]=
γ.
Заменив неравенство |Θ –
Θ*|<δ
равносильным ему двойным неравенством
-δ <Θ
– Θ*< δ,
или Θ*- δ <Θ<
Θ* + δ,
имеем
Р[Θ* – δ
<Θ< Θ* + δ]
= γ.
Это соотношение следует
понимать так: вероятность того, что
интервал(Θ*-δ,
Θ*+δ)
заключает в себе (покрывает) неизвестный
параметр Θ, равна γ.
Доверительным называют
интервал (Θ*-δ,
Θ*+δ),
который покрывает неизвестный параметр
с заданной надежностью γ.
Замечание.
Интервал (Θ*-δ,
Θ*+δ)
имеет случайные концы (их называют
доверительными границами). Действительно,
в разных выборках получаются различные
значения Θ*. Следовательно, от выборки
к выборке будут изменяться и концы
доверительного интервала, т. е.
доверительные границы сами являются
случайными величинами – функциями от
х1,
x2,
…,
хn.
Так
как случайной величиной является не
оцениваемый параметр Θ, а доверительный
интервал, то более правильно говорить
не о вероятности попадания Θ в доверительный
интервал, а о вероятности того, что
доверительный интервал покроет Θ.
Метод доверительных интервалов разработал
американский статистик Ю. Нейман, исходя
из идей английского статистика Р. Фишера.
§ 15. Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ
Пусть количественный признак
X
генеральной совокупности
распределен нормально, причем среднее
квадратическое отклонение σ
этого распределения известно. Требуется
оценить неизвестное математическое
ожидание а
по выборочной средней
.
Поставим своей задачей
найти доверительные интервалы, покрывающие
параметр а с
надежностью γ.
Будем рассматривать
выборочную среднюю
как случайную величину(
изменяется от выборки к выборке) и
выборочные значения признаках1,
x2,
…,хn
– как одинаково распределенные независимые
случайные величины Х1,
Х2,
…,Хn
(эти числа также
изменяются от выборки к выборке). Другими
словами, математическое ожидание каждой
из этих величин равно а
и среднее квадратическое
отклонение – σ.
Примем без доказательства,
что если случайная величина X
распределена нормально,
то выборочная средняя
,
найденная по
независимым наблюдениям, также
распределена нормально. Параметры
распределения
таковы (см. гл. VIII,
§ 9):
M()=a,
.
Потребуем, чтобы выполнялось соотношение
Р(|Х
– а| < δ)
= γ,
где γ
– заданная
надежность.
Пользуясь формулой (см. гл.
XII,
§ 6)
Р(|Х-а|
< δ)
= 2Ф(δ/σ),
заменив X
на
и σ
на
,
получим
Р(|Х-а|)
<δ)
= 2Ф(δ)
= 2Ф (t),
где t
=
δ.
Найдя из последнего равенства
, можем написать
Р (|—а
| <
)
= 2Ф(t).
Приняв во внимание, что
вероятность P
задана и равна γ,
окончательно
имеем (чтобы получить рабочую формулу,
выборочную среднюю вновь обозначим
через
)
Смысл полученного соотношения
таков: с надежностью γ
можно утверждать,
что доверительный интервал (,
) покрывает неизвестный
параметр а;
точность оценки
.
Итак, поставленная выше
задача полностью решена. Укажем еще,
что число t
определяется из равенства 2Ф(t)
= γ. или Ф(t)=
γ /2;
по таблице функции
Лапласа (см. приложение 2) находят аргумент
t, которому
соответствует значение функции Лапласа,
равное γ /2.
Замечание
1.
Оценку
называют
классической. Из формулы
,
определяющей
точность классической оценки, можно
сделать следующие выводы:
1) при
возрастании объема выборки п
число
δ
убывает
и, следовательно, точность оценки
увеличивается;
2)
увеличение надежности оценки γ
= 2Ф(t)
приводит к увеличению t(Ф
(t)
— возрастающая функция), следовательно,
и к возрастанию δ;
другими словами, увеличение надежности
классической оценки влечет за собой
уменьшение ее точности.
Пример.
Случайная величина X
имеет
нормальное распределение с известным
средним квадратическим отклонением σ
= 3. Найти доверительные интервалы для
оценки неизвестного математического
ожидания а
по
выборочным средним
,
если
объем выборки n
= 36 и задана надежность оценки
γ= 0,95.
Решение.
Найдем
t.
Из
соотношения 2Ф(t)=0,95
получим Ф(t)
= 0,475. По таблице приложения 2 находим
t=1,96.
Найдем точность
оценки:
.
Доверительный
интервал таков: (-0,98;
+ 0,98). Например, если
= 4,1, то доверительный интервал имеет
следующие доверительные границы:
–
0,98
= 4,1- 0,98 = 3,12;
+
0,98 = 4,1 + 0,98 = 5,08.
Таким
образом, значения неизвестного параметра
а,
согласующиеся
с данными выборки, удовлетворяют
неравенству 3,12 < а
< 5,08.
Подчеркнем, что было бы ошибочным
написать Р(3,12
<
а < 5,08) = 0,95. Действительно, так как а
–
постоянная величина, то либо она заключена
в найденном интервале (тогда событие
3,12 < а
< 5,08
достоверно и его вероятность равна
единице), либо в нем не заключена (в
этом
случае событие 3,12 < а
<
5,08 невозможно и его вероятность равна
нулю). Другими словами, доверительную
вероятность не следует связывать с
оцениваемым параметром; она связана
лишь с границами доверительного
интервала, которые, как уже было указано,
изменяются от выборки к выборке.
Поясним
смысл, который имеет заданная надежность.
Надежность γ = 0,95 указывает, что если
произведено достаточно большое число
выборок, то 95% из них определяет такие
доверительные интервалы, в которых
параметр действительно заключен; лишь
в 5% случаев он может выйти за границы
доверительного интервала.
Замечание
2.
Если требуется оценить математическое
ожидание с наперед заданной точностью
δ
и
надежностью γ, то минимальный объем
выборки, который обеспечит эту точность,
находят по формуле
(следствие
равенства
).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Погрешность и доверительный интервал: в чем разница?
17 авг. 2022 г.
читать 2 мин
Часто в статистике мы используем доверительные интервалы для оценки значения параметра совокупности с определенным уровнем достоверности.
Каждый доверительный интервал принимает следующий вид:
Доверительный интервал = [нижняя граница, верхняя граница]
Погрешность равна половине ширины всего доверительного интервала.
Например, предположим, что у нас есть следующий доверительный интервал для среднего значения генеральной совокупности:
95% доверительный интервал = [12,5, 18,5]
Ширина доверительного интервала составляет 18,5 – 12,5 = 6. Допустимая погрешность равна половине ширины, которая будет равна 6/2 = 3 .
В следующих примерах показано, как рассчитать доверительный интервал вместе с погрешностью для нескольких различных сценариев.
Пример 1: Доверительный интервал и допустимая погрешность для среднего значения генеральной совокупности
Мы используем следующую формулу для расчета доверительного интервала для среднего значения генеральной совокупности:
Доверительный интервал = x +/- z*(s/ √n )
куда:
- x : выборочное среднее
- z: z-критическое значение
- s: стандартное отклонение выборки
- n: размер выборки
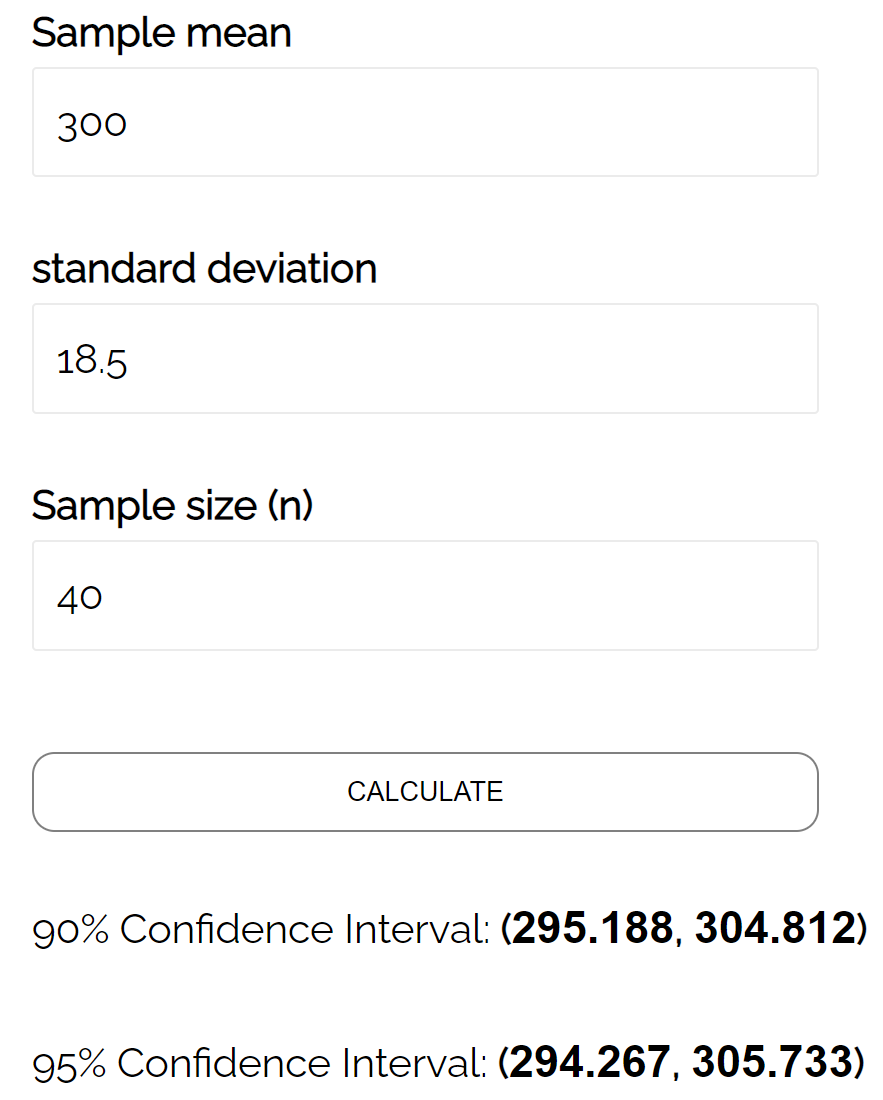
Пример: Предположим, мы собираем случайную выборку дельфинов со следующей информацией:
- Размер выборки n = 40
- Средний вес выборки x = 300
- Стандартное отклонение выборки s = 18,5
Мы можем подставить эти числа в калькулятор доверительного интервала , чтобы найти 95% доверительный интервал:
95% доверительный интервал для истинного среднего веса популяции черепах составляет [294,267, 305,733] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (305,733 – 294,267) / 2 = 5,733 .
Пример 2: Доверительный интервал и допустимая погрешность для доли населения
Мы используем следующую формулу для расчета доверительного интервала для доли населения:
Доверительный интервал = p +/- z * (√ p (1-p) / n )
куда:
- p: доля выборки
- z: выбранное значение z
- n: размер выборки
Пример: Предположим, мы хотим оценить долю жителей округа, поддерживающих определенный закон. Мы выбираем случайную выборку из 100 жителей и спрашиваем их об их отношении к закону. Вот результаты:
- Размер выборки n = 100
- Доля в пользу закона p = 0,56
Мы можем подставить эти числа в доверительный интервал для калькулятора пропорций , чтобы найти 95% доверительный интервал:
95% доверительный интервал для истинной доли населения составляет [0,4627, 0,6573] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (0,6573 – 0,4627) / 2 = 0,0973 .
Дополнительные ресурсы
Погрешность и стандартная ошибка: в чем разница?
Как найти погрешность в Excel
Как найти погрешность на калькуляторе TI-84
Содержание:
- Точечные и интервальные оценки параметров распределения
- Примеры решения задач
Точечные и интервальные оценки параметров распределения
Оценка параметра распределения совокупности 
Оценка называется обоснованной, если она совпадает по вероятности с соответствующим параметром при
Оценка называется несмещенной, если ее математическое ожидание совпадает со значением параметра.
В случае выбора из всех известных несмещенных обоснованных оценок определенной оценки, необходимо указать критерий, по которому сделан выбор.
Чаще всего используется критерий, который состоит в выборе оценки, имеющей наименьшую возможную дисперсию. Такая оценка называется эффективной. Нижняя граница дисперсии несмещенной оценки параметра 

где 

Оценки параметров распределения находят методами максимальной правдоподобности и моментов. Метод максимальной правдоподобности состоит вот в чем. Пусть закон распределения случайной величины определяется через параметр 


За оценки максимальной правдоподобности параметров 
Использование метода моментов основывается на сходстве (по вероятности) статистических моментов распределения с соответствующими теоретическими моментами распределения, которые в этом случае должны существовать. Как известно, теоретические моменты распределения выражаются через параметры распределения. Составим систему 
Пусть есть точечная оценка 











Примеры решения задач
Пример 1. Выборка объемом 
Найти оценку для параметра 
Решение. Применим метод максимальной правдоподобности. Построим функцию правдоподобности, составим и решим уравнение для определения оценки:
Проверим оценку на несмещенность, найдя ее математическое ожидание:
Преобразование выполнено согласно свойствам математического ожидания и с учетом того, что результаты выборки являются независимыми одинаково распределенными случайными величинами. Найдем 
Тогда 
Проверку обоснованности оценки выполним, второй формой неравенства Чебышева, то есть оценим вероятность 
(Последний интервал, который является математическим ожиданием квадрата случайной величины, равен 

Подставляя дисперсию оценки в неравенство Чебышева, получим:

Следовательно, оценка обоснованная.
Находим дисперсию эффективной оценки:
Дисперсия эффективной оценки совпадает с дисперсией найденной оценки для 
Пример 2. Методом моментов найти оценку параметра 
Решение. Геометрический закон распределения определяется формулой 
Пример 3. По данным выборки объемом 


Решение. Интервальная оценка для математического ожидания, если дисперсия совокупности 



Для построения оценки рассматривалась выборочная функция 
Пример 4. Решить предыдущую задачу для случая, когда дисперсия совокупности неизвестна.
Решение. В этом случае интервальную оценку построим с помощью выборочной функции 





Пример 5. По результатам выборки объемом 

Решение. Для определения доверительного интервала берем выборочную функцию 






Пример 6. Найти с надежностью 



Решение. Для определения доверительного интервала берем выборочную функцию 
где 


Получим интервал
Пример 7. Определить минимальный объем выборки 



Решение. Воспользовавшись формулой 




Пример 8. Из партии однотипных высокоомных сопротивлений взяли для контроля 10 штук. Измерения показали такие отклонения от номинала, кОм:
Найти выборочную среднюю и дисперсию отклонения фактического значения сопротивления от номинала в этой партии и определить точность оценки математического ожидания выборочной средней величиной с надежностью 
Решение. Считаем, что отклонение 








Следовательно, получим такой доверительный интервал для математического ожидания:
Пример 9. В ВТК были измерены диаметры 200 валов, изготовленных на станке-автомате. Отклонения измеренных диаметров от номинала, мкм, приведены в таблице.
Считая, что выборка сделана из нормально распределенной совокупности, определить с надежностью 

Решение. С помощью условных моментов распределения, вычислим выборочную дисперсию 
найдем условные моменты распределения и выборочную дисперсию на основании расчетов в таблице:
Точность оценки 












Выборочная функция 
Выполним преобразование для определения границ доверительного интервала:
Следовательно, доверительный интервал для дисперсии такой:
Найдем точность оценки как половину длины доверительного интервала:
Согласно значению 
Окончательно получим:
Лекции:
- Проверка статистических гипотез
- Дисперсионный анализ
- Элементы теории корреляции
- Выборка из генеральной совокупности. Вариационный ряд. Гистограмма относительных частот
- Выборочная функция распределения
- Закон больших чисел в форме Чебышева
- Теорема Бернулли
- Центральная предельная теорема
- Теория случайных процессов и теория массового обслуживания
- Первичная обработка и графическое представление выборочных данных