При измерении
длин отрезков и площадей фигур, при взвешивании тел и других измерениях
получаются числа, выражающие эти величины.
Ввиду
погрешностей измерения полученные числа являются приближёнными значениями измеряемой
величины.
У каждого из
вас есть линейка и карандаш. Давайте попытаемся измерить длину карандаша.
Из рисунка
видно, что длина карандаша чуть меньше 10 см. Если бы на этой линейке не было
миллиметровых делений, то мы бы сказали, что длина карандаша равна 10 см. Но
это было бы не совсем точное измерение.
Такую
неточность называют погрешностью измерения.
В нашем случае,
на линейке есть миллиметровые деления, поэтому мы можем измерить длину
карандаша с более высокой точностью – 9,8 см.
Приближённое
значение отличается от точного значения в этом случае на 0,2 см. Чтобы узнать,
на сколько приближённое значение отличается от точного, надо из большего числа
вычесть меньшее, т.е. найти модуль разности точного и приближённого значений.
Этот модуль разности называют абсолютной погрешностью.
Определение:
Абсолютной
погрешностью приближённого значения называют модуль разности точного и приближённого значений.
Значение
абсолютной погрешности не всегда можно найти. Но обычно известна её оценка
сверху – например, при измерении длины отрезка линейкой с сантиметровыми
делениями абсолютная погрешность измерения не превышает 1 сантиметра, а при
взвешивании на весах с гирями 100 грамм, 200 грамм, 500 грамм и 1 килограмм
абсолютная погрешность взвешивания не превышает ста грамм.
Посмотрите, на слайде
изображён отрезок CD.
Его длина
расположена между цифрами 7 см и 8 см. Понятно, что 7 см – это приближённое
значение длины отрезка CD с недостатком, а 8 см – это приближённое значение длины отрезка CD с
избытком.
Если истинную длину
отрезка обозначить за х, то получим, что длина отрезка CD удовлетворяет
неравенству:
Пусть истинное
значение измеряемой величины равно .
Измерение дало
результат .
Тогда разность – это абсолютная погрешность измерения.
Число называют границей абсолютной погрешности
измерения, если выполняется неравенство:
Принято писать
Точность
приближённого значения зависит от многих причин. Если приближённое значение
получено в процессе измерения, то, конечно же, его точность будет зависеть от
прибора, с помощью которого выполнялось это измерение.
Вот, например,
комнатный термометр. На нём деления нанесены через один градус. Это даёт
возможность измерять температуру воздуха с точностью до 1 градуса. А на весах,
у которых цена деления шкалы 20 г, можно взвешивать с точностью до 20 г. Или, к примеру, ещё, механические часы. Цена одного
деления, которых 1 мин. По ним можно сказать время с точностью до 1 минуты.
Для оценки
качества измерения можно использовать относительную погрешность приближённого
значения.
Определение:
Относительной
погрешностью приближённого значения называется отношение абсолютной погрешности к модулю приближённого
значения.
Относительную
погрешность принято выражать в процентах. В тех случаях, когда абсолютная
погрешность приближенного значения неизвестна, а известна лишь его точность,
ограничиваются оценкой относительной погрешности.
Например: при измерении (в сантиметрах) длины книжной полки и
толщины компакт-диска получили следующие результаты:
Чем меньше
относительная погрешность измерения, тем оно точнее.
Итоги:
Абсолютной
погрешностью приближенного значения
называют модуль разности точного и приближенного значений.
Число называют границей абсолютной погрешности измерения,
если выполняется неравенство:
Относительной
погрешностью приближенного значения называется
отношение абсолютной погрешности к модулю приближенного значения.
Чем меньше
относительная погрешность измерения, тем оно
точнее.
Как найти точность приближенного значения
Количественного понятия «точность» в науке не существует. Это качественное понятие. При защите диссертаций говорят только о погрешности (например, измерений). И даже если прозвучало слово «точность», то следует иметь в виду весьма расплывчатую меру величины, обратной погрешности.

Инструкция
Небольшой анализ понятия «приблизительное значение». Возможно, что имеется в виду приблизительный результат вычисления. Погрешность (точность) здесь задает сам исполнитель работы. В таблицах эта погрешность указывается, например «до 10 в минус четвертой степени». Если же погрешность относительная – то в процентах или долях процента. Если вычисления велись на основе числового ряда (чаще всего Тейлора) – на основе модуля остаточного члена ряда.
О приблизительных значениях величин часто говорят как об оценочных их значениях. Результаты измерений случайны. Поэтому это те же случайные величины, обладающие своими характеристиками разброса значений, как та же дисперсия или с.к.о. (среднее квадратичное отклонение). В математической статистике вопросам оценок параметров посвящены целые разделы. При этом различают точечные и интервальные оценки. Последние здесь не рассматриваются. Точечную оценку некоторого параметра λ, подлежащего определению договоримся обозначать λ*. Оценки параметров просто вычисляются по каким-то формулам (статистикам), удовлетворяющим своим требованиям, называемыми критериями качества оценки.
Первый критерий называется несмещенность. Имеется в виду то, что среднее значение (математическое ожидание) оценки λ* равно ее истинному значению, то есть M[λ*]=λ. Об остальных критерия качества говорить пока не стоит. Ими иногда и пренебрегают, обосновывая вопрос тем, что самое главное, чтобы оценка достаточно «слабо» отличалась от истины. Поэтому берется основная характеристика разброса – дисперсия оценки и просто вычисляется. Если исследователь принимает самостоятельное решение, что она достаточно мала, то этим и ограничиваются.
Наиболее часто оценивается среднее значение (математическое ожидание). Это среднее выборочное, вычисляемое, как среднее арифметическое имеющихся результатов наблюдений mx*=(1/n)(x1+x2+ … +xn). Легко показать, что М[mx*]=mx, то есть mx* оценка несмещенная. Дисперсию оценки математического ожидания найдите следуя выкладкам, приведенным на рисунке 1а. Так как истинное значение Dх недоступно, взамен возьмите среднюю выборочную дисперсию (см. рис.1b).
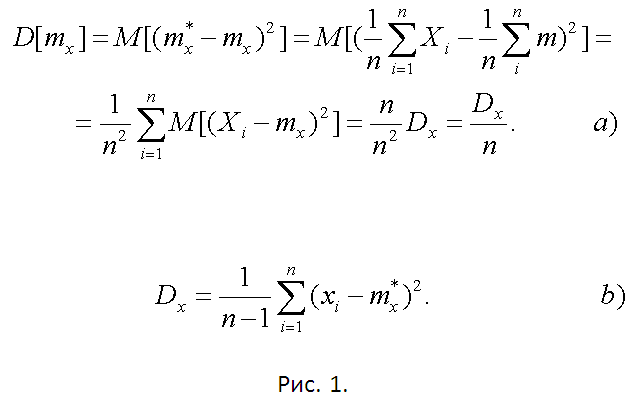
Источники:
- Тихонов В.И. Статистическая радиотехника. – М.: Радио и связь, 1982. – 624 с.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Погрешность и точность приближения
План урока
- Абсолютная погрешность приближенного значения
- Относительная погрешность приближенного значения
Цели урока
- Знать определения абсолютной и относительной погрешности приближенного значения
- Уметь находить абсолютную и относительную погрешность приближенного значения
Разминка
- Округлите до сотых число:
а) 5,113; б) 5,124; в) 5,553; г) 5,067.
Абсолютная погрешность приближенного значения
На практике в вычислениях используют, как правило, десятичные дроби с ограниченным числом десятичных знаков. Если дробь бесконечная или с большим количеством десятичных знаков, ее округляют. Так число π выражается бесконечной десятичной непериодической дробью 3,1415926… В зависимости от задачи его округляют до десятых, сотых, тысячных и т.д. И тогда получают приближенные значения: 3,1; 3,14; 3,142 и т.д.
По графику функции y=x2 можно найти приближенные значения этой функции при x=1,6 и x=2,3: если x=1,6, то y≈2,6; если x=2,3, то y≈5,3.
Точные значения квадратов чисел:
если x=1,6, то y=1,62=2,56; если x=2,3, то y=2,32=5,29.
В первом случае отличие приближенного значения от точного значения равно 0,04, во втором – 0,01:
2,6-2,56=0,04; 5,3-5,29=0,01.
Абсолютной погрешностью
приближенного значения называют модуль разности точного и приближенного значений.
Так, в рассмотренном примере абсолютная погрешность определяется следующим образом:
|2,56-2,6|=|-0,04|=0,04; |5,29-5,3|=|-0,01|=0,01.
Найти абсолютную погрешность не всегда возможно. Например, при измерении длины отрезка с помощью линейки мы можем сказать, что абсолютная погрешность не превосходит цены деления. Цена деления обычной линейки 0,1 см, поэтому абсолютная погрешность приближенного значения не больше 0,1.
Если x≈a и абсолютная погрешность этого приближенного значения не превосходит некоторого числа h, то число a называют приближенным значением x с точностью до h.
Пишут:
x≈a с точностью h.
Обычно используют другую запись:
x=a±h.
Эта запись означает, что
a-h≤x≤a+h.
Например, если x=15±0,2, то 14,8≤x≤15,2.
Точность приближенного значения зависит от многих причин. На практике в процессе измерения, его точность зависит от прибора, с помощью которого выполнялось измерение, от его точности.
1. Округлите числа 1,526; 13,56; 5,753 до десятых и найдите абсолютную погрешность каждого из приближенных значений.
2. Приближенное значение числа x равно a. Найдите абсолютную погрешность приближения, если:
а) x=3,76; a=3,8; б) x=9,653; a=9,7; в) x=38,1; a=38;
г) x=26,48; a=26.
3. Запишите в виде двойного неравенства:
а) x=7±1; б) x=27±3; в) x=23±0,1; г) x=16,5±0,5;
д) x=5,82±0,01; е) x=30,42±0,05.
Относительная погрешность приближенного значения
Допустим, мы измерили толщину h монеты и ее диаметр d в сантиметрах:
h=0,2±0,1; d=2,5±0,1
Тогда качество измерения можно оценить как отношение точности измерения к приближенному значению: для толщины 0,10,2=0,5, а для диаметра 0,12,5=0,04. Чем меньше отношение, тем точнее измерение.
Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения.
Относительную погрешность принято выражать в процентах:
|x-aa|⋅100%.
Тогда 0,10,2⋅100%=50%, 0,12,5⋅100%=4%. Тогда говорят, что измерение толщины выполнено с относительной точностью до 50%, а измерение диаметра — с относительной точностью до 4%. Качество второго измерения значительно выше, чем первого.
Округлите число до единиц и найдите относительную погрешность округления (в процентах):
а) 2,1; б) 5,12; в) 9,736; г) 49,54.
1. Что называется абсолютной погрешностью приближенного значения? Поясните смысл записи x=a±h.
2. Что называется относительной погрешностью приближенного значения?
Ответы
Упражнение 1
1. 0,026; 0,04; 0,047.
2. а) 0,04; б) 0,047; в) 0,1; г) 0,48.
3. Запишите в виде двойного неравенства:
а) 6≤x≤8; б) 24≤x≤30; в) 22,9≤x≤23,1; г) 16≤x≤17; д) 5,81≤x≤5,83;
е)30,37≤x≤30,47.
Упражнение 2
а) 5%; б) 2,4%; в) 2,64%; г) 0,92%.
Содержание:
- Приближённые вычисления
- Абсолютная и относительная погрешности
- Выполнение действий над приближёнными числами
- Выполнение действий без точного учёта погрешности
Приближённые вычисления
Приближённые вычисления — вычисления, в которых данные и результат (или только результат) являются числами, приближенно представляющими истинные значения соответствующих величин. Числовые данные, полученные измерением реальных объектов, редко бывают точными значениями соответствующей величины, а обычно имеют некоторую погрешность
Абсолютная и относительная погрешности
При решении практических задач часто приходится иметь дело с приближёнными значениями разных числовых величин. К ним относятся: результаты измерения разных величин с помощью приборов; значения полученные при считывании на графиках, диаграммах, номограммах; проектные данные; результаты округления чисел; результаты действий над приближёнными числами; табличные значения некоторых величин; результаты вычислений значений функции. Приближённые значения (приближение, приближённые числа) могут значительно отличаться от точных, либо быть близкими к ним.
Для оценки отклонения приближённых чисел от точных используют такие понятия как абсолютная и относительная погрешности.
Абсолютной погрешностью приближённой называется модуль разности между точным значением величины 
Пример.
Абсолютная погрешность приближённого числа 
Если точное число неизвестно, то найти абсолютную погрешность 

При записи приближённых чисел часто используют понятия верной и сомнительной цифры.
Цифра 
Например: в числе 

В конечной записи приближённого числа сохраняют только верные цифры. Так число 



Например: если 
Если в целом числе последние нули являются сомнительными, их исключают из записи числа.
Именно поэтому при работе с приближёнными числами широко используют стандартную форму записи числа.
Например: в числе 
Следовательно, в десятичной записи приближённого числа последняя цифра указывает на точность приближённости, то есть предел абсолютной погрешности не превышает единицу последнего разряда.
Например:
1. Запись 

2. Запись
3. Если
В десятичной записи числа значимыми цифрами называются все его верные цифры начиная с первой слева, отличной от нуля.
Например: в числе 1,13 — три значимых цифры, в числе 0,017 — две, в числе 0,303 — три, в числе 5,200 — четыре, в числе 25*103 — две значимых цифры.
При таком подходе к записи приближенного числа необходимо уметь округлять числа.
Правила округления чисел:
— Если первая цифра, которую отбрасываем является меньше пяти, то в основном разряде, который сохраняется цифра не меняется. Например: 879,673≈879,67.
— Если первая цифра, которую отбрасываем больше пяти, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 456,87≈456,9.
— Если первая цифра, которая отбрасывается пять и за ней есть ещё отличны от нуля, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 1246,5002≈1247.
— Если первая цифра, которая отбрасывается — пять и за ней нет больше никаких цифра, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 0,275≈0,28; 1,865≈1,86.
Абсолютная погрешность не полностью характеризует точность приближения. Например, 
Относительной погрешностью 


Поскольку абсолютная погрешность 
Число 
Предел относительной погрешности можно вычислить по формуле:
Конечно относительная погрешность выражается в процентах.
С помощью относительной погрешности легко установить точность приближённости.
Пример 1. Найти относительную погрешность числа
Решение: Имеем
Следовательно
Пример 2. Сравнить точность измерения толщины книги d (см) и высоты стола H (см), если известно, что 
Решение:
Как видим, точность измерения высоты стола значительно выше.
Выполнение действий над приближёнными числами
Результат арифметических действий над приближёнными числами является также приближённым числом.
Необходимо уметь устанавливать погрешности результатов вычислений. Их находят с точным и без точного учёта погрешностей исходных данных. Правила нахождения погрешностей результатов действий с точным учётом погрешности приведены в таблице (обозначения – 


Пример 3. Вычислить приближение значения выражения 
Решение: находим значение квадрата числа 5,62 и квадратного корня из числа 18,50.
Найдём границу относительной погрешности результата:
Граница абсолютной погрешности результата:
Ответ:
Пример 4. Вычислить приближение значения выражения 
Решение: находим значение квадратного корня из числа 6,24 и 
Граница относительной погрешности результата:
Граница абсолютной погрешности результата:
Ответ:
Выполнение действий без точного учёта погрешности
Точный учёт погрешности усложняет вычисление. Поэтому, если не надо учитывать погрешность промежуточных результатов, можно использовать более простые правила.
Сложение и вычитание приближённых вычислений рекомендуется выполнять так:
а) выделить слагаемое с наименьшим числом верных десятичных знаков;
б) округлить другие слагаемые так, чтобы каждое из них содержало на один десятичный знак больше чем выделенное;
в) выполнить действия, учитывая все сохранённые десятичные знаки;
г) результаты округлить и сохранить столько десятичных знаков, сколько их есть в приближённом числе с наименьшим числом десятичных знаков.
Умножение и деление приближённых вычислений рекомендуется выполнять так:
а) выделить среди данных чисел, число с наименьшим количеством верных значимых цифр;
б) округлить оставшиеся данные так, чтобы каждое из них содержало на одну значащую цифру больше, чем в выделенном;
в) выполнить действия — сохранить все значимые цифры;
г) сохранять в результате столько значащих цифр, сколько их имеет выделенное число с наименьшим количеством верных значимых цифр.
При возведении в степень приближённого числа в результате сохраняют столько значимых цифр, сколько верных значимых цифр имеет основа степени.
При извлечении корня из приближённого числа в результате сохраняют столько верных цифр, сколько имеет подкоренное число.
Лекции:
- Уравнение сферы
- Пределы: примеры решения
- Площадь поверхности конуса
- Целые рациональные выражения
- Числовые ряды. Числовой ряд. Сумма ряда
- Свойства логарифмов
- Линейные дифференциальные уравнения первого порядка
- Скрещивающиеся прямые
- Скалярное призведение двух векторов
- Теоремы, связанные с понятием производной
Автор: Софронова Наталия Андреевна,
учитель математики МОУ «Упшинская ООШ»
Оршанского района Республики Марий Эл
( К учебнику Ю.А.Макарычева Алгебра 8)
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
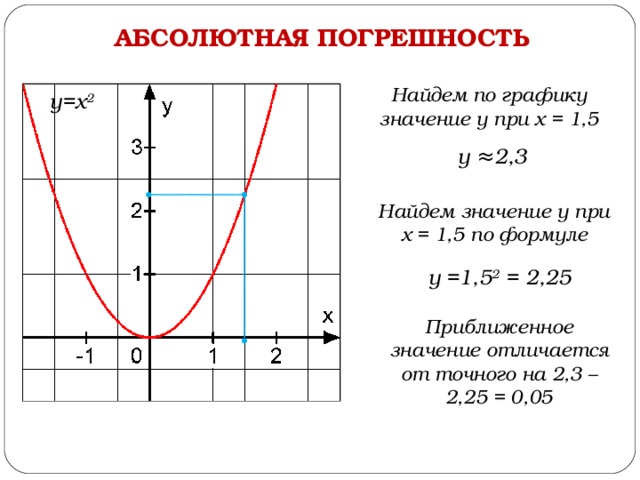
Найдем по графику значение у при х = 1,5
у=х 2
у ≈2,3
Найдем значение у при х = 1,5 по формуле
у =1,5 2 = 2,25
Приближенное значение отличается от точного на 2,3 – 2,25 = 0,05
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
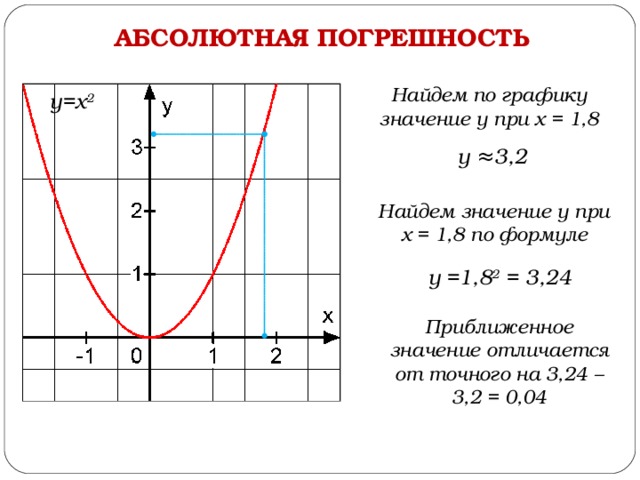
Найдем по графику значение у при х = 1,8
у=х 2
у ≈3,2
Найдем значение у при х = 1,8 по формуле
у =1,8 2 = 3,24
Приближенное значение отличается от точного на 3,24 – 3,2 = 0,04
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
х
1,5
Точное значение у
(по формуле)
1,8
2,25
Приближенное значение у (по графику)
3,24
2,3
3,2
у=х 2
Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.
у = 2,3 А.П. = |2,25 – 2,3| = |- 0,0 5| = 0,05
у = 3,2 А.П. = |3,24 – 3,2| = | 0,0 4| = 0,04
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.
Пример 1 . Старинная русская мера массы пуд равна 16,38. Округлите это значение до целых и найдите абсолютную погрешность приближенного значения.
Решение. 1 6 ,38 ≈ 16
16,38 – точное значение;
16 – приближенное значение.
А.П. = | 16,38 – 16 | = |0 ,38 | = 0, 38
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.
Пример 2 . Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков и найдите абсолютную погрешность приближенного значения.
Решение. 10 6 7 ≈ 1070
1067 – точное значение;
1070 – приближенное значение.
А.П. = | 1067 – 1070 | = |-3| = 3
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
Определение. Абсолютной погрешностью приближенного значения называют модуль разности точного и приближенного значений.
Пример 3 . Старинная русская мера длины сажень равна 2,13 м. Округлите это значение до десятых и найдите абсолютную погрешность приближенного значения.
Решение. 2, 1 3 ≈ 2,1
2,13 – точное значение;
2,1 – приближенное значение.
А.П. = | 2,13 – 2,1 | = | 0,03 | = 0,03
АБСОЛЮТНАЯ ПОГРЕШНОСТЬ
Пример 4 . Представьте дробь в виде бесконечной периодической дроби. Округлите результат до сотых и найдите абсолютную погрешность приближенного значения.
Решение.
ТОЧНОСТЬ ПРИБЛИЖЕНИЯ
Всегда ли можно найти абсолютную погрешность ?
АВ ≈ 5,3 см
Найдем длину отрезка АВ
А
В
Точного значения длины отрезка АВ мы определить не можем, поэтому и абсолютную погрешность приближенного значения найти невозможно.
В подобных случаях в качестве погрешности указывают такое число, больше которого абсолютная погрешность быть не может.
В нашем примере в качестве такого числа можно взять число 0,1.
ПОЧЕМУ? Цена деления линейки равна 0,1 см и поэтому абсолютная погрешность приближенного значения 5,3 не больше 0,1.
ТОЧНОСТЬ ПРИБЛИЖЕНИЯ
А
В
Говорят, что число 5,3 есть приближенное значение длины отрезка АВ (в санти-метрах) с точностью до 0,1
АВ ≈ 5,3 см
t ≈ 28 0 с точностью до 1
t ≈ 14 0 с точностью до 2
Определите точность приближенных значений величин, полученных при измерении приборами, изображенными на рисунках 1- 4
Рис.2
Рис.1
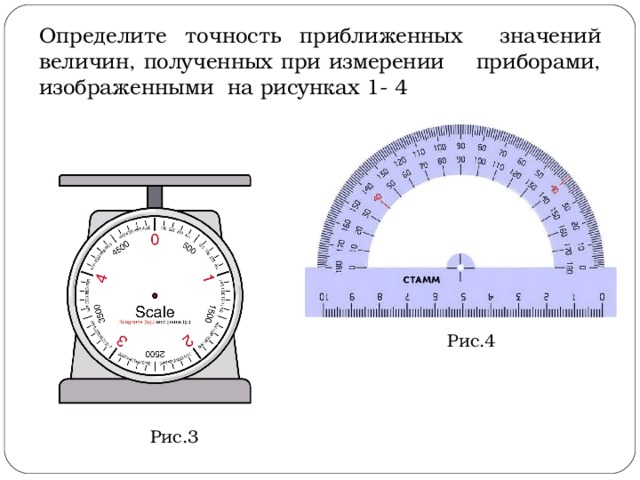
Определите точность приближенных значений величин, полученных при измерении приборами, изображенными на рисунках 1- 4
Рис.4
Рис.3
ТОЧНОСТЬ ПРИБЛИЖЕНИЯ
Говорят, что число 5,3 есть приближенное значение длины отрезка АВ (в сантиметрах) с точностью до 0,1
АВ ≈ 5,3 см
Если х ≈ а и абсолютная погрешность приближенного значения не превосходит некоторого числа h , то число а называют приближенным значением х с точностью до h
х ≈ а с точностью до h
х = а ± h
Длина рулона 10,5 ± 0,5
ТОЧНОСТЬ ПРИБЛИЖЕНИЯ
А
В
АВ ≈ 5,3 см
с точностью до 0,1
t ≈ 28 0 с точностью до 1
t ≈ 14 0
с точностью до 2
Определение . Относительной погрешностью (точностью) приближенного значения называется отношение абсолютной погрешности (точности) к модулю приближенного значения
Для оценки качества измерения можно использовать определения относительной погрешности и относительной точности
l = 100,0 ± 0,1
b = 0,4 ± 0,1
ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ
Определение . Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения
Пример 5 . Старинная русская мера массы пуд равна 16,38. Округлите это значение до целых и найдите относительную погрешность приближенного значения.
Решение. 1 6 ,38 ≈ 16
16,38 – точное значение;
16 – приближенное значение.
А.П. = | 16,38 – 16 | = |0 ,38 | = 0, 38
ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ
Определение . Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения
Пример 6 . Старинная русская мера длины верста равна 1067 м. Округлите это значение до десятков и найдите относительную погрешность приближенного значения.
Решение. 10 6 7 ≈ 1070
1067 – точное значение;
1070 – приближенное значение.
А.П. = | 1067 – 1070 | = |-3| = 3
ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ
Пример 7 . Представьте дробь в виде бесконечной периодической дроби. Округлите результат до сотых и найдите относительную погрешность приближенного значения.
Решение.