Как найти ток через плотность тока - Сайт, где вы сможете решить свои вопросы

Сила тока I для тока, протекающего через некоторую площадь сечения проводника S эквивалентна производной заряда q по времени t и количественно характеризует электрический ток.

Определение 1

Таким образом выходит, что сила тока — это поток заряженных частиц через некоторую поверхность S.

Определение 2

Электрический ток является процессом движения как отрицательных, так и положительных зарядов.

Перенос заряда одного знака в определенную сторону равен переносу заряда, обладающего противоположным знаком, в обратном направлении. В ситуации, когда ток образуется зарядами и положительного, и отрицательного знаков (dq+ и dq−), справедливым будет заключение о том, что сила тока равна следующему выражению:

I=dq+dt+dq-dt.

В качестве положительного определяют направление движения положительных зарядов. Ток может быть постоянным, когда ни сила тока, ни его направление не претерпевают изменений с течением времени, или, наоборот, переменным. При условии постоянства, формула силы тока может выражаться в следующем виде:

I=q∆t,

где сила тока определена в качестве заряда, который пересекает некоторую поверхность S в единицу времени. В системе СИ роль основной единицы измерения силы тока играет Ампер (А).

1A=1 Кл1 с.

Плотность тока. Связь плотности тока с зарядом и силой тока, напряженностью

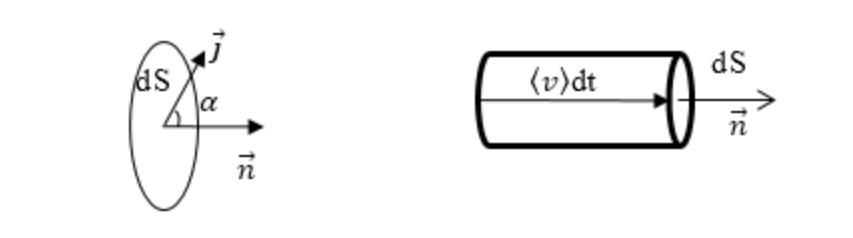
Выделим в проводнике, в котором протекает ток, малый объем dV случайной формы. С помощью следующего обозначения υ определим среднюю скорость движения носителей зарядов в проводнике. Пускай n0 представляет собой концентрацию носителей заряда. На поверхности проводника выберем пренебрежительно малую площадку dS, которая расположена ортогонально скорости υ (рис. 1).

Рисунок 1

Проиллюстрируем на поверхности площадки dS очень короткий прямой цилиндр, имеющий высоту υdt. Весь массив частиц, которые располагались внутри такого цилиндра за время dt пересекут плоскость dS и перенесут через нее, в направлении скорости υ, заряд, выражающийся в виде следующего выражения:

dq=n0qeυdSdt,

где qe=1,6·10-19 Кл является зарядом электрона, другими словами отдельной частицы или же носителя тока. Разделим приведенную формулу на dSdt и получим:

j=dqdSdt,

где j представляет собой модуль плотности электрического тока.

j=n0qeυ,

где j является модулем плотности электрического тока в проводнике, в котором заряд переносится электронами. В случае, если ток появляется как результат движения нескольких типов зарядов, то формула плотности тока может быть определена в виде следующего выражения:

j=∑niqiυii,

где i представляет собой носитель заряда. Плотность тока — это векторная величина. Снова обратим внимание на рисунок 1. Пускай n→ представляет собой единичный перпендикуляр к плоскости dS. В случае, если частицы, переносящие заряд, являются положительными, то переносимый ими заряд в направлении нормали больше нуля. В общем случае переносимый в единицу времени элементарный заряд может быть записана в следующем виде:

dqdt=j→n→dS=jndS.

Формула приведенная выше справедлива также в том случае, когда плоскость площадки dS неортогональная по отношению к вектору плотности тока. По той причине, что составляющая вектора j→, направленная под прямым углом к нормали, через сечение dS электричества не переносит. Исходя из всего вышесказанного, плотность тока в проводнике окончательно запишем, применяя формулу j=n0qeυ в таком виде:

j→=-n0qeυ→.

Таким образом, плотность тока эквивалентна количеству электричества, другими словами заряду, который протекает за одну секунду через единицу сечения проводника. В отношении однородного цилиндрического проводника справедливым будет записать, что:

j=IS∆t,

где S играет роль площади сечения проводника. Плотность постоянного тока равна по всей площади сечения проводника. Для двух разных сечений проводника (S1,S2) с постоянным током справедливо следующее равенство:

j1j2=S2S1.

Основываясь на законе Ома для плотности токов можно записать такое выражение:

j→=λE→,

где λ обозначает коэффициент удельной электропроводности. Определив плотность тока, мы имеем возможность выразить силу тока в следующем виде:

I=∫SjndS,

где интегрирование происходит по всей поверхности S любого сечения проводника. Единица плотности тока Aм2.

Линии тока

Определение 3

Линии, вдоль которых движутся заряженные частицы, носят название линий тока.

Направления движения положительных зарядов также определяются в качестве направлений линий тока. Изобразив линии тока, можно получить наглядное представление о движении электронов и ионов, которые формируют собой ток. Если внутри проводника выделить трубку с током, у которой боковая поверхность состоит из линий тока, то движущиеся заряженные частицы не будут пересекать боковую поверхность данной трубки. Такую трубка представляет собой так называемую трубку тока. К примеру, поверхность металлической проволоки в изоляторе будет определяться как труба тока.

Пример 1

Сила тока в проводнике равномерно возрастает от 0 до 5 А на протяжении 20 с. Определите заряд, который прошел через поперечное сечение проводника за данный отрезок времени.

Решение

В качестве основы решения данной задачи возьмем формулу, которая характеризует собой силу тока, то есть:

I=dqdt.

Таким образом, заряд будет найден как:

q=∫t1t2Idt.

В условии задачи сказано, что сила тока изменяется равномерно, а это означает то, что мы можем записать закон изменения силы тока в следующем виде:

I=kt.

Найдем коэффициент пропорциональности в приведенном выражении, для чего необходимо запишем закон изменения силы тока еще раз для момента времени, при котором сила тока эквивалентна I2=3А (t2):

I2=kt2→k=I2t2.

Подставим выражение выше в I=kt и проинтегрируем в соответствии с q=∫t1t2Idt, получим формулу такого вида: q=∫t1t2ktdt=∫t1t2I2t2tdt=I2t2∫t1t2tdt=t22t1t2=I22t2t22-t12.

В качестве начального момента времени возьмем момент, когда сила тока эквивалентна нулю, другими словами t1=0, I1=0 A; t2=20, I2=5 А. Проведем следующие вычисления:

q=I22t2t22=I2t22=5·202=50 (Кл).

Ответ: q=50 Кл.

Пример 2

Определите среднюю скорость движения электронов в проводнике, молярная масса вещества которого эквивалентна μ, поперечное сечение проводника S. Сила тока в проводнике I. Примем, что на каждый атом вещества в проводнике приходится два свободных электрона.

Решение

Силу тока (I) в проводнике можно считать постоянной, что позволяет нам записать следующее выражение:

I=q∆t=Nqe∆t,

где заряд q определим как произведение числа электронов проводимости в проводнике, на заряд одного электрона qe, представляющего собой известную величину. ∆t играет роль промежутка времени, за который через поперечное сечение проводника проходит заряд q. Найти N можно, если применять известное в молекулярной физике соотношение:

N’NА=mμ=ρVμ,

где N′ играет роль количества атомов в проводнике, объем которого V, плотность ρ, а молярная масса μ. NA представляет собой число Авогадро. По условию задачи N=2N′. Найдем из N’NА=mμ=ρVμ число свободных электронов: N=2ρVμNA.

Подставим выражение, приведенное выше, в I=q∆t=Nqe∆t, в результате чего получим:

I=2ρVμNAqe∆t=2ρqeNASlμ∆t,

где объем проводника найден как V=Sl, где l – длина проводника. Выразим ее.

l=μ∆tI2ρqeNAS.

Среднюю скорость движения электронов или, другими словами, скорость тока в проводнике можно определить следующим образом: υ=l∆t=μI2ρqeNAS.

Ответ: υ=μI2ρqeNAS.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 июля 2021 года; проверки требуют 5 правок.

Плотность тока

Размерность	L⁻²I
Единицы измерения
СИ	А/м²
Примечания
векторная величина

Пло́тность то́ка — векторная физическая величина, характеризующая плотность потока электрического заряда в рассматриваемой точке. В СИ измеряется в Кл/м²/c или, что то же самое, А/м².

Если все носители заряда имеют одинаковый заряд , плотность тока вычисляется по формуле

где (м^-3) — концентрация носителей, а vec{v} — средняя скорость их движения. В более сложных случаях производится суммирование по носителям разных сортов.

Плотность тока имеет технический смысл силы электрического тока, протекающего через элемент поверхности единичной площади^[1]. При равномерном распределении плотности тока и сонаправленности её с нормалью к поверхности, через которую протекает ток, для величины вектора плотности тока выполняется:

${displaystyle j=|{vec {j}}|={frac {I}{S}}}$

где I — сила тока через поперечное сечение проводника площадью S. Иногда говорится о скалярной^[2] плотности тока, в таких случаях под ней подразумевается величина в формуле выше.

Варианты вычисления плотности тока[править | править код]

В простейшем предположении, что все носители тока (заряженные частицы) двигаются с одинаковым вектором скорости {vec v} и имеют одинаковые заряды (такое предположение может иногда быть приближенно верным; оно позволяет лучше всего понять физический смысл плотности тока), а концентрация их ,

${displaystyle {vec {j}}=n,q,{vec {v}}=rho _{q}{vec {v}},}$

где ${displaystyle rho _{q}}$ — плотность заряда этих носителей. Направление вектора vec j соответствует направлению вектора скорости {vec v} , с которой движутся заряды, создающие ток, если q положительно. В реальности даже носители одного типа движутся вообще говоря и как правило с различными скоростями. Тогда под следует понимать среднюю скорость.

В сложных системах (с различными типами носителей заряда, например, в плазме или электролитах)

${displaystyle {vec {j}}=sum _{s}n_{s}q_{s}{vec {v}}_{s}}$

то есть вектор плотности тока есть сумма плотностей тока по всем разновидностям (сортам) подвижных носителей; где n_s — концентрация частиц, ${displaystyle q_{s}}$ — заряд частицы, ${displaystyle {vec {v}}_{s}}$ — вектор средней скорости частиц -го сорта.

Выражение для общего случая может быть записано также через сумму по всем индивидуальным частицам из некоторого малого объёма , содержащего рассматриваемую точку:

${displaystyle {vec {j}}={frac {1}{V}}sum _{i}q_{i}{vec {v}}_{i}}$

Сама формула почти совпадает с формулой, приведенной чуть выше, но теперь индекс суммирования i означает не номер типа частицы, а номер каждой индивидуальной частицы, не важно, имеют они одинаковые заряды или разные, при этом концентрации оказываются уже не нужны.

Плотность тока и сила тока[править | править код]

Связь между током и плотностью тока

В общем случае сила тока (полный ток) может быть рассчитана исходя из плотности тока по формуле

${displaystyle I=left|int limits _{S}({vec {j}}cdot d{vec {S}})right|=left|int limits _{S}j_{n},dSright|}$

где j_n — нормальная (ортогональная) составляющая вектора плотности тока по отношению к элементу поверхности площадью ; вектор — специально вводимый вектор элемента поверхности, ортогональный элементарной площадке и имеющий абсолютную величину, равную её площади, позволяющий записать подынтегральное выражение как обычное скалярное произведение. Обратное нахождение плотности тока по известной силе тока невозможно; в предположении равноплотного токопротекания перпендикулярно площадке будет .

Сила тока представляет собой поток вектора плотности тока через заданную фиксированную поверхность. Часто в качестве такой поверхности рассматривается поперечное сечение проводника.

Величиной плотности тока обычно оперируют при решении физических задач, в которых анализируется движение заряженных носителей (электронов, ионов, дырок и других). Напротив, использование силы тока удобнее в задачах электротехники, особенно когда рассматриваются электрические цепи с сосредоточенными элементами.

Плотность тока и законы электродинамики[править | править код]

Величина плотности тока фигурирует в ряде важнейших формул классической электродинамики, некоторые из них представлены ниже.

Уравнения Максвелла[править | править код]

Плотность тока в явном виде входит в одно из четырёх уравнений Максвелла, а именно в уравнение для ротора напряжённости магнитного поля

${displaystyle nabla times {vec {H}}={vec {j}}+{frac {partial {vec {D}}}{partial t}}}$

физическое содержание которого в том, что вихревое магнитное поле порождается электрическим током, а также изменением электрической индукции ; значок partial обозначает частную производную (по времени ). Это уравнение приведено здесь в системе СИ.

Уравнение непрерывности[править | править код]

Уравнение непрерывности выводится из уравнений Максвелла и утверждает, что дивергенция плотности тока равна изменению плотности заряда со знаком минус, то есть

${displaystyle nabla cdot {vec {j}}+{partial rho _{q} over partial t}=0}$

Закон Ома в дифференциальной форме[править | править код]

В линейной и изотропной проводящей среде плотность тока связана с напряжённостью электрического поля в данной точке по закону Ома (в дифференциальной форме):

где sigma — удельная проводимость среды, vec E — напряжённость электрического поля. Или:

${displaystyle {vec {j}}={frac {1}{rho }},{vec {E}}}$

где rho — удельное сопротивление.

В линейной анизотропной среде имеет место такое же соотношение, однако удельная электропроводность sigma в этом случае, вообще говоря, должна рассматриваться как тензор, а умножение на неё — как умножение вектора на матрицу.

Плотность тока и мощность[править | править код]

Работа, совершаемая электрическим полем над носителями тока, характеризуется^[3] плотностью мощности [энергия/(время•объем)]:

{displaystyle w={vec {E}}cdot {vec {j}}}

где точкой обозначено скалярное произведение.

Чаще всего эта мощность рассеивается в среду в виде тепла, но вообще говоря она связана с полной работой электрического поля и часть её может переходить в другие виды энергии, например такие, как энергия того или иного вида излучения, механическая работа (особенно — в электродвигателях) и т. д.

С использованием закона Ома формула для изотропной среды переписывается как

${displaystyle w=sigma E^{2}={frac {j^{2}}{sigma }}equiv rho j^{2}}$

где sigma и rho — скаляры. Для анизотропного случая будет

{displaystyle w={vec {E}}sigma {vec {E}}={vec {j}}rho {vec {j}}}

где подразумевается матричное умножение (справа налево) вектора-столбца на матрицу и на вектор-строку, а тензор sigma и тензор rho порождают соответствующие квадратичные формы.

4-вектор плотности тока[править | править код]

Основная статья: 4-ток

В теории относительности вводится четырёхвектор плотности тока (4-ток), составленный из объёмной плотности заряда ${displaystyle rho _{q}}$ и 3-вектора плотности тока vec{j}:

${displaystyle J^{mu }=(crho _{q},{vec {j}}),}$

где — скорость света.

4-ток является прямым и естественным обобщением понятия плотности тока на четырёхмерный пространственно-временной формализм и позволяет, в частности, записывать уравнения электродинамики в ковариантном виде.

Примечания[править | править код]

↑ Тур А. В., Яновский В. В. Плотность электрического тока // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 639. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
↑ Чаще в таких случаях она даже не называется явно скаляром, но просто не упоминается её векторный характер.
↑ Это прямо следует из формул, приведенных выше вкупе с определением работы или с формулой мощности .

Источник

В электродинамике
— разделе учения об электричестве, в
котором рассматриваются явления и
процессы, обусловленные движением
электрических зарядов или макроскопических
заряженных тел, — важнейшим понятием
является понятие электрического тока.
Электрическим
током
называется любое упорядоченное
(направленное) движение электрических
зарядов. В проводнике под действием
приложенного электрического поля Е
свободные электрические заряды
перемещаются: положительные — по полю,
отрицательные — против поля (рис. 146,
а),
т. е. в проводнике возникает электрический
ток, называемый током
проводимости.
Если же упорядоченное движение
электрических зарядов осуществляется
перемещением в пространстве заряженного
макроскопического тела (рис. 146, б),
то возникает так называемый конвекционный
ток.

Для возникновения
и существования электрического тока
необходимо, с одной стороны, наличие
свободных носителей
тока —
заряженных частиц, способных перемещаться
упорядоченно, а с другой — наличие
электрического поля,
энергия которого, каким-то образом
восполняясь, расходовалась бы на их
упорядоченное движение. За направление
тока условно
принимают направление движения
положительных
зарядов.

Количественной
мерой электрического тока служит сила
тока I
скалярная
физическая величина, определяемая
электрическим зарядом, проходящим через
поперечное сечение проводника в единицу
времени:

Если сила тока и
его направление не изменяются со
временем, то такой ток называется
постоянным.
Для постоянного тока

где Q
— электрический
заряд, проходящий за время t
через поперечное сечение проводника.
Единила силы тока — ампер (А).

Физическая величина,
определяемая силой тока, проходящего
через единицу площади поперечного
сечения проводника, перпендикулярного
направлению тока, называется плотностью
тока:

Выразим силу и
плотность тока через скорость v
упорядоченного движения зарядов в
проводнике. Если концентрация носителей
тока равна n
и каждый носитель имеет элементарный
заряд е
(что не обязательно для ионов), то за
время dt
через поперечное сечение S
проводника переносится заряд dQ=ne
v
S
dt.
Сила тока

а плотность тока

(96.1)

Плотность тока —
вектор,
ориентированный по направлению тока,
т. е. направление вектора j
совпадает с направлением упорядоченного
движения положительных зарядов. Единица
плотности тока — ампер на метр в квадрате
(А/м²).

Сила тока сквозь
произвольную поверхность S
определяется как поток вектора j,
т. е.

(96.2)

где dS=ndS
(n
— единичный вектор нормали к площадке
dS,
составляющей с вектором j
угол ).

16. Сторонние силы. Электродвижущая сила и напряжение

Если в цепи на
носители тока действуют только силы

электростатического
поля, то происходит перемещение носителей
(они предполагаются положительными) от
точек с большим потенциалом к точкам с
меньшим потенциалом. Это приведет к
выравниванию потенциалов во всех
точках цепи и к исчезновению электрического
поля. Поэтому для существования
постоянного тока необходимо наличие в
цепи устройства, способного создавать
и поддерживать разность потенциалов
за счет работы сил неэлектростатического
происхождения. Такие устройства
называются
источниками тока.
Силы неэлектростатического
происхождения,
действующие на заряды со стороны
источников тока, называются
сторонними.

Природа сторонних
сил может быть различной. Например, в
гальванических элементах они возникают
за счет энергии химических реакций
между электродами и электролитами; в
генераторе — за счет механической
энергии вращения ротора генератора и
т. п. Роль источника тока в электрической
цепи, образно говоря, такая же, как роль
насоса, который необходим для перекачивания
жидкости в гидравлической системе. Под
действием создаваемого поля сторонних
сил электрические заряды движутся
внутри источника тока против сил
электростатического поля, благодаря
чему на концах цепи поддерживается
разность потенциалов и в цепи течет
постоянный электрический ток.

Сторонние силы
совершают работу по перемещению
электрических зарядов. Физическая
величина, определяемая работой,
совершаемой сторонними силами при
перемещении единичного положительного
заряда, называется
электродвижущей силой
(э.д.с.),
действующей
в цепи:

(97.1)

Эта работа
производятся за счет энергии, затрачиваемой
в источнике тока, поэтому величину
можно также называть электродвижущей
силой источника тока, включенного в
цепь. Часто, вместо того чтобы сказать:
«в цепи действуют сторонние силы»,
говорят: «в цепи действует э.д.с.», т. е.
термин «электродвижущая сила»
употребляется как характеристика
сторонних сил. Э.д.с., как и потенциал,
выражается в вольтах (ср. (84.9) и (97.1)).

Сторонняя сила
F_ст,
действующая на заряд Q₀,
может быть выражена как

где Е
— напряженность поля сторонних сил.
Работа же сторонних сил по перемещению
заряда Q₀
на замкнутом участке цепи равна

(97.2)

Разделив (97.2) на
Q₀,
получим выражение для э. д. с., действующей
в цепи:

т. е. э.д.с., действующая
в замкнутой цепи, может быть определена
как циркуляция вектора напряженности
поля сторонних сил. Э.д.с., действующая
на участке 1—2,
равна

(97.3)

На заряд Q₀
помимо сторонних сил действуют также
силы электростатического поля F_e=Q₀E.
Таким образом, результирующая сила,
действующая в цепи на заряд Q₀,
равна

Работа, совершаемая
результирующей силой над зарядом Q₀
на участке 1—2,
равна

Используя выражения
(97.3) и (84.8), можем записать

(97.4)

Для замкнутой цепи
работа электростатических сил равна
нулю (см. § 83), поэтому в данном случае

Напряжением
U
на участке 1—2
называется физическая величина,
определяемая работой, совершаемой
суммарным полем электростатических
(кулоновских) и сторонних сил при
перемещении единичного положительного
заряда на данном участке цепи. Таким
образом, согласно (97.4),

Понятие напряжения
является обобщением понятия разности
потенциалов: напряжение на концах
участка цепи равно разности потенциалов
в том случае, если на этом участке не
действует Э.д.с., т. е. сторонние силы
отсутствуют.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В этой статье мы познакомим вас с плотностью электрического тока. Мы объясним, почему это величина важна в электротехнике, покажем ее формулу, а также проведем несколько примеров расчетов.

Простое объяснение

Плотность тока J — векторная физическая величина, характеризующая плотность потока электрического заряда в рассматриваемой точке.

Википедия

Высокая плотность электрического тока вызывает нагрев кабеля. Поэтому необходимо следить за тем, чтобы не превысить допустимую допустимую силу тока в линии или проводнике. Кроме того, эффективное сечение проводника может уменьшаться при воздействии высокочастотных сигналов (скин-эффект), что увеличивает плотность тока. Поэтому при выборе проводника необходимо учитывать не только фактический ток, но и частоту сигнала.

Формулы

Как уже упоминалось выше, плотность тока J описывает отношение электрического тока к площади, через которую он протекает, то есть: J = I / S . Здесь J — плотность тока, I — сила тока, S — площадь поперечного сечения.

Единица измерения — соответственно амперы на квадратный метр, то есть [ J ] = А / м² .

Однако часто плотность тока также указывают в амперах на квадратный миллиметр ( А / мм² ), поскольку сечения обычных проводников (проводов, кабелей) имеют такой порядок величины.

Пример расчёта

В общем случае для расчета плотности тока учитываются геометрические свойства кабеля. На их основе можно сначала рассчитать площадь поперечного сечения, а затем, при известной силе тока, плотность тока.

Медный провод

Ниже приводится расчет плотности тока для медного провода диаметром 1 мм, по которому течет ток 8 А. Предполагается, что линия имеет круглое поперечное сечение.

Сначала рассчитаем площадь поперечного сечения провода, зная, что его диаметр d = 1 мм:

S = r² * π = π * d² / 4 = π * 1² / 4 = 0, 785 мм² .

Тогда плотность тока J может быть рассчитана по приведенной выше формуле. Для тока I = 8А и площади поперечного сечения S = 0,785 мм² получаем: J = 8 / 0,785 = 10, 2 А / мм² .

Токопроводящие дорожки

В отличие от кабеля, сечение токопроводящей дорожки не круглое, а прямоугольное. Здесь мы рассматриваем медную проводниковую дорожку шириной 0,5 мм и толщиной 0,035 мм.

Рис. 1. Расчёт плотности тока в токопроводящей дорожке

Вы можете рассчитать площадь прямоугольного поперечного сечения токопроводящей дорожки, умножив ширину токопроводящей дорожки на толщину меди: S = 0,5 * 0,035 = 0,0175 мм² .

Для тока I, равного 200 мА, плотность тока J составляет: J = I / S = 0,2 / 0,0175 = 11,43 А / мм² .

Применение

Плотность тока особенно важна в тех случаях, когда необходимо оптимизировать сечение проводника по соображениям стоимости, площади и веса. Как правило, сечение проводника выбирается как можно меньше, чтобы соответствовать условиям применения.

Здесь важно, чтобы фактическая плотность тока в проводнике не превышала максимально допустимую плотность тока. Причина этого в том, что каждый электрический проводник имеет электрическое сопротивление. При протекании электрического тока на этом сопротивлении возникает падение электрического напряжения. В результате происходит преобразование энергии и нагрев линии. Чрезмерный нагрев может повредить изоляцию проводника и вызвать серьезные повреждения.

Именно поэтому, например, допустимые плотности тока для бытовых установок регламентируются соответствующими стандартами. Кроме того, все кабели в домашних хозяйствах оснащены предохранителем, который срабатывает до достижения максимально допустимой плотности электрического тока.

В автомобильном секторе важную роль играет экономия веса и пространства. Поэтому здесь также тщательно подбираются кабели, чтобы найти компромисс между нагревом и весом/пространством.

Источник

Current is defined as the flow of the electron in a wire under a voltage difference. Current is the most common type of energy used in our daily life it provides electrical energy which is responsible for the working of all the electrical appliances which we used in our daily life.

Current density is defined as the amount of current flowing through the per unit area of the wire. It is measured in ampere/m². Before learning more about current density we have to learn about current.

In this article, we will learn about current, its types, and current density in detail.

Current Definition

The flow of electrons or holes in the conductor is defined as the electric current. Electric current flows because of the electro-potential force generated at the end of the conductor by battery or AC sources. The current is defined by the symbol “I “and is measured in the Ampere.

The following image shows current flowing through the circuit which lights up the bulb.

Current is the fundamental quantity and its dimensional symbol is [I].

The formula for calculating the current is,

i = q/t

where,
i is the current,
q is charge following in the conductor,
t is the time taken

One Ampere is defined as one Coulomb of the charge flowing through the conductor in one sec. I amp current is defined as 6.24×10¹⁸ electrons flowing through the conductor in one sec.

Types of Current

The current which we use is divided into two categories which are,

Direct Current
Alternating Current

Direct Current

A current that always flows in one direction is called a direct current (DC) and it is generated by electrochemical and batteries.

Alternating Current

A current which changes its direction repeatedly is called an alternating current (AC) and is generated by AC generators.

What is Current Density?

The rate of charge flow across the cross-section of a conductor is referred to as current density.

A flow of electrons is what an electric current is commonly thought to be. Electrons flow out of one end of the battery, through the wire, and enter the other end of the battery when two ends of the battery are connected by metal wire. If the size and direction of the current are both constant, the current produced is usually considered steady.

The density of current flow in a conductor is defined as current density. The letter J is used to represent it. Current Density and its measurement are particularly essential in the study of electromagnetism. The charge per unit time per unit area of an electrical conductor is called the current Density and it is a vector quantity as it has both magnitude and direction.

Formula for Current density

The current density formula is as follows:

J = I/A

where,
J is the Current Density (A/m²)
I is the flow of current through the conductor (A)
A is the Cross sectional area (m²)

Unit and Dimensional of Current Density

The SI unit for measuring the current density is Ampere/m²
The dimensional formula for density is [M⁰L^-2T⁰I¹]

Derivation of Current Density Formula

The current density formula is derived from the definition of the current density. We know that the current density is defined as the current flowing through the per unit area of the conductor then,

J = dI/dA

where,
dI/dA is the Current change with the unit area.

which implies,

dI = J × dA

dI = J × dAcosθ

when
dA is perpendicular to J, (if θ = 90^o so, cos θ = 1).

Therefore,

dI = J × dA

integrating both sides

∫₀^JdI = J × ∫₀ ^AdA

I = J×A

J = I/A

Do Check,

What is Alternating Current?

Electric Current in Conductors

Difference Between Electric Potential and Potential Difference

Solved Example on Current Density Formula

Example 1: What is the current density in a wire with a cross-section area of 23 mm² and a current of 8 mA running through it?

Solution:

Given,

A = 23 mm²
= 0.000023 m²,

I = 8 mA = 0.008 A

Since,

J = I/A

= 0.008 / 0.000023

= 347.82 A/m²

Example 2: A copper wire with a diameter of 3 mm² has a current of 9 mA flowing through it. Find the current density of the conductor.

Solution:

Given,

A = 3 mm²
= 0.000003 m²,

I = 9 mA
= 0.009 A

Since,

J = I/A

= 0.009 / 0.000003

= 3000 A/m²

Example 3: If 42 A of current flows through the battery in an 8 m² region, what is the current density of the conductor?

Solution:

Given,

A = 8 m²,

I = 42 A

Since,

J = I/A

= 42 / 8

= 5.25 A/m²

Example 4: If the current density is 4 A/m² and the current through the conductor is 24 A. Find the cross-sectional area.

Solution:

Given,

J = 4 A/m²

I = 24 A

Since,

J = I/A

A = I/J

= 24/4

= 6 m²

FAQs on Current Density

Q1: What is Current Density?

Answer:

The rate of charge flow across any cross-section of any conductor is referred to as current density of the conductor.

Q2: Is current density scalar or vector quantity?

Answer:

Current Density is a vector quantity as it has both magnitude and direction.

Q3: What is the current density formula?

Answer:

The current density of any material is measured with the formula,

J = I/A

Q4: Why current density is a vector density?

Answer:

Current density has both magnitude and direction and thus it is a vector quantity as vector quantities have direction.

Q5: What is current?

Answer:

The rate of flow of electric charge through a conductor is defined as the electric current. It can be classified as,

Direct Current

Alternating Current

Last Updated :
18 Apr, 2023

Like Article

Save Article

Источник

Плотность тока. Связь плотности тока с зарядом и силой тока, напряженностью

Линии тока

Варианты вычисления плотности тока[править | править код]

Плотность тока и сила тока[править | править код]

Плотность тока и законы электродинамики[править | править код]

Уравнения Максвелла[править | править код]

Уравнение непрерывности[править | править код]

Закон Ома в дифференциальной форме[править | править код]

Плотность тока и мощность[править | править код]

4-вектор плотности тока[править | править код]

Примечания[править | править код]

16. Сторонние силы. Электродвижущая сила и напряжение

Простое объяснение

Формулы

Пример расчёта

Медный провод

Токопроводящие дорожки

Применение

Current Definition

Types of Current

Direct Current

Alternating Current

What is Current Density?

Formula for Current density

Unit and Dimensional of Current Density

Derivation of Current Density Formula

Solved Example on Current Density Formula

FAQs on Current Density

Q1: What is Current Density?

Q2: Is current density scalar or vector quantity?

Q3: What is the current density formula?

Q4: Why current density is a vector density?

Q5: What is current?

Вам также может понравиться

Как найти время тела по наклонной плоскости

Как найти инстаграм по фото бот

Как найти сообщение в телеграмме которое удалил

Добавить комментарий Отменить ответ